2. 中国航发沈阳发动机研究所,辽宁 沈阳 110015
2. AECC Shenyang Engine Institute, Shenyang 110015, China
航空发动机中用于涡轮冷却和转静间隙封严的内部冷却空气主要引自高压压气机。从高压压气机到盘轴间隙位置的径向内流过程会对冷却气体造成较大的压力损失。
从20世纪80年代开始,国内外就陆续展开了对降低引气压力损失方法的研究,所采用的降低压力损失的结构被称为减涡器,常见的减涡器结构主要有三种:无管式(去旋喷嘴式)减涡器、管式减涡器和翅片式减涡器。其中去旋喷嘴式减涡器由于其体积小重量轻且结构稳定性好的优点,成为了研究人员的研究重点。Farthing等[1]首次在旋转盘腔中引入去旋喷嘴,并进行了流场结构的分析,发现当转速不变时,无量纲流量会随着压力损失呈现出S型曲线变化规律;Farthing等[2]研究发现去旋喷嘴能将盘腔内的压力损失减小到零,但是如果包括喷嘴内压力损失时,总压力损失总是比刚体旋转时大;Pfitzner等[3]对应用于BR700系列发动机的两种形式的减涡器进行了对比分析;Negulescu等[4]分析了去旋喷嘴性能变化的S型曲线各阶段出现的原因,首次对完整引气流路流路中的压力损失进行了分析,研究了去旋喷嘴的瞬态响应行为;Young Colin等[5]对盘腔径向内流流路进行了数值模拟研究,重点研究了鼓筒孔内的流动状态以及其对下游盘腔的影响规律;Friedl等[6]将无管式减涡器的概念引入BR715型航空发动机高压涡轮盘冷却系统中,在高压涡轮转子叶片的根部引进了一组去旋喷嘴;白洛林等[7]对带有微型涡轮的共转盘腔内的流动和换热进行了试验和数值研究,试验结果表明换热效果随无量纲质量流量、旋转雷诺数和浮升力的增大而增强;武亚勇[8]对去旋喷嘴的旋转盘腔内部流场特性进行了实验与三维数值计算对比研究;Andre等[9]对减涡器在径向不同的布置方式进行了试验研究,得到了压力分布随流量的变化规律;黄爱霞[10]应用RNG k-ε湍流模型对围屏上带反旋喷嘴的径向内流旋转涡轮盘腔内的流动与换热进行了数值模拟;陈阳春[11]对去旋角、旋转雷诺数、去旋喷嘴进气无量纲流量系数等参数对共转盘腔内的流动结构、压力损失和换热效果的影响进行了研究。杨守辉等[12]研究了去旋角对盘腔内流场的影响规律;May David等[13]研究了无管式减涡器的迟滞效应;建立了一个基础的旋流盘腔的瞬态模型,可更准确的预测盘风阻,切向速度和涡流压力梯度。廖乃冰等[14]对有/无导流盘引气结构的径向内流引气进行了数值研究,通过对比两者的流场和气流沿程总温证明了导流盘能显著降低引气过程的沿程总温,减少气流的流动阻力。目前国内外对去旋喷嘴式减涡器的研究主要停留在对流动结构以及换热特性的机理性研究,提出了限制去旋喷嘴式减涡器应用的一些问题:如喷嘴结构本身所造成的压力损失过大以及S型变化规律对喷嘴去旋效率的不利影响等,但是缺乏对解决这些问题相关方法的研究。其中对喷嘴结构设计方法的研究匮乏是导致去旋喷嘴式减涡器迟迟无法在航空发动机中推广应用的重要原因。
为了探究去旋喷嘴结构本身对去旋系统降低压力损失性能的影响规律,本文通过对喷嘴的不同结构进行分析,总结出几种基本的结构变化因素;通过对安装具有单一结构变化因素的去旋喷嘴的共转盘腔内流体流动进行数值模拟,得到各结构因素对盘腔内气流结构和减涡器减压损性能的影响规律。
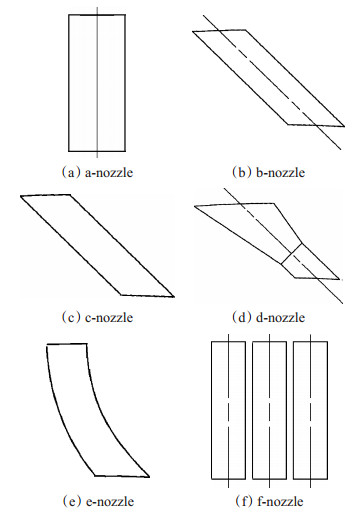
2 物理模型和计算方法 2.1 几何模型和网格划分如图 1(a)所示,本文选取从鼓筒孔入口开始,依次通过鼓筒孔、去旋喷嘴上游盘腔、去旋喷嘴以及去旋喷嘴下游盘腔,最终到盘腔出口的腔体空间作为研究区域。为了避免盘腔型面的不同对研究结果的普遍性产生不利影响,将盘腔型面简化为矩形截面盘腔。根据文献[4]可知,鼓筒孔出口气流周向速度约等于对应半径位置转盘旋转速度,而流量入口边界条件选择的是垂直于入口面,不具备初始周向速度。故将鼓筒孔长度加长,通过鼓筒孔壁施加的周向力为气流提供周向速度。计算结果显示鼓筒孔出口处的气流旋转速度近似等于转盘旋转速度,满足工况要求。最终确定的计算域几何模型如图 1(b)所示,图中r0 = 219mm,r1/r0 = 0.86,r2/r0 = 0.80,r3/r0 = 0.18,盘腔宽度为16.5mm。本文重点研究了喷嘴几何结构对去选系统减阻特性的影响。如图 2所示,a结构作为无去旋参照,喷嘴直径为5mm,个数为1;b结构为基础型去旋喷嘴,去旋角等于45°,喷嘴直径为5mm,个数为1;c结构截面形状为矩形;d结构为收缩喷嘴,e结构喷嘴入口为垂直进气,f结构为沿轴向排布的三个基础型喷嘴。c,d,e,f的去旋角以及流通截面积均与b结构喷嘴相等。选取盘腔的1/36作为计算域,最终确定的计算域模型如图 1所示。所有计算模型均采用结构化网格,调整第一层边界层网格厚度,保证壁面Y+介于30~300。进行网格独立性验证,确定了所有模型网格数都在100万左右。

|
Fig. 1 Co-rotating cavity with de-swirl nozzle |
|
Fig. 2 Varied de-swirl nozzles |
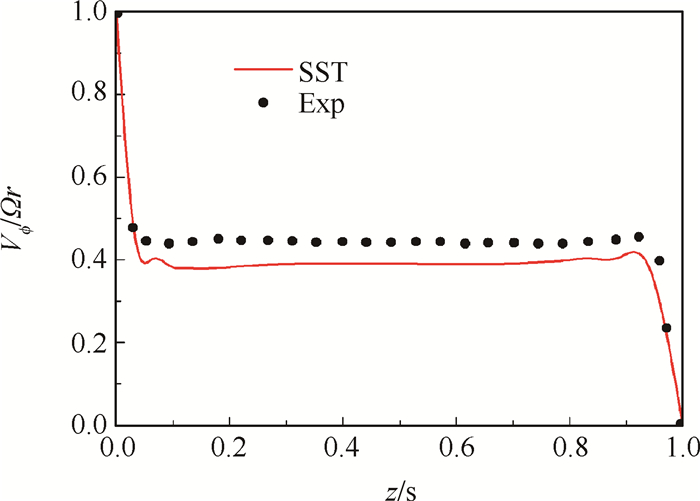
本文的数值计算采用Fluent软件,选用基于压力的稳态解算器,湍流模型采用文献[15]中验证通过的k-ω SST湍流模型,不勾选Low-Re Corrections和Intermittency transition model选项以降低对边界层网格的要求,以可压缩气体作为计算流体,采用流体域旋转、壁面相对于流体域静止来模拟盘腔内的流动特征。当出口流量与入口流量误差小于0.1%,且入口总压的波动范围低于平均总压值的5%时,视为计算收敛。为了验证数值方法的可靠性,选用参考文献[16]中的试验数据进行对比验证。计算结果如图 3所示。计算结果与试验结果很接近,最大误差不超过15%。
|
Fig. 3 Comparison of computed result and experimental data |
进口采用流量进口边界条件,进口流量为0.972kg/s,总温为500K,出口为压力出口,出口静压为1114575Pa。计算工况转速为2500r/min到17500r/min,每2500r/min取一计算点。
2.4 参数定义旋转雷诺数
| $ \mathit{R}{{\mathit{e}}_{\phi }}\rm{=}\mathit{\rho \Omega }{{\mathit{b}}^{\rm{2}}}\rm{/}\mathit{\mu } $ | (1) |
式中ρ为流体密度,Ω为盘腔旋转角速度,b为特征长度(本文选用盘腔外半径),μ为气体的动力粘度。
总压损失系数
| $ {{\mathit{C}}_{\mathit{p}}}\rm{=2}\mathit{\rho }{{\mathit{A}}^{\rm{2}}}\rm{(}{{\mathit{p}}_{\rm{1}}}\rm{-}{{\mathit{p}}_{\rm{3}}}\rm{)/}{{{\mathit{\dot{m}}}}^{\rm{2}}} $ | (2) |
式中A为鼓筒孔入口面积,p1为喷嘴入口总压,p3为盘腔出口总压,
喷嘴总压损失系数
| $ {{\mathit{C}}_{\mathit{p}\rm{, n}}}\rm{= 2}\mathit{\rho }{{\mathit{A}}^{\rm{2}}}\rm{(}{{\mathit{p}}_{\rm{1}}}\rm{-}{{\mathit{p}}_{\rm{2}}}\rm{)/}{{{\mathit{\dot{m}}}}^{\rm{2}}} $ | (3) |
式中p2为喷嘴出口总压。
盘腔总压损失系数
| $ {{\mathit{C}}_{\mathit{p}\rm{, c}}}\rm{= 2}\mathit{\rho }{{\mathit{A}}^{\rm{2}}}\rm{(}{{\mathit{p}}_{\rm{2}}}\rm{-}{{\mathit{p}}_{\rm{3}}}\rm{)/}{{{\mathit{\dot{m}}}}^{\rm{2}}} $ | (4) |
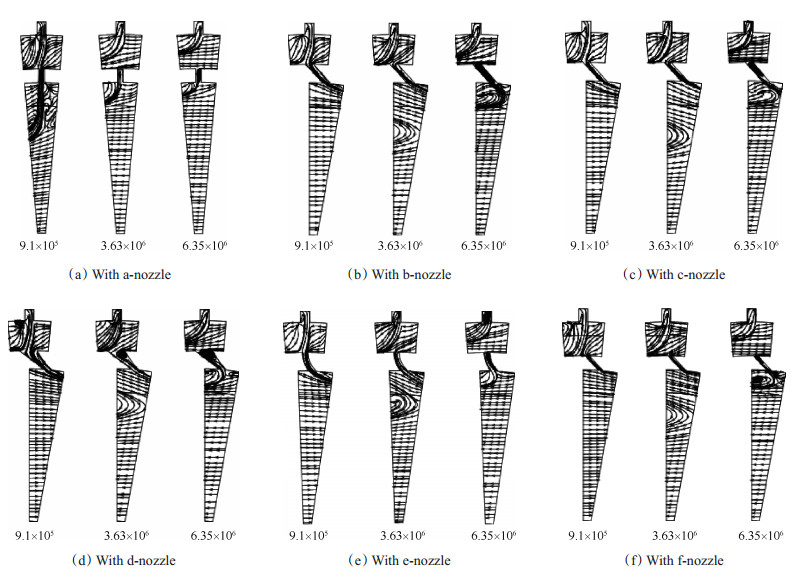
图 4为不同转速和喷嘴结构下x=0/z=0截面的盘腔流线图,由于篇幅限制,本文只选择旋转雷诺数为9.1×105,3.63×106和6.35×106三种转速下的流线图进行展示,图中均为逆时针旋转。
|
Fig. 4 Streamlines on cross section |
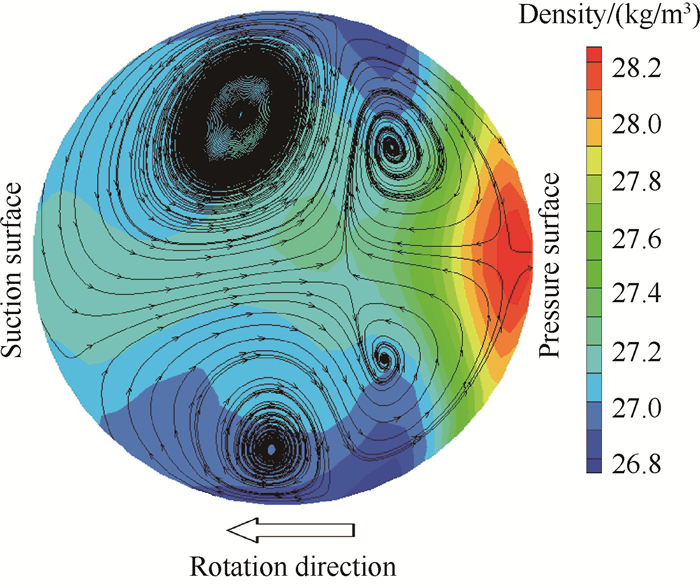
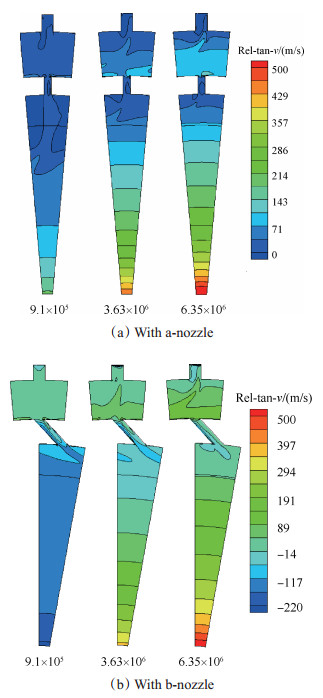
由图 4可以看出,在同一转速下所有的上游盘腔内整体流场结构基本相同,这是因为下游喷嘴形状及由其引起的下游流动状态的不同对上游盘腔内流场结构所产生的影响有限。流体在鼓筒孔中会有一定的回流,回流主要集中在鼓筒孔的吸力面侧(见图 5),并且回流在到达鼓筒孔入口之前会恢复到沿盘腔径向入流的方向,径向入流主要集中于鼓筒孔的压力面侧。回流区和内流区各形成两个旋转方向相反的涡,如图 5所示,内流区涡处于压力面侧,由于压缩作用,相对于处于吸力面侧的回流区涡更小,但是其流体密度相对较大,所以鼓筒孔内总的流量效果依然是内流,这也是流量入口的必然结果。鼓筒孔形成的射流旋转速度与盘腔旋转速度接近,如图 6所示,在进入上游盘腔后,由于切向哥氏力的加速效果,旋转速度逐渐增加,射流逐渐被拉弯,此时的射流对于盘腔内具有更高转速的流体而言相当于一个扰流柱,在射流柱的背风面区域形成分离区,分离区内的一部分流体会重新流入鼓筒孔中,成为上文所述的回流部分;另一部分则会在盘腔中继续发展。进入去旋喷嘴的流体来源会随着盘腔旋转速度的变化而变化。低转速时,其一部分来源于同一周向位置的鼓筒孔,另一部分则来源于沿与盘腔旋转方向相反的下一个鼓筒孔。随着转速的增加,前者的比重逐渐减小,后者的比重先增加后减小,并且越来越多的旋转方向下游的鼓筒孔加入供气行列,最终所有鼓筒孔的进气都会在进入去旋喷嘴之前完全掺混,共同为全部去旋喷嘴供气。气流在所有形状喷嘴中的流动形式基本相同,吸力面的流动速度高于压力面附近的流动速度,流动形式稳定。气流进入喷嘴时,由于初始速度与喷嘴方向存在一定的角度,所以会在压力面靠近入口处形成一个分离区。分离区内压力较小,两侧气流流入分离区,然后回流到入口位置汇入主流并向喷嘴下游流动。随着转速的增加,分离区逐渐向下游扩张,并最终扩展到整个喷嘴,此时下游盘腔内的部分气体加入到分离区的回流过程,形成类似于鼓筒孔内的回流情况。气流从喷嘴进入到下游盘腔后,形成类似于上游盘腔中鼓筒孔射流所产生的射流柱。由于有去旋效果的喷嘴出口气流方向与盘腔旋转方向相反,所产生的去旋效果使下游盘腔中的气流具有一定的与盘腔旋转方向相反的流动速度,如图 6(b)所示。低转速时,去旋的影响能扩散到整个盘腔,使整个下游盘腔内的气流相对于盘腔反向旋转;随着转速的增加,盘腔内旋转作用的增强,将去旋的影响区域逐渐向下游盘腔的高半径压缩,低半径处的气流则恢复到以高于转盘的转速正向旋转。
|
Fig. 5 Streamlines and distribution of density on the cross section of drum hole |
|
Fig. 6 Distribution of rel-tangential-velocity on the cross section with a and b nozzle |
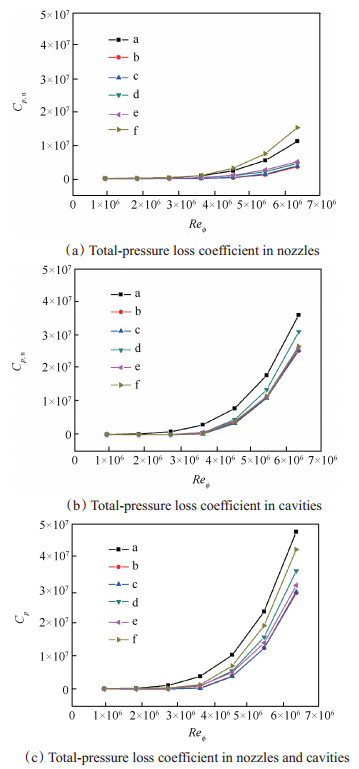
从喷嘴入口半径到喷嘴出口半径的总压损失系数Cp, n可用于衡量喷嘴本身所造成的压力损失;从喷嘴出口到盘腔出口半径的总压损失系数Cp, c则可以反映喷嘴的去旋效果;从喷嘴入口半径到盘腔出口半径的总压损失系数Cp可以用来表示安装该喷嘴的共转盘腔的总的压力损失大小。
带不同结构去旋喷嘴的盘腔内压力损失分布曲线如图 7所示。图(a),(b),(c)分别对应喷嘴内总压损失系数Cp, n,盘腔内总压损失系数Cp, c以及从喷嘴入口到盘腔出口总的总压损失系数Cp对旋转雷诺数的变化规律。低转速时带去旋喷嘴的盘腔内压力损失与带a型垂直进气喷嘴的盘腔内压力损失非常接近。这是因为低转速时盘腔内形成的旋转作用较弱,由此引起的压力损失与由安装喷嘴导致的流通截面变化引起的局部损失以及摩擦耗散所引起的沿程损失都较小,所以去旋的作用并不明显。由于f型喷嘴在同样的流通面积下,流体与壁面之间的接触面比a型喷嘴大得多,这也就意味着更高的沿程损失,所以f型喷嘴本身所造成的压力损失明显高于a型喷嘴,这也导致安装有f型喷嘴的盘腔内总的压力损失在低半径时略高于无去旋的盘腔。随着转速的增加,盘腔内旋转作用和喷嘴本身所导致的压力损失都在增加,但是旋转作用所导致的压力损失增加较快,逐渐占据主导地位,带有去旋喷嘴的盘腔总的压力损失低于无去旋喷嘴的盘腔。整体来看,去旋喷嘴的使用可以提高压力损失开始急剧上升的临界转速。
|
Fig. 7 Total-pressure loss coefficient of the disc cavity with different nozzles |
为了判断几种结构因素对去旋喷嘴的减压损效果是否有利,下面将c,d,e,f四种变型喷嘴分别与基础型喷嘴b的去旋减压损效果进行对比分析。
c型喷嘴为将b型喷嘴截面变为正方形的一种变型。图中可以看出所有转速下,二者的各部分压力损失以及总的压力损失相差都低于20%。这是因为c型喷嘴与b型喷嘴具有相同的进气角,而且在结构上比较接近,所以在低转速时,二者由于喷嘴本身所造成的压力损失非常接近。根据上文的分析,安装有c型喷嘴和安装b型喷嘴的盘腔内的流场结构很接近,所以二者的去旋效果也非常接近。高转速时,虽然c型喷嘴的沿程损失略高于b型喷嘴,但是由于此时旋转作用所导致的压力损失占主导,所以二者总的压力损失依然非常接近。
d型喷嘴为将b型喷嘴的进口改为渐缩型的一种变型。由图可以看出,d型喷嘴本身所造成的压力损失在所有转速下都高于b型喷嘴,而且随着转速的增加,差距有所增大。这是因为d型喷嘴的渐缩型入口使上游盘腔中气流的流动方向与喷嘴入口方向的夹角比b型喷嘴更大,这导致流体需要更高的压差才能流入d型喷嘴内,而且随着转速增加,这种劣势越发明显。而对于喷嘴的去旋效果,在低转速时,d型喷嘴的去旋效果略强于b型喷嘴。这是因为d型喷嘴的渐缩型设计有利于提高喷嘴出口射流速度,从而增强去旋效果。但是随着转速的增加,进气条件的劣势完全抵消了这种优势,所以在高转速时,d型喷嘴的去旋效果弱于b型喷嘴,而且这种差距随着转速的增加逐渐拉大。对于总体的压力损失,二者在低转速时相差很小,而在高转速时,安装有d型喷嘴的盘腔的总压损失会逐渐高于安装b型喷嘴的盘腔,最大高出52.41%。
e型喷嘴为b型喷嘴将进口进行渐变调整为垂直进气方向时的一种变型。图中可以看出当旋转雷诺数在2.72×106及其以下时,安装有垂直进气去旋喷嘴的盘腔内压力损失较小,旋转雷诺数在3.63×106以及3.63×106以上时,反之。这是因为在低转速时,由于入口方向的优化,e型喷嘴内流动分离较弱,其优势足以抵消e型喷嘴由于流道更长所导致的沿程损失的增加,这保证了其出口速度高于b型喷嘴出口流速,所以e型喷嘴的去旋效果更优。但是随着转速的增加,e型喷嘴内的流动分离也愈发严重,这削弱了e型喷嘴在进气条件上的优势,导致其去旋效果逐渐低于b型喷嘴。两种结构的去旋喷嘴在喷嘴结构上各具优势,在低转速时,二者由于喷嘴结构本身所导致的压力损失很接近,随着转速的增加,e型喷嘴的进气优势消失殆尽,e型喷嘴由喷嘴本身所导致的压力损失逐渐高于b型喷嘴。安装有两种喷嘴的盘腔内总的压力损失在低转速时非常接近,但是随着转速的增加,差距逐渐拉大。最大相对差距为56.43%。
f型喷嘴采用在同一周向位置,沿轴向均匀分布三个b型去旋喷嘴的布置方式。由图 6可知,二者的去旋效果非常接近,但是由于同样的流通面积,f型喷嘴的沿程损失远远高于e型喷嘴,这也就导致安装有f型去旋喷嘴的盘腔内压力损失高于安装e型喷嘴的盘腔,而且随着转速的增加,差距逐渐增大,最大相对差距为76.84%。
4 结论通过本文研究,得到如下结论:
(1) 去旋喷嘴可有效提高共转盘腔内压力损失开始急剧增长的临界转速。
(2) 方形喷嘴与圆形喷嘴去旋减压损效果非常接近,总压损失相差低于20%。
(3) 减小喷嘴入口方向与气流旋转速度方向之间的夹角可有效改善喷嘴的进气条件。
(4) 渐缩型入口对喷嘴的去旋效果是有利的。
(5) 同一周向位置,保持总流通面积不变,沿轴向增加喷嘴数目不能提高去旋效果;而且其结构本身也会造成更多的压力损失,当喷嘴数由一个增加到三个时,系统总压损失最大增加76.84%。
| [1] |
Farthing P R, Chew J W, Owen J M. The Use of Deswirl Nozzles to Reduce the Pressure Drop in a Rotating Cavity with a Radial Inflow[J]. Journal of Turbomachinery, 1991, 113: 106-114. DOI:10.1115/1.2927727
(  0) 0) |
| [2] |
Farthing P R, Owen J M. De-Swirled Radial Inflow in a Rotating Cavity[J]. International Journal of Heat & Fluid Flow, 1991, 12(1): 63-70.
(  0) 0) |
| [3] |
Pfitzner M, Waschka W. Development of an Aeroengine Secondary Air System Employing Vortex Reducers[C]. Yokohama: 22nd ICAS Congress, 2000.
(  0) 0) |
| [4] |
Negulescu D, Pfitzner M. Secondary Air Systems in Aeroengines Employing Vortex Reducers[R]. ASME 2001-GT-0198.
(  0) 0) |
| [5] |
Young C, Snowsill G D. CFD Optimization of Cooling Air Offtake Passages within Rotor Cavities[J]. Journal of Turbomachinery, 2003, 125(2): 915-923.
(  0) 0) |
| [6] |
Friedl W H, Peitsch D, Negulescu D. Improvement of High Pressure Turbine Air Systems by De-Swirl Nozzles [R]. DETC2002/CIE-34449.
(  0) 0) |
| [7] |
白洛林, 郑光华, 冯青, 等. 带有微型涡轮的旋转盘腔局部换热特性[J]. 推进技术, 2005, 26(3): 223-228. (BAI Luo-lin, ZHENG Guang-hua, FENG Qing, et al. Experimental Investigation of Local Heat Transfer Characteristic in a Rotating Cavity with Micro-Turbine[J]. Journal of Propulsion Technology, 2005, 26(3): 223-228.)
(  0) 0) |
| [8] |
武亚勇. 反预旋进气旋转盘腔系统的流场实验与计算研究[D]. 西安: 西北工业大学, 2007. http://cdmd.cnki.com.cn/article/cdmd-10699-2007057930.htm
(  0) 0) |
| [9] |
Günther A, Uffrecht W, Kaiser E, et al. Experimental Analysis of Varied Vortex Reducer Configurations for the Internal Air System of Jet Engine Gas Turbines[R]. ASME GT 2008-50738.
(  0) 0) |
| [10] |
黄爱霞, 王锁芳. 反旋进气盘腔内流动与换热的数值模拟[J]. 航空动力学报, 2008, 23(9): 1684-1688. (  0) 0) |
| [11] |
陈阳春. 带去旋系统的旋转盘腔内流动和换热的数值研究[D]. 南京: 南京航空航天大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10287-1011252204.htm
(  0) 0) |
| [12] |
杨守辉, 王锁芳. 不同去旋角度进气共转盘腔内流动与换热研究[J]. 航空发动机, 2011, 37(6): 17-20. (  0) 0) |
| [13] |
May D, Chew J W, Scanlon T J. Prediction of De-Swirled Radial Inflow in Rotating Cavities with Hysteresis[J]. Journal of Turbomachinery, 2012, 135(4).
(  0) 0) |
| [14] |
廖乃冰, 周志翔, 邱长波. 空气系统径向内流引气的流动特性数值分析[J]. 推进技术, 2014, 35(3): 378-383. (LIAO Nai-bin, ZHOU Zhi-xiang, QIU Chang-bo. Numerical Simulation of Radial Inflow in Air System[J]. Journal of Propulsion Technology, 2014, 35(3): 378-383.)
(  0) 0) |
| [15] |
呼艳丽, 郭文, 王蕾, 等. 反旋喷嘴进气旋转盘腔压力损失特性[J]. 航空动力学报, 2016, 31(8): 1866-1873. (  0) 0) |
| [16] |
Gan X, Kilic M, Owen J M. Superposed Flow Between Two Discs Contrarotating at Differential Speeds[J]. International Journal of Heat & Fluid Flow, 1994, 15(6): 438-446.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

