2. 中国科学院大学 工程科学学院, 北京 100049
2. School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
空间引力波探测和地球重力场测量卫星的关键技术之一就是微推进技术, 为微、纳卫星在太空中姿态调整、轨道维持和无拖曳飞行控制提供技术支撑[1~3]。目前国内外适用于空间引力波探测的微牛级推进技术主要包括场发射电推力器FEEP(Field Emission Electric Propulsion)、射频离子微推力器(Micro-Newton Radio-Frequency Ion Thruster)、胶质离子推力器(Colloid Micro-Newton Thruster)和冷气微推力器[4]。而研制一套在地面上能够准确测得微推力器的推力范围和分辨力等性能参数的测量系统, 是研制FEEP、μRIT等微推力器的关键环节, 也是其在轨运行的技术保障。
目前, 国内外测量推力器推力的方式主要分为直接测量和间接测量, 直接测量精度较高;间接测量误差较大, 但能分析尾气成分和扩散角等[5]。法国国家航空航天局的Denis Packan和Jean Bonnet研制出一套基于倒摆结构的微推力测量装置, 并测得奥地利研究中心研制的FEEP推力范围为1~20μN, 后经过改进, 利用电容式位移传感器和重力加速计检测摆臂位置变化, 在标定臂上放置标定质量块标定较大推力(>10μN), 以及通过钟摆底部安装的通电线圈在磁场中产生的安培力标定较小推力(< 10μN), 该套系统测量推力范围较大(0~700μN), 且噪声水平在0.001~4Hz内为1μN/Hz, 在0.01~1Hz内为0.1μN/Hz, 已应用于测量冷气推力器, 但该套系统结构比较复杂, 倒摆刀口支撑点处摩擦力产生误差较大, 平台振动对该装置精度影响较大, 而且在标定弱力大于100μN时, 精度仅为1%[6];北京航空航天大学的汤海滨教授研制出一套全弹性微小推力系统, 利用电磁力标定该测量装置, 其推力测量范围为0~200mN, 精度达到1%, 并应用于测量冷气微推力器产生的推力大小, 但精度仅限于毫牛级推力器推力测量[7];此外, 意大利的Paolucci F[8]针对FEEP研制出一套基于扭秤原理测量推力装置, 扭摆通过上下两段扭丝连接, 上部扭丝承担扭摆扭转, 下部扭丝松弛, 且两段扭丝作为FEEP电路一部分, 扭摆扭转角位移通过光杠杆测量装置测得, 最终利用推力产生的力矩与扭丝偏转力矩平衡计算得到推力。但该套推力测量系统无磁阻尼装置, 无法测量微推力;日本针对电推力器研制的单摆结构和双摆结构推力测量系统, 其结构复杂, 且测量推力范围为毫牛量级[9, 10];西北工业大学研制的三丝扭摆推力测量系统仅在测量毫牛级推力时保证精度, 且其结构安装更加复杂[11]。
针对微牛级推力器研制出一套基于扭秤的微推力测量系统, 其结构简单, 易于安装使用;扭秤系统在扭转和水平方向非常灵敏, 对微小推力能够很快响应;不同的扭丝直径及拉力大小对扭秤系统的灵敏度和扭转角度影响较大, 可以根据不同的推力范围和最小响应推力进行调整;相比Paolucci F研制的测量系统, 本套微推力测量系统能够测得推力为1~ 200μN, 达到0.4μN的分辨力, 且包含磁阻尼系统, 使测量系统能够快速稳定; 利用高精度双激光位移传感器差动测量系统标定扭秤系统, 减小系统误差;同时分析环境和结构对扭秤系统测量结构的影响。
2 扭秤系统测量原理 2.1 微推力测量原理通过分析比较国内外弱力测量系统[6, 8, 12, 13]的优缺点, 设计出一套基于扭秤的双丝扭摆结构, 主要包括:固定支架、扭摆、Ga-Feep、配重、标准力产生装置、扭秤标定系统和磁阻尼系统, 如图 1所示。
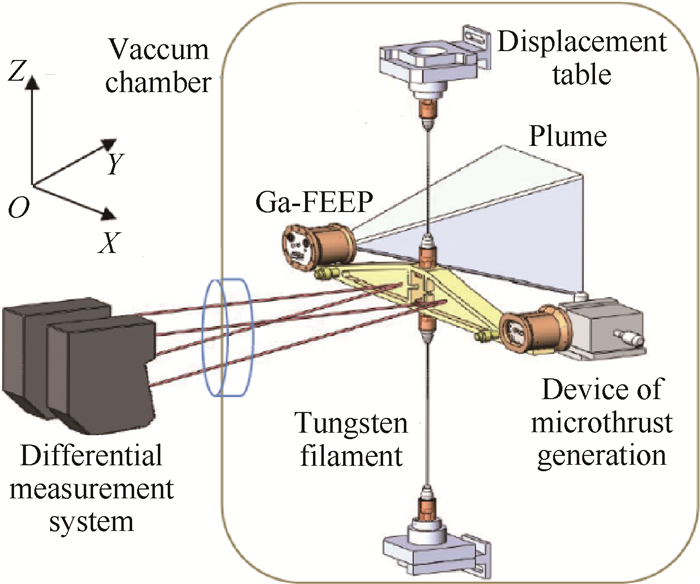
|
Fig. 1 Microthrust measurement system with torsion balance |
采用标准的模态分析方法求解扭秤的本征频率, 如图 2建立的坐标系可给出扭秤的位置坐标, α1, β1, α2, β2, γ五个自由度, 由于扭秤做小角度运动, 忽略纵向位移, 系统的总动能为
| $ T = \frac{1}{2}M\left[ {{{\left( {l{{\dot \alpha }_2} + h{{\dot \alpha }_1}} \right)}^2} + {{\left( {l{{\dot \beta }_2} + h{{\dot \beta }_1}} \right)}^2}} \right] + \frac{1}{2}{I_x}\dot \alpha _1^2 + \frac{1}{2}{I_y}\dot \beta _1^2 + \frac{1}{2}{I_z}{{\dot \gamma }^2} $ | (1) |

|
Fig. 2 Principle of two-wire torsion balance |
总势能为
| $ V = \frac{1}{2}Th\left( {\alpha _1^2 + \beta _1^2} \right) + \frac{1}{2}Tl\left( {\alpha _2^2 + \beta _2^2} \right) + \frac{1}{2}k{{\dot \gamma }^2} $ | (2) |
式中 T为扭秤上端拉力, M为总系统重量, l为扭摆长度, 2h为扭杆高度, k为扭丝扭转弹性系数, Ix, Iy, Iz为主转动惯量。由拉格朗日方程
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_i}}}} \right) - \frac{{\partial L}}{{\partial {q_i}}} = 0 $ | (3) |
得到矩阵形式的扭秤系统动力学方程
| $ \begin{array}{l} \left( {\begin{array}{*{20}{c}} {M{h^2} + {I_x}}&0&{Mlh}&0&0\\ 0&{M{h^2} + {I_y}}&0&{Mlh}&0\\ {Mlh}&0&{M{l^2}}&0&0\\ 0&{Mlh}&0&{M{l^2}}&0\\ 0&0&0&0&{{I_z}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\ddot \alpha }_1}}\\ {{{\ddot \beta }_1}}\\ {{{\ddot \alpha }_2}}\\ {{{\ddot \beta }_2}}\\ {\ddot \gamma } \end{array}} \right) + \\ \left( {\begin{array}{*{20}{c}} {Th}&0&0&0&0\\ 0&{Th}&0&0&0\\ 0&0&{Th}&0&0\\ 0&0&0&{Th}&0\\ 0&0&0&0&{Th} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\alpha _1}}\\ {{\beta _1}}\\ {{\alpha _2}}\\ {{\beta _2}}\\ \gamma \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) \end{array} $ | (4) |
将扭秤系统参数代入式(4), 可得扭秤系统本征频率:α1=8.25Hz, α2 =0.86Hz, β1 =1.09Hz, β2 =0.72Hz, γ=0.17Hz。扭转是扭秤的主要振动模式, 对应的恢复系数小, 是扭秤最灵敏的运动模式, 其他4个本征振动频率相对扭转频率较大, 可通过滤波消除。
扭摆由两根钨丝拉紧安装在真空环境中, 一端安装已研制的Ga-FEEP, 另一端安装标准力产生装置及配重, 使扭摆水平。当微推力器发射羽流电脉冲, 扭摆经过扭转振荡一段时间后趋于稳定在某一平衡位置。此时, 由微推力器在垂直于扭摆方向的分力产生的力矩与钨丝的偏转力矩相等。扭秤的扭转运动方程为
| $ J\ddot \theta + \lambda \dot \theta + k\theta = Fb $ | (5) |
式中J为扭摆的转动惯量, λ为阻尼因子, k为扭丝的扭转弹性系数, F为微推力器在垂直扭摆方向的分力, b为微推力器与扭丝的距离, θ 为扭摆的扭转角位移。当扭秤受到外力时, 扭秤的运动规律可表示为
| $ \theta = {\theta _\tau }{{\rm{e}}^{ - \zeta t}}\sin \left( {\omega t + \varphi } \right) + Fb/J{\omega ^2} $ | (6) |
式中θτ为扭摆振荡的最大振幅, ζ = λ/2J为扭摆运动的阻尼系数, ω =(ω02 -ζ2)1/2为扭摆的自由振荡频率, ω0 =(K/J)1/2为扭摆在无阻尼时的自由振荡频率。当扭秤系统在高真空环境中时, 阻尼系数ζ可忽略不计, 测得ω ≈ ω0, 则推力F大小为
| $ F = J{\omega ^2}\Delta \theta /b = k\Delta \theta /b $ | (7) |
| $ \mathit{\boldsymbol{F}} \times b = k \times \Delta \theta $ | (8) |
式中Δθ为扭摆在外力作用下扭转角位移改变量。由式(8)可知, 当扭秤系统扭丝材料、尺寸和扭摆尺寸确定后, 被测推力F与扭摆扭转角位移成线性关系[14]。
根据扭秤系统的运动规律, 微推力的测量原理为:利用高精度电子天平标定弱力产生装置;将微推力器、标准力产生装置和配重安装到扭摆两端;利用标准力产生装置标定扭秤系统, 最终给出标准力FC和扭摆扭转角Δθ的关系[15]
| $ {F_{\rm{C}}} = a \times \Delta \theta + b $ | (9) |
静电梳状驱动结构是微机电系统中重要的组成部分, 在插入方向上, 其交叉齿间产生的静电引力与输入电压的二次方具有良好的线性关系[16]
| $ {F_{{\rm{ESC}}}} = {\varepsilon _0}N{U^2}\left( {h/g} \right) $ | (10) |
式中ε0为真空介电常数, N为静电梳齿对数, U为加载电压, h为静电梳高度, g为静电梳交叉齿间距。由式(10)可知, 产生的静电力与齿交插深度无关, 而其他参数均为固定值[16]。
图 3为实验中所使用的静电梳状弱力产生装置, 其中接地电极为对称扇形结构, 高压电极为8mm× 8mm×0.5mm条形极板, 交叉极板为6对, 交叉齿间距为0.5mm, 当交叉深度约为4mm时, 该实验装置满足式(10)要求。
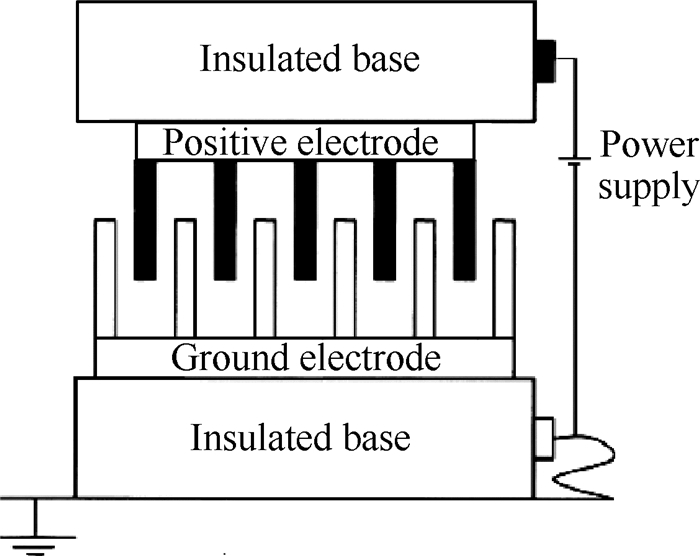
|
Fig. 3 Device of weak force generation |
为了精确测量扭摆对微推力的响应, 实验中利用两路高精度激光位移传感器, 通过差动法测量扭摆相对扭转角, 原理如图 4所示。t0为扭秤系统初始位置;对扭秤系统施加微推力, 扭摆绕z轴扭转和y方向平动后稳定在平衡位置t′, 两路激光位移传感器测得的位移变化值分别为λα和λb;两路激光位移传感器测量点与扭丝的距离分别为x1和x2, 传感器间距为γ[17]。
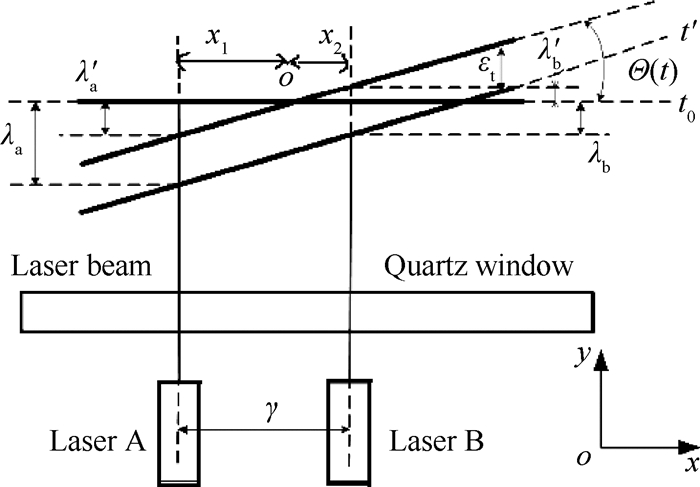
|
Fig. 4 Principle of differential measurement |
扭摆在xy平面的位移主要由y方向的振动和绕z轴的扭转组成, 当激光束与x轴垂直时, 传感器测量量λ由绕z轴转动量λ′和y方向平动量εt组成, 利用差动测量原理对两路位移传感器测量值分析, 得到扭摆相对扭转角θ(t)。
| $ {\lambda _{\rm{a}}} = {{\lambda '}_{\rm{a}}} + {\varepsilon _{\rm{t}}} $ | (11) |
| $ {\lambda _{\rm{b}}} = - {{\lambda '}_{\rm{b}}} + {\varepsilon _{\rm{t}}} $ | (12) |
| $ \theta \left( t \right) = \frac{{{{\lambda '}_{\rm{a}}}}}{{{x_1}}} $ | (13) |
| $ \theta \left( t \right) = \frac{{{{\lambda '}_{\rm{b}}}}}{{{x_2}}} $ | (14) |
| $ {x_1} + {x_2} = \gamma $ | (15) |
由上式得到
| $ \theta \left( t \right) = \frac{{{{\lambda '}_{\rm{a}}} + {{\lambda '}_{\rm{b}}}}}{\gamma } = \frac{{{\lambda _{\rm{a}}} + {\lambda _{\rm{b}}}}}{\gamma } $ | (16) |
差动测量系统利用两路激光位移传感器测量扭秤系统对微推力的响应, 有效地消除了扭秤系统单摆效应和偏移对测量结果的影响, 具有测量范围大、测量精度高等优点;此外, 差动测量系统不需要安装在真空室内, 其结构简单, 操作方便。
实验中使用的一对激光位移传感器的分辨力分别为0.1μm和0.25μm, 两传感器间距为133mm ± 1mm, 计算得到差动测量系统扭转角分辨力为7.519× 10-7rad。根据扭秤系统测量原理和胡克定律, 得到
| $ \Delta \theta = \frac{{4Fbl\left( {1 + \mu } \right)}}{{{\rm{ \mathsf{ π} }}{R^4}E}} $ | (17) |
式中F为施加的推力, b为微推力器与扭丝的距离, l 为扭丝并联后的等效长度, μ为泊松比, R为扭丝半径, E 为扭丝弹性模量[14]。将差动测量系统扭转角分辨力代入式(17), 得到微牛级扭秤系统的分辨力为0.078μN。理论上, 本套微牛级扭秤测量系统能够测量亚微牛级弱力。
2.4 磁阻尼装置对扭秤系统施加微推力后, 为保证扭摆能够尽快稳定在平衡位置, 在扭秤系统中安装磁阻尼系统, 其原理如图 5所示。对扭秤系统施加微推力后, 由于穿过扭摆的磁通量发生变化, 扭摆内部产生感应涡流, 通过涡流耗损抑制扭摆转动和平动, 扭秤系统在5个振荡周期内稳定在平衡位置, 其衰减系数及阻尼比为
| $ \eta = \frac{{{x_n}}}{{{x_{n + 1}}}} = 1.901 $ | (18) |
| $ \xi = \frac{1}{{\sqrt {1 + 4{{\rm{ \mathsf{ π} }}^2}/{{\ln }^2}\eta } }} \approx 0.102 $ | (19) |
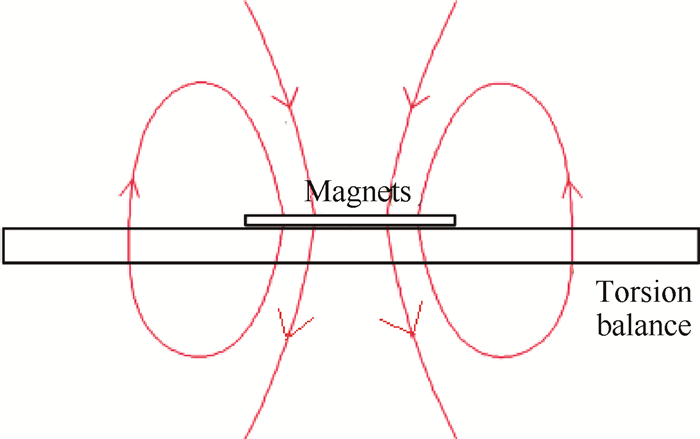
|
Fig. 5 Principle of structure of magnetic damping |
式中xn, xn + 1 为衰减过程中相邻振幅, η为磁阻尼装置衰减系数, ξ为阻尼比。
3 实验与标定 3.1 弱力产生装置标定由于环境和加工等因素, 实际操作中得到的弱力与理论值之间存在误差, 故利用高精度电子天平对静电梳进行标定, 如图 6所示。将接地电极水平放置在电子天平托盘中央, 高压电极安装在位移调节平台上, 连接电路并调节静电梳指间距及插入深度, 输入不同电压值, 记录电子天平示数, 得到弱力与电压二次方的关系。

|
Fig. 6 Calibrating the device of weak force generation |
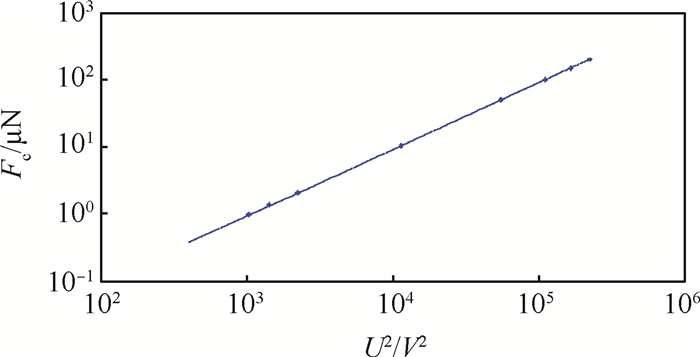
将表 1中的电压值输入到弱力产生装置中, 利用高精度电子秤测得相应的静电力, 由北京市重力加速度g=9.8015N/kg, 将电子秤示数转换为力。图 7中星号表示实验记录点, 直线为对前9个实验点进行线性拟合的结果。根据9个实验点计算弱力标定结果最小二乘线性度
| $ {\xi _{{\rm{LS}}}} = \frac{{\left| {{{\left( {\Delta {y_{\rm{L}}}} \right)}_{\max }}} \right|}}{{{y_{{\rm{FS}}}}}} \times 100\% $ | (20) |
|
|
Table 1 Calibrating result of the weak force generator |
|
Fig. 7 Fitting of the force calibration |
式中yFS为满量程输出, (ΔyL)max为标定点与最小二乘直线的最大偏差, 得到最小二乘线性度ξLS = 0.091%, 该套标准力产生装置线性度良好。标准力与电压平方值的线性拟合关系式为
| $ {F_{\rm{C}}} = a{U^2} + b $ | (21) |
式中a=0.000907μN/V2, b=0.02μN, 相对不确定度为2.9%[14]。
3.2 扭秤系统标定扭秤系统标定将在真空环境下进行, 故扭秤系统安装及调试在真空室内完成。将已标定的弱力产生装置安装在扭秤系统中, 位移调节平台接入高压电极并做绝缘处理, 扭摆通过钨丝接入接地电极, 避免扭摆与真空室壁的静电力影响标定结果;调节位移调节平台使静电梳齿间距和交叉深度与标定状态相同;利用两线水平仪校准扭摆水平度和两段扭丝的同轴度;磁阻尼装置固定于扭秤板架, 磁阻尼效果由强磁铁与扭摆的间距决定, 故两者间距保持在1mm内;差动测量系统安装在真空室外, 两路激光位移传感器通过观察窗测量扭摆响应位移, 利用电子水平仪校准激光位移传感器水平度。标定工作在预抽真空的真空室内完成, 标定工作中需将机械泵和分子泵关闭, 以减小平台振动对标定结果的影响。
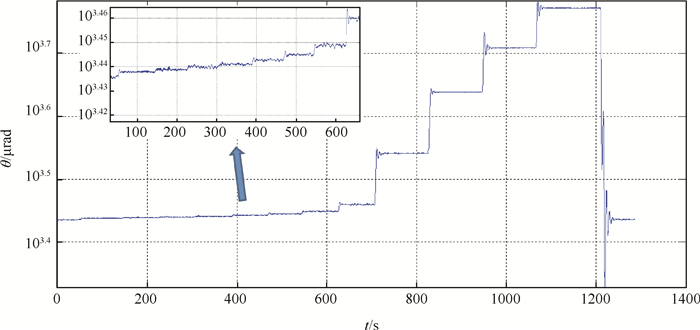
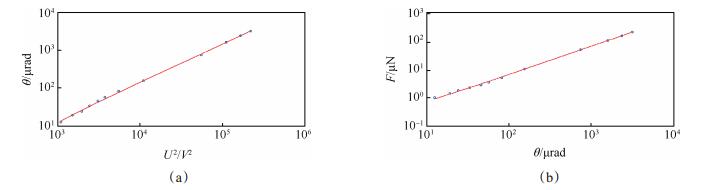
将表 2中的电压值依次输入扭秤系统中的弱力产生装置, 各项电压值对应的推力按式(17)计算得到, 利用差动测量系统记录的数据, 得到如图 8所示的标定台阶。从图中能清晰地看到14个台阶, 分别对应大小不同的标准力。分别对前13个台阶进行线性分析, 取每个台阶稳定段作为扭秤系统对标准力响应的角位移值。考虑扭秤系统中非线性因素, 对上述角位移值做关于电压二次方的二阶非线性拟合, 如图 9(a)所示。
|
|
Table 2 Calibrating result of micronewton torsion balance system |
|
Fig. 8 Calibrating steps of micronewton torsion balance system |
|
Fig. 9 Nonlinear fitting of microthrust torsion balance system |
最后, 利用电子天平拟合结果和差动系统测量结果, 建立标准力与扭转角位移之间的关系, 同样考虑扭秤系统二阶非线性因素, 如图 9(b)所示, 图中圆圈为实际测量值, 直线为二阶非线性拟合, 得到
| $ F = a{\theta ^2} + b\theta + c $ | (22) |
式中a=-1.88 × 10-7μN/μrad2, b=0.0631μN/μrad, c=0.09μN, 相对不确定度为1.1%[19]。
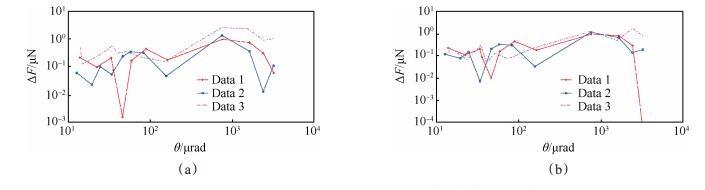
对整套微推力测量系统的绝对误差分析如图 10所示。对测量的三组数据分别进行一阶线性拟合和二阶非线性拟合, 当推力为1μN时, 一阶拟合重复度为60.7%, 二阶拟合重复度为80.5%;当推力为200μN时, 一阶拟合重复度为99.41%, 二阶拟合重复度为99.94%, 可见二阶拟合结果相比一阶拟合结果重复度高。图 10(a)为一阶线性拟合绝对误差分析图, 图 10(b)为二阶非线性拟合绝对误差分析图, 通过两幅图对比, 能够清晰地看到二阶非线性拟合绝对误差较小。因此, 双丝扭秤微推力测量系统利用二阶非线性拟合作为微推力与扭摆角位移的表达式(22)。在图 10(b)中, 对应推力约为50μN和100μN两点绝对误差较大, 其它值均在0.4μN以内, 产生较大误差原因可能为电压源在该两点的电压输出不稳, 存在1V左右跳动, 对微推力测量系统测量精度影响较小。综上, 微牛级扭秤测量系统可靠性较好, 能够达到测量范围为1~200μN, 分辨力为0.4μN。
|
Fig. 10 Absolute errors of microthrust torsion balance system |
扭秤系统扭转角位移的测量误差主要由实验室环境下热噪声干扰造成, 也是限制扭秤系统测量精度的根本因素, 根据Luther等[19]从理论上估计出热噪声对扭秤转动周期影响的表达式, 计算出热噪声对本套微牛级扭秤系统转动周期的影响为0.317μs, 即热噪声对微牛级扭秤系统的影响为高频信号, 可利用激光位移传感器控制器低通滤波消除。
实际测量推力器时, 推力器的热效应会影响扭丝的扭转弹性系数, 从而引起测量误差。温度对扭丝弹性系数的影响可表示为
| $ K\left( t \right) = {K_0}\left[ {1 + {\alpha _k}\left( {t - {t_0}} \right)} \right] $ | (23) |
式中K0为温度t0时的扭转弹性系数, αk为扭转弹性系数的线性温度系数。由于扭秤周期T = 2π(I/K)1/2, 其中I为扭摆转动惯量, I和K均为温度的函数, 所以αk可以通过测量不同温度下扭秤周期转换计算得到。根据华中科技大学的杨山清[20]研究温度对钨丝热弹性效应的测试结果, 可计算得到:当测量环境升高10℃时, 推力测量误差约为0.15%, 即推力器工作时的热效应对微推力测量系统测量精度影响较小。
微牛级扭秤系统对地面及真空系统的振动非常灵敏, 通过悬丝点影响扭秤系统的单摆运动, 具有较强的随机性, 无法通过低通滤波消除, 对扭秤系统测量精度影响较大。实验中, 通过角位移差动测量系统测得振动对扭秤系统产生的角位移振幅小于7.52μrad, 满足精度要求。
连接扭摆的两段扭丝通过夹具咬合固定, 扭丝与连接件之间的摩擦力易产生测量误差。从图 7中的台阶标定中发现无明显零点漂移现象, 即扭摆在扭转时扭丝与连接件之间无明显相对滑动;而较小的摩擦力所产生的测量误差通过扭秤标定修正, 所以扭丝与连接件之间的摩擦力对微推力测量系统测量精度的影响可忽略不计。
作为高精度测量工具, 微牛级扭秤系统的加工精度、安装和调试过程是其能否满足测量精度要求的前提。本套扭秤测量系统加工精度较高, 粗糙度为1.6μm, 对称性良好, 不会对测量结果有影响;在安装和调试过程中, 两段钨丝同轴偏差小于0.2mm, 扭摆水平度偏差小于0.1°, 弱力产生装置梳齿间距偏差小于0.1mm, 两台激光位移传感器固定水平度偏差小于0.1°, 故扭秤系统安装对测量结果产生的系统误差较小, 可忽略不计。
微推力与扭摆的垂直度对扭秤系统测量结果影响较大, 但在安装中很难保证两者完全垂直, 经过理论分析, 两者垂直度偏差弧度在允许范围±5.6×10-3rad内即可满足测量要求。此外, 两路激光位移传感器间距γ和标准力产生装置与扭丝的距离b存在测量误差, 但属于恒定偏差, 通过扭秤系统标定修正了测量误差对扭秤系统的影响。
5 结论在实验标定中, 通过两步标定法:弱力产生装置标定和扭秤系统标定, 对微推力扭秤测量系统标定, 得到以下结论:
(1)弱力产生装置产生的弱力与输入电压的二次方线性度比较小, 产生的标准力可靠性高。
(2)差动测量系统测量精度和分辨力较高, 理论上微推力测量系统能够达到微牛级分辨力。
(3)准确得到标准力与扭转角位移的关系式(22), 微推力测量范围为1~200μN, 分辨力为0.4μN, 相对不确定度为1.1%, 满足微推力器微牛级推力的静态测量的要求。
本套微牛级测量系统仅限于静态推力测量, 而无拖曳技术要求推力器能够快速响应, 这就需要一套能够测量推力器动态特性的测量工具, 即微推力动态测量装置, 这也是下一步对本套微牛级扭秤系统的改进目标。
| [1] |
萨顿. 火箭发动机基础[M]. 北京: 科学出版社, 2003.
(  0) 0) |
| [2] |
韩先伟. 微波等离子推力器真空实验研究与卫星应用探索[D]. 西安: 西北工业大学, 2002.
(  0) 0) |
| [3] |
吴汉基, 冯学章, 刘文喜, 等. 地球静止卫星南北位置保持控制系统的选择[J]. 中国空间科学技术, 1994(5): 17-24. (  0) 0) |
| [4] |
于达仁, 刘辉, 丁永杰, 等. 空间电推进原理[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014.
(  0) 0) |
| [5] |
刘慎秋, 郭华菊. 对扭秤法测量万有引力常数实验的探讨[J]. 物理实验, 1998, 19(4): 3-4. (  0) 0) |
| [6] |
Denis Packan, Jean Bonnet, Simone Rocca. Thrust Measurements with the ONERA MicroNewton Balance [C]. Florence, Italy: 30th International Electric Propulsion Conference, 2007.
(  0) 0) |
| [7] |
汤海滨, 刘畅, 向民, 等. 微推力全弹性测量装置[J]. 推进技术, 2007, 28(6): 703-706. (TANG Hai-bin, LIU Chang, XIANG Min, et al. Full Elastic Microthrust Measurement Equipment[J]. Journal of Propulsion Technology, 2007, 28(6): 703-706.)
(  0) 0) |
| [8] |
Paolucci F, d'Agostino L, Burgoni S. Design and Performance Study of a Micro-Newton Thrust Stand for FEEP[C]. Noordwijk, Netherlands: 2th European Spacecraft Propulsion Conference, 1997.
(  0) 0) |
| [9] |
Toshiaki Edamitsu, Hirokazu Tahara. Performance Measurement and Flowfield Calculation of an Electrothermal Pulsed Plasma Thruster with a Propellant Feeding Mechanism[C]. New Jersey, USA: 29th International Electric Propulsion Conference, 2005.
(  0) 0) |
| [10] |
Naoki Nagao, Shigeru Yokata, Kimiya Komurasaki, et al. Development of a Two-Axis Dual Pendulum Thrust Stand for Thrust Vector Measurement of Hall Thrusters [C]. Florence, Italy: 30th International Electric Propulsion Conference, 2007.
(  0) 0) |
| [11] |
杨娟, 刘宪闯, 王与权, 等. 微波推力器独立系统的三丝扭摆推力测量[J]. 推进技术, 2016, 37(2): 362-371. (YANG Juan, LIU Xian-chuang, WANG Yu-quan, et al. Thrust Measurement of an Independent Microwave Thruster Propulsion Device with Three-Wire Torsion Pendulum Thrust Measurement System[J]. Journal of Propulsion Technology, 2016, 37(2): 362-371.)
(  0) 0) |
| [12] |
Diamant K D. Thrust Stand Characterization of the NASA Evolutionary Xenon Thruster(NEXT)[C]. Nashville, Tennessee: 46th Joint Propulsion Conference and Exhibit, 2010.
(  0) 0) |
| [13] |
John K Ziemer. Performance Measurements Using a Sub-MicroNewton Resolution Thrust Stand[C]. California, USA: 27th International Electric Propulsion Conference, 2001.
(  0) 0) |
| [14] |
申波. 微推力测量实验装置的设计与研究[D]. 沈阳: 东北大学, 2012.
(  0) 0) |
| [15] |
赵凤鸣. 基于扭秤的弱力测量的初步分析和校验[D]. 沈阳: 东北大学, 2013.
(  0) 0) |
| [16] |
Chichung Chen, Chengkuo Lee. Design and Modeling for Comb Drive Actuator with Enlarged Static Displacement[J]. Sensors and Actuators A, 2004, 115(2): 530-539.
(  0) 0) |
| [17] |
高辉. 基于镓的场发射电推力器机理研究及样机研制[D]. 北京: 中国科学院力学研究所, 2013.
(  0) 0) |
| [18] |
国家质量技术监督局计量司. 测量不确定度评定与表示指南[M]. 北京: 中国计量出版社, 2000.
(  0) 0) |
| [19] |
Charles Bagley H, Gabriel Luther G. Preliminary Results of a Determination of the Newtonian Constant of Gravitation: a Test of the Kuroda Hypotheis[J]. Physical Review Letters, 1997, 78(16): 3047-3050. DOI:10.1103/PhysRevLett.78.3047
(  0) 0) |
| [20] |
杨山清. 扭丝滞弹性效应的精确测量[D]. 武汉: 华中科技大学, 2009. 编辑: 朱立影
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

