新一代火箭发动机比冲和推力要求越来越高,提高液体火箭发动机燃烧室压力是发动机设计中的主要方向之一[1~3]。由于燃烧室内壁热流密度随燃烧室压力增加几乎呈线性增加[4],所以压力的升高会导致内壁热流密度显著提高。准确获得燃烧室内壁热流密度,既是发动机安全工作的必要保证,也是计算发动机性能和寿命的重要依据。
很多研究者针对发动机内壁热流密度开展了研究。作为比较容易实现的研究手段,数值计算方法大量应用于发动机内壁热载研究中,计算结果也为工程应用提供了广泛参考[5, 6]。Betti等[5]使用简化的Reynolds-Averaged Navier-Stokes(RANS)方法计算液氧/甲烷发动机内壁热流密度,并用亚声速气膜和超声速气膜工况算例进行了验证。Lin等[6]提出两种方法用于模拟气氢-气氧单喷嘴燃烧室内壁的热流分布。然而,数值计算结果往往是基于若干假设与简化的模型,计算方法也很难完全模拟实际情况。因此,进行能够直接测量得到热载数据的试验研究十分必要。为了得到燃烧室内壁热载分布及传热规律,研究者应用各种热流密度的测量及计算方法,开展了大量的地面发动机试验研究。
量热法作为发动机长时间稳态工作状态下测量热流密度的传统方法,用于不少发动机试验中[7]。量热法通过测量冷却剂入口和出口集液环处冷却剂温度,得到该试验段长度上的平均热流。在地面试验中,大多使用蒸馏水作为冷却燃烧室内壁材料的冷却剂。Negishi等[8]在试验中设计了一个7段水冷量热式燃烧室,测量得到各段燃烧室内壁的平均热流,并将数值计算结果与试验值进行了对比研究。Arnold等[9]在头部气膜冷却试验研究中,燃烧室下游试验段和喷管段均采用量热法进行热流测量,得到对应位置的平均热流密度。
在近年来的一些试验中,稳态梯度法也被应用于稳态工作状态下进行热流密度测量,通过测量两个及以上个不同深度位置上的稳态温度,可以得到对应位置处内壁热流密度。Suslov等[10~12]为了研究气氢液氧燃烧室内壁面在有无头部气膜状态下的二维热载分布,设计了采用稳态梯度法测量内壁热流密度的缩尺燃烧室。
在短时间工作的热容燃烧室试验中,多使用两点瞬态计算方法,即通过测量热容燃烧室材料两个不同深度位置处瞬态温度,使用数值计算方法,得到对应位置的瞬态热流密度。Locke等[13]在单喷嘴气氢气氧燃烧室热容试验中,使用两点瞬态计算方法测量不同喷注器结构工况中燃烧室内壁热流密度的轴向分布,并作为验证数值计算方法的参考来衡量各计算方法的准确性。Conley[14]在传统两点瞬态计算方法的基础上,提出一种不限定外壁边界条件的两点计算方法,并给出了两点深度比的最佳范围。汪小卫等[15]针对单喷嘴热容燃烧室给出了壁面热流密度的测量方法,并获得了其轴向分布。
在不同条件下,以上提到的方法可以用于测量热流密度。但是量热法和稳态梯度法只能用于稳态工况,在热容燃烧室中不能使用。而两点瞬态法虽然能得到热容燃烧室瞬态热流密度,但其结果受每一点测量温度影响很大,在实际测量中经常得不到理想的数据,同时,特制的同轴热电偶加工困难,在使用过程中也容易损坏失效[13],所以在本文研究中不予采用。
为了获得内壁热流密度,研究多喷嘴缩尺燃烧室内壁热流分布及传热特性,本文开展了热容燃烧室试验。试验中每一个被测位置安装一个同轴热电偶,以热容燃烧室材料单点测量温度为输入条件,使用本文提出的三种计算方法,处理数据得到热流密度。
2 热容燃烧室本文试验在北京航空航天大学宇航学院热防护实验平台上进行,试验中所使用的热容试验燃烧室如图 1所示。燃烧室采用气氢气氧为推进剂,设计混合比为6,燃烧室压力为3.0MPa,设计压力稳定工作时长为3s。

|
Fig. 1 Experimental heat sink rocket chamber |
试验燃烧室由火炬式点火器、喷注器、水冷圆柱段、热容圆柱段和喷管组成。火炬式点火器同样采用气氢气氧燃烧产生点火火炬,流量约为5.0g/s,混合比为1,点火设计压力为2.5MPa。为了减小点火推进剂流量对主燃烧室压力影响,点火火炬在主燃烧室压力完全建立后关闭。喷注器采用多喷嘴直流剪切气气喷注器,其设计流程与文献[16, 17]采用的方法相同。水冷圆柱段由紫铜内壁和不锈钢外套配合组成,其矩形槽冷却通道数目为20个,冷却水流量为4.0kg/s,以确保燃烧室喷注器下游壁面得到充分冷却。热容圆柱段和喷管段材料为紫铜,为试验温度测量对象。试验段上布置两列同轴热电偶,用于测量试验中距内壁一定深度材料上的温度。两列热电偶分别位于喷注器外围喷嘴和相邻喷嘴间下游对应的直线上,相互间成30°,热电偶和喷注器的相对位置如图 2所示。

|
Fig. 2 Location of the thermocouples comparing with injector |
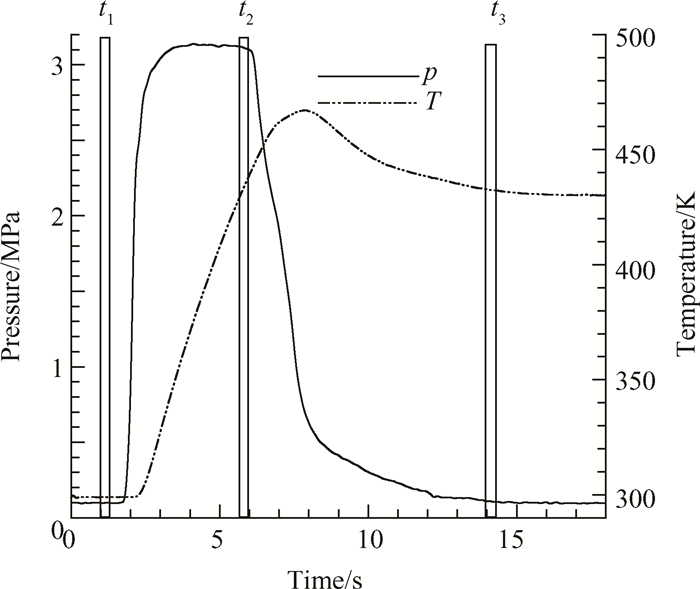
图 3所示为当前试验工况下的试验压力数据以及其中一个测点得到的温度数据。由图 3可见,试验能够得到稳定3s的燃烧室压力。同时,壁面温度随时间增加而升高,在压力上升段温度剧烈上升,在压力稳定阶段温度上升相对缓慢。图中所示t1,t2和t3分别为选取的试验前、试验压力稳态和试验后时长为0.4s时间段,用于数据处理计算热流密度。
|
Fig. 3 Experimental pressure and temperature |
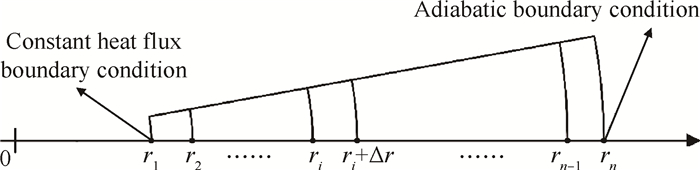
根据单点温度数据,使用本节提出的方法可以计算得到内壁瞬态热流密度和温度。由于热容试验段为圆柱结构,对于任意轴向截面上,计算模型可以表示为如图 4所示。其中,Dc和Do分别为燃烧室材料内径和外径,ri = Dc/2, rn = Do/2, Δr =(Do-Dc)/(2n-2)。
|
Fig. 4 One-dimensional calculation model |
由于试验段轴向和周向位置温差较小,所以忽略试验段热容材料轴向与周向的传热,计算模型简化为一维瞬态导热模型。本方法中使用柱坐标下的一维瞬态导热控制方程[18]。
在本文进行的3s试验中,由于热容材料足够厚,试验中外壁面温度变化很小,所以可以忽略外壁与外界环境之间的换热,即计算模型外边界为绝热边界条件[18]。计算过程中,假设从点火开始到计算时间点燃气对内壁面热流密度保持不变,即燃气侧壁面为定热流边界条件。同时,环境温度设置为试验段初始温度,在计算中取t1时间段平均温度为初始温度。
为了得到瞬态热流密度和内壁温度,计算过程主要分两步进行。
第一步:通过求解控制方程、边界条件和初始条件并进行迭代,得到点火开始到任意时间节点tk对应的平均热流密度
| $ \varepsilon = \frac{{\left| {{T_{k,{\rm{e}}}} - {T_{k,{\rm{c}}}}} \right|}}{{{T_{k,{\rm{e}}}}}} $ | (1) |
当ε < 10-4时,即认为输入热流为所求的平均热流;否则,根据式(2)修正输入热流
| $ {{\dot q}_{{\rm{av}}}} = {\left( {{{\dot q}_{\rm{a}}}} \right)_{{\rm{old}}}} + {C_1}\left( {{T_{k,{\rm{e}}}} - {T_{k,{\rm{c}}}}} \right) $ | (2) |
其中
| $ {C_1} = \frac{{\rho {c_{\rm{v}}}\left( {D_{\rm{o}}^2 - D_{\rm{c}}^2} \right)}}{{4{D_{\rm{c}}}{t_k}}} $ | (3) |
将热流修正值代入控制方程、边界条件和初始条件重新进行迭代求解,直到满足ε < 10-4,认为当前计算输入热流为平均热流密度
第二步:根据平均热流密度结果,得到瞬态热流密度。由高温燃气传入燃烧室壁面的单位面积上的热量可以表示为
| $ {Q_{{t_k} - {t_{k - 1}}}} = {Q_{{t_k}}} - {Q_{{t_{k - 1}}}} $ | (4) |
所以,由式(5)可以得到时间节点
| $ {{\dot q}_{\frac{{{t_k} + {t_{k - 1}}}}{2}}} = \frac{{{t_k} \times {{\dot q}_{{t_k},{\rm{a}}}} - {t_{k - 1}} \times {{\dot q}_{{t_{k - 1}},{\rm{a}}}}}}{{{t_k} - {t_{k - 1}}}} $ | (5) |
由以上两步可以得到点火时间范围内各时刻瞬态热流密度。将得到的瞬态热流密度作为燃气侧壁面定热流边界条件,可以求得内壁的瞬态温度。
3.2 由热平衡方法计算平均热流根据热量守恒定律,以热容燃烧室壁面材料整体为研究对象,有热平衡方程
| $ {Q_{{\rm{in}}}} - {Q_{{\rm{out}}}} = {Q_{{\rm{sto}}}} $ | (6) |
在燃烧室压力稳定段,认为燃烧室材料整体温度变化率相同[19],取试验测量点的温度梯度为整体温度梯度。同时,假设外壁面为绝热边界,由外壁面损失的热流Qout为0。从而,由式(7)可以求得内壁平均热流
| $ {{\dot q}_{{t_{\rm{f}}},{\rm{a}}}} = {{\dot q}_{{\rm{in}}}} = \frac{{\rho {c_{\rm{v}}}\left( {D_{\rm{o}}^2 - D_{\rm{c}}^2} \right)}}{{4{D_{\rm{c}}}}}\frac{{\Delta T}}{{\Delta t}} $ | (7) |
式中
由热平衡方法得到的t2时间段内平均热流密度,可以作为压力稳定段内的平均热流密度。
3.3 由热积累方法计算平均热流在试验中,若不考虑热容燃烧室外壁的热量损失,可以由点火实验前和关机后材料的热积累求得点火时间段内由燃气向燃烧室内壁传递的热量,从而得到该时间段内的平均热流。点火时间内所传递的热流由式(8)表示
| $ Q = m\left[ {{c_{v,{t_3}}}{T_{{t_3}}} - {c_{v,{t_1}}}{T_{{t_1}}}} \right] $ | (8) |
其中,试验前的温度取t1时间段内的平均温度值,试验后的温度取t3时间段内的平均温度值,认为t3时间段开始温度基本维持不变。所以,内壁平均热流密度为
| $ {{\dot q}_{{t_{\rm{f}}},{\rm{a}}}} = \frac{{\left( {{\rho _{{t_3}}}{c_{v,{t_3}}}{T_{{t_3}}} - {\rho _{{t_1}}}{c_{v,{t_1}}}{T_{{t_1}}}} \right)\left( {D_{\rm{o}}^2 - D_{\rm{c}}^2} \right)}}{{4{D_{\rm{c}}}\Delta {t_{\rm{f}}}}} $ | (9) |
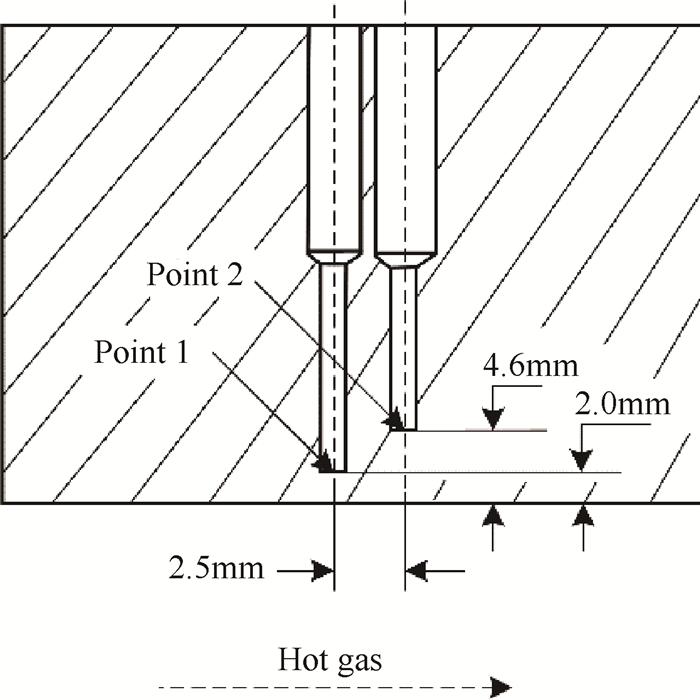
为了对比本文的单点瞬态方法与文献[14, 20]提出的两点瞬态法,试验中在燃烧室圆柱段布置了3组热电偶测量两个不同深度上的温度,测量孔尺寸如图 5所示。两个测点位置距离燃气侧壁面距离比为2.3,在轴向位置上两点相距很小,认为试验温度测量值为同一轴向位置不同深度上的温度。在试验过程中,由于壁面材料温度随时间剧烈变化,材料发生体积变化会影响热电偶与测孔壁面的接触情况。为了减小接触热阻的变化对温度测量的影响,试验采用了弹簧固定装置,提供恒定13N的压力。
|
Fig. 5 Location of measured points for method validation |
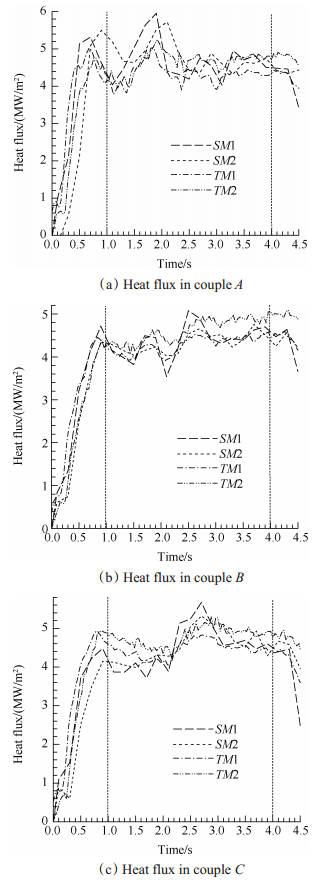
图 6所示为根据不同位置上3组温度测量数据计算得到的瞬态热流密度,其中SM1和SM2分别表示运用单点瞬态法在点1和点2处得到的结果,TM1和TM2分别表示运用文献[14, 20]中的两点瞬态法计算得到的结果。从图中可以看出,两种方法得到的瞬态热流密度相差较小,并且热流随时间的变化具有相同的趋势。在各点位置上,点火后的压力建立时间段(约0.8s)内,热流密度从0迅速上升到接近稳态的热流值,并在关机后下降。同样的热流时间曲线在文献[14, 20]已经得到。
|
Fig. 6 Comparison of heat fluxes between two method |
为了定量分析单点方法与两点法得到结果的差异,通过计算稳定工作时间段(1~4s)内热流密度平均值,可以求得单点法相对于两点法的计算结果误差,对比结果如表 1所示。可以看出,两种方法计算结果相对误差在10%以内。同时,除A组外,由点1和点2得到的结果均略小于文献[20]中方法的计算结果,而略大于文献[14]中方法的计算结果。这说明对于相同的试验数据,与两点法相比,运用单点法同样可以得到可用的热流密度。
|
|
Table 1 Relative error of the average heat fluxes (%) |
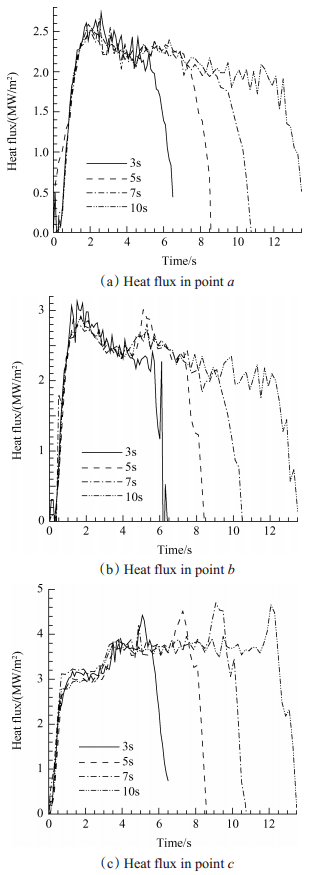
图 7所示为不同点火时长工况下得到的热流密度结果,其中图 7(a)位于燃烧室圆柱段,图 7(b)位于喷管收缩段,图 7(c)位于喷管扩张段。可以看出,增加点火时长基本不影响相同时间段计算得到的瞬态热流,说明单点瞬态法受点火时长的影响较小。同时,在燃烧室圆柱段和喷管段得到的热流密度在压力稳定阶段随时间的变化规律完全相反,即在圆柱段热流密度随着点火时长的增加而减小,而在喷管段热流密度随点火时长增加而增加。这是由于利用单点法计算瞬态热流,假设外壁为完全绝热条件,然而在试验状态下,外壁温度会随时间逐渐升高,外壁的热损失也会逐渐增加。所以试验过程中测量得到的温度值会略小于外壁完全绝热条件下的温度,而在采用主动冷却状态下稳定工作时间段内壁热流一般为恒定值,从而由此测量温度计算得到的热流密度会逐渐减低。在喷管段,虽然外壁面同样存在温度升高的问题,但由于在轴向上温度梯度比较大,尤其在喉部附近温度远高于收缩段和扩张段,轴向传热对热流密度的影响高于外壁热损失的影响,从而热流密度在试验过程中随时间增长而增加。
|
Fig. 7 Transient heat flux in different work time |
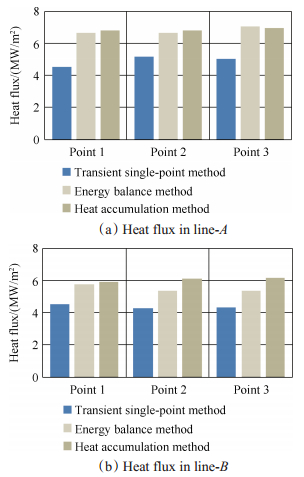
本节分别使用单点瞬态方法、热平衡方法和热积累方法对试验得到的壁面温度数据进行计算处理,得到相应的热流密度平均值。对于单点瞬态方法,平均值的计算与表 1中相同,在压力稳定段取平均热流密度。三种方法计算结果如图 8所示,其中图 8(a)为喷注器喷嘴下游测点处内壁热流密度,图 8(b)为两喷嘴中心线下游测点处内壁热流密度。
|
Fig. 8 Heat flux comparisons among the three methods |
可以看出,三种方法得到的结果没有数量级的差别,并且热平衡方法和热积累方法得到的热流密度值均略高于瞬态方法。同时,几乎对于所有测点运用热积累方法得到的热流密度最高,这个现象在图 8(b)中更明显。这是由于在后两种计算方法中,将壁面固体材料视为一个整体,认为材料所有位置在压力稳定段具有相同的温度梯度或关机后温度完全相同,而实际过程中温度以及温度梯度会随距内壁距离增大而降低。所以试验测量得到距内壁1mm处温度及温度梯度会高于整体材料的平均值,得到的平均热流密度会高于实际值。对于热积累方法,忽略压力稳定阶段之外时间段燃气对内壁的传热,计算得到的热量高于实际压力稳定阶段传入的值,所以计算得到的平均热流密度结果偏高。在不同周向位置,Line-A上的热流高于Line-B上的值,这种现象满足多喷嘴喷注器燃烧室内壁的热载分布。
通过对比可以看出,热平衡方法和热积累方法得到的热流密度值偏大,在工程设计中更为保守,而热平衡方法偏差更小,所以在试验工程中可以使用热平衡方法作为快速计算方法,得到热流密度参考值。
5 结论本文通过试验研究测量得到单点温度数据,提出并采用三种方法计算内壁热流密度,其中瞬态方法可以得到瞬态热流。得到的主要结论如下:
(1)燃烧室壁面测量的温度数据可分为两段,为温度剧烈变化段和平滑变化段,在平滑段燃烧室压力达到稳态,热流基本保持不变。
(2)根据单点温度计算得到的瞬态热流与瞬态两点梯度法得到的结果相差很小,在热容试验中,可以使用单点法计算内壁热流。
(3)在相同燃烧室参数工况下,不同工作时长温度及热流重复性很好。在燃烧室圆柱段,热流密度随工作时间增加而降低,在喷管段变化趋势相反。
(4)在计算平均热流密度的三种方法中,热积累方法和热平衡方法得到的值高于瞬态方法,其中热积累方法得到的值最高。在工程应用中,热平衡方法可以作为获得平均热流密度的快速计算方法,得到更为保守的热流密度。
| [1] |
Huzel D K, Huang D H. Modern Engineering for Design of Liquid-Propellant Rocket Engines[R]. AIAA 1992-0147.
(  0) 0) |
| [2] |
王之任. 近代大型液体火箭发动机的特点[J]. 推进技术, 1991, 12(4): 29-35. (WANG Zhi-ren. Characteristics of Modern Large Liquid Rocket Engine[J]. Journal of Propulsion Technology, 1991, 12(4): 29-35.)
(  0) 0) |
| [3] |
刘国球, 胡平信. 液体火箭发动机技术的回顾与展望[J]. 推进技术, 1998, 19(4): 3-7. (LIU Guo-qiu, HU Ping-xin. Review of Liquid Propellant Rocket Engine[J]. Journal of Propulsion Technology, 1998, 19(4): 3-7.)
(  0) 0) |
| [4] |
Bartz D R. A Simple Equation for Rapid Estimation of Rocket Nozzle Convective Heat Transfer Coefficients[J]. Journal of Jet Propulsion, 1957, 27(1): 49-51. DOI:10.2514/8.12572
(  0) 0) |
| [5] |
Betti B, Martelli E, Nasuti F. Heat Flux Evaluation in Oxygen/Methane Thrust Chambers by RANS Approach [R]. AIAA 2010-6721.
(  0) 0) |
| [6] |
Lin J, West J, Williams R, et al. CFD Code Validation of Wall Heat Fluxes for a GO2/GH2 Single Element Combustor[R]. AIAA 2013-4524.
(  0) 0) |
| [7] |
Suslov D, Woschnak A, Greuel D, et al. Measurement Techniques for Investigation of Heat Transfer Processes at European Research and Technology Test Facility P8[J]. Journal of Physics Condensed Matter, 2005, 17(41): 6405-6413. DOI:10.1088/0953-8984/17/41/011
(  0) 0) |
| [8] |
Negishi, H, Kumakawa A, Yamanishi N, et al. Heat Transfer Simulations in Liquid Rocket Engine Subscale Thrust Chambers[R]. AIAA 2008-5241.
(  0) 0) |
| [9] |
Arnold R, Suslov D I, Haidn O J. Experimental Investigation of Film Cooling with Tangential Slot Injection in a LOX/CH4 Subscale Rocket Combustion Chamber[J]. Transactions of the Japan Society for Aeronautical and space Sciences, Space Technology Japan, 2009, 7(26): 81-86.
(  0) 0) |
| [10] |
Suslov D I, Arnold R, Haidn O. Investigation of Two Dimensional Thermal Loads in the Region near the Injector Head of a High Pressure Subscale Combustion Chamber[R]. AIAA 2009-450.
(  0) 0) |
| [11] |
Suslov D I, Arnold R, Haidn O. Investigation of Film Cooling Efficiency in a High Pressure Subscale LOX/H2 Combustion Chamber[R]. AIAA 2011-5778.
(  0) 0) |
| [12] |
Arnold R, Suslov D I, Haidn O. Circumferential Film Cooling Effectiveness in a LOX/H2 Subscale Combustion Chamber[J]. Journal of Propulsion and Power, 2009, 25(3): 25-770.
(  0) 0) |
| [13] |
Locke J M, Pal S, Woodward R D, et al. Chamber Wall Heat Flux Measurements for a LOX/CH4 Uni-Element Rocket[R]. AIAA 2007-5547.
(  0) 0) |
| [14] |
Conley A, Vaidyanathan A, Segal C. Heat Flux Measurements for a GO2/GH2 Single-Element, Shear Injector[J]. Journal of Spacecraft and Rockets, 2007, 44(3): 633-639. DOI:10.2514/1.26678
(  0) 0) |
| [15] |
汪小卫, 金平, 蔡国飙, 等. 单喷嘴燃烧室传热特性的测量方法[J]. 推进技术, 2008, 29(6): 726-732. (WANG Xiao-wei, JIN Ping, CAI Guo-biao, et al. Method for Measurement of Single-Injector Heat Transfer Characteristics[J]. Journal of Propulsion Technology, 2008, 29(6): 726-732.)
(  0) 0) |
| [16] |
汪小卫, 高玉闪, 金平, 等. 单喷嘴大流量气-气喷注器设计与试验[J]. 航空动力学报, 2010, 25(3): 691-698. (  0) 0) |
| [17] |
汪小卫, 高玉闪, 金平, 等. 单喷嘴气-气喷注器推力室燃烧流场相似性[J]. 航空学报, 2010, 31(8): 1538-1545. (  0) 0) |
| [18] |
陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2003.
(  0) 0) |
| [19] |
Celano M P, Silvestri S, Schlieben G, et al. Injector Characterization for a GOX-GCH4 Single Element Combustion Chamber[C]. Munich: 5th European Conference for Aeronautics and Space Sciences(EUCASS), 2013.
(  0) 0) |
| [20] |
Coy E. An Efficient Method for Calculating Surface Temperature and Heat Flux Based on Embedded Temperature Sensors[R]. AIAA 2008-3952.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

