2. 中国船舶工业系统 工程研究院,北京 100094;
3. 青岛大学 应用技术学院,山东 青岛 266071
2. China Ship Building Industry System Engineering Research Institute, Beijing 100094, China;
3. Applied Technology Institute of Qingdao University, Qingdao 266071, China
传统修补技术是通过螺接、铆接或者焊接等方式将金属补强板固定到飞机结构损伤位置,金属补强板改善了修补区域的应力分布,但造成了修补区域临近位置处的应力集中,同时该方法也会引入新的损伤源,使应力集中问题更加严重[1~3]。复合材料胶接修补可以改变力的传递路线,使结构损伤处应力有效地传递到补片,改善损伤处应力集中[4, 5]。含裂纹结构贴补补片后,有效降低了裂纹尖端的应力强度因子值,延缓或者阻止了裂纹的再起始、再扩展,大大提高了损伤结构的剩余强度和耐久性能[1~5]。
复合材料补片的材料类型主要有玻璃纤维/环氧树脂,碳纤维/环氧树脂以及硼纤维/环氧树脂三类。从强度性能来说,玻璃纤维/环氧树脂材料小于其他两类材料,但由于其制备简单、价格低廉,得到了广泛应用。同修补结构基板热膨胀系数相比,硼纤维/环氧树脂与碳纤维/环氧树脂相对较低,会产生较大残余热应力。而玻璃纤维/环氧树脂的热膨胀系数远大于其他两类材料,对其进行相对低温的热固化处理,可以显著减小修补结构的残余应力。Crooks[6]对碳纤维/环氧树脂补片单面修补铝合金板的残余应力进行了实验研究,发现当固化温度为120℃时,修补结构的残余应力达到最大值6.8MPa,当固化温度从120℃变为93℃时,残余应力降低了20%。硼纤维与碳纤维材料还具备一定的导电性,在高温潮湿的环境下易与基板发生电化学腐蚀,而玻璃纤维绝缘性能较好。
考察修补结构疲劳性能是评价修补效果的指标之一。很多学者对复合材料胶接修补结构进行了疲劳试验和数值分析。Schubbe等[7]对复合材料单面修补铝合金结构的疲劳裂纹扩展进行了实验研究。Chukwujekwu等[8]建立二维有限元模型,对复合材料单面修补铝合金薄板和厚板结构的疲劳扩展进行了分析。Seo等[9],Hosseini等[10, 11],以及杨孚标[12]对复合材料单面修补薄板和厚板结构的疲劳裂纹扩展前沿进行了相关研究,通过原位逆向电流检测设备观测发现,沿金属板厚度方向裂纹扩展呈曲线形状。Lee等[13]利用数值方法模拟了碳纤维复合材料单面修补含中心穿透裂纹铝合金板的疲劳裂纹扩展,仿真结果与试验结果一致。本文根据玻璃纤维/环氧树脂复合材料单面修补含单边穿透裂纹铝合金板疲劳试验的裂纹前沿形状,进行适当简化,建立了基于UCF和SCF修补结构有限元模型,对基板厚度方向的应力强度因子进行数理统计分析,定义ESIF,利用Paris公式对疲劳寿命进行预测,并与试验结果进行对比分析。
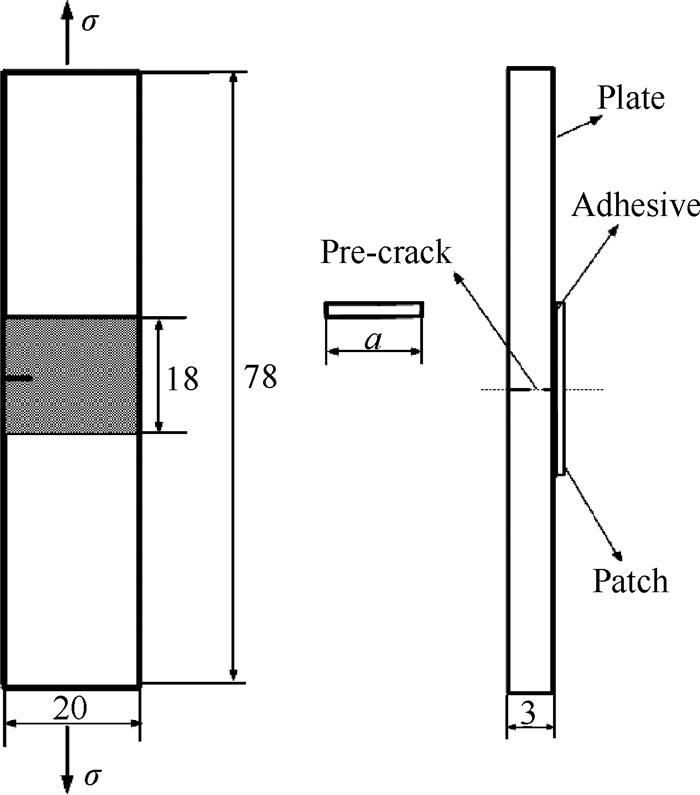
2 疲劳实验方法复合材料单面修补结构的几何示意图如图 1所示,金属板材料为LD2CS铝合金,其几何尺寸为78mm(长)×20mm(宽)×3mm(厚),金属板一侧中心位置处利用线切割预制长度a = 4 mm的单边穿透裂纹,裂纹宽度为0.2mm,裂纹方向与金属板长度方向垂直。利用玻璃纤维/环氧树脂复合材料补片对含裂纹铝合金板进行修补,复合材料补片由6层单向玻璃纤维组成,纤维层的尺寸为18mm(长)×20mm(宽)× 0.3mm(厚),铺层方式为正交铺层,0°方向与裂纹长度方向垂直。首先对金属板表面损伤处进行喷砂,之后使用E44/聚酰胺环氧树脂将复合材料补片贴补到损伤区域表面,并在100℃,0.1MPa环境下进行2h的共固化处理。
|
Fig. 1 Geometrical model of repair structure with singleside patch(mm) |
利用液压伺服试验机进行疲劳试验。试验时加载频率为10Hz,施加疲劳载荷的最大值为97MPa,应力比R = 0.1,波形为正弦波。疲劳过程中引入少量超载谱块,以记录试件中一定循环次数下的疲劳裂纹扩展前缘线,通过测量前缘线之间的距离测得疲劳裂纹扩展长度a与循环周次N的关系。具体做法为施加五千次正常的等幅交变载荷循环后,加入循环次数为20次,最大应力σmax = 130MPa,最小应力σmin = 25MPa,频率为5Hz的超载谱块。
3 有限元分析含穿透裂纹铝合金板复合材料单面修补结构疲劳裂纹扩展过程中,沿金属板厚度方向裂纹扩展长度不一致,裂纹前沿与厚度方向不垂直,如图 2所示。这是因为沿金属板厚度方向SIF值存在差异,裂纹扩展速度不一致,靠近贴补补片面的SIF值较小,扩展速度慢。因此,在分析含穿透裂纹铝合金板复合材料单面修补结构时,贴补补片面和未贴补补片面裂纹扩展长度差异不能忽略。通过观察断裂试验件的横断面,贴补补片面和未贴补补片面之间裂纹扩展差异大约为4mm/16mm。假定其他裂纹长度时修补面和未修补面裂纹扩展长度差异从0到4mm线性变化。从图 2中还可以看出,在试验中裂纹扩展前沿形状为椭圆形,在斜裂纹有限元模型分析时简化为直线形裂纹尖端。

|
图 2 Cross section of fractured specimen |
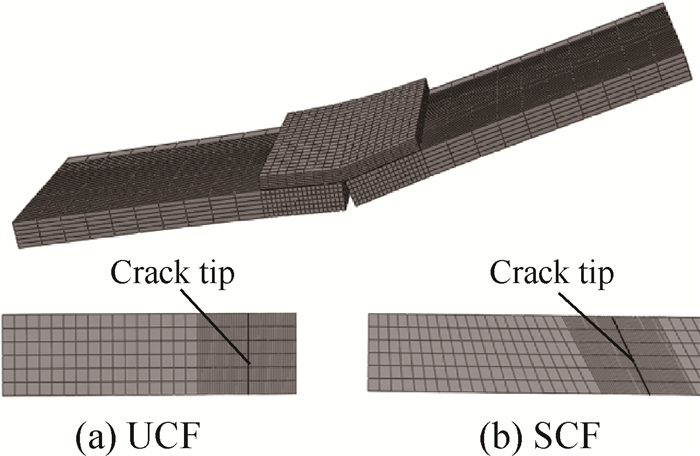
利用商业有限元软件Abaqus[14]建立两类有限元模型,以研究复合材料单面修补结构的疲劳裂纹扩展,建立的有限元模型如图 3所示。第一类为基于UCF有限元模型,假定裂纹扩展过程中裂纹前沿长度一致,即疲劳裂纹扩展前沿始终垂直于金属板厚度方向,贴补面和未贴补面裂纹扩展速率一致;第二类为基于SCF有限元模型,其裂纹前沿与金属板厚度方向是斜交的,即疲劳裂纹扩展中裂纹前沿与金属板厚度方向成一定角度,贴补补片面和未贴补补片面裂纹扩展速率不一致。
|
Fig. 3 Finite element model of repaired structure and crack front modeling |
有限元分析时取全尺寸建模,对金属板建模采用C3D20R(20节点六面体二次减缩积分单元)单元仿真,利用SEAM模拟穿透裂纹,并在裂纹尖端设置1/4奇异单元。胶层采用C3D8R(8节点六面体二次减缩积分单元)单元仿真,初始厚度为0.1mm;补片采用SC8R(4节点连续壳单元)单元模拟[15]。布局全局种子大小为3mm,设置补片、胶层和修补处的局部种子大小为0.5mm,胶层厚度方向设置为1层,补片的厚度方向层数与实际层数一致,金属板的厚度方向设置6层。裂纹尖端处要进行网格细化,设置网格密度为0.1mm。使用绑定约束(Tie)将不同材料界面节点的自由度完全绑定,模拟胶层与铝合金板、胶层与补片的协调变形关系。边界条件(Boundary)采用铝合金板一端固定,一端施加载荷的方式。
分析时假定胶层和补片未发生损伤。铝合金板、玻璃纤维/环氧树脂补片以及胶层的材料属性如表 1所示。利用两类模型计算了施加最大应力时,裂纹长度a分别为4mm,6mm,8mm,10mm,12mm,14mm,16mm以及18mm时沿板厚度方向裂纹尖端处应力强度因子值SIF。
|
|
Table 1 Material properties of aluminum plate, adhesive and patch |
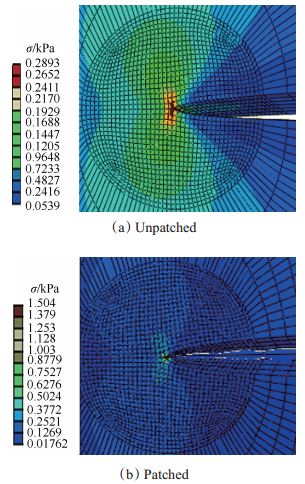
由有限元模型得到贴补补片前后裂纹尖端附近应力分布图(如图 4所示),从图中可以看出,由于补片的补强作用,裂纹附近应力集中现象明显得到改善,SIF值减小。
|
Fig. 4 Stress distribution around crack tip of patched and unpatched aluminum plates |
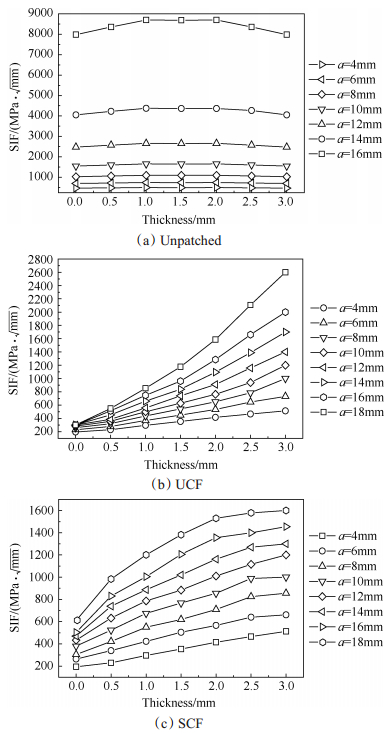
由于分析中应用补片进行单面贴补,受力后产生附加弯矩,沿厚度方向SIF值存在差异。图 5为未修补以及修补试验件两类有限元模型计算得到的沿厚度方向SIF值变化曲线,横轴0刻度表示贴补补片面。从图中可以看出,未贴补面的SIF要比贴补面高很多。在基于SCF修补有限元模型中,贴补面和未贴补面SIF差值比基于UCF修补有限元模型要小,这是因为基于SCF修补有限元模型贴补面裂纹长度比基于UCF修补有限元模型要短,剩余断面的宽大部分抑制了裂纹张开,导致SIF值减小。
|
Fig. 5 Stress intensity factor variation along the thickness direction for different models |
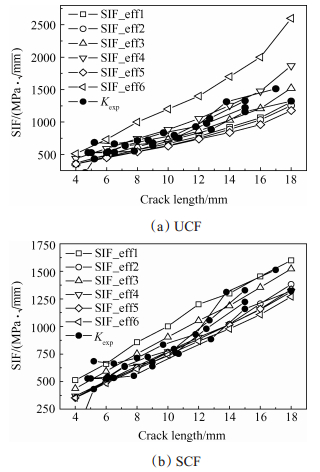
由于未贴补补片面与贴补补片面裂纹尖端SIF值差异较大,因此需要定义给定裂纹长度时的有效SIF值。利用数理统计中统计参量定义有效SIF值:对厚度方向的所有值求解平均值(SIF_eff1),去掉最大值最小值求解平均值(SIF_eff2),对所有值求解均方根(SIF_eff3),对未贴补面到中间点的值求解平均值(SIF_eff4),金属板中心点处的值作为有效值(SIF_eff5),以及未贴补面的值作为有效值(SIF_eff6)。对上述SIF统计量进行求解,画出多个有效SIF值随裂纹长度变化的曲线,如图 6所示。
|
Fig. 6 Stress intensity factor of patched specimen as a function of crack length for two types of FEM with various statistical methods |
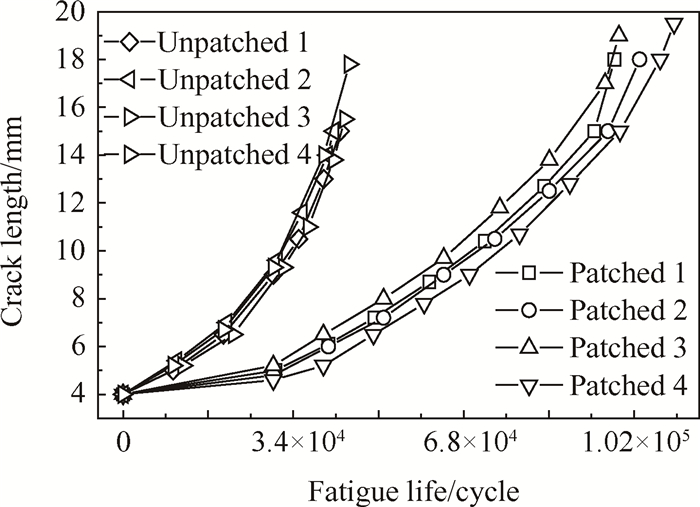
为了获得未修补结构和修补结构的疲劳裂纹扩展行为,进行了两类试验件的疲劳试验,得到疲劳载荷循环数-裂纹长度曲线图(如图 7所示)。从图 7中可以看出,疲劳试验结果存在一定的分散性,但分散性较小。使用ASTM标准E-647中推荐的七点增量多项式法求解裂纹的扩展速率。对于含穿透裂纹未修补试验件的应力强度因子K,其计算公式为
| $ K = \sigma \sqrt {{\rm{ \mathit{ π} }}a} F\left( {a/b} \right) $ | (1) |
| $ \begin{array}{l} F\left( {a/b} \right) = \\ \left[ {\frac{{0.752 + 2.02\left( {\frac{a}{b}} \right) + 0.37{{\left( {1 - \sin \left( {\frac{{{\rm{ \mathit{ π} }}a}}{{2b}}} \right)} \right)}^3}}}{{\cos \left( {\frac{{{\rm{ \mathit{ π} }}a}}{{2b}}} \right)}}} \right] \times \sqrt {\frac{{2b}}{{{\rm{ \mathit{ π} }}a}}\tan \left( {\frac{{{\rm{ \mathit{ π} }}a}}{b}} \right)} \end{array} $ | (2) |
|
图 7 Fatigue crack growth of patched specimen as a function of cycle |
式中a和b分别为裂纹长度和铝合金板宽度。
4.2 利用实验结果计算SIF裂纹扩展的Paris公式为
| $ {\rm{d}}a/{\rm{d}}N = C{\left( {\Delta K} \right)^m} $ | (3) |
式中N疲劳载荷的循环数;C,m为材料常数;ΔK为SIF值的增量,用以研究未修补和修补试验件的疲劳扩展行为。本实验中ΔK = 0.9Kσmax,Kσmax为施加最大载荷时裂纹尖端的SIF值。利用SIF修正法进行疲劳扩展分析,即假定修补试验件和未修补试验件的材料常数C和m是相同的,复合材料补片的作用是减小修补试验件裂纹尖端处SIF值。
将式(3)两边取自然对数,可得到
| $ \ln \left( {{\rm{d}}a/{\rm{d}}N} \right) = \ln C + m\ln \left( {\Delta K} \right) $ | (4) |
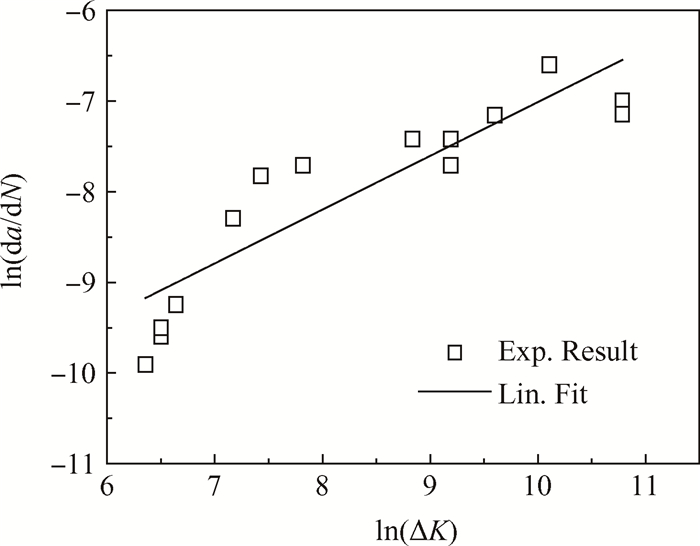
通过试验测得的ln(da/dN)和ln(ΔK)之间的关系,结果如图 8所示。取置信水平α = 0.05,进行线性拟合,得到方程的相关系数R2 = 0.88,说明回归方程显著,回归方程是成立的,其表达式为
| $ \ln \left( {{\rm{d}}a/{\rm{d}}N} \right) = - 12.94 + 0.5931\ln \left( {\Delta K} \right) $ | (5) |
|
Fig. 8 ln(ΔK) -ln(da/dN) curve of the single-side cracked plate |
由该直线的斜率和截距得到实验条件下材料常数C = 2.4 × 10-6和m = 0.5931。
通过图 7计算得到修补试验件裂纹扩展速率da/dN,利用式(5)可以求解修补结构不同裂纹长度时的ΔKexp,并进一步求得施加最大应力时的应力强度因子Kexp,并绘于图 6中,与两类有限元模型得到的SIF值进行对比分析验证。从图 6中可以看出,两类有限元模型得到的SIF值与试验方法得到的结果变化趋势一致。在基于UCF有限元模型中,Kexp的值介于SIF_eff3与SIF_eff4之间,而Kexp的值与基于SCF有限模型各有效SIF值吻合较好。
4.3 疲劳寿命预测文献[12]对式(3)进行了积分和简化处理,得到了修补结构疲劳裂纹在稳定扩展时寿命计算方法。当裂纹长度从aj增加到aj + 1时,修补结构所经历的疲劳周次
| $ \Delta {N_j} = \frac{{\Delta {a_j}}}{{C{{\left[ {\Delta {K_{j + 1}}\left( {{a_{j + 1}}} \right)} \right]}^m}}} $ | (6) |
| $ {N_{j + 1}} = {N_j} + \Delta {N_j} = {N_j} + \frac{{\Delta {a_j}}}{{C{{\left[ {\Delta {K_{j + 1}}\left( {{a_{j + 1}}} \right)} \right]}^m}}} $ | (7) |
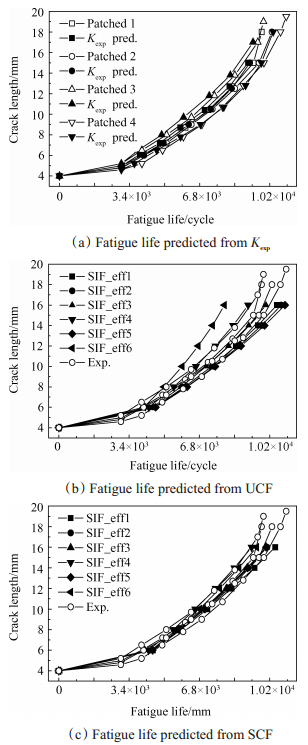
利用式(6)和式(7),根据试验结果得到的应力强度因子Kexp,以及两类有限元模型ESIF可以对修补试验件疲劳裂纹寿命进行预测,将预测结果绘于图 9,并与实验结果进行对比分析。
|
Fig. 9 Comparison of fatigue life predicted from different models and experimental result |
在图 9(a)中,利用四件修补试验件得到的Kexp对四件修补件的疲劳寿命进行预测,可以发现,其预测结果与试验件疲劳试验结果十分接近,但比实际试验值要小,是一个保守值。图 9(b)和图 9(c)分别为基于UCF和基于SCF修补结构有限元模型预测疲劳寿命与试验结果对比图,从图 9(b)可以看出,四类试验件的疲劳寿命曲线都落于SIF_eff3与SIF_eff4的预测范围之内,SIF_eff6的预测值过于保守,与试验中值寿命的误差为19%。疲劳裂纹较短时,SIF_eff1,SIF_eff2与SIF_eff5的疲劳寿命预测值与试验值差异较小,随着裂纹长度增加,其误差变大,与试验中值寿命的误差为13%。这主要是因为随着裂纹长度的增加,修补面和未修补面裂纹长度差异变大,而此模型未考虑造成的,因此模型只可使用SIF_eff3与SIF_eff4进行疲劳寿命的估测。从图 9(c)可以看出,基于SCF有限元模型各有效SIF疲劳寿命预测值与疲劳试验结果吻合较好,与试验中值寿命的误差都在6%以内,这主要是由于此模型考虑到了单面修补结构疲劳过程中修补面和未修补面裂纹扩展长度存在差异,得到的结果较为理想。
5 结论通过本文研究,得到以下结论:
(1)修补结构的SIF沿金属板方向变化明显,利用数理统计方法定义了多类有效SIF,同基于UCF有限元模型相比,基于SCF有限元模型的各有效SIF值与试验获得的SIF值更接近,精度更高。
(2)通过试验获得的Kexp与有限元模型得到的ESIF对疲劳寿命进行预测和对比,发现Kexp预测结果比实际值小,相对保守。基于垂直裂纹有限元模型中SIF_eff3与SIF_eff4的预测结果与实验值较接近,其他有效SIF值预测误差较大,与试验中值寿命的最大误差可达19%。基于SCF有限元模型各SIF值的预测结果与试验值吻合较好,与试验中值寿命的最大误差都在6%以内,更适合于疲劳寿命的预测。
| [1] |
Baker A A. Repair of Cracked or Defective Metallic Aircraft Components with Advanced Fiber Composites[J]. Composite Structure, 1984, 2(2): 153-234. DOI:10.1016/0263-8223(84)90025-4
(  0) 0) |
| [2] |
苏维国, 穆志韬, 朱做涛, 等. 金属裂纹复合材料单面胶接修补结构应力分析[J]. 复合材料学报, 2014, 31(3): 772-780. (  0) 0) |
| [3] |
郝建滨, 李旭东, 穆志韬. 金属裂纹板复合材料胶接修补强度的弹塑性有限元预测[J]. 复合材料学报, 2015, 33(3): 643-649. (  0) 0) |
| [4] |
韩允, 刘元海, 肖晓辉. 复合材料胶接修补结构有限元分析方法研究[J]. 直升机技术, 2016, 3: 32-35. DOI:10.3969/j.issn.1673-1220.2016.03.006 (  0) 0) |
| [5] |
Baker A A. Bonded Composite Repair of FatigueCracked Primary Aircraft Structure[J]. Composite Structure, 1999, 47: 431-437. DOI:10.1016/S0263-8223(00)00011-8
(  0) 0) |
| [6] |
Crooks H. Reduction of Thermal Residual Strains in Adhesively Bonded Composite Repairs[D]. USAF: MSc Thesis, Air Force Institute of Technology, 2003.
(  0) 0) |
| [7] |
Schubbe J J, Mall S. Investigation of a Cracked Thick Aluminum Panel Repaired with a Bonded Composite Patch[J]. Engineering Fracture Mechanics, 1999, 63: 305-323. DOI:10.1016/S0013-7944(99)00032-6
(  0) 0) |
| [8] |
Chukwujekwu O A, Singh N, Enemuoh U, et al. Design, Analysis and Performance of Adhesively Bonded Composite Patch Repair of Cracked Aluminum Aircraft Panels[J]. Composite Structure, 2005, 71(2): 258-270. DOI:10.1016/j.compstruct.2005.02.023
(  0) 0) |
| [9] |
Seo D C, Lee J J. Fatigue Crack Growth Behavior of Cracked Aluminum Plate Repaired with Composite Patch[J]. Composite Structure, 2002, 57(1-4): 323-330. DOI:10.1016/S0263-8223(02)00095-8
(  0) 0) |
| [10] |
Hosseini-Toudeshky H, Sadeghi G, Daghyani H R. Three-dimensional Approach to Fatigue Crack Propagation for Aluminum Panels Repaired with Single-Sided Composite Laminates[C]. Australia: 4th Asian-Australasian Conference on Composite Material, 2004.
(  0) 0) |
| [11] |
Hosseini-Toudeshky H, Sadeghi G, Daghyani H R. Experimental Fatigue Crack Growth and Crack-Front Shape Analysis of Asymmetric Repaired Aluminum Panels with Glass/Epoxy Composite Patches[J]. Composite Structure, 2005, 71: 401-406. DOI:10.1016/j.compstruct.2005.09.032
(  0) 0) |
| [12] |
杨孚标. 复合材料修补含中心裂纹铝合金板的静态与疲劳特性研究[D]. 长沙: 国防科学技术大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-90002-2007141062.htm
(  0) 0) |
| [13] |
Lee W Y, Lee J J. Successive 3D FE Analysis Technique for Characterization of Fatigue Crack Growth Behavior in Composite-Repaired Aluminum Plate[J]. Composite Structure, 2004, 66(1-4): 513-520. DOI:10.1016/j.compstruct.2004.04.074
(  0) 0) |
| [14] |
石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2006.
(  0) 0) |
| [15] |
刘万雷, 常新龙, 张晓军, 等. 缠绕复合材料壳体低速冲击损伤试验与仿真研究[J]. 推进技术, 2017, 38(1): 172-178. (LIU Wan-lei, CHANG Xin-long, ZHANG Xiao-jun, et al. Experimental and Numerical Analysis of Filament Winding Composite Shell under Low-Velocity Impact[J]. Journal of Propulsion Technology, 2017, 38(1): 172-178.)
(  0) 0) |
| [16] |
高海朋, 刘猛, 王浚. 基于疲劳寿命的复合材料舱体分级优化分析[J]. 推进技术, 2013, 34(11): 1549-1556. (GAO Hai-peng, LIU Meng, WANG Jun. Graded Optimization and Analysis of Composite Cabin Based on Fatigue Life[J]. Journal of Propulsion Technology, 2013, 34(11): 1549-1556.)
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

