涡轮叶盘结构是一种工况极其恶劣的热端部件,处于循环高温、高压、高转速的燃气区,其性能衰退是导致航空发动机非计划换发的重要因素,严重制约着发动机可靠性和经济性[1~3]。叶片和轮盘广泛采用枞树型榫齿连接,榫头和榫槽间存在配合间隙,以保证叶片自动进入正常工作位置、自由膨胀以及吹风冷却[4]。然而,过渡状态下,配合间隙会随工况的转换而改变,稳态下,由于离心力、热载荷、振动负荷等因素的共同作用,同样会导致配合间隙发生变化,榫齿处每时每刻都呈现出复杂的应力循环和多样的接触状态[4~8],于是叶片与轮盘榫齿处的接触问题也成为了当下的研究热点,大量的数值模拟和试验研究结果表明,该结构的绝大多数失效模式均与疲劳有关,显著影响着涡轮部件的使用寿命[9~12],因此,合理的设计榫齿结构的几何尺寸,提高其疲劳寿命,保障航空发动机的安全可靠性,是十分有必要的。
随着航空发动机性能的提高以及诸多新型材料的出现,带来更多的不确定性,配合间隙的变化难免引起接触状态和应力水平的改变,与此同时,叠加载荷、材料参数的随机性,可能会导致叶盘结构的疲劳寿命存在较大概率区间,在随机因素的影响下,寿命预测结果与确定性分析结果相比,会存在一定偏差,传统的确定性分析结果已无法满足设计需要。稳健性优化方法被证明能够有效减小结构疲劳寿命的概率区间,使其对随机变量的敏感程度降低,有利于更加准确的进行寿命评估[13~18]。
综上,在探究榫槽/榫齿配合间隙的变化对叶盘结构疲劳寿命的影响程度的基础上,建立配合间隙与疲劳寿命间的函数关系,对疲劳寿命进行稳健性优化,为确定一个最优的榫槽/榫齿配合间隙,提供一套定性的分析方法,是十分有意义的。
基于有限元计算,本文研究和分析了叶盘结构疲劳寿命随榫齿配合间隙的变化规律,综合考虑载荷、材料、榫齿配合间隙等随机因素的不确定性,将二次多项式响应面法与果蝇优化算法相结合,针对叶盘结构的疲劳寿命进行了稳健性优化研究。
2 计算模型和边界条件对叶盘结构的一个循环对称段进行建模,在建模过程中不考虑叶片、盘内部及榫齿处的冷却通气孔,忽略叶根圆角等,见图 1。叶片材料为定向凝固合金DZ125,涡轮盘材料为高温合金GH4169。接触问题采用罚函数法求解,六个榫齿的接触方式为面-面接触,接触摩擦系数取0.3。约束轮盘前后套筒端面的轴向和周向位移,限制叶片榫齿前后端面轴向位移,尽可能真实模拟叶盘结构的工况边界条件。进行网格划分时,在叶盘榫齿处、尺寸变化处进行网格细化,生成有限元模型。忽略涡轮叶片受到的振动应力和气动力,仅考虑离心力和热负荷,离心力按载荷谱中典型功率状态计算,热负荷为相应功率状态的稳态温度场,以n=16300r/min的转速状态为例,温度场计算结果为图 2,将其作为结构分析的边界条件。

|
Fig. 1 Model of blade-disk |

|
Fig. 2 Steady-state temperature field |
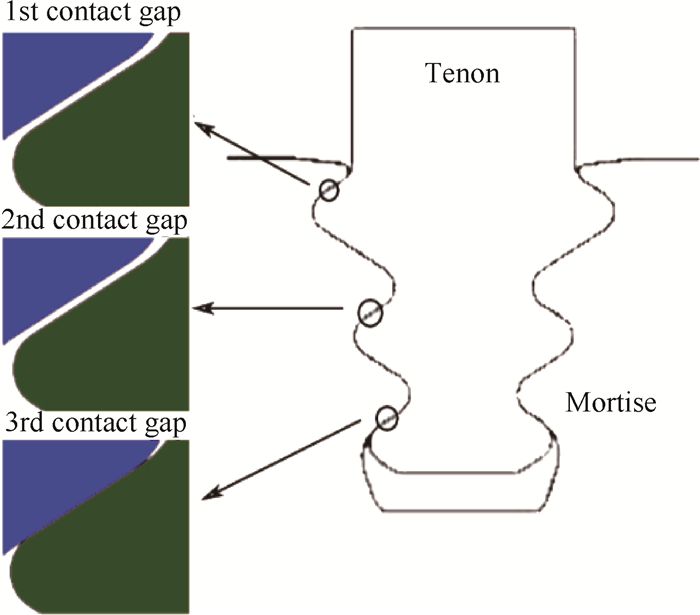
该型航空发动一、二榫齿的理论配合间隙为5μm,第三榫齿啮合,如图 3所示,现采用控制变量法,分别改变一、二榫齿的配合间隙值,来研究配合间隙对叶盘结构榫齿处疲劳寿命的影响,寿命计算仅考虑0~16300r/min~0主循环,图 4~6反映了不同配合间隙下涡轮叶片、涡轮盘的应力状态。
理论上轮盘危险点应处于盘心,但本文研究重点在于榫槽,因此提取榫槽最大应力,盘心处暂不考虑。
|
Fig. 3 Contact gap between tenon and mortise |
|
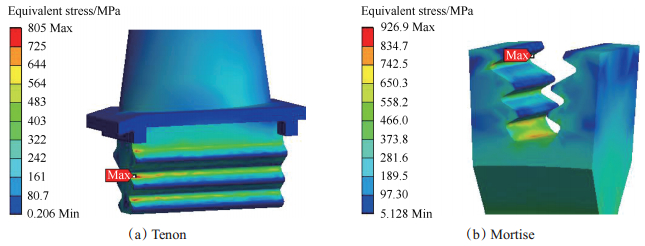
Fig. 4 Stress distribution of blade-disk when contact gap=4μm |
|
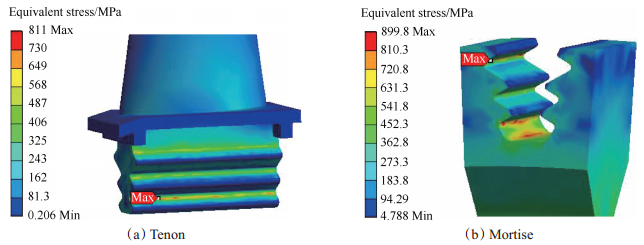
Fig. 5 Stress distribution of blade-disk when contact gap=5μm |
|
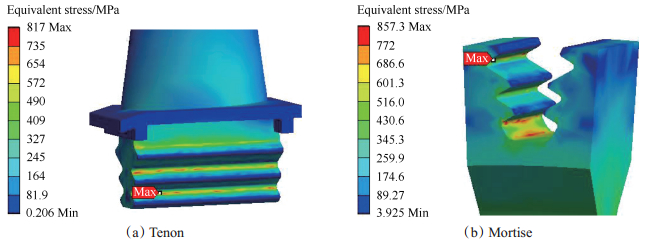
Fig. 6 Stress distribution of blade-disk when contact gap=6μm |
计算结果表明:在理论配合间隙下,叶片最大应力位于在叶背第三榫齿进气边,榫槽最大应力位于第一榫齿进气边。配合间隙为4μm时,叶片的危险点转移至第二榫齿叶背进气边,榫槽处危险点转移至第一榫齿排气边;配合间隙为6μm时,叶片的危险点与理论配合间隙下相比并没有发生改变,只是在应力分布和应力水平上有所区别。显然,配合间隙的变化在影响榫齿处应力状态的同时,叶盘结构的危险点也在不断转移,因此,在不同的应力水平下,叶盘结构的疲劳寿命会存在一定差异,这可能会导致疲劳裂纹萌生、扩展,最终引起疲劳断裂。
疲劳寿命计算采用带Morrow平均应力修正的Manson-Coffin公式。
| $ \frac{{{\varepsilon _{{\rm{eq}}}}}}{2} = \frac{{{{\sigma '}_{\rm{f}}} - {\sigma _{\rm{m}}}}}{E}{\left( {2N} \right)^b} + {{\varepsilon '}_{\rm{f}}}{\left( {2N} \right)^c} $ | (1) |
式中εeq为等效应变幅;σ'f为疲劳强度系数;ε'f为疲劳塑性系数;b为疲劳强度指数;c为疲劳塑性指数;N为低循环疲劳寿命循环数;E为弹性模量,对于正交各向异性材料,该值按照作用力的方向和工况温度选取。
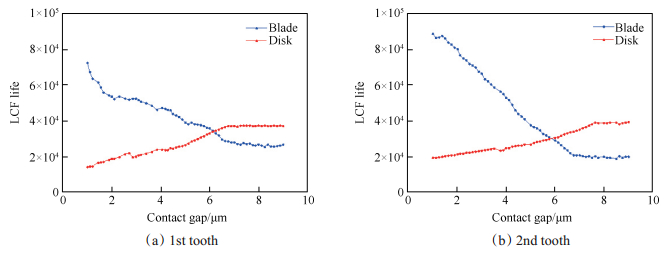
图 7详细给出了1~9μm配合间隙下涡轮叶片、涡轮盘的低循环疲劳寿命变化曲线。
|
Fig. 7 Variation regularity of LCF life with contact gaps |
分析图 7(a)可知,叶片疲劳寿命随第一榫齿配合间隙的增加而呈现出先减小后逐渐稳定的趋势,最大寿命循环为72563,当配合间隙小于2μm时,叶片疲劳寿命大幅下降,配合间隙对叶片疲劳寿命的影响显著,当配合间隙在2~7μm范围变化时,叶片疲劳寿命下降趋势平缓、下降幅度均匀,当配合间隙大于7μm时,叶片疲劳寿命变化趋于稳定,仅在小范围波动,基本不受配合间隙变化的影响,稳定寿命循环约为26571;然而,涡轮盘的疲劳寿命则呈现出相反的变化规律,最小寿命循环为14185,配合间隙小于6.5μm时,涡轮盘疲劳寿命平稳增加,配合间隙大于6.5μm时,寿命值趋于稳定,稳定寿命循环约为37064;与涡轮盘相比,叶片疲劳寿命对第一榫齿的配合间隙敏感程度较高,其疲劳寿命波动范围约为轮盘的2倍。同理可分析图 7(b),叶片和轮盘的低循环疲劳寿命随第二榫齿配合间隙的变化规律与图 7(a)类似,寿命循环最大值88405,叶片疲劳寿命在配合间隙小于6.75μm时逐渐下降,后趋于稳定,稳定寿命循环约为19996;轮盘疲劳寿命在配合间隙小于6.25μm时逐渐上升,后趋于稳定,稳定寿命均值约为36716;值得一提的是,第二榫齿的配合间隙对叶片疲劳寿命影响更加显著,其疲劳寿命变化范围约为轮盘的3.4倍。综合图 7分析结果可得,叶片疲劳寿命对榫齿配合间隙变化的敏感程度高于轮盘,尤其针对第二榫齿的配合间隙;而第一、二榫齿配合间隙对轮盘寿命的影响程度相当。
4 叶盘结构疲劳寿命的概率分析和稳健性优化研究在实际工况下,由于离心力、热载荷、振动负荷等因素不确定性,配合间隙具有一定的随机性,由此导致了榫齿齿面的接触程度存在明显差异,进而影响叶盘结构的疲劳寿命,因此,需要同时考虑载荷、材料参数、配合间隙的不确定性,对其叶盘结构疲劳寿命进行概率分析和稳健性优化。
4.1 基于响应面法的叶盘结构疲劳寿命概率分析直接调用有限元程序进行抽样计算会耗费大量时间,工程上常采用响应面法(Response Surface Methodology,RSM)来代替繁琐的有限元计算,其基本思想是利用有限的样本点拟合出一个简单响应函数来等效真实的输出函数。含交叉项的二次多项式函数拟合精度高,各随机变量能够被充分覆盖,适用于非线性程度较强的情况,因此用其拟合叶盘结构疲劳寿命与随机变量的关系更加合理[15, 16]
| $ N\left( X \right) = {a_0} + \sum\limits_{i = 1}^n {{a_i}{X_i}} + \sum\limits_{i = 1}^n {\sum\limits_{j \ge i}^n {{a_{ij}}{X_i}{X_j}} } $ | (2) |
式中a0,ai,aij均为响应面方程待定系数,Xi代表载荷、材料参数等随机变量,N代表涡轮叶片低循环疲劳寿命。通过数值模拟将主要随机变量引入到寿命预测中,考虑载荷,材料、配合间隙等参数的随机性,分别构造叶片、轮盘疲劳寿命的响应面模型,并进行概率分析。
表 1,2分别给出了工况参数和材料参数的分布规律及其数字特征,假定各变量之间相互独立且服从正态分布,具体来讲,转速ω,盘心温度T1,榫槽温度T2,叶尖温度T3,对流换热系数h代表了工况载荷的不确定性,d1, d2体现了榫槽/榫齿配合间隙的不确定性,弹性模量E,泊松比υ,疲劳强度系数σ'f,热导率λ,线膨胀系数α,疲劳强度指数b,疲劳塑性指数c,表明了材料性能参数存在不确定性。根据所选取的随机变量,在有限元软件中采用中心组合抽样法进行250次抽样计算,其中200组数据用于拟合响应面方程,剩余50组数据用来检验拟合效果。
|
|
Table 1 Random variables of working condition and its distribution |
|
|
Table 2 Random variables of material property and its distribution |
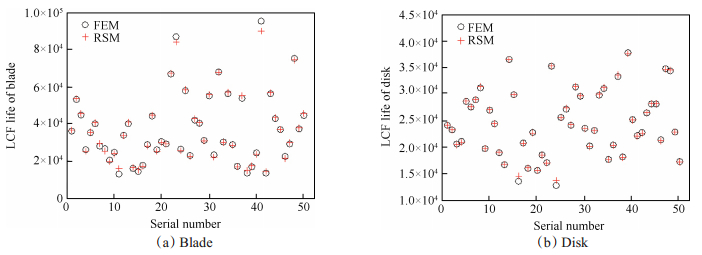
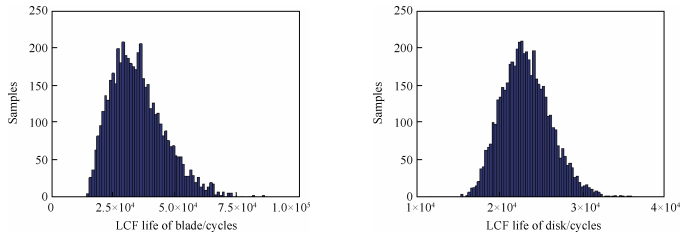
图 8为理论计算结果与响应面方程计算结果的对比,拟合结果表明,叶片和轮盘疲劳寿命的拟合平均相对误差分别为0.98%和0.61%,精度良好。图 9为叶片、轮盘疲劳寿命分布,是利用拟合好的响应面方程代替有限元计算,采用蒙特卡洛法进行1×104次随机抽样得到的,显然,叶片、轮盘疲劳寿命近似服从正态分布,与轮盘相比,叶片疲劳寿命分散性更大。边缘点处的疲劳寿命出现频次低,属于极限状态,实际情况下可能不存在,因此在后续的优化过程不考虑这一部分,利用概率为0.05和0.95的下侧分位数进行限制。
|
Fig. 8 Results comparison between FEM and RSM |
|
Fig. 9 Distribution of LCF life |
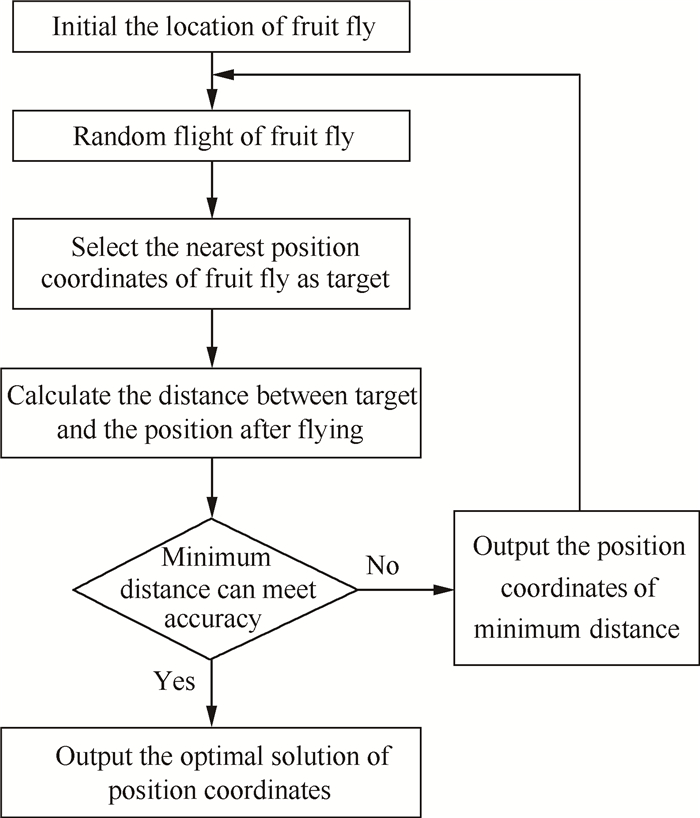
果蝇优化算法(Fruit Fly Optimization Algorithm,FFOA)是台湾学者潘文超提出的一种全局人工智能优化算法,其代码简单,收敛能力强,因此得到了广泛应用[19, 20]。该算法模拟了果蝇的觅食过程,主要流程见图 10,具体步骤如下:
|
Fig. 10 Flowchart of FFOA |
(a)给定果蝇的种群规模Sizepop、最大迭代次数Maxgen、随机初始化种群位置坐标X_axis、Y_axis。
(b)果蝇利用强大的嗅觉定位食物的位置,在算法中,搜索的位置和方向是随机的:
| $ {X_i} = X\_{\rm{axis}} + {\rm{Random}}\;{\rm{value}} $ | (3) |
| $ {Y_i} = Y\_{\rm{axis}} + {\rm{Random}}\;{\rm{value}} $ | (4) |
(c)味道浓度S反映了食物与原点之间的距离D,两者成反比:
| $ {D_i} = \sqrt {X_i^2 + Y_i^2} $ | (5) |
| $ {S_i} = 1/{D_i} $ | (6) |
(d)通过味道浓度判定函数F(s),即迭代函数,筛选出浓度最高的果蝇初始位置:
| $ \left[ {{\rm{bestSmell}}\;{\rm{bestIndex}}} \right] = \max \left( {{\rm{Smel}}{{\rm{l}}_i}} \right) $ | (7) |
(e)最佳浓度位置坐标确定后,果蝇种群利用视觉飞向该位置
| $ {\rm{Smellbest}} = {\rm{bestSmell}} $ | (8) |
| $ X\_{\rm{axis}} = X\left( {{\rm{bestIndex}}} \right) $ | (9) |
| $ Y\_{\rm{axis}} = Y\left( {{\rm{bestIndex}}} \right) $ | (10) |
(f)迭代寻优,重复步骤(b)~(d),每次的计算结果均与前一次迭代结果进行比较,若出现更优浓度,则进行替换,若未出现更优浓度,继续进行迭代计算,直至达到最大迭代次数Maxgen。
几乎现实世界中的所有问题都存在多个目标,随着研究问题的复杂度越来越高,优化目标的个数也在增多,多目标优化理想点法便应运而生,其核心思想是:假设对叶盘结构疲劳寿命稳健性有影响的因素有f1(x),f2(x),…,fn(x),共n个,对于每个目标函数均有其最优值fi* = min fi(x)(x ∈ X),若能够使所有目标函数值均达到最优时的自变量x相同,定义为x*,则称x*为该多目标优化问题的一个理想点,事实上,这种情况出现的概率很小,但可以找出一点x*,权衡偏差|fi(x*)-fi*|,于是构造评价函数,求使其达到最小值时的x*
| $ \min U\left( x \right) = \sum\limits_{i = 1}^n {{\lambda _i}{{\left[ {{f_i}\left( {{x^ * }} \right) - f_i^ * } \right]}^2}} $ | (11) |
随机变量的波动导致叶盘结构疲劳寿命分布具有较大的概率分布区间,因此,需要合理地选取优化可控变量,对涡轮叶片进行稳健性优化研究,稳健性优化基于两点原则:一方面使目标值接近最优均值,另一方面使目标值的波动范围越小越好。解决多目标优化问题的思路主要是通过降维,将其转化为两个单目标优化问题,即分别求解叶片、轮盘疲劳寿命稳健性最优结果,随后采用理想点法求全局最优解。
单目标优化模型选取加权均方差法
| $ \left\{ \begin{array}{l} {\rm{find}}:{d_1},{d_2} \in \left[ {4,6} \right]\\ {f_i} = {\alpha _i}{\left( {\mu - m{u_i}} \right)^2} + \left( {1 - {\alpha _i}} \right){\left( {\sigma - sigm{a_i}} \right)^2}\\ {\mathop{\rm minimize}\nolimits} :{f_i} = f_i^ * \\ {\rm{s}}.{\rm{t}}.{\left( {{N^{0.95}} - {N^{0.05}}} \right)_{i - after}} < {\left( {{N^{0.95}} - {N^{0.05}}} \right)_{i - before}}\\ 4 \le {d_i} \le 6\left( {i = 1,2} \right) \end{array} \right. $ | (12) |
多目标优化模型选取理想点法
| $ \left\{ \begin{array}{l} {\rm{find}}:{d_1},{d_2} \in \left[ {4,6} \right]\\ {\mathop{\rm minimize}\nolimits} :\sum\limits_{i = 1}^2 {{\lambda _i}{{\left[ {{f_i}\left( x \right) - f_i^ * } \right]}^2}} \\ {\rm{s}}.{\rm{t}}.{\left( {{N^{0.95}} - {N^{0.05}}} \right)_{i - after}} < {\left( {{N^{0.95}} - {N^{0.05}}} \right)_{i - before}}\\ 4 \le {d_i} \le 6\left( {i = 1,2} \right) \end{array} \right. $ | (13) |
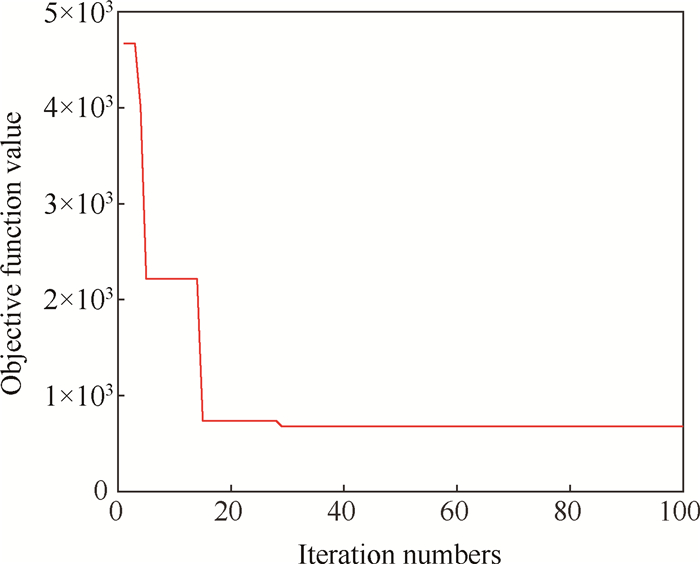
式中mui, sigmai分别为疲劳寿命均值和标准差的设计目标值,αi为综合考虑目标均值与标准差的权重系数,fi*为单目标优化最优值,λi为多目标优化权重系数,i = 1时代表叶片,i = 2时代表轮盘;利用分位数限制寿命分布的概率区间长度,并作为边界约束条件,保证优化后的寿命概率分布区间减小,配合间隙d1,d2作为稳健性优化中的可控随机变量,即设计变量,其余参数作为不可控随机变量。图 11为目标函数的迭代过程,表 3及图 12对比了优化前后结果。
|
Fig. 11 Iteration progress |
|
|
Table 3 Comparison of results before and after optimization |
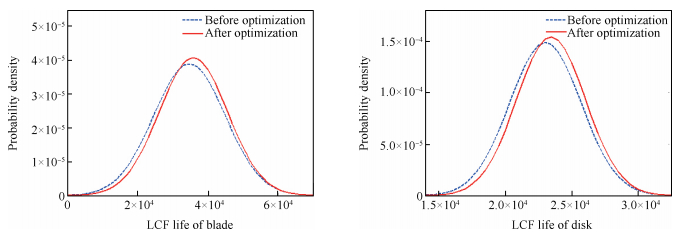
|
Fig. 12 Probability density distributions before and after optimization |
从多目标优化结果的变化趋势上分析,叶片、轮盘疲劳寿命均值分别提高了3.24%、1.93%,疲劳寿命标准差分别降低了4.23%和3.84%,概率区间分别减小了10.13%、8.16%,从数值上看,叶片疲劳寿命均值、标准差、概率区间的变化幅度均高于轮盘,分析其原因可能是叶片疲劳寿命对配合间隙等随机变量的敏感程度更高,这一点也在疲劳寿命随配合间隙的变化规律中得到证实。
多目标稳健性优化方法提高了叶盘结构疲劳寿命抵抗随机变量波动的能力,概率区间的减小能够使寿命预测结果与确定性分析结果的偏差降低,有利于准确的对叶盘结构疲劳寿命进行评估。
5 结论本文在分析配合间隙对叶盘结构疲劳寿命影响的基础上,综合考虑载荷、材料、榫齿配合间隙等随机因素的不确定性,针对叶盘结构的疲劳寿命进行了稳健性优化研究,结论如下:
(1)榫槽/榫齿配合间隙的不确定性在影响榫齿处应力状态、应力水平的同时,叶盘结构的危险点也在不断转移。
(2)榫槽/榫齿配合间隙的不确定性导致叶盘结构的疲劳寿命存在较大分散性,叶片疲劳寿命对榫齿配合间隙变化的敏感程度高于轮盘,尤其针对第二榫齿的配合间隙的变化;而第一、二榫齿配合间隙的变化对轮盘寿命的影响程度大体相近。
(3)多目标优化结果表明:与优化前相比,优化后的叶片、轮盘疲劳寿命均值分别增加了3.24%,1.93%,概率区间分别减小了10.13%,8.16%,提高了叶盘结构的疲劳寿命稳健性。
| [1] |
李其汉, 王延荣. 航空发动机结构强度设计问题[M]. 上海: 上海交通大学出版社, 2014.
(  0) 0) |
| [2] |
李骏, 宋友辉, 刘汉斌, 等. 涡轮叶片-榫头-轮盘的蠕变与低循环疲劳寿命预测[J]. 推进技术, 2015, 36(11): 1699-1704. (LI Jun, SONG You-hui, LIU Han-bin, et al. Creep and Low Cycle Fatigue Life Prediction for Turbine Blade-Tenon-Disk Structure[J]. Journal of Propulsion Technology, 2015, 36(11): 1699-1704.)
(  0) 0) |
| [3] |
唐俊星, 陆山. 轮盘应变疲劳寿命可靠性分析方法[J]. 推进技术, 2005, 26(4): 344-347. (TANG Junxing, LU Shan. Reliability Analysis Method for the Strain Fatigue Life of a Disk[J]. Journal of Propulsion Technology, 2005, 26(4): 344-347.)
(  0) 0) |
| [4] |
彭茂林, 杨自春, 曹跃云, 等. 配合间隙对涡轮盘-片结构的接触响应影响分析[J]. 航空动力学报, 2011, 26(4): 779-786. (  0) 0) |
| [5] |
Guo T, Deng W, Xia Q, et al. An Experiment Method for Measuring the Stress Distribution of the Turbine Blade Tenon[J]. Mechanical Science & Technology for Aerospace Engineering, 2014, 33(8): 1277-1280.
(  0) 0) |
| [6] |
王少飞, 温志勋, 郜玉芬, 等. 配合间隙对涡轮叶片榫头/榫槽接触的影响[J]. 推进技术, 2015, 36(1): 112-118. (WANG Shao-fei, WEN Zhi-xun, GAO Yufen, et al. Effects of Contact Gap on Contact Properties of Turbine Blade Tenon/Mortise[J]. Journal of Propulsion Technology, 2015, 36(1): 112-118.)
(  0) 0) |
| [7] |
魏大盛, 王延荣. 榫连结构几何参数对接触应力的影响[J]. 推进技术, 2010, 31(4): 473-477. (WEI Dasheng, WANG Yan-rong. Effect of Critical Geometrical Parameters on Distribution of Contact Stress in a Tenonjointing[J]. Journal of Propulsion Technology, 2010, 31(4): 473-477.)
(  0) 0) |
| [8] |
黄文周, 张俊杰, 张乘齐. 枞树形榫联接结构参数选取及其与应力的关系[J]. 燃气涡轮试验与研究, 2013(1): 22-25. (  0) 0) |
| [9] |
古远兴, 温卫东, 崔海涛. 高低周载荷作用下燕尾榫结构的微动疲劳寿命预测[J]. 推进技术, 2008, 29(2): 240-243. (GU Yuan-xing, WEN Wei-dong, CUI Hai-tao. Prediction of Fretting Fatigue Life of Dovetail Joint under High-Cycle and Low-Cycle Load[J]. Journal of Propulsion Technology, 2008, 29(2): 240-243.)
(  0) 0) |
| [10] |
张中奎. 镍基单晶涡轮叶片榫头疲劳裂纹扩展寿命研究[J]. 机械强度, 2015(4): 725-729. (  0) 0) |
| [11] |
Yao Z H, Hong C M, Dong J X, et al. Failure Analysis of Gas Turbine Rotor Blades[J]. Failure Analysis & Prevention, 2008, 45(1): 234-244.
(  0) 0) |
| [12] |
Hu D, Wang R, Hou G. Life Assessment of Turbine Components Through Experimental and Numerical Investigations[J]. Journal of Pressure Vessel Technology, 2013, 135(2).
(  0) 0) |
| [13] |
陈立周. 稳健设计[M]. 北京: 机械工业出版社, 2000.
(  0) 0) |
| [14] |
Ghisu T, Parks G T, Jarrett J P, et al. Robust Design Optimization of Gas Turbine Compression Systems[J]. Journal of Propulsion & Power, 1971, 27(2).
(  0) 0) |
| [15] |
周平, 白广忱. 基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计[J]. 航空动力学报, 2013, 28(5): 1013-1018. (  0) 0) |
| [16] |
贺谦, 李元生, 温志勋, 等. 涡轮叶片多学科可靠性及稳健设计优化[J]. 推进技术, 2010, 31(2): 193-197. (HE Qian, LI Yuan-sheng, WEN Zhi-xun, et al. Multidisciplinary Probabilistic and Robust Design Optimization for Turbine Blade[J]. Journal of Propulsion Technology, 2010, 31(2): 193-197.)
(  0) 0) |
| [17] |
刘宏蕾, 陈志英, 周平. 航空发动机套齿结构配合稳健性优化设计[J]. 航空发动机, 2016, 42(6). (  0) 0) |
| [18] |
彭茂林, 杨自春, 曹跃云, 等. 涡轮叶片低周疲劳可靠性稳健设计优化研究[J]. 中国电机工程学报, 2013, 33(11): 104-111. (  0) 0) |
| [19] |
潘文超. 应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J]. 太原理工大学学报(社会科学版), 2011, 29(4): 1-5. (  0) 0) |
| [20] |
Pan W T. A New Fruit Fly Optimization Algorithm: Taking the Financial Distress Model As an Example[J]. Knowledge-Based Systems, 2012, 26(2): 69-74.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

