放热率是燃烧诊断中标识反应区和监控燃烧状态的重要参数之一,其分布是燃烧与湍流相互作用、燃烧不稳定性等过程综合作用的结果。精确测量火焰的放热率分布一直是燃烧学领域研究的热点。随着燃烧器的发展趋于复杂,在诸如工业燃气轮机和航天发动机等复杂燃烧环境中直接测量火焰的放热率变得十分困难[1]。火焰的自发辐射测量作为一种非接触式的测量手段在燃烧诊断中广泛应用。自发辐射诊断技术利用激发态粒子的化学发光,可以表征反应区位置[2],标识反应放热率[3],确定局部当量比[4]。与其他燃烧诊断技术相比[5],它适用于复杂燃烧环境,在其基础上发展起来的化学发光计算断层成像技术可实现瞬时的三维测量[6],具有很大的发展潜力。
对各种类型火焰的化学发光特性及发射光谱的实验研究确定了发光光强与放热率之间存在密切联系。Haber等[7]最早开始研究OH*和CH*化学发光特性与放热率之间的关系。他们研究了本生灯火焰和陶瓷蜂窝平面火焰两种燃烧反应器的化学发光特性,实验结果显示,OH*是标识放热率的良好指示剂,而大范围的工况下CH*并不能很好地反应放热率。Hardalupas[3]和Kathrotia[8]等都在实验研究中发现了OH*和CH*标识放热率的重要作用,但他们的实验仅总结了不同工况下激发态粒子光强分布的变化规律,并没有直接得到光强与放热率的关系。Lauer[9]通过实验测得了湍流预混火焰的放热率,并研究了放热率与OH*和CH*发光光强之间的关系,但是实验结果仅表明光强可以标识总放热率,不能准确体现放热率的分布。Prabasena[10]和Nori[11]也分别通过实验得到了OH*,CH*总光强与总放热率之间的比例关系。国内的研究人员,如王宝璐等[12]还研究了扩散火焰中激发态粒子的光谱特性。
激发态粒子化学反应机理成熟,使数值模拟成为研究火焰化学发光特性的重要方法。Panoutsos[13]对比八种不同的激发态反应模型,研究对冲火焰中OH*和CH*化学发光与燃烧信息之间的关系。结果表明OH*可以表征放热区的位置;峰值比随当量比的单调变化进一步证明了化学发光用于预测当量比的可行性,但是他们并未研究光强与放热率的定量关系。Hossain等[14]对无碳烟情况下的甲烷/丙烷空气对冲扩散火焰进行了数值模拟,探讨反应机理、气体流速、稀释气体以及激发态粒子的输运特性对CH*分布的影响,并得到了总反应放热率与粒子摩尔浓度之间的定量关系,但是他们得出的比例关系仅在气体流速小于1.5m/s时成立,表明使用CH*标识放热率具有一定的局限性。Nikolaou[15]采用数值模拟方法对预混火焰中放热率标识粒子进行研究,虽然他们没有开展激发态粒子标识放热率的工作,但是研究方法是十分有效的参考。
目前,国内外学者对甲烷-空气层流预混火焰的化学发光特性研究还局限于定性阶段,化学发光与放热率之间的定量化研究鲜有报道;对于激发态粒子标识放热率的理论依据,也尚未有深入研究。
本文利用Chemkin对甲烷-空气预混火焰开展数值模拟,研究预混火焰燃烧过程中的放热率标识粒子,重点研究激发态粒子定量化标识放热率的特性,为化学发光定量化测量放热率提供数值依据。
2 甲烷燃烧化学反应机理 2.1 激发态粒子化学反应机理为准确模拟甲烷的燃烧过程,本文考察了包含激发态粒子反应在内的多种甲烷燃烧反应机理。基态粒子化学反应模型采用发展较为成熟的GRIMech 3.0机理[16],共包含53个组分,325个基元反应,完整地描述了基态粒子的产生与消耗,这是模拟激发态粒子浓度分布的基础。
激发态粒子的化学反应机理,是对化学发光进行数值模拟的关键所在。本文重点研究激发态粒子OH*和CH*的分布特性。在甲烷燃烧过程中,激发态化学反应机理并不明确。被广泛认可的OH*的生成反应R1由Gaydon[17]提出,但不同的研究人员在实验中测得的反应速率常数并不相同,本文取Carl等[18]推荐的值k1=4.82×1010exp(-167/RT)。
| $ {\rm{CH}} + {{\rm{O}}_{\rm{2}}} = {\rm{CO}} + {\rm{O}}{{\rm{H}}^ * } $ | (R1) |
Smith等[19]在研究低压H2-Air和CH4-N2O火焰时,发现OH*还存在R2,R3两个生成途径
| $ {\rm{H}} + {\rm{O}} + {\rm{M}} = {\rm{O}}{{\rm{H}}^ * } + {\rm{M}} $ | (R2) |
| $ {\rm{OH}} + {\rm{OH}} + {\rm{H = O}}{{\rm{H}}^ * } + {{\rm{H}}_{\rm{2}}}{\rm{O}} $ | (R3) |
R2,R3的化学反应速率常数分别为:k2 =5.45·(±2.3)×1012和k3=1.45(±0.6)×1012。
早期的多数文献在对甲烷-空气火焰进行数值模拟时,均没有添加R2和R3两个反应;但在最近的文献中,研究发现反应R2的加入可以模拟OH*达到峰值后减速下降过程,与实验符合很好,因此本文采取R1,R2来模拟OH*的生成。
对于CH*的来源,Glass等[20]提出的生成反应R4,R5已得到公认。本文采用最新的Elsamra [21]测得的速率常数,k4 =6.02 × 10-4T4.4exp(-2285.1/RT)和k5 = 6.02×1012exp(475/RT),他们的结果在文献中使用最广。
| $ {{\rm{C}}_{\rm{2}}}{\rm{H}} + {{\rm{O}}_{\rm{2}}} = {\rm{C}}{{\rm{O}}_{\rm{2}}} + {\rm{C}}{{\rm{H}}^ * } $ | (R4) |
| $ {{\rm{C}}_{\rm{2}}}{\rm{H}} + {\rm{O}} = {\rm{CO}} + {\rm{C}}{{\rm{H}}^ * } $ | (R5) |
两种粒子的消耗反应及速率常数已经有公认的结果,本文所采用的OH*和CH*化学反应机理见表 1 [18, 21, 22]。
|
|
Table 1 Chemkical reaction mechanism for excited-state species |
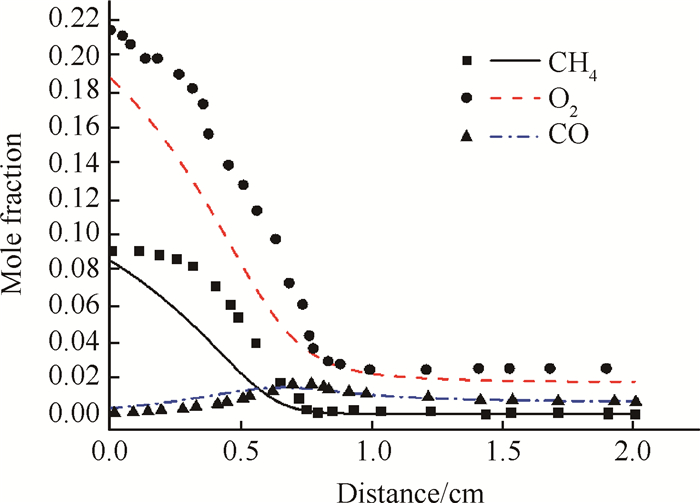
为检验数值模拟的正确性,对照Dupont[23]所开展的甲烷燃烧实验,在相同的工况下进行数值模拟,并与实验结果进行对比。该实验对甲烷-空气预混平面火焰进行研究,测量得到了燃烧过程中组分的浓度分布,其采用的工况如表 2所示。实验工况下,燃烧器上方不同位置处CH4,O2,CO三种组分浓度分布的实验值与模拟值如图 1所示。数值模拟的结果与实验拟合得很好,可以准确模拟三种组分的变化趋势。在小于0.5cm时,CH4和O2的模拟值和实验值存在一些误差,最大误差均小于15%,数值模拟的结果具有较高的准确度。
|
|
Table 2 Flame parameters |
|
Fig. 1 Comparison between experimental data(symbols) and computational results(lines) |
采用两种方法开展激发态粒子标识放热率的研究。第一种方法分析不同基元反应的放热特性,重点研究不同反应的放热贡献率以及反应速率与放热率的关系,为激发态粒子标记放热率提供理论依据。第二种方法提出误差估计系数,研究粒子浓度分布与放热率分布之间存在的差异,确定放热率标记效果较好的目标粒子。针对上述两种方法,定义放热贡献率及误差估计系数两个参数对数据进行分析。
3.1 放热贡献率火焰中粒子的浓度分布由与该粒子生成消耗相关的基元反应决定,若粒子可以很好地标记火焰的放热区,则表明该粒子的生成过程与放热密切相关。燃烧过程中,总放热率Q与基元反应r的放热率qr满足
| $ Q = \sum\limits_r {{q_r}} $ | (1) |
基元反应r的放热率qr由式(2)给出
| $ {q_r} = \int_x {\sum\limits_r {h_{j, r}^0{{\dot \omega }_{j, r}}\left( x \right){\rm{d}}\mathit{x}} } $ | (2) |
式中
若某基元反应放热率大,在总反应放热率中占比重高,则参与该基元反应的粒子与放热率密切相关,可能作为标识放热率的粒子。但是,激发态粒子是反应过程中及其微量的组分,与其相关的反应放热几乎不对总放热率产生贡献;影响总反应放热率的主要是基态粒子的反应。本文首先研究基态粒子对放热率的标识作用,进一步分析基态粒子与激发态粒子之间的关系,从而合理的解释激发态粒子对放热率的标识。
定义放热贡献率fr
| $ {f_r} = \frac{{{q_r}}}{Q} \times 100\% $ | (3) |
研究放热贡献率较大的基元反应,分析影响放热率的重要基态粒子,作为研究激发态粒子的媒介,开展激发态粒子标记放热率的研究。
3.2 误差估计系数层流预混火焰的研究表明,剧烈的化学反应和大量热仅在很窄的反应区产生,火焰的放热率呈单峰分布。为评价粒子分布与放热率分布的相似性,研究粒子标识放热率效果的优劣,定义误差估计系数Z,对标识效果进行衡量
| $ Z\left( v \right) = \int\limits_x {\left| {\frac{{Q\left( x \right)}}{{{Q_{\max }}}} - \frac{{\chi \left( x \right)}}{{{\chi _{\max }}}}} \right|} {\rm{d}}\mathit{x} $ | (4) |
式中Q为放热率,Qmax为放热率峰值;χ是粒子浓度,χmax是对应的峰值。Z越小,则表明该粒子的分布与放热率相似,对放热率的标识效果越好。
4 结果与分析本文对甲烷-空气平面预混火焰进行数值模拟,反应物初始温度为298K,压力为0.1MPa,当量比在0.8~1.4变化,预混气体流速在5~25cm/s变化,研究不同当量比、预混气体流速下粒子浓度与放热率的分布特性。
4.1 基元反应放热特性预混气体出口流速10cm/s工况下,统计0.8~1.2五种当量比下基元反应放热率,表 3统计了不同当量比下放热贡献率fr均较大的9个基元反应。
|
|
Table 3 Primary exothermic reaction at v=10cm/s |
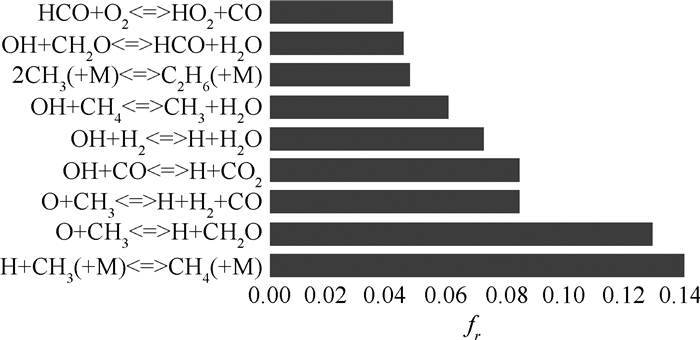
当量比为1.0时,图 2所示为以上9个基元反应的放热贡献率。
|
Fig. 2 Contribution of each reaction to the total heat release rate at φ=1.0, v=10cm/s |
以上9个基元反应放热占总放热比重的71.12%,放热率的分布主要由这些反应决定,参与这些反应的粒子最可能作为放热率的标记物。有OH参加的4个反应R99,R84,R98,R101放热贡献率的和达到26.43%,表明OH与反应放热密切相关;R101和R168两个反应分别为HCO的生成反应与消耗反应,在反应放热中也占较大比例,说明HCO应大量存在于热量释放的区域,可能是放热率的良好指示剂。以上基元反应和参与反应的粒子与放热率关系密切,但是仅由放热贡献并不能确定它们对放热率的标记作用。
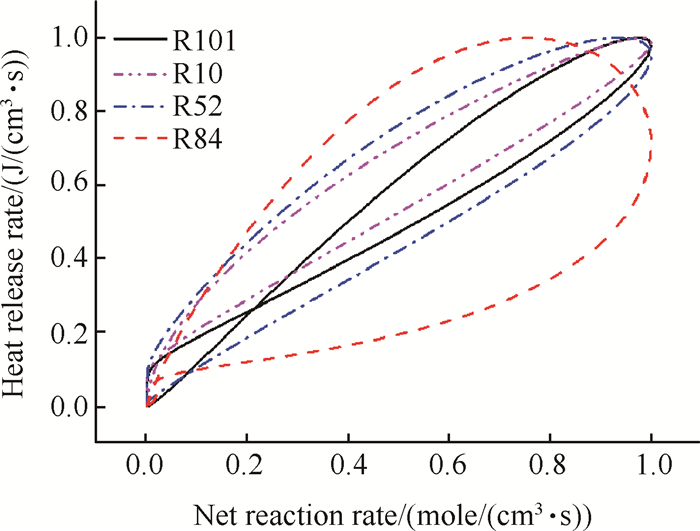
用反应速率峰值及放热率峰值将两者标准化,取横坐标为标准化的基元反应反应速率,纵坐标为标准化的总放热率,对比甲烷燃烧过程中四个主要基元反应的反应速率与放热率的线性关系,得到的结果如图 3所示。
|
Fig. 3 Correlation between HRR and the net reaction rate |
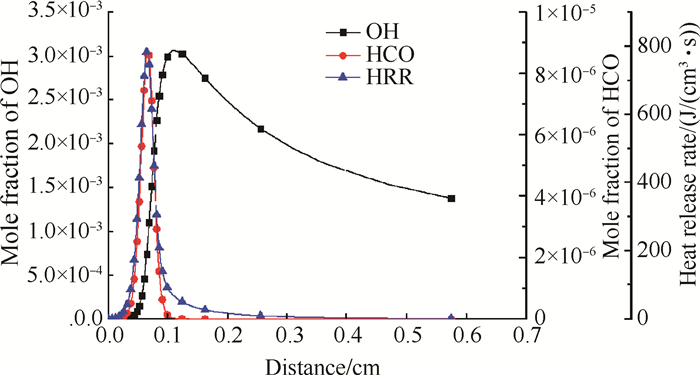
分别对上述四个反应的反应速率-放热率曲线做最小二乘拟合,相关系数分别为0.9755,0.9506,0.8993,0.6349,线性相关性依次降低,只有HCO生成反应OH+CH2O=HCO+H2O(R101)的反应速率与总放热率存在很强的线性相关关系。表明反应在R101反应速率较大的位置,总放热率也大,进一步说明了R101对总放热率的标识作用。而放热比重同样较大其余三个反应则不存在类似的线性关系;图 4所示为OH摩尔分数、HCO摩尔分数与放热率的分布图,可见OH在反应区之后没有马上被消耗,在产物区仍然大量存在;而HCO仅在大量热量释放的剧烈反应区集中存在,这说明HCO适合作为放热的标记粒子,而OH则不适合。
|
Fig. 4 OH, HCO mole fraction profiles and heat release rate |
HCO的生成反应与总放热率分布关系密切,HCO主要由OH和CH2O反应产生,因此,参与反应的OH,CH2O两种粒子的乘积以及HCO都可以标记放热率。
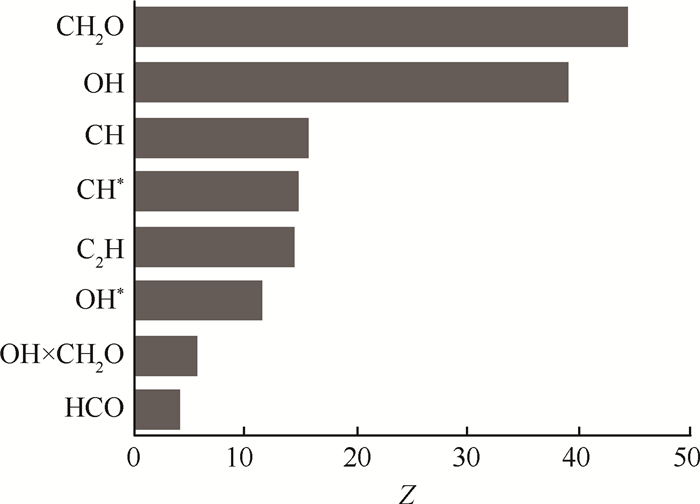
4.2 激发态粒子对放热率标记效果经过上一节的分析,确定HCO,OH×CH2O可以作为放热率的标记物;以上述基态粒子为参照,对比粒子摩尔浓度与总放热率的误差估计系数,研究激发态粒子对放热率的标记效果与理论依据。OH × CH2O,HCO,OH*和CH*以及它们的来源CH,C2H,上述6种粒子的摩尔浓度与总放热率的误差估计系数Z如图 5所示。
|
Fig. 5 Error estimator for different species |
HCO,OH×CH2O浓度分布与放热率分布的误差估计系数最小,两种分布的相似程度最高,印证了基态粒子HCO的生成反应对放热率的标识作用;OH*的误差估计系数与HCO相差不大,其值小于CH*,表明OH*浓度分布与放热率分布相似程度也很高,且高于CH*,因此,OH*对放热率有较好的标记效果。
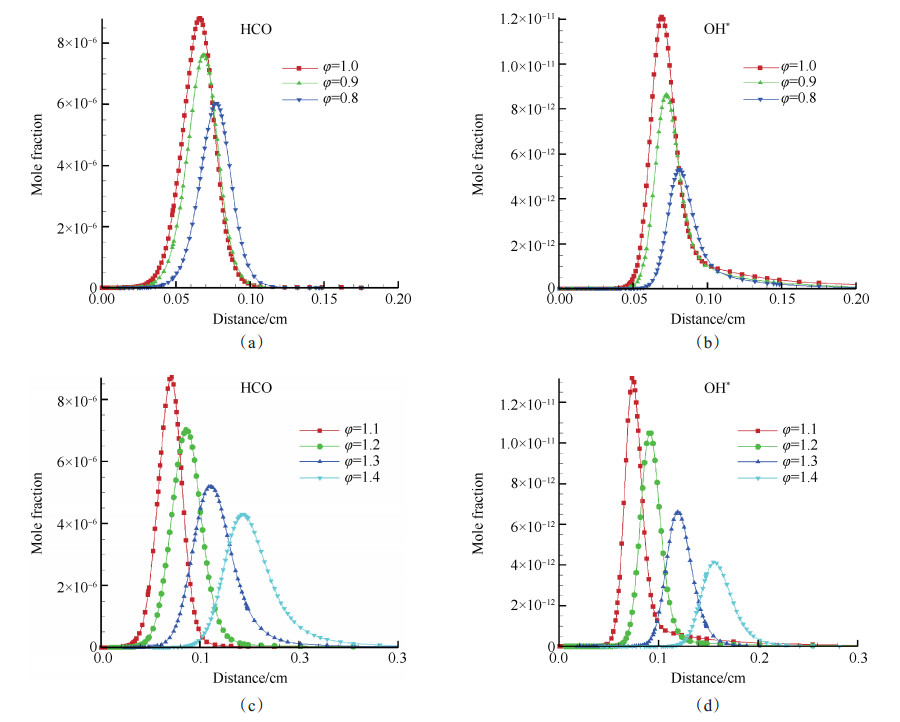
进一步分析气体流速为10cm/s,当量比变化时,HCO与OH*两种粒子的摩尔分数变化,变化规律如图 6所示。
图 6(a)、(b)所示为当量比从0.8变化至1.0,HCO与OH*峰值均逐渐增大,峰值位置左移;图 6(c)、(d)所示为当量比从1.1变化至1.4,HCO与OH*峰值均逐渐减小,峰值位置右移,当量比为1.0时,峰值浓度最大。OH*与HCO的变化规律完全相同。
|
Fig. 6 Mole fraction of HCO and OH* change with the equivalence ratio |
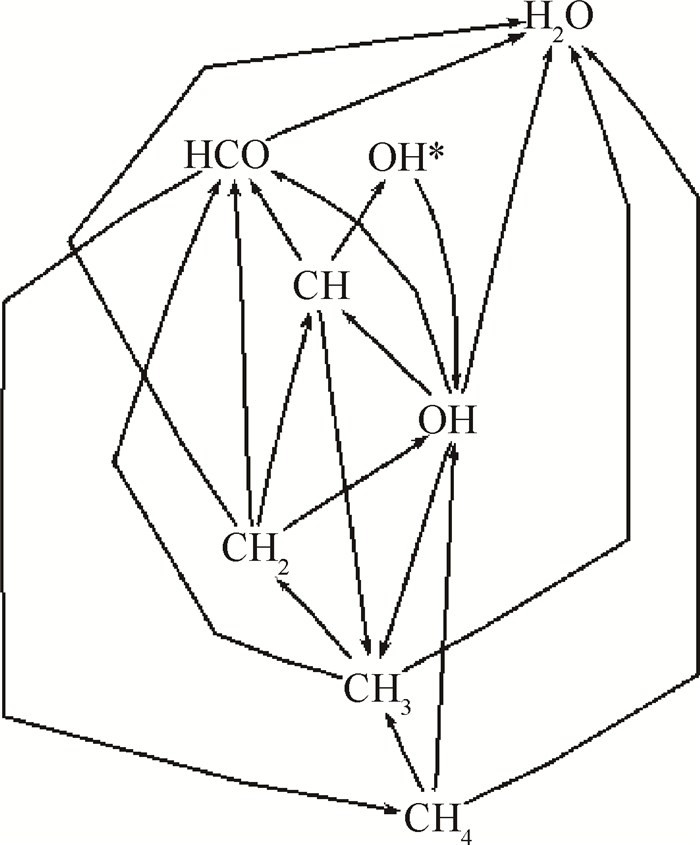
在甲烷燃烧过程中,存在如图 7所示氧化途径。CH及OH两种粒子是HCO的主要来源,HCO的浓度增大及减小由CH和OH决定;OH*主要由CH与O2反应产生,则HCO的浓度将显著影响OH*的浓度,因此随当量比变化,OH*峰值大小、分布位置的变化趋势与HCO相同,激发态粒子OH*在分布上与基态粒子HCO有相同的特性,OH*与HCO一样,对放热率有很好的标记效果。
|
Fig. 7 Observation of the reaction path when OH* is produced from methane-air flame |
利用激发态粒子的化学发光定量化测量反应的放热率,关键是得到激发态粒子浓度与放热率之间的定量关系。对当量比0.9~1.2,同一当量比下出口流速为5~25cm/s的数值模拟结果进行分析,研究OH*浓度峰值与放热率峰值之间的关系。
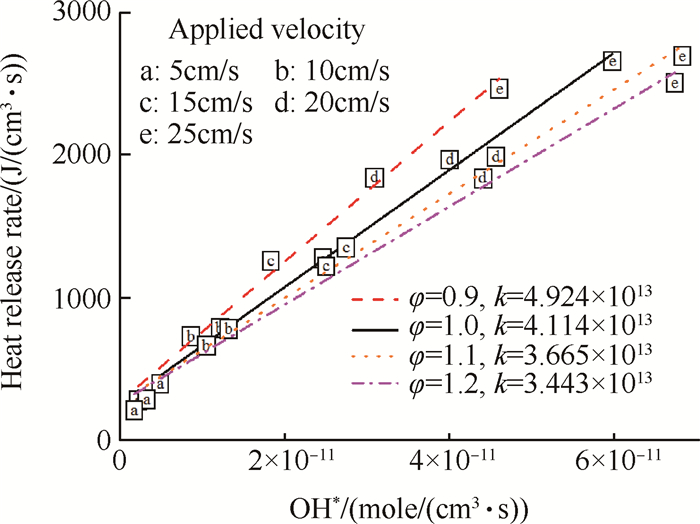
如图 8所示为不同当量比下OH*浓度峰值与放热率峰值拟合曲线。当量比相同,预混气体流速变化时,OH*峰值浓度与峰值放热率呈线性关系,线性相关性系数均大于0.99;比例系数随当量比单调变化,当量比越大,比例系数越小。在95%置信区间下,比例系数k与当量比φ的拟合函数为
| $ k = 1.45 \times {10^{14}}{\varphi ^2} - 3.53 \times {10^{14}}\varphi + 2.50 \times {10^{14}} $ |
|
Fig. 8 Correlation between peak concentration of OH* and peak of heat release rate |
由该定量关系,即可用OH*的浓度峰值预测不同当量比下的放热率峰值。
5 结论通过本文研究,得到如下结论:
(1)HCO的生成与消耗反应在整个反应放热中占较大比重,HCO大量存在于放热区域,可作为放热率的标记粒子。
(2)虽然OH*的生成反应几乎不产生热量,但是OH*的浓度分布随当量比的变化规律与HCO十分相似,两者峰值浓度均在当量比等于1.0时达到最大值,OH*也是标记放热率的重要粒子。
(3)OH*浓度分布与放热率分布的相似性高于CH*,OH*标识放热率的效果优于CH*。
(4)在同一当量比下,随流速变化,OH*浓度峰值与放热率峰值呈线性关系;线性比例系数随当量比变化,当量比越大,比例系数越小,两者的函数关系为:k=(1.45φ2-3.53φ+2.50)×1014。在确定燃烧当量比的情况下,可由OH*浓度峰值定量化测量反应的放热率峰值。
在实际应用中,利用激发态粒子的自发辐射强度进行燃烧诊断;而自发辐射光强分布与粒子浓度分布之间的定量关系还需进一步研究,这是未来研究的重点。
| [1] |
Gazi A, Vourliotakis G, Skevis G, et al. Assessment of Chemical Markers for Heat Release Rate Correlations in Laminar Premixed Flames[J]. Combustion Science and Technology, 2013, 185(10): 1482-1508. DOI:10.1080/00102202.2013.804517
(  0) 0) |
| [2] |
Kojima J, Ikeda Y, Nakajima T. Basic Aspects of OH (A), CH(A), and C2(d) Chemiluminescence in the Reaction Zone of Laminar Methane-Air Premixed Flames[J]. Combustion and Flame, 2004, 140(1-2): 34-45.
(  0) 0) |
| [3] |
Hardalupas Y, Orain M. Local Measurements of the Time-Dependent Heat Release Rate and Equivalence Ratio Using Chemiluminescent Emission from a Flame[J]. Combustion and Flame, 2004, 139(3): 188-207. DOI:10.1016/j.combustflame.2004.08.003
(  0) 0) |
| [4] |
Tripathi M M, Krishnan S R, Srinivasan K K, et al. Chemiluminescence-Based Multivariate Sensing of Local Equivalence Ratios in Premixed Atmospheric Methane–Air Flames[J]. Fuel, 2012, 93: 684-691. DOI:10.1016/j.fuel.2011.08.038
(  0) 0) |
| [5] |
范周琴, 刘卫东, 林志勇, 等. 凹腔喷射超声速燃烧火焰结构实验研究[J]. 推进技术, 2013, 34(1): 62-68. (FAN Zhou-qin, LIU Wei-dong, LIN Zhi-yong, et al. Experimental Investigation on Supersonic Combustion Flame Structure with Cavity Injectors[J]. Journal of Propulsion Technology, 2013, 34(1): 62-68.)
(  0) 0) |
| [6] |
Floyd J, Geipel P, Kempf A M. Computed Tomography of Chemiluminescence (CTC) : Instantaneous 3D Measurements and Phantom Studies of a Turbulent Opposed Jet Flame[J]. Combustion and Flame, 2011, 158(2): 376-391. DOI:10.1016/j.combustflame.2010.09.006
(  0) 0) |
| [7] |
Haber L C, Vandsburger U, Saunders W R, et al. An Experimental Examination of the Relationship Between Chemiluminescent Light Emissions and Heat-Release Rate Under Non-Adiabatic Conditions[R]. ASME 2000-GT-0121.
(  0) 0) |
| [8] |
Kathrotia T, Riedel U, Warnatz J. A Numerical Study on the Relation of OH*, CH*, and C2* Chemiluminescence and Heat Release in Premixed Methane Flames [C]. Vienna: Proceedings of the European Combustion Meeting, 2009.
(  0) 0) |
| [9] |
Lauer M, Sattelmayer T. On the Adequacy of Chemiluminescence as a Measure for Heat Release in Turbulent Flames with Mixture Gradients[J]. Journal of Engineering for Gas Turbine and Power, 2010, 132(1): 1-8.
(  0) 0) |
| [10] |
Prabasena B, Röder M, Kathrotia T, et al. Strain Rate and Fuel Composition Dependence of Chemiluminescent Species Profiles in Non-Premixed Counterflow Flames: Comparison with Model Results[J]. Apply Physics B, 2012, 107(3): 561-569. DOI:10.1007/s00340-012-4989-6
(  0) 0) |
| [11] |
Nori V N, Seitzman J M. CH* Chemiluminescence Modeling for Combustion Diagnostics[J]. Proceedings of the Combustion Institute, 2009, 32(1): 895-903. DOI:10.1016/j.proci.2008.05.050
(  0) 0) |
| [12] |
王宝璐, 额日其太. 甲烷反扩散火焰光谱特性实验研究[J]. 推进技术, 2016, 37(1): 105-111. (WANG Bao-lu, Eriqitai. Experiment Study of Inverse Methane/ Air Diffusion Flame Emission Spectrum Properties[J]. Journal of Propulsion Technology, 2016, 37(1): 105-111.)
(  0) 0) |
| [13] |
Panoutsos C S, Hardalupas Y, Taylor A M K P. Numerical Evaluation of Equivalence Ratio Measurement Using OH* and CH* Chemiluminescence in Premixed and Non – Premixed Methane-Air Flames[J]. Combustion and Flame, 2009, 156(2): 273-291. DOI:10.1016/j.combustflame.2008.11.008
(  0) 0) |
| [14] |
Hossain A, Nakamura Y. A Numerical Study on the Ability to Predict the Heat Release Rate Using CH* Chemiluminescence in Non-Sooting Counterflow Diffusion Flames[J]. Combustion and Flame, 2014, 161(1): 162-172. DOI:10.1016/j.combustflame.2013.08.021
(  0) 0) |
| [15] |
Nikolaou Z M, Swaminathan N. Heat Release Rate Markers for Premixed Combustion[J]. Combustion and Flame, 2014, 161(12): 3073-3084. DOI:10.1016/j.combustflame.2014.05.019
(  0) 0) |
| [16] |
姚强, 李水清, 王宇. 燃烧学导论:概念与应用(第二版)[M]. 北京: 清华大学出版社, 2014.
(  0) 0) |
| [17] |
Gaydon A G. Spectroscopy of Flames[M]. London: Chapman and Hall, 1957.
(  0) 0) |
| [18] |
Carl S A, Poppel M V, Peeters J. Identification of the CH+O2 →OH(A)+CO Reaction as the Source of OH(AX) Chemiluminescence in C2H2/O/H/O2 Atomic Flames and Determination of Its Absolute Rate Constant Over the Range T=296 to 511K[J]. Journal of Physical Chemistry A, 2003, 107(50): 11001-11007. DOI:10.1021/jp035568j
(  0) 0) |
| [19] |
Smith G P, Park C, Schneiderman J, et al. C2 Swan Band Laser-Induced Fluorescence and Chemiluminescence in Low-Pressure Hydrocarbon Flame[J]. Combustion and Flame, 2005, 141(1-2): 66-77. DOI:10.1016/j.combustflame.2004.12.010
(  0) 0) |
| [20] |
Glass G P, Kistiakowsky G B, Michael J V, et al. Mechanism of the Acetylene-Oxygen Reaction in Shock Waves[J]. The Journal of Chemistry Physics, 1965, 42(2): 608-621. DOI:10.1063/1.1695981
(  0) 0) |
| [21] |
Elsamra R M I, Vranckx S, Carl S A. CH(A2Δ)Formation in Hydrocarbon Combustion: the Temperature Dependence of the Rate Constant of the Reaction C2H+O2→ CH(A2Δ)+ CO2[J]. Journal of Physical Chemistry A, 2005, 109(45): 10287-10293. DOI:10.1021/jp053684b
(  0) 0) |
| [22] |
Tamura M, Berg P A, Harrington J E, et al. Collisional Quenching of CH(A), OH(A), and NO(A) in Low Pressure Hydrocarbon Flames[J]. Combustion and Flame, 1998, 114(3-4): 502-514. DOI:10.1016/S0010-2180(97)00324-6
(  0) 0) |
| [23] |
Dupont L, Bakali A E, Pauwels J F, et al. Investigation of Stoichiometric Methne/Air/Benzene(1.5%)and Methane/Air Low Pressure Flames[J]. Combustion and Flame, 2003, 135(1-2): 171-183. DOI:10.1016/S0010-2180(03)00158-5
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

