2. 中国科学院 可再生能源重点实验室,广东 广州 510640;
3. 广东省新能源和可再生能源研究开发与应用重点实验室,广东 广州 510640;
4. 中国科学院大学,北京 100049
2. Key Laboratory of Renewable Energy, Chinese Academy of Sciences, Guangzhou 510640, China;
3. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development, Guangzhou 510640, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
大推力(高能量密度燃烧)、高推重比(温度、压力及流速不断增加)、高效率是未来先进发动机发展的主要目标。与常规的固体、气体燃料相比,液体碳氢燃料具有很高的能量密度和热沉,且容易存储和便于携带,在一些有特殊应用环境和高功率密度输出要求的前沿科技领域具有更广阔的应用前景,如超声速发动机、各种尺度的飞行器、推进器等[1, 2]。在这些装置中,液体碳氢燃料在一个被高温燃气充分加热的进气(冷却)通道中提前吸热裂解成为燃烧性能优良的小分子碳氢燃料或者中间体[3, 4],提高了燃料在燃烧室的燃烧效率,而且由于液体燃料强烈的化学吸热能力,为燃烧器部件提供了优良的冷却和保护作用[5, 6]。
发动机工作时,燃烧室壁面热流很高。通道的几何尺寸、壁面材料对燃料的对流传热也有着非常重要的影响,并最终影响其裂解特性。因此,针对碳氢燃料主动冷却通道内的流动传热以及裂解反应进行数值研究,可以综合考虑各个因素的影响,并准确把握通道内燃料裂解特性以及规律,这对深入研究超燃冲压发动机的主动再生冷却机理,和发动机部件结构设计及运行优化等有着重要意义。
当前国内外许多学者[7~13]对碳氢燃料在主动冷却通道中的裂解开展了大量实验和数值模拟方面的研究。而目前数值研究主要采用一步总包反应机理。Ward等[8]在假设产物比例保持不变的基础上,提出了PPD(Proportional Product Distribution)裂解反应机理并进行了二维稳态数值模拟,但该机理只适用于低裂解率的情况,在高裂解率时存在较大偏差[9]。鲍文等[10]采用Ward的PPD机理建立了一维的瞬态模型研究了正癸烷在主动冷却通道中的裂解过程。Nicolas Gascoin等[11]采用一个包含1185个化学反应的详细机理建立了一维瞬态模型来研究正十二烷的裂解过程,由于详细机理需要知道所有的反应路径以及反应速率常数,因此化学计算耗时很长,如推广到二维或三维计算有一定难度。侯凌云等[12]基于实验结果,建立了一步裂解总包反应机理,并引入了两相流数值模拟。这些研究主要考虑主动冷却通道内部的各化学组分的变化,而冷却通道的整体吸热性能应综合考虑通道内部化学反应和壁面换热的耦合作用。
本文利用控制容积法,采用自行构建的正庚烷详细基元化学反应机理研究二维主动冷却通道内化学反应及壁面传热特性,探索了热解反应与壁面传热、流动之间的耦合作用规律,以此为高超声速发动机冷却结构的设计提供有效的指导。
2 数值模型 2.1 物理模型冷却通道假设为圆管如图 1所示,全长1000mm; 流体的入口温度为Tin;min为入口的质量流量;忽略管壁的厚度,管壁的温度边界条件为Tw;x为流动方向。
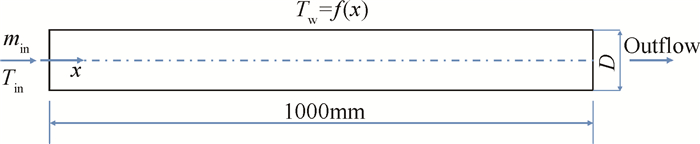
|
Fig. 1 Schematic of physical model |
质量守恒方程
| $ \nabla \cdot \left( {\rho u} \right) = 0 $ | (1) |
动量守恒方程
| $ \nabla \cdot \left( {\rho uu} \right) = - \nabla p - \nabla \cdot \tau $ | (2) |
组分守恒方程
| $ \nabla \cdot \left( {\rho {Y_i}u} \right) = - \nabla \cdot \left( {\rho {Y_i}{u_{{\rm{d}}, \mathit{i}}}} \right) - {S_i} $ | (3) |
能量守恒方程
| $ \nabla \cdot \left( {\rho u{e_{\rm{t}}}} \right) = - \nabla \cdot \left( {\lambda \nabla T} \right) - \nabla \cdot \left( {\rho u} \right) $ | (4) |
式中ρ为流体密度,u为速度,p为流体压力,τ为黏性应力项,Yi组分i的质量分数,ud, i为组分i的扩散速度,Si为化学反应源项,et为流体内能,λ为热传导系数。
本文根据实际工况,将通道的入口设置为质量流量入口(Mass-flow inlet)的边界条件。通道出口设置为自由流动出口(Outflow),满足以下条件
| $ \frac{{\partial u}}{{\partial x}} = \frac{{\partial v}}{{\partial y}} = \frac{{\partial T}}{{\partial x}} = 0 $ | (5) |
式中u和v为轴向和径向的速度。高温壁面的边界条件满足以下条件
| $ u = v = 0 $ | (6) |
| $ T = f\left( x \right) $ | (7) |
计算所采用的离散格式为二阶迎风差分,采用压力速度的耦合算法进行层流化学反应的计算。
2.3 简化反应动力学机理本文所采用的机理是参照Held等[14]和劳伦斯利弗莫尔国家实验室(LLNL)Curran[15]等提出的详细基元反应,简化得到一个46个组分374步反应的详细正庚烷裂解机理。计算中物性参数以tran和therm文件导入Fluent中,与流动传热计算过程耦合。利用该机理模拟文献[16]中的实验工况,图 2为主要组分的产率对比,结果表明本文所采用的机理与实验结果吻合较好,可以用于后续的计算。
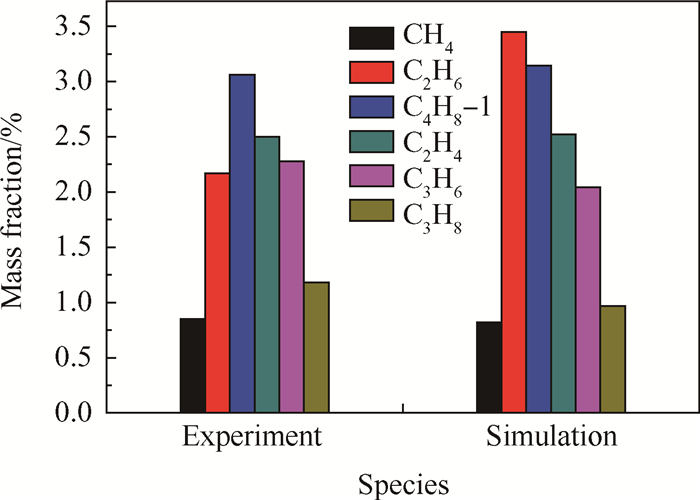
|
Fig. 2 Comparison between simulation and experimental results |
本文在数值模拟之前,首先对网格独立性进行了分析。如表 1所示,Case A为径向和轴向网格数分别为15,3×103,总数为4.5×104的四边形结构化网格,而Case B是在Case 1计算结果的基础上对近壁面处和入口处加密后得到的总数为76126的计算网格。通过对比,网格数目增加将近一倍时,计算结果的偏差仅为0.014%。考虑计算精度和计算速度,最终选择径向比例为0.9,轴向比例为1.0,总网格数目为4.5×104的结构化网格。
|
|
Table 1 Grids for calculation |
表 2为本文中的所有计算工况。
|
|
Table 2 Conditions of numerical cases |
首先,通过数值模拟来研究考虑裂解反应、不考虑裂解反应两种条件下的流动传热情况,并进行对比分析。不考虑裂解反应的条件下,计算过程不求解组分方程。计算工况如表 2中的工况3所示。
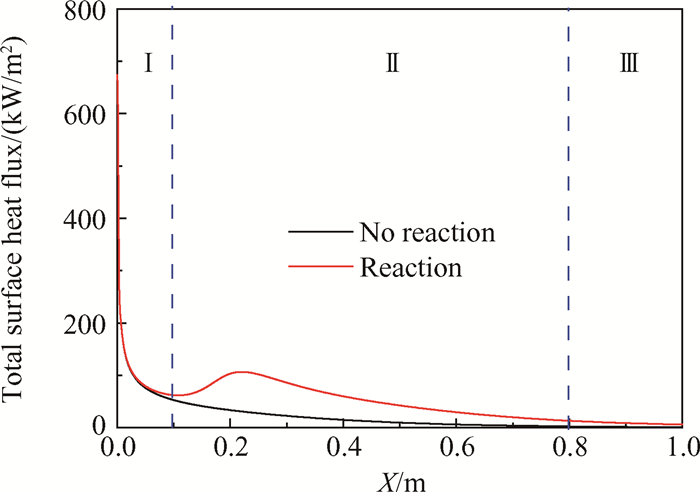
图 3(a)、图 3(b)分别给出了两种条件下通道内温度分布云图,对比两图可以明显看出考虑裂解反应时通道内流体温度较低。图 4为通道中心轴线温度的沿程变化,可以看出约从x=0.2m处起正庚烷的裂解反应速率加快,裂解反应对流体温度的影响逐渐明显。两种计算工况下,流体的最大温差为63K。图 5为壁面向燃料传递热流的沿程变化,从图中可以看出考虑裂解反应时,燃料能够从高温壁面吸收更多热量。综上可知,燃料流经高温壁面发生裂解反应能够有效吸收壁面的热量,起到热防护的作用。定义单位时间内面积为dSw的壁面微元向通道内部流体传递的热量为Qw
| $ {Q_{\rm{w}}} = \int {q{\rm{d}}{\mathit{S}_{\rm{w}}}} $ | (8) |
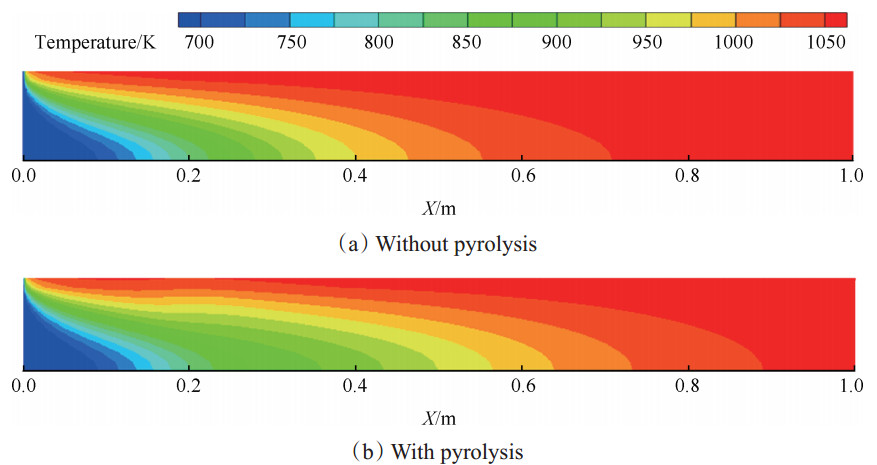
|
Fig. 3 Contours of temperature in tube(figure not to scale) |
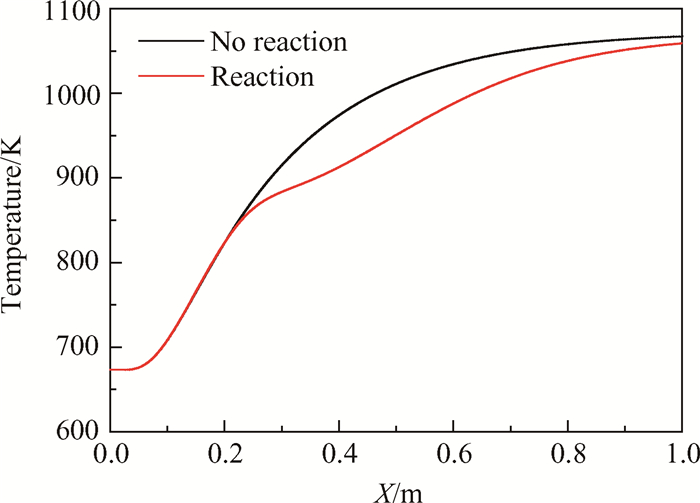
|
Fig. 4 Comparison of temperature of axis in tube with/without pyrolysis |
|
Fig. 5 Comparison of surface heat flux with/without pyrolysis |
式中q为面积微元的热流密度。
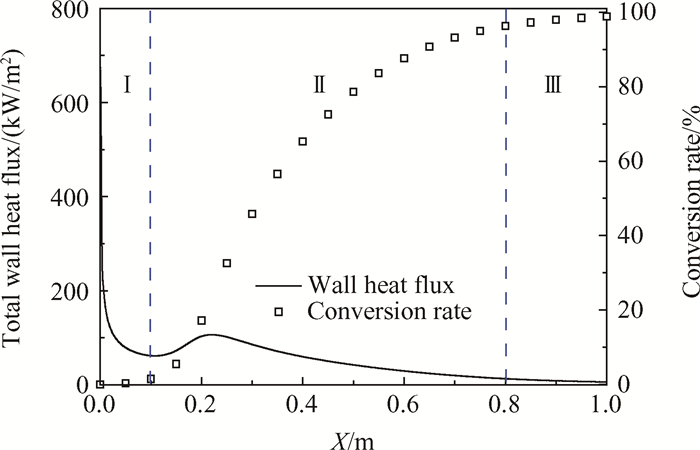
图 6为考虑裂解反应时通道内正庚烷积分平均转化率以及壁面热流传递量的沿程变化。根据以上模拟结果,可以将主动冷却通道按其化学反应特征以及传热特性划分为以下三个区域:
|
Fig. 6 Variations of wall heat flux and conversion rate of nheptane along the tube |
Ⅰ区:热入口区。从入口到壁面传递热流的极小值处,即0~0.1m段,正庚烷处于预热段,燃料从高温壁面吸收热量,为物理吸热过程。
Ⅱ区:主反应区。其中从壁面热流的极小值处到极大值处,即0.1~0.2m段,正庚烷开始裂解。0.2~0.8m段,燃料裂解率开始升高,并且逐渐达到反应平衡状态。
Ⅲ区:充分反应区。反应后的高温产物与壁面之间达到热平衡。
根据式(8)可以算出,燃料流经主动冷却通道共吸收壁面热流为158.6W,其中Ⅰ区吸热36.6W,占总吸收热流的23.07%,Ⅱ区116.4W,占73.39%,Ⅲ区5.6W,占3.54%。
5 换热特性的影响因素分析 5.1 入口温度的影响本节给出了三组不同入口温度的计算工况,如表 2中的工况1,2,3。
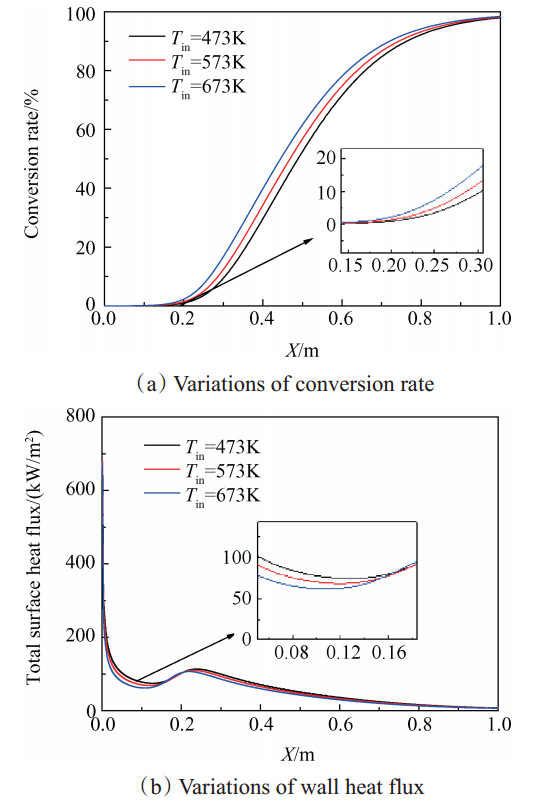
从图 7(a)中可以看出,较高的入口温度会使燃料的裂解起始位置小幅提前,但在不同的入口温度条件下,正庚烷的裂解起始位置基本都位于x=0.2m处。三种工况下正庚烷的转化率在反应未达到平衡前(0.2m<x<0.8m),在相同位置处入口温度越高转化率也较高,但三种工况下最终转化率分别为98.01%,98.24%,98.47%。上述计算结果表明,入口温度对反应最终转化率的影响很小。
|
Fig. 7 Variations of performance at different inlet temperatures |
图 7(b)为壁面热流密度沿程变化,可以看出入口温度对壁面传热的影响主要在通道的入口段,即Ⅰ区(物理吸热)。入口温度越低,燃料从壁面吸收的热流也相应越多。但当燃料发生裂解反应后,入口温度的影响基本消除。表 3是根据公式
|
|
Table 3 Computational results for different inlet temperature |
本节给出了四组不同运行压力的计算工况,如表 2中的工况4,5,6,7。
图 8(a)和图 8(b)分别为不同压力下正庚烷的转化率和壁面热流密度沿流动方向的变化情况。从图 8(a)中可以看出,燃料的裂解率随着运行压力的升高而提高,当压力从0.1MPa升高到0.5MPa,转化率从57.24%升高到91.1%,而当压力从0.5MPa升高到2MPa,转化率仅从91.1%升高到98.03%。根据公式

|
Fig. 8 Variations of performance at different pressures |
|
|
Table 4 Variation of wall heat fluxes and heat absorption by zone Ⅰ |
本节给出了三组不同壁面温度的计算工况,如表 2中的工况6,8,9。
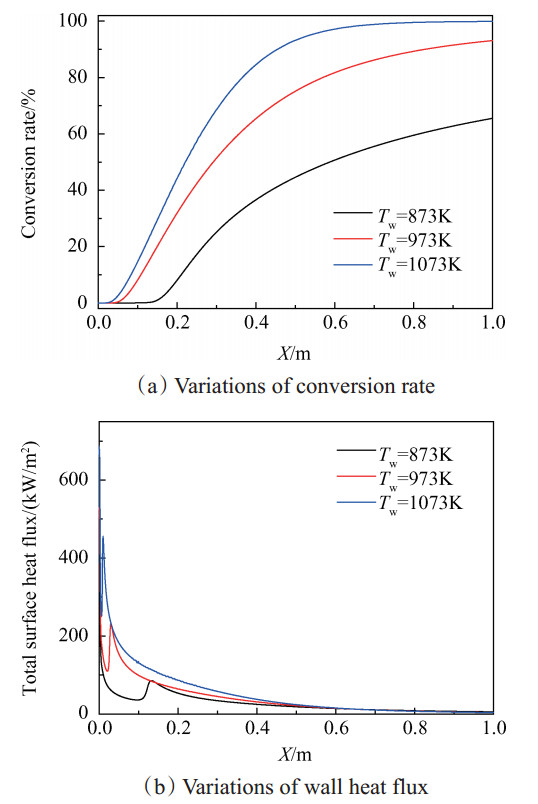
图 9(a)为正庚烷转化率沿程变化,壁面温度的升高有利于正庚烷的裂解。如表 5,当壁面温度从873K升高到1073K,燃料的转化率从65.51%升高到99.91%。从图 9(b)中也可以看出随着壁面温度的升高,燃料的裂解起始位置也逐渐提前,从而导致Ⅰ区的长度缩短,根据式(8)计算可知,其物理吸热量下降。如表 5所示,随着壁面温度的升高,物理吸热量和其所占的百分比都随之降低。说明壁面温度的升高在促进化学热沉释放的同时也一定程度上抑制了物理热沉的释放。根据文献[18]对温度非均匀系数的定义,如式(9)。可计算出三种工况下通道的出口温度非均匀系数分别为2.32%,1.24%和0.79%。表明燃料在较低转化率的工况下通道出口温度的不均匀性比较强。
| $ {R_T} = \frac{{{T_{\max }} - {T_{\min }}}}{{{T_{{\rm{mean}}}}}} \times 100\% $ | (9) |
|
Fig. 9 Variations of performance at different wall temperatures |
|
|
Table 5 Computational results for different wall temperatures |
式中Tmax为某一位置的最高温度,Tmin为该位置的最低温度,Tmean为该处的积分平均温度。
5.4 通道尺寸的影响本节给出了三组不同通道直径的计算工况,如表 2中的工况7,10,11。
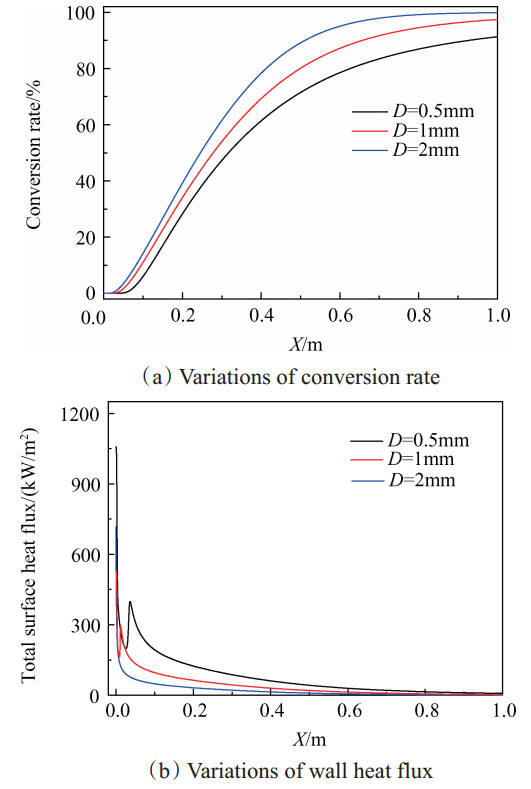
图 10(a)为正庚烷转化率沿程变化,可以看出,在壁面温度和入口质量流率相同的条件下通道直径的增大促进了燃料的转化率,主要原因是由于在大通道中燃料的停留时间增长。通道直径从0.5mm增加到2mm,燃料的停留时间从0.03s增加到0.45s。从图 10(b)中可以看出,随着管径的增大壁面热流的极小值与极大值位置前移。在管径为0.5mm的通道中,可以明显地观察到物理吸热段和化学吸热段;当管径增大到1mm时,由于停留时间的增加,Ⅰ区长度明显缩短,燃料的裂解起始位置提前;当通道管径增大到2mm时,由于停留时间长,Ⅰ区的长度已经非常短,即燃料在入口位置附近已经开始发生裂解反应。表 6为三种工况下燃料吸收壁面热流的变化,可以看出燃料吸收的热流并未与通道的表面积呈线性增加的关系,小通道中壁面传递的平均热流最大。在D=0.5mm的通道中Ⅰ区的吸热为14.28W,占总吸热量的11.8%;在D=1mm的通道中Ⅰ区的吸热为8.17W,占总吸热量的6.61%。
|
Fig. 10 Variations of performance with different tube diameters |
|
|
Table 6 Computational results for different diameters |
如表 6所示,三种通道的出口温度非均匀系数分别为1.15%,0.8%,0.5%。表明在质量流率相同的工况下,小通道内流速高,温度不均匀性强,对流换热强,使得高温壁面的热量能够更快速地被燃料吸收。
5.5 压力与通道尺度的耦合作用由以上对各个影响因素的分析可知,入口温度的影响较小。本节在保持壁面温度和入口温度恒定的条件下,探索运行压力和通道尺度的耦合作用。选取表 2中的工况5,6,7,10,11,13,14,16,17进行综合分析。
根据式(8),并结合通道中的对流传热过程,可知冷却通道通过壁面向燃料传递的热量可表示为
| $ {\mathit{Q}_{\rm{t}}} = \overline {{h_{\rm{s}}}} \left( {{T_{\rm{w}}} - {T_{\rm{f}}}} \right){S_{\rm{w}}} $ | (10) |
式中
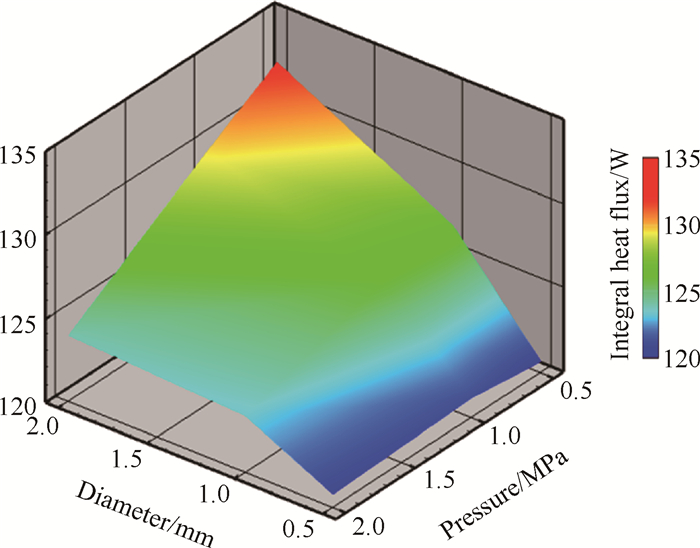
从表 7和图 11可知,当通道半径从0.5mm增大到2mm时,通道表面积Sw增大了16倍,但通道整体的吸热量并未随表面积的增大而显著提高。根据前几节的分析可知,在壁面温度一定的情况下,式(10)中(Tw -Tf)项对通道整体的吸热量Qt的影响很小。
|
|
Table 7 Variations of integral wall heat flux under different conditions(W) |
|
Fig. 11 Variations of integral wall heat flux |
|
|
Table 8 Variations of average wall heat flux under different conditions(W/m2) |
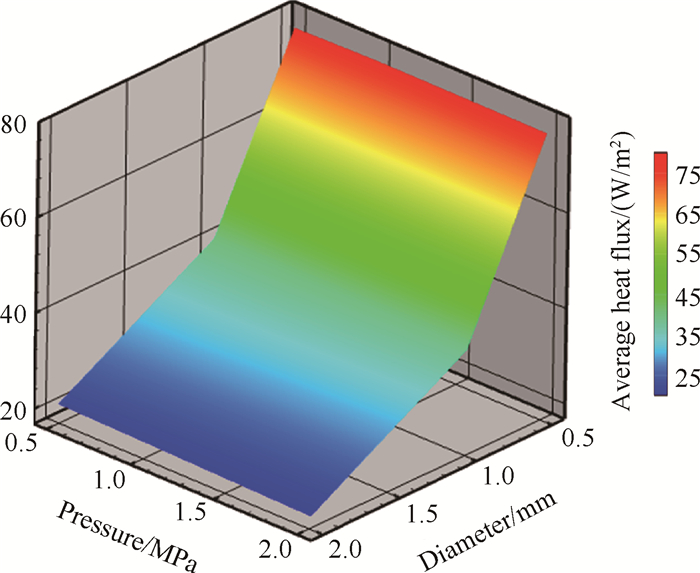
图 12是冷却通道单位面积的传热量,从图中可以看出在相同的运行压力下小通道的单位面积换热特性要明显优于大通道。这说明通道尺寸的减小,有利于加强通道内热量的传递,弥补了停留时间变小带来的不利影响。
|
Fig. 12 Variations of average wall heat fluxf |
本文对模化通道内正庚烷裂解特性进行了数值研究。分别探究了燃料入口温度、压力、壁面温度、通道尺寸对裂解反应以及高温壁面传热的影响,结果表明:
(1)根据燃料的裂解特性和壁面传热特性,可将通道划分为三个吸热区域,热入口区,主反应区和充分反应区。
(2)在保证汽化的条件下,燃料的入口温度对通道内的裂解反应和传热特性的影响较小,且影响主要集中在通道入口段;压力升高会导致燃料转化率的提高,主要原因是压力升高导致燃料在通道内的停留时间增长;壁面温度的升高会促进燃料的化学吸热,但同时也会一定程度上抑制其物理吸热能力。
(3)通道的直径变小导致通道内的流动、传热和化学反应之间的耦合作用增强,因此小尺度通道的单位面积换热特性要由于大通道。同一压力和质量流率下,通道直径减小50%,其单位面积的换热性能提升约1倍。
| [1] |
Fernandez-Pello A C. Micropower Generation Using Combustion: Issues and Approaches[J]. Proceedings of the Combustion Institute, 2002, 29(1): 883-899. DOI:10.1016/S1540-7489(02)80113-4
(  0) 0) |
| [2] |
Tim Edwards. Liquid Fuels and Propellants for Aerospace Propulsion[J]. Journal of Propulsion and Power, 2003, 19(6): 1089-1107. DOI:10.2514/2.6946
(  0) 0) |
| [3] |
Lander H, Nixon A C. Endothermic Fuels for Hypersonic Vehicles[J]. Aircraft, 1971, 8(4): 200-207. DOI:10.2514/3.44255
(  0) 0) |
| [4] |
贺芳, 禹天福, 李亚裕. 吸热型碳氢燃料的研究进展[J]. 导弹与航天运载技术, 2005, 274(1): 26-29. (  0) 0) |
| [5] |
Sobel D R, Spadaccini L J. Hydrocarbon Fuel Cooling Technologies for Advanced Propulsion[J]. ASME Journal of Engineering for Gas Turbines and Power, 1997, 119(2): 344-351. DOI:10.1115/1.2815581
(  0) 0) |
| [6] |
Huang H, Sobel D R, Spadaccini L J. Endothermic Heat-Sink of Hydrocarbon Fuels for Scramjet Cooling [R]. AIAA 2002-3871.
(  0) 0) |
| [7] |
张琴, 刘国柱, 李国柱, 等. 主动冷却通道内甲醇催化分解吸热过程[J]. 推进技术, 2015, 36(6): 927-932. (ZHANG Qin, LIU Guo-zhu, LI Guo-zhu, et al. Endothermic Process of Methanol Catalysis Decomposition in Active Fuel Cooling Channels[J]. Journal of Propulsion Technology, 2015, 36(6): 927-932.)
(  0) 0) |
| [8] |
Ward T A, Ervin J S, Striebich R C, et al. Simulation of Flowing Mildly-Cracked Normal Alkanes Incorporating Proportional Product Distributions[J]. Journal of Propulsion and Power, 2004, 20(3): 394-402. DOI:10.2514/1.10380
(  0) 0) |
| [9] |
阮波, 孟华. 碳氢燃料裂解吸热反应及超临界传热现象数值模型的构建与验证[J]. 航空学报, 2011, 32(12): 2220-2226. (  0) 0) |
| [10] |
鲍文, 李献领, 秦江, 等. 碳氢燃料流动换热与裂解反应的建模及仿真[J]. 工程热物理学报, 2011, 32(10): 1705-1771. (  0) 0) |
| [11] |
Gascoin N, Gillard P, Dufour E, et al. Validation of Transient Cooling Modelling for Hypersonic Application[J]. Journal of Thermophysics Heat Transfer, 2007, 21(1): 86-94. DOI:10.2514/1.26022
(  0) 0) |
| [12] |
侯凌云, 董宁, 孙大鹏. 矩形冷却槽道内煤油热裂解过程数值研究[J]. 推进技术, 2014, 35(1): 128-132. (HOU Ling-yun, DONG Ning, SUN Da-peng. Numerical Study on Thermal Cracking Process of Kerosene in a Rectangular Cooling Channel[J]. Journal of Propulsion Technology, 2014, 35(1): 128-132.)
(  0) 0) |
| [13] |
杨样, 张磊, 张若凌, 等. 超燃冲压发动机燃烧室主动冷却设计研究[J]. 推进技术, 2014, 35(2): 208-212. (YANG Yang, ZHANG Lei, ZHANG Ruoling, et al. Design Research of an Actively Fuel-Cooled Scramjet Combustor[J]. Journal of Propulsion Technology, 2014, 35(2): 208-212.)
(  0) 0) |
| [14] |
Held T J, Marchese A J, Dryer F L. A Semi-Empirical Reaction Mechanism for n-Heptane Oxidation and Pyrolysis[J]. Combustion Science and Technology, 1997, 123(1-6): 107-146. DOI:10.1080/00102209708935624
(  0) 0) |
| [15] |
Curran H J, Gaffuri P, Pitz W J, et al. A Comprehensive Modeling Study of n-Heptane Oxidation[J]. Combustion and Flame, 1998, 114(1): 149-177.
(  0) 0) |
| [16] |
Xie W, Fang W, Li D, et al. Coking of Model Hydrocarbon Fuels Under Supercritical Condition[J]. Energy & Fuels, 2009, 23(6): 2997-3001.
(  0) 0) |
| [17] |
Chakraborty J P, Kunzru D. High Pressure Pyrolysis of n-Heptane[J]. Journal of Analytical & Applied Pyrolysis, 2009, 86(1): 44-52.
(  0) 0) |
| [18] |
Wen Bao, Silong Zhang, Jiang Qin, et al. Numerical Analysis of Flowing Cracked Hydrocarbon Fuel Inside Cooling Channels in View of Thermal Management[J]. Energy, 2014, 67: 149-161. DOI:10.1016/j.energy.2014.01.044
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

