2. 兰州空间技术物理研究院 真空技术与物理重点实验室,甘肃 兰州 730000
2. Science and Technology on Vacuum Technology and Physics Laboratory, Lanzhou Institute of Physics, Lanzhou 730000, China
高超声速飞行器在大气层中高速飞行过程中的气动加热效应会产生极高的热流密度,为保证红外观测窗口等温度敏感部件可以安全可靠的工作,必须对其进行冷却,受飞行器结构的约束,所用的冷却结构必须是高效紧凑结构。传统的单相对流冷却换热强度低,难以满足高效紧凑换热的要求,微尺度相变对流换热的研究表明微尺度结构的沸腾换热可以实现高效紧凑的换热功能,但随着管道尺寸减小,气泡的脱离直径与微通道尺寸逐渐接近,通道内气泡更易合并,并有可能形成气塞,从而微尺度管道内沸流动腾换热机理与常规尺度管道相比就会产生很大的差异,换热特性也将发生很大的改变。近年来,很多国内外学者纷纷展开了微细管道内流动沸腾换热的研究。Yang[1]利用数值模拟和实验研究了制冷剂R141b在水平蛇形管内的流动沸腾过程,给出了泡状流,搅拌状流,和环状流等不同流型的特点,发现二次流会影响泡状流区域的传热特性;Kew[2]等通过实验研究制冷剂R141b在直径为1.39~3.69mm管道内的流动沸腾特性,根据汽泡的特点将流体流型分为四个区域:单一气泡流、受限泡状流、环状流、“干涸”流,随着干度的提高,对流换热逐渐增强,当干度增大到一定数值之后,出现蒸干现象,换热情况恶化。Bertsch[3]等研究发现在水力直径为1.09mm的平行微通道组中R134a流动沸腾传热系数随热流密度的升高而增大,并在干度约0.2时达到最大值;Coleman和Garimella[4]研究表明制冷剂在直径小于10mm的细通道内流动沸腾,表面张力和管径对流型的产生和变化起重要作用,矩形细通道的高宽比是流型变化的重要影响因素。张小艳等[5]对R417A在水平光滑管和内螺纹管中的流动沸腾换热进行了实验研究,结果表明传热系数随着质量流速的增大而增大;葛琪林[6]等通过实验研究了R290在微细通道内流动沸腾换热特性,结果表明随着热流密度、质量流速和饱和温度的增加,传热系数增大,干度和热流密度对传热系数的影响最为显著;张良等[7]对CO2在微细通道内流动沸腾换热特性进行了实验研究,结果表明传热系数随质量流量的增大而增大,随热流密度增大而先增大后减小,随管径、蒸发温度的减小而增大;郭雷[8]等对水在竖直矩形细通道内的沸腾换热过程进行了数值研究,结果发现通道直径的不同对汽泡生长方式和气泡形态产生很大影响,并且随着通道尺寸的减小,压降和换热系数明显增大;琚忠云[9]模拟研究了水在不同间隙尺寸窄通道内的沸腾换热过程,结果表明间隙尺寸小的窄通道出口平均温度、进出口压差以及平均表面换热系数较大,ONB点产生较早;王志奇[10]等基于CFD平台对制冷剂R245fa在水平光滑管和微肋管沸腾传热特性进行了数值模拟,结果表明传热系数随着质量流速与热流密度的增加而提高;随着干度的增加,传热系数先增加再降低,相比光滑管,微肋管内制冷剂的沸腾传热系数能提高10%~25%;黄秀杰[11]研究发现R32在水平微细光管内的流动沸腾过程中质量流速的增加削弱了重力对两相分布的影响;热流密度的增加强化了壁面附近的核态沸腾。
尽管许多学者对此进行了很多研究工作,也获得了许多相关数据,但至今尚未形成公认的微尺度管道内流动沸腾换热机理。目前针对微尺度流动沸腾换热的研究方法为理论研究、数值模拟计算和实验研究,其中数值模拟方法研究周期短,成本低,可为微尺度管道内流动沸腾换热实验研究提供理论基础,已广泛应用于多种研究领域。本文利用数值模拟方法,研究了制冷剂R141b在微细管道内流动沸腾过程中流型、温度及速度分布,分析了制冷剂R141b在微细管道内流动沸腾换热的基本特性和气泡运动特点,以及表面传热系数的变化规律。
2 物理模型和计算方法 2.1 物理模型及网格划分目前针对高速飞行器的气动加热设计的微尺度高效换热防护系统主要由制冷剂进口,多排微小管道,制冷剂出口等结构组成。本文将物理模型简化为单根二维矩形微细管道,管道长度为500mm,管道直径为0.5mm。利用Gambit软件对计算区域划分结构化四边形网格,网格数量为3×105,通过划分边界层网格对壁面附近区域的网格进行加密,边界层第一层网格高度为0.005mm,增长率为1.2,共10层,并进行了网格无关性验证,计算区域局部网格如图 1所示。

|
Fig. 1 Schematic diagram of computing grid |
本文数值模拟的制冷剂R141b在饱和温度下的物性参数设定如表 1所示,制冷剂R141b物性参数数据来源为NIST。在本文数值计算的温度范围内,液相物性随温度变化较小,数值计算中采用常物性,气相物性随温度变化较大,数值计算中采用变物性,考虑了气相物性随温度的变化。本文数值模拟的工况如表 2所示。
|
|
Table 1 Properties of R141b |
|
|
Table 2 Cases in simulations |
(1)VOF多相流模型
微细管道内[12, 13]制冷剂流动沸腾问题属气液两相流范畴,涉及流动和换热综合问题,本文选用VOF多相流模型[14, 15]对制冷剂在微细管道流动沸腾过程中气泡的产生、生长和脱离过程进行数值模拟。VOF多相流模型通过求解单一的动量方程和各相体积分数的连续性方程及能量守恒方程来模拟制冷剂气液两相流动与换热。VOF多相流模型中的两相之间没有互相穿插,气相和液相的体积分数分别为αv和αl,每个控制体积内两相体积分数之和为1。当αv =1时为气相区域,当αl =1时为液相区域。对于气液两相共存界面,则αv和αl在0~1之间。
VOF多相流模型跟踪气液相间界面是通过求解各相体积分数的连续方程来完成的,气液各相的连续性方程如下
| $ \frac{{\partial {\alpha _{\rm{l}}}}}{{\partial t}} + \nabla \cdot \left( {{\mathit{\boldsymbol{v}}_{\rm{l}}}{\alpha _{\rm{l}}}} \right) = \frac{1}{{{\rho _{\rm{l}}}}}\left( {S{\alpha _{\rm{l}}} + {m_{{\rm{vl}}}} - {m_{{\rm{lv}}}}} \right) $ | (1) |
| $ \frac{{\partial {\alpha _{\rm{v}}}}}{{\partial t}} + \nabla \cdot \left( {{\mathit{\boldsymbol{v}}_{\rm{v}}}{\alpha _{\rm{v}}}} \right) = \frac{1}{{{\rho _{\rm{v}}}}}\left( {S{\alpha _{\rm{v}}} + {m_{{\rm{lv}}}} - {m_{{\rm{vl}}}}} \right) $ | (2) |
| $ {\alpha _{\rm{l}}} + {\alpha _{\rm{v}}} = 1 $ | (3) |
VOF多相流模型通过求解整个控制体积内单一的动量方程,作为结果的速度场是由各相共享的。综合考虑重力、表面张力和相间相互作用力的影响,两相动量方程如下所示
| $ \frac{\partial }{{\partial t}}\left( {\rho \mathit{\boldsymbol{v}}} \right) + \nabla \cdot \left( {\rho \mathit{\boldsymbol{vv}}} \right) = - \nabla p + \nabla \left[{\mu \left( {\nabla \mathit{\boldsymbol{v + }}\nabla _\mathit{\boldsymbol{v}}^{\rm{T}}} \right)} \right] + \rho \mathit{\boldsymbol{g}} + \mathit{\boldsymbol{F}} $ | (4) |
VOF多相流模型中的所有相均遵循相同的能量方程,能量E作为质量平均变量处理,如下所示
| $ \frac{\partial }{{\partial t}}\left( {\rho \mathit{\boldsymbol{v}}} \right) + \nabla \left[{\mathit{\boldsymbol{v}}\left( {\rho E\mathit{\boldsymbol{ + }}\mathit{p}} \right)} \right] = \nabla \cdot \left( {{k_{{\rm{eff}}}}\nabla T} \right) + {S_{\rm{h}}} $ | (5) |
| $\rho = {\alpha _{\rm{l}}}{\rho _{\rm{l}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}} $ | (6) |
| $ E = \frac{{{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{E_{\rm{l}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}}{E_{\rm{l}}}}}{{{\alpha _{\rm{l}}}{\rho _{\rm{l}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}}}} $ | (7) |
| $ \mu = {\mu _{\rm{l}}}{\alpha _{\rm{l}}} + {\mu _{\rm{v}}}{\alpha _{\rm{v}}} $ | (8) |
| $ \mathit{\boldsymbol{F}} = {\sigma _{{\rm{lv}}}}\frac{{{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{\kappa _{\rm{v}}}\nabla {\alpha _{\rm{v}}} + {\alpha _{\rm{v}}}{\rho _{\rm{v}}}{\kappa _{\rm{l}}}\nabla {\alpha _{\rm{l}}}}}{{0.5\left( {{\rho _{\rm{l}}} + {\rho _{\rm{v}}}} \right)}} $ | (9) |
式中αl和αv分别为液相、气相的体积分数,vl和vv分别为液相、气相的速度,ρl和ρv分别为液相、气相的密度,mvl和mlv为气液两相间的质量传递,Sαl,Sαv,Sh为源项,keff为有效导热系数,F为体积力,ρ为混合相密度,E为能量。
表面张力为表面力,可通过CFS(Continuum Surface Force)模型[16]将表面力转化为体积力,其中σlv为气液界面表面张力,气相和液相的曲率分别定义如下
| $ {\kappa _{\rm{l}}} = \frac{{\Delta {\alpha _{\rm{l}}}}}{{\left| {\nabla {\alpha _{\rm{l}}}} \right|}}\;\;\;\;\;\;{\kappa _{\rm{v}}} = \frac{{\Delta {\alpha _{\rm{v}}}}}{{\left| {\nabla {\alpha _{\rm{v}}}} \right|}} $ | (10) |
(2)相变模型
本文选用的相变模型是由Lee[17]提出的蒸发冷凝模型,此模型假定相变是在恒定压力和标准热平衡状态下发生的,质量传递主要取决于饱和温度,质量传递源项如下式所示
| $ {m_{{\rm{lv}}}} = {\gamma _{\rm{l}}}{\alpha _{\rm{l}}}{\rho _{\rm{l}}}\frac{{T - {T_{{\rm{sat}}}}}}{{{T_{{\rm{sat}}}}}}\;\;\;\;\;\;\;{T_1} > {T_{{\rm{sat}}}} $ | (11) |
| $ {m_{{\rm{vl}}}} = {\gamma _{\rm{v}}}{\alpha _{\rm{v}}}{\rho _{\rm{v}}}\frac{{{T_{{\rm{sat}}}} - T}}{{{T_{{\rm{sat}}}}}}\;\;\;\;\;\;\;{T_{\rm{v}}} < {T_{{\rm{sat}}}} $ | (12) |
在本文中,为保证气液界面温度接近饱和温度,时间松弛因子γl和γv规定为10s-1,时间松弛因子过大会导致数值计算发散,时间松弛因子过小会造成气液界面温度偏离饱和温度较多。
能量传递源项可由气化潜热和质量传递源项的乘积得到
| $ Q = - {h_{{\rm{fg}}}}m $ | (13) |
(3)湍流模型
本文数值计算选用RNG k-ε湍流模型。制冷剂在微细管道内流动沸腾时,壁面附近流动较为复杂,且雷诺数较低,湍流发展不充分,RNG k-ε模型结合壁面函数法对低雷诺数和近壁流有更好的表现[10]。
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[{{\alpha _{k{\mathsf{ u} \rm{ eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + \rho \varepsilon $ | (14) |
| $ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{{\alpha _{\varepsilon {\mathsf{ u}\rm{ eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + \frac{{G_{2\varepsilon }^ * }}{k}{G_k} - {G_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} $ | (15) |
式中k为湍流脉动动能,ε为湍流脉动动能耗散率,Gk为由于时均速度梯度产生的湍流动能,C2ε*,C2ε为常数。
2.3 边界条件边界条件设置:本文管道入口处选用速度入口(Velocity-inlet)边界条件,流动方向沿X轴正方向,并设定入口温度为293K,出口边界条件采用自由流(Outflow)边界条件,设定上下壁面为无滑移壁面(Wall)边界条件,保持制冷剂流动管道壁面外部边界为固定的热流密度,见图 2。

|
Fig. 2 Boundary conditions |
本文使用Fluent 16.0进行数值模拟计算,采用VOF多相流模型追踪气液界面,选用RNG k-ε模型湍流模型,压力速度耦合采用PISO算法,压力插值格式选择PRESTO格式,体积分数方程选用Geo-Reconstruct算法,动量方程、湍流方程和能量方程对流项的差分格式都选用二阶迎风格式,时间步长选择为10μs,每个时间步长迭代20次,残差收敛标准为10-5。
2.5 计算方法验证文献[18]对制冷剂R141b在微细管道内流动沸腾换热进行了实验研究,为验证本文的数值计算方法,选用文献[18]的实验数据进行对比。
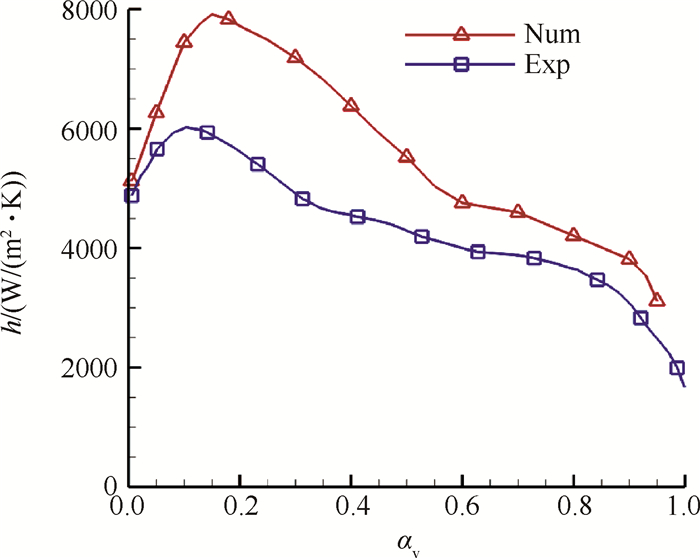
图 3为文献[18]传热系数随含气率变化趋势的实验数据与数值模拟数据的对比,方形间断点表示实验数据,三角形间断点表示模拟数据。结果表明,本文数值计算得到制冷剂在微细管道内的沸腾传热系数变化趋势与实验得到的变化趋势基本一致,数值上存在一定偏差,沸腾传热系数的模拟值高出相应工况下的实验值约10%~40%。沸腾对流换热数值计算偏差主要是由计算所用的湍流模型和多相流沸腾模型引起的,现有的湍流模型和多相流模型参数是在特定条件下得到的,对不同工况下管内沸腾换热的数值计算都会存在一定偏差,大量研究结果表明沸腾传热系数模拟值与实验值的偏差较大是一个普遍现象,只要数值计算得到变化规律与实验得到的变化规律一致,数值偏差在50%以内是可以接受的,例如文献[19]对多个工况下水在竖直矩形微细通道内流动沸腾现象进行了实验和数值研究,发现沸腾传热系数的模拟值高出相应工况下的实验值约20%~70%,可见本文的计算偏差是相对较小的,在合理范围内,所以本文的计算方法是可行的。
|
Fig. 3 Comparison of calculated data and experimental data |
本文以微细通道内制冷剂R141b的流型、温度、速度、表面传热系数为研究要素来探究微细通道内制冷剂流动沸腾换热机理。由于本文采用非稳态数值计算,故选取各工况下制冷剂R141b在微细管道内流动沸腾达到时均稳定状态时的计算结果来分析微细通道内制冷剂气液两相流动沸腾换热特性。
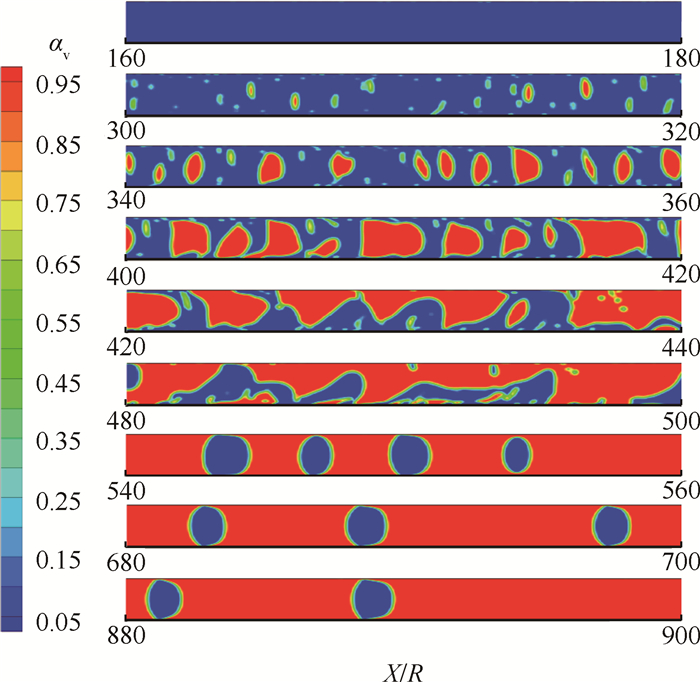
3.1 管道内流型分布图 4~图 6分别为三种不同工况下制冷剂R141b在d=0.5mm管道内不同位置流型变化图。制冷剂R141b在管道内流动沸腾依次出现了单相流,泡状流,受限泡状流,弹状流,间歇流,雾状流。
|
Fig. 4 Micro/mini-channel two-phase flow regimes (q=22258W/m2, G=890kg/(m2·s)) |
|
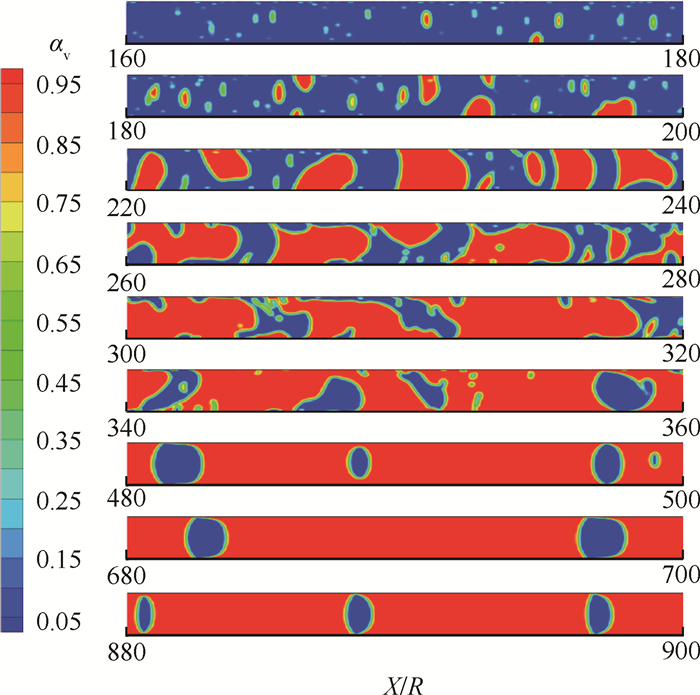
Fig. 5 Micro/mini-channel two-phase flow regimes (q=22258W/m2, G=500kg/(m2·s)) |
|
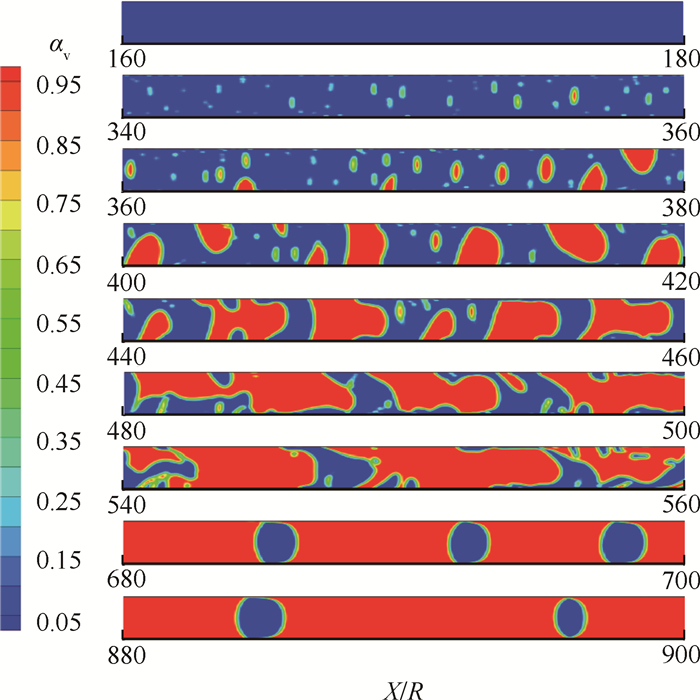
Fig. 6 Micro/mini-channel two-phase flow regimes (q=11000W/m2, G=500kg/(m2·s)) |
由于制冷剂R141b在进入管道时为纯液体,并存在13K的过冷度,故在管道入口出现一段单相流;制冷剂不断吸热,温度逐渐升高达到饱和温度,壁面处开始出现气泡,气泡逐渐长大,合并形成更大的气泡并脱离壁面,气泡四周被液膜包围,分布于连续的液相,称为泡状流;由于管径较小,气泡径向生长受到抑制,逐渐贴近壁面,形成受限泡状流;受限气泡在运动过程中继续扩张,受限气泡间的液块也不断的变小,相邻的受限气泡聚合成弹状流,相邻气弹间充满着小液块或小气泡;制冷剂继续吸热,含气率增加,气泡速度增大,弹状流继续扩张、合并形成间歇流;壁面附近被气相占据,液滴被夹带在气相中移动,并出现局部蒸干现象,流型发展为雾状流。
相同加热条件下,随着质量流速的增加,相同位置管道内含气率逐渐减小,相同流型出现的位置不断推后,这是由于质量流速的增大使得制冷剂两相流动速度增加,单位时间交换更多的热量,液相向气相得转变速度减慢,流型变化较慢,含气率增加较慢。
相同质量流速下,随着热流密度的增加,相同位置管道内含气率逐渐增大,相同流型出现的位置不断提前,这是由于热流密度的增大加快了制冷剂液相向气相转变的速度,含气率增加较快,气相速度增大,相间剪切力随之增大,沸腾过程更加剧烈,流型变化较快。
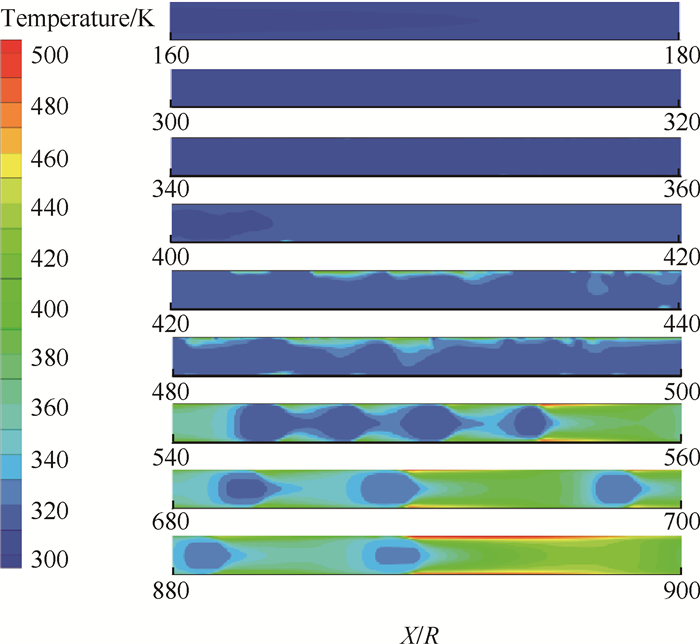
3.2 温度分布图 7~图 9分别为三种不同工况下制冷剂R141b在d=0.5mm管道内不同位置温度分布图。
|
Fig. 7 Contours of temperature distribution (q=22258W/m2, G=890kg/(m2·s)) |
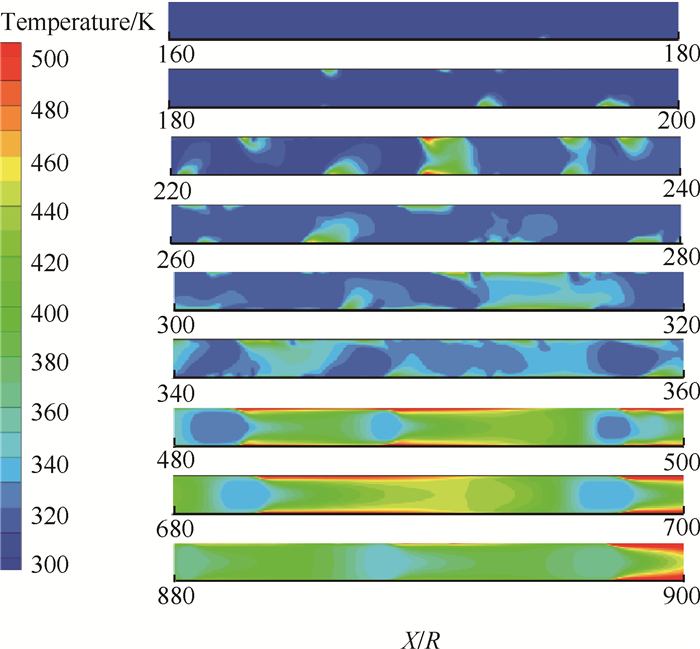
|
Fig. 8 Contours of temperature distribution (q=22258W/m2, G=500kg/(m2·s)) |
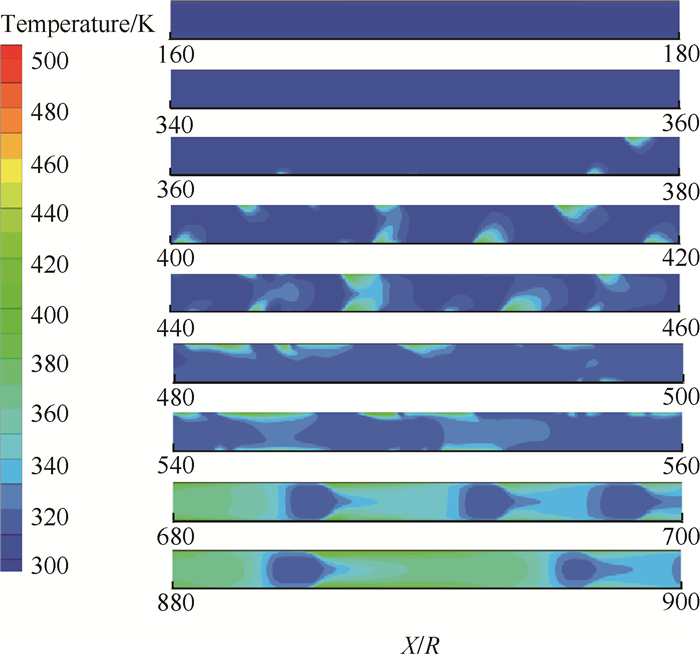
|
Fig. 9 Contours of temperature distribution (q=11000W/m2, G=500kg/(m2·s)) |
制冷剂R141b在管道流动沸腾换热过程中,温度沿轴向逐渐升高,这是由于管道壁面受热,靠近壁面处的温度高于主流温度,壁面处气泡核心温度最高,并逐渐向中心扩散,而且越靠近壁面,温度梯度越大,管道主流含气率较高处温度也较高。
相同加热条件下,随着质量流速的增加,相同位置管道内温度逐渐降低,这是由于质量流速的增加使得制冷剂两相流动速度增加,单位时间交换更多的热量,使得壁面温度降低,液相向气相得转变速度减慢,含气率增加较慢,所以相同位置管道内温度随着质量流速的增加而降低。
相同质量流速下,随着热流密度的增加,相同位置管道内温度逐渐升高,这是由于热流密度的增大加快了制冷剂液相向气相转变的速度,含气率增加较快,气相速度增大,相间剪切力随之增大,沸腾过程更加剧烈,所以相同位置管道内温度随热流密度的增加而升高。
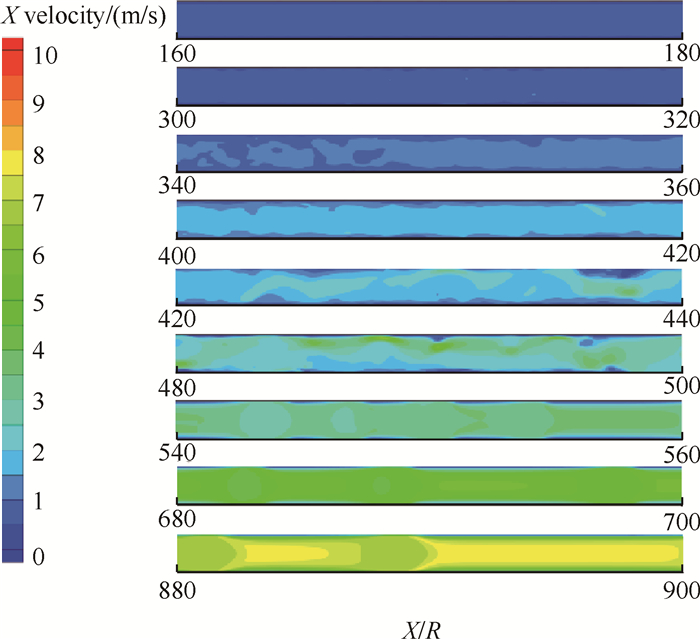
3.3 速度分布图 10~ 图 12分别为三种不同工况下制冷剂R141b在d=0.5mm管道内不同位置速度分布图。
|
Fig. 10 Contours of velocity distribution (q=22258W/m2, G=890kg/(m2·s)) |
|
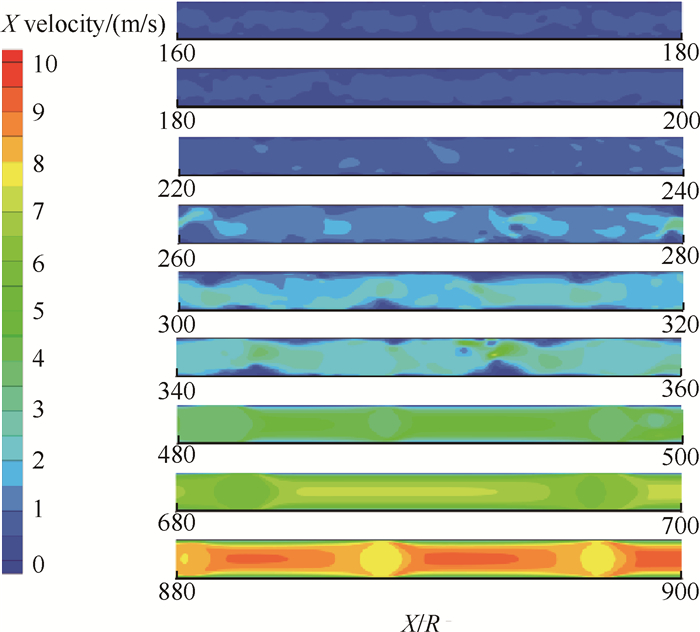
Fig. 11 Contours of velocity distribution (q=22258W/m2, G=500kg/(m2·s)) |
|
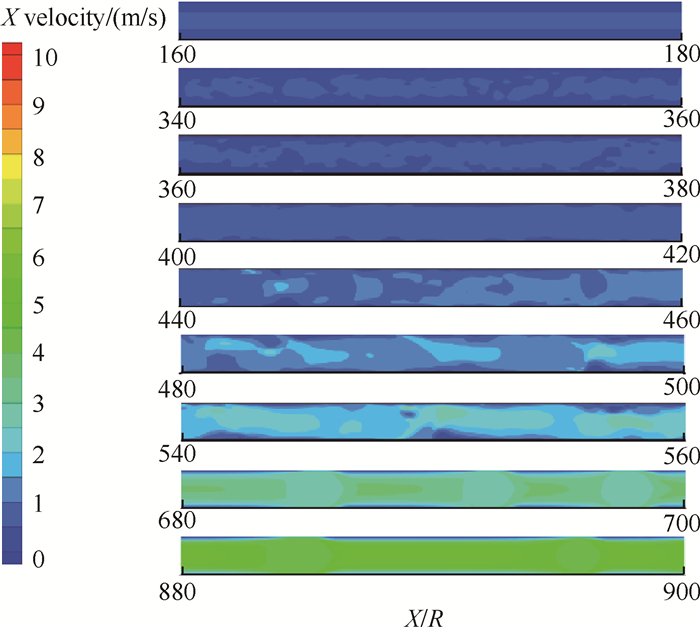
Fig. 12 Contours of velocity distribution (q=11000W/m2, G=500kg/(m2·s)) |
制冷剂R141b在管道内流动沸腾换热过程中,轴向速度逐渐增大。管道主流速度和气泡聚集区的速度较大。在粘性力的作用下,壁面附近形成热边界层,速度较小,且沿管径方向呈现较大的速度梯度。在管道出口,含气率较高,沿程阻力减小,气相速度增大,但气相中夹带的液滴会减慢局部流速。
相同加热条件下,随着质量流速的增加,相同位置管道内速度逐渐减小,这是由于质量流速的增加使得制冷剂两相流动速度增加,单位时间交换更多的热量,液相向气相转变的速度减慢,含气率增加较慢,沿程阻力增大,所以相同位置管道内速度随着质量流速的增加而减小。
相同质量流速下,随着热流密度的增加,相同位置管道内速度逐渐增大,这是由于热流密度的增大加快了制冷剂液相向气相转变的速度,含气率增加较快,沿程阻力减小,所以相同位置管道内速度随热流密度的增加而升高。
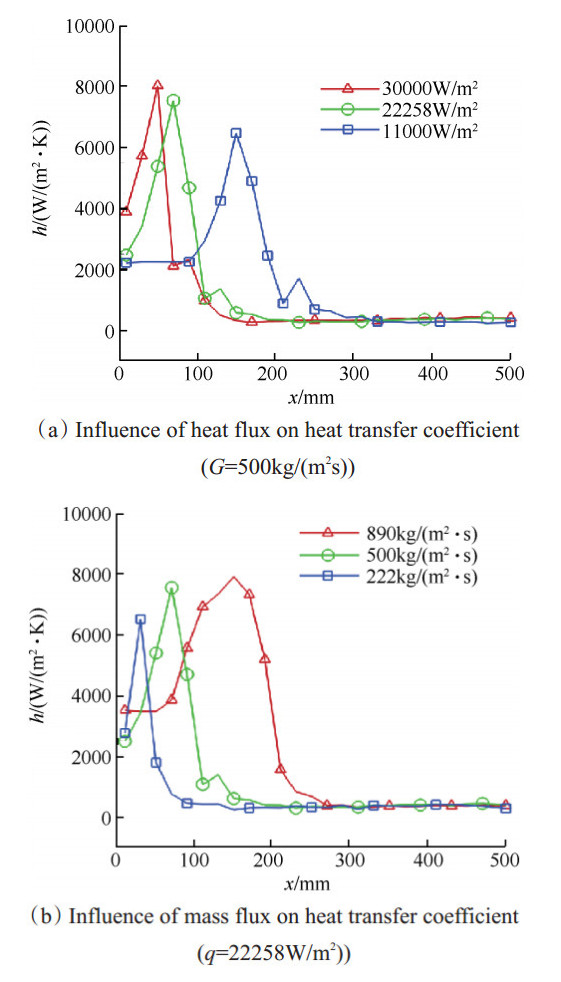
3.4 表面传热系数图 13(a)和(b)分别为不同工况下制冷剂R141b在d=0.5mm管道内不同位置表面传热系数变化图。
|
Fig. 13 Effects of heat flux and mass flux on heat transfer coefficient |
制冷剂R141b在微细管道流动沸腾换热过程中,表面传热系数沿轴向先增大后减小。管道入口段是单相流体的对流换热,表面传热系数略低;管道中间段,壁面上产生气泡,破坏了边界层的稳定,扰动增加,换热增强,表面传热系数增大,较大的气泡脱离壁面进入主流,并相互影响,形成气块或气柱,引起主流的扰动,换热得到强化,表面传热系数继续增大达到峰值;随后小气泡不断合并,形成的气泡体积越来越大,逐渐占据整个流动截面,换热恶化,表面传热系数急剧减小;在表面传热系数下降的后半段出现一个小波峰,这是由于此处的流型处于过渡状态,气泡会扩张、聚合并变形,从而对管内制冷剂流动产生扰动,在一定程度上强化了局部换热,使得表面传热系数增大。管内温度继续升高,蒸汽夹带的液滴几乎完全蒸发,出现“蒸干”现象,表面传热系数达到最低,由于管道内制冷剂的含气率几乎不再变化,故表面传热系数逐渐趋于稳定。
随着质量流速的增大,表面传热系数峰值逐渐增大,表面传热系数峰值出现的位置不断推后,这是由于质量流速的增大使得制冷剂的两相流动速度增加,单位时间内制冷剂与壁面发生更多的热量交换,壁面温度下降更多,主流扰动增强,强化了换热,故表面传热系数增大,热流密度为30000W/m2的工况较热流密度为11000W/m2工况的表面传热系数平均增幅为23.9%。
随着热流密度的增大,表面传热系数峰值逐渐增大,表面传热系数峰值出现的位置不断提前,这是由于热流密度的增大加快了制冷剂液相向气相转变的速度,气相体积增大速率较快,相间传热面积增大,强化气液相间热量交换,提升沸腾换热效率,质量流速为890kg/(m2·s)的工况较质量流速为222kg/(m2·s)工况的表面传热系数平均增幅为21.4%。
4 结论本文数值研究了制冷剂R141b在水平微细管道内的流动沸腾换热特性,得到如下结论:
(1)制冷剂R141b在微细管道内流动沸腾依次出现单相流,泡状流,受限泡状流,弹状流,间歇状流,雾状流,经历了单相对流换热,过冷沸腾换热,核态沸腾换热,膜态沸腾换热。
(2)制冷剂R141b在管道内流动沸腾换热过程中,温度沿轴向逐渐升高,随质量流速的增加而降低,随热流密度的增大而升高;速度沿轴向逐渐增大,随质量流速的增加而减小,随热流密度的增大而增大。
(3)制冷剂R141b在管道内流动沸腾换热过程中,表面传热系数沿轴向先增大后减小;质量流速的增大使得制冷剂的两相流动速度增加,单位时间内制冷剂与壁面发生更多的热量交换,表面传热系数随之增大;热流密度的增大加快了制冷剂液相向气相转变的速度,相间传热面积增大,强化气液相间的热量交换,表面传热系数随之增大。
(4)本文虽然通过数值研究对微尺度管道内沸腾气液两相流动与换热机理有了进一步的认识,但是由于沸腾气液两相流动与换热过程的复杂性,还需要对一些影响因素进行更为深入的研究,例如壁面粗糙度对制冷剂在微细管道内流动沸腾换热的影响。
| [1] |
Yang Z, Peng X F, Ye P. Numerical and Experimental Investigation of Two Phase Flow during Boiling in a Coil Tube[J]. International Journal of Heat and Mass Transfer, 2008, 51(5-6): 1003-1016. DOI:10.1016/j.ijheatmasstransfer.2007.05.025
(  0) 0) |
| [2] |
Kew P, Cornwell K. Correlations for the Prediction of Boiling Heat Transfer in Small Diameter Channels[J]. Applied Thermal Engineering, 1997, 17(8-10): 705-715. DOI:10.1016/S1359-4311(96)00071-3
(  0) 0) |
| [3] |
Bertsch S S, Groll E A, Garimella S V. Refrigerant Flow Boiling Heat Transfer in Parallel Micro-Channels as a Function of Local Vapor Quality[J]. International Journal of Heat and Mass Transfer, 2008, 51(19-20): 4775-4787. DOI:10.1016/j.ijheatmasstransfer.2008.01.026
(  0) 0) |
| [4] |
Coleman J W, Garimella S. Characterization of TwoPhase Flow Patterns in Small Diameter Round and Rectangular Tubes[J]. International Journal of Heat and Mass Transfer, 1999, 42(15): 2869-2881. DOI:10.1016/S0017-9310(98)00362-7
(  0) 0) |
| [5] | |
| [6] |
葛琪林, 柳建华. R290微通道内沸腾换热实验研究[J]. 热能动力工程, 2015, 30(5): 672-817. (  0) 0) |
| [7] |
张良, 柳建华, 叶方平. 细微通道内低温CO2流动沸腾换热特性研究[J]. 热能动力工程, 2014, 29(3): 262-266. (  0) 0) |
| [8] |
郭雷, 张树生, 程林. 竖直矩形细通道内水沸腾换热的数值模拟[J]. 热能动力工程, 2011, 26(1): 31-35. (  0) 0) |
| [9] |
琚忠云, 周涛. 窄通道内水沸腾换热的数值模拟研究[J]. 工业安全与环保, 2014, 40(8): 5-11. (  0) 0) |
| [10] |
王志奇, 夏小霞. 水平管内制冷剂沸腾传热特性的数值模拟[J]. 工业加热, 2015, 44(1): 32-34. (  0) 0) |
| [11] |
黄秀杰. R32在微细通道内流动沸腾特性的实验及数值研究[D]. 北京: 清华大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10003-1015007315.htm
(  0) 0) |
| [12] |
郑杰, 朱惠人, 郭涛. 微尺度冲击冷却通道换热特性实验研究[J]. 推进技术, 2015, 36(1): 82-88. (ZHENG Jie, ZHU Hui-ren, GUO Tao. Experimental Investigation on Jet Impingement Heat Transfer for Micro-Channel[J]. Journal of Propulsion Technology, 2015, 36(1): 82-88.)
(  0) 0) |
| [13] |
吴峰, 王秋旺, 罗来勤, 等. 液体火箭发动机推力室冷却通道流动与传热数值研究[J]. 推进技术, 2005, 26(5): 389-393. (WU Feng, WANG Qiuwang, LUO Lai-qin, et al. Numerical Investigation of Heat Transfer and Fluid Flow in Cooling Channel of Liquid Rocket Engine Thrust Chamber[J]. Journal of Propulsion Technology, 2005, 26(5): 389-393.)
(  0) 0) |
| [14] |
姜玉廷, 郑群, 罗铭聪. 叶片前缘两相流冲击冷却的耦合数值模拟[J]. 推进技术, 2015, 36(3): 443-449. (JIANG Yu-ting, ZHENG Qun, LUO Ming-cong. Congjugate Simulation of Two Phase Flow Impingement Cooling on Blade Leading Edge[J]. Journal of Propulsion Technology, 2015, 36(3): 443-449.)
(  0) 0) |
| [15] |
Swapna S R, Vivek V B. Volume-of-Fluid(VOF)Simulations of Rise of Single/Multiple Bubbles in Sheared Liquids[J]. Chemical Engineering Science, 2010(65): 527-537.
(  0) 0) |
| [16] |
Brackbill J U, Kothe D B, Zemach C. A Continuum Method of Modeling Surface Tension[J]. Journal of Computational Physics, 1992, 10(2): 335-354.
(  0) 0) |
| [17] |
Lee W H. A Pressure Iteration Scheme for Two-Phase Flow Modeling[R]. LA-UR-79-975.
(  0) 0) |
| [18] |
Lin S, Kew P A, Cornwell K. Two-Phase Heat Transfer to a Refrigerant in a 1mm Diameter Tube[J]. International Journal of Refrigeration, 2001(24): 51-56.
(  0) 0) |
| [19] |
常威. 矩形细通道内流动沸腾特性分析及实验研究[D]. 山东: 山东大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10422-1012460978.htm
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


