进气道和发动机的匹配工作是推进系统中的重要研究内容[1]。随着先进战斗机的隐身性能日益凸显,发动机的进气形式也由最初的直进气道改成了S型进气道,然而这种进气道在飞机做高强度机动或者侧滑时易产生强度较大的旋流畸变,影响发动机的稳定性,甚至会导致严重事故[2~4]。因此航空燃气涡轮发动机界也将旋流畸变列为除总温、总压等畸变以外推进系统设计中必须考虑的畸变类型。
旋流畸变即为发动机进口处的气流偏转现象,具有两种基本形式,即整体涡和对涡[5]。国内外对于旋流畸变也开展了一些研究。美国的阿诺德工程发展中心(Arnold Engineering Development Center,AEDC)利用平行压气机模型和平均线模型研究旋流畸变对压气机性能的影响,但是精度不高[6]。Sheoran等利用了滑动网格技术和冻结转子法分析了整体涡、对涡旋流畸变对压气机性能的影响,并验证了CFD数据的可靠性[7]。Ried开展了一系列的试验给出了不同进气畸变对压气机影响的普遍趋势,指出喘振边界和畸变指数密切相关[8]。欧洲Tornado战斗机在发生喘振后,因当时没有先进的数值仿真技术,经过大量的重复测试与试验使得问题得以解决[9, 10]。Sheoran等采用了压力远场边界条件和内部突出钟形口的腔室旋流器,给仿真过程中网格划分、边界条件设定带来较大的工作量[7, 11],也未对气动交界面(Aerodynamic Interface Plane,AIP)上的流畅细节进行细致的分析。国内对于旋流畸变的研究较少,空军工程大学的胡伟波等通过直接改变压气机进口气流参数来模拟旋流研究了整体涡对压气机性能的影响[12],程邦勤等利用同样的研究方法研究了对涡[13],但是这种研究方法将流场简化,与实际流场有一定差别。周游天和屠宝锋等均设计了叶片式旋流发生器,通过改变叶片的安装角和叶片数来改变旋流的种类和强度[5, 14]。但是,目前国内外对于旋流畸变的研究集中于整体涡而且主要考虑的是旋流角,忽略了旋流的方向、范围等特征;在研究压气机性能和稳定性时几乎没有涉猎旋流的作用机理;国内旋流评价指标基本以AIP上0.87R0流场参数为依据不具有通用性。综上可见,在旋流的产生以及细致量化方面开展更为细致的研究尤为迫切。
减少甚至消除旋流畸变对压气机性能和稳定性的影响早已成为燃气涡轮发动机设计面临的主要问题。因此,能够产生强度和种类可以预测的旋流并对其进行量化,评价旋流对压气机性能和稳定性的影响对于今后推进系统的设计与保持稳定工作具有重要的借鉴意义。旋流畸变多产生于S弯进气道中,但是设计制作弯曲的进气道来研究旋流畸变对压气机性能及稳定性的影响有诸多不利因素:(1)几何外形控制,制作工艺复杂。(2)实验时难以调整位置,不能产生模式可预见的旋流,灵活性差。(3)会有混合畸变产生,不能单一地评价旋流畸变的影响。因此,出于后续旋流实验考虑,本文设计了腔室型旋流发生器并利用数值模拟方法对AIP和压气机进口截面上的旋流进行了分析,也为后续开展旋流器与压气机的联合仿真和实验提供数值依据。
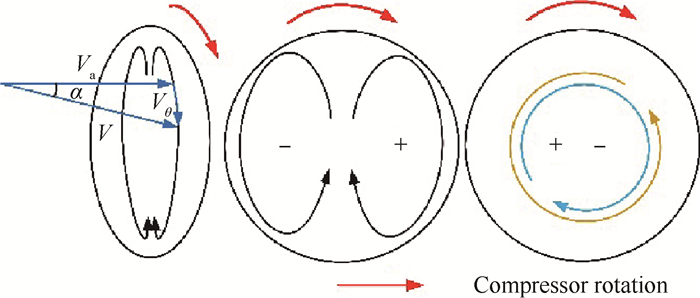
2 旋流畸变的类型与评定 2.1 分类旋流畸变使得气流具有一定的切向和径向速度,其中以整体涡和对涡最为常见。整体涡表现为进口截面气流都沿同一方向旋转,对涡表现为两个漩涡对称分布且气流旋转方向相反。为了进一步对旋流进行细致的量化与分类,先引入旋流角的概念。定义为截面上一点速度方向与轴向分速度的夹角。定义式表示为
| $ \alpha = {\tan ^{-1}}\left( {\frac{{{V_\theta }}}{{{V_{\rm{a}}}}}} \right) $ | (1) |
式中Vθ代表切向速度,Va代表轴向速度。其正负判别方式如图 1所示,切向速度与压气机转向相同为正,反之为负。
|
Fig. 1 Definition of swirl angle |
汽车工程师协会(Society of Automotive Engineers,SAE)制定了一套新的旋流评价指标,即包括旋流扇区(Sector Swirl,SS)、旋流强度(Swirl Intensity,SI)、旋流方向(Swirl Directivity,SD)旋流对数(Swirl Paired,SP) [15]。用该指标能够清楚地反映旋流的种类,强度和范围,且相比于国内其他研究旋流畸变所采用的旋流强度
正旋流扇区
| $ SS_{\rm{i}}^ + = \frac{1}{{\theta _{\rm{i}}^ + }}\int\limits_{\theta _{\rm{i}}^ + } {\alpha {{\left( \theta \right)}_{\rm{i}}}{\rm{d}}\theta } $ | (2) |
负旋流扇区
| $ SS_{\rm{i}}^-= \frac{1}{{\theta _{\rm{i}}^-}}\int\limits_{\theta _{\rm{i}}^-} {\alpha {{\left( \theta \right)}_{\rm{i}}}{\rm{d}}\theta } $ | (3) |
SD,SI,SP等参数均可通过旋流扇区和周向范围计算得出[15]。
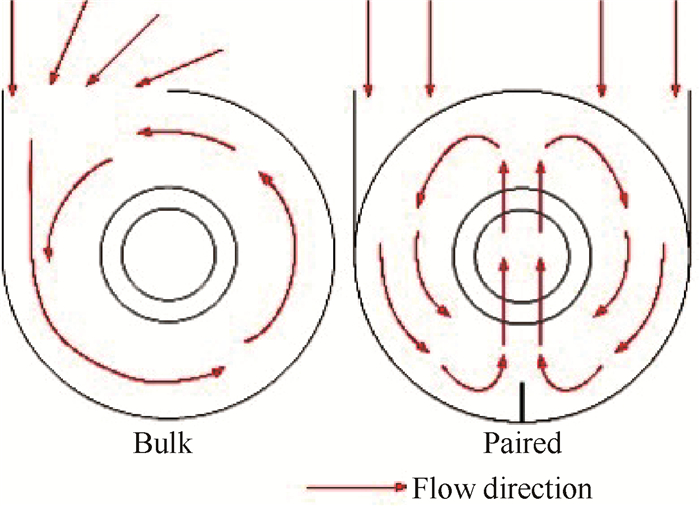
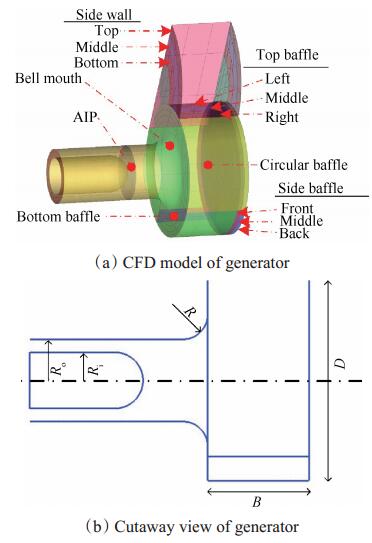
3 旋流器设计与计算方法 3.1 旋流器结构尺寸本文中旋流发生器的设计主要是针对Stage35跨音速轴流压气机进行,因该压气机气动性能良好,且可以获得足够的几何参数数据和实验特性数据[16],利于后续的联合仿真研究。旋流器进气方向及其形成旋流原理如图 2所示,其几何结构主要包括进气口、腔室、底部挡板、钟形口、环形出口。腔室用于产生旋流,底部挡板阻流形成对涡,钟形口均匀过度可减少流动损失,出口采用与压气机进口截面相同的环形出口形式。腔室半径为D为625mm;钟形口半径R为153.9mm;环形出口保持与Stage35进口几何尺寸相同,内环半径Ri为175.26mm;外环半径Ro为256.5mm;AIP在离腔室右侧边缘两倍直径处,CFD模型及剖视图如图 3(a)、(b)所示。
|
Fig. 2 Sketch of generator |
|
Fig. 3 Geometric structure of swirl generator |
整体涡和对涡旋流器采用不同的进气方式。形成整体涡时,采用单侧进气方式,通过改变进气口顶部挡板的数量(共3块,分别标示为Left,Middle,Right)来改变进气口的宽度,侧板(Side wall)的高度根据顶部挡板数量协同改变,从而改变进口几何布局来调整整体涡强度。本文设计了四种强度的整体涡旋流器布局,对应顶部挡板宽度分别为0°,10°,20°,30°圆心角所对应的曲面,侧板高度随着挡板宽度调整以保证进气方向垂直于进口曲面。
形成对涡时,采用腔室上侧进气,腔室底部加一个横板(Bottom baffle)以保证形成标准模式对涡。通过前后移动侧板(Side baffle)来调节腔室厚度从而达到改变对涡强度的目的。本文设置了三种强度的对涡布局(对应侧板位置标示为Front,Middle,Back),对应腔室厚度B分别为575mm,525mm,475mm。参照CFD模型图,表 1给出了旋流器在形成不同种类与强度旋流时的几何布局说明,其中对于不同几何构件,表格中利用Off表示移除,On表示采用。
|
|
Table 1 Analyzed swirl distortion generator configurations |
由于计算域均由曲面包围而成,结构网格在曲面过渡时质量较差,故全部采用非结构四面体混合网格,考虑其具有良好的贴合性且对于复杂的外形具有很好的适应能力,易于控制网格单元的大小形状及网格点的位置[17]。经网格无关性检验,最终确定网格数量在400万左右,生成后质量较好,网格质量检验结果如图 4所示。

|
Fig. 4 Mesh quality histogram |
本文所计算的均为高雷诺数湍流工况,故采用标准k-ε求解模型,计算域采用流量进口边界条件,给定平均静压作为出口边界条件,采用绝热静止无滑移光滑的壁面条件。整个计算过程在一台64核心,128GB的高性能服务器上进行。
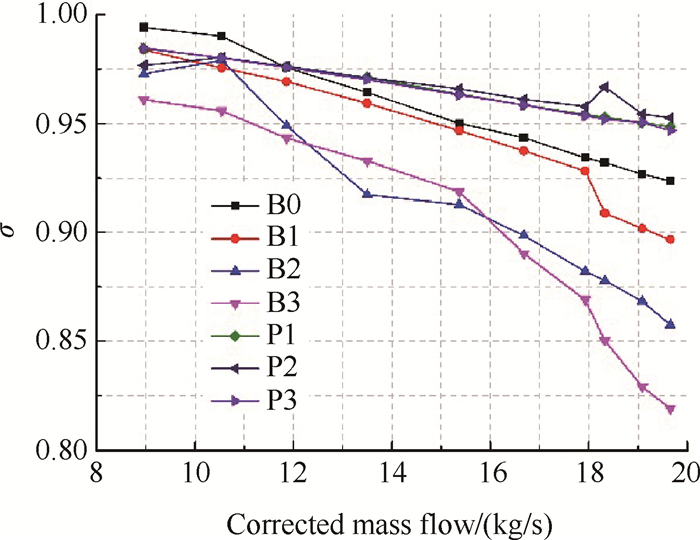
旋流种类主要靠改变腔室结构获得,旋流强度同时还将会受到流量大小的影响。本文设计了四种整体涡旋流发生器和三种对涡发生器来模拟能够产生两种涡的进气装置。不同布局在不同流量工况下的总压恢复系数如图 5所示,可知B0布局总压恢复最高,B3最低,且总体随着流量的增加总压恢复系数降低。其原因可能是B3挡板宽度大,下流流体对其压力阻碍,进口气流流动损失增加,且随着流量的增加,内部流体分离流增大和粘性剪切力的作用也会使总压损失变大。
|
Fig. 5 Total pressure recovery coefficient |
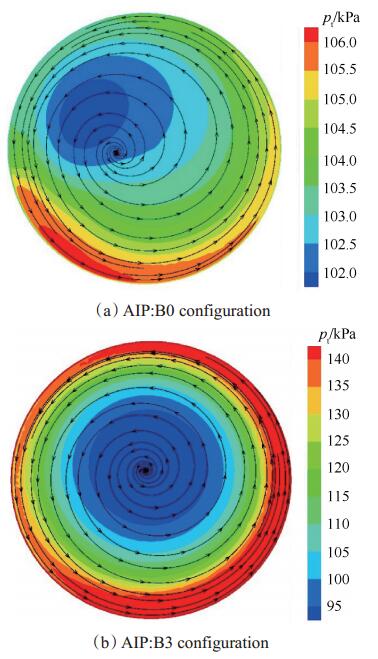
根据NASA对Stage35开展的地面试验数据可知,此压气机不同转速下的流量可达8.96~19.66kg/s。因此本文量化了不同布局的腔室型旋流器在不同流量工作状态下所产生的旋流。为了清晰对比不同流量工况下的AIP处流场,图 6分别给出了B0布局下13.5kg/s和B3布局下19.66kg/s时AIP上所形成整体涡的速度矢量-总压云图,其中pt表示总压,单位为kPa。从图中可以明显地看出,气流在管道中形成了整体涡,涡心为低压区,高能气流分布在近壁面处。流量较小时,壁面底部形成局部高压区,流量较大时,流场分布均匀,中心低压区域变大,高能气流区主要在近壁面周向均匀分布。经过对比,导致涡心偏移的主要影响因素是顶部挡板宽度,宽度增加则涡心更为居中。
|
Fig. 6 Velocity vectors-total pressure contours of AIP for bulk swirl |
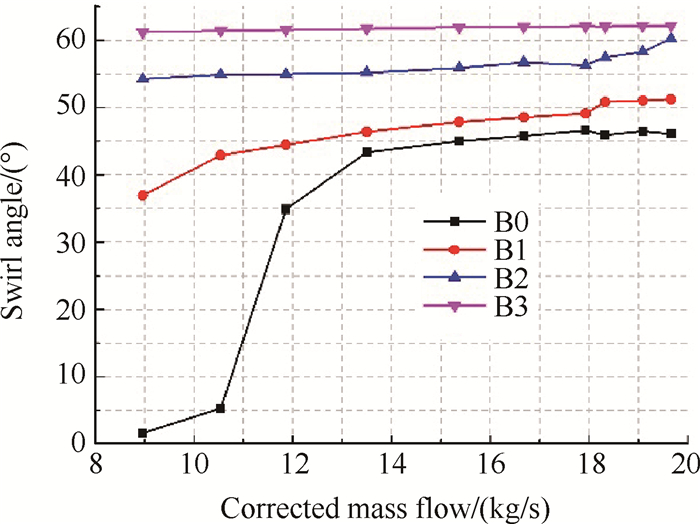
旋流角度作为评价旋流的一个重要指标,对于整体涡而言SD,SP为定值,因此旋流角度很大程度上说明了旋流强度的大小。仿真结果表明整体涡旋流角度虽然在每一个周向位置具有不同的数值,但是数值变化范围较小,因此比较周向平均值更为方便直观。为了表明不同的发生器构型在不同流量时所产生的整体涡的旋流角度的变化情况,图 7给出了各个构型旋流器所产生旋流的旋流角度周向平均值随着流量的变化趋势。选取轴向AIP处,径向90%R0处观察,可以明显看出,旋流角度平均值达到62.14°,旋流角度随流量的增大和腔室顶部挡板宽度变宽而增加;挡板宽度越大,则腔室进口越以切向速度为主导,旋流角度受流量影响程度也就越小;当流量增加到一定程度后,由于气流在腔室内部的阻滞作用,旋流角度基本不再增加。
|
Fig. 7 Swirl angle of bulk vs. mass flow |
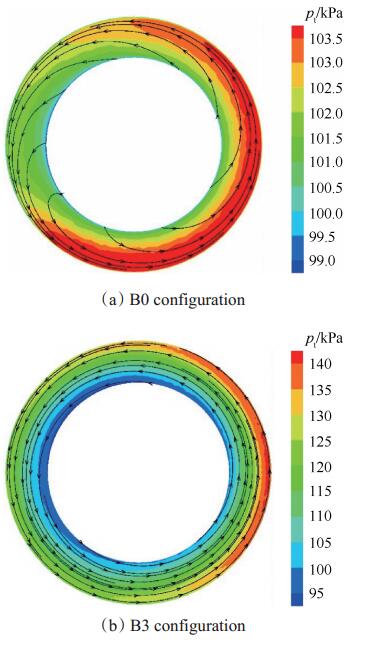
旋流器出口将与Stage35压气机相连接,为了方便对不同径向位置流场表征,将环形进口不同径向分别定义为叶尖、叶中和叶根。为了研究压气机在此旋流下的工作状态,就必须对进口截面旋流分布情况进行分析。观察旋流在直管道中充分发展并受整流罩的扰动后到达压气机情况,图 8给出了上述两种工况下压气机进口截面处的速度矢量-总压云图。注意到,切向速度差别明显,流量较小时气流具有明显的径向速度和局部回流区,流量较大时径向速度几乎消失。经过整流罩气流总压损失,涡心低压低速区扩散包围在压气机叶根处,叶尖处切向速度较大,表现为高压区。
|
Fig. 8 Velocity vectors-total pressure contours at the inlet section of compressor for bulk swirl |
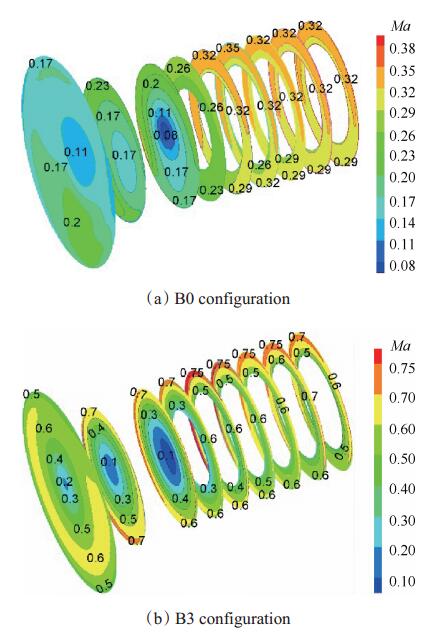
图 9分别给出了上述工况下整体涡旋流器管道轴向各个截面的马赫数变化云图,可以看出不同流量时流场的演变情况,主要受到流量大小和整流罩扰动的影响。在逐渐靠近压气机进口截面时,中心处扰动使得速度有所增大,由于涡心偏移,偏移方向环面局部Ma高。流经整流罩后,由于流通面积减小,气流切向速度明显增大,但之后在轴向基本不再变化,达到了稳定流动。
|
Fig. 9 Mach number distribution at cross stream plane for bulk swirl |
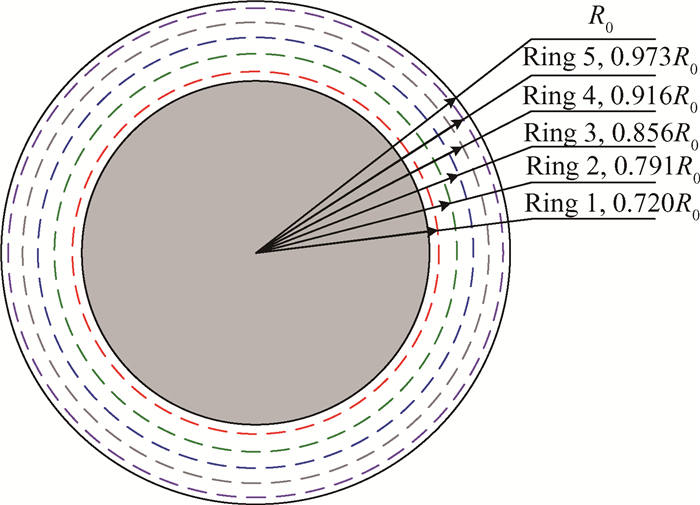
一般情况下,在压气机进口截面某一半径处的旋流角度值不能确定整个环面的流动情况,因此需要从叶根到叶尖选择不同的位置对旋流角度进行测量,从而确定整个环面的旋流状况。图 10给出了五个监测环位置。
|
Fig. 10 Positions of monitoring rings |
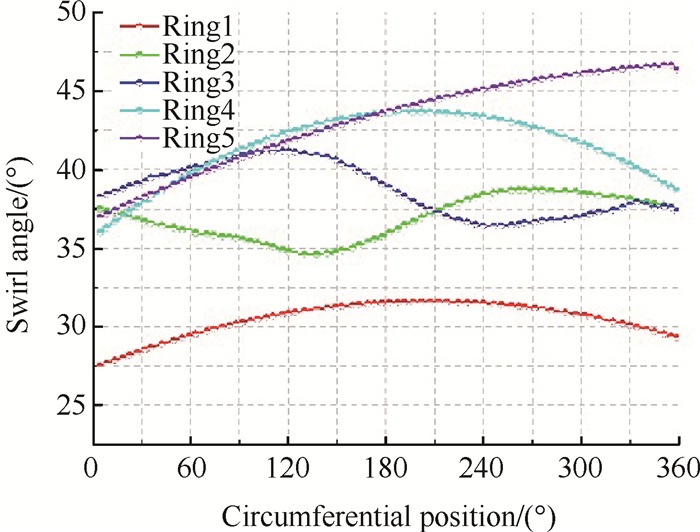
图 11给出了B3布局流量为19.66kg/s情况下五个监测环旋流角度在周向位置的分布情况。由图可知旋流角在周向分布有波动,因其涡心不居中所以切向速度不均匀。由于整流罩的扰动使得气流经过压气机进口截面时旋流角度减小,随着半径的增大,旋流角度基本呈现增大的趋势,说明该状态下靠近叶尖处周向速度分量更大,因此可知整体涡最主要影响的是压气机的叶尖流动。相比于AIP上的旋流角度值减小幅度较大,由于气体粘性及整流罩的扰动作用使得气流旋转动能减弱,周向速度减小。
|
Fig. 11 Swirl angles distribution at different monitor rings of B3 configuration |
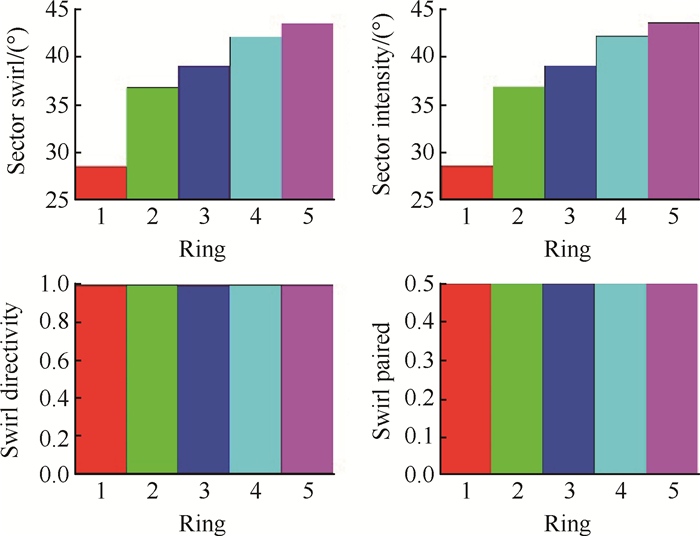
为了能够清晰地表示五个监测环各个旋流指标,参照SAE给出的量化方法,绘制了旋流指标柱状图,分别用五种不同的颜色代表五个监测环。对于整体涡而言,SD的值为1.0,SP的值为0.5。对于整体涡其他布局也是如此。此布局下,旋流强度和旋流扇区均随着半径的增加而增大,如图 12所示。
|
Fig. 12 Swirl distortion descriptors of 5 rings at the inlet section of compressor of B3 configuration |
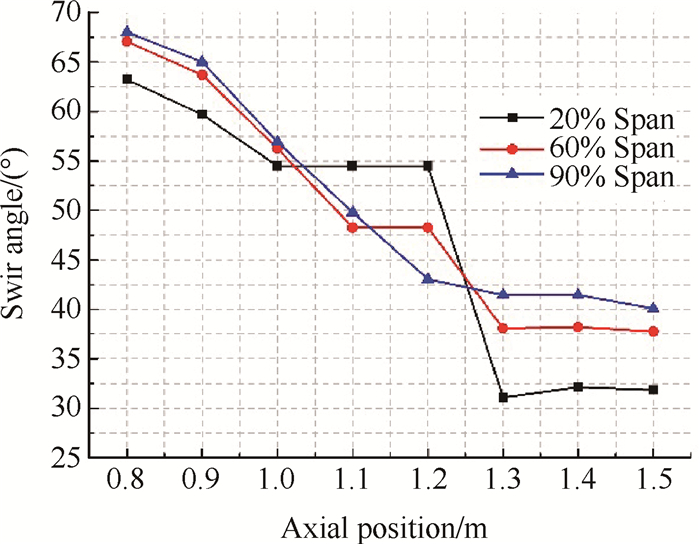
为了分析此布局下气流角度随着轴向位置和径向高度的共同影响,图 13给出了在20% Span,60% Span,90% Span三种叶高时旋流角度随着轴向距离变化特性,三种叶高分别对应半径191.56mm,224.02mm,248mm。纵坐标表示旋流角度的最大值。由图可知,旋流角度随气流在管道中的发展逐渐减小,通过整流罩时减小更快,之后基本保持平稳。整流罩对于叶根处旋流角度的影响最为明显,旋流角达到稳定时,相比于AIP处下降幅度达到了47%。
|
Fig. 13 Distribution of maximum bulk swirl angle at different axial positions of B3 configuration |
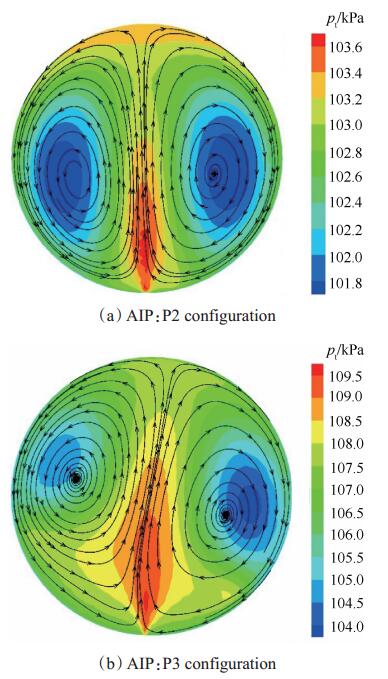
对涡旋流器的主要几何部件、仿真流量范围与整体涡相同,不同之处在于可以改变腔室厚度。图 14给出了P2布局下流量为8.96kg/s和P3布局下19.66kg/s时的AIP速度矢量-总压云图,可见此旋流器能够产生明显的对涡旋流。涡心为低压区,均呈现对称分布,涡的结构基本不受腔室布局和流量的影响,但是流量增大时,出现了对涡向一侧偏移现象,导致一侧高压区域变大。
|
Fig. 14 Velocity vectors-total pressure contours of AIP for paired swirl |
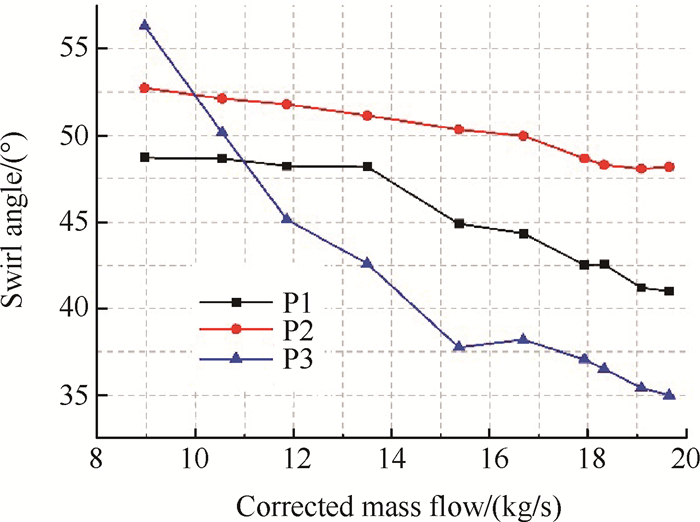
与整体涡相同,取AIP上90%R0处的监测位置,对涡发生器各个布局下的旋流角度随流量的变化如图 15所示。相比于整体涡旋流器,不同之处在于形成对涡时,旋流角度随流量的增加而减少,在小流量工况下P3受流量影响最为明显,最大降幅达到了38.6%。
|
Fig. 15 Swirl angle of paired vs. mass flow |
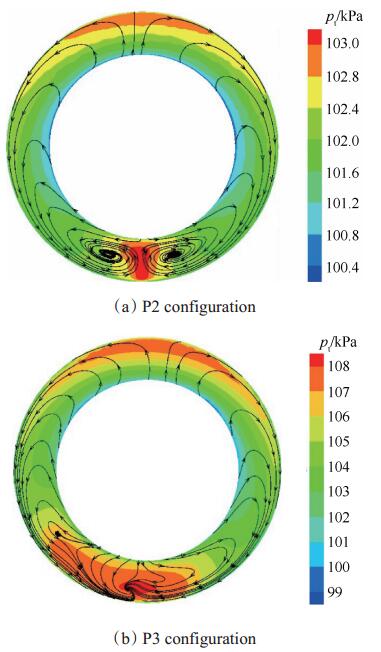
图 16给出了两种工况下压气机进口截面处的速度矢量-总压云图。可见流场受流量影响有明显变化。对涡经过整流罩后两侧涡心被压缩变形聚集在底部,涡心周围形成局部高压区域。环面气流有切向、径向速度分量,形成回流区。其中叶尖和叶根处切向速度较大,当流量增大时,底部高压区域向一侧扩散,涡逐渐破裂。
|
Fig. 16 Velocity vectors-total pressure contours at the inlet section of compressor for paired swirl |
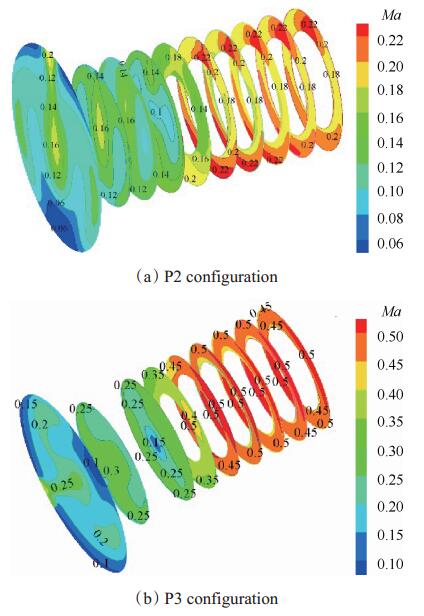
图 17给出了上述两种对涡布局下的轴向切面Ma数的分布云图,由图可知无论腔室内部还是管道内部,Ma均呈现对称分布。相比小流量,大流量工况下环面上侧和下侧高Ma区域分布偏移。因此,对涡旋流对压气机局部气动性能影响明显,且随着涡心的偏移,影响剧烈区域位置也会变化。
|
Fig. 17 Mach number distribution at cross stream plane for paired swirl |
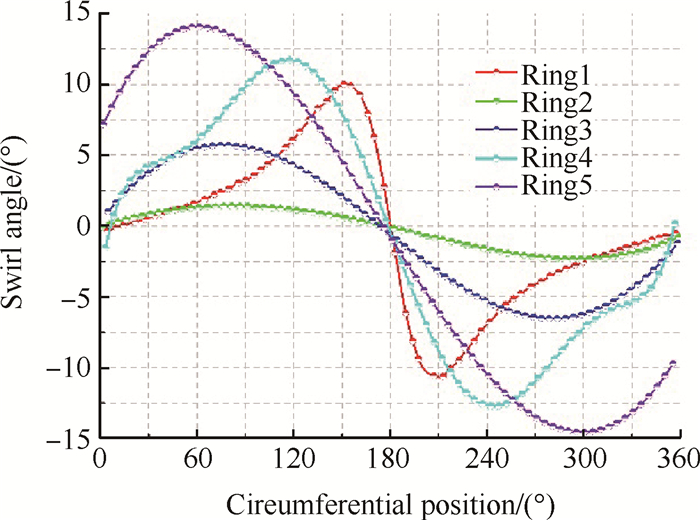
利用图 10给出的监测方法对P2布局下8.96kg/s工况时压气机进口截面全周向位置的旋流角度进行量化,监测环各径向位置的旋流角度随着周向位置变化情况如图 18所示。可知,所有角度近似于正弦函数分布,正与AIR5686里描述的对涡旋流角分布相同。因形成对涡,由上图的流线图可知近壁面处流线密集,切向速度大。旋流角度在叶根和叶尖处较大,在中间部位较小,因此对涡旋流主要影响叶尖和叶根流场来影响压气机性能。叶尖处最大旋流角度可以达到14.05°。
|
Fig. 18 Swirl angles distribution at different monitor rings of P2 configuration |
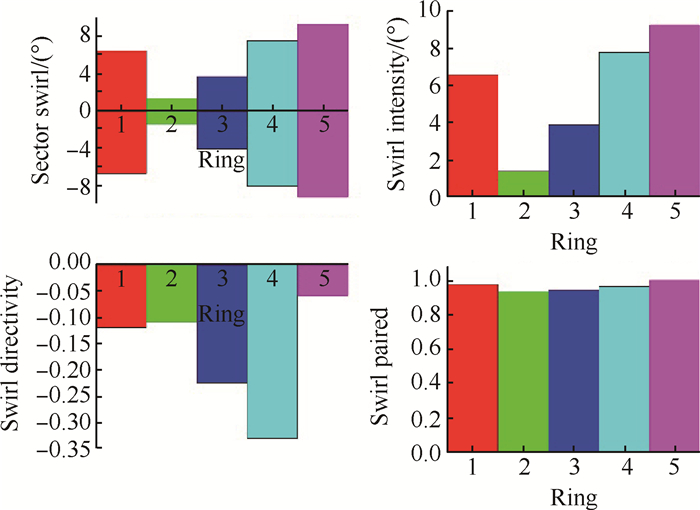
图 19给出了P2布局下压气机进口截面五个监测环的旋流评价指标柱状图。其中Ring1和Ring5相比于其他监测环具有较大强度的对涡畸变,强度最大可以达到9.26。
|
Fig. 19 Swirl distortion descriptors of 5 rings at the inlet section of compressor of P2 configuration |
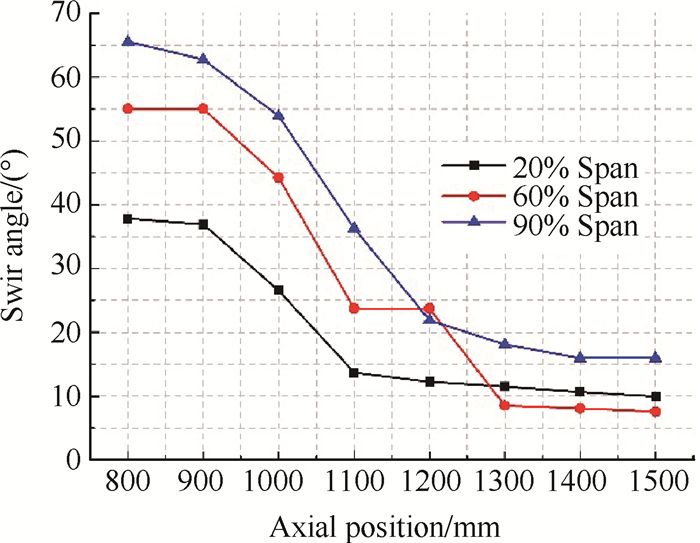
对涡旋流角度的分布均近似于正弦函数,且其正、负周向范围大致分布在0~ π,π~2π,因此观察对涡旋流随管道轴向和径向位置变化的情况可以通过观察旋流角度的变化。由仿真结果可知,P3布局下8.96kg/s时旋流角度最大,因其变化趋势明显,便于观察,故图 20给出了此工况下的不同径向位置对涡最大旋流角度值随着轴向的变化趋势图。如图所示,对涡在管道中发展其切向速度衰减程度相比于整体涡时更大,对涡经过整流罩达到稳定时角度相比于AIP处,叶中处最大降幅为84%,相比于整体涡而言对涡旋流受整流罩的影响更大。
|
Fig. 20 Distribution of average paired swirl angle at different axial positions of P3 configuration |
整体涡和对涡是进气系统中最为常见的两种旋流畸变类型,通过对狂风战斗机、战斧巡航导弹和APU等案例的分析可知,在类型和流场细节方面,本文设计所产生的旋流畸变与实际AIP上的进气畸变相同;在强度上,实际旋流强度受到飞行马赫数、攻角和侧滑角的影响因此并不是定值,所以可以利用腔室型旋流器旋流可调范围大的特点来对压气机进行仿真与试验的研究;实际的压气机进气旋流还受到转子转动带来的反压影响,所以与实际情况更为相似的旋流畸变需要进一步进行旋流器与压气机的联合仿真确定。
5 结论通过仿真,可以得出以下结论:
(1) 所设计的旋流器能产生种类和强度可调的旋流,整体涡AIP上最大旋流角度可以达到65.8°,压气机进口截面处最大可达46.64°;对涡AIP上旋流角度可以达到58.2°,压气机进口截面处最大可达14.05°。
(2) 当整体涡旋流器器顶部挡板宽度较小时,总压恢复系数高,旋流角度小且随流量增加变化明显;当宽度较大时,涡心居中,旋流角度增大且受流量变化影响较弱,总压恢复系数降低。
(3) 三种厚度的对涡旋流器旋流角度均随着流量的增大而减小。腔室厚度减小导致大流量工况下气流将以轴向速度为主导,腔室厚度增大会导致内部空间增大,使得气流不能达到较大的切向速度。
(4) 在压气机进口截面处,整体涡强度随着半径的增加而增大,最大可达43.5,对涡则是叶根和叶尖部位旋流强度较大,最大可达9.26,说明整体涡主要影响压气机转子叶尖,对涡则同时影响叶根和叶尖的气动性能。相比整体涡,对涡对流场的影响较小。
| [1] |
Sheoran Y, Bruce Bouldin P, Krishnan M. Compressor Performance and Operability in Swirl Distortion[J]. ASME Journal of Turbomachinery, 2012, 134(7): 1-13.
(  0) 0) |
| [2] |
Xu Dong, Dakun Sun, Fanyu Li. Effect of Inlet Distortion on Compressor Stability with Stall Precursor-Suppressed Casing Treatment[J]. ASME Journal of Fluids Engineering, 2014, 136(11): 1-15.
(  0) 0) |
| [3] |
刘大响, 叶培梁, 胡骏, 等. 航空燃气涡轮发动机稳定性设计与评定技术[M]. 北京: 航空工业出版社, 2004.
(  0) 0) |
| [4] |
Beale D K, Cramer K B, King Dr P S. Development of Improved Methods for Simulating Aircraft Inlet Distortion in Turbine Engine Ground Tests[R]. AIAA 2002-3045. http://arc.aiaa.org/doi/abs/10.2514/6.2002-3045
(  0) 0) |
| [5] |
周游天, 李军, 李成龙, 等. 进气旋流畸变对压气机性能的影响[J]. 航空动力学报, 2015, 30(8): 1936-1943. (  0) 0) |
| [6] |
Chetan Mistry, Pradeep A M. Influence of Circumferential Inflow Distortion on the Performance of a Low Speed, High Aspect Ratio Contra Rotating Axial Fan[J]. ASME Journal of Turbomachinery, 2014, 136(7): 1-11.
(  0) 0) |
| [7] |
Sheoran Y, Bruce Bouldin P, Krishnan M. Advancements in the Design of an Adaptable Swirl Distortion Generator for Testing Gas Turbine Engines[R]. ASME 2009-GT-59146. http://www.researchgate.net/publication/267501424_Advancements_in_the_Design_of_an_Adaptable_Swirl_Distortion_Generator_for_Testing_Gas_Turbine_Engines
(  0) 0) |
| [8] |
Reid C. The Response of Axial Flow Compressors to Intake Flow Distortion[C]. Cleveland: ASME 1969 Gas Turbine Conference and Products Show, 1969. https://www.researchgate.net/publication/299390129_The_Response_of_Axial_Flow_Compressors_to_Intake_Flow_Distortion
(  0) 0) |
| [9] |
Milt D, Dave B, Sheoran Y. Integrated Test and Evaluation Techniques as Applied to an Inlet Swirl Investigation Using the F109 Gas Turbine Engine[R]. ASME 2008-GT-50074. https://www.researchgate.net/publication/267500753_Integrated_Test_and_Evaluation_Techniques_as_Applied_to_an_Inlet_Swirl_Investigation_Using_the_F109_Gas_Turbine_Engine
(  0) 0) |
| [10] |
Aulehla F. Intake Swirl-a Major Disturbance Parameter in Engine/Intake Compatibility[C]. Seattle: 13th Congress of ICAS/AIAA, 1982. http://www.mysciencework.com/publication/show/intake-swirl-major-disturbance-parameter-engine-intake-compatibility-a761bdbf
(  0) 0) |
| [11] |
Sheoran Y, Bruce Bouldin. A Versatile Design of a Controlled Swirl Distortion Generator for Testing Gas Turbine Engines [R]. ASME 2008-GT-50657. https://www.researchgate.net/publication/267501117_A_Versatile_Design_of_a_Controlled_Swirl_Distortion_Generator_for_Testing_Gas_Turbine_Engines
(  0) 0) |
| [12] |
胡伟波, 程邦勤, 陈志敏, 等. 整体涡旋流畸变对压气机性能影响的研究[J]. 推进技术, 2015, 36(9): 1324-1330. (HU Wei-bo, CHENG Bang-qin, CHEN Zhi-min, et al. Investigation on Effects of Bulk Swirl Distortion on Compressor Performance[J]. Journal of Propulsion Technology, 2015, 36(9): 1324-1330.)
(  0) 0) |
| [13] |
程邦勤, 纪振伟, 胡伟波, 等. 对涡旋流畸变对跨声速压气机性能影响的数值研究[J]. 推进技术, 2017, 38(8): 1776-1786. (CHENG Bang-qin, JI Zhen-wei, HU Wei-bo, et al. Effects of Paired Swirl Distortion on Single Stage Transonic Compressor Performance Using Numerical Simulation[J]. Journal of Propulsion Technology, 2017, 38(8): 1776-1786.)
(  0) 0) |
| [14] |
屠宝锋, 胡骏, 尹超. 叶片式旋流畸变发生器数值模拟研究[J]. 推进技术, 2015, 36(12): 1817-1824. (TU Bao-feng, HU Jun, YIN Chao. Numerical Simulation for Blade Type Swirl Distortion Generator[J]. Journal of Propulsion Technology, 2015, 36(12): 1817-1824.)
(  0) 0) |
| [15] |
Society of Automotive Engineers. A Method for Assessing Inlet Swirl Distortion[R]. AIR 5686, 2010.
(  0) 0) |
| [16] |
Lonnie Reid, Royce D Moore. Performance of SingleStage Axial-Flow Transonic Compressor with Rotor and Stator Aspect Ratios of 1. 19 and 1. 26, Respectively, and with Design Pressure Ratio of 1. 82[R]. NASA Technical, 1338, 1978. https://www.researchgate.net/publication/24384941_Performance_of_single_axial_flow_transonic_compressor_with_rotor_and_stator_aspect_ratio_of_119_and_126_respectively_and_with_design_pressure_ratio_of_205
(  0) 0) |
| [17] |
许和勇, 叶正寅. 三维非结构自适应多重网格技术[J]. 空气动力学学报, 2011, 29(3): 365-369. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39

