2. 火箭军工程大学 发射工程系, 陕西 西安 710025
2. Department of Launch Engineering, Rocket Force University of Engineering, Xi' an 710025, China
大惯量起竖系统可完成重型负载的快速起竖,保证武器装备的高机动性和快速反应能力,在军事领域应用广泛[1]。传统起竖装置多采用液压力作为驱动源,该方式可充分发挥液压系统大推力、大行程的优点,但由于动力源能量密度、机械空间尺寸的限制,液压驱动存在起竖相对缓慢、能量密度不足等问题[2]。为优化起竖液压和控制系统,国内许多学者做了大量卓有成效的工作。姚晓光等[3]通过分析起竖过程的重力矩模型、风载荷模型和油缸作用力模型,对各系统参量做了定量分析;马长林等[4]将仿人工智能积分控制策略应用于起竖过程的跟踪控制;李良等[5],谢政等[6]基于滑模理论分别设计了自适应滑模控制器、多面滑模控制器,实现了对起竖参量的精确跟踪,提高了起竖过程的稳定性;冯江涛等[7]则对起竖过程的多级缸及级间缓冲进行了研究。此外,还有部分学者尝试通过改变起竖系统的驱动结构来提高起竖效率[8],以上研究均对提高现有大惯量起竖系统的稳定性、快速性具有一定的指导意义。但要大幅提升系统起竖速度,达到秒级高速起竖的先进水平,还需对起竖动力源进行改进和优化。
增大液压动力源流量会造成装机功率和体积的增加。电驱动技术具有“安全高效、精确易控”等优点,且电驱动方式用于起竖机构能量转换直接,降低了系统的复杂度,目前,在火炮和中小型起竖装置中得到了成功应用,但受限于机械传动功率和电源功率,电驱动在实现大惯量系统的高速起竖方面尚存在诸多难题,也未见公开报道的应用实例,即大负载的快速起竖通常仍依赖液压起竖方案。
俄罗斯白杨M系列导弹采用燃气助力液压起竖的方式,将起竖时间控制在10s以内[9]。燃气助力装置通常以高温、高压燃气为动力源,多用于弹射[10, 11]、无人机发射[12, 13]等场合,在大惯量起竖系统中,可提供较大的初始动能,是实现高速起竖的关键。但目前关于燃气驱动机理和应用的研究却鲜有报道,美国学者Charles K等[14]利用爆炸气体压缩油液来驱动前起落架缓存器伸长,实现飞机的短距起降,但该方式控制系统复杂、安全威胁较大,很难适用于安全性要求高的高速起竖系统。邵亚军等[15]提出了一种燃气-液压混合驱动的快速起竖方式,对起竖系统内弹道进行了合理化设计,得出了一种兼顾快速性和平稳性的混合起竖方案。
为进一步满足大惯量起竖系统的高速性,且不影响起竖过程的平稳,结合上述分析,本文基于燃气-液压混合驱动的快速起竖方式,以某固体复合推进剂为动力源,设计了一种变截面实心圆柱形端燃药柱,利用燃烧释放的能量驱动负载快速起竖到一定角度,液压机构负责提供传动介质和补油单元。本文主要对系统前端的燃气助力加速起竖过程进行研究,在分析燃气助力机制的基础上,重点讨论了动力源的设计过程和方法。考虑了点火药燃烧、装药燃面推移对助力过程内弹道特性的影响;基于燃烧产物的两相流特性,分析了混合燃气温度、压强特性及各单一成分质量流量在起竖过程中的动态变化规律;结合起竖机构的机械模型,建立了动力源和起竖过程的一体化动力学模型。以某大惯量起竖系统为研究对象,设定起竖角速度目标曲线,利用遗传算法进行装药结构参数匹配和燃面优化;通过正向内弹道计算验证设计过程的合理性。
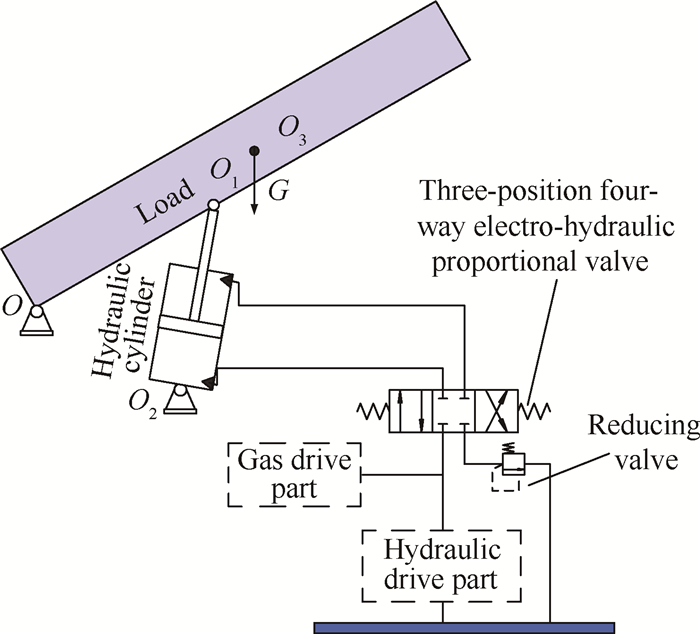
2 燃气-液压混合驱动物理模型燃气-液压混合驱动系统包括燃气助力单元和液压起竖机构。燃气助力单元由燃气发生器、固体装药和初容室等组成;液压起竖机构由液压油源、起竖油缸、电液比例阀、负载等组成。起竖系统的结构组成示意如图 1所示。
|
Fig. 1 Sketch of gas-hydraulic hybrid drive erecting system |
图 1中,减压阀用来确保起竖油缸有杆腔有一定的压力,从而起到一定的缓冲作用,避免燃气对系统造成较大冲击。系统采用燃气助力的方式,以液压油为工质,实现大惯量系统快速起竖。燃气助力单元与液压油源单元作为两个独立的动力源,通过油管衔接并入起竖系统,燃气助力单元负责提供较大的初始动能,使系统在较短的时间内(5~8s)起竖至较大角度(
整个起竖过程按工作逻辑顺序可分为燃气助力阶段、动力源切换阶段和液压起竖阶段。本文重点分析燃气驱动过程及动力源的参数优化,对液压系统和具体的机械结构(机械强度、机械间配合、热防护等)不作过多阐述,且认为动力源切换平稳、液压系统满足起竖过程的流量、压力需求。前期在对系统整体分析的基础上,明确了几个关键参数的取值范围:最大负载力约为31.5kN,最大输出压强(低压室内燃气作用于推力活塞的压强)约为5MPa。
燃气助力单元的结构组成如图 2所示。

|
Fig. 2 Sketch of gas assistor |
以具有大能量密度的某固体复合推进剂为动力源,考虑设计的合理性、简便性和可实现性,设计药形为实心圆柱形端燃药柱,以自由装填的方式固定在燃气发生器内。动力源的结构参数决定起竖过程的状态,在内弹道计算的基础上,对动力源结构进行优化设计,并对系统作如下假设:
(1) 结构强度满足要求,连接紧固,密封完好。
(2) 机械结构性能良好,忽略起竖系统阻尼的影响。
(3) 燃气与油液之间隔热性能完好,油液性质不发生改变。
(4) 燃气冲击不会造成系统的损坏及油液性质的改变。
结合图 1,图 2,综合上述分析,液压动力源和燃气助力单元之间的配合可表述为:在起竖初始阶段,由燃气助力单元为起竖系统提供动能,高压气体推动储存好的油液进入系统实现快速起竖;当燃气助力单元完成快速起竖动作后,液压动力源提供较小的压力即可满足负载起竖需求,此时,卸掉燃气助力单元的压力,由液压动力源提供起竖所需流量,完成最后的起竖动作。
3 燃气助力单元内弹道模型由于高温燃气的温度在整个助力过程中的变化幅度相对较大,燃气的比热会发生相应的变化,需要考虑比热随温度的变化情况。参考文献[16]中所述,比热随温度的变化可通过如下方式拟合得到
| $ {C_p} = {a_0} + {a_1}T + {a_2}{T^2} + {a_3}{T^3} $ | (1) |
式中a0,a1,a2,a3均为常系数,可查表得到。
在推进剂选定以后,结合其燃烧特性,可初步确定其燃烧产物中各组分。本文所用推进剂,燃烧后混合气体主要由CO,N2,HCl,H2,CO2,H2O等组成。混合气体的比热可通过下式计算
| $ {C_{p{\rm m}}} = \sum\limits_{i = 1}^n {{x_i}{C_{pi}}} $ | (2) |
式中Cpi组分i的比热,xi为组分i的质量百分数,∑xi = 1。结合各组分的质量占比,可得到混合气体的比热约为
| $ {C_p} = 1579.3 + 0.03T $ | (3) |
分别计算气体在800K和1800K两种温度下的比热,并比较,得到误差约为1.84%。
考虑比热在本文工况下随温度变化较小,且对文中分析重点影响不大,故文中视燃气比热为常量。
3.1 点火药量确定适当的点火压强是装药可靠点燃的必要保证,点火药量mig是决定点火压强pig的唯一因素。依据气体状态方程,可建立如下平衡
| $ {p_{{\rm{ig}}}}\left( {{V_{10}} - \frac{{{m_{{\rm{ig}}}}{\varepsilon _1}}}{{{\rho _{{\rm{igp}}}}}}} \right) = {m_{{\rm{ig}}}}\left( {1 - {\varepsilon _1}} \right)\frac{R}{{{M_1}}}{T_1} $ | (4) |
式中点火压强需满足pig ≥ pcr,pcr为装药的临界压强,V10为装药状态下高压室的自由容积,ρigp为点火药燃烧产物中凝固相微粒密度,ε1为点火药燃烧产物中凝固相微粒的质量比,R为摩尔气体常数,M1为气相成分的平均分子量,T1为高压室温度。
3.2 高压室内弹道数学模型装药燃烧过程中,高压室内同时存在两种燃烧产物的气、凝(固)相成分,视产物中气相成分为两种单一成分的均匀掺混,同时忽略凝相成分的团聚、破碎等细观过程,不考虑相变引起的热效应。根据质量守恒原则,点火药、装药气相燃烧产物的质量流量为
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{m_1}}}{{{\rm{d}}t}} = - \frac{{{m_1}}}{{{m_1} + {m_2}}}{Q_{\rm{m}}}\\ \frac{{{\rm{d}}{m_2}}}{{{\rm{d}}t}} = {M_{\rm{b}}} - \frac{{{m_2}}}{{{m_1} + {m_2}}}{Q_{\rm{m}}} \end{array} \right. $ | (5) |
式中m1,m2分别为点火药、装药气相燃烧产物的质量,Mb为装药燃烧时燃气的生成速率
| $ {M_{\rm{b}}} = {\rho _{\rm{P}}}{A_{\rm{b}}}u\left( {1 - {\varepsilon _2}} \right) $ | (6) |
式中ρP为装药密度,Ab为燃面面积,ε2为装药燃烧产物中凝固相微粒的质量比。u为燃速,服从指数燃速定律
| $ u = \left\{ \begin{array}{l} a{p^n}\;\;\;\;\;t \le {t_{\rm{k}}}\\ 0\;\;\;\;\;\;\;\;t > {t_{\rm{k}}} \end{array} \right. $ | (7) |
式中a为燃速系数,n为压强指数,二者均根据实验结果确定,tk为药柱燃烧时间,依据燃气驱动时间tg确定,初期计算时,取tk = 0.9tg。
Qm为由高压室到低压室的气体质量流量,其值由混合气体特性决定
| $ {Q_{\rm{m}}} = \left\{ \begin{array}{l} \varphi \frac{{{p_1}{A_{\rm{t}}}}}{{\sqrt {{R_{\rm{g}}}{T_1}} }}\sqrt {\frac{{2k}}{{k - 1}}\left[ {{{\left( {\frac{{{p_2}}}{{{p_1}}}} \right)}^{\frac{2}{k}}} - {{\left( {\frac{{{p_2}}}{{{p_1}}}} \right)}^{\frac{{k + 1}}{k}}}} \right]} \;\;\;\;\;\;\;{\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}} < \frac{{{p_2}}}{{{p_1}}} < 1\\ \varphi \sqrt k {\left( {\frac{2}{{k + 1}}} \right)^{\frac{{k + 1}}{{2\left( {k - 1} \right)}}}}\frac{{{p_1}{A_{\rm{t}}}}}{{\sqrt {{R_{\rm{g}}}{T_1}} }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{p_2}}}{{{p_1}}} < {\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}} \end{array} \right. $ | (8) |
式中φ为流量修正系数,k为燃气绝热指数,At为喷喉截面积,p1,p2分别为高、低压室压强,混合气体常数Rg = R/Mh,其中,Mh为混合气体的平均分子量,参考文献[17],可得
| $ {M_{\rm{h}}} = \frac{{{m_1} + {m_1}}}{{\frac{{{m_1}}}{{{M_1}}} + \frac{{{m_2}}}{{{M_2}}}}} $ | (9) |
式中M2为装药气相燃烧产物的分子量。
高压室容积通常较低压室要小很多,且凝相产物占据一定比例,为更精确分析其对内弹道及起竖过程的影响,文中计算均考虑凝相对体积的贡献值,视颗粒在空间中的分布满足统计规律。凝相微粒占有的总体积为
| $ V = \frac{{\sum\limits_{i = 1}^n {{m_i}} }}{{{\rho _1}}} $ | (10) |
式中mi为第i个粒子的质量,n为总粒子数,ρl为凝相微粒密度。
由于凝相粒子的布朗运动比气相要小得多,可以忽略不计,所以它不提供压强。高压室内凝相微粒到喷管喉部下游变为固相,忽略壁面粘性造成颗粒附着现象、颗粒堆积对喉部面积的改变。由于凝相成分在气相中均匀掺混,视气流中凝相、气相成分质量占比保持不变,可得出高压室内气相占有体积为
| $ {V_1} = {V_{10}} - \frac{{{m_1}{\varepsilon _1}}}{{{\rho _{{\rm{igp}}}}\left( {1 - {\varepsilon _1}} \right)}} - \frac{{{m_2}{\varepsilon _2}}}{{{\rho _{{\rm{zyp}}}}\left( {1 - {\varepsilon _2}} \right)}} $ | (11) |
式中ρzyp为装药燃烧产物中凝固相微粒密度。考虑药柱燃烧过程中的燃面推移会造成自由容积的变化,也直接影响内弹道特性[18],本文假设药柱燃面作一维推移,可得
| $ \frac{{{\rm{d}}{V_{10}}}}{{{\rm{d}}t}} = {A_{\rm{b}}}u $ | (12) |
由能量守恒,可得
| $ \frac{{{\rm{d}}\left( {{m_1} + {m_2}} \right){C_{\rm{v}}}{T_1}}}{{{\rm{d}}t}} = {\chi _1}{M_{\rm{b}}}{C_{p2}}{T_{\rm{a}}} - {Q_{\rm{m}}}{C_p}{T_1} $ | (13) |
式中χ1 为高压室热损失修正系数,Cp2,Ta分别为装药燃气定压比热、定压燃烧温度,Cp,Cv分别为混合气体的定压、定容比热,其值可由下式确定
| $ {C_v} = {C_p}/k = \sum {{Y_j}{C_{{\rm{v}},j}}} $ | (14) |
式中Yj,Cv, j 分别为组分j的质量分数、定容比热。
3.3 低压室内弹道数学模型低压室内充斥着常态下的干空气,热物性参数参考文献[19]。令初容室内气体质量为m3,则其变化主要决定于喷管处的质量流量。
| $ \frac{{{\rm{d}}{m_3}}}{{{\rm{d}}t}} = {Q_{\rm{m}}} $ | (15) |
流入低压室内的燃气推动执行机构运动,根据低压室内能量守恒原则
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{C_{{\rm{v'}}}}{m_3}{T_2}} \right) = {\chi _2}{C_p}{T_1}{Q_{\rm{m}}} - {p_2}S\frac{{{\rm{d}}l}}{{{\rm{d}}t}} $ | (16) |
式中Cv'为低压室混合气体的定容比热,T2为低压室温度,S为推力活塞横截面积,l为图 1中O1,O2两点之间的距离。
分析气体的流动过程,结合各成分在封闭系统中的质量守恒,可推算出低压室内气体的平均分子量为
| $ {M_1} = \frac{{{m_3}}}{{\frac{{{m_{{\rm{ig}}}}\left( {1 - {\varepsilon _2}} \right) - {m_1}}}{{{M_1}}} + \frac{{{m_3} - {m_{{\rm{ig}}}}\left( {1 - {\varepsilon _2}} \right) + {m_1}}}{{{M_2}}}}} $ | (17) |
结合图 1中起竖机构的三角结构,其函数关系可表述为
| $ {l_1}^2 + {l_3}^2 - 2{l_1}{l_3}\cos \left( {\theta + {\theta _0}} \right) = {l^2} = {\left( {{l_2} + {l_{\rm{s}}}} \right)^2} $ | (18) |
式中l2为初始状态下O1,O2之间的距离,ls为活塞杆伸出位移,θ0为∠O1OO2的初始状态值。
推力活塞移动速度为
| $ \frac{{{\rm{d}}l}}{{{\rm{d}}t}} = \frac{{{l_1}{l_3}\sin \left( {\theta + {\theta _0}} \right)}}{{\sqrt {l_1^2 + l_3^2 - 2{l_1}{l_3}\cos \left( {\theta + {\theta _0}} \right)} }}\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} $ | (19) |
式中
根据牛顿第二定律,负载起竖过程受力分析,可推导出系统转动过程的动力学微分方程
| $ J\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = \frac{{{p_2}S{l_1}{l_3}\sin \left( {\theta + {\theta _0}} \right)}}{{\sqrt {l_1^2 + l_3^2 - 2{l_1}{l_3}\cos \left( {\theta + {\theta _0}} \right)} }} - G{l_4}\cos \left( {\theta + {\theta _0}} \right) $ | (20) |
式中
| $ \left\{ \begin{array}{l} {{\dot X}_1} = - \frac{{{X_1}}}{{{X_1} + {X_2}}}{Q_{\rm{m}}}\\ {{\dot X}_2} = {M_{\rm{b}}} - \frac{{{X_2}}}{{{X_1} + {X_2}}}{Q_{\rm{m}}}\\ {{\dot X}_3} = {A_{\rm{b}}}u\\ {{\dot X}_4} = \frac{{{\chi _1}{M_{\rm{b}}}{C_{p2}}{T_{\rm{a}}} - {Q_{\rm{m}}}{C_p}{X_4} - \frac{{\left( {{C_{{\rm{v2}}}} - {C_{{\rm{v1}}}}} \right){M_{\rm{b}}}{X_1}{X_4}}}{{{X_1} + {X_2}}} - {C_{\rm{v}}}\left( {{M_{\rm{b}}} - {Q_{\rm{m}}}} \right){X_4}}}{{\left( {{X_1} + {X_2}} \right){C_{\rm{v}}}}}\\ {{\dot X}_5} = {Q_{\rm{m}}}\\ {{\dot X}_6} = \left\{ {{\chi _2}{Q_{\rm{m}}}{C_p}{X_4} - \frac{{{p_2}S{l_1}{l_3}\sin \left( {{X_7} + {\theta _0}} \right)}}{{\sqrt {l_1^2 + l_3^2 - 2{l_1}{l_3}\cos \left( {{X_7} + {\theta _0}} \right)} }} - {C_{v'}}{X_6}{Q_{\rm{m}}} - \\\left[ {\frac{{{X_1}{X_5}}}{{{X_1} + {X_2}}} - {m_{i{\rm{g}}}}\left( {1 - {\varepsilon _1}} \right) + {X_1}} \right]{Q_{\rm{m}}}/{X_5}\left( {{C_{{\rm{v1}}}} - {C_{{\rm{v2}}}}} \right)} \right\}/{X_5}{C_{{\rm{v'}}}}\\ {{\dot X}_7} = {X_8}\\ {{\dot X}_8} = \left\{ \begin{array}{l} \frac{{\frac{{{p_2}S{l_1}{l_3}\sin \left( {{X_7} + {\theta _0}} \right)}}{{\sqrt {l_1^2 + l_3^2 - 2{l_1}{l_3}\cos \left( {{X_7} + {\theta _0}} \right)} }} - G{l_4}\cos \left( {{X_7} + {\theta _0}} \right)}}{J}\;\;\;\\{p_2} \ge \frac{{G{l_4}\cos \left( {{X_7} + {\theta _0}} \right)\sqrt {l_1^2 + l_3^2 - 2{l_1}{l_3}\cos \left( {{X_7} + {\theta _0}} \right)} }}{{S{l_1}{l_3}\sin \left( {{X_7} + {\theta _0}} \right)}}\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\{p_2} < \frac{{G{l_4}\cos \left( {{X_7} + {\theta _0}} \right)\sqrt {l_1^2 + l_3^2 - 2{l_1}{l_3}\cos \left( {{X_7} + {\theta _0}} \right)} }}{{S{l_1}{l_3}\sin \left( {{X_7} + {\theta _0}} \right)}} \end{array} \right. \end{array} \right. $ | (21) |
结合上述内弹道模型及起竖过程的整体动力学模型,为满足数值求解的需要,设定8个待求变量,分别为:X1 = m1,X2 = m2,X3 = V10,X4 = T1,X5 = m3,X6 = T2,X7 = θ,X8 = ω,则可建立如下起竖过程封闭状态微分方程组。
式中Cv2为装药燃气的定容比热。
5 动力源参数匹配及优化整个匹配及优化过程可分为两步:第一步首先确定能够在规定时间内达到起竖角度的定截面药柱直径,为后续优化提供参考和约束范围,第二步针对定截面药柱的不足,对药柱进行变截面优化设计。
5.1 目标曲线及模型参数为满足高速起竖需求,同时不对负载造成过大的冲击,且便于安全制动和精准控制,基于内弹道分析和前期数值试验积累,参考传统起竖方式的经典起竖轨迹,初步规划燃气驱动8s,负载起竖至1.28rad。即燃气驱动过程起竖目标曲线的数学表达为
| $ \omega = 0.04t $ | (22) |
公式(22)所示轨迹可保持起竖过程匀加速,而在燃气驱动8s结束后,仍留有部分角度空间实现负载减速,使负载平稳起竖到位且速度降为0。燃气驱动仅负责加速过程,而减速过程由液压辅助装置完成,不作本文的分析重点。
点火药使用小粒黑火药,燃烧产物中的凝相微粒密度[20]为ρigp = 3203.6 kg /m3,ε1 = 0.6,R = 8.314J/(mol ·K),由公式(4)确定mig = 0.02kg。装药采用复合固体推进剂,ρP = 2409 kg /m3,ε2 = 0.32,ρzyp = 3000kg/m3。φ = 0.96,k = 1.33,χ1 = 0.9,χ2 = 0.8,S=0.07m2,r= 10m,m=10000kg,At =12.56mm2。忽略点火药的燃烧过程,认为其瞬间被引燃,且在点燃药柱前,高压室温度保持平衡,药柱点燃与喷管喉部堵盖破裂同时发生,考虑到能量损失,取初始状态T1 = 2000K,V10 = 11cm2,T2 = 298.15K,θ0 = 0.33rad。
5.2 动力源参数匹配为提高装药结构的设计效率,初始阶段,基于药柱恒面燃烧进行内弹道正向分析。以药柱燃面直径d为优化参数,采用遗传算法匹配规划的起竖角度值。本文以8s时刻起竖到位角为判定参数,通过与设定的理想角度(θid = 1.28 rad)对比,确定对应药柱燃面的合理性。
| $ smk = \left| {{\theta _{t = 8{\rm{s}}}} - {\theta _{{\rm{id}}}}} \right| $ | (23) |
smk表示匹配角度θt = 8s与理想角度θid差的绝对值,smk值越小,说明匹配得到的起竖角度与理想角度越接近,匹配效果越好。
通过调用ODE45求解器对微分方程组(19)进行解算,并将其嵌入遗传算法主程序,优选过程以适应度的大小区分个体优劣,文中涉及的约束条件为极小值问题,将其转化为适应度函数,可表述如下
| $ Fit = C - smk $ | (24) |
式中C为选定的大正数值。
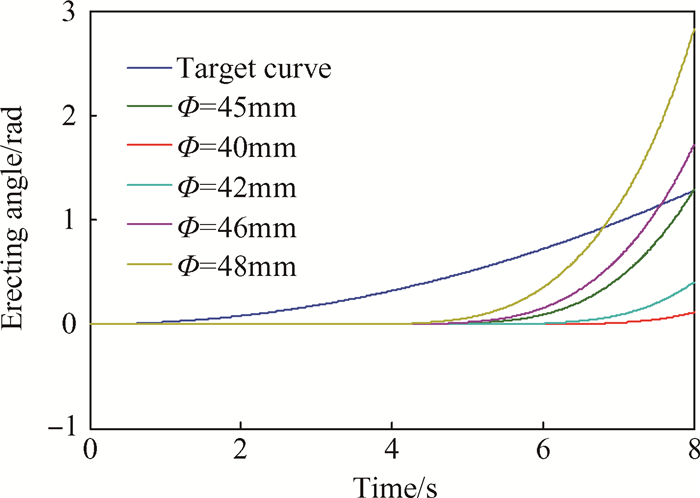
考虑到药柱的结构强度、生产的便利性及燃气发生器空间尺寸的约束,匹配过程将药柱直径限制在[0.02 0.2]范围内,该范围是在前期估算的基础上,确定药柱直径的大致范围,以方便后面遗传算法的匹配和减少运算量、提高解算效率。而药柱长度可通过燃烧时间和药柱燃速加以确定。通过遗传算法程序优选,得出最佳尺寸为45mm,并和直径在40mm,42mm,46mm,48mm下的起竖角度曲线同时与理想角度变化曲线对比,结果如图 3所示。
|
Fig. 3 Erection angle curves of different burning surface |
由图 3可知,规划的目标曲线呈抛物线形式增长,而直径45mm的工况下在8s时的到位角度为1.289rad,与目标角度的误差仅为0.7%。其余四组取值均与理想结果相差较远。但从图中曲线发展规律和离散数据分析可知,45mm工况下的起竖曲线存在蓄气时间过长、加速时间过短的不足,由负载开始运动到起竖至设定角度时间为3.8s,起竖过程的最大过载达到7m/s2,不仅造成起竖过程滞后,还会对机械安全构成威胁。由图中曲线规律,可通过增大药柱直径的方式缩短蓄气时间,而为了兼顾起竖的平稳性,需要将药柱直径限制在较小范围内,且随起竖过程的推进而改变。本文提出一种大截面蓄气、小截面起竖的变截面药柱,即药柱前端直径较大,实现快速蓄能、短时起动;后端直径较小,助力系统平稳、快速起竖。
5.3 动力源结构优化在对动力源结构进行优化时,以药柱直径为优化参数,以起竖时间为优化目标,在确定装药特性的基础上,对直径进行全程优化。优化过程可分为两个阶段:一是蓄气阶段,二是起竖阶段。
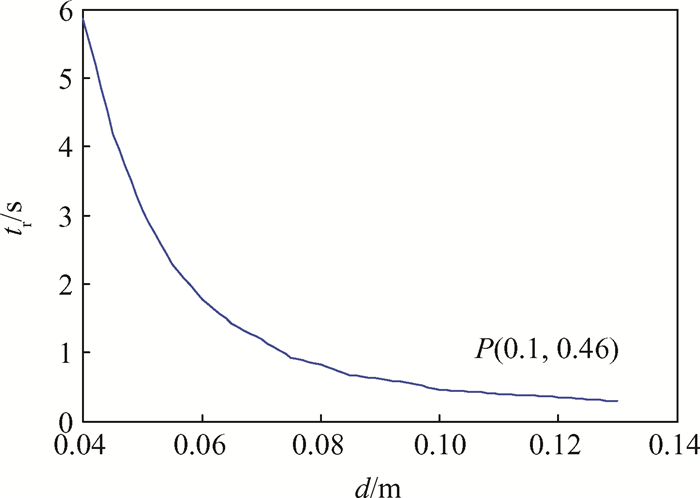
蓄气阶段,通过正向内弹道计算,得出几组直径下对应的蓄气时间tr,并通过插值、线性拟合的方式获取了两者对应的关系曲线,如图 4所示。
|
Fig. 4 Relation of gas inflation time and grain diameter |
图 4中两个变量之间近似呈反比例关系。为缩短蓄气时间,选取0.1m作为蓄气段的药柱直径,如图中P点所示,蓄气时间为0.46s。在0至0.46s内对燃速曲线积分,可得到药柱燃烧的长度约为27mm。
起竖阶段,对药柱前端直径0.1m的工况进行燃烧7.2s,驱动8s条件下的内弹道分析,在药柱后端直径[0.02 0.2]的约束范围内,难以匹配满足起竖角度要求的尺寸。即使将药柱直径缩小至0.01m,8s起竖到位时的角度也远大于设定角度。
由上述分析可知,燃气起竖过程的药柱燃烧时间取值方法与弹射过程有所不同,应另行确定。同时确定合理的药柱直径d,燃烧时间tk和燃气驱动时间tg,需要考虑起竖角度θ,最大过载αmax,起竖时间tg等多个因素,即在满足最大过载要求的前提下,使系统起竖至角度θid的时间最短。采用遗传算法实现上述过程。数学表达可描述为
| $ \left\{ \begin{array}{l} \left| {\theta \left( {I,P} \right) - {\theta _{i{\rm{d}}}}} \right| = \min \left| {{\theta _i}\left( {I,P} \right) - {\theta _{i{\rm{d}}}}} \right|\\ {I^0} \le I \le {I^1}\\ {\alpha _{\max }} \le {\alpha _{\rm{s}}}\\ {t_{\rm{g}}} \to {t_{{\rm{gmin}}}} \end{array} \right. $ | (25) |
式中I为设计变量,i为样本序号,I1,I0为变量的上、下限,P为系统已知参量,αs为设定的过载阈值。
为避免求解过程局部最优解对结果造成的影响,结合药柱的长径比限制、装填的简便性等实际因素,从优化结果中初步确定三组参量组合,Result 1:d = 0.02m, tk = 2s, tg = 5.74s;Result 2:d = 0.03m, tk = 2s, tg = 5.02s;Result 3:d = 0.04m, tk = 1.5s, tg = 4.62s。三组参量组合最终起竖到位角度均为1.28rad,表 1为三种组合下各限制条件的对比结果。
|
|
Table 1 Comparison of three results |
由表 1可知,第三种组合起竖时间较短,更利于快速起竖的要求;且所需药柱的长度相对另外两组也较小,便于实现药柱自由装填和燃气发生器在空间的安装;同时,药柱后端直径达到0.04m,相对前端的0.1m减幅较小,增加了药柱整体的结构强度。虽然第三种组合下产生的最大过载较其他两种略大,但均在负载承受范围之内。综合上述分析,针对本文中的大惯量起竖系统,采用Result 3对应的动力源,起竖效果最佳。
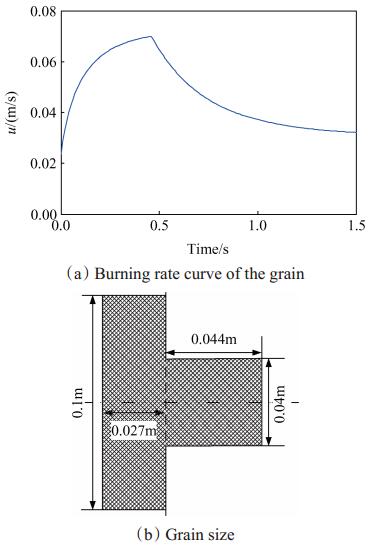
6 结果分析文中设计的动力源为变截面固体药柱,图 5为药柱燃速、燃面随时间变化的对应关系,图 6所示分别为高压室气体压强、温度曲线。
|
Fig. 5 Burning rate and grain size |
|
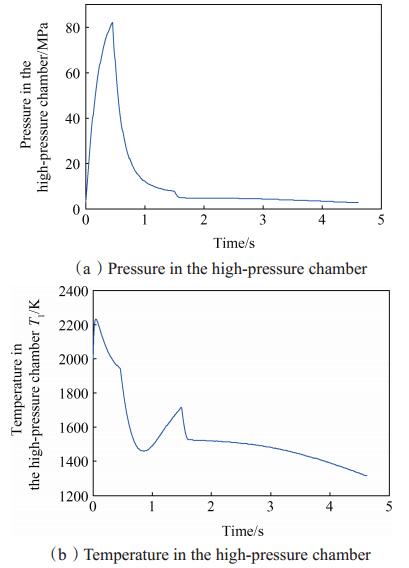
Fig. 6 Pressure and temperature in the high-pressure chamber |
由图 5可知,药柱燃速先增后减,与图 6(a)中高压室压强曲线相互印证。图 6(b)中,高压室温度在短时内增加,其余时间则基本保持减小趋势,究其原因,是高压室自由容积的增加和燃气的不断外流所致。
气体质量决定高压室压强的变化,0.46s之前,压强逐渐增加,而曲线上升率逐渐减小,这是因为高压室自由容积增大的同时,由高压室到低压室的质量流量增加(图 7所示)。0.46s之后,药柱直径由0.1m突变为0.04m,导致燃气生成速率迅速下降,同时,低压室容积增大,高压室内混合气体质量逐渐减小、低压室内气体质量逐渐增加、自由容积继续增大,结合图 7中0.46s之后的流量曲线,可知燃气生成速率远小于流出速率,致使高压室压强下降,与图 6(a)中曲线相吻合。燃速也开始减小,与图 5中曲线相吻合。
|
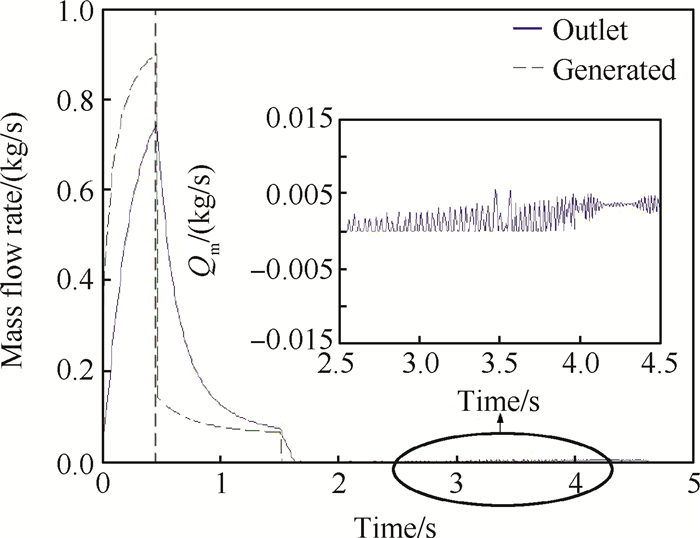
Fig. 7 Mass flow rate curves |
随着药柱直径的变化,燃气生成速率减小,质量流量也逐渐减小,如图 7所示。
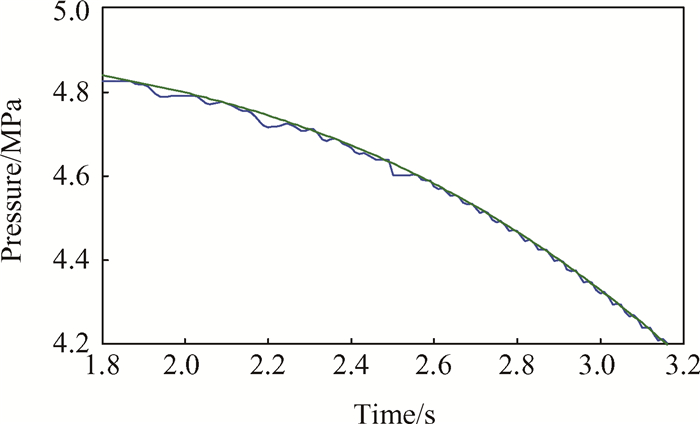
图 7中所示喷口流出气体质量流量曲线的变化趋势与图 6(a)高压室压强曲线的变化趋势极为相似,究其原因,由公式(8)可知,质量流量的大小主要取决于高压室与低压室压差,而高压室压强远大于低压室压强,因此,质量流量受高压室压强影响较大。随着高温高压燃气不断由高压室流入低压室,高、低压室压差逐渐变小,质量流量也不断减小。药柱直径的突变加剧了该过程,1.5s之后,质量流量基本为0,即高、低压室内的气体质量保持恒定。在2~ 4.5s之间,质量流量会有小幅的波动。究其原因,当高、低压室压强相等时,质量流量为0,而负载继续运动,低压室压强继续下降,质量流量有所增加,达到一定值又开始下降,如此反复数个周期。图 8,图 9所示为低压室压强变化及稳定段高、低压室压强交替增减的过程。
|
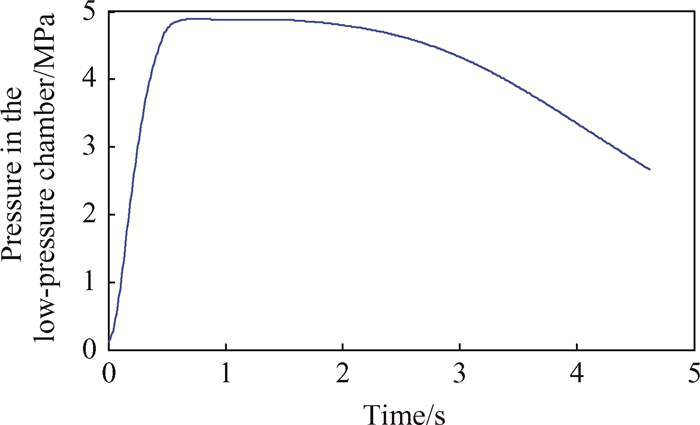
Fig. 8 Pressure in the low-pressure chamber |
|
Fig. 9 Pressure in the high-pressure chamber and lowpressure chamber in stability |
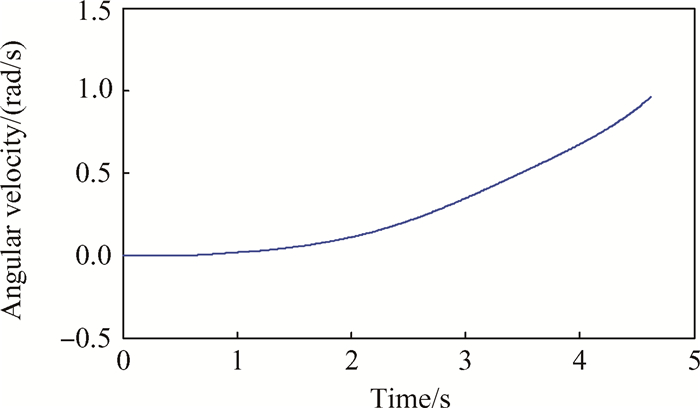
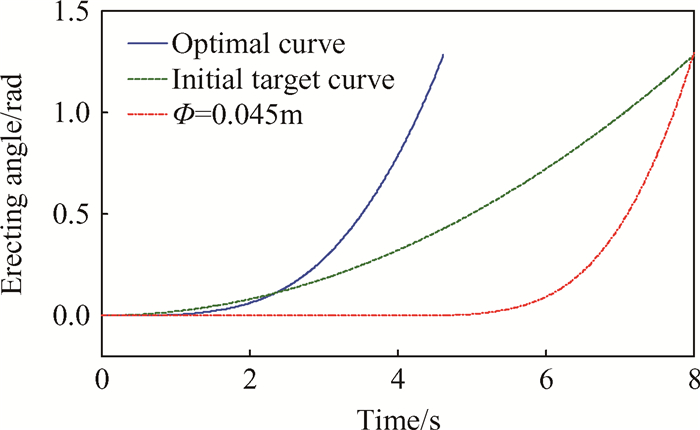
随着气体不断由喷口流入低压室(图 7所示),低压室内气体质量随之增加,低压室压强也逐渐增大,但压强增大的同时,低压室体积也随着负载的运动而增加,从而降低了低压室压强增长的速率,0.46s之后,质量流量开始减小,压强开始减小。由图 8可知,当低压室压强增加至4.8MPa后开始缓慢下降,在0.5~2s基本保持恒定,2~4.6s下降段也相对较为平缓,即可确保负载保持匀加速运动起竖至设定角度,最大过载为0.35g,如图 10,11所示,说明所设计动力源可实现文中大惯量起竖系统快速、平稳起竖。且从图 11中优化曲线与药柱直径为45mm时角度曲线的对比结果可看出,优化曲线较大幅度的缩短了蓄气时间;与初始设定的目标曲线对比看出,整个起竖过程所需要的时间也大幅缩短,实现了快速起竖的目的。
|
Fig. 10 Erection angular velocity curve |
|
Fig. 11 Optimal result of the erection angle curve |
通过本文研究,得出以下结论:
(1) 采用燃气-液压混合驱动的起竖方案可解决传统起竖方式起竖缓慢、动力源能量密度低等问题,但要对动力源进行设计和优化,需采用变截面固体药柱实现该方案的高速、平稳起竖要求。
(2) 在考虑燃气气粒两相性的起竖系统一体化模型基础上,设定了燃气驱动8s,起竖至1.28rad的初步方案,计算得到一种直径为45mm的药柱,并采用遗传算法对该药柱进行了优化,最终确定一种前端直径0.1m,后端直径0.04m的变截面药柱。
(3) 通过正向内弹道分析,得出本文设计方案可使负载在4.62s起竖至1.28rad,且整个起竖过程的最大过载小于0.35g,可实现快速、平稳起竖的要求。
| [1] |
李良, 谢建, 黄建招. 大型起竖系统建模与辨识研究[J]. 机床与液压, 2013, 41(16): 147-150. DOI:10.3969/j.issn.1001-3881.2013.16.044 (  0) 0) |
| [2] |
黄先祥, 高钦和, 郭晓松. 大型装置起竖过程的动力学建模研究[J]. 系统仿真学报, 2002, 14(3): 271-273. (  0) 0) |
| [3] |
姚晓光, 郭晓松, 冯永保, 等. 导弹起竖过程的载荷研究[J]. 兵工学报, 2008, 29(6): 718-722. (  0) 0) |
| [4] |
马长林, 黄先祥, 李锋, 等. 大型装置起竖系统智能积分控制仿真研究[J]. 兵工学报, 2008, 29(2): 227-231. (  0) 0) |
| [5] |
李良, 李锋, 冯永保, 等. 基于自适应模糊滑模的大型液压起竖系统控制策略研究[J]. 兵工学报, 2016, 37(1): 71-76. (  0) 0) |
| [6] |
谢政, 谢建, 杜文正, 等. 大型发射装置液压起竖系统的滑模控制研究[J]. 兵工学报, 2015, 36(4): 674-680. (  0) 0) |
| [7] |
冯江涛, 高钦和, 管文良, 等. 多级液压缸建模及级间缓冲研究[J]. 兵工学报, 2016, 37(12): 2268-2276. DOI:10.3969/j.issn.1000-1093.2016.12.012 (  0) 0) |
| [8] |
唐卫华, 王三民, 袁茹. 发射装置起竖动力学分析及驱动方式优选[J]. 弹箭与制导学报, 2006, 27(2): 325-327. (  0) 0) |
| [9] |
田桂, 谢建, 陈永宁, 等. 导弹起竖过程轨迹规划及跟踪控制研究[J]. 系统仿真学报, 2012, 24(11): 2356-2371. (  0) 0) |
| [10] |
Yongquan Liu, Anmin Xi. An Interior Trajectory Simulation of the Gas-Steam Missile Ejection[J]. Journal of Computers, 2013, 8(5): 235-237.
(  0) 0) |
| [11] |
蒋淑园, 王浩, 阮文俊. 高压弹射装置内弹道二维模型及发射腔内流场特性分析[J]. 兵工学报, 2015, 36(6): 1009-1014. (  0) 0) |
| [12] |
Mortazavi M, Askari A. The Utilization of High Fidelity Simulation in the Support of UAV Launch Phase Design: Three Case Studies[J]. Journal of Aerospace Science & Technology, 2012, 9(2): 45-54.
(  0) 0) |
| [13] |
蔡云鹏, 闫建国, 王亮. 无人机发射过程建模与控制方法研究[J]. 飞行力学, 2010, 28(1): 80-83. (  0) 0) |
| [14] |
Charles K, Marietta G. Jump Strut Landing Gear Apparatus and System[P]. US: 4687158, 1987-08-18.
(  0) 0) |
| [15] |
邵亚军, 张炜, 高钦和, 等. 燃气-液压混合驱动的大型起竖系统内弹道设计[J]. 推进技术, 2017, 38(9): 1956-1962. (SHAO Ya-jun, ZHANG Wei, GAO Qin-he, et al. Interior Ballistic Design for Large Erecting System Based on Hybrid Drive of Gas and Hydraulics[J]. Journal of Propulsion Technology, 2017, 38(9): 1956-1962.)
(  0) 0) |
| [16] |
Cengel Yunus A, Boles Michael A. Thermodynamicsan Engineering Approach[M]. USA: McGraw-Hill, 2002.
(  0) 0) |
| [17] |
胡松启, 李葆萱. 固体火箭发动机燃烧基础[M]. 西安: 西北工业大学出版社, 2014.
(  0) 0) |
| [18] |
向红军, 方国尧. 翼柱型装药燃烧室三维非定常湍流的数值模拟[J]. 推进技术, 2000, 21(4): 27-31. (XIANG Hong-jun, FANG Guo-yao. Numerical Simulation of 3-D Unsteady Turbulent Flow in SRM Chamber with Finocyl Grain[J]. Journal of Propulsion Technology, 2000, 21(4): 27-31.)
(  0) 0) |
| [19] |
姚琳, 马大为, 马吴宁, 等. 两级提拉式单侧弹射装置内弹道建模与优化[J]. 兵工学报, 2017, 38(3): 466-475. (  0) 0) |
| [20] |
张小飞. 凝聚相微粒对固体火箭发动机点火过程影响[D]. 哈尔滨: 哈尔滨工程大学, 2009. http://d.wanfangdata.com.cn/Thesis/Y1654536
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

