吸气式高超声速飞行器利用空气作为氧化剂,发动机比冲高,极具发展潜力和研究价值,各国对吸气式高超声速飞行器的研发热情巨大。相对于火箭动力飞行器,吸气式高超声速飞行器一般采用机体/推进一体化构型,一体化问题是该类飞行器的关键技术,飞行器内流和外流之间存在严重的耦合关系,主要表现在自由空气来流经进气道和隔离段后为燃烧室提供氧化剂,压缩空气与燃料混合燃烧后经尾喷管膨胀加速产生推力,但在亚燃模态下,燃烧室流场壅塞产生的反压会反作用于隔离段,改变隔离段中的波系组织,进而导致燃烧室流态的改变,两者相互作用最终达到平衡。早期的吸气式飞行器一体化问题分析主要基于工程估算。常用的方法包括激波-膨胀波法和零维燃烧室分析模型等,主要用于前期的吸气式飞行器的动力学特性分析[1]。但工程估算精度难以满足现在的工程需求,风洞试验和CFD是当今研究一体化的主流手段。
为了研究一体化构型的气动特性,NASA设计了一个HXLV(包括助推器、连接段和X-43A)的3%尺寸缩比模型,在LRC20英寸马赫数为6的风洞和31英寸马赫数为10的风洞中进行吹风试验,同时为了研究HXLV级间分离的稳定性问题,在AEDC(Arnold Engineering Development Center)Von Karman实验室对8.33%尺寸缩比模型进行了马赫数为6的风洞试验[2, 3]。
由于实验成本高、周期长,尤其对于大尺寸吸气式飞行器,地面设施无法对全尺寸飞行器进行风洞试验,故CFD在机体/推进一体化研究中发挥了很大的作用。Cockrell等[4]使用商业软件GASP(General Aerodynamics Simulation Program)对X-43A的气动/推进一体化流场进行数值模拟,得到了大量的气动数据,包括流场特征、表面压强分布以及全机的气动力和力矩,并与实验数据进行了大量对比,发现CFD计算结果与实验结果吻合较好;Parikh等[5]使用NASA LRC开发的非结构CFD软件包TetrUSS对HXLV整机进行了数值模拟,考察了不同马赫数、攻角、侧滑角和舵面偏转角的影响,并将结果与试验数据进行对比发现,两者吻合良好。
由于气动和推进学科的数值计算分析方法存在较大差异,主要体现在推进学科分析需考虑燃烧室中复杂的燃烧化学反应问题,且燃烧的数值计算和外气动的数值计算时间尺度差异较大,故采用完全的数值方法分析气动/推进一体化性能将会导致计算量过大,故一般采用分段松耦合计算的方法,将气动和推进学科人为地分开后分别进行计算。
郭金磊等[6]改进了冲压发动机燃烧室计算的一维流方法,石喜勤,Chen Bing等[7, 8]通过数值CFD方法分别计算外流场和燃烧室,通过预先给定一个进气道背压,计算得到进气道出口气流特性数据,作为燃烧室的计算入口边界条件,燃烧室计算过程中通过外插手段反馈得到燃烧室入口压强,以此作为进气道计算的新的背压,通过数轮相互迭代耦合从而实现内外流场相互匹配。Kerith Numbers[9, 10]通过CFD和一维流相结合的方法研究了气动/推进的耦合分析方法,通过引入特征线法计算扰动的传播问题,并通过时间步迭代完成气动/推进耦合界面的匹配。此外,Malcolm Rowe[11]和William等[12]通过试验手段研究了进气道和燃烧室之间的数据匹配问题,Denny A G等[13]基于NS方程求解和零维发动机模型研究了F-16,F-18和A-10等飞机的进气道和发动机的耦合问题,Murma S M等[14]针对F16战机利用数值方法对外流和进气道、发动机的内部流场之间的耦合问题进行了分析,Campbell J L[15, 16],Beverly Duncan[17],Sung[18, 19]和Rodrick V Chima[20]等分别针对不同的构型利用不同的方法研究了进气道和发动机界面之间的耦合分析问题。
吸气式飞行器内外流一体化快速分析是前期设计和飞行动力学特性分析的前提和关键,一维流理论是吸气式动力系统快速分析的常用手段,基于一维流理论代替复杂的燃烧室和预燃激波串模型,通过与CFD方法相结合,可完成一体化性能的快速分析。
本文针对双模态超燃冲压发动机的背压耦合求解存在较大困难的问题,基于准一维流方法建立预燃激波串和冲压燃烧室的准一维流模型,在亚燃模态,考虑热力喉道及背压问题,实现双模态超燃冲压发动机的内流耦合分析,通过迭代方法实现隔离段中激波串和燃烧室中反压的匹配,计算结果分别与相关文献的直连试验和本课题组的自由射流试验结果对比,验证了方法的有效性,具有重要的工程应用背景和理论研究价值。
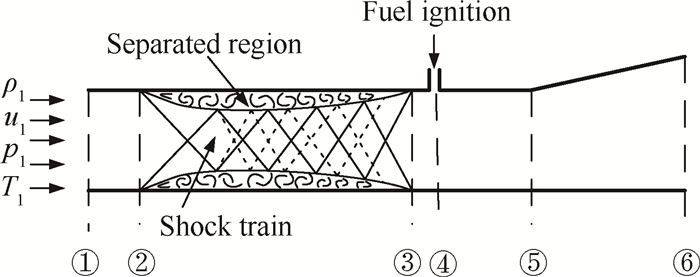
2 准一维流分析方法双模态冲压发动机准一维流分析需考虑亚燃、超燃以及亚/超混合等工作模态,在冲压燃烧室的背压作用下,隔离段中会出现伪激波串,而燃烧室下游则出现热力喉道等现象,如图 1所示。为得到准确的发动机性能,需通过一维流理论描述上述流动现象。
|
Fig. 1 Flow characteristic of dual mode scramjet |
一般给定隔离段入口气流参数,作为耦合求解的边界条件。对于冲压发动机,燃料从喷注点注入流道后经燃烧释热,增大流道压强进而产生推力,当加热量达到一定程度将会出现热壅塞,进而产生背压,改变燃烧室的进口气流参数,隔离段出现分离区,核心流产生激波串,使隔离段出口气流减速增压以匹配燃烧室入口条件。
2.1 隔离段准一维流控制方程基于隔离段控制体的分析可知,马赫数、速度、温度、压强、密度和核心流面积等均为未知流动特性(非独立变量),而几何面积、摩擦和热增长均为独立变量。
对于附着流,核心流面积可认为与几何面积相等,则马赫数的常微分方程为
| $ \begin{array}{l} \frac{{{\rm{d}}M{a^2}}}{{M{a^2}}} = - \frac{{2\left( {1 + \left( {\gamma - 1/2} \right)M{a^2}} \right)}}{{1 - M{a^2}}}\frac{{{\rm{d}}A}}{A} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{\left( {1 + \gamma M{a^2}} \right)\left( {1 + \left( {\gamma - 1/2} \right)M{a^2}} \right)}}{{1 - M{a^2}}}\frac{{{\rm{d}}{T_{\rm{t}}}}}{{{T_{\rm{t}}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{\gamma M{a^2}\left( {1 + \left( {\gamma - 1/2} \right)M{a^2}} \right)}}{{1 - M{a^2}}}\frac{{4{C_{\rm{f}}}{\rm{d}}x}}{{{D_{\rm{H}}}}} \end{array} $ | (1) |
给定管道的面积分布A(x),水利直径DH(x),总温分布Tt(x)和蒙皮阻力系数Cf(x),可通过积分求解上式。
对于分离流,气流的实际有效流通面积一般小于几何面积,额外的核心流面积分布函数Ac(x)必须给定[21]。
| $ \begin{array}{l} \frac{{{\rm{d}}\left( {{A_{\rm{c}}}/A} \right)}}{{{A_{\rm{c}}}/A}} = \left[ {\frac{{1 - M{a^2}\left( {1 - \gamma \left( {1 - {A_{\rm{c}}}/A} \right)} \right)}}{{\gamma M{a^2}{A_{\rm{c}}}/A}}} \right]\frac{{{\rm{d}}p}}{p} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\frac{{1 + \left( {\gamma - 1} \right)M{a^2}}}{{2{A_{\rm{c}}}/A}}} \right)4{C_{\rm{f}}}\frac{{{\rm{d}}x}}{D} + \left( {1 + \frac{{\gamma - 1}}{2}M{a^2}} \right)\frac{{{\rm{d}}{T_{\rm{t}}}}}{{{T_{\rm{t}}}}} \end{array} $ | (2) |
气流马赫数和核心流通面积方程可通过多方程的ODE求解器进行积分求解。但求解之前需预知压强分布。对于该情况,Ortwerth基于试验数据发展了管流中压力梯度计算经验公式[22]。
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}x}} = \frac{k}{{2{D_{\rm{H}}}}}{C_{{\rm{f0}}}}\left( {\gamma pMa} \right) $ | (3) |
式中DH是管道的水力直径,Cf0是分离点处的摩擦系数,(γpMa)/2表示气流动压,k是经验常数,本文取100.5。
2.2 燃烧室准一维流控制方程燃烧室准一维流控制方程参考文献[23]。为简化一维流分析,利用经验公式计算燃料喷注后的释热规律[24]。
| $ \tau \left( x \right) = 1 + \left( {{\tau _{\rm{b}}} - 1} \right)\frac{{\theta \bar x}}{{1 + \left( {\theta - 1} \right)\bar x}}\left( {\theta \ge 1} \right) $ | (4) |
| $ \tau \left( x \right) = {T_{\rm{t}}}/{T_{{{\rm{t}}_2}}} $ | (5) |
| $ \bar x = \left( {x - {x_{\rm{i}}}} \right)/\left( {{x^4} - {x_{\rm{i}}}} \right) $ | (6) |
式中xi为加热或超声速燃烧开始的轴向位置。θ为经验常数,一般取1~10,取决于燃油喷射和油气混合的模式。
| $ {\tau _{\rm{b}}} = {T_{{{\rm{t}}_4}}}/{T_{{{\rm{t}}_2}}} $ | (7) |
基于释热经验公式可得到燃烧室沿程的总温分布,代入燃烧室守恒控制方程,利用ODE求解器可得到沿程的其他流动参数。
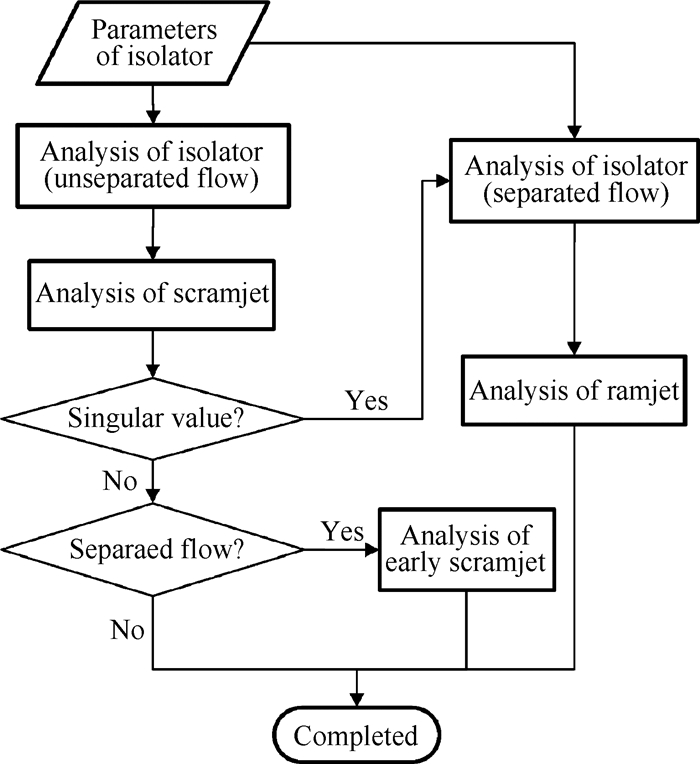
3 内流耦合求解方法耦合分析主要处理燃烧室背压的产生和匹配问题,基于迭代的思想实现隔离段和燃烧室之间的流动参数匹配。针对耦合求解过程中可能出现的情况,需通过适当的方法加以判别,耦合求解流程如图 2所示。双模态超燃冲压发动机的工作过程主要包括亚燃模态、超燃模态和亚/超混合模态(早期超燃模态),其中亚燃模态和亚/超混合模态均出现大范围的边界层流动分离现象,求解方法类似。
|
Fig. 2 Solution process of dual mode scramjet |
对于给定的隔离段入口数据,假定未出现任何分离流,进行超燃模态分析,基于超燃模态分析结果进行判断:(1)若求解过程出现奇异(Ma=1)现象,则进行亚燃模态分析;(2)若求解过程未出现奇异现象,则判定是否出现早期超燃模态,若未出现则发动机处于超燃模态,分析求解完成。
3.1 燃烧室壅塞问题分析对于超声速燃烧,直接求解常微分方程组,但对于亚声速燃烧,需考虑热壅塞问题,管流中的马赫数控制方程(忽略摩擦和质量添加)为
| $ \begin{array}{l} \frac{1}{{M{a^2}}}\frac{{{\rm{d}}M{a^2}}}{{{\rm{d}}x}} = - \frac{{2\left( {1 + \left( {\gamma - 1/2} \right)M{a^2}} \right)}}{{1 - M{a^2}}}\frac{1}{A}\frac{{{\rm{d}}A}}{{{\rm{d}}x}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\left( {1 + \gamma M{a^2}} \right)\left( {1 + \left( {\gamma - 1/2} \right)M{a^2}} \right)}}{{1 - M{a^2}}}\frac{1}{{{T_{\rm{t}}}}}\frac{{{\rm{d}}{T_{\rm{t}}}}}{{{\rm{d}}x}} \end{array} $ | (8) |
引入函数G将式(8)改写为
| $ \frac{1}{{M{a^2}}}\frac{{{\rm{d}}M{a^2}}}{{{\rm{d}}x}} = \frac{{G\left( x \right)}}{{1 - M{a^2}}} $ | (9) |
其中
| $ G = \left( {1 + \frac{{\gamma - 1}}{2}M{a^2}} \right) \times \left[ { - 2\frac{1}{A}\frac{{{\rm{d}}A}}{{{\rm{d}}x}} + \left( {1 + \gamma M{a^2}} \right)\frac{1}{{{T_{\rm{t}}}}}\frac{{{\rm{d}}{T_{\rm{t}}}}}{{{\rm{d}}x}}} \right] $ | (10) |
为保证方程在壅塞点(Ma=1)处解的存在性,G函数必须等于0,采用洛必达法则可知
| $ {\left( {\frac{1}{{M{a^2}}}\frac{{{\rm{d}}M{a^2}}}{{{\rm{d}}x}}} \right)^ * } = \frac{{\left( {{\rm{d}}G\left( x \right)/{\rm{d}}x} \right)}}{{ - \left( {{\rm{d}}M{a^2}/{\rm{d}}x} \right)}} $ | (11) |
重组上式可得
| $ \frac{{M{a^3}}}{{{{\left( {Ma - 1} \right)}^2}}}\frac{{{\rm{d}}{{\left( {Ma - 1} \right)}^2}}}{{{\rm{d}}x}} = \frac{{ - G\left( x \right)}}{{{{\left( {Ma - 1} \right)}^2}\left( {Ma + 1} \right)}} $ | (12) |
由上式可知,当G > 0时,驱使马赫数逐渐趋近于1,当G < 0时,驱使马赫数远离1。故在亚燃模态下,沿流道通过壅塞点时,G函数应从正到负并在壅塞点处等于0。在实际求解过程中,流道沿程可能出现两次G函数穿越0的情形,其中G函数从负到正的零点并非燃烧室的真实壅塞点,求解过程中可以忽略。
对于燃烧室壅塞问题,假设壅塞点位置为xs,壅塞点之前(xs-)的流道性能参数可采用燃烧室守恒控制方程组进行常微分求解得到,该方法也适用于壅塞点后(xs+)的流场求解。但由于微分方程在壅塞点处求解存在一定的困难,亚声速燃烧控制方程求解将在此处中止,壅塞点后的流场求解需重新给定初值。此处采用“激波跳跃”关系式求解特征点后的流场参数,经激波跳跃后亚声速气流转变为超声速。
| $ Ma_{{{\rm{s}}^ + }}^2 = \frac{{1 + \frac{{\gamma - 1}}{2}Ma_{{{\rm{s}}^ - }}^2}}{{\gamma Ma_{{{\rm{s}}^ - }}^2 - \frac{{\gamma - 1}}{2}}} $ | (13) |
| $ \frac{{{\rho _{{{\rm{s}}^ + }}}}}{{{\rho _{{{\rm{s}}^ - }}}}} = \frac{{\gamma - 1}}{{\gamma + 1}} + \frac{2}{{\left( {\gamma + 1} \right)Ma_{{{\rm{s}}^ + }}^2}} $ | (14) |
| $ \frac{{{T_{{{\rm{s}}^ + }}}}}{{{T_{{{\rm{s}}^ - }}}}} = \frac{{{{\left( {\gamma + 1} \right)}^2}Ma_{{{\rm{s}}^ + }}^2}}{{\left[ {2 + \left( {\gamma - 1} \right)Ma_{{{\rm{s}}^ + }}^2} \right]\left[ {2\gamma Ma_{{{\rm{s}}^ + }}^2 - \left( {\gamma - 1} \right)} \right]}} $ | (15) |
| $ \frac{{{\rho _{{{\rm{s}}^ + }}}}}{{{\rho _{{{\rm{s}}^ - }}}}} = \frac{{\gamma + 1}}{{2\gamma Ma_{{{\rm{s}}^ + }}^2 - \left( {\gamma - 1} \right)}} $ | (16) |
激波跳跃关系是气流在极端条件下产生的正激波的逆过程,通过激波跳跃关系给出壅塞点后的气流参数,以此为初值求解燃烧室的剩余部分。
3.2 隔离段与燃烧室参数匹配对于亚燃冲压燃烧室,假设其入口马赫数为Ma4i,且Ma4i < 1,根据给定的隔离段入口状态确定燃烧室入口(即隔离段出口)的其他气流参数(如p4i,ρ4i和T4i等),通过迭代寻找到合适的Ma4i,并计算得到壅塞点位置xs,该位置应满足如下关系
| $ \begin{array}{*{20}{c}} {{x_{\rm{s}}} = x\left( {Ma = 1} \right) = x\left( {G = 0} \right)}\\ {{G_{{{\rm{s}}^ - }}} > 0,{G_{{{\rm{s}}^ + }}} < 0} \end{array} $ | (17) |
由于初始马赫数的猜测值并无严格的理论依据,故可能会出现以下两类情形:
(1) 初始猜测值过小。当初始猜测值过小,燃烧室中燃料释放的热量可能无法保证气流在流道中发生热壅塞,此时燃烧室流道中出现最大马赫数Mamax < 1的情形。
(2) 初始猜测值过大。当初始猜测值过大,则在燃料释热的影响下管流中的马赫数快速趋近于1,但此时函数G并不等于0,即该结果并非最终的收敛结果,燃烧室会产生背压驱使入口气流参数发生改变,并最终达到式(17)的平衡关系。
为确保得到合理的入口条件,通过打靶法确定燃烧室的入口马赫数。在亚燃模态,燃烧室入口气流为亚声速,引入一个小数ε1作为误差因子,令入口的最大可能马赫数Ma4i, max = 1 -ε1;在燃烧室背压作用下,分离区的再附点可能会被完全推出燃烧室,即整个分离区均位于隔离段内,此时再附点处的马赫数MaR是燃烧室入口可能出现的最小马赫数,但考虑到核心流和隔离段壁面附近低速气流的相互掺混作用而导致最终气流马赫数仍可能进一步降低,故燃烧室入口的最小可能马赫数Ma4i, min = kMaR,其中k是比例因子,本文取0.8。最大和最小马赫数的取值并不影响最终的计算结果精度,但会影响迭代次数,若为早期超燃模态,最大马赫数Ma4i, min应为超声速,可取为隔离段的入口马赫数。
匹配分析的输入条件包括:燃油喷注位置xi,燃油喷注量
隔离段与燃烧室参数匹配分析过程为:
(1) 设置燃烧室入口气流马赫数初始猜测值Maguess =(Ma4i, min + Ma4i, max)/2,基于隔离段入口参数Si和分离区分析结果,得到燃烧室入口的初始状态参数Sguess。
(2) 已知燃烧室入口气流状态参数、燃油喷注位置和喷注量,通过ODE方法求解燃烧室守恒控制方程,得到燃烧室性能数据。计算过程若出现奇异(Ma = 1)情况,则迭代中止,仅记录该位置之前的状态参数。
(3) 基于燃烧室分析结果,计算迭代误差e,若误差满足要求,则中止迭代,结合激波跳跃关系求解壅塞点后的燃烧室状态参数。否则进行如下判断:(1)若燃烧室全流道的最大马赫数小于1,则令Ma4i, min = Maguess,并转入步骤(1)重新分析。(2)若流道中出现奇异值,则令Ma4i, max = Maguess,并转入(1)重新分析。
为保证迭代收敛,需给出合理的误差判别方法。由燃烧室中热壅塞的分析可知,当热壅塞现象出现时,应满足xs = xMa = 1 = xG = 0,引入误差因子ε2,当迭代收敛时,误差应满足式(18)的要求。
| $ e = \left| {{x_{Ma = 1}} - {x_{G = 0}}} \right| \le {\varepsilon _2} $ | (18) |
当迭代未收敛时,流道沿程可能并无函数G等于0的点出现,故在正式迭代分析之前,针对Ma4i, min的状态进行燃烧室分析,并记录最大马赫数Mamax出现的位置xMamax,此位置是热壅塞最可能发生的位置,当迭代过程中没有出现G = 0的情况时,用xMamax代替xG = 0计算误差函数e。
4 计算结果与讨论为量化分析和试验结果的对比,采用了两类误差:(1)关键位置(分离点、峰值压强点等)预测误差。(2)压强预测误差。
位置误差可表示为
| $ err = \frac{{\left| {{x_{\rm{a}}} - {x_{\rm{t}}}} \right|}}{{{L_{\rm{c}}}}} \times 100\% $ | (19) |
式中xa是分析位置点,xt是测试位置点,Lc是流道长度。
压强误差可表示为
| $ err = \frac{{\left| {{p_{\rm{a}}} - {p_{\rm{t}}}} \right|}}{{{p_{\rm{t}}}}} \times 100\% $ | (20) |
式中pa是计算压强,pt是试验压强。平均压强误差为沿流道取若干点处的压强误差后取平均,可表示为
| $ err = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {\frac{{\left| {{p_{\rm{a}}} - {p_{\rm{t}}}} \right|}}{{{p_{\rm{t}}}}}} \right)}_i} \times 100\% } $ | (21) |
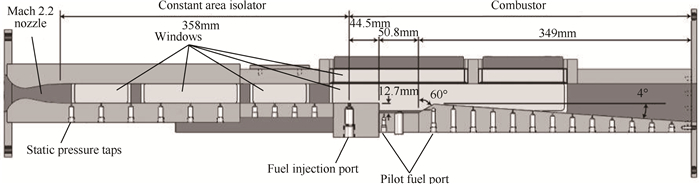
通过试验对比以验证准一维流耦合分析方法,参考文献[25]中的双模态超燃冲压发动机直连试验结果,该试验的试验模型如图 3所示。
|
Fig. 3 Model of connect-direct test |
试验模型的隔离段入口尺寸为25.4mm × 28.1mm,其它尺寸可参考图 3。试验模型采用等直隔离段,燃烧室为等直和微扩张的两段式布局。选取文献中的6个试验状态结果进行对比,试验状态(马赫数、总压、总温、当量比)如表 1所示。
|
|
Table 1 Test states |
以燃料喷注点作为坐标原点,基于准一维流方法计算隔离段和燃烧室的流场参数,选取压强作为计算和试验的对比参数,给出流道的沿程压强分布曲线,最终的一维流分析结果与试验测试结果的对比如图 4所示。

|
Fig. 4 Comparison of pressure distribution in the channel |
图 4中,x=0位置是燃料喷注点。试验状态1~3的模型入口马赫数、总压和当量比均相同,总温不断增大。低总温下发动机处于亚燃工作模态,随着来流总温增加,燃烧室释热效率不断减小,在1400K总温下释热不足以产生热壅塞,发动机由亚燃转入超燃模态。试验状态4~6的模型入口马赫数、总压和总温均相同,燃油当量比不断减小,随着燃料喷注量减少,燃烧室中释热量不足以产生热壅塞,发动机由亚燃模态转为超燃模态。
当发动机处于亚燃模态,隔离段出现压升现象,对比试验和分析结果可知,准一维流可很好地预测隔离段中的流动分离点(压升起始点),在不同的来流参数下,预测位置的相对误差在1.4%~11.2%,但预测的流道峰值压强相对于试验结果偏大,误差在15.6%~21.6%,在稳焰凹腔作用下,亚燃燃烧室在燃油喷注点后压强变化平缓,准一维流分析并未考虑凹腔作用,故预测的压降位置较试验结果有所提前,但整体上计算结果与试验结果变化趋势基本一致,流道沿程的压强预测平均误差在9.6%以内。
在超燃模态,等直隔离段中无分离流出现,沿程压强基本一致。在燃料喷注点后,由于燃烧释热,流道压强增大,但进入扩张段,由于流道面积的增加,燃烧室出现压降。超燃模态下的数值计算结果与试验结果变化趋势基本一致,尤其是峰值压强及其发生位置,峰值压强预测误差小于3.75%,峰值压强的发生位置预测误差小于2%。
由对比结果可知,本文方法在亚燃模态下的隔离段压升预测和背压匹配问题上均有较好的预测精度,在超燃模态下,沿程压强与试验结果基本一致。
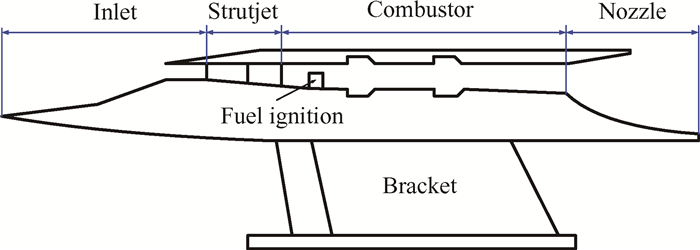
4.2 RBCC动力系统准一维流分析亚燃模态和超燃模态是RBCC动力系统的两个主要工作模态,由于存在引射火箭,故准一维流分析时流道处理方式与一般的双模态超燃冲压发动机有所区别。本文针对中心支板式RBCC飞行器,研究其一体化性能,自由射流试验模型示意图如图 5所示。
|
Fig. 5 Free jet test model of RBCC vehicle |
一体化试验飞行器总长3.75m,由于主火箭支板具有一定的长度和厚度,在准一维流分析中需考虑流道面积的突变。
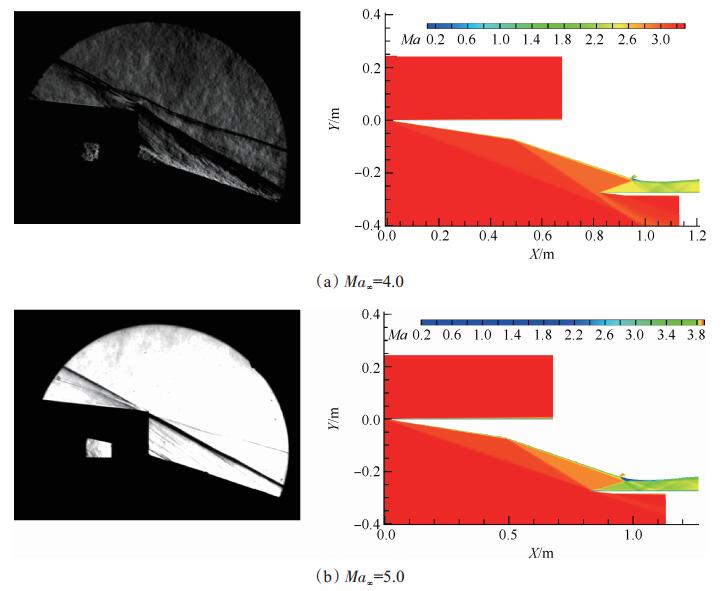
一体化自由射流试验在马赫4和5状态下进行,试验攻角为0°。准一维流分析包含隔离段和燃烧室两部分,隔离段入口边界条件通过进气道的CFD计算得到,计算条件与试验来流条件一致,采用KOmega SST湍流模型,进气道出口设为压力出口,经CFD计算后采用质量平均得到出口气流参数,该参数是准一维流分析的入口边界条件。进气道的马赫数计算云图和试验纹影图如图 6所示。
|
Fig. 6 Schlieren and nephogram of inlet |
进气道设计马赫数为5,在马赫5状态下激波封口,马赫4状态下出现溢流。CFD计算结果和试验纹影图均验证了该现象,且两者所描述的进气道外压缩波系位置基本一致。
基于CFD计算结果得到进气道出口条件如表 2所示。该参数是准一维流求解的入口边界条件。
|
|
表 2 Performance of the inlet |
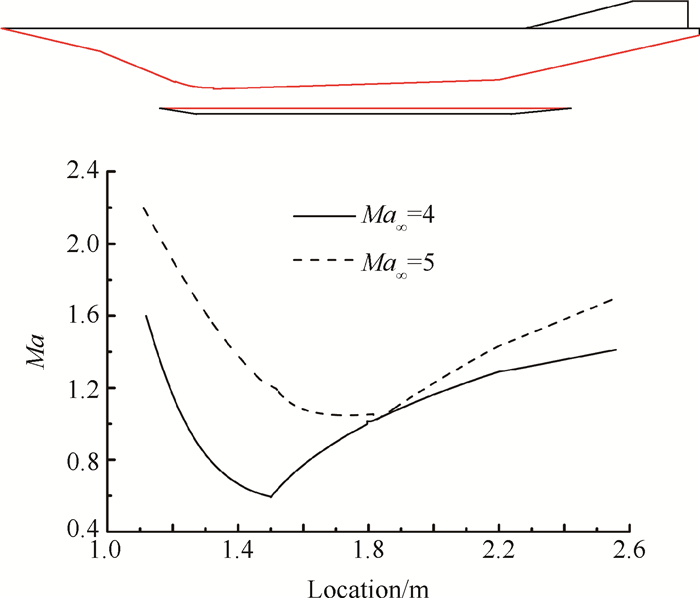
流道全长3.75m,沿程参数分布以飞行器头部作为坐标原点,基于准一维流分析可得到流道的沿程马赫数曲线,如图 7所示。
|
Fig. 7 Mach number distribution of the channel |
由马赫数曲线可知RBCC发动机在Ma4试验条件处于亚燃模态,并在沿程x=1.82m处发生热壅塞。Ma5条件下发动机流道全程超声速,但出现了大范围的流动分离现象,隔离段中的斜激波串使流道内的气流马赫数大大减小,该条件下发动机处于早期超燃模态。
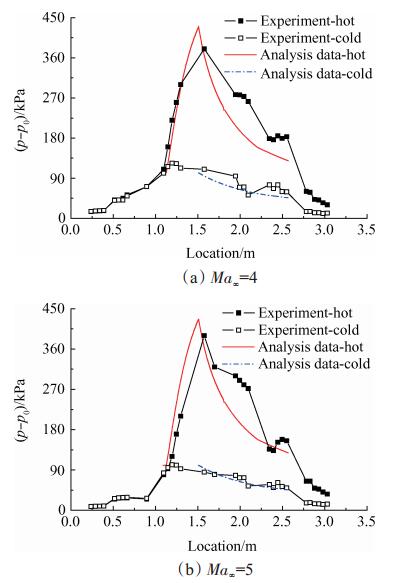
基于准一维流的压强分析结果和飞行器全流道自由射流试验结果对比如图 8所示。
|
Fig. 8 Channel pressure distribution of RBCC vehicle |
基于准一维流的耦合分析结果包括隔离段和燃烧室,自由射流试验结果给出了全流道(进气道、隔离段、燃烧室和内喷管)沿程压强分布,计算和试验包括热态(发动机工作)结果和冷态(发动机不工作)结果。
在冷态条件下,由于燃烧室中稳焰凹腔的作用,流道沿程压强在x=2.0m和x=2.5m处出现振荡,导致计算结果与试验结果出现一定误差,但整体变化趋势基本一致。
在热态条件下,由于燃烧室热壅塞导致室压大幅上升,隔离段中出现陡峭的压升曲线,由对比结果可知,基于准一维流的隔离段压升点预测与试验基本相同,误差不大于2.1%,压升曲线的上升趋势与试验结果基本一致,流道沿程压强的平均误差在10.5%以内,峰值压强的分析结果略大于试验结果,Ma4试验条件下误差为13.2%,Ma5试验条件下误差为10.8%。燃料喷注点后压强处于下降趋势,计算结果与试验值误差较上升段略大,但趋势基本一致,误差增大的主要原因是试验结果在燃烧室凹腔的作用延缓了压强的下降趋势,尤其在凹腔处,压强变化平缓,但准一维流求解时并未考虑凹腔问题。
由于准一维流是对三维流动的简化,流动参数由三维转一维的过程中将不可避免的引入误差。此外,准一维流求解过程中采用了经验公式,包括隔离段中的压升公式和燃烧室中的释热规律,经验公式基于试验数据得到,具有一定的可信度,但其对各类模型的适用性需通过试验进一步确认,也是准一维流分析结果误差的一个主要来源。燃烧效率是准一维流分析的输入参数,但燃烧室中燃料的燃烧效率取决于多方面的因素,如来流性能、进气道设计、燃料喷注和燃烧室设计等,难以准确给出,可以根据CFD计算或试验结果反推得到,但会带来误差,进而影响准一维流分析精度。
5 结论本文基于准一维流方法发展了一套可用于亚/超双模态的内流计算方法,并基于风洞试验结果进行验证,得到以下结论:
(1) 本文方法可适用于双模态超燃冲压发动机的隔离段和燃烧室的耦合分析,且对于RBCC组合动力在亚燃和超燃模态下也具有一定的计算精度。
(2) 在亚燃模态下,基于准一维流方法可很好地预测隔离段中的流动分离点,误差小于10%,峰值压强和沿程压强平均值的预测结果不大于22%和10.5%。
(3) 在超燃模态下,准一维流的求解精度较高,对于燃烧室中的峰值压强预测误差小于3.75%,峰值压强的发生位置预测误差小于2%。
由于本文暂未考虑准一维流计算中的凹腔、经验公式等引入的误差,后续将改进准一维流耦合分析方法,考虑凹腔对燃烧室有效流通面积的影响,进一步确认准一维流中的误差因素并加以改善。
| [1] |
Michael A Bolender, David B Doman. A Non-Linear Model for the Longitudinal Dynamics of a Hypersonic Air-Breathing Vehicle[R]. AIAA 2005-6255 http://arc.aiaa.org/doi/abs/10.2514/6.2005-6255
(  0) 0) |
| [2] |
Engelund W C, Holland S D, Crockrell C E, et al. Aerodynamic Database Development for the Hyper-X Airframe Integrated Scramjet Propulsion Experiments[J]. Journal of Spacecraft and Rockets, 2001, 38(6): 803-810. DOI:10.2514/2.3768
(  0) 0) |
| [3] |
Woods W C, Holland S D, DiFuvio M. Hyper-X Stage Separation Wind-Tunnel Test Program[J]. Journal of Spacecraft and Rockets, 2001, 38(6): 811-819. DOI:10.2514/2.3770
(  0) 0) |
| [4] |
Cockrell C E Jr, Engelund W C. Integrated Aero-Propulsive CFD Methodology for the Hyper-X Flight Experiment[R]. AIAA 2000-4010. http://dl.acm.org/citation.cfm?id=886025
(  0) 0) |
| [5] |
Parikh P, Engelund W, Armand S, et al. Evaluation of a CFD Method for Aerodynamic Database Development using the Hyper-X Stack Configuration[R]. AIAA 2004-5385. http://arc.aiaa.org/doi/abs/10.2514/6.2004-5385
(  0) 0) |
| [6] |
郭金磊, 谷良贤, 龚春林. 一种改进的冲压发动机一维流分析模型[J]. 推进技术, 2014, 35(5): 584-590. (GUO Jin-lei, GU Liang-xian, GONG Chun-lin. An Improved One-Dimensional Analysis Model for Ramjet[J]. Journal of Propulsion Technology, 2014, 35(5): 584-590.)
(  0) 0) |
| [7] |
石喜勤, 陈兵, 徐旭, 等. 冲压发动机进气道/燃烧室/尾喷管耦合流场计算[J]. 推进技术, 2008, 29(5): 557-561. (SHI Xi-qin, CHEN Bing, XU Xu, et al. Inlet/Combustor/Nozzle Coupled Flow Field Calculation for Ramjet[J]. Journal of Propulsion Technology, 2008, 29(5): 557-561.)
(  0) 0) |
| [8] |
Chen Bing, Xu Xu, Cai Guobiao. A Multi-Code CFD Solver for the Efficient Simulation of Ramjet/Scramjet Inlet-Engine Coupled Flowfields[R]. AIAA 2007-5414. http://arc.aiaa.org/doi/abs/10.2514/6.2007-5414
(  0) 0) |
| [9] |
Keith Numbers. Development of a Coupled Inlet-Engine Dynamic Analysis Method[R]. AIAA 97-2880. http://arc.aiaa.org/doi/pdf/10.2514/6.1997-2880
(  0) 0) |
| [10] |
Keith Numbers. Conservation Coupling Technique for Dynamic Inlet-Engine Analysis[J]. Journal of Propulsion and Power, 2003, 19(3): 444-455. DOI:10.2514/2.6128
(  0) 0) |
| [11] |
Malcolm Rowe, Andmark B Sussman. Development of High-Response Data Analysis AIDS for Inlet-Engine Testing[J]. Journal of Aircraft, 1971, 8(5): 307-311. DOI:10.2514/3.44275
(  0) 0) |
| [12] |
William M Shain, Palmer E Burris. Dynamic Test Method for Supersonic Inlet/Engine Development[C]. Washington DC: Aerodynamic Testing Conference, 1966. http://arc.aiaa.org/doi/abs/10.2514/6.1966-741
(  0) 0) |
| [13] |
Denny A G, Horine J T, Nichols R H, et al. Inlet/Engine Integration Examples Using Coupled Transient and Steady Engine Performance Models with Kestrel[R]. AIAA 2014-0753. http://www.researchgate.net/publication/269200632_InletEngine_Integration_Examples_Using_Coupled_Transient_and_Steady_Engine_Performance_Models_with_Kestrel
(  0) 0) |
| [14] |
Murma S M. Coupled Numerical Simulation of the External and Engine Inlet Flows for the F-18 at Large Incidence[R]. AIAA 92-2621. http://www.sciencedirect.com/science/article/pii/S1369886900000070
(  0) 0) |
| [15] |
Campbell J L, Ellisf S H. Engine/Inlet Compatibility Analysis Procedure[J]. Journal of Aircraft, 1971, 8(5): 301-307. DOI:10.2514/3.59101
(  0) 0) |
| [16] |
Campbell J L, Ellis S. Inlet-Engine Compatability Analysis [R]. AIAA 70-0941. http://arc.aiaa.org/doi/abs/10.2514/6.1970-941
(  0) 0) |
| [17] |
Beverly Duncan. Computational Analysis of Ramjet Engine Inlet Interaction[R]. AIAA 92-3102. http://arc.aiaa.org/doi/pdf/10.2514/6.1992-3102
(  0) 0) |
| [18] |
Hong-Gye Sung. A Unified Analysis of Ramjet Operation in an Integrated Rocket Ramjet Engine Part Ⅰ. Transition from Rocket Booster to Ramjet Sustainer[R]. AIAA 2001-3460. http://arc.aiaa.org/doi/abs/10.2514/6.2001-3460
(  0) 0) |
| [19] |
Sung H G, Hsieh S Y, Yang V. A Unified Analysis of Ramjet Operation in an Integrated Rocket Ramjet Engine Part Ⅱ. Combustion Dynamics of Ramjet Engine [R]. AIAA 2001-3192. http://arc.aiaa.org/doi/abs/10.2514/6.2001-3192
(  0) 0) |
| [20] |
Rodrick V Chima. Coupled Analysis of an Inlet and Fan for a Quiet Supersonic Jet [R]. AIAA 2010-479. http://arc.aiaa.org/doi/pdf/10.2514/6.2010-479
(  0) 0) |
| [21] |
Smart M K. Flow Modeling of Pseudoshocks in Backpressured Ducts[J]. AIAA Journal, 2015, 53(12): 3577-3588. DOI:10.2514/1.J054021
(  0) 0) |
| [22] |
Ortwerth P J. Scramjet Vehicle Integration[M]. Reston: American Institute of Aeronautics and Astronautics, Inc., 2001.
(  0) 0) |
| [23] |
余勇, 刘卫东, 王振国. 超声速燃烧室性能一维数值模拟[J]. 流体力学实验与测量, 2004, 18(3): 36-41. (  0) 0) |
| [24] |
Heiser W H, Pratt D T. Hypersonic Airbreathing Propulsion[M]. Washington DC: American Institute of Aeronautics and Astronautics, Inc., 1994, 237-242.
(  0) 0) |
| [25] |
Matthew L F, James F D. Isolator-Combustor Interactions in a Direct-Connect Ramjet-Scramjet Experiment[J]. Journal of Propulsion and Power, 2012, 28(1): 83-95. DOI:10.2514/1.B34367
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

