2. 航天低温推进剂技术国家重点实验室,北京 100028
2. State Key Laboratory of Technologies in Space Cryogenic Propellants, Beijing 100028, China
航天低温推进剂主要包括液氧、液氢和液态甲烷等。以液氢液氧火箭推进剂为例,其比重比常温推进剂高30%~40%,低温推进剂的应用可显著提高火箭运载能力。然而,液氢的沸点是-253℃,在此温度下,氧气、氮气、二氧化碳和水分等都会发生固化。这些机械杂质容易堵塞管路中的过滤器或阀门等部件,严重影响低温液体输送过程的稳定性,进而引起液氢加注系统或火箭动力装置系统部件故障。此外,液氢中的固态氧或固态空气遇到摩擦或冲击还极易引发爆炸。为了保证安全性,低温加注系统在加注前需进行气体置换,使杂质含量降低到技术要求所规定的指标内[1, 2]。美国土星五号液氧加注系统就曾由于流动不稳定问题导致了部分管路严重损坏[3]。俄罗斯的低温系统也曾因严重的水击而发生管路、阀门损坏的事故[4]。此外,国内的航天系统也遇到过类似的问题。
为了保证低温推进剂加注过程的安全性,前人对推进剂系统的气体置换过程开展了一系列的研究。符锡理对运载火箭液氢液氧推进剂的加注过程存在的问题及技术难点进行了较为全面的研究和分析[5],主要针对发射场液氮加注系统的加注压力自动控制及自动补加流量调节方法[6]。张亮亮等[7]针对发射场氢箱低压置换过程搭建了缩比试验装置,考察不同气体流量控制方法的流量调节特征,发现采用气体调节阀进行气体流量控制的方法响应时间短,流量调节结果平稳可控,是较优的控制方法。在理论计算方面,王红雨[8]对液氢加注系统的置换方案进行了探讨,指出氦气是一种比较理想的置换介质,但考虑到其资源稀缺且价格昂贵,可采用氢气作为介质进行增压至稀释置换,或者先采用高纯氮气置换稀释,再用氢气或氦气置换。为将杂质含量降低到规定指标,何明飞[9]和叶欣等[10]对氢气置换过程时所需的置换次数、用量及用时进行了较为全面的数值计算。为研究置换过程中的动态过程,研究人员还针对贮箱本身的充放气过程开展了数学建模工作[11~13]。
然而,目前对于低温加注系统置换过程的分析仅针对加注系统本身进行建模,缺乏对整个置换流程中流动状态及流量控制的分析计算。受安全条件的限制,常规置换实验一般多采用氮作为置换系统的测试工作介质。氮和氢在物性、安全性等方面都存在很大的差别,在置换系统中的流量以及流动稳定性也存在较大的差异。因此,考察氮气置换测试所得的流动特性对于指导以氢气为介质置换系统的流量调节与控制措施非常有必要。
本文针对新一代航天推进系统的低温推进剂加注系统的气体置换流程,为了保证安全、可靠地为加注系统供给稳定压力和流量的氢气,对置换系统的气化、回温和充气等过程进行仿真计算,重点考察低温液体增压罐的工作压力、气路调节阀开度对于系统中流动状态和流量调节的影响。分别以氮和氢作为置换介质,分析氮、氢在置换系统中流动状态和流量控制方面的相似性,从而评估以氮气作为置换介质的流动特性测试结果对于氢气置换系统的流量调节策略的可参照性。
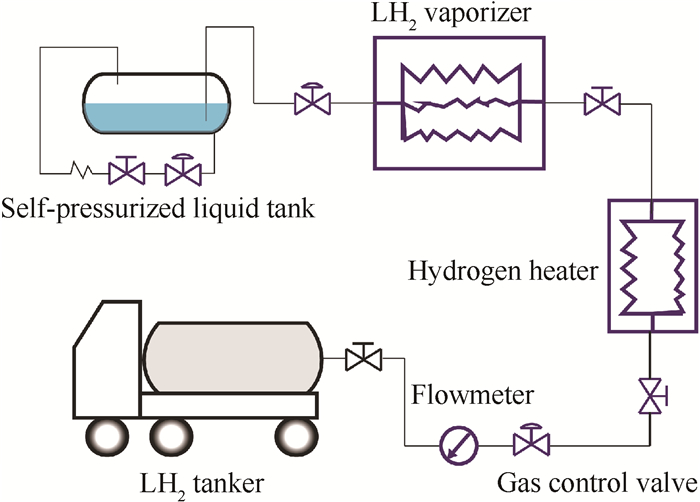
2 计算模型拟以容积为72m3的地面液氢车作为气体置换的模拟计算对象,图 1为地面液氢车置换系统简图。配置一套液氢复温流程为加注系统的置换提供连续的氢气。通过气化器将液氢气化并加温至80K左右,利用空浴式回温器将低温氢气复温至常温水平,对加注系统进行增压置换。主要计算工况如下:
|
Fig. 1 Schematic of gas replacement process for liquid hydrogen loading |
氢气流量控制目标范围:m=0.0125~0.15kg/s,环境温度:Ta=293K,环境压力:pa=0.1MPa,液氢进口压力:pi=0.7~0.9MPa,液氢进口温度:Ti=20K,氢车充压压力:pmax=0.3MPa,气阀调节阀开度:0~100%。
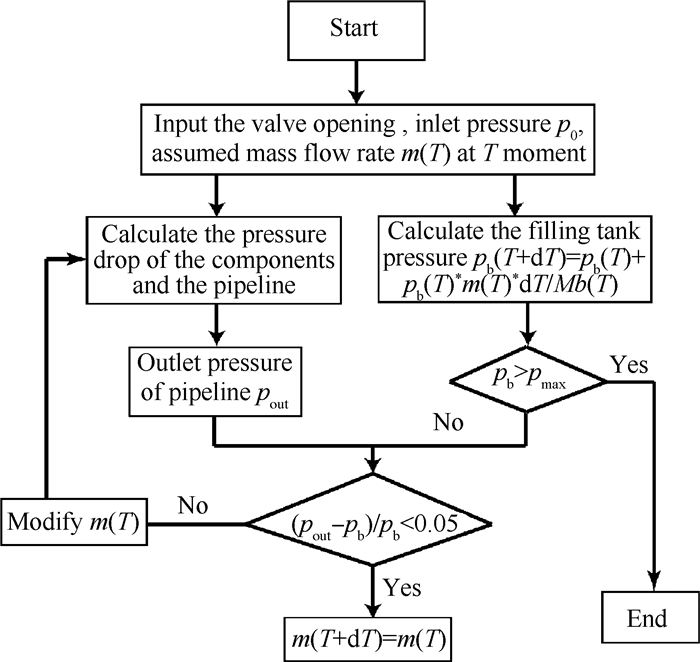
计算中,忽略气化器内的压降,充气过程中,液氢车内气体均匀且压缩性系数不变,温度均匀且不变,不发生吸附或化学反应。采用稳态分布参数模型[14],应用Matlab软件编程,调用Refprop软件中氮和氢的物性参数,可进行置换系统流动状态的仿真计算。假设T时刻的初始流量为m,计算从增压罐出口到总管路出口的压降,得到总管路出口(即氢车气体置换入口)处的压力pout,图 2为计算程序流程图。根据计算的出口压力pout与氢车背压pb是否相等,来判断该初始流量m是否为实际的流量。在判断是否相等时,根据本身工艺流程的控制需求,允许5%的计算容差。继而,将计算得到的T时刻的实际流量m作为T+dT时刻的假设流量,进入下一个循环。当背压pb超过最大充气压力0.3MPa时,计算过程终止。
|
Fig. 2 Diagram of computational procedure |
管路局部阻力和沿程阻力分别利用式(1)和式(2)进行计算[15]
| $ \Delta {p_{\rm{j}}} = \zeta \frac{{\rho {v^2}}}{2} $ | (1) |
| $ \Delta {p_{\rm{f}}} = f\frac{L}{{{d_{\rm{H}}}}}\frac{{\rho {v^2}}}{2} $ | (2) |
式中ρ为流体密度,v为流体流速,L为流道长度,dH为水力直径;ζ为局部损失系数,其值主要取决于流动的局部变化、边界的几何形状和尺寸,可通过具体情况查表得到;f为沿程损失系数,可以通过穆迪图得到。
气路调节阀采用的是气动薄膜低温笼式单座调节阀,为等百分比调节阀。根据下列公式可求出各阀门流通能力Kv值下调节阀的压降[16~18]:
对液体
| $ K = \sqrt {\frac{{10{Q_{\rm{L}}}}}{{\left( {{p_1} + {p_2}} \right)/{\gamma _{\rm{L}}}}}} $ | (3) |
对气体
| $ {K_{\rm{v}}} = \frac{{{Q_{\rm{N}}}}}{{3.34}}\sqrt {\frac{{{\gamma _{\rm{N}}}\left( {273 + t} \right)}}{{\left( {{p_1} - {p_1}} \right)\left( {{p_1} + {p_2}} \right)}}} $ | (4) |
式中QL为液体流量,m3/h;γL为液体密度,g/cm3;p1为阀前压力(绝),kPa;p2为阀后压力(绝),kPa;QN和γN分别为标准状态气体流量(Nm3/h)和密度(kg/Nm3);t为气体温度,℃。
程序中使用的管路特性、工况等参数来源于氢气置换系统,因而可针对氢气置换过程中系统每个部位仿真计算不同时刻的流量、压力、速度和物性等变化,从而将计算结果用来指导实际的氢气置换过程。
3 置换系统流动特性分析本节以氢作为置换介质,考察低温液体增压罐的工作压力、气路调节阀开度对于系统中流动状态和流量调节的影响。
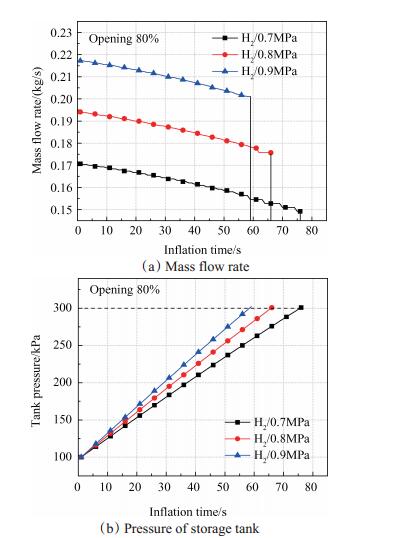
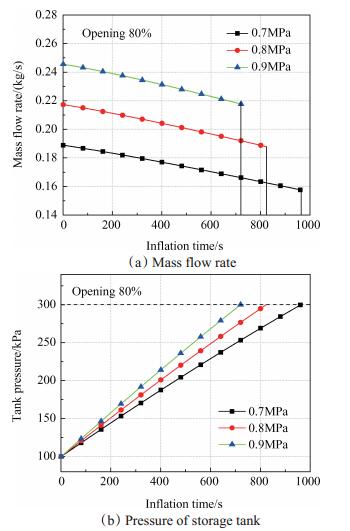
3.1 增压罐工作压力对流动状态的影响图 3给出了气路调节阀开度设为80%,自增压储罐工作压力为0.7~0.9MPa,在以氢气作为介质的置换系统中,质量流量、液氢车背压在充气过程中的变化情况。可以看出,随着时间的推移,在各个不同的压力工况下,质量流量都呈线性下降,容器背压增速变缓。对于以氢气作为介质的系统来说,自增压储罐工作压力为0.7MPa时的流量在0.1493~0.1707kg/s(5981~6838Nm3/h),工作压力为0.8MPa时的流量在0.1757~0.1941kg/s(7039~7776Nm3/h),工作压力为0.9MPa时的流量在0.2011~0.2172kg/s(8056~ 8701Nm3/h)。增压罐的工作压力越高,质量流量越大,且流量递减的幅度明显缩小,分别为857Nm3/h,737Nm3/h和645Nm3/h,而充气时间随压力升高呈现缩短趋势。综合可知,增压罐的工作压力越高,虽然充气时间越短,但流量下降越快,则管路流速越高。因此,高工作压力并不利于充压过程保持稳定性。
|
Fig. 3 Variation of hydrogen mass flow rate and pressure of GH2 storage tank during inflation with different operating pressure of LH2 storage tank |
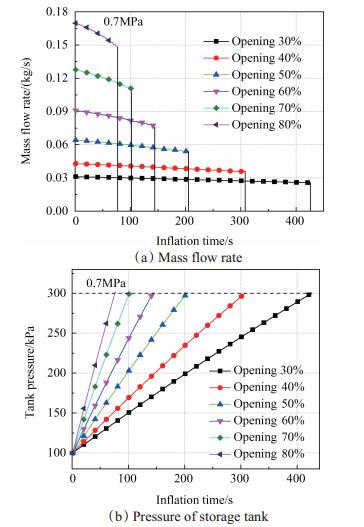
图 4分别给出了自增压储罐工作压力为0.7 MPa,气路调节阀K2开度从30%~80%变化时,置换系统中质量流量、液氢车背压在充气过程中的变化情况。整体而言,无论在多大的气路调节阀开度下,随着充气过程的进行,质量流量都逐渐下降,液氢车背压增速变缓。不同的是,气阀开度越大,流量越大。例如,液阀20%开度、气阀80%开度时的流量在0.1489~0.1696kg/s(5962~6792Nm3/h),而液阀20%开度、气阀30%开度时的流量在0.02561~0.03105kg/s(1025~1243Nm3/h)。可见,气阀对系统流量调节的作用非常显著。阀门开度越大,流量显著升高,背压升高较快,并且流量下降速度也越快,这些都不利于系统流动状态的稳定和安全。
|
Fig. 4 Variation of hydrogen mass flow rate and pressure of GH2 storage tank during inflation with different opening of gas control valve |
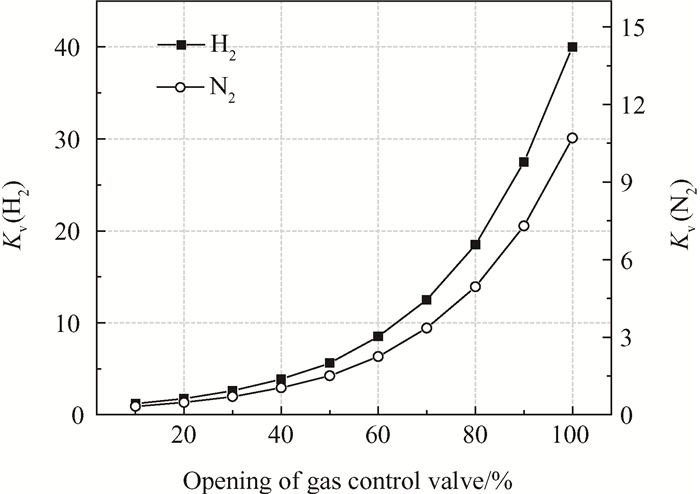
为考察以氮作为介质的置换系统流动特性对于氢气置换流程的流量调节与控制策略的可参照性,下面将针对氮气置换系统进行仿真计算,分析不同工况下置换系统的流动状态,并着重对比分析置换系统中流量分布规律中的氮、氢相似性。气路调节阀采用的是浙江蒙德克流体控制有限公司生产的气动薄膜低温单座调节阀,型号MDK-126M,该阀门属于等百分比调节阀,以氢气作为工质的额定流通能力Kv值为40。Kv值与阀门开度的关系如图 5所示,根据阀门开度与Kv值关系求出每个开度对应的Kv值。再根据式(3)和(4)求出各阀门Kv值下调节阀的压降。
|
Fig. 5 Variation of Kv with opening of gas control valve for GH2 and GN2 |
图 6分别给出了在以氮气作为介质的置换系统中,气路调节阀开度为80%,自增压储罐工作压力为0.7~0.9MPa时,系统质量流量、液氢车背压在充气过程中的变化情况。由图可知,与氢气置换流动规律类似,随着时间的推移,在各个不同的压力工况下,质量流量都呈线性下降,液氢车背压增速变缓。自增压储罐工作压力为0.7 MPa时的流量在0.1576~ 0.1889kg/s(454~544Nm3/h),压力为0.8MPa时的流量在0.1879~0.2173kg/s(541~626Nm3/h),压力为0.9 MPa时的流量波动在0.2178~0.2456kg/s(627~ 707Nm3/h)。自增压工作压力越高,流量相应越大,流量递减的幅度变化很小,分别为90Nm3/h,85Nm3/h和80Nm3/h。但依然可以看出,流量递减的幅度是随工作压力的升高而减小的。这一点与氢气置换系统一致。
|
Fig. 6 Variation of nitrogen mass flow rate and pressure of GH2 storage tank during inflation with different operating pressure of LN2 storage tank |
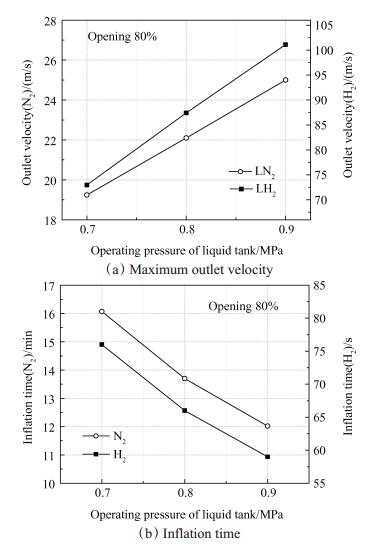
图 7给出了分别采用氮气和氢气作为介质时,系统充气时间与最大流速在充气过程中的变化情况,最大流速即流量最大时的出口流速。充气时间都随压力升高而缩短,且几乎呈线性趋势;其次,压力越高,系统最大流速(即管路出口流速)越高。
|
Fig. 7 Variation of maximum outlet velocity and inflation time with different operating pressure of LN2 storage tank |
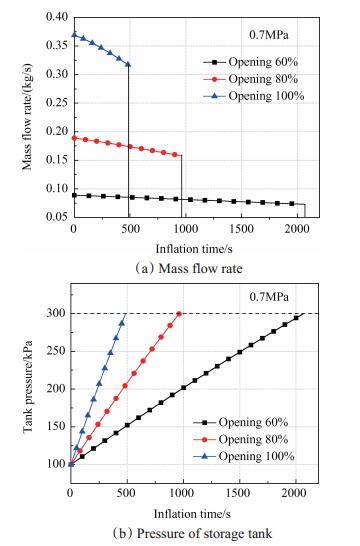
针对以氮气作为介质的置换系统,图 8给出了增压罐工作压力为0.7MPa,气路调节阀开度从60%~ 100%变化时,置换系统中质量流量、液氢车背压在充气过程中的变化情况。可以看出,随着充气过程的进行,质量流量逐渐下降,因而相应的液氢车增压速度变缓。对比图 4中氢气置换系统质量流量变化曲线,情况基本类似。气路调节阀开度越大,流量越大,容器增压越快,流动越不稳定,且气阀对系统流量调节作用非常显著。
|
Fig. 8 Variation of nitrogen mass flow rate and pressure of GN2 storage tank during inflation with different opening of gas control valve |
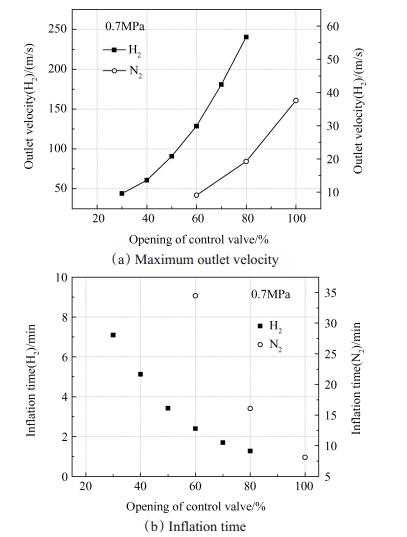
图 9给出了出口最大流速及充气时间与气路调节阀开度变化关系图。无论对于氮气还是氢气,气阀开度越大,充气时间则越短,并且缩短趋势逐渐平缓;而气阀开度越大,流量递减的斜率越大,即递减速度越快,这是由于充气时间越短则液氢车背压变化越快,因而反馈给流量的变化也越大。这种反馈和变化对于以氢气为介质时更加明显。
|
Fig. 9 Variation of maximum outlet velocity and inflation time with different opening of gas control valve |
综上可知,在定性变化方面,氮气和氢气是基本相似的,随着增压罐工作压力的升高,调节阀开度增大,充气时间减短,系统内质量流量增大,流速也随之增大,充压过程越不稳定。而在定量分析时,氮气的充气时间是氢气的十几倍,最大流速是氢气流速的1/5左右。对于该置换系统,在相同工作压力、管径、换热量要求工况下,氮和氢的密度、粘度以及导热系数可能相差十几倍,对于系统的流动特性造成以上量级的差别影响在意料之中。
5 结论(1)在置换充气过程中,氢的质量流量随时间的变化近似呈线性变化,液氢罐内气压逐渐升高,并且呈现先增压较快,尔后减慢的规律。增压罐工作压力越高,流量越大且充气时间越短,但流量下降也越快,管路出口流速过高,不利于充压过程保持稳定。气路调节阀对于系统的影响非常明显,阀门开度越大,流量越大,但流量的递减趋势也越明显,出口流速越大,容易导致流动越不稳定。
(2)氢气和氮气分别作为置换介质时,自增压储罐工作压力和调节阀开度对于置换系统的影响都是相似的。然而,在相同自增压罐工作压力、控制阀开度下,氢气系统内的最大流速可达到氮气系统最大流速的5倍,因而氢气系统的安全性还需进一步得以重视。
(3)总体而言,氮气系统所得的流量压力调节控制策略能为氢气置换系统的工作在影响因素和变化趋势等方面提供参考,进而为氢气置换系统确定基本的调节控制策略。但在实际工作中,仍应对氢气系统进行更加全面的测试,从而确定更完善的流量控制方案,以保证系统的安全运行。
| [1] |
刘海飞, 陈虹, 王天祥, 等. 液氢和液氧低温推进剂加注系统中的管路瞬变特性研究[J]. 水动力学研究与进展, 2014, 29(6): 642-648. (  0) 0) |
| [2] |
吴文跃. 空间站的在轨推进剂再加注问题[J]. 推进技术, 1988, 9(2): 50-56. (WU Wen-yue. The Problem of on-Orbit Propellant Refueling for Space Stations[J]. Journal of Propulsion Technology, 1988, 9(2): 50-56.)
(  0) 0) |
| [3] |
Moore W I, Arnold R J. Failure of Liquid Oxygen Filling System of Saturn V[J]. Missiles and Space Vehicles, 1979, 2: 69-74.
(  0) 0) |
| [4] |
瓦费林·尼亚波部拉诺夫. 液体低温系统[M]. 北京: 低温工程编辑部, 1993.
(  0) 0) |
| [5] |
符锡理. 运载火箭液氢液氧低温推进剂加注技术[J]. 低温工程, 1995(6): 1-8. (  0) 0) |
| [6] |
符锡理. 运载火箭发射场液氮加注系统[J]. 低温工程, 1995(1): 7-11. (  0) 0) |
| [7] |
张亮亮, 陈虹, 高旭, 等. 氢箱置换过程中气体流量控制技术试验研究[J]. 低温与超导, 2015(10): 17-21. (  0) 0) |
| [8] |
王红雨. 液氢加注系统的气体置换方法探讨[J]. 低温与特气, 2007, 25(6): 20-22. (  0) 0) |
| [9] |
何明飞. 氢气置换用量及用时计算[J]. 低温工程, 2010(6): 46-49. (  0) 0) |
| [10] |
叶欣, 张青, 张邦双. 液氢加注系统氢气置换计算[J]. 低温工程, 2014(6): 38-41. (  0) 0) |
| [12] |
朱子勇, 孙万民, 王占林. 某试验台LH2贮箱气体置换过程数值模拟[J]. 火箭推进, 2011, 37(6): 52-60. (  0) 0) |
| [13] |
张永敬. 战略导弹液体推进剂加注定量方式的改进[J]. 推进技术, 1992, 13(5): 59-61. (ZHANG Yong-jing. The Improvement of Quantitative Filling Method of Liquid Propellant in a Strategic Missile[J]. Journal of Propulsion Technology, 1992, 13(5): 59-61.)
(  0) 0) |
| [14] |
马鸿武, 杨金岩, 王衍文. 液体火箭推进剂加注模拟仿真系统的设计与实现[J]. 推进技术, 1993, 14(1): 46-50. (MA Hong-wu, YANG Jin-yan, WANG Yan-wen. The Design and Implementation of Simulation System of Propellant Filling in Liquid Rocket[J]. Journal of Propulsion Technology, 1993, 14(1): 46-50.)
(  0) 0) |
| [15] |
杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 1998.
(  0) 0) |
| [16] |
陆亚俊, 马最良, 邹平华. 暖通空调(第二版)[M]. 北京: 中国建筑工业出版社, 2007.
(  0) 0) |
| [17] |
Paul Wing. Determining and Using the Control Valve Pressure Recovery Factor[J]. Instrumentation Technology, 1979, 26(8): 55-59.
(  0) 0) |
| [18] |
Driskell L. Control Valve Sizing with ISA Formulas[J]. Instrumentation Technology, 1974, 21(7): 33-48.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


