短距起飞/垂直降落飞行器(STOVL)由于兼具了固定翼飞机和旋翼飞机的优点,一经问世便成为各航空大国研究的热点。20世纪六七十年代,英国研究制造出了“鹞”式亚声速单座单发垂直/短距起落战斗机;美国在联合攻击战斗机计划(JSF)中设计制造出性能强大的F-35B垂直起降战斗机等[1, 2]。
F-35B的垂直起降系统采用的是“前置垂直对转升力风扇+90°转向尾喷口+每侧翼根处各有一个滚转喷管”的方式,最早由Bevilaqua等提出[3]。在水平飞行时,垂直升力风扇的舱门关闭,水平方向的推力由主发动机独立完成。在垂直升降时,对转升力风扇由主发动机的低压轴驱动,通过变速箱齿轮咬合的方式驱动,输出垂直向推力。尾喷口在这时候会向下偏转到一定角度,共同输出垂直升力,两者提供大部分升力,约占总升力的91%。滚转喷管提供较小的推力,主要用于平衡以及姿态调整[4~6]。
虽然采用升力风扇发动机进行垂直起飞会影响飞行器的载荷[7],但是由于其在应对复杂起降环境(如山区、战场、甲板)方面不可忽视的优越性[8],因此关于升力风扇发动机的研究一直是航空领域的热点问题。关于对转升力风扇,606所的徐雪从强度要求和结构布局方面对对转升力风扇的尺寸以及机匣的结构进行了设计与论证[9];西工大的郑志成将升力风扇与桨叶结构相类比,提出了基于无人机上用的小型风扇性能估算模型,但与大型飞行器上带进气道及喷管的升力风扇模型有较大差异[10]。沈飞的杨琳从叶片机级理论的角度出发,针对叶片从叶根到叶尖的差异,对发动机用的单级常规对转风扇的叶片进行了详尽的气动设计[11]。
关于升力风扇发动机建模,西工大的刘帅采用了普通风扇作为升力风扇,在所建升力风扇发动机数学模型的基础上进行了性能模拟,侧重于发动机部分的调节与分析,但对升力风扇部分的仿真甚少;且未详细介绍建模方法原理与思路[12]。南航的任冰涛详述了各部件建模理论并仿真出了该发动机的高度特性和升力风扇的起动过程,但升力风扇的特性图由对多级轴流式压气机的特性图缩放而来,缺乏对对转升力风扇的设计研究,在非设计点上会有较大的误差[13]。
采用对转风扇作为升力风扇有着一系列非常显著的优点,包括消减陀螺力矩、减小尺寸、结构更紧凑、减轻重量等[14~16]。因此研究对转风扇特性及对转升力风扇发动机性能对垂直起降推进系统的设计有着重要的意义。而国内尚未开展基于常规升力风扇和相同设计点性能要求下的对转风扇的设计工作;以及结合发动机联合运行时,不同升力风扇与发动机耦合作用下的非设计点性能对比工作。
本文的建模对象是美国海军研究院在F-35B垂直起降推进系统的基础上为重型运输机设计的升力风扇发动机[17]。其中做了以下预设:
(1) 由于滚转喷嘴主要用于姿态调整与平衡[4],提供的升力较少,在设计时忽略了滚转喷嘴。相应的,设计点处,升力风扇与尾喷管提供的升力应该相平衡,消除力矩。
(2) 主发动机是F-135发动机的衍生类型。
(3) 由于升力风扇与主发动机之间通过舱门隔开,两者不存在气路耦合[4]。
(4) 先采用一级转子一级静子的普通风扇作为升力风扇开展建模,然后在相同性能要求的前提下,进行对转风扇的设计与研究。进而对两者进行比较。
结构上,对转风扇由两级转子构成,包括一级正转级和一级反转级。两者通过两对锥齿轮由发动机低压轴或传动轴从垂直方向驱动,实现同轴反向旋转,转子的转速由两对啮合副的传动比确定[18, 19]。
2 升力风扇发动机模型理论 2.1 升力风扇系统工作原理升力风扇系统主要由进气道、升力风扇、喷管三部分组成。
2.1.1 升力风扇系统-进气道由于升力风扇系统用于地面低马赫数垂直起降,进气道对来流减速增压的作用并不显著,因此,升力风扇系统的进气道在专门的起飞进气门作用下为收敛型,并将低速来流加速到高速的升力风扇进口气流。
对于亚声速进气道,总是有正的阻力作用在包围着进入发动机进气道的空气的流管上[16],这个力就是通常所说的“附加阻力”Dadd,如图 1所示。
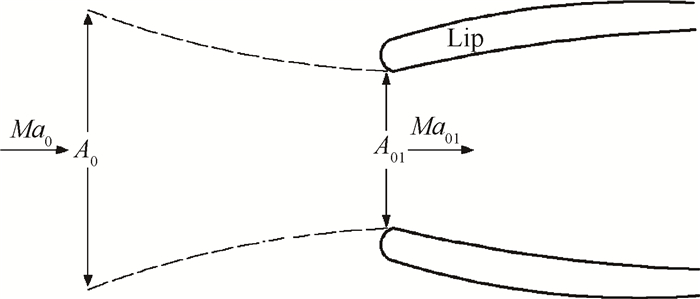
|
Fig. 1 Formation of additional resistance |
如果将0~1段作为等熵、一维流完全气体看待,那么
| $ {D_{{\rm{add}}}} = {p_1}{A_1}\left( {1 + \gamma Ma_1^2} \right) - {p_0}{A_{01}}\left( {\frac{{{A_1}}}{{{A_{01}}}} + \gamma Ma_{01}^2} \right) $ | (1) |
再将式(1)与质量守恒定律以及常用的完全气体关系式来表达,从而得出
| $ \begin{array}{l} {\phi _{{\rm{inlet}}}} = \frac{{{D_{{\rm{add}}}}}}{F} = \frac{{{D_{{\rm{add}}}}}}{{{m_0}\left( {F/{m_0}} \right)}} = \\ \;\;\;\;\;\;\;\;\;\frac{{\frac{{M{a_0}}}{{M{a_{01}}}}\sqrt {\frac{{T_{01}^ * }}{{T_0^ * }}} \left( {1 + \gamma Ma_{01}^2} \right) - \left( {\frac{{{A_1}}}{{{A_0}}} + \gamma Ma_0^2} \right)}}{{\gamma M{a_0}\left( {F{g_{\rm{c}}}/{m_0}{a_0}} \right)}} \end{array} $ | (2) |
式中gc为重力加速度,a0为当地声速。式(2)表明,如果Ma0接近Ma01,则ϕinlet不大。而当Ma0 = 0时,ϕinlet值很高,且随着Ma01的增大而增大。升力风扇系统主要用于地面缓慢垂直起降状态,因此,Ma0接近于0。为了获取较低的ϕinlet值,需要在进气道上设专门的进气门,从而降低Ma01,降低ϕinlet,并且能有效地防止附面层分离。
2.1.2 升力风扇本文基于性能要求为升力风扇系统设计了两套升力风扇,一种是已有的建模文献中普遍采用的单级风扇,包括进口导向叶片、一级转子、一级静子。一种是F-35B上已得到实际应用的双级对转升力风扇,包括进口导向叶片、一级正转级、一级反转级以及出口导向叶片。
为了获取较为准确的非设计点风扇特性,本文基于叶片机基元级理论[20]计算了升力风扇的特性,即在一定的相对流量Qf, cr和相对转速nf, cr输入下获取风扇的压比πf。其中
| $ {Q_{{\rm{f}},{\rm{cr}}}} = \frac{{{Q_{\rm{f}}}\sqrt {T_1^ * /288.15} }}{{p_1^ * /101325}} $ | (3) |
| $ {n_{{\rm{f}},{\rm{cr}}}} = {n_{\rm{f}}}/{n_{{\rm{fd}}}} \cdot \sqrt {288.15/T_1^ * } $ | (4) |
式中nfd为风扇的设计点转速。
在计算特性时,不考虑叶片及气流从叶根到叶尖的变化,而只选取中性面上的基元级作为分析对象。常规风扇中性面上的基元级及速度三角形如图 2所示。图中W为相对流速,C为绝对流速,U为中性面上叶尖线速度。
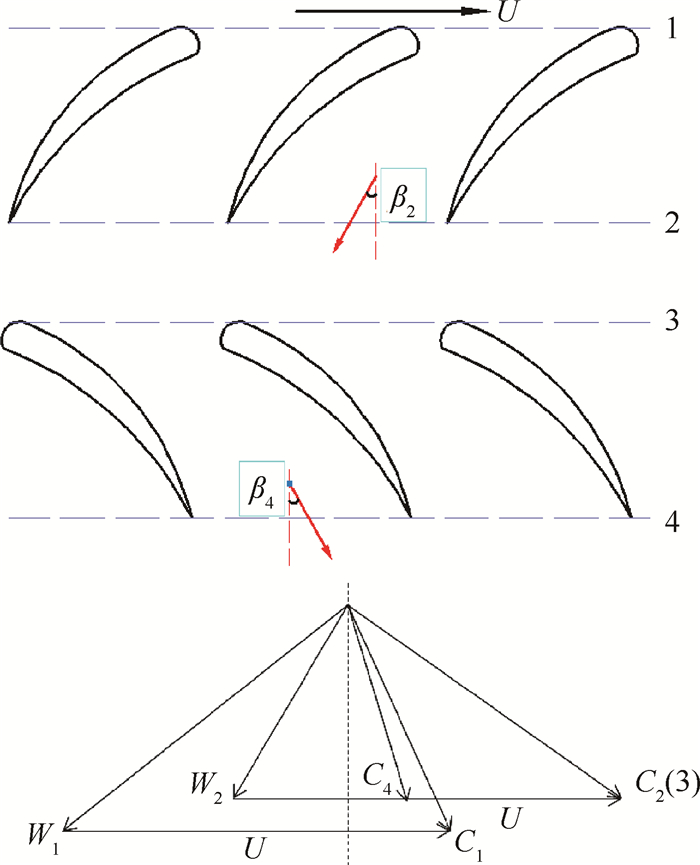
|
Fig. 2 Elementary stage of common lift fan and velocity triangle |
在常规风扇正常工作状态下,可以假设空气是沿着叶片设计的方向流动的,即β2 = β2d,α4 = β4 = β4d。转子进口的绝对气流角为进口导流叶片的出口角α1 = αi2。常规风扇各进出口气流角有如下关系式
| $ \begin{array}{*{20}{c}} \begin{array}{l} {\alpha _{i1}} = {\beta _{i2}} = 0\\ {\alpha _1} = {\alpha _{i2}}\\ {\alpha _2} = {\alpha _{2,k}}\\ {\alpha _3} = {\beta _3} = {\alpha _2}\\ {\alpha _{{\rm{e1}}}} = {\beta _{{\rm{e2}}}} = {\alpha _4} \end{array}&\begin{array}{l} {\alpha _{i2}} = {\beta _{i2}} = {\beta _{i{\rm{d}}}}\\ {\beta _1} = {\beta _{1,k}}\\ {\beta _2} = {\beta _{2{\rm{d}}}}\\ {\alpha _4} = {\beta _4} = {\beta _{4{\rm{d}}}}\\ {\alpha _{{\rm{e2}}}} = {\beta _{{\rm{e2}}}} = 0 \end{array} \end{array} $ | (5) |
式中k表示不同工作状态。利用速度三角形求解,用Ca表示轴向速度,即
| $ \frac{{{U_{\rm{c}}}}}{{{C_{{\rm{a1}}}}}} = \tan {\alpha _1} + \tan {\beta _{1,k}} $ | (6) |
| $ \frac{{{U_{\rm{c}}}}}{{{C_{{\rm{a2}}}}}} = \tan {\alpha _{2,k}} + \tan {\beta _2} $ | (7) |
首先对转子进行分析。在理想绝热状态下,出口气流的静温和总温满足下式
| $ T_2^ * = {T_2} + \frac{{C_2^2}}{{2{C_P}}} $ | (8) |
式中根据进出口流量平衡,ρ1A1Ca1 = ρ2A2Ca2,以及密度与静温的关系
| $ T_2^ * = {T_1} \cdot {\left( {\frac{{{A_1}{C_{{\rm{a1}}}}}}{{{A_2}{C_{{\rm{a2}}}}}}} \right)^{\gamma - 1}} + \frac{{C_{{\rm{a2}}}^2}}{{2{C_P}{{\cos }^2}{\alpha _2}}} $ | (9) |
风扇对气流的做功可表示为
| $ {C_P}\left( {T_2^ * - T_1^ * } \right) = U\left( {{C_{{\rm{a2}}}}\tan {\alpha _2} - {C_{{\rm{a1}}}}\tan {\alpha _1}} \right) $ | (10) |
综合式(7),(9),(10),建立方程组,可解出方程组的未知数T2*,Ca2,α2。本文采用代入法先求Ca2,再代入式(9)获取T2*
| $ C_{{\rm{a2}}}^{\gamma + 1} + {a_1}C_{{\rm{a2}}}^{\gamma - 1} + {a_2} = 0 $ | (11) |
方程系数分别表示为
| $ {a_1} = - \left( {{U^2} - 2{C_{{\rm{a1}}}}U\tan {\alpha _1} + 2{C_P}T_1^ * } \right){\cos ^2}{\beta _2} $ | (12) |
| $ {a_2} = 2{C_P}T_1^ * \cdot {\cos ^2}{\beta _2}{\left( {\frac{{{C_{{\rm{a1}}}}{A_1}}}{{{A_2}}}} \right)^{\gamma - 1}} $ | (13) |
与转子相比,静子可看作U =0,代入求解出静子出口的T4*,并根据出口总温T4*求出温比τf,再根据理想绝热状态下温比与压比的关系方程得出压比πf
| $ \eta \left( {\tau - 1} \right) = {\pi ^{\frac{{\gamma - 1}}{\gamma }}} - 1 $ | (14) |
式中η为等熵压缩效率,取
对转风扇中性面上的基元级及速度三角形如图 3所示。
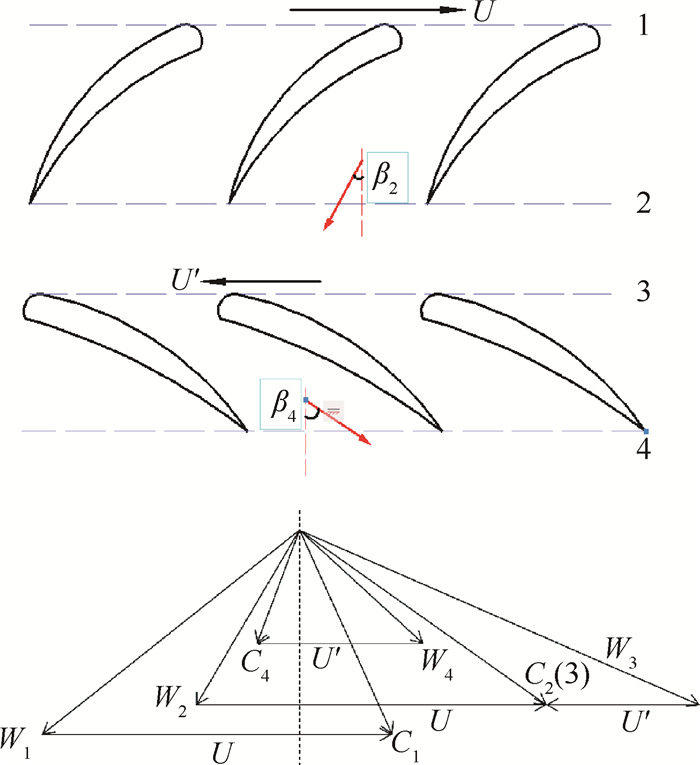
|
Fig. 3 Elementary stage of contra lift fan and velocity triangle |
正转级的工作情况及Ca2的求解与常规风扇转子类似,反转级可以看作是预旋CU与转速U方向相反的反预旋转动,即α3 < 0。因此,反转级出口Ca4的计算可以采用与正转级相同的方法,但α3 = -α2。
另外,η = η1∙η2,η1,η2分别为正转级与反转级的等熵压缩效率,计算方法与常规风扇转子效率的类似,如式(14)所示。
出口导向叶片起修正气流流动角度的作用,在理想绝热状态下,忽略流动损失,总压恢复系数σo接近于1。
综上,即可获取升力风扇在不同工作状态(转速、流量、进口气流状况)下的工作压比并求取相关出口参数。
2.1.3 升力风扇系统-尾喷管本文升力风扇系统采用普通的收敛型喷管。首先根据喷管总压恢复系数σe计算出口总压p5*。接着通过比较实际压比p0/p5*与空气临界压比βcr来确定升力风扇喷管工作状态。当p0/p5* > βcr,升力风扇喷管为亚临界状态;当p0/p5* = βcr,升力风扇喷管处于临界状态;当p0/p5* < βcr,升力风扇喷管处于超临界状态。接着根据喷管状态与流量公式求解喷管出口总压p5C*,若p5* = p5C*,则升力风扇模型处于平衡状态,否则通过重设升力风扇压比πf值进行迭代平衡求解。
综上所述,升力风扇模型的平衡方程为
| $ p_5^ * = p_{5{\rm{C}}}^ * $ | (15) |
由于喷管处于亚临界工作状态,出口气流完全膨胀;再考虑到起降低马赫数下的进气道入口的附加阻力Dadd,升力风扇的推力公式为
| $ {F_{\rm{f}}} = {Q_{\rm{f}}}\left( {{C_5} - {C_1}} \right) \cdot \left( {1 - {\phi _{{\rm{inlet}}}}} \right) $ | (16) |
功率根据风扇对气流的做功来计算
| $ {P_{\rm{f}}} = {Q_{\rm{f}}}{C_P}\left( {T_4^ * - T_1^ * } \right)/\eta $ | (17) |
升力风扇和涡扇发动机之间通过传动轴相联,但它们可以看作是相互独立工作的。升力风扇的转速nf由低压轴的转速nl及齿轮箱的传动比确定,在该转速下,升力风扇独立工作,结合气流进口条件,获得升力风扇在该工作状态下的性能参数,包括推力Ff,轴功率Pf。轴功率作为一个需求量,传至发动机低压轴,对发动机产生影响。
发动机稳态工作时,存在流量连续、功率平衡以及压力平衡的要求。除了公式(15)中升力风扇需满足的出口总压平衡方程以外,带有升力风扇的双轴涡扇主发动机模型还需满足
(1) 低压转子功率平衡方程
| $ {P_{\rm{f}}} + {P_{{\rm{fan}}}} = {P_{{\rm{lt}}}} \cdot {\eta _{\rm{l}}} $ | (18) |
式中Pfan为涡扇发动机风扇的耗功量。
(2) 高压转子功率平衡方程
| $ {P_{{\rm{ex}}}} + {P_{{\rm{com}}}} = {P_{{\rm{ht}}}} \cdot {\eta _{\rm{h}}} $ | (19) |
式中Pex为发动机高压轴的抽功量。
(3) 低压涡轮出口流量连续方程
| $ {Q_{{\rm{lt}}}} = {Q_{{\rm{lt}},{\rm{C}}}} $ | (20) |
式中Qlt, C为根据进口求解出的涡轮出口流量;Qlt为根据涡轮特性线获取的涡轮流量。
(4) 高压涡轮出口流量连续方程
| $ {Q_{{\rm{ht}}}} = {Q_{{\rm{ht}},{\rm{C}}}} $ | (21) |
(5) 内、外涵出口静压平衡方程
| $ {p_{16}} = {p_6} $ | (22) |
(6) 尾喷管喉道总压平衡方程
| $ p_8^ * = p_{8{\rm{C}}}^ * $ | (23) |
动态工作时需要考虑转动惯量对加速性的影响。即高低压转子的功率关系改为
| $ \frac{{{\rm{d}}{n_{\rm{h}}}}}{{{\rm{d}}t}} = \frac{{\left( {{P_{{\rm{ht}}}}{\eta _{\rm{h}}} - {P_{{\rm{com}}}} - {P_{{\rm{ex}}}}} \right)}}{{{N_{\rm{h}}}{J_{\rm{h}}}{{\left( {\frac{\pi }{{30}}} \right)}^2}}} $ | (24) |
| $ \frac{{{\rm{d}}{n_{\rm{l}}}}}{{{\rm{d}}t}} = \frac{{\left( {{P_{{\rm{lt}}}}{\eta _{\rm{l}}} - {P_{\rm{f}}} - {P_{{\rm{fan}}}}} \right)}}{{{N_{\rm{l}}}{J_{\rm{l}}}{{\left( {\frac{\pi }{{30}}} \right)}^2}}} $ | (25) |
式中Jl中包括升力风扇附加的转动惯量Jadd。首先要计算升力风扇的转动惯量Jf,通过微元法积分算取。根据理论力学,已知功率、转速及转动惯量之间的关系如下
| $ P = J{\omega ^2} $ | (26) |
由于发动机低压轴转速nl与升力风扇转速nf不相等,即ω不同,因此不能将Jf直接附加到发动机低压轴上。根据功率平衡,附加在发动机低压轴的升力风扇转动惯量Jadd计算如下
| $ \frac{{{J_{{\rm{add}}}}}}{{{J_{\rm{f}}}}} = {\left( {\frac{{{n_{\rm{f}}}}}{{{n_{\rm{l}}}}}} \right)^2} $ | (27) |
美国海军研究院在文献[17]中基于F-35B垂直起降推进系统为某重型运输机配置了升力风扇发动机,其中升力风扇系统采用了单级常规风扇。相关参数如表 1所示。
|
|
Table 1 Design parameters of lift fan system |
本文采用基元级理论算取升力风扇的特性。首先需要在设计点状态下,半设计半计算出合适的叶片角度、尺寸等参数,使设计点(即取定相似流量Qf, cr =1773.5kg/s,转速nfd =2576r min时)计算所得的πfd与表 1中要求的相一致。风扇各进出口截面迭代设计结果如表 2所示。经过非设计点计算,常规升力风扇特性图如图 4所示。
|
|
Table 2 Airflow parameters of common lift fan on design point |

|
Fig. 4 Pressure ratio characteristics of common lift fan |
(1) 设计点压比πfd = 2.29(标红点处)。
(2) 由于只有单级,不需为下级产生预旋,因此可以使静子叶片的设计出口角β4d = 0,从而在正常工作状态下,α4 = 0,可以省略出口导向叶片,减轻重量。
(3) 理想绝热状态下,通过转子,绝对流速和总压增加,机械能增加。轴向流速减小,此现象可以从流量连续角度解释,温度上升,密度上升,因此轴向流速减小。
(4) 通过静子,总压不受影响,轴向流速不变,但绝对流速减小,动压减小,静压增大,即动能转化为势能,总机械能不变。该普通升力风扇的中性面上的反力度Ω = 0.5441,静增压分配合理[21]。
(5) 单级常规升力风扇有着较广阔的工作范围(两蓝色虚线之间)。
3.2 常规升力风扇建模低马赫数垂直起降时,进气道前的附加阻力Dadd比较大,因此需要合理地选择Ma01的值,并使阻力系数ϕinlet处于较低值且推力满足要求。
阻力系数可在设计状态下确定。先根据3.1节的设计点参数,建立常规升力风扇设计点稳态计算模型,并计算出初步推力,该推力未考虑阻力系数且与尾喷管出口面积设定值有关。接着做出远方来流马赫数Ma0 = 0.0015时(C0 = 0.5m/s,即设计点处飞行器缓慢起降的速度)的阻力系数与修正推力随进气道进口截面马赫数变化的曲线,如图 5所示。
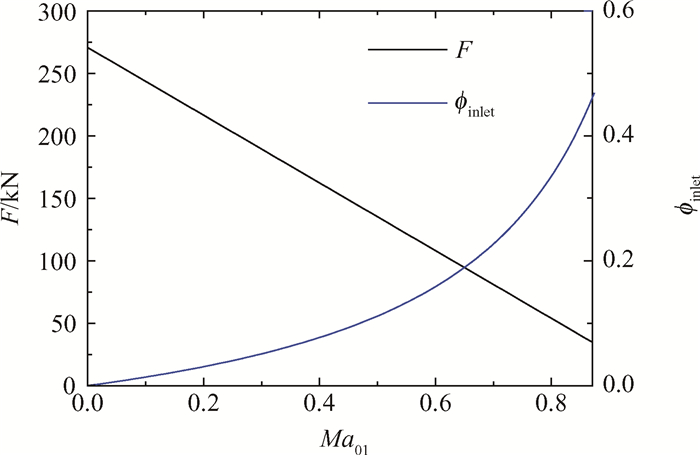
|
Fig. 5 Drag coefficient and thrust changing along with inlet Mach number |
需要升力风扇提供的推力为193857.95N,利用该变化曲线图进行插值,则当F = 193857.95N时,Ma01 =0.2836(C01 = 96.42 m/s),及ϕinlet =0.0470,符合ϕinlet < 0.05的标准[16]。设计点处,风扇的进口流速C1 = 160.65m/s,因此,在专门的起飞进气门和后方升力风扇进口反压的作用下,垂直起降时,升力风扇系统的进气道对进口气流起加速作用。
基于常规升力风扇设计点稳态计算模型,添加非设计点特性图及进气道阻力系数,引入特性图插值法与平衡条件,可建立升力风扇系统全状态稳态模型,并进行设计点处配平。模型在设计点处的相关参数与文献[17]的需求参数比较见表 3。
|
|
Table 3 Contrast between common lift fan model and design requirements |
表 3表明,在设计点处,升力风扇系统模型的性能参数与实际升力风扇系统的性能要求非常接近,所建模型具有一定准确性。
3.3 对转升力风扇的设计与特性获取在满足与文献[17]中相同性能要求的前提下,可基于常规升力风扇设计参数的基础上,设计对应的对转风扇。设计步骤如下:
(1) 保持正转级角度参数不变,在与原常规风扇相同的正转级转速和风扇流量下,合理设计反转级角度参数和转速,并获取压比πfd, C,为方便起见,此时的对转风扇简称为中介对转风扇C。
(2) 在升力风扇的设计点稳态计算模型中,输入风扇C的设计点压比、流量及转速,配平后,得到性能参数推力FC和轴功率PC。不难预见,由于πfd, C的增大,FC和PC会与原常规风扇的对应值有较大的误差,设κ = Ffd/FC。根据推力计算公式Ff = Qf(C5 -C1)∙ϕinlet以及轴功率计算公式Pf = QfCP(T4* -T1*)/η可知,该误差可以在保证C1,C5,T1*,T4*等参数不变的情况下,通过改变Qf来实现对推力和功率等性能参数的修正。
(3) 将相关参数按下式修正
| $ \begin{array}{l} {{Q'}_{\rm{f}}} = {Q_{\rm{f}}} \cdot \kappa \\ {{A'}_{\rm{i}}} = {A_{\rm{i}}} \cdot \kappa \\ {{A'}_{\rm{m}}} = {A_{\rm{m}}} \cdot \sqrt \kappa \\ {{A'}_{\rm{f}}} = {A_{\rm{f}}}/\sqrt \kappa \end{array} $ | (28) |
式中Ai为升力风扇系统的所有特征截面,包括进气道进口截面、风扇各截面、尾喷管出口面积等,从而确保在流量变化κ倍的情况下,各截面的流动情况、总温总压等参数与原设计值下的保持一致。对应的对转风扇中性面半径值变化
通过以上修正公式,对转升力风扇稳态模型设计点处的推力结果与常规升力风扇参数下的模型推力结果完全一致,轴功率有较小误差。至此,实现了基于常规升力风扇,在一定性能要求下的对转升力风扇的设计与建模。
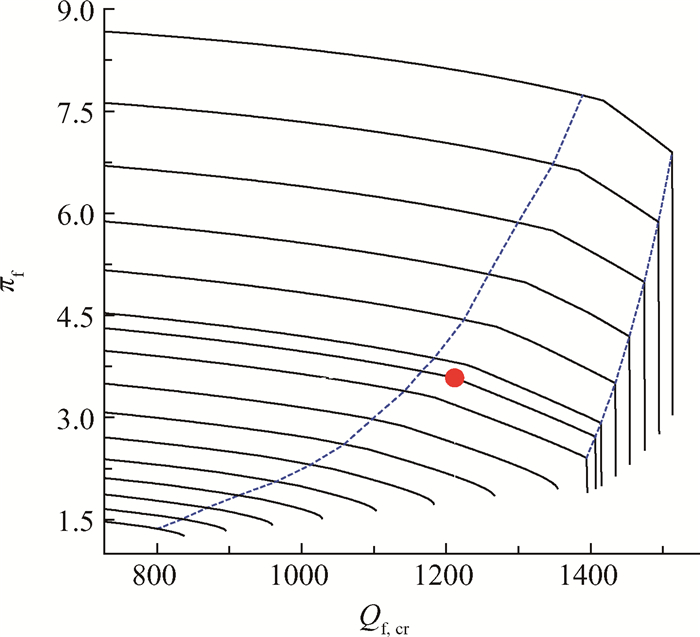
在新的对转升力风扇参数下,设计点处的风扇迭代设计参数结果如表 4所示。经过非设计点计算,对转升力风扇特性图如图 6所示。
|
|
Table 4 Airflow parameters of contra lift fan on design point |
|
Fig. 6 Pressure ratio characteristics of contra lift fan |
常规升力风扇与对转升力风扇系统设计点处的性能参数对比如表 5所示,其中对转升力风扇轴功率为修正前的数值。
|
|
Table 5 Contrast between contra lift fan and non-contra |
(1) 压比πfd = 3.5828,与普通风扇相比,压比明显增大。
(2) 采用对转风扇可以减小升力风扇系统的尺寸和重量,但转速增大,对材料强度要求增大,减速器的传动比减小,尺寸减小。
(3) 通过反转级,出口气流的绝对速度α4不为0,因此,需要出口导流叶片将气流修正为轴向。
(4) 反转级进口气流的相对进口角β3较大,因此,如图 2和图 3所示,对转升力风扇的反转级比常规风扇的静子更“偏”,进口角更大。
(5) 通过反转级,气流轴向速度Ca进一步降低。与常规风扇静子相比,经过反转级,气流绝对速度C下降的更多,静压增加的更多,体现对转风扇在将动压转化为静压方面极佳的性能。反力度Ω = 0.7826,远大于普通风扇。
(6) 反转级的转速需要降低,从而降低周向线速度U。原因在于,轴向速度Ca的减小迫使U减小,从而确保气流角度不会太大,速度三角形合理。
(7) 对转升力风扇的工作范围比常规升力风扇的要小得多。验证了对转风扇工作的不稳定性与对工作环境要求的严格性。
(8) 该修改方法下,对转升力风扇与常规风扇的设计点推力误差为0,轴功率误差很小。
3.4 升力风扇发动机动态建模与升力风扇相匹配的发动机模型的建立是基于参考文献[17]的设计基础上的。利用GASTURB软件在一款现实已有并且掌握了参数的常规发动机的基础上进行修改,从而设计出一款设计点性能满足要求的升力风扇发动机,非设计点状态未处理。在GASTURB中输入常规基准发动机的参数,该发动机以高空状态为设计点;将基准发动机地面状态的非设计点数据中的前面部件(包括风扇、压气机、燃烧室等)的参数作为设计点数据,而后面部件(包括涡轮尾喷管等)的设计点参数选用原基准发动机的高空设计点参数,从而将设计点从高空转移到地面。另外用设计面板中的低压轴机械效率参数(设计点η=0.6)来代替升力风扇的作用效果,体现低压轴加上升力风扇后的工作情况。
本文在发动机建模时采用了实验室的发动机模型,通过修改各尺寸参数如面积等,修改低压轴转动惯量,修改各部件设计点数据,利用设计点修正法修改压气机特性图,以及部分缺失参数如引气量采用修正系数配凑法建立了与参考文献性能需求相匹配的发动机模型,在建模过程中进行了反复迭代设计,以2.2节6个平衡方程残差为标志量进行设计点配平与Newton-Raphson法迭代计算后的再平衡工作。
由于对转风扇与常规风扇设计点性能一致,因此,可以采用同一台发动机模型驱动,该发动机模型设计点参数如表 6所示。
|
|
Table 6 Contrast between engine model and design requirements |
表 6中,发动机部分的性能参数与实际要求的非常接近,修正的发动机模型具有一定的准确性。且结合升力风扇系统的稳态模型,发动机与升力风扇之间耦合工作关系,以及修正后的双轴涡扇发动机模型即可建立升力风扇发动机动态模型。设计点处,带升力风扇发动机提供的总推力Ft = 352159.89N。
4 模型仿真与分析 4.1 升力风扇系统多转速输入稳态仿真首先对升力风扇系统稳态模型进行独立仿真,即在不同的发动机低压轴转速nl的驱动下,比较两种类型的升力风扇的性能参数的差别。
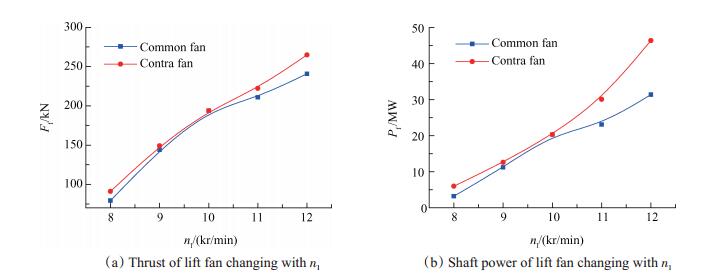
如图 7所示,红色对应对转升力风扇模型,蓝色对应常规升力风扇模型。其中nl = 10kr/min为设计点处的发动机低压轴转速。
|
Fig. 7 Differences of performance parameters of 2 lift fans changing along with nl |
由图 7明显看出,对转风扇和常规风扇在设计点处有相同的推力和轴功率。而在非设计点处,由于在风扇压比特性图上的差异,对应相同的发动机低压轴驱动转速,对转风扇的升力略微大些。又由于两者在效率特性图上的差异(对转升力风扇有两级对转转子,因此其非设计点上的等熵压缩效率低于常规升力风扇的),对转风扇需要消耗的轴功率也要略微大一点,且离设计点越远,差异越明显。
4.2 升力风扇发动机变燃油流量稳态仿真发动机喷管喉道面积一定A8 = 0.336kg/s,燃油流量输入不同的情况下,升力风扇发动机模型的参数情况如图 8所示(红色为对转升力风扇发动机,蓝色为常规的)。其中,Wfb=4.551kg/s为设计点处燃油流量值,此时,两种升力风扇发动机的各项特性参数相同。
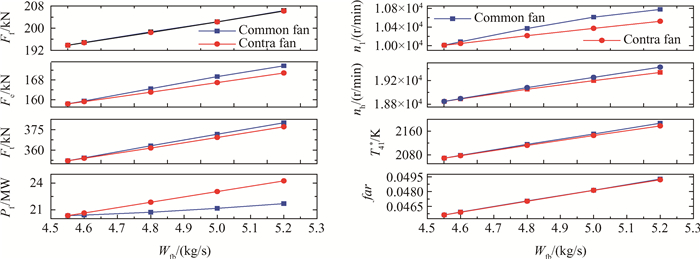
|
Fig. 8 Main parameters of lift fan engine changing with different fuel input on steady state |
从图 8中可以看出,不同燃油流量下,两种升力风扇系统产生的升力Ff是几乎一致的,而发动机部分产生的升力Fe是不同的,且Fe′ < Fe。结合其他参数变化曲线,分析如下:
在不同燃油流量输入下的升力风扇发动机性能参数对比仿真图 8中,首先观察的是far图,分别带对转升力风扇与常规升力风扇的发动机模型在油气比(far)参数上始终相等,说明同一非设计点燃油流量下,不同升力风扇发动机的部分空气流量始终相等。即Qfan′ = Qfan,式中Qfan′为带对转升力风扇的发动机空气流量,Qfan为带常规升力风扇的发动机空气流量。根据4.1节图 7的结论,同一低压轴驱动转速下,由于非设计点特性图的影响,对转升力风扇的耗功率更大Pf′ > Pf,因此由Plt = Pf + Pfan可知,Pfan′ < Pfan与图 8中Pfan差异相符。由于发动机空气流量相同,因此,发动机风扇耗功率上的差异由发动机风扇压比的差异来体现,即πfan′ < πfan。由一般的发动机风扇部件特性图可知,流量相同,压比越小,则转速越小,因此带对转升力风扇的发动机的低压轴转速小于带常规升力风扇的发动机低压轴转速,即nl′ < nl,与图 8中低压轴转速nl差异相符。4.1节的图 7中,非设计点处,当对转升力风扇发动机的低压轴驱动转速略低于常规升力风扇发动机的低压轴转速时,两种升力风扇产生的升力差异会减小,甚至会出现相同的情况,正如图 8中所示两种发动机的升力风扇升力Ff曲线几乎重合。同时,由于带对转风扇的发动机低压轴转速略低,故发动机推力更低Fe′ < Fe,总推力Ft′ < Ft,与图 8中的差异相符。
| $ \begin{array}{l} {{P'}_{\rm{f}}} = {P_{\rm{f}}} \Rightarrow {{P'}_{{\rm{fan}}}} < {P_{{\rm{fan}}}} \Rightarrow \left\{ \begin{array}{l} {{\pi '}_{{\rm{fan}}}} < {\pi _{{\rm{fan}}}}\\ {{Q'}_{{\rm{fan}}}} = {Q_{{\rm{fan}}}}\left( {far' = far} \right) \end{array} \right.\\ \Rightarrow {{n'}_{\rm{l}}} < {n_{\rm{l}}} \Rightarrow \left\{ \begin{array}{l} {{F'}_{\rm{f}}} \approx {F_{\rm{f}}}\\ {{F'}_{\rm{e}}} < {F_{\rm{e}}} \end{array} \right. \Rightarrow \;\;\;{{F'}_{\rm{t}}} < {F_{\rm{t}}} \end{array} $ |
分析表明,当发动机连接特性不同的升力风扇时,某个状态下,发动机会通过自动调节自身的转速以尽量消除不同升力风扇的在推力、轴功率和总推力等方面的差异,体现其“趋同”的特点。
4.3 升力风扇发动机变燃油流量动态对比仿真本文还研究了燃油流量缓慢变化下的两款升力风扇发动机的特性参数随时间的变化情况。燃油流量按式(29)变化,如图 9所示。

|
Fig. 9 Fuel flow changing along with time |
| $ {W_{{\rm{fb}}}} = \left\{ \begin{array}{l} 3.0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t < 1\\ 3.0 + 0.1\left( {t - 1} \right)\;\;\;\;1 \le t \le 3\\ 4\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t > 3 \end{array} \right. $ | (29) |
据动态仿真所示,升力风扇发动机模型非设计点处的动态运行较为平稳良好,见图 10。由于压比特性图与效率特性图的不同,带对转升力风扇和带常规升力风扇的发动机在稳态处,性能参数的数值略有差异,差异规律满足4.2节中的分析结论。在设计垂直起降推进系统时,可以通过综合考量对转风扇在减重减小尺寸等方面的优势以及非设计点推力较小等方面的劣势,从而选择合适的风扇类型作为升力风扇。

|
Fig. 10 Main parameters of two lift fan engines changing along with time in dynamic simulation |
通过本文研究,得到以下结论:
(1) 为了使模型产生推力满足需求,采用函数作图插值法,将设计点处升力风扇进气道进口截面马赫数设为0.2836,且进气道阻力系数为0.0470。此时进气道为收敛加速型,对应于实际的进气道设计中起飞进气门的作用效果,避免出现太厚的附面层。
(2) 本文提出的基于叶片基元级理论的气流参数计算模型可广泛用于风扇或压气机非设计点特性的半设计半计算中。本文提出的中介推力修正系数法可用于基于常规风扇的对转风扇的半设计半计算中,此方法下,两风扇推力相等,修正前的轴功率误差仅为0.0265。对比两者设计参数与非设计点特性图,指出对转风扇尺寸更小,重量更轻,反转级转速低,反力度大,抗陀螺力矩等优点;以及特性图工作区较小,正转级转速大,非设计点效率较低等缺点。
(3) 进一步的结合发动机的动稳态仿真表明,由于压比特性不同,在相同的发动机低压轴驱动转速下,非设计点处对转风扇产生的推力更大;由于效率特性不同,对转风扇消耗的轴功率也更大。且当发动机连接特性不同的升力风扇时,发动机会产生“趋同”的作用效果,即通过调节自身的转速以尽量消除搭载不同升力风扇时在升力风扇推力、轴功率和发动机总推力等方面的差异。从总推力角度来看,带对转升力风扇的发动机在非设计点处会略小。
| [1] |
刘大响. 航空发动机技术的发展和建议[J]. 中国工程科学, 1999, 1(2): 24-29. (  0) 0) |
| [2] |
宋笔锋. 航空航天技术概论[M]. 北京: 国防工业出版社, 2006.
(  0) 0) |
| [3] |
Bevilaqua P, Eshleman J, Falabella D, et al. ASTOVL Aircraft Technology Demonstration Program[R]. Lockheed Martin Skunk Works Report, TR-96-1, 1996.
(  0) 0) |
| [4] |
Armsrtong. CAN科普_"闪电"之心—谈谈F135发动机[J]. 空军之翼, 2016(1). (  0) 0) |
| [5] |
叶代勇, 滕健, 郭捷, 等. 短距起飞/垂直降落战斗机发动机发展及关键技术分析[J]. 航空发动机, 2013, 39(1): 74-78. (  0) 0) |
| [6] |
Sellers J F, Szuch J R. Control of Turbofan Lift Engines for VTOL Aircraft[R]. NASA-TM X-68175, 1973.
(  0) 0) |
| [7] |
郭捷, 杨琳, 郑宁, 等. 短距/垂直起落战斗机升力风扇关键技术的探讨[J]. 航空科学技术, 2008(2): 30-35. (  0) 0) |
| [8] |
K evin M McCarthy. STOVL Strike Fighter Concept Definition Work at NAWC AD Warminster[R]. AIAA-92-4197-CP.
(  0) 0) |
| [9] |
徐雪, 黄爱华, 郭捷. 基于关键结构特征的升力风扇结构布局方案设计[J]. 航空发动机, 2014, 40(4): 14-19. (  0) 0) |
| [10] |
郑志成, 周洲. 垂直起降飞机设计中升力风扇估算模型分析[J]. 飞行力学, 2010, 28(3): 21-23. (  0) 0) |
| [11] |
杨琳, 陈雷, 孙海, 等. 对转风扇设计技术研究[J]. 航空学报, 2014, 35(5): 1226-1235. (  0) 0) |
| [12] |
刘帅, 王占学, 蔡元虎, 等. 升力风扇和涡扇发动机组合动力系统性能模拟与分析[J]. 航空动力学报, 2013, 28(5): 1095-1100. (  0) 0) |
| [13] |
任冰涛, 李秋红. 短距起飞/垂直降落发动机建模技术研究[J]. 航空动力学报, 2015, 30(10): 2531-2538. (  0) 0) |
| [14] |
季路成. 对转叶轮机技术挑战分析[J]. 推进技术, 2007, 28(1): 40-44. (JI Lu-cheng. Analysis for Technique Challenges on Counter-Rotating Turbomachinery[J]. Journal of Propulsion Technology, 2007, 28(1): 40-44.)
(  0) 0) |
| [15] |
钱锟. F-35的改进项目和试飞进展[J]. 国际航空, 2010(4): 31-35. (  0) 0) |
| [16] |
马丁利J D, 海泽W H. 航空发动机设计[M]. 北京: 科学出版社, 1992.
(  0) 0) |
| [17] |
James E Goebel. Design of a Lift Fan Engine for a Heavy Lift Aircraft[D]. South Bend: University of Notre Dame, Monterey: Naval Postgraduate School, 2003.
(  0) 0) |
| [18] |
杨小贺, 单鹏. 两类对转风扇的设计与气动特征数值研究[J]. 航空动力学报, 2011, 26(10): 2313-2322. (  0) 0) |
| [19] |
张恒铭, 黄秀全, 张翔, 等. 两级对转风扇非定常特性分析[J]. 推进技术, 2016, 37(2): 209-217. (ZHANG Heng-ming, HUANG Xiu-quan, ZHANG Xiang, et al. Unsteady Characteristic Analysis of a Two-Stage Counter-Rotating Fan[J]. Journal of Propulsion Technology, 2016, 37(2): 209-217.)
(  0) 0) |
| [20] |
Naveen Kumar Vallabhaneni. Continuously Variable Rotatorcraft Propulsion System: Modeling and Simulation[D]. Knoxville: University of Tennessee, 2011.
(  0) 0) |
| [21] |
胡骏, 吴铁鹰, 曹人靖. 航空叶片机原理[M]. 北京: 科学出版社, 2005.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

