2. 中国东方航空江苏有限公司 飞机维修部,江苏 南京 211113;
3. 扬州大学 机械工程学院,江苏 扬州 225127
2. Department of Aircraft Maintenance, China Eastern Airlines Jiangsu Limited, Nanjing 211113, China;
3. College of Mechanical Engineering, Yangzhou University, Yangzhou 225127, China
时间限制派遣(Time Limited Dispatch,TLD)的概念来源于波音767飞机的全权限数字式发动机控制(Full Authority Digital Electronic Control,FADEC)系统的研制与审定之中[1]。TLD是指当系统的冗余单元出现故障时,不需要立即进行维修,允许系统带故障运行一段预定长度的时间[2]。TLD运行是民用飞机与商用航空发动机型号合格审定的可选要求,一旦TLD运行获得批准,飞机运营商可将系统冗余单元的故障安排在计划的维修间隔期进行维修,而不必在下一次飞行前完成所有故障维修,避免了由于非计划维修导致航班延误或取消,从而提高了飞机的可派遣性[2, 3]。
TLD分析是在系统能够满足平均完整性要求的条件下确定各故障的派遣时间间隔。目前,TLD分析的方法主要包括时间加权平均法、马尔可夫模型法以及蒙特卡罗仿真方法。时间加权平均法是一种基于故障树分析的近似方法,由于精度较低,在适航审定中并不被广泛采用。马尔可夫模型法包括开环马尔可夫模型方法与闭环马尔可夫模型方法,它们求得的系统平均完整性要求相差一个因子,通常认为闭环马尔可夫模型求得平均完整性要求的准确值,因此,闭环马尔可夫模型也是适航当局推荐使用的TLD分析方法。马尔可夫模型适用于单故障TLD分析,即只考虑直接导致推力控制丧失(Loss of Thrust Control,LOTC)的单个故障、可派遣的单个故障以及单故障派遣时导致LOTC的单个继发故障; 若考虑多故障状态,马尔可夫模型的复杂度将随着系统组成单元数量的增加呈指数级增长、出现状态空间爆炸,从而导致求解过程异常复杂。蒙特卡罗仿真方法是一种数值仿真方法,基本思想是生成服从单元寿命分布的随机数来模拟单元寿命、进而根据系统失效与单元失效的关系得到系统的LOTC状态时间间隔,该时间平均值的倒数即为发动机控制系统的平均完整性要求。若在TLD分析中考虑多故障状态,蒙特卡罗仿真方法能够避免状态空间爆炸,是多故障TLD分析的有效方法[2, 4]。
在上述方法中,航空发动机控制系统的平均完整性水平通常被认为是“平均LOTC率”。运输类飞机发动机控制系统的平均完整性水平必须小于1×10-5(单位:1/h,下同)。当故障发生后,根据瞬时LOTC率的值,可将发动机控制系统带故障运行的派遣类别分为三类[1, 3, 4]:
(1) 不允许派遣(ND):若瞬时LOTC率大于1×10-4时,则不允许带故障运行,故障必须立即修复。
(2) 短时派遣(ST):当瞬时LOTC率在区间[7.5×10-5, 1×10-4)内时,可带故障派遣较短的时间间隔TST,即故障必须在时间区间[0, TST]内修复。
(3) 长时派遣(LT):当瞬时LOTC率在区间[1×10-5, 7.5×10-5)内时,可带故障派遣较长的时间间隔[TLT(TLT>TST)],故障必须在时间区间[0, TLT]内修复。
TLD分析可具体描述为在发动机控制系统平均完整性要求小于1×10-5的条件下,确定TST与TLT的值。
当前,FADEC技术是航空发动机控制的发展方向[5, 6],TLD运行业已广泛应用于安装FADEC系统的发动机的研制与审定,以及安装此类发动机的飞机的研制与审定。TLD分析也已经成为针对25.1309“设备、系统及安装”、33.28“发动机控制系统”等适航条款开展符合性验证的重要内容[7~10]。
本文将对发动机控制系统TLD分析的若干可靠性基本理论问题进行研究,重新定义航空发动机控制系统平均完整性水平,分析单故障与多故障TLD模型的特点,并且提出周期检查维修方式下故障暴露时间计算方法。
2 平均完整性水平定义研究通常认为航空发动机控制系统的平均完整性水平由平均LOTC率表示[2, 11~15]。LOTC事件定义为:(1)不能通过油门杆动作,在任何飞行状态下对发动机推力在慢车与90%的最大额定推力之间进行调节; (2)发动机不能满足CCAR33部的工作特性要求; (3)发动机推力以不可接受的方式振荡[1, 2]。由此定义可知,发生LOTC意味着航空发动机控制系统失效,因此可将平均LOTC率视为发动机控制系统的平均失效率。根据上述分析,平均LOTC率应当定义为
| $ {{\bar \lambda }_{{\rm{LOTC}}}}\left( {{t_1},{t_2}} \right) = \frac{1}{{{t_2} - {t_1}}}\int_{{t_1}}^{{t_2}} {{\lambda _{\rm{S}}}\left( t \right){\rm{d}}t} $ | (1) |
上式表示系统在时间区间[t1, t2]内的平均LOTC率,式中λS(t)为系统瞬时失效率,其一般表达式如下
| $ {\lambda _{\rm{S}}}\left( t \right) = - \frac{{{\rm{d}}{R_{\rm{S}}}\left( t \right)/{\rm{d}}t}}{{{R_{\rm{S}}}\left( t \right)}} $ | (2) |
式中RS(t)为系统在t时刻的可靠度。
根据非齐次泊松过程的相关理论可知,平均失效率实质上是采用最小维修时,系统在时间区间[t1, t2]内的故障频率[16]。因此平均LOTC率为采用最小维修时,系统在时间区间[t1, t2]内LOTC发生的频率,即在[t1, t2]内单位时间发生LOTC的次数。显然,平均LOTC率的值并非常数,而是t1,t2的函数。而实际分析中,无论采用何种方法计算得到的发动机电子控制系统的平均完整性水平均为常数[2, 11~15],因此将发动机控制系统的平均完整性水平定义为平均LOTC率是不正确的,至少是不严谨的。
发动机控制系统开展TLD分析的最主要方法是马尔可夫模型法,通常认为闭环马尔可夫模型能够求得准确的平均完整性水平,而开环马尔可夫模型只能求得平均完整性水平的近似值[2]。但是现有的文献并没有分析开环与闭环马尔可夫模型在求解平均完整性水平时的本质区别。
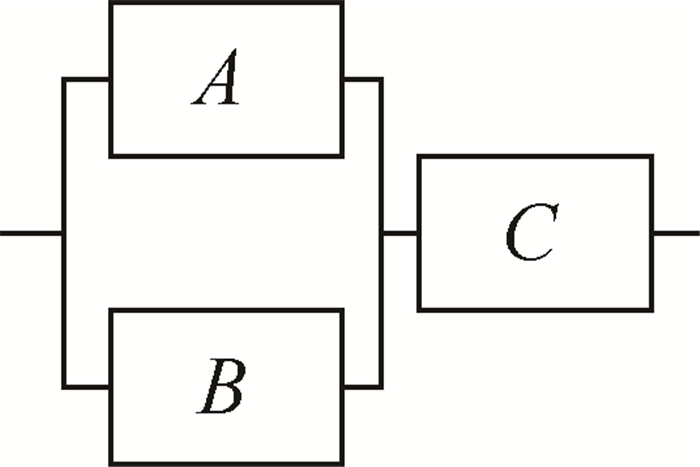
以图 1所示系统为例,图中各单元失效率分别为λA=8×10-5,λB=2×10-5及λC=7×10-6。
|
Fig. 1 Case 1 |
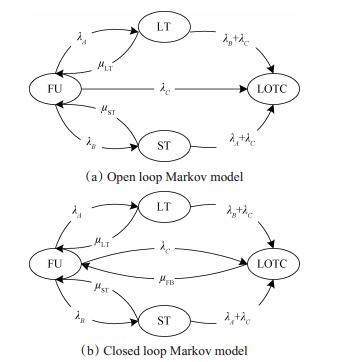
当单元A失效后,系统瞬时LOTC率为λB+λC=2.7×10-5,同理可得单元B失效后系统的瞬时LOTC率为8.7×10-5,而单元C失效后系统将失效。由前述派遣类别可知,单元A、B与C失效后,系统将分别进入LT,ST与LOTC状态。与图 1对应的开环与闭环马尔可夫模型见图 2。
|
Fig. 2 Open and closed Markov models of case 1 |
图 2中,FU,LT,ST与LOTC分别表示系统处于完好状态、长时派遣状态、短时派遣状态以及LOTC状态。μST,μLT与μFB分别为系统处于LT,ST与LOTC状态的修复率,其中μST=1/TST,μLT=1/TLT。由于系统处于LOTC状态时必须立刻进行维修,允许带故障派遣的时间为0,μFB理论上应当为无穷大,实际计算时可取一较大的数值。开环与闭环马尔可夫模型的区别在于闭环模型多了从LOTC状态到FU状态的反馈。
基于马尔可夫模型的发动机控制系统平均完整性水平(现有文献中均称其为平均LOTC率)定义如下[2]
| $ {{\bar \lambda }_{{\rm{LOTC}}}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{{P_{{\rm{into}} - {\rm{LOTC}}}}\left( t \right)}}{{1 - {P_{{\rm{LOTC}}}}\left( t \right)}} $ | (3) |
式中PLOTC(t)]是发动机控制系统在t时刻处于LOTC状态的概率,Pinto-LOTC(t)是t时刻流入LOTC状态的概率。
以图 2所示的马尔可夫模型为例,Pinto-LOTC(t)]可表示如下
| $ {P_{{\rm{into}} - {\rm{LOTC}}}}\left( t \right) = {\lambda _C}{P_{{\rm{FU}}}}\left( t \right) + \left( {{\lambda _A} + {\lambda _C}} \right){P_{{\rm{ST}}}}\left( t \right) + \left( {{\lambda _B} + {\lambda _C}} \right){P_{{\rm{LT}}}}\left( t \right) $ | (4) |
式中PFU(t),PST(t)与PLT(t)分别是t时刻系统处于FU,ST与LT状态的概率。
2.1 基于开环马尔可夫模型的平均完整性水平由连续时间马尔可夫过程的Fokker-Planck方程可得[17]
| $ \frac{{{\rm{d}}{P_{{\rm{LOTC}}}}\left( t \right)}}{{{\rm{d}}t}} = {P_{{\rm{into}} - {\rm{LOTC}}}}\left( t \right) - {P_{{\rm{out}} - {\rm{LOTC}}}}\left( t \right) $ | (5) |
在开环马尔可夫模型中,不存在从LOTC状态到FU状态的反馈,因此t时刻不存在流出LOTC状态的概率,即Pout-LOTC(t)=0,结合式(5)可得
| $ \frac{{{\rm{d}}{P_{{\rm{LOTC}}}}\left( t \right)}}{{{\rm{d}}t}} = {P_{{\rm{into}} - {\rm{LOTC}}}}\left( t \right) $ | (6) |
由LOTC事件定义可知LOTC状态为系统失效状态,因此PLOTC(t)可表示为
| $ {P_{{\rm{LOTC}}}}\left( t \right) = 1 - {R_{\rm{S}}}\left( t \right) $ | (7) |
综合式(2)、(3)、(6)和(7)可得
| $ {{\bar \lambda }_{{\rm{LOTC}}}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{{\rm{d}}{P_{{\rm{LOTC}}}}\left( t \right)/{\rm{d}}t}}{{1 - {P_{{\rm{LOTC}}}}\left( t \right)}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{ - {\rm{d}}{R_{\rm{S}}}\left( t \right)/{\rm{d}}t}}{{{R_{\rm{S}}}\left( t \right)}} = \mathop {\lim }\limits_{t \to + \infty } {\lambda _{\rm{S}}}\left( t \right) $ | (8) |
由式(8)可知,在开环马尔可夫模型中,发动机控制系统的平均完整性水平为系统瞬时LOTC率的稳态值,即时间趋向无穷时的系统失效率值,并非式(1)给出的系统平均LOTC率。
2.2 基于闭环马尔可夫模型的平均完整性水平令Q为连续时间马尔可夫过程的转移率矩阵
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {{q_{11}}}&{{q_{12}}}& \cdots &{{q_{1n}}}\\ {{q_{21}}}&{{q_{22}}}& \cdots &{{q_{2n}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{q_{n1}}}&{{q_{n2}}}& \cdots &{{q_{nn}}} \end{array}} \right] $ | (9) |
则该马尔可夫过程的Fokker-Planck方程组可表示为
| $ \frac{{{\rm{d}}P\left( t \right)}}{{{\rm{d}}t}} = P\left( t \right)\mathit{\boldsymbol{Q}} $ | (10) |
当时间趋于无穷时,该马尔可夫过程将趋于稳定,并且极限概率不再随时间变化,可得
| $ \mathit{\boldsymbol{\bar \pi Q}} = \mathit{\boldsymbol{\bar 0}} $ | (11) |
式中π=[π1 π2…πn]为各状态极限概率组成的向量,πi表示状态i的极限概率,0为所有元素均为0的向量。
在基于马尔可夫过程的可靠性模型中,系统稳态故障频率可表示为[18]
| $ {f_{{\rm{up}} - {\rm{down}}}} = \sum\limits_{k \in W} {{\pi _k}\left( {\sum\limits_{j \in F} {{q_{kj}}} } \right)} $ | (12) |
式中W为所有工作状态的集合,F为所有失效状态的集合,πk为第k个状态的极限概率,qkj为状态k到j的转移概率。
在TLD分析的马尔可夫模型中,LOTC状态是集合F的唯一元素,其他状态均属于集合W,假定LOTC状态为第n个状态,则F={n},可得系统处于稳态时流入LOTC状态的概率为
| $ \mathop {\lim }\limits_{t \to \infty } {P_{{\rm{into}} - {\rm{LOTC}}}}\left( t \right) = \sum\limits_{k = 1,2, \cdots ,n - 1} {{\pi _k}{q_{kn}}} $ | (13) |
由式(10)与式(11)可得
| $ {f_{{\rm{up}} - {\rm{down}}}} = \mathop {\lim }\limits_{t \to \infty } {P_{{\rm{into}} - {\rm{LOTC}}}}\left( t \right) $ | (14) |
由于LOTC状态是唯一的失效状态,系统稳态可用度可表示如下
| $ A = 1 - \mathop {\lim }\limits_{t \to \infty } {P_{{\rm{LOTC}}}}\left( t \right) $ | (15) |
根据式(3)、式(14)与式(15)可得
| $ {{\bar \lambda }_{{\rm{LOTC}}}} = \frac{{{f_{{\rm{up}} - {\rm{down}}}}}}{A} $ | (16) |
系统稳态故障频率的一般表达式为
| $ {f_{{\rm{up}} - {\rm{down}}}} = \frac{1}{{MTTR + MTBF}} $ | (17) |
式中MTBF为平均故障间隔时间,MTTR为平均修复时间。
系统稳态可用度的一般表达式为
| $ A = \frac{{MTBF}}{{MTTR + MTBF}} $ | (18) |
由式(15)~(17)可得
| $ {{\bar \lambda }_{{\rm{LOTC}}}} = \frac{1}{{MTBF}} $ | (19) |
由式(18)可得,基于闭环马尔可夫过程求得的系统平均安全性水平本质上是系统MTBF的倒数,即平均LOTC间隔时间的倒数,也可称为不考虑将系统从LOTC状态恢复到FU状态所需维修时间的LOTC频率。由于不考虑系统从LOTC状态恢复到FU状态所需维修时间,因此式(18)求得的平均完整性要求与μFB无关,该结论与文献[2]是一致的。
式(1)是平均失效率,表示系统失效后采用最小维修策略时在[t1, t2]内的故障频率,其特点是系统修复后的瞬时失效率等于系统失效前的瞬时失效率,即修复不会改变系统瞬时失效率的发展趋势,该过程用非齐次泊松过程来描述; 式(18)表示的LOTC频率实质上是采用最大维修策略时的故障频率,系统进入LOTC状态后将被完全修复(即修复如新),该过程用更新过程来表示; 式(8)则是稳态LOTC率,即不考虑从LOTC状态恢复到FU状态的维修时的系统瞬时LOTC率的稳定值。
综合上述分析可得,发动机控制系统的平均完整性水平既不是平均LOTC率,也不是稳态LOTC率,而应当是LOTC频率(不考虑维修时间)。只有当系统寿命服从指数分布,即系统的瞬时LOTC率为常数时,上述三者才相等。通常假定发动机控制系统的各部件的寿命服从指数分布[2],但是发动机控制系统则是由这些部件组成的冗余系统,其寿命显然不可能服从指数分布,即发动机控制系统的瞬时LOTC率不可能为常数,因此上述三者一般是不相等的。
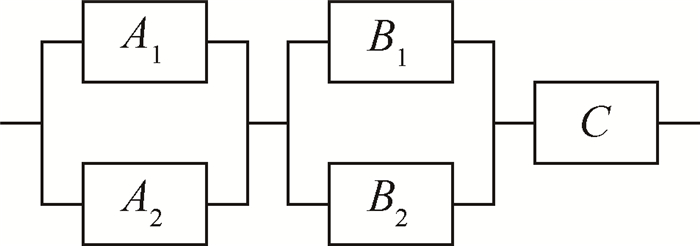
3 单故障与多故障TLD模型特点分析 3.1 单故障TLD模型及其特点目前广泛使用的TLD模型为单故障模型,其只考虑单个故障状态、以及单故障派遣时导致系统进入LOTC状态的继发单个故障[2]。图 3所示系统中,单元A1与A2的失效率均为λA,单元B1与B2的失效率为λB,单元C的失效率为λC。
|
Fig. 3 Case 2 |
在单故障模型中考虑的单个故障,以及该故障发生后导致系统由进入LOTC状态的单个继发故障见表 1。
|
|
Table 1 Single faults and additional single faults |
表 1中,C故障将直接导致系统进入LOTC状态,因此不存在继发的导致LOTC状态的故障,也没有瞬时LOTC率。令λA=8×10-5,λB=2×10-5及λC=7×10-6,则λA+λC与λB+λC分别在[7.5×10-5, 1×10-4)与[1×10-5, 7.5×10-5)内。因此,A1或A2故障后系统进入ST状态,B1或B2故障后系统则进入LT状态。
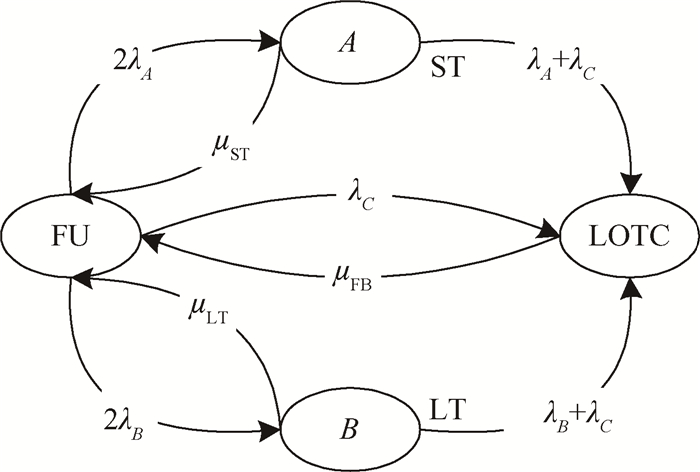
图 4给出了图 3所示系统的单故障TLD分析的闭环马尔可夫模型。图中,A表示单元A1或A2故障,B表示单元B1或B2故障。
|
Fig. 4 Single fault TLD model of case 2 |
单故障TLD模型忽略了除LOTC状态外的所有组合故障,图 3中被忽略的组合故障包括:A1故障未修复B1又故障、A1故障未修复B2又故障、A2故障未修复B1又故障、以及A2故障未修复B2又故障。由于组合故障被忽略,单故障TLD模型具有如下特点:
(1) 单故障发生后的瞬时LOTC率为常数,其值等于继发的单故障的失效率加上由FU状态进入LOTC状态的失效率,如A1故障后的瞬时LOTC率等于A2的失效率加上C的失效率。
(2) 通常假定冗余部件的单故障不会是ND状态,若单故障状态即为ND状态,则表明设计是不合理的,即冗余设计会极大地降低飞机的出勤可靠度,工程实际中应当避免这种情况的发生。
(3) 单故障发生后,只有将该故障修恢复到FU状态一种维修策略,在单故障TLD模型中,所有与修复率相关的有向弧的箭头都指向FU状态。
3.2 多故障TLD模型特点单故障TLD模型从本质上讲是一种状态简化的模型,由于忽略了除LOTC状态外的所有多故障状态,只能通过式(3)求得故障派遣时间间隔(TLT与TST)与平均完整性水平(λLOTC)的近似关系。在给定发动机控制系统的λLOTC小于1×10-5的条件下,也只能确定TST与TLT的近似值。当忽略的多故障状态较多时,会导致求得的近似值与真实值存在较大误差,因此当系统组成单元较多时,有必要建立多故障TLD模型。与单故障TLD模型相比,多故障TLD模型的特点可概述如下:
(1) 故障发生后的瞬时LOTC率通常是时间的函数,该函数可由式(2)求得。
(2) 多故障TLD模型中可能存在ND状态,由于ND状态需要立刻修复,与ND状态相关的修复率理论上应当无穷大。
(3) 多故障发生后可能存在多种维修策略,不同的维修策略必然对应于不同的TLD模型。
3.3 多故障TLD模型示例以图 3所示系统为例,若考虑所有多故障状态,则Ai(i=1,2.下同)故障后的系统可靠度函数为
| $ {R_{\rm{S}}}\left( t \right) = {R_A}\left( t \right) \times \left( {2{R_B}\left( t \right) - {R_B}{{\left( t \right)}^2}} \right) \times {R_C}\left( t \right) $ | (20) |
式中RA(t),RB(t),RC(t)分别为单元Ai、单元Bi、以及单元C的可靠度函数。将式(20)带入式(2),可求得
| $ {\lambda _{{\rm{LOTC}}}}\left( t \right) = {\lambda _A} + {\lambda _C} + \frac{{2{\lambda _B}\left( {1 - {{\rm{e}}^{ - {\lambda _B}t}}} \right)}}{{2 - {{\rm{e}}^{ - {\lambda _B}t}}}} $ | (21) |
同理可得Bi故障后的瞬时LOTC率为
| $ {\lambda _{{\rm{LOTC}}}}\left( t \right) = {\lambda _B} + {\lambda _C} + \frac{{2{\lambda _A}\left( {1 - {{\rm{e}}^{ - {\lambda _A}t}}} \right)}}{{2 - {{\rm{e}}^{ - {\lambda _A}t}}}} $ | (22) |
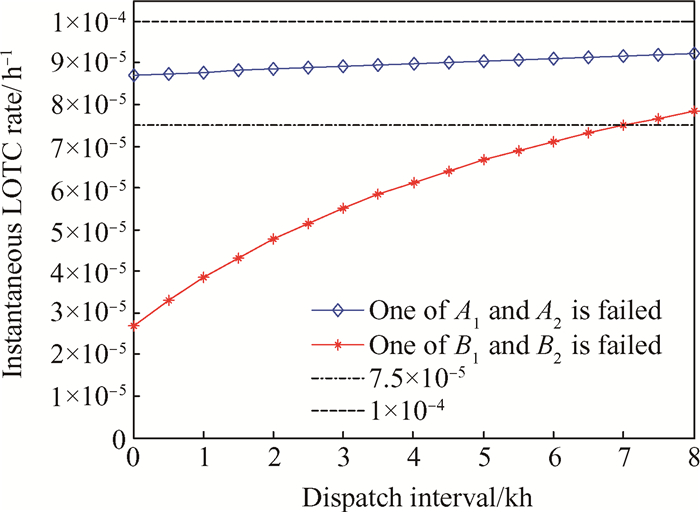
将λA,λB与λC的数值分别代入式(21)与式(22),可得Ai或Bi故障后的系统瞬时LOTC率曲线,见图 5。
|
Fig. 5 Curve of instantaneous LOTC rate |
显然,图 5所示的瞬时LOTC率为时间的函数,并且该函数值并不总是位于前述派遣类别所要求的瞬时LOTC率的区间内,因此无法直接利用该分类方法来确定故障后的派遣类别,此时可利用瞬时LOTC率函数在预定的派遣间隔内的最大值来确定故障后的派遣类别[4]。图 5中,Ai故障后的瞬时LOTC率在8kh以内时一直处于[7.5×10-5, 1×10-4),而短时派遣间隔TST一般都小于500h,因此在TST内,瞬时LOTC率在7.5×10-5, 1×10-4),因此Ai故障为ST状态。同样由图 5可知,Bi故障后的瞬时LOTC率在6.995kh以内时位于[1×10-5, 7.5×10-5),在6.995~8kh时位于[7.5×10-5, 1×10-4),因此若长时派遣间隔TLT小于6.995kh,则Bi故障为LT状态,否则为ST状态。
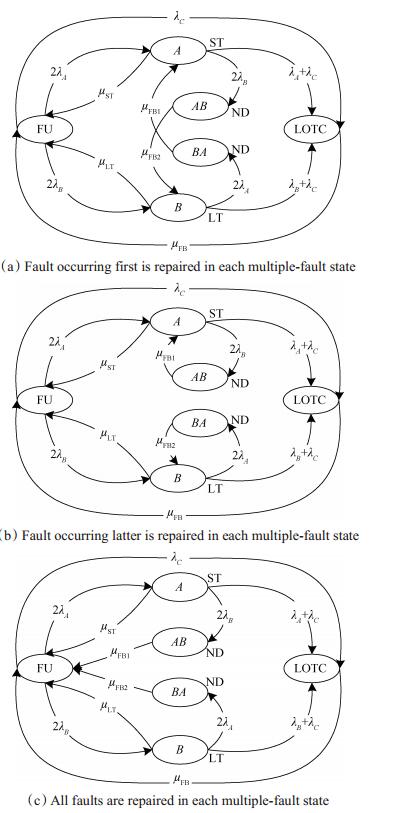
同样以图 3所示系统为例,若Ai故障未修复Bi又故障,此时的瞬时LOTC率为λA+λB+λC,其值为1.07×10-4,根据派遣分类方法,该状态应当属于ND状态,因此与该状态相关的修复率理论上应当为无穷大。同时该状态是典型的多故障状态,有立即修复先发生的故障(Ai故障)、立即修复后发生的故障(Bi故障)、以及立即将所有故障(Ai故障与Bi故障)均修复三种不同的维修策略; 同理,Bi故障未修复Ai又故障也属于ND状态,也有三种不同的维修策略。当TLT小于6.995kh,这三种维修策略相对应的多状态TLD模型如图 6所示。
|
Fig. 6 Multiple-fault TLD models |
图中,A表示单元Ai故障,B表示单元Bi故障,AB表示Ai故障未修复时Bi又故障,BA表示Bi故障未修复时Ai又故障,μFB1与μFB2分别是与AB、BA状态相关的修复率,由于AB与BA状态均为ND状态,因此μFB1与μFB2的值理论上应当无穷大,实际计算时可取较大的数值。若TLT大于6995h,图 6中的B状态也应当是ST状态,此时与B状态相关的修复率应当为μST。
4 周期检查维修方式下故障暴露时间分析飞机故障发生通常有两种维修方式,即“MEL(Minimum Equipment List)维修方式”与“周期检查维修方式”。MEL维修方式也称为视情维修,在该维修方式下飞机具有对相关故障状态的检测与告警功能,故障发生时刻是已知的,故障暴露时间从故障发生时刻开始到故障维修时刻结束,短时派遣故障通常采用这种维修策略。周期检查维修方式则是在固定的检测间隔期检查故障是否发生,长时派遣故障通常采用该维修方式[2, 19, 20]。
采用周期检查维修方式时,无法获知故障发生的具体时刻,为了求得故障暴露时间,通常假定故障在检测间隔期的中点发生。以某长时派遣故障为例:假定飞机允许带该故障派遣的时间间隔为250h,该故障的检测间隔期为400h,若检查时发现故障,申请人可以假设故障发生在检测间隔期的中间点,即已经发生了200h,因此必须在随后的50h内修复以满足派遣间隔的要求。这种假设并不严谨,只有故障前时间在检测间隔期内服从均匀分布时才成立。本部分将给出故障前时间服从一般分布时,在检测间隔期发现故障的条件下,平均故障暴露时间的推导过程。
假设故障检测间隔期为TI,x为产品的故障前时间,在TI时刻发现故障的条件下,故障发生在时刻t的概率为
| $ P\left( {x = t\left| {x < {T_I}} \right.} \right) = \left\{ \begin{array}{l} \frac{{P\left( {x = t} \right)}}{{P\left( {x < {T_I}} \right)}}\;\;\;\;\;t < {T_{\rm{I}}}\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \ge {T_{\rm{I}}} \end{array} \right. $ | (23) |
若f(t)为故障密度函数,则在TI时刻发现故障条件下的故障密度函数为
| $ f\left( {t\left| {{T_{\rm{I}}}} \right.} \right) = \left\{ \begin{array}{l} \frac{{f\left( t \right)}}{{\int_0^{{T_1}} {f\left( t \right){\rm{d}}t} }}\;\;\;\;t < {T_{\rm{I}}}\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \ge {T_{\rm{I}}} \end{array} \right. $ | (24) |
由此可得TI时刻发现故障条件下的平均故障前时间为
| $ {\theta _{{T_{\rm{I}}}}} = \int_0^{ + \infty } {tf\left( {t\left| {{T_{\rm{I}}}} \right.} \right){\rm{d}}t} = \frac{{\int_0^{{T_1}} {tf\left( t \right){\rm{d}}t} }}{{\int_0^{{T_1}} {f\left( t \right){\rm{d}}t} }} $ | (25) |
由于通常假设发动机控制系统各部件的寿命服从指数分布[2],即各部件的故障前时间服从指数分布,若某个长时派遣故障的失效率为λLT,由式(25)可得TI时刻发现故障条件下,该长时故障的平均故障前时间
| $ {\theta _{{T_{\rm{I}}}}} = \frac{{\int_0^{{T_{\rm{I}}}} {{\lambda _{{\rm{LT}}}}t{{\rm{e}}^{ - {\lambda _{{\rm{LT}}}}t}}{\rm{d}}t} }}{{1 - {{\rm{e}}^{ - {\lambda _{{\rm{LT}}}}{T_{\rm{I}}}}}}} = \frac{1}{{{\lambda _{{\rm{LT}}}}}} + \frac{{{T_{\rm{I}}}}}{{1 - {{\rm{e}}^{ - {\lambda _{{\rm{LT}}}}{T_{\rm{I}}}}}}} $ | (26) |
在TI时刻(故障发现时刻),该故障的平均暴露时间为
| $ {T_{\rm{E}}} = {T_{\rm{I}}} - {\theta _{{T_{\rm{I}}}}} = \frac{{{T_{\rm{I}}}}}{{1 - {{\rm{e}}^{ - {\lambda _{{\rm{LT}}}}{T_{\rm{I}}}}}}} - \frac{1}{{{\lambda _{{\rm{LT}}}}}} $ | (27) |
若该长时故障的派遣时间间隔为TLT,则在TI时刻发现故障后,允许继续带故障派遣时间为
| $ {{T'}_{{\rm{LT}}}} = {T_{{\rm{LT}}}} - {T_{\rm{E}}} = {T_{{\rm{LT}}}} - \frac{{{T_1}}}{{1 - {{\rm{e}}^{ - {\lambda _{{\rm{LT}}}}{T_{\rm{I}}}}}}} + \frac{1}{{{\lambda _{{\rm{LT}}}}}} $ | (28) |
由式(28)可求得,采用周期检查维修方式时,在检测间隔期发现故障后,仍然允许继续派遣的时间间隔。
5 实例分析某型FADEC系统由发动机控制组件(ECU)、液压机械组件(HMU)、电源、传感器部件组成。ECU包括两个完全相同的通道Ⅰ与Ⅱ,均接收输入信号并进行计算,但是只有一个通道向HMU输出控制指令,通道Ⅰ与Ⅱ通过CCDL进行通讯,任一通道的所有输入信号都可以通过CCDL提供给另一通道,保证在某一通道的重要输入信号失效的情况下,两个通道仍然能够正常工作。所有控制信号传感器都是双余度的,分别与通道Ⅰ与Ⅱ相连。发动机起动后通道Ⅰ与Ⅱ分别由专用电源的两个独立线圈供电。HMU将源于ECU的控制指令转换为液压压力,驱动燃油计量活门(FMV)实现燃油控制,驱动可变静子叶片(VSV)与可变放气活门(VBV)实现压气机气流控制。ECU计算FMV、VSV以及VBV控制指令所需输入信号包括:高压转子转速(N2)、压气机排气温度(T3)、油门杆角度(TLA)以及HMU中执行机构(FMV、VSV与VBV)的位置反馈信号。
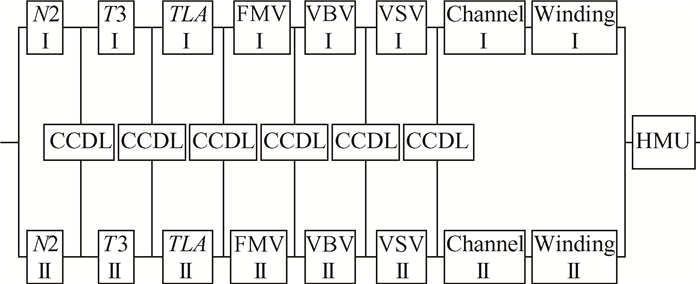
发动机燃油控制功能丧失和压气机气流控制功能丧失会均会导致LOTC状态。因此,要保证发动机运行过程中不出现LOTC状态,HMU以及至少一个ECU通道及其对应的传感器与电源线圈必须处于非故障状态。综合上述分析,给出该FADEC系统的可靠性模型,见图 7[4]。
|
Fig. 7 Reliability block diagram of the FADEC system |
|
|
Table 2 Failure Rate of Components(1/h) |
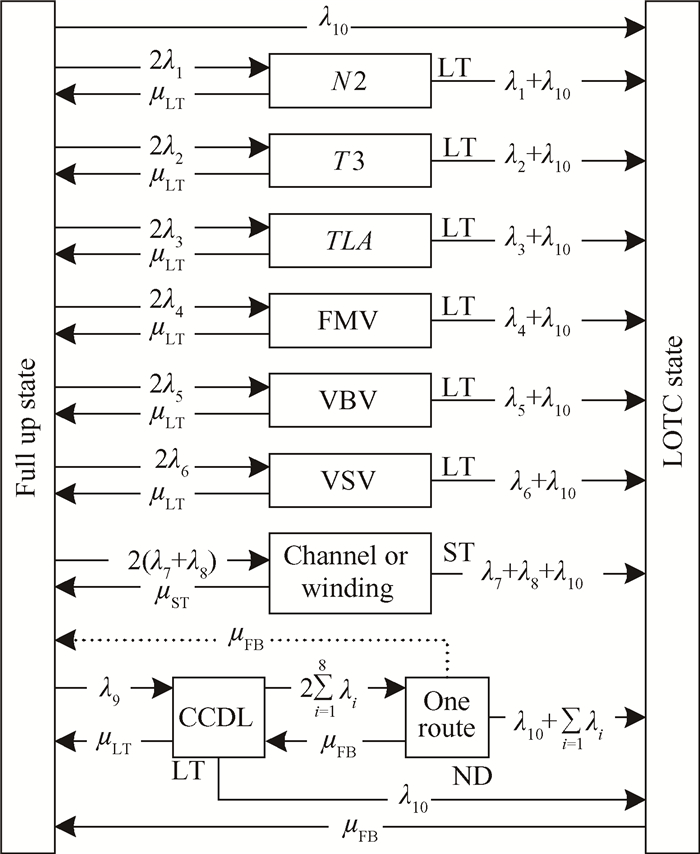
图 8给出了该FADEC系统的多故障TLD分析闭环马尔可夫模型。由于该系统组成单元数量较多,图 8并没有给出系统的所有故障状态,而是参考文献[13]给出了一种简化的多状态马尔可夫模型。在该模型中,CCDL失效并且一个ECU通道或其对应的传感器、电源线圈失效(One Route)是多故障状态,该状态的瞬时失效率大于1×10-4,因此属于ND状态,该状态具有将其修复到“CCDL”状态(最小维修)和“Full up”(完全修复)状态两种维修策略。此外,在该模型中,“CCDL”状态下系统瞬时失效率为时间的函数而不是常数。
|
Fig. 8 State-reduced Markov model of FADEC system |
图 8中,如删除“One Route”状态,即为单故障TLD分析闭环马尔可夫模型,该模型中不存在多故障状态,也不存在ND状态。单故障发生后的瞬时效率均为常数,并且所有单故障状态只有恢复到“Full up”一种维修策略。
上述特点与3.2节给出的“多故障TLD模型特点”相符。
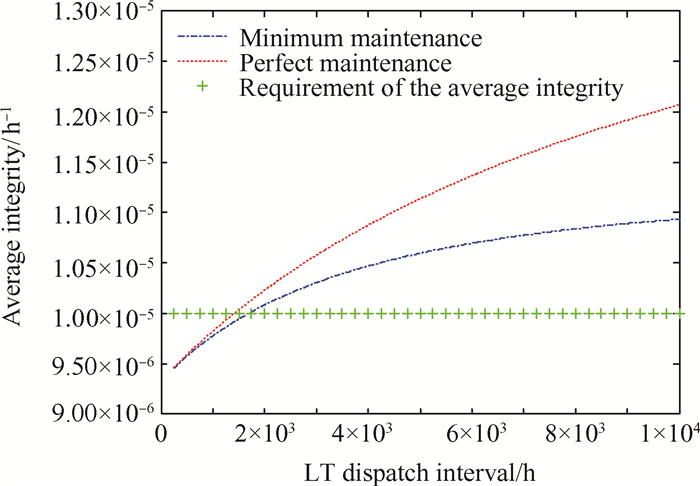
5.2 系统平均完整性要求的计算根据联邦航空局(FAA)要求,给定TST=250h[2],由式(9)~(19)可求得λLOTC与TLT的函数关系。图 9给出了最小维修和完全修复时的λLOTC曲线,采用最小维修策略时,满足平均完整性要求的TLT最大值为1696h,采用完全修复策略时,满足平均完整性要求的TLT最大值为1443h。
|
Fig. 9 Curves of the average integrity |
由图 9可知,采用完全修复策略得到的λLOTC值要大于采用最小维修策略得到的λLOTC值。其原因在于图 8中含有ND状态,与最小维修相比,采用完全维修策略时系统处于ND状态的稳态概率会减小,进而导致系统处于LOTC状态的稳态概率变大,由式(3)可知,此时的λLOTC值也将变大。
5.3 周期检查维修方式下故障暴露时间长时派遣(LT)故障一般采用“周期检查维修方式”[1, 2]。本例中所有LT类故障的失效率之和为
| $ {\lambda _{{\rm{LT}}}} = 2\sum\limits_{i = 1}^6 {{\lambda _i}} + {\lambda _9} = 2.132 \times {10^{ - 4}} $ |
若检查周期为400h,并且在检查间隔期发现故障,由式(26)可得该相应的平均故障前时间为197h;由式(27)可得故障的平均暴露时间为203h。若TLT为500h,则在检查间隔期发现故障后,允许系统继续带故障派遣的时间为297h。
6 结论本文对发动机控制系统TLD分析的若干可靠性理论问题进行了研究,给出了发动机控制系统平均完整性水平的准确定义,分析并确定了单故障与多故障TLD模型的特点,针对周期检查维修方式,提出了在检测间隔期发现故障条件下的平均故障暴露时间计算公式。
本文的研究成果可应用于民用飞机与商用航空发动机的安全性评估与型号合格审定之中,能够指导适航审定工程师与系统安全性工程师开展TLD分析工作,对于保证飞机安全运行、降低航班延误具有重要作用。
| [1] |
United States Department of Transportation. ANE-1993-33. 28TLD-R1 Policy for Time-Limited Dispatch (TLD) of Engines Fitted with Full Authority Digital Engine Control Systems[M]. Washington D C: Federal Aviation Administration, 1993.
(  0) 0) |
| [2] |
SAE International Group. ARP5107B Guidelines for Time-Limited-Dispatch (TLD) Analysis for Electronic Engine Control Systems[M]. Washington D C: Society of Automotive Engineers, 2006.
(  0) 0) |
| [3] |
SAE International S-18 Committee. ARP4761 Guidelines and Methods for Conducting the Safety Assessment Process on Civil Airborne System and Equipment[M]. Washington D C: Society of Automotive Engineers, 1996.
(  0) 0) |
| [4] |
陆中, 戎翔, 周伽, 等. 基于蒙特卡罗仿真的FADEC系统多故障TLD分析方法[J]. 航空学报, 2015, 36(12): 3970-3979. (  0) 0) |
| [5] |
赵皓岑, 王彬, 叶志锋. 数控燃油计量装置联合建模方法研究[J]. 推进技术, 2016, 37(9): 1752-1758. (ZHAO Hao-cen, WANG Bin, YE Zhi-feng. Study on Co-Modeling Method for Digital Control Fuel Metering Unit[J]. Journal of Propulsion Technology, 2016, 37(9): 1752-1758.)
(  0) 0) |
| [6] |
李睿超, 郭迎清, 李岩, 等. 基于数据集中器的超燃冲压发动机分布式控制系统通信方案设计[J]. 推进技术, 2016, 37(9): 1766-1773. (LI Rui-chao, GUO Ying-qing, LI Yan, et al. Communication Scheme Design of Distributed Control System for Scramjet Engine Based on Data Concentrators[J]. Journal of Propulsion Technology, 2016, 37(9): 1766-1773.)
(  0) 0) |
| [7] |
United States Department of Transportation. Code of Federal Regulation Part 25 (Amendment 25-123) Airworthiness Standards: Transport Category Airplanes[M]. Washington D C: Federal Aviation Administration, 2007.
(  0) 0) |
| [8] |
United States Department of Transportation. AC25. 1309-1A, System Design and Analysis[M]. Washington D C: Federal Aviation Administration, 1988.
(  0) 0) |
| [9] |
European Aviation Safety Agency. CS-E (Amendment 3) Certification Specifications for Engines[M]. Koln: European Aviation Safety Agency, 2010.
(  0) 0) |
| [10] |
United States Department of Transportation. AC33. 28-3 Guidance Material for 14 CFR33. 28 Engine Control Systems[M]. Washington D C: Federal Aviation Administration, 2014.
(  0) 0) |
| [11] |
Prescott D R, Andrews J D. Aircraft Safety Modeling for Time-Limited Dispatch[C]. Virginia: Proceedings of 2005 Annual Reliability and Maintainability Symposium, 2005: 139-145.
(  0) 0) |
| [12] |
Prescott D R, Andrews J D. A Comparison of Modelling Approaches for the Time-Limited Dispatch (TLD) of Aircraft[J]. Journal of Risk and Reliability, 2006, 220(1): 9-20.
(  0) 0) |
| [13] |
Prescott D R, Andrews J D. Modeling and Specification of Time-Limited Dispatch Categories for Commercial Aircraft[J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130(2): 1-10.
(  0) 0) |
| [14] |
Prescott D R, Andrews J D. The Safe Dispatch of Aircraft with Known Faults[J]. International Journal of Performability Engineering, 2008, 4(3): 243-253.
(  0) 0) |
| [15] |
Prescott D R, Andrews J D. Monte Carlo Simulation Modelling of Aircraft Dispatch with Known Faults[C]. Chengdu: 8th International Conference on Reliability, Maintainability and Safety, 2009: 532-535.
(  0) 0) |
| [16] |
Finkelstein M. Failure Rate Modelling for Reliability and Risk[M]. Berlin: Springer, 2008, 72-73.
(  0) 0) |
| [17] |
Lawler G F. Introduction to Stochastic Processes[M]. Florada: CRC Press, 2006, 81-82.
(  0) 0) |
| [18] |
Birolini A. Reliability Engineering: Theory and Practice, Seventh Edition[M]. Berlin: Springer, 2007, 498-500.
(  0) 0) |
| [19] |
Limnios N. Maintenance Optimization of a Digital Engine Control System with Limit Failure Rate Constrain[C]. Harrogate: 22nd Congress of International Council of the Aeronautical Sciences, 2000: 1-10.
(  0) 0) |
| [20] |
Sung B, Schrage D P. Optimal Maintenance of a Multi-Unit System under Dependencies[C]. Fort Worth: Proceedings of 2009 Annual Reliability and Maintainability Symposium, 2009: 118-123.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

