航空发动机是由成千上万个零件组成的高精度复杂工业产品[1, 2],研制过程中存在高精度、高效率、结构复杂、多迭代修改、短周期等特点和要求。作为制造过程中的一个独立环节,发动机的装配过程是实现其功能的关键环节之一[3],装配质量与发动机的整体性能有着密切联系[4, 5],影响着发动机的成本、质量以及研制周期[6, 7],而装配成功率是衡量装配质量的一个重要指标。对于航空发动机这一高精度复杂产品来说,为满足不断提升的产品研制需求[8~10],装配成功率在计算精度和效率上有着异于其它工业产品的高要求。
在进行装配成功率计算之前,要进行公差分析[11]。传统的公差分析方法中,极值法是以最大误差代数和的方法为基础,即只考虑组成环尺寸的最大极限值与最小极限值[12, 13],建立在零件100%互换的基础上,是公差分析的一种最简单方法。但实际上尺寸链中各组成环和封闭环的尺寸公差是随机变量,由于极值法没有考虑实际值在上下范围内的分布情况,得出的结果往往过于极端,同时造成制造成本的增加。统计法包括均方根法、蒙特卡洛法、Taguchi方法以及卷积法等[8~10],其中均方根法虽然考虑了各个组成环尺寸的分布情况,但其假设前提过于理想,只有在大批量生产并且组成环的数目足够多时才能比较准确地反映封闭环的尺寸值[14];蒙特卡洛法在公差分析中的应用最为广泛[15~17],其优点是能够处理组成环为不同分布类型的情况,对于装配响应函数的类型也没有限制,适用性强,并且计算精度也能够得到保证,但是蒙特卡洛法的计算精度与样本数量的平方根成正比,足够的计算精度要求大量计算样本的支撑,计算时间长,效率低;卷积法在理论上也能够处理组成环为不同分布类型的情况[18],但其计算过程复杂,需要借助数值积分和计算机编程技术进行计算;Taguchi方法由于其简单易行[19],应用也十分广发,但是应用Taguchi方法对统计量的高阶矩进行计算时,精度欠佳。
目前,装配成功率的计算方法主要有矩估计法(二阶矩估计法、四阶矩估计法)和蒙特卡洛法等[11],二阶矩法能够准确地估计出统计量的前两阶矩,但是前两阶矩并不能准确地反映出统计量的分布类型,因而得出的装配成功率在精度上不够高;而蒙特卡洛法虽然能够处理组成环服从不同分布类型的装配成功率估算问题,但其在对数据处理的效率上则明显低于矩估计法。蒙特卡洛方法虽然存在对计算样本要求大、计算效率低等缺点,但其在计算精度上的优势可以对其他方法的有效性进行验证。
综上所述,Taguchi方法在公差分析问题上应用广泛,能够准确估计出统计量的前两阶矩,但其在对统计量的高阶矩进行估计时,计算精度不够,无法准确反映封闭环的分布类型。针对航空发动机对装配过程的高精度和高效率的要求,本文介绍了一种基于Taguchi方法的改进试验设计方法,在试验设计中对每一个因素的不同水平值都赋予相应的权重因子,该方法可以准确地估算出统计量的前四阶矩。结合Pearson分布理论,建立了航空发动机装配成功率的计算模型。最后以某型航空发动机涡轮转子的装配成功率计算求解为例,通过与蒙特卡洛仿真结果进行对比,对本文所提方法的适用性和有效性进行验证。
2 基本理论 2.1 改进的Taguchi方法传统的Taguchi方法在进行试验设计时,每个因素X1, X2, …, Xi, …, XN(1≤i≤N)设为正态分布,因素的三水平分别取为μi-
| $ {m_1} = \sum\limits_1^N {{Y_i}/N} $ | (1) |
| $ {m_2} = \sum\limits_1^N {{{\left( {{Y_i} - {m_1}} \right)}^2}/N} $ | (2) |
| $ {m_3} = \sum\limits_1^N {{{\left( {{Y_i} - {m_1}} \right)}^3}/N} $ | (3) |
| $ {m_4} = \sum\limits_1^N {{{\left( {{Y_i} - {m_1}} \right)}^4}/N} $ | (4) |
统计系数为
均值
| $ \mu = {m_1} $ | (5) |
方差
| $ {\sigma ^2} = {m_2} $ | (6) |
偏度
| $ \sqrt {{\beta _1}} = {m_3}/{\left( {{m_2}} \right)^{1.5}} $ | (7) |
峰度
| $ {\beta _2} = {m_4}/{\left( {{m_2}} \right)^2} $ | (8) |
传统的Taguchi方法假设所有的因素符合正态分布,因素的三水平值分别取为
| $ {m_1} = \sum\limits_1^N {{\omega _i}{Y_i}} $ | (9) |
| $ {m_2} = \sum\limits_1^N {{\omega _i}{{\left( {{Y_i} - {m_1}} \right)}^2}} $ | (10) |
| $ {m_3} = \sum\limits_1^N {{\omega _i}{{\left( {{Y_i} - {m_1}} \right)}^3}} $ | (11) |
| $ {m_4} = \sum\limits_1^N {{\omega _i}{{\left( {{Y_i} - {m_1}} \right)}^4}} $ | (12) |
式中ωi为试验组合中各因素相应水平权重因子的乘积。
2.2 装配响应函数在用统计法进行公差分析时,将每个组成环(因素)X1, X2, …, Xi, …, XN(1≤i≤N)的取值看作随机变量[20],都有其各自的分布类型,然后需要构造装配公差分析模型,即确定装配响应函数。装配响应函数是指尺寸链中各组成环和封闭环之间的函数关系表达式,它是进行公差分析的依据[11]。装配响应函数可表示为
| $ Y = g\left( {{X_1},{X_2}, \cdots ,{X_i}, \cdots ,{X_N}} \right) $ | (13) |
式中Y为封闭环尺寸(输出特性),N为设计变量个数。可知,当组成环的尺寸值为随机变量时,封闭环的尺寸值也是一个随机变量,如图 1所示。
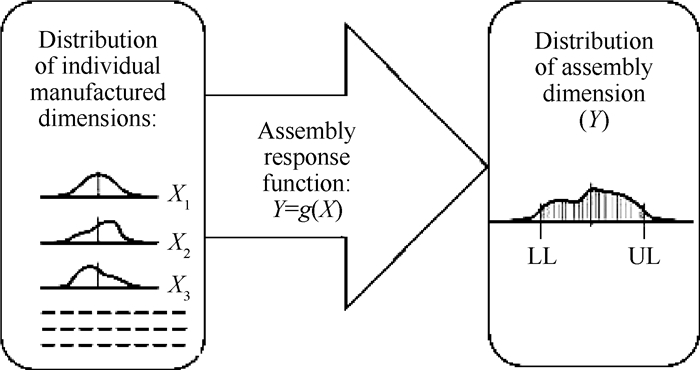
|
Fig. 1 Tolerance analysis of mechanical assemblies |
例如,某活塞发动机中[9],气缸、活塞的装配图如图 2所示,缸膛与活塞之间的直径间隙既要大于0以保证活塞在气缸中能够自由移动,又要小于某一特定值以防止油液流过活塞。此时我们关注的是活塞外径X1和气缸内径X2,则该装配过程中X1,X2为装配尺寸链中的组成环,缸膛与活塞之间的直径间隙Y为输出特性,装配响应函数为
| $ Y = {X_2} - {X_1} $ |
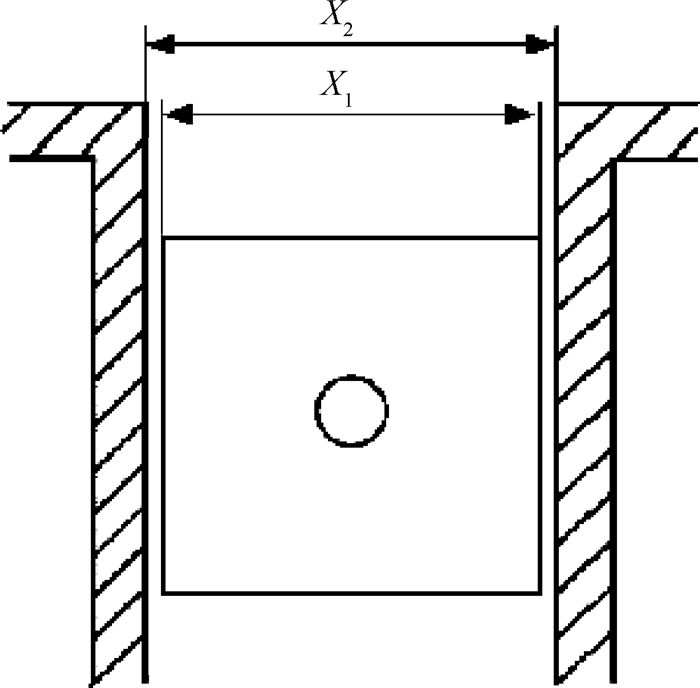
|
Fig. 2 Cylinder-Piston engine assembly drawing |
装配响应函数是尺寸的函数,其响应值并不是统一的,需要根据尺寸链的几何关系等因素确定,一般来说装配响应函数可表示为
| $ Y = \sum\limits_{i = 1}^N {{\xi _i}{L_i}} $ | (14) |
式中系数ξi称作传递比或影响系数(按照机械精度理论),代表组成环对封闭环的影响程度,ξi>0时,第i个组成环为增环,ξi < 0时,第i个组成环为减环。
2.3 装配响应的分布类型基于蒙特卡洛模拟方法的基本原理,Karl Pearson提出了一种包括多种分布类型的统一模型[23]
| $ \frac{{{\rm{d}}p\left( x \right)}}{{{\rm{d}}x}} = - \frac{{\left( {a + x} \right)p\left( x \right)}}{{{c_0} + {c_1}x + {c_2}{x^2}}} $ | (15) |
式中p(x)为概率密度函数;a,c0,c1,c2为分布参数,它们是概率密度函数的前四阶矩的函数。因此只需要得到样本的前四阶矩,便可以根据Pearson微分方程(15)解得概率密度函数。根据不同的参数取值可以得到不同的概率密度函数。由Pearson分布模型建立的分布族见表 1。
|
|
Table 1 Pearson distribution family |
由表 1可以看出,Pearson分布包含了任意给定均值、标准差、偏度和峰度的常见分布类型,如正态分布、β分布、γ分布、t分布等。
2.4 装配成功率的计算通过试验设计得到装配响应的N个值Y1, Y2, …, YN后,计算得到统计量的均值、标准差、偏度和峰度四个统计系数,可以运用Matlab中的Pearsonrnd函数构建合适的皮尔逊族分布模型,根据分布模型便可计算得到在指定装配间隙下的装配成功率
| $ P = {P_{\rm{r}}}\left( {{Y_{\min }} \le Y \le {Y_{\max }}} \right) $ | (16) |
式中Ymin, Ymax为装配间隙的上下限。
基于Taguchi方法的装配成功率计算过程如图 3所示。
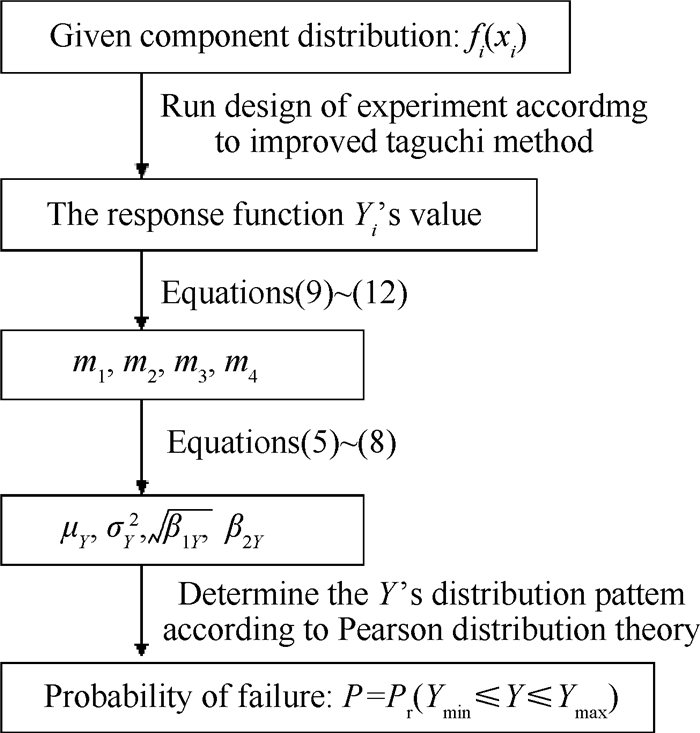
|
Fig. 3 Flow chart for the calculation of assembly success rate based on improved Taguchi method |
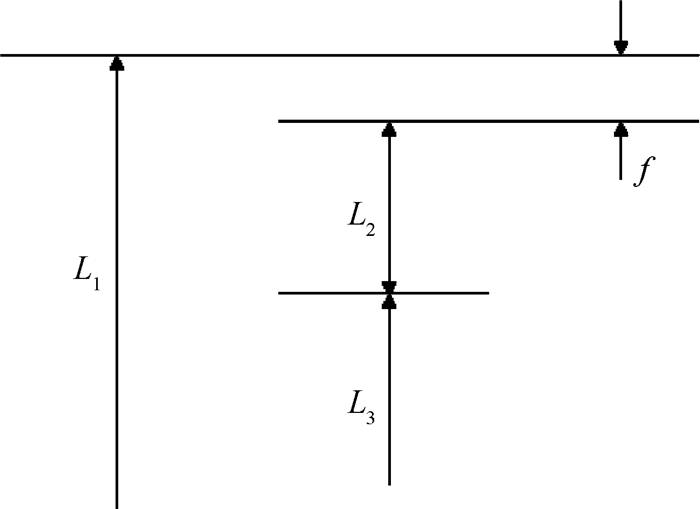
为验证基于改进的Taguchi方法的装配成功率计算模型的有效性,本文以某航空发动机涡轮转子高压一级涡轮的径向装配尺寸链为例进行装配成功率的估算。如图 4所示,f为高压一级涡轮叶尖与机匣的间隙,L1为机匣内径,L2为叶尖到涡轮盘外沿长度,L3为涡轮盘直径。要求叶尖间隙f符合:2.8mm≤f≤3.3mm,为装配成功。各组成环的尺寸参数见表 2。
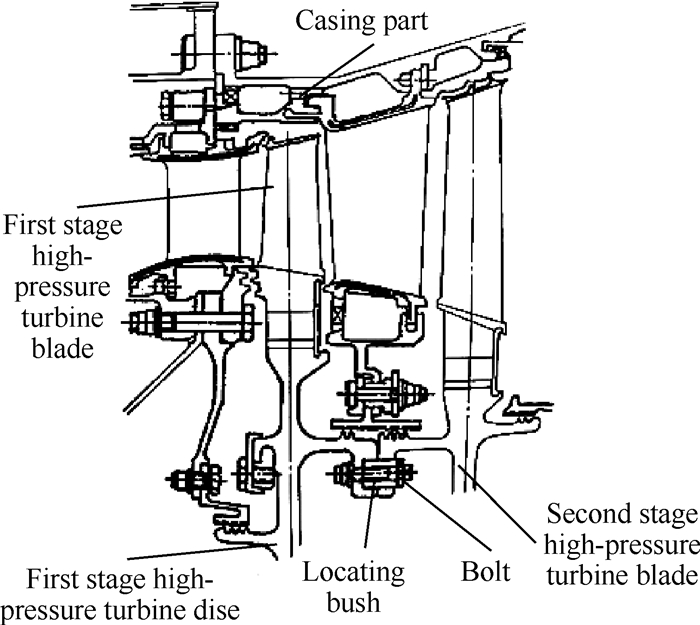
|
Fig. 4 High-pressure turbine of aero-engine |
|
|
Table 2 Size of the individual dimensions |
由装配尺寸链图 5可以确定,组成环L1为增环,L2,L3为减环,则封闭环f的值可由式(14)计算到。
|
Fig. 5 Assembly dimensional chain |
假设各组成环的实际尺寸都服从正态分布,分布范围与各自的公差带宽度一致,分布中心与公差带中心重合,根据“3σ原则”可确定公差与标准差之间的关系为
| $ {\sigma _i} = \frac{{{T_i}}}{6} $ | (17) |
式中Ti为公差,σi为标准差。
根据改进的Taguchi方法,因素的三水平分别取为μi-
|
|
Table 3 Three level values of individual dimensions |
|
|
Table 4 Calculation results of assembly dimension |
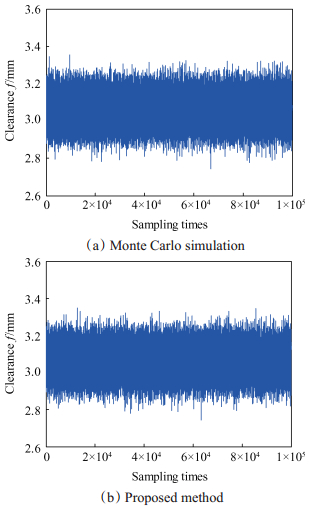
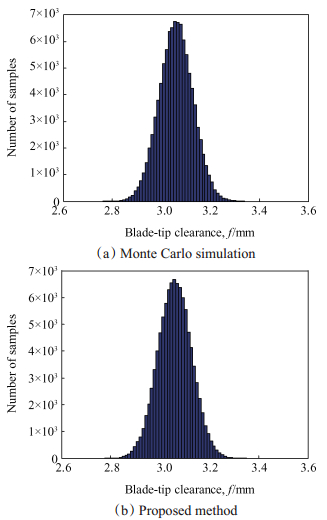
根据表 4中的数据可以得到间隙值f的27个样本值,由公式(9)~(12)得到均值、方差、偏度及峰度值列于表 5中,表 5同时给出了基于传统Taguchi方法得出的统计系数。为方便对比,进行了1×105次的蒙特卡洛模拟,结果同样列于表 5中。用蒙特卡洛法及本文方法得到的模拟抽样结果和装配间隙的分布情况如图 6和图 7所示。
|
|
Table 5 Statistical coefficients calculation results |
|
Fig. 6 Assembly gap simulation results |
|
Fig. 7 Distribution map of assembly gap |
由表 5中的数据可以看出,在对装配间隙的均值、方差以及偏度进行估计时,Taguchi方法以及改进的Taguchi方法均能取得较好的效果,但是在对峰度进行估计时,Taguchi方法相对于蒙特卡洛方法的误差为19.38%,改进的Taguchi方法相对于蒙特卡洛方法的误差为0.21%,估算的准确度大幅提高,这也验证了改进的Taguchi方法在估算系统响应的高阶矩时比传统的Taguchi方法具有更高的准确度。
3.3 装配成功率的计算根据Pearson统一模型和表 5中的数据,由修正的Taguchi方法得到装配间隙f服从正态分布,并且该分布的统计系数已知,由此可计算出装配成功率为
| $ P = {P_r}\left( {2.8 \le f \le 3.3} \right) = 0.9998 $ |
进行1×105次的蒙特卡洛模拟,得到的装配成功率为:P=Pr(2.8≤f≤3.3)=0.9996。可知用本文所提方法计算得出的装配成功率与经过1×105次蒙特卡洛模拟得出的结果非常接近,相对误差仅为0.02%。
4 结论本文提出了改进的Taguchi方法,结合Pearson分布理论,建立了装配成功率的计算模型。以某型航空发动机的高压一级涡轮叶尖间隙的装配成功率的估算为例,通过与蒙特卡洛仿真结果的对比得出以下结论:
(1) 改进的Taguchi方法与传统Taguchi方法对装配间隙的均值、方差和偏度的估计均较为准确,但是在对峰度(四阶矩)进行估计时,改进的Taguchi方法在准确度上比传统Taguchi方法有明显优势,使相对误差由原来的19.38%减小到0.21%。
(2) 用本文所提方法得出的装配成功率与蒙特卡洛仿真结果十分接近,相对误差仅为0.02%,说明本文所提方法能够准确地估算出装配成功率,弥补了传统的Taguchi方法在计算精度上的不足。
本文仅对组成环为正态分布的情况进行了分析,对于非正态分布的情况没有涉及,这将是下一步的工作。
| [1] |
McDonald C F, Massardo A F, Rodgers C, et al. Recuperated Gas Turbine Aeroengines, Part Ⅱ: Engine Design Studies Following Early Development Testing[J]. Aircraft Engineering and Aerospace Technology, 2008, 80(3): 280-294. DOI:10.1108/00022660810873719
(  0) 0) |
| [2] |
Fei C, Bai G. Distributed Collaborative Extremum Response Surface Method for Mechanical Dynamic Assembly Reliability Analysis[J]. Journal of Central South University, 2013, 20: 2414-2422. DOI:10.1007/s11771-013-1751-0
(  0) 0) |
| [3] |
Yang Z, Hussain T, Popov A A, et al. Novel Optimization Technique for Variation Propagation Control in an Aero-Engine Assembly[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2011, 225(1): 100-111. DOI:10.1243/09544054JEM2043
(  0) 0) |
| [4] |
费成巍, 白广忱, 范觉超, 等. 涡轮转子多尺寸装配可靠性优化分析[J]. 推进技术, 2013, 34(1): 15-18. (FEI Cheng-wei, BAI Guang-chen, FAN Jue-chao, et al. Optimization and Analysis for Multi-Dimensions Assembly Reliability of Turbine Rotor[J]. Journal of Propulsion Technology, 2013, 34(1): 15-18.)
(  0) 0) |
| [5] |
桑潇潇, 廖明夫, 吴法勇, 等. 发动机轴承内环装配工艺对转子动力学特性影响的试验研究[J]. 推进技术, 2015, 36(12): 1874-1880. (SANG Xiao-xiao, LIAO Ming-fu, WU Fa-yong, et al. Experimental Study on Rotor-Dynamic Behavior Development on Aero-Engine Bearing Inner Ring Assembly Technologies[J]. Journal of Propulsion Technology, 2015, 36(12): 1874-1880.)
(  0) 0) |
| [6] |
Feng C X J, Kusiak A. Robust Tolerance Synthesis with the Design of Experiments Approach[J]. Journal of Manufacturing Science and Engineering, 2000, 122(3): 520-528. DOI:10.1115/1.1285860
(  0) 0) |
| [7] |
邵锦文, 张振家, 袁宁, 等. 航空发动机涡轮叶尖间隙损失的统计设计[J]. 推进技术, 2003, 24(2): 122-124. (SHAO Jin-wen, ZHANG Zhen-jia, YUAN Ning, et al. Statical Design for Turbine Blades Tip Clearance Loss Analysis[J]. Journal of Propulsion Technology, 2003, 24(2): 122-124.)
(  0) 0) |
| [8] |
石宏. 航空发动机装配工艺技术[M]. 北京: 北京航空航天大学, 2015, 28-30.
(  0) 0) |
| [9] |
Singh P K, Jain P K, Jain S C. Important Issues in Tolerance Design of Mechanical Assemblies, Part 1: Tolerance Analysis[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2009, 223(10): 1225-1247. DOI:10.1243/09544054JEM1304A
(  0) 0) |
| [10] |
朱彬, 于乃江, 孟祥海, 等. 航空发动机装配尺寸链公差设计方法研究[J]. 测试技术学报, 2015, 29(2): 177-184. (  0) 0) |
| [11] |
张岩, 莫蓉. 基于低偏差序列样本的装配公差分析方法[J]. 计算机集成制造系统, 2014, 20(3): 579-585. (  0) 0) |
| [12] |
Tian M W, Shi R C J. Worst Case Tolerance Analysis of Linear Analog Circuits Using Sensitivity Bands[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, 47(8): 1138-1145. DOI:10.1109/81.873869
(  0) 0) |
| [13] |
Mansuy M, Giordano M, Hernandez P. A New Calculation Method for the Worst Case Tolerance Analysis and Synthesis in Stack-Type Assemblies[J]. Computer-Aided Design, 2011, 43(9): 1118-1125. DOI:10.1016/j.cad.2011.04.010
(  0) 0) |
| [14] |
Yan-long CAO, Jiang-xin Y, Zhao-tong WU, et al. A Robust Tolerance Design Method Based on Process Capability[J]. Journal of Zhejiang University-Science A, 2004, 5(1): 81-85. DOI:10.1631/jzus.2004.0081
(  0) 0) |
| [15] |
Cao Y, Yan H, Liu T, et al. Application of Quasi-Monte Carlo Method Based on Good Point Set in Tolerance Analysis[J]. Journal of Computing and Information Science in Engineering, 2016, 16(2): 021008. DOI:10.1115/1.4032909
(  0) 0) |
| [16] |
Wu F, Dantan J Y, Etienne A, et al. Improved Algorithm for Tolerance Allocation Based on Monte Carlo Simulation and Discrete Optimization[J]. Computers & Industrial Engineering, 2009, 56(4): 1402-1413.
(  0) 0) |
| [17] |
Qureshi A J, Dantan J Y, Sabri V, et al. A Statistical Tolerance Analysis Approach for Over-Constrained Mechanism Based on Optimization and Monte Carlo Simulation[J]. Computer-Aided Design, 2012, 44(2): 132-142. DOI:10.1016/j.cad.2011.10.004
(  0) 0) |
| [18] |
Shen Z, Ameta G, Shah J J, et al. A Comparative Study of Tolerance Analysis Methods[J]. Journal of Computing and Information Science in Engineering, 2005, 5(3): 247-256. DOI:10.1115/1.1979509
(  0) 0) |
| [19] |
Ghani J A, Choudhury I A, Hassan H H. Application of Taguchi Method in the Optimization of End Milling Parameters[J]. Journal of Materials Processing Technology, 2004, 145(1): 84-92. DOI:10.1016/S0924-0136(03)00865-3
(  0) 0) |
| [20] |
Taguchi G, Chowdhury S, Wu Y. Taguchi's Quality Engineering Handbook[M]. New York: Wiley, 2005.
(  0) 0) |
| [21] |
D'Errico J R, Zaino N A. Statistical Tolerancing Using a Modification of Taguchi's Method[J]. Technometrics, 1988, 30(4): 397-405. DOI:10.1080/00401706.1988.10488434
(  0) 0) |
| [22] |
Seo H S, Kwak B M. Efficient Statistical Tolerance Analysis for General Distributions Using Three-Point Information[J]. International Journal of Production Research, 2002, 40(4): 931-944. DOI:10.1080/00207540110095709
(  0) 0) |
| [23] |
Johnson N L, Kotz S, Balakrishnan N. Continuous Univariate Distributions[M]. New York: John Wiley & Sons, 1994, 15-25.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

