2. 中国航发沈阳发动机研究所,辽宁 沈阳 110015
2. AECC Shenyang Engine Institute, Shenyang 110015, China
先进的转子和静子间的动密封技术可显著提高大功率旋转机械工作效率和可靠性[1]。刷式密封是继迷宫密封之后发展起来的一种新型动密封技术,有效降低了旋转机械的泄漏损失[2],被广泛应用于航空发动机、汽轮机、燃气轮机等旋转机械[3, 4]。近年来,随着旋转机械逐渐向高性能方向发展,刷丝颤振现象越来越严重,直接影响刷式密封封严性能和使用寿命[5, 6]。
国内外学者对刷式密封做了大量的研究工作,国外Dogu等[7]建立了定常稳态刷式密封多孔介质模型,对零间隙刷式密封的泄漏流动特性进行了数值研究。Hogg[5]基于稳态多孔介质模型,合理解释了在气流力作用下由刷丝变形引起的疲劳断裂现象。国内张艾萍[8]、迟佳栋[9]等基于稳态多孔介质模型,研究了刷式密封滞后效应及其影响因素、并对结构优化进行了分析;李军[10]、胡丹梅[11]、黄学民[12]等基于稳态多孔介质模型,采用定常稳态数值求解方法,研究了压比、刷丝直径、保护高度、径向间隙等参数对泄漏流动影响规律。王之栎等[13]采用各项异性多孔介质模型,研究了刷式密封的流场分布、泄漏量以及刷丝束厚度与泄漏率的关系。研究表明,多孔介质模型采用的经验公式需要定义多孔介质上的流动阻力,本质上仅仅是在动量方程上叠加了一个动量消耗源项[14],具有一定的局限性。国外Lelli等[15]建立了流体域与刷丝实体域分别建模的刷式密封三维实体稳态求解模型,数值研究了刷丝在气流力作用下的变形规律。Zhao等[16, 17]计算了在均布力的作用下单根刷丝的变形情况,并分析了尖端接触反力及刷丝束内摩擦力对滞后效应的影响。国内黄首清[18]建立了刷式密封三维切片模型,应用定常稳态数值方法研究了刷式密封流场及温度场分布特性。研究表明,刷式密封刷丝在流体的作用下会产生变形,刷丝变形进一步影响流体分布,刷丝与流体之间的相互作用是典型的瞬态双向流固耦合问题[19, 20]。现有文献关于刷式密封研究主要基于多孔介质模型及三维实体模型,且采用定常稳态求解方法,集中在流场特性方面,对瞬态双向流固耦合法的刷式密封刷丝颤振特性研究较少。
本文采用双向流固耦合与动网格技术,建立基于能量法的刷式密封刷丝颤振特性瞬态流固耦合求解模型,分别从泄漏量及非定长气动力做功角度对实验得到的泄漏量和采用理论模型得出流体非定常气动力做功与本文双向流固耦合数值计算结果进行对比验证,在此基础上,研究了刷丝束间隙中的流体速度和压力分布特性,并分析刷丝变形规律以及刷丝颤振特性,并研究了刷式密封结构参数对刷式颤振特性的影响规律。
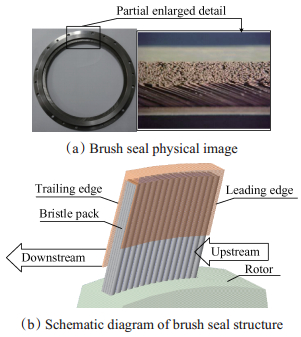
2 刷式密封刷丝颤振特性理论分析 2.1 刷式密封流固耦合特性分析刷式密封是具有优良密封性能的接触式动密封。如图 1所示,刷丝束是由柔软而纤细的刷丝交错层叠构成,并沿着转子旋转方向呈一定角度排列,保证了刷式密封能够适应转子的瞬间径向变形或偏心运动而保持良好的密封性能。研究表明,刷丝在气流力的作用下产生变形,刷丝变形进一步影响流场分布[21],刷丝与流体之间的相互作用是典型的瞬态双向流固耦合问题。在气流力作用下,刷丝的轴向变形使密封与转子面间隙增大[22],进而增加泄漏量,降低刷式密封封严性能。
|
Fig. 1 Sketch of image of brush seal and the structure |
对于刷式密封的刷丝而言,在与流场流固耦合作用的过程中,流场中非定常气动力对刷丝做功,并以弹性势能的形式将能量存储在变形的刷丝中。即在瞬态流固耦合过程中,流场中的非定常气动力对刷丝做功,使刷丝产生变形。若非定常气动力对刷丝做正功,刷丝吸收了流场中的能量,则经过一段时间的积累,刷丝弹性势能累积,刷丝振动变形加剧,刷丝丧失稳定性,出现颤振。若非定常气动力对刷丝做负功,刷丝通过流场放出部分吸收的能量,则经过一段时间的积累,刷丝弹性势能减少,刷丝振动趋于平稳,变形程度逐渐变小,从而保持其稳定性。因此,判别刷式密封刷丝的颤振特性,可通过一段时间内刷丝的能量情况而得出结论[23],能量法公式如下
| $ W = \int {\mathit{\boldsymbol{w}}\left( t \right){\rm{d}}t} $ | (1) |
式中W表示非定常气动力做功,w(t)表示单位时间步非定常气动力对刷丝做的功。
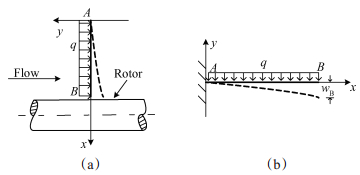
2.3 稳态下的刷丝颤振理论分析刷式密封在径向具有优良的密封性能,但是在轴向,由于受到所气流力的作用,刷丝轴向发生弯曲变形,其受力分析如图 2(a)所示,简化为在均布载荷作用下的悬臂梁模型[24~26]
|
Fig. 2 Force analysis of a bristle |
刷丝任意截面上的弯矩为
| $ \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{x}} \right) = - \frac{1}{2}\mathit{\boldsymbol{q}}{\left( {l - x} \right)^2} $ | (2) |
刷丝在纯弯曲情况下,弯矩与曲率间的关系为
| $ \frac{1}{\rho } = \frac{\mathit{\boldsymbol{M}}}{{EI}} $ | (3) |
式中M和皆
如图 2(b)所示,在弯曲变形时,刷丝梁的轴线将成为xy平面内的一条曲线,称为挠曲线,挠曲线上横坐标为x的任意点的纵坐标用y表示,称为挠度,它代表坐标为x的横截面的形心沿y方向的位移。弯曲变形中,刷丝梁的横截面相对原来位置转过的角度为θ,刷丝梁挠曲线的方程可以写成
| $ W = \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) $ | (4) |
实际工况中刷丝的变形远小于跨度,转角θ是一个非常小的角度,并且根据曲线斜率为该点导数,可得
| $ \frac{1}{\rho } = \frac{{{\rm{d}}\theta }}{{{\rm{d}}\mathit{\boldsymbol{x}}}} = \frac{{{{\rm{d}}^2}\mathit{\boldsymbol{w}}}}{{{\rm{d}}{\mathit{\boldsymbol{x}}^2}}} $ | (5) |
根据式(2)、式(3)及式(5)可以得到刷丝梁曲线的近似挠曲线微分方程
| $ EI\mathit{\boldsymbol{w''}} = - \frac{1}{2}\mathit{\boldsymbol{q}}{\left( {l - \mathit{\boldsymbol{x}}} \right)^2} $ | (6) |
式(6)积分可得刷丝转角方程(7)与刷丝挠曲线方程(8)
| $ EI\theta = - \frac{1}{6}\mathit{\boldsymbol{q}}{\left( {l - \mathit{\boldsymbol{x}}} \right)^3} + {C_1} $ | (7) |
| $ EI\mathit{\boldsymbol{\omega }} = \frac{1}{{24}}\mathit{\boldsymbol{q}}{\left( {l - \mathit{\boldsymbol{x}}} \right)^4} + {C_1}\mathit{\boldsymbol{x}} + {C_2} $ | (8) |
对于刷丝固定端A,转角和挠度均等于零,可得即θA=0;ωA=0,代入式(7)与(8)可得刷丝梁挠曲线方程
| $ \mathit{\boldsymbol{\omega }} = \frac{\mathit{\boldsymbol{q}}}{{24EI}}\left[ {{{\left( {l - \mathit{\boldsymbol{x}}} \right)}^4} + 4{l^3}\mathit{\boldsymbol{x}} - {l^4}} \right] $ | (9) |
对于截面B的横坐标为XB=l,代入式(11),可得截面B的挠度即变形量。
均布力q由气流压力作用在刷丝柱上产生,故气流力为
| $ \mathit{\boldsymbol{q}} = \mathit{\boldsymbol{p}}s $ | (10) |
| $ s = ld $ | (11) |
式中p为作用在刷丝表面上的流体压强,s为气流力作用下的面积,将式(11)代入式(10)得
| $ \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{q}}d $ | (12) |
气流力使刷丝微元产生微小变形产生的功为
| $ W = \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{\omega }}\left( \mathit{\boldsymbol{x}} \right) $ | (13) |
将式(9)与式(12)代入上式并积分得气流力对整根刷丝做功为
| $ W = \frac{{13{\mathit{\boldsymbol{p}}^2}{l^5}{d^2}}}{{360EI}} $ | (14) |
刷式密封刷丝在设计工况下,发生了变形,变形后的刷丝改变了流体的速度及压力分布。因此,必须要从流固耦合的角度去分析。将流固耦合求解过程划分为若干个时间步,得到单位时间步内刷丝单位面积获得的气动功
| $ W\left( {\tilde x} \right) = \int_{{t_o}}^{{t_0} + T} {\mathit{\boldsymbol{F}}\left( {\bar x,t} \right)\mathit{\boldsymbol{V}}\left( {\bar x,t} \right) \cdot \mathit{\boldsymbol{n}}\left( {\bar x,t} \right){\rm{d}}t} ,\forall \bar x \in S $ | (15) |
式中t0为计算开始时间,T为时间步长,F(x, t)为t时刻的刷丝静压力,V(x, t)为t时刻的刷丝速度,n(x, t)为t时刻的刷丝表面方向矢量,S为刷丝表面积。
为了全面考察刷丝在流固耦合中是否会出现颤振失稳现象,需要对刷丝的气动功进行分析。本文中,计算非定常气动力做功时根据刷丝各个节点上的非定常气动力和对应节点的位移来计算非定常气动力做功;气动功可以视为每个时间步中功的叠加。因此,在具体计算时,单位时间步内的气动功可由下式计算
| $ W = \sum\nolimits_i^n {{w_{ij}}} $ | (16) |
式中wij=
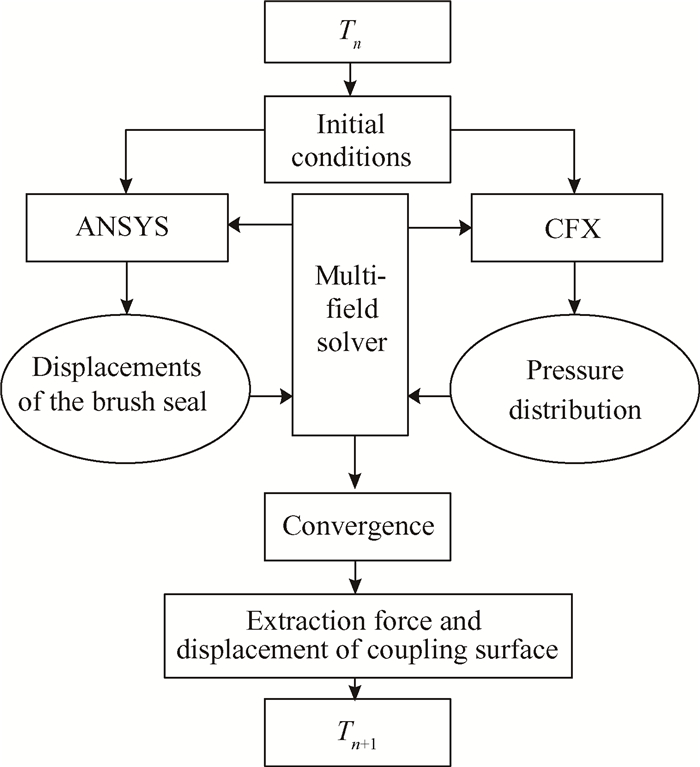
本文通过ANSYS Workbench数据交换平台提供的System Coupling模块实现刷丝和流场的双向耦合。刷丝变形分析采用ANSYS软件中的瞬态结构动力学分析方法,流场特性采用CFX中RNG k-ε湍流模型进行分析。刷式密封双向流固耦合求解采用双重循环迭代方法[27]。耦合流程如图 3,Tn时刻循环开始,以Tn+1时刻流场p,v的分布和刷丝变形的位移结果信息作为初始条件,流体域进行若干子步计算收敛后,通过网格插值将得出流场压力、速度等分布信息传递于刷丝固体域耦合面,刷丝固体域耦合面以其为边界条件计算得到刷丝瞬态动力响应,然后刷丝变形的位移x等信息再通过网格插值传递给流场耦合面,作为流场耦合面的边界条件,至此流体域与固体域的位移、载荷都达到收敛状态时,此时基于能量法提取收敛状态下刷丝流固耦合面上的力和位移,利用能量公式(16)提取此刻刷丝从流体中吸收的能量,随后继续进入Tn-1时刻循环。在双向流固耦合方法下,可获得任一时刻刷式密封刷丝运动变形特性及流体对刷丝做的功,该方法求解方式比较灵活,可以选择适合各物理场自身特点的计算方法进行求解,以达到较高的计算精度。
|
Fig. 3 FSI simulations with two-way coupling |
本文为提高数值结果的计算精度,将刷式密封流体域网格加密,这将引起耦合界面上流体域与固体域的网格不匹配,不能直接进行数据的交换,为此本文刷式密封流固耦合计算中采用守恒插值法,将气动载荷、网格变形等信息在刷丝与流体域间传递,即在耦合面上满足求解精度的情况下,保证能量传递守恒。若刷丝网格位移为Xs,通过传递函数[T]将刷丝网格位移转换为流场的网格位移Xf,表达式如下[30]
| $ {\mathit{\boldsymbol{X}}_{\rm{f}}} = \left[ \mathit{\boldsymbol{T}} \right]{X_{\rm{s}}} $ | (17) |
在流体载荷的作用下,刷丝与流体域耦合面应满足能量传递守恒,即
| $ \mathit{\boldsymbol{F}}_{\rm{f}}^{\rm{T}}{\mathit{\boldsymbol{X}}_{\rm{f}}} = \mathit{\boldsymbol{F}}_{\rm{s}}^{\rm{T}}{\mathit{\boldsymbol{X}}_{\rm{s}}} = \mathit{\boldsymbol{F}}_{\rm{f}}^{\rm{T}}\left[ T \right]{\mathit{\boldsymbol{X}}_{\rm{s}}} $ | (18) |
则可以得出载荷在两个物理场之间传递关系
| $ {\mathit{\boldsymbol{F}}_{\rm{s}}} = {\left[ \mathit{\boldsymbol{T}} \right]^{\rm{T}}}{\mathit{\boldsymbol{F}}_{\rm{f}}} $ | (19) |
式中Ff,Fs分别为作用在耦合面上的流体与刷丝载荷。
3.2 流固耦合建模理论 3.2.1 流体动力学模型在本文双向流固耦合瞬态计算工况下,满足的湍流流动守恒方程包括动量方程和连续方程[28]
| $ \frac{{\partial \rho }}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{u}}} \right) = 0 $ | (20) |
| $ \left\{ \begin{array}{l} \frac{{\partial \left( {\rho \mathit{\boldsymbol{u}}} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{Uu}}} \right) = {\rm{div}}\left( {\mathit{\Gamma }{\rm{grad}}\mathit{\boldsymbol{u}}} \right) - \frac{{\partial \mathit{\boldsymbol{p}}}}{{\partial x}} + {S_u}\\ \frac{{\partial \left( {\rho \mathit{\boldsymbol{v}}} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{U\nu }}} \right) = {\rm{div}}\left( {\mathit{\Gamma }{\rm{grad}}\mathit{\boldsymbol{v}}} \right) - \frac{{\partial \mathit{\boldsymbol{p}}}}{{\partial y}} + {S_v}\\ \frac{{\partial \left( {\rho \mathit{\boldsymbol{w}}} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{Uw}}} \right) = {\rm{div}}\left( {\mathit{\Gamma }{\rm{grad}}\mathit{\boldsymbol{w}}} \right) - \frac{{\partial \mathit{\boldsymbol{p}}}}{{\partial z}} + {S_w} \end{array} \right. $ | (21) |
式中ρ为密度,t为时间,p为流体微元体上的压力,U为速度矢量,u,v和w是速度矢量U在x、y和z方向的分量,Г为扩散系数,Su,Sv和Sw为动量守恒方程的广义源项,即
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{S}}_u} = {\mathit{\boldsymbol{F}}_x} + \frac{\partial }{{\partial \mathit{\boldsymbol{x}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial \mathit{\boldsymbol{x}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{y}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial \mathit{\boldsymbol{x}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{z}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial \mathit{\boldsymbol{x}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{x}}}}\left( {\lambda {\rm{div}}\mathit{\boldsymbol{U}}} \right)\\ {\mathit{\boldsymbol{S}}_v} = {\mathit{\boldsymbol{F}}_y} + \frac{\partial }{{\partial \mathit{\boldsymbol{x}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial \mathit{\boldsymbol{y}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{y}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial \mathit{\boldsymbol{y}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{z}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial \mathit{\boldsymbol{y}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{y}}}}\left( {\lambda {\rm{div}}\mathit{\boldsymbol{U}}} \right)\\ {\mathit{\boldsymbol{S}}_w} = {\mathit{\boldsymbol{F}}_z} + \frac{\partial }{{\partial \mathit{\boldsymbol{x}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial \mathit{\boldsymbol{z}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{y}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial \mathit{\boldsymbol{z}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{z}}}}\left( {\mu \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial \mathit{\boldsymbol{z}}}}} \right) + \frac{\partial }{{\partial \mathit{\boldsymbol{z}}}}\left( {\lambda {\rm{div}}\mathit{\boldsymbol{U}}} \right) \end{array} \right. $ | (22) |
式中Fx,Fy和Fz是流体微元体上的体力,若体力只有重力,且z轴竖直向上,则Fx=0,Fy=0和Fz=-ρg,μ为动力黏度,λ是第二黏度,一般可取λ=-2μ/3。
当刷丝受气动载荷作用弯曲变形时,刷丝束间隙流道高度弯曲变形,流场变得极其复杂。在弯曲流线的情况下,湍流是各项异性的,黏性系数是各向异性的张量,然而标准k-ε模型中对于Reynolds应力的各个分量,假定黏性系数是相同的,因此标准k-ε模型用于包含有强旋流、弯曲壁面流动和弯曲流线流动的刷式密封流场时,会产生一定的失真,需要对标准k-ε模型进行修正[29, 30],修正模型RNG k-ε模型为
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {\mathit{\boldsymbol{u}}_j}k} \right)}}{{\partial {\mathit{\boldsymbol{x}}_j}}} = \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}\left[ {\frac{{{\mu _{\rm{t}}}}}{{{\sigma _\kappa }}}\frac{{\partial \mathit{\boldsymbol{k}}}}{{\partial {\mathit{\boldsymbol{x}}_j}}}} \right] + G - \rho \varepsilon $ | (23) |
| $ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {\mathit{\boldsymbol{u}}_j}\varepsilon } \right)}}{{\partial {\mathit{\boldsymbol{x}}_j}}} = \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}\left[ {\frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial {\mathit{\boldsymbol{x}}_j}}}} \right] + {C_{\varepsilon 1}}G\frac{\varepsilon }{\kappa } - \rho {C_{\varepsilon 2}}\frac{{{\varepsilon ^2}}}{\kappa } $ | (24) |
式中
综合比较式(20)~(24)可得,RNG k-ε模型考虑了刷式密封流场中气体旋转等复杂流动,并且RNG k-ε模型不仅与流动情况有关,而且也是空间坐标函数,因此其可以更准确地求解刷式密封流场复杂的流体流动。
3.2.2 结构动力学模型刷式密封刷丝在流体作用下的瞬态响应可通过求解结构动力学方程获得,有限自由度为n的结构动力学方程表示为[31]
| $ \left[ \mathit{\boldsymbol{M}} \right]\mathit{\boldsymbol{\ddot x}} + \left[ \mathit{\boldsymbol{C}} \right]\mathit{\boldsymbol{\dot x}} + \left[ \mathit{\boldsymbol{K}} \right]\mathit{\boldsymbol{x}} = p\left( t \right) $ | (25) |
即
| $ \left( {\begin{array}{*{20}{c}} {{m_{11}}{m_{12}} \cdots {m_{1n}}}\\ {{m_{21}}{m_{22}} \cdots {m_{2n}}}\\ \vdots \\ {{m_{n1}}{m_{n2}} \cdots {m_{nn}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot x}}}_1}}\\ {{{\mathit{\boldsymbol{\ddot x}}}_2}}\\ \vdots \\ {{{\mathit{\boldsymbol{\ddot x}}}_n}} \end{array}} \right) + \left[ \mathit{\boldsymbol{C}} \right]\dot x + \\\left( {\begin{array}{*{20}{c}} {{k_{11}}{k_{12}} \cdots {k_{1n}}}\\ {{k_{21}}{k_{22}} \cdots {k_{2n}}}\\ \vdots \\ {{k_{n1}}{k_{n2}} \cdots {k_{nn}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_1}}\\ {{\mathit{\boldsymbol{x}}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{x}}_n}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_1}\left( t \right)}\\ {{\mathit{\boldsymbol{p}}_2}\left( t \right)}\\ \vdots \\ {{\mathit{\boldsymbol{p}}_n}\left( t \right)} \end{array}} \right) $ | (26) |
式中M为质量矩阵,其中元素mij是使刷丝仅在第j个坐标上产生单位加速度而相应于第i个坐标上所需施加的力;C为阻尼矩阵,其在工程实际中常由实验测定计算出来;K为刚度矩阵,其中元素kij是使刷丝仅在第j个坐标上产生单位位移而相应于第i个坐标上所需施加的力。
刷丝变形瞬态分析和流场的非定常计算采用相同的物理时间步长,在每个物理时间步里,采用双向顺序耦合求解方式,即先求解刷丝束间隙中瞬态流场,再用瞬态流场分析结果求解刷丝的瞬态动力特性,随后再将瞬态动力特性分析结果求解刷丝束间隙中的瞬态流场,如此往复相互作用,直至收敛。
3.2.3 刷丝颤振动网格技术分析为准确模拟刷丝在流体作用下随时间的颤振变形特性,本文采用动网格技术建立了刷式密封瞬态求解模型。当刷丝发生变形时,刷丝周围的网格的每个边看成一个弹簧,使用基于拉伸和扭转弹簧模拟的动网格方法,将刷丝变形信息传递给与它相邻的流体域耦合面每一个节点,进而将刷丝变形信息扩散到整个流体域。考虑到守恒性,每个节点上的合力必须为零,拉伸和扭转弹簧受力平衡方程分别为[29]
| $ {\mathit{\boldsymbol{F}}_1} = K_1^{ij}{\mathit{\boldsymbol{q}}^{ij}} $ | (27) |
| $ \mathit{\boldsymbol{F}}_l^{ijk} = \left( {{R^{ijkT}}{C^{ijk}}{R^{ijk}}} \right){\mathit{\boldsymbol{q}}^{ijk}} $ | (28) |
式中Klij和(RijkTCijkRijk)分别为拉伸弹簧和扭转弹簧的平衡刚度矩阵,qij和qijk分别为表示拉伸弹簧与扭转弹簧的位移矢量。
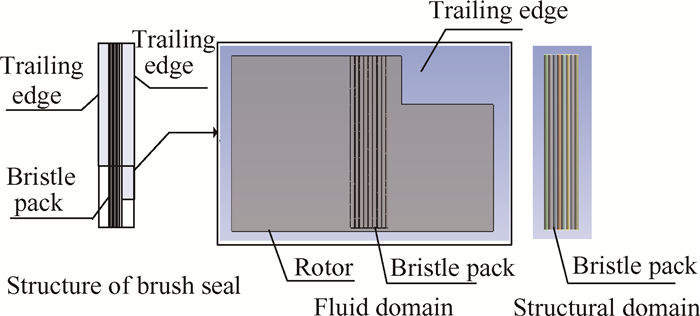
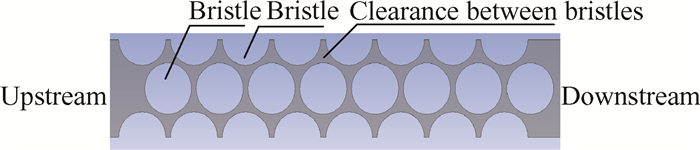
3.3 刷式密封数值求解模型 3.3.1 求解模型本文以国内航空发动机内流系统高压压气机出口与卸荷腔之间的刷式密封为研究对象,采用流固耦合与动网格技术,建立了考虑刷丝变形的刷式密封力学特性的流固耦合三维求解模型。本文选取刷式密封前挡板以下区域内的刷丝束为研究对象,图 4给出了刷丝排数为八排的刷式密封三维模型,包括固体域和流体域。图 5为刷丝束间隙流场模型横截面示意图,其中刷丝长度为5mm,直径为0.15mm,刷丝间距为15μm,刷丝束与后挡板的轴向距离为0.5mm,后挡板高度为1.4mm,厚度为3.4mm,刷丝端部与转子面距离为0.1mm。刷丝材料为镍基高温合金,弹性模量为213.7GPa,泊松比为0.29。
|
Fig. 4 Computational domain of brush seal |
|
Fig. 5 Sketch of bristles gap flow model |
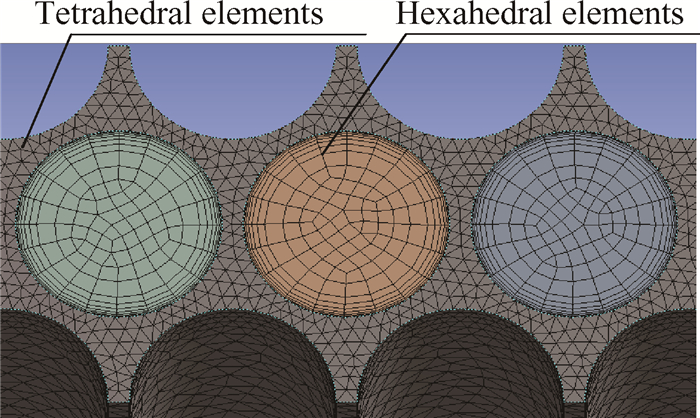
由于刷丝间隙的细长比较大,为了满足计算精度,需要细化网格。图 6给出了刷式密封计算网格示意图,本文采用混合网格形式,流体区域几何形状比较复杂,采用精细的四面体网格,使流体的流动迹线与网格分布的脉络相适应。刷丝区域几何形状简单,采用六面体网格。考虑了边界层网格对计算结果的影响,对边界层网格进行了加密处理。本文在网格质量及网格敏感性测试良好前提下,考虑计算精度与计算时间等因素,最终选定流体域网格数为40万,固体域网格数为10万。
|
Fig. 6 Meshing sketch of brush seals |
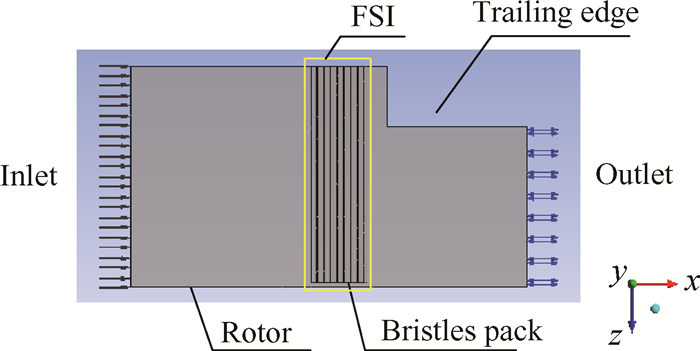
图 7给出了刷式密封流固耦合建模的边界条件示意图。文中涉及的压力均为相对压力,参考压力为标准大气压。模型流体域进出口采用压力边界条件,入口采用总压为0.08MPa,出口压力为0。双向流固耦合面边界如图 7虚线框位置,包括两部分,由每排刷丝周向圆柱面和自由端圆面组成的固体域耦合面和与固体耦合面相邻的流体域面为流体耦合面,耦合面在瞬态多场求解器中设置为可移动边界条件。流场周向对称壁面采用不指定壁面边界条件,以便其能追随耦合面变形运动。转子面设置为指定变形边界,在笛卡尔坐标下,转子面在z轴方向上按照正弦规律运动,表达式为:Asin(wt-1),A取0.1mm;w=2π/T,T为周期;转子旋转表面线速度为300m/s。为了便于计算收敛,非定常求解计算以定常计算结果作为初始值。
|
Fig. 7 Sketch of FSI model boundary conditions |
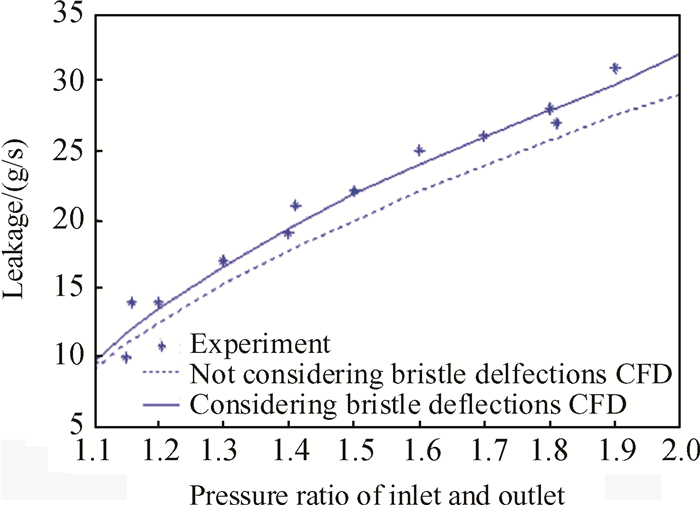
本文将考虑/未考虑刷丝变形的泄漏量数值计算结果分别与实验结果进行对比分析。图 8给出了以文献[23]的刷式密封结构为研究对象,采用考虑刷丝变形瞬态双向流固耦合数值方法和未考虑刷丝变形稳态数值方法计算得到的泄漏量分别与文献[23]实验结果进行对比。由图中可以看出,在相同工况下,考虑刷丝变形流固耦合数值方法的泄漏量计算值与实验结果更吻合。在进出口压比较小时,考虑/未考虑刷丝变形泄漏量计算值相差较小,随着进出口压比的增大,二者差值逐渐增大,这主要是由于在轴向气流力作用下,刷丝的轴向变形使密封与转子面间隙增大,造成泄漏量增大,同时随着进出口压比的增大,刷丝的轴向弯曲变形逐渐增大,因此考虑刷丝变形流固耦合数值方法更能真实反映刷式密封的泄漏特性。由此可以得出,本文考虑刷丝变形的瞬态双向流固耦合数值方法可以准确地模拟刷式密封泄漏流动特性。
|
Fig. 8 Comparison of experimental leakage with CFD results |
本文对刷丝密封颤振特性分别采用稳态理论求解与双向流固耦合求解,并对计算结果进行对比分析,相互验证稳态理论方法与瞬态流固耦合理论方法的准确性。
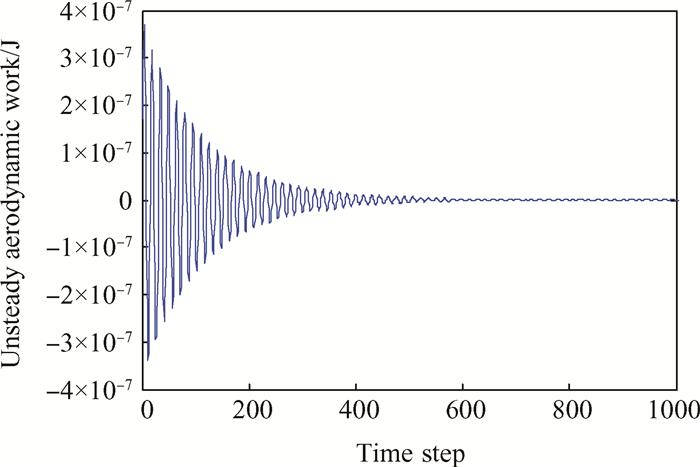
图 9给出了利用双向流固耦合数值方法得到的刷丝受非定常气动力做功的变化规律。表 1给出了流体对刷丝做功的稳态理论值与流固耦合计算值。由图 9可以看出,瞬态流固耦合模型下非定常气动力做功呈现振荡周期变化规律。表 1中瞬态流固耦合计算值在此振荡周期变化规律中得到,而稳态理论计算值是以受均布载荷的悬臂梁模型为基础,分析均布力做功计算得到。双向瞬态流固耦合计算值是以流体力学模型及结构力学模型为基础双向耦合计算的结果,是基于能量法的刷丝与流场信息交互的整个耦合过程的求解,稳态理论值是以结构力学模型为主要研究对象进行推导计算的结果,未能充分地体现刷丝与流体耦合过程中的能量交换。因此双向瞬态流固耦合计算值与稳态理论值存在一定的误差。
|
Fig. 9 Change of bristle energy with time |
|
|
Table 1 Comparison of theoretical values and transient fluid-solid coupling calculation values |
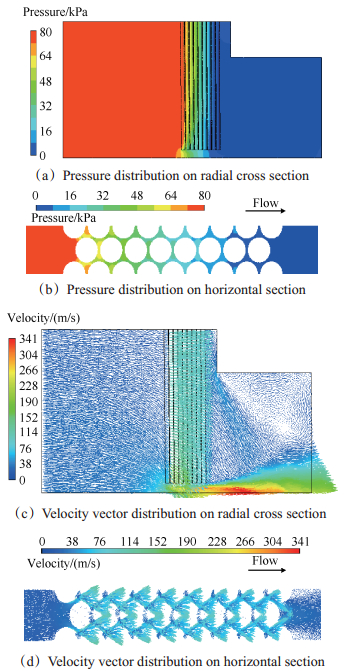
图 10给出了刷丝排数为八排的刷式密封对称面与刷丝束横截面的压力与速度分布图。由图 10(a)、(b)可以看出,上游入口区域压力保持基本不变,当流体进入刷丝束区域后,流体受到刷丝阻碍作用产生压降,压降主要集中在刷丝束间隙区域,压力沿着轴向逐渐降低。由图 10(c)、(d)可以看出,流体以相同的初始速度进入刷式密封刷丝间隙以及刷丝与转子面间隙内,在压差的作用下流向后挡板和出口,当流经刷丝束后流体的轴向速度开始逐渐增大,而径向速度在后挡板附近急剧增大。刷丝束靠近上游和根部区域的流动非常微弱,最大速度发生在刷丝与转子面间隙处,流体成射流状射出。
|
Fig. 10 Pressure distribution of the brush seal and sketch of flow field distribution |
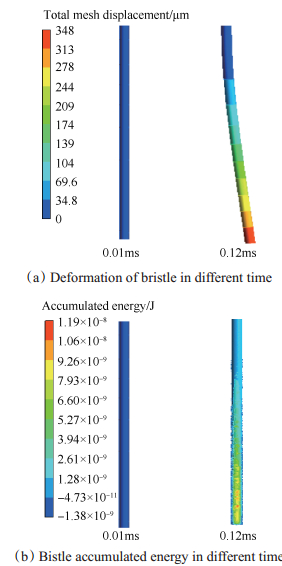
图 11给出了不同时刻刷丝受到非定常气动力作用下的变形云图与气动力累积功图。由图 11(a)左图及图 11(b)左图可以看出,在刷丝与流体耦合作用初始阶段,在0.01ms时刷丝自由端变形较小,刷丝从流体中仅吸收少量能量,刷丝将此能量以弹性势能与动能的形式存储在运动变形的刷丝中。此时,刷丝受流体的非定常气动力与自身的弹性恢复力合力不为零,非定常气动力明显大于自身的弹性恢复力,刷丝自由端在合力的作用下沿着非定常气动力的方向断续移动;在0~0.12ms时间段,刷丝所受合力持续做正功,刷丝能量持续累积,并在0.12ms时达到最大,如图 11(b)右图所示,此时刷丝由非定常气动力做功累积的能量以弹性势能的形式存储在变形的刷丝中,如图 11(a)右图所示。
|
Fig. 11 Deformation and accumulated energy in different time |
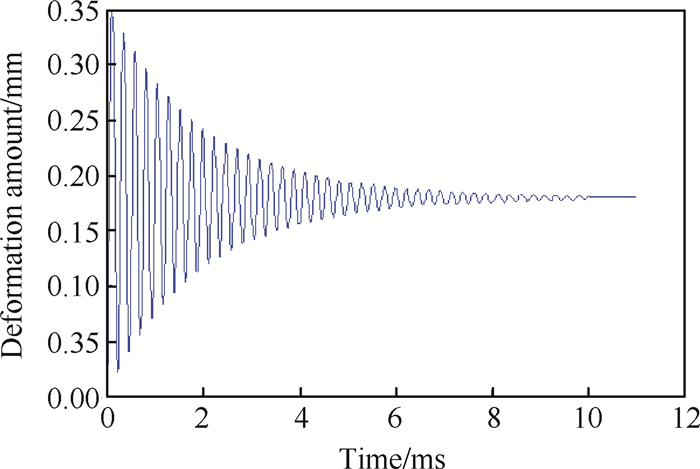
图 12给出了刷丝的刷式密封刷丝自由端变形随时间变化规律。如图所示,刷丝在上下游压差气流力的作用下产生变形,在此变形过程中,刷丝在气动力的作用下发生最大位移,刷丝从流体中吸收能量,此时刷丝弹性恢复力达到最大,大于刷丝非定常气流力,因而变形量降低,刷丝的弹性势能减小,转化为刷丝的动力势能。经刷丝与流体的多次往复作用,刷丝所受气流力与刷丝弹性恢复力达到平衡。
|
Fig. 12 Change of maximum displacement with time |
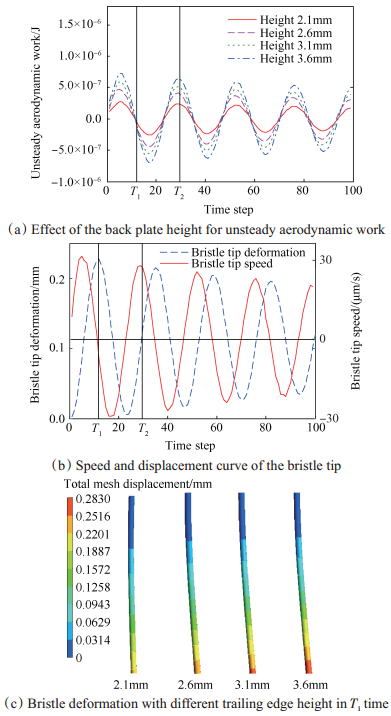
图 13给出了后挡板保护高度对刷丝颤振的影响,其中图 13(a),(b)为后挡板保护高度对非定常气动力做功的影响及与之对应的刷丝自由端速度、位移曲线图,图 13(c)为T1时刻不同后挡板保护高度下的刷丝变形云图。由图 13(a),(b)可以看出,不同后挡板保护高度下的非定常气动力做功均呈振荡变化趋势,且非定常气动力做功周期不随后挡板保护高度的变化而变化。由图 13(a),(c)可以看出,随着后挡板保护高度的增加,非定常气动力做功也增加(图 13(a)中T2时刻),刷丝变形也越剧烈,刷丝越不稳定,越易引发颤振。
|
Fig. 13 Effect of baffle height on the bristle flutter |
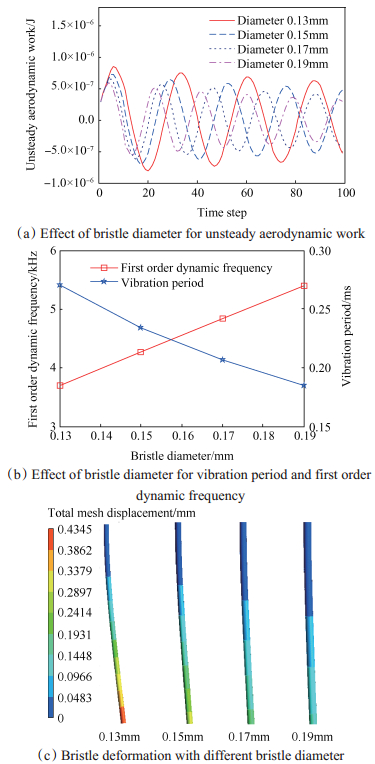
图 14给出了刷丝直径对刷丝颤振的影响,其中图 14(a)为不同刷丝直径对非定常气动力做功的影响,图 14(b)为刷丝直径对刷丝一阶动频和振动周期的影响,图 14(c)为不同刷丝直径下的刷丝变形云图。由图 14(a),(b)可以看出,不同刷丝直径下的非定常气动力做功均呈振荡变化趋势,且非定常气动力做功周期随刷丝直径的减小而增加,与模态分析下的一阶动频及振动周期相对应。由图 14(a),(c)可以看出,随着刷丝直径的减小,非定常气动力做功增加,刷丝变形也越来剧烈,刷丝越不稳定,越易引发颤振。
|
Fig. 14 Effect of bristle diameter on the bristle flutte |
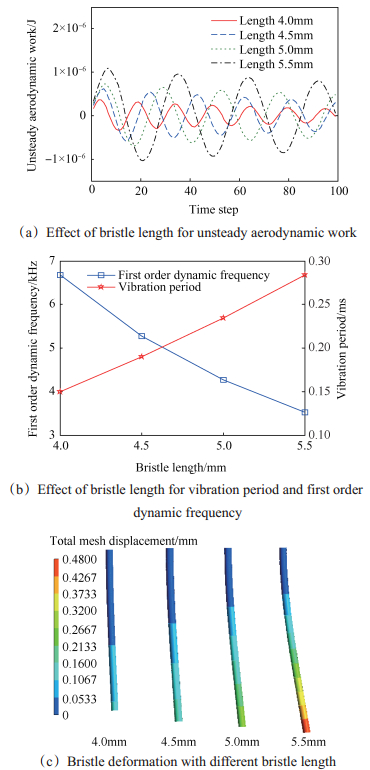
图 15给出了刷丝长度对刷丝颤振的影响图,其中图 15(a)为不同刷丝长度对非定常气动力做功的影响,图 15(b)为不同刷丝长度对刷丝一阶动频和振动周期的影响,图 15(c)为不同刷丝长度对刷丝变形的影响。由图 15(a)、(b)可以看出,不同刷丝长度下非定常力动力做功均呈振荡变化趋势,且非定常气动力做功周期随刷丝长度的增加而增加,与模态分析下的一阶动频及振动周期相对应。由图 15(a)、(c)可以看出,随着刷丝长度的增加,非定常气动力做功增加,刷丝变形也越来越剧烈,越不稳定,越易引发颤振。
|
Fig. 15 Effect of bristle length on the bristle flutter |
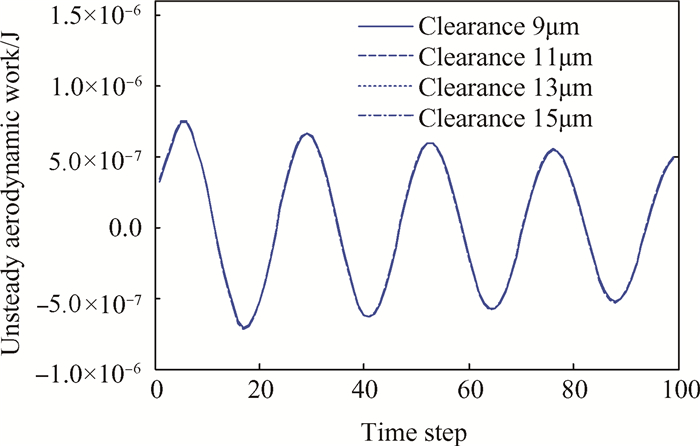
图 16和图 17分别给出了不同刷丝束与后挡板轴向间隙及刷丝间隙对非定常气动力做功的影响。从图 16和图 17可以看出,非定常气动力做功均呈振荡变化趋势。不同刷丝束与后挡板轴向间隙及刷丝间隙对非定常气动力做功周期、做功数值没有明显的影响,刷丝束与后挡板轴向间隙及刷丝间隙对刷丝颤振的影响不大。

|
Fig. 16 Effect of the clearance between the black palte and bristle for unsteady aerodynamic work |
|
Fig. 17 Effect of bristle clearance for unsteady aerodynamic work |
本文建立了基于能量法的刷式密封刷丝颤振特性瞬态流固耦合求解模型,分析刷丝变形规律以及刷丝颤振特性,研究了刷式密封结构参数对刷丝颤振特性的影响,得出以下结论:
(1) 刷丝在非定常气动力作用下做功并发生变形,变形的刷丝又反作用于流体,影响非定常气动力做功,非定常气动力做功和刷丝变形均随时间呈振荡趋势变化。
(2) 随着刷丝长度从4.0~5.5mm及后挡板保护高度从2.1~3.6mm,非定常气动力做功增加,刷丝变形越剧烈,越易引发颤振。后挡板保护高度对非定常气动力做功的周期没有明显影响,但随着刷丝长度增加非定常气动力做功周期也增加。
(3) 刷丝直径从0.13~0.19mm,非定常气动力对刷丝做功减小,非定常气动力做功的周期变短。刷丝束与后挡板轴向间隙及刷丝间隙的变化对非定常气动力做功的大小与周期没有明显影响。
(4) 增加刷丝直径、减少刷丝长度及后挡板保护高度有利于抑制刷丝颤振,刷丝束与后挡板轴向间隙及刷丝间隙对刷丝颤振的影响不大。
| [1] |
Dinc S, Demiroglu M, Turnquist N, et al. Fundamental Design Issues of Brush Seals for Industrial Applications[J]. ASME Journal of Turbomachinery, 2002, 124(2): 293-300. DOI:10.1115/1.1451847
(  0) 0) |
| [2] |
何立东, 袁新, 尹新. 刷式密封研究的进展[J]. 中国电机工程学报, 2001, 21(12): 28-32. DOI:10.3321/j.issn:0258-8013.2001.12.007 (  0) 0) |
| [3] |
Steinetz B M, Hendricks R C. Advanced Seal Technology in Meeting Next Generation Turbine Engine Goal[R]. NASA/TM-1998-06961, 1998.
(  0) 0) |
| [4] |
丁水汀, 陶智, 徐国强. 刷式封严流动和换热的数值模拟[J]. 推进技术, 1999, 20(1): 65-67. (DING Shui-ting, TAO Zhi, XU Guo-qiang. Numerical Simulation on Fluid Flow and Heat Transfer of a Brush Seal Configuration[J]. Journal of Propulsion Technology, 1999, 20(1): 65-67.)
(  0) 0) |
| [5] |
Hogg S L, Chew J W. Porosity Modeling of Brush Seal[J]. Journal of Tribology, 1997, 119(4): 769-775. DOI:10.1115/1.2833883
(  0) 0) |
| [6] |
曹广州, 吉洪湖, 纪国剑. 刷式封严初期使用特性的实验和数值研究[J]. 推进技术, 2010, 31(4): 478-489. (CAO Guang-zhou, JI Hong-hu, JI Guo-jian. Experimental and Numerical Study on the Leakage Characteristics of Brush Seals at the Early Stage of Operating[J]. Journal of Propulsion Technology, 2010, 31(4): 478-489.)
(  0) 0) |
| [7] |
Do gu. Investigation of Brush Seal Flow Characteristics Using Bulk Porous Medium Approach[J]. Journal of Engineering for Gas Turbines and Power, 2005, 127(1): 136-144. DOI:10.1115/1.1808425
(  0) 0) |
| [8] |
张艾萍, 张帅. 低滞后刷式密封泄漏流动数值模拟及结构优化[J]. 润滑与密封, 2015, 40(2): 67-72. (  0) 0) |
| [9] |
迟佳栋, 王之栎. 前板结构对低滞后刷式密封性能影响因素分析[J]. 航空动力学报, 2012, 27(8): 1902-1906. (  0) 0) |
| [10] |
李军, 晏鑫, 丰镇平, 等. 基于多孔介质模型的刷式密封泄漏流动特性研究[J]. 西安交通大学学报, 2007, 41(7): 768-771. DOI:10.7652/xjtuxb200707003 (  0) 0) |
| [11] |
胡丹梅, 黄烨. 汽轮机刷式密封优化设计[J]. 润滑与密封, 2010, 35(5): 70-73. (  0) 0) |
| [12] |
黄学民, 史伟. 刷式密封中泄漏流动的多孔介质数值模拟[J]. 航空动力学报, 2000, 15(1): 55-58. (  0) 0) |
| [13] |
王之栎, 梁小峰. 低滞后刷式密封数值分析[J]. 北京航空航天大学学报, 2008, 4(9): 1080-1083. (  0) 0) |
| [14] |
曹广州, 吉洪湖, 袁艳平. 模拟刷式封严泄漏流动的多孔介质模型[J]. 航空动力学报, 2008, 23(3): 443-447. (  0) 0) |
| [15] |
Lelli D, Chew J W. Combined 3D Fluid Dynamics and Mechanical of Brush Seal[J]. Journal of Tubomachinery, 2006, 128(1): 188-195. DOI:10.1115/1.2103093
(  0) 0) |
| [16] |
Zhao H, Stango R J. Effect of Flow-Induced Radial Load on Brush Seal/Rotor Contact Mechanics[J]. Journal of Tribology, 2004, 126(1): 208-215. DOI:10.1115/1.1609492
(  0) 0) |
| [17] |
Zhao H, Stango R J. Role of Distributed Interbristle Friction Force on Brush Seal Hysteresis[J]. Journal of Tribology, 2007, 129(1): 199-204. DOI:10.1115/1.2401218
(  0) 0) |
| [18] |
黄首清, 索双富, 李永健. 刷式密封流场和温度场的三维数值计算[J]. 清华大学学报(自然科学版), 2014, 54(6): 805-810. (  0) 0) |
| [19] |
白花蕾, 吉洪湖, 曹广州, 等. 指尖密封泄漏特性的实验研究[J]. 航空动力学报, 2009, 24(3): 532-535. (  0) 0) |
| [20] |
邢景棠, 周盛. 流固耦合力学概述[J]. 力学进展, 1997, 27(1): 19-38. DOI:10.6052/1000-0992-1997-1-J1998-223 (  0) 0) |
| [21] |
宗兆科, 苏华. 动压式指尖密封工作状态及其影响的流固耦合分析[J]. 航空动力学报, 2010, 25(9): 2156-2162. (  0) 0) |
| [22] |
Tolga Duran E. Brush Seal Structural Analysis and Correlation with Tests for Turbine Conditions[J]. ASME Journal of Engineering for Gas Turbines and Power, 2016, 138(1): 201-213.
(  0) 0) |
| [23] |
张潇, 王延荣. 基于能量法的叶片颤振边界预测方法[D]. 北京: 北京航空航天大学, 2010.
(  0) 0) |
| [24] |
陈春新, 李军. 刷式密封刷丝束与转子接触力的数值研究[J]. 西安交通大学学报, 2002, 17(5): 636-640. (  0) 0) |
| [25] |
刘占生, 叶建槐. 刷式密封接触动力学特性研究[J]. 航空动力学报, 2002, 17(5): 636-640. (  0) 0) |
| [26] |
刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2008.
(  0) 0) |
| [27] |
钱若军, 董石麟. 流固耦合理论研究进展[J]. 空间结构, 2008, 14(1): 4-15. (  0) 0) |
| [28] |
王福军. 计算流体动力学析-CFD软件的原理与应用[M]. 北京: 清华大学出版社, 2004, 10-11.
(  0) 0) |
| [29] |
Yakhot V. Renormalization Group Analysis of Turbulence: Basic Theory[J]. Journal of Scientific Computing, 1986, 1(1): 3-51. DOI:10.1007/BF01061452
(  0) 0) |
| [30] |
Wissink J G. DNS of Separating, Low Reynolds Number Flow in a Turbine Cascade with Incoming Wakes[J]. Journal of Heat and Fluid Flow, 2003, 24(4): 626-635. DOI:10.1016/S0142-727X(03)00056-0
(  0) 0) |
| [31] |
张小伟, 王延荣. 涡轮机械叶片的流固耦合数值计算方法[J]. 航空动力学报, 2009, 7(24): 1622-1626. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39

