2. 华北电力大学 能源动力与机械工程学院, 北京 102206
2. School of Energy, Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China
传统燃气轮机一般采用扩散燃烧室, 污染物排放相对较高[1, 2]。为了控制污染物排放, 干式低污染排放(DLE)技术在燃气轮机领域得到了广泛的应用[1, 2]。新技术的应用也带来燃烧不稳定性、熄火以及回火等一系列的负面问题[3, 4]。通过结构或运行参数的优化提高燃烧室性能已成为国内外学者的研究重点[4~11]。
目前, 针对旋流数、雷诺数、值班燃料比等燃烧器参数优化的文献相对较多[4~9]。旋流数和雷诺数决定了涡旋破碎的位置及类型, 影响燃烧室内回流区范围、温度分布以及NOx的生成过程[5]。强旋流条件下, 涡旋绕中心轴做低频进动形成进动涡核, 并可能导致燃烧不稳定性现象的发生[6]。由于主燃区与值班区的燃烧组织方式的不同, 值班燃料比影响燃烧室内温度分布以及NOx生成过程[6, 7]。此外, 贫燃预混燃烧过程中容易出现热-声振荡现象, 而扩散火焰可有效抑制该现象的发生, 因此, 提高值班燃料比有利于抑制燃烧室内燃烧不稳定现象[8, 9]。燃烧室的结构及大小同样影响燃烧室内速度、压强梯度的分布以及涡旋破碎过程[10, 11]。在功率一定的条件下, 燃烧室的大小还决定了比面积热强度Qm的大小, 进而影响燃烧室内温度分布及NOx生成过程。然而, 国内外公开发表的相关文献相对较少, 且多针对于某一方面性能的影响展开研究。Fu等[10]采用实验方法研究了燃烧室大小对双旋流喷嘴下游流场的影响, 研究表明, 燃烧室内回流区的范围与燃烧室尺寸密切相关。Duwig[11]采用实验方法研究了燃烧室大小对燃烧室内压力振荡的影响, 研究表明, 增大燃烧室横截面积Af可降低压力振幅。
雷诺时均(RANS)、大涡模拟(LES)及直接数值模拟(DNS)是湍流燃烧过程的主要数值方法[12, 13]。RANS方法不计算各种尺度的湍流脉动, 因而丢失了脉动运动中大量有用的信息, 计算精确性最差[14, 15]。DNS方法直接求解流动控制方程, 计算量最大, 目前仅限于求解较低雷诺数的简单湍流运动[14, 15]。LES方法则介于二者之间, 直接求解大尺度湍流, 并通过模型求解小尺度脉动, 可较为精确地求解实验手段无法得到的流场空间和时间上的动态信息[16, 17]。目前, 已成为燃烧室内湍流燃烧过程研究的重要手段[16, 17]。
某分管形燃烧室具有微、小型燃气轮机燃烧室典型的结构特征, 燃烧室的最大热功率约为1MW, 横截面积Af约为0.026m2。进气压力为0.6MPa时, 燃烧室的比面积热强度Qm约为0.24MJ·m-1·h-1·Pa-1[12, 13]。为了确保燃烧区的流速处于合理的范围, 本文在设计值的基础上对燃烧室横截面积Af进行了小幅调整, 采用LES方法研究了横截面积Af对流动、燃烧、压力振荡以及污染物生成过程等方面的影响, 为燃烧室设计提供参考。
2 物理模型和计算方法 2.1 物理模型燃气轮机燃烧室气动计算及基本尺寸的设计过程中, 首先根据理论公式以及经验参数计算得到燃烧室的最大横截面积Aref[12, 13]
| $ {A_{{\rm{ref}}}} = \frac{{{M_{\rm{a}}}\sqrt {T_2^ * } }}{{P_2^ * }}\sqrt {\frac{{R{\varphi _{{\rm{ref}}}}}}{{2{\delta _{\rm{b}}}}}} $ | (1) |
式中Ma, R, φref, δb分别为空气流量、气体常数、燃烧室阻力系数以及燃烧室总压损失系数[8, 9]。
燃烧室横截面积为
| $ {A_{\rm{f}}} = \left( {0.5 \sim 0.76} \right){A_{{\rm{ref}}}} $ | (2) |
计算结果还需通过比面积热强度Qm校核
| $ {Q_{\rm{m}}} = 3600{M_{\rm{f}}}{H_{\rm{u}}}\eta /{A_{\rm{f}}}p_2^ * $ | (3) |
式中Mf, Hu, η分别为燃料质量流量、低位发热量以及燃烧效率[12, 13]。比面积热强度Qm经验值的取值范围为0.20~0.45MJ·m-1·h-1·Pa-1[12, 13]。
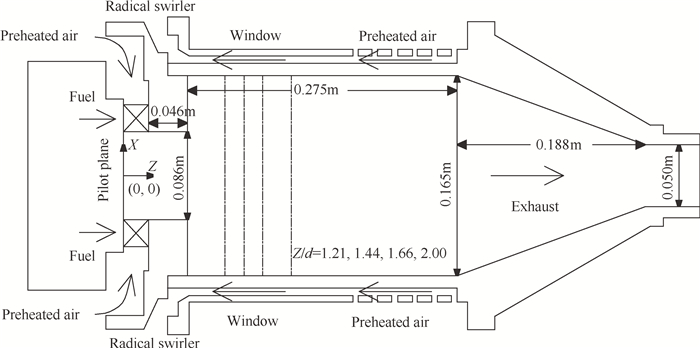
模型燃烧室如图 1所示, 燃烧室采用逆流式结构, 头部安装有1个DLE混合型燃烧器, 以径向旋流器作为一次配气机构, 属于微、小型燃气轮机中应用较多的结构形式, 因此, 具有一定的代表性[12, 13]。DLE燃烧器与实际燃气轮机完全一致, 径向旋流器内设有12个矩形通道, 旋流数为1.3[12]。预混段横截面的内径为86mm, 长度为46mm[12~14]。实际燃烧室横截面为圆形, 为了便于安装观测设备, 模型燃烧室横截面设计成带倒角的正方形, 二者的横截面积Af近似相等, 约为0.026m2[12~14]。燃烧室的长度为0.275m, 过渡段的长度为0.188m, 出口横截面内径则为0.05m[12~14]。主燃料喷口位于近旋流器入口的矩形通道内, 与预热空气在矩形通道内均匀混合形成预混燃料, 值班燃料喷口则位于值班平面。本文中, 值班燃料比为0%。
|
Fig. 1 Gas turbine model combustion chamber |
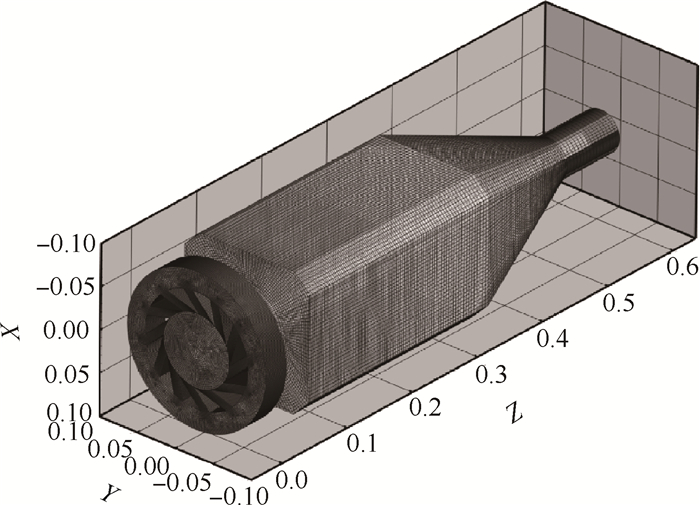
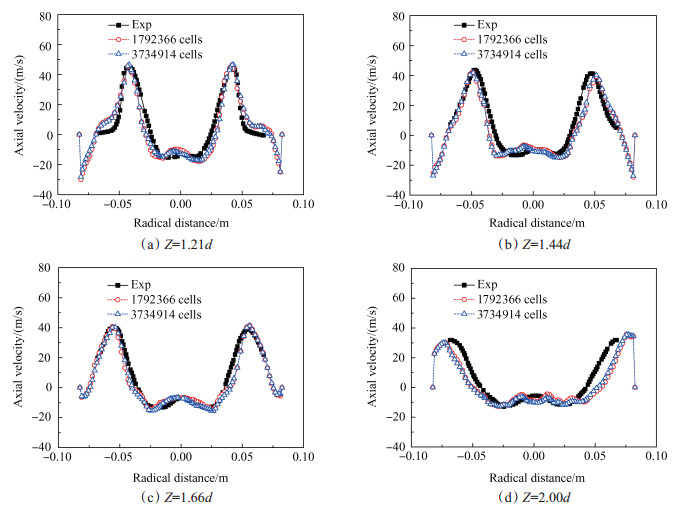
采用Gambit软件进行建模及网格划分, 网格如图 2所示。建模过程中, 忽略燃烧室外层壳体的具体结构, 通过设置相应的边界条件反映其影响[13]。采用分区网格划分的方法对径向燃烧器及其附近区域进行网格加密[13~15]。为了分析网格数量对于计算结果的影响, 对网格数目分别为179万和373万两种网格模型进行了计算与分析。图 3给出了两种网格模型y平面上的热态速度分布的对比。如图 3所示, 两种网格模型y平面上的速度分布情况近似, 均能较好地反映燃烧室内时均轴向速度的分布规律, 相对误差均小于5 %, 因此, 采用网格数为179万的模型可以保证计算精度。采用克朗数Co准则确定计算时间步长Δt, 即:Co=Δt·ui/Δxi。计算域中, 流向上最小的网格尺度Δx < 1mm。计算过程中, 确保克朗数Co < 0.5, 最终的计算时间步长Δt取为2μs[16~18]。每个时间步长Δt迭代20步, 每个工况各计算约2.5×105个时间步长, 约5×106步。对于相同网格数量的模型, 采用LES和RANS方法计算1步的计算时间大致相同, 而采用RANS方法计算约10000步则可以确保计算收敛, 因此, 由于采用LES方法的计算时间为RANS方法的500倍以上。
|
Fig. 2 Computational field and gird generation |
|
Fig. 3 Comparison between LES results of time-average axial velocity under different mesh number |
LES方法的第一步是将湍流分解为大尺度湍流运动以及小尺度脉动。
| $ {u_i}\left( {x,t} \right) = {{\bar u}_i}\left( {x,t} \right) + {{u'}_i}\left( {x,t} \right) $ | (4) |
式中ui(x, t)为大尺度湍流运动; u″i(x, t)为小尺度脉动[14, 15]。
滤波之后的控制方程
| $ \frac{{\partial \bar \rho }}{{\partial t}} + \frac{{\partial \left( {\bar \rho {{\tilde u}_i}} \right)}}{{\partial {x_i}}} = 0 $ | (5) |
| $ \frac{{\partial \left( {\bar \rho {{\tilde u}_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho {{\tilde u}_i}{{\tilde u}_j} + \bar p{\delta _{ij}}} \right)}}{{\partial {x_j}}} = \frac{{\partial \left( {{{\bar \tau }_{ij}} + \bar \tau _{ij}^{{\rm{sgs}}}} \right)}}{{\partial {x_j}}} $ | (6) |
| $ \frac{{\partial \left( {\bar \rho \tilde E} \right)}}{{\partial t}} + \frac{{\partial \left( {\left( {\bar \rho \tilde E + \bar p} \right){{\tilde u}_i}} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_i}}}\left( {{{\tilde u}_j}{{\tilde \tau }_{ij}} + \lambda \frac{{\partial \tilde T}}{{\partial {x_i}}} - H_i^{{\rm{sgs}}} + \sigma _i^{{\rm{sgs}}}} \right) $ | (7) |
式中τijsgs, Hisgs, σisgs分别为亚网格应力张量、亚格子焓通量以及亚格子黏性项, 表达式如公式(8)~(10)所示[16~18]
| $ \tau _{ij}^{{\rm{sgs}}} = \bar \rho \left( {{u_i}{u_j} - {{\tilde u}_i}{{\tilde u}_j}} \right) $ | (8) |
| $ H_i^{{\rm{sgs}}} = \bar \rho \left( {{u_i}E - {{\tilde u}_i}\tilde E} \right) + \overline {p{u_i}} - \bar p{{\tilde u}_i} $ | (9) |
| $ \sigma _{ij}^{{\rm{sgs}}} = - \left( {{\tau _{ij}}{u_j} - {{\tilde \tau }_{ij}}{{\tilde u}_j}} \right) $ | (10) |
采用有限速率/涡耗散模型对湍流燃烧速率进行描述[9]。采用文献[13]中给出的M4简化反应机理。该机理包含4步化学反应以及6种反应物(CH4, O2, CO, H2, CO2, H2O)[13]。具体反应机理及反应速率如公式(11)~(18)所示。燃烧室内生成的NOx主要有热力型及快速型两种[13]。本文采用文献[13]中给出的3步NOx反应机理进行计算, 该反应机理包括:扩展型热力型NOx机理、快速型NOx机理以及N2O机理[13]。
| $ {\left[ {{\rm{C}}{{\rm{H}}_4}} \right]^{0.7}} + 1.5{\left[ {{{\rm{O}}_2}} \right]^{0.97}} \rightleftharpoons {\rm{CO}} + 2{{\rm{H}}_2} $ | (11) |
| $ {\left[ {{{\rm{H}}_2}} \right]^{0.55}} + 0.5{\left[ {{{\rm{O}}_2}} \right]^{1.01}} \rightleftharpoons {{\rm{H}}_2}{\rm{O}} $ | (12) |
| $ \left[ {{\rm{CO}}} \right] + 0.5{\left[ {{{\rm{O}}_2}} \right]^{0.5}} \rightleftharpoons {\rm{C}}{{\rm{O}}_2} $ | (13) |
| $ \left[ {{\rm{CO}}} \right] + \left[ {{{\rm{H}}_2}{\rm{O}}} \right] \rightleftharpoons {\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_2} $ | (14) |
具体反应速率表达式如下
| $ {R_1} = {A_1}{T^{{\rm{B1}}}}{{\rm{e}}^{\frac{{ - {E_{{\rm{a1}}}}}}{{RT}}}}{\left[ {{\rm{C}}{{\rm{H}}_4}} \right]^{0.7}}{\left[ {{{\rm{O}}_2}} \right]^{0.97}} $ | (15) |
| $ {R_2} = {\left( {{p_{{\rm{atm}}}}/p} \right)^n}{A_2}{T^{{{\rm{B}}_2}}}{{\rm{e}}^{\frac{{ - {E_{{\rm{a2}}}}}}{{RT}}}}{\left[ {{{\rm{H}}_2}} \right]^{0.55}}{\left[ {{{\rm{O}}_2}} \right]^{1.01}} $ | (16) |
| $ {R_3} = {A_3}{T^{{{\rm{B}}_3}}}{{\rm{e}}^{\frac{{ - {E_{{\rm{a3}}}}}}{{RT}}}}\left[ {{\rm{CO}}} \right]{\left[ {{{\rm{O}}_2}} \right]^{0.5}} $ | (17) |
| $ {R_4} = {A_4}{T^{{{\rm{B}}_4}}}{{\rm{e}}^{\frac{{ - {E_{{\rm{a4}}}}}}{{RT}}}}\left[ {{\rm{CO}}} \right]\left[ {{{\rm{H}}_2}{\rm{O}}} \right] $ | (18) |
表 1给出了不同计算工况时的参数设置。工况1~4中, 径向旋流燃烧器及预混段的结构保持一致, 预混段横截面积A约为60cm2。工况1~4中, 燃烧室横截面积Af分别为0.024, 0.026, 0.029及0.032m2, 其中, 工况2为基准工况, 燃烧室横截面积Af为0.026m2。进气压力p为0.6MPa时, 比面积热强度Qm分别为0.26, 0.24, 0.22及0.20MJ·m-1·h-1·Pa-1, 而其经验值的取值范围则为0.20~0.45MJ·m-1·h-1·Pa-1。燃料和空气的入口设为质量入口边界, 燃料的质量流量及温度分别为6.2g/s及483K, 空气的质量流量及预热温度则分别为175g/s及685K[12~14]。工况1~4中, 值班燃料比为0%, 所有燃料经由主燃料喷口与预热空气在矩形通道内均匀混合形成预混燃料, 燃料的当量比约为0.6[12~14]。由于采用LES方法计算1个工况的时间为RANS方法的500倍以上。为了减少计算量, 对燃料组分进行了适当的简化, 简化后燃料的热值保持不变, 约为39.4MJ/(N·m3)。CH4, CO2及N2的摩尔分数则分别为98.97%, 0.27%及0.76%[13]。燃烧室壁面设为绝热壁面, 忽略壁面之间的辐射换热。燃烧室出口设为压力出口边界, 压损率约为1%[13]。
|
|
Table 1 Parameter settings of different simulation cases |
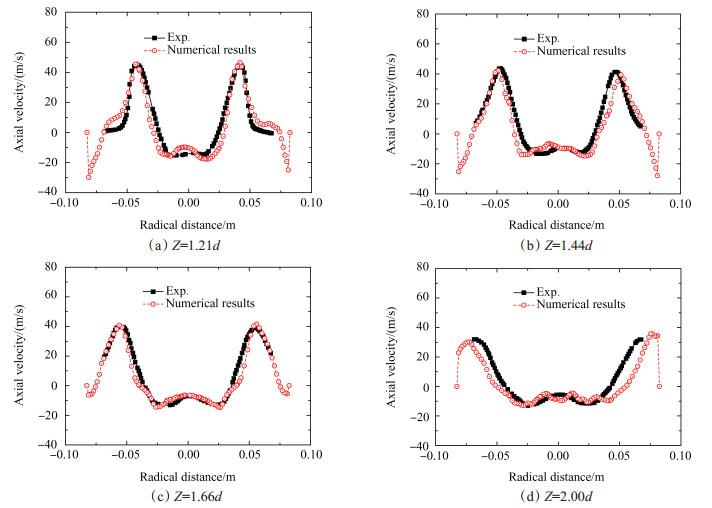
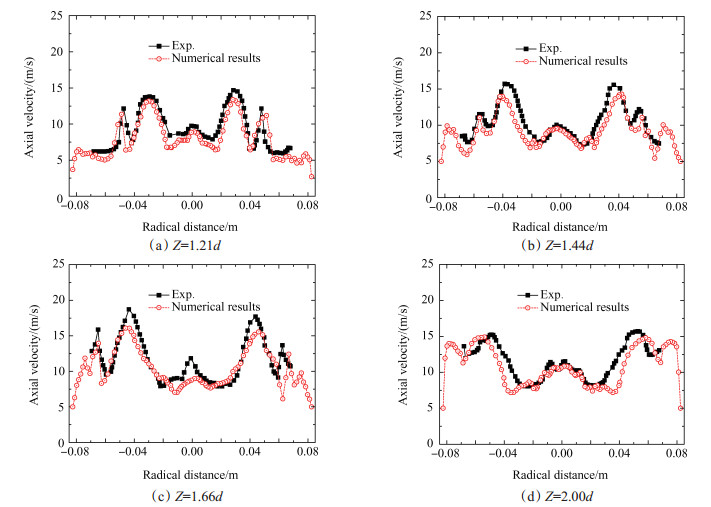
时均速度及均方根速度分别用于描述某一时间段内平均速度及速度波动的大小[18]。图 4给出了工况2中, y平面上不同轴向位置处时均轴向速度的计算值与文献[12]中实验值的对比(热态流场)。不同的轴向位置如图 1所示, Z, d分别为轴向距离、预混段横截面的内径[12~14]。如图 4所示, 计算结果较好地反映了燃烧室内时均轴向速度的分布规律, 相对误差小于5 %, 速度峰值um的计算值与实验值接近, 回流区的宽度则略大于实验值。燃烧室内, 存在沿中轴线对称的速度峰值um, 中心回流区位于中轴线附近, 外部回流区则位于壁面附近。图 5给出了均方根轴向速度的计算值与实验值的对比。如图 5所示, 计算结果较好地反映了均方根轴向速度的分布规律, 速度峰值um的计算值略低于实验值, 而峰值点之间的距离则正好相反。燃烧室内, 内、外剪切层附近的速度波动最为剧烈, 其他区域的速度波动幅度则相对较小。速度波动幅度随轴向距离的增加而减小。
|
Fig. 4 Comparison between LES and experiment results of time-average axial velocity |
|
Fig. 5 Comparison between LES and experiment results of root mean square axial velocity |
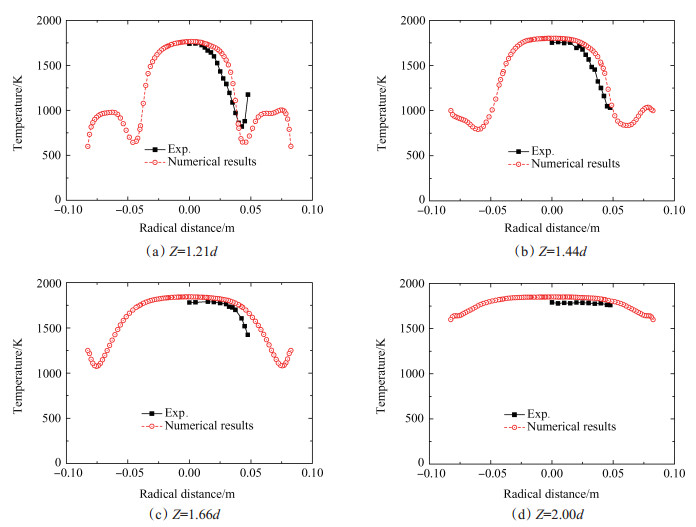
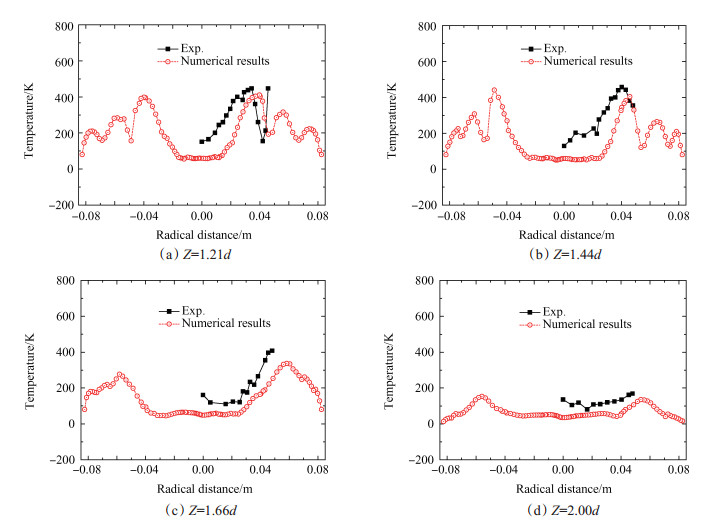
图 6给出了工况2中, y平面上不同轴向位置处时均温度的计算值与文献[12]中实验值的对比。如图 6所示, 计算结果较好地反映了燃烧室内时均温度的分布规律, 相对误差小于10 %, 温度及高温区的范围的计算值则略大于实验值。燃烧室内, 高温区位于中轴线附近, 主流区的温度最低, 内、外剪切层附近的温度梯度则相对较大。图 7给出了均方根温度的计算值与实验值的对比。如图 7所示, 计算结果较好地反映了均方根温度的分布规律, 均方根温度的计算值则略低于实验值。对比图 5与图 7可知, 均方根温度与速度的分布规律相似, 内、外剪切层附近的温度波动最为剧烈, 波动幅度随轴向距离的增加而减小。对比图 6与图 7可知, 中轴线附近, 时均温度最高而温度波动幅度则最小。此外, 燃烧室内压力振荡主频f及NOx排放浓度的计算值分别为194.4Hz及12.9mL/m3(15% O2), 均与文献[12]中的实验数据较好地吻合。LES方法的精确性较好, 可用于研究燃烧室横截面积Af对流动、燃烧、压力振荡以及污染物生成过程的影响规律。
|
Fig. 6 Comparison between LES and experiment results of time-average flame temperature |
|
Fig. 7 Comparison between LES and experiment results of root mean square flame temperature |
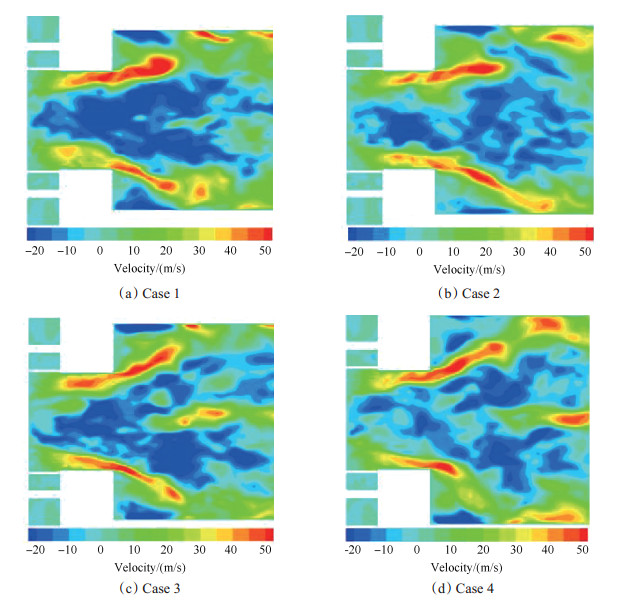
图 8给出了不同工况中, y平面上瞬态轴向速度分布的对比(热态流场)。如图 8所示, 受离心力的影响, 旋转气流在燃烧室内发生径向扩张, 从而形成环状主流区。中轴线附近, 由于流体的抽吸作用, 形成了中心回流区, 回流区延伸至值班平面。由于中心回流区的边界存在大量大小不等的涡旋, 瞬态速度场的对称性相对较差。由于通流面积发生突扩, 燃烧室入口截面与流体再附点之间形成了外部回流区, 外部回流区的范围则相对较小。向下流发展过程中, 流场发生径向扩张, 从而导致中心回流区的宽度增大, 回流速度则有所降低。中轴线附近, 由于正压的恢复, 逐渐形成了一股正向流动的气流。由于燃烧室内的速度以及压强分布明显受燃烧室壁面的影响, 因此, 增大横截面积Af使得燃烧室内的中心回流区的范围扩大, 回流速度则有所降低。中轴线附近, 正向流动区域的范围也有所扩大。
|
Fig. 8 Comparison of the instantons axial velocity of different simulation cases |
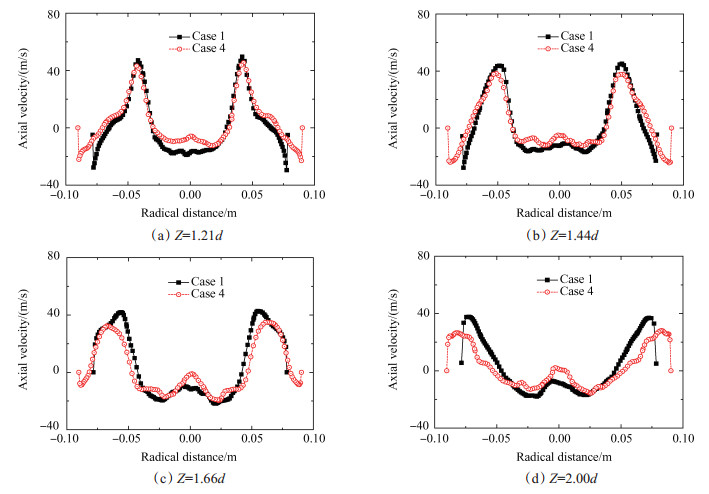
图 9给出不同工况中, y平面上不同轴向位置处的时均轴向速度分布的对比(热态流场)。由于变化趋势相同, 且相邻两组数据之间差异较小, 因此, 仅给出了工况1与工况4的两组数据的对比。如图 9所示, 靠近燃烧室入口的轴向位置上, 不同工况的峰值速度um分别为48.4, 44.3m/s, 中心回流区的宽度则分别为57mm, 60mm, 两者的差异相对较小。当轴向距离Z>1.44d时, 增大横截面积Af明显地加速了射流的衰减过程。工况4中, 流体的发散角明显增大, 峰值点的位置向壁面方向移动, 峰值的大小则有所降低。此外, 由于中心回流区的宽度增加, 中轴线附近, 正向流动区域的范围扩大, 速度也有所增加。壁面附近, 增大横截面积Af也使得流体再附点向下游移动, 外部回流区范围扩大, 工况1中, 流体再附点位于Z=1.21d附近, 工况4中, 流体再附点则移动至Z=1.44d附近。
|
Fig. 9 Comparison of the time-averaged axial velocity of different simulation cases |
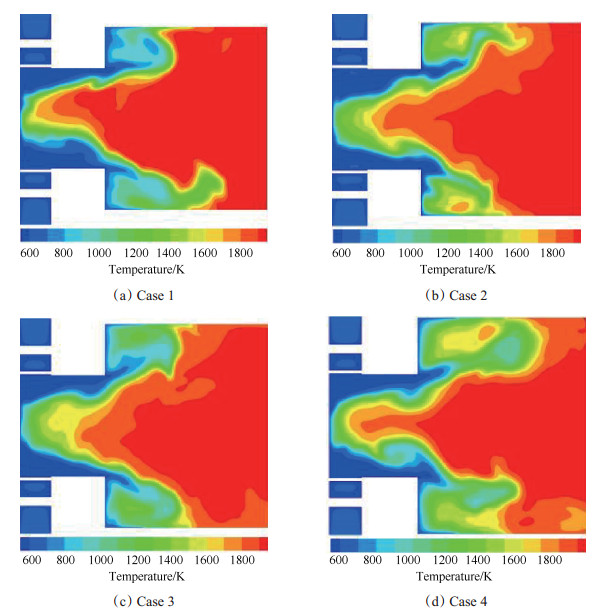
图 10给出了不同工况中, y平面上瞬态温度分布的对比。对比图 8与图 10可知, 燃烧室内火焰特性与回流区分布密切相关。预混段内, 中心回流区延伸至值班平面, 回流的高温燃烧产物不断地与燃料气流交换热量和活化分子, 燃料气流在与预混段内即开始着火与燃烧, 为火焰的稳定提供了良好的基础。燃烧室内, 中心回流区火焰温度相对较高, 高温区范围随轴向距离的增加而扩大。回流区边界上存在的涡旋扭曲了火焰形状, 瞬态温度场的对称性相对较差。增大横截面积Af使得比面积热强度Qm减小, 燃烧室内温度水平降低。中轴线附近, 高温区的范围缩小。壁面附近, 外部回流区范围扩大, 低温区范围有所扩大。
|
Fig. 10 Comparison of the instantons temperature of different simulation cases |
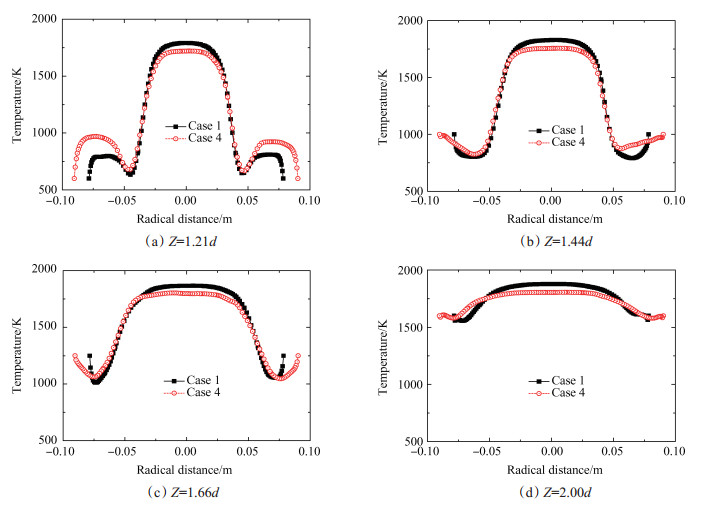
图 11给出不同工况中, y平面上不同轴向位置处的时均温度分布的对比。如图 11所示, 燃烧室内, 温度最高的区域位于中轴线附近。向下流发展过程中, 高温区范围发生了明显的径向扩张, 温度也有所升高。工况1中, 中轴线上不同轴向位置处的温度分别为1789.8, 1829.6, 1866.7及1877.6K, 增幅随轴向距离的增加而降低。壁面附近, 由于外部回流区温度的升高, 燃烧室内温度的径向分布趋于均匀。增大横截面积Af使得比面积热强度Qm减小, 燃烧室内的温度水平降低。工况1~4中, 燃烧室内峰值温度Tm分别为1896.9, 1859.7, 1836.2及1824.5K, 降幅随截面积Af的增大而降低。不同工况中, 峰值温度Tm均超过1800 K, 根据泽尔道维奇机理(Zeldovich), 增大横截面积Af所导致的峰值温度Tm降低可有效降低NOx的生成速率。
|
Fig. 11 Comparison of the time-averaged temperature of different simulation cases |
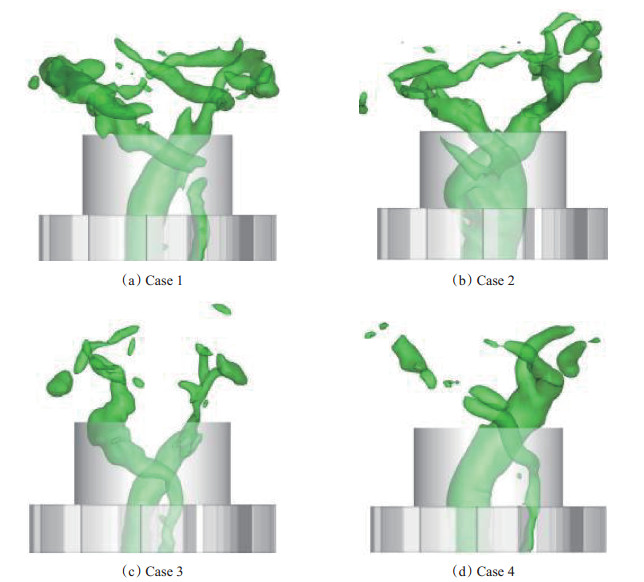
为了抵消切向速度所导致的离心力, 进动涡核周围的压力通常相对较低, 因此, 可用压力等值面定性地描述进动涡核结构[18]。图 12给出了用压力等值面(p≈0.299MPa)表示的进动涡核结构。如图 12所示, 不同工况中, 燃烧室内出现大小不同的两个螺旋形进动涡核, 进动涡核结构延伸至值班平面[18]。受预混段结构的限制, 预混段内进动涡核的间距相对较小。燃烧室内, 流场发生明显的径向扩张, 中心回流区的范围明显扩大, 进动涡核的间距也明显扩大。向下游发展过程中, 涡核结构破碎成随机的小尺度涡旋后逐渐消失, 因此, 完整的进动涡核结构主要存在于上游流场中。工况1~4中, 由于径向旋流器及预混段结构保持一致, 上游流场中的进动涡核结构类似。这说明, 横截面积Af的改变对进动涡核结构的影响相对较小。
|
Fig. 12 Comparison of the precession vortex core structures of different simulation cases |
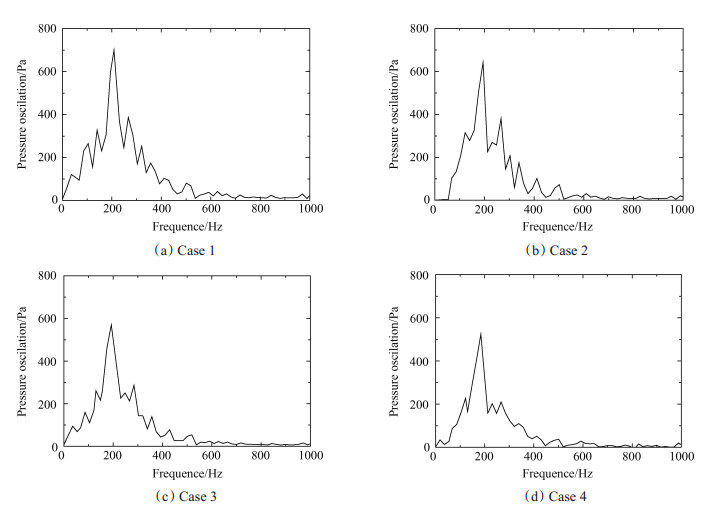
热态计算过程中, 监测压力振荡随时间变化的规律, 并采用傅里叶变换方法(FFT)进一步求得压力振荡主频f[18]。图 13给出了不同燃烧室横截面积Af时, 燃烧室内压力振荡的频谱分析结果的对比。如图 13所示, 工况2中, 压力振荡主频f计算值为194.4Hz, 与文献[12]中的实验值吻合较好, 计算精度较好。工况1~4中, 燃烧室内均出现明显的压力振荡主频f, 振荡主频f之间的差异相对较小。工况1~4中, 振荡幅值Δp分别为700.4, 642.3, 569.8以及523.7Pa, 降幅明显, 这说明增大横截面积Af使得燃烧室的声学耗散作用增强, 从而有效降低了压力振荡幅值Δp。由于压力振荡幅值Δp是表征燃烧不稳定性现象产生的重要指标, 因此, 增大燃烧室横截面积Af有利于降低压力振荡幅值Δp, 抑制燃烧不稳定性现象的发生。
|
Fig. 13 Comparison of the pressure occasions characteristic of different simulation cases |
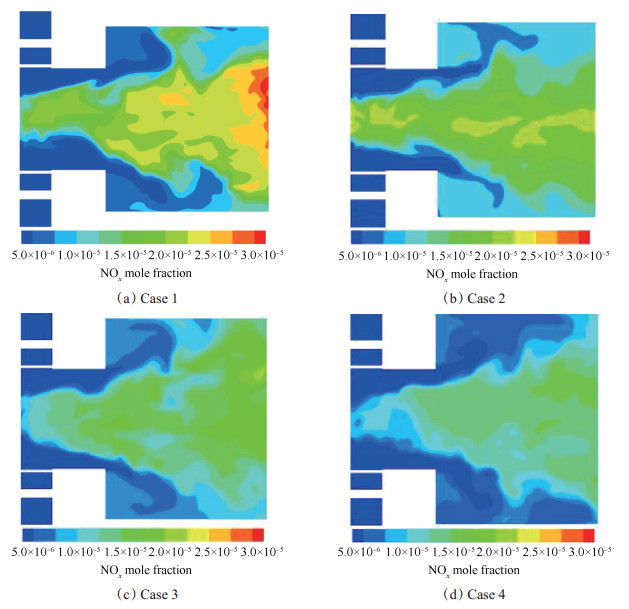
图 14给出了不同工况中, y平面上瞬态NOx摩尔分数分布的对比。如图 14所示, 燃烧室内NOx摩尔分数与其生成速率以及流动状况相关。预混段内, 火焰温度较低, 而NOx摩尔分数却相对较高。这是由于, 中心回流区内回流的高温燃烧产物中NOx浓度较高, 高温燃烧产物的回流导致该区域的NOx摩尔分数升高。燃烧室内, 中轴线附近的火焰温度相对较高, 高温明显地促进了NOx的生成, NOx摩尔分数也相对较高。由于温度较低, 主流区及外部回流区附近的NOx摩尔分数则相对较低。此外, 瞬态速度场及温度场的不对称明显导致了NOx摩尔分数分布的不对称。增大燃烧室横截面积Af使得燃烧室的比面积热强度Qm减小, 燃烧室内温度降低, NOx摩尔分数明显下降。
|
Fig. 14 Comparison of the instantons NOx mole fraction of different simulation cases |
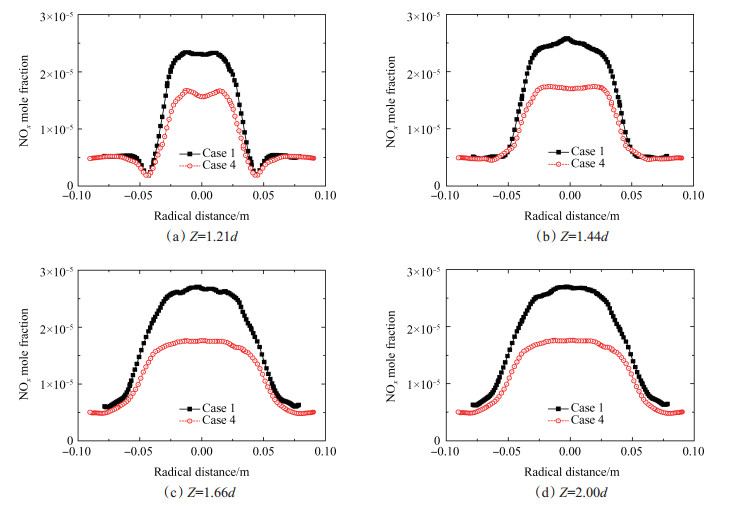
图 15给出不同工况中, y平面上不同轴向位置处的时均NOx摩尔分数分布的对比。对比图 11与图 15可知, 燃烧室内, NOx摩尔分数与温度分布规律相似。中轴线附近, 温度及NOx摩尔分数均相对较高, 其他区域则相对较低。随着轴向距离的增加, 燃烧室内高温区范围扩大, NOx摩尔分数高的区域也相应扩大。增大横截面积Af使得燃烧室内NOx摩尔分数降低, 燃烧室出口NOx的排放浓度下降。工况1~4中, 燃烧室出口NOx浓度分别为15.2, 12.9, 10.6及9.8mL/m3(15%O2)。这说明, 增大横截面积Af虽然延长了燃料气流在燃烧室内的滞留时间, 不利于控制燃烧室内NOx的生成, 但由于燃烧室内的峰值温度Tm均已超过1800K, 根据泽尔道维奇机理, 增大横截面积Af所导致的温度降低对于NOx生成速率的影响更为明显, 并最终导致了燃烧室出口NOx排放浓度下降。因此, 采用较大燃烧室横截面积Af有利于降低烧室内温度水平, 控制NOx排放。
|
Fig. 15 Comparison of the time-averaged NOx mole fraction of different simulation cases |
(1) 增大横截面积加速了射流的衰减过程, 流体的发散角增大, 速度峰值则有所降低, 中心回流区的宽度增加。壁面附近, 外部回流区范围扩大, 流体再附点向下游移动。当横截面积由0.024m2增大至0.032m2时, 流体再附点由Z=1.21d附近移动至Z=1.44d附近。
(2) 增大燃烧室横截面积增强了燃烧室的声学耗散作用, 压力振荡幅值降低。当横截面积由0.024m2增大至0.032m2时, 压力振荡幅值Δp由700.4Pa降低至523.7Pa, 降幅明显。因此, 采用较大的燃烧室横截面积有利于控制燃烧不稳定性现象的发生。
(3) 增大燃烧室横截面积降低了燃烧室内温度水平及NOx生成速率。当横截面积由0.024m2增大至0.032m2时, 燃烧室出口NOx浓度由15.2mL/m3降低至9.8mL/m3(15%O2), 降幅明显。因此, 采用较大的燃烧室横截面积有利于控制NOx排放。
| [1] |
T S. On Stationary and Travelling Vortex Breakdowns[J]. Journal of Fluid Mechanics, 1971, 45(3): 545-559. DOI:10.1017/S0022112071000181
(  0) 0) |
| [2] |
Huang Y, Yang V. Dynamics and Stability of Lean-Premixed Swirl-Stabilized Combustion[J]. Progress in Energy & Combustion Science, 2009, 35(4): 293-364.
(  0) 0) |
| [3] |
朱文中, 杨渐志, 陈靖, 等. 湍流扩散火焰局部熄火现象的大涡模拟研究[J]. 推进技术, 2015, 36(6): 808-815. (ZHU Wen-zhong, YANG Jian-zhi, CHEN Jing, et al. Large Eddy Simulation of Local Extinction of Turbulent Non-Premixed Flame[J]. Journal of Propulsion Technology, 2015, 36(6): 808-815.)
(  0) 0) |
| [4] |
张昊, 朱民. 热声耦合振荡燃烧的实验研究与分析[J]. 推进技术, 2010, 31(6): 730-744. (ZHANG Hao, ZHU Min. Experimental Study and Analysis of Thermo-Acoustic Instabilities in Natural Gas Premixed Flames[J]. Journal of Propulsion Technology, 2010, 31(6): 730-744.)
(  0) 0) |
| [5] |
Oberleithner K, Stöhr M, Im S H, et al. Formation and Flame-Induced Suppression of the Precessing Vortex Core in a Swirl Combustor:Experiments and Linear Stability Analysis[J]. Combustion and Flame, 2015, 162(8): 3100-3114. DOI:10.1016/j.combustflame.2015.02.015
(  0) 0) |
| [6] |
Silva C F, Leyko M, Nicoud F, et al. Assessment of Combustion Noise in a Premixed Swirled Combustor Via Large-Eddy Simulation[J]. Computers & Fluids, 2013, 78(12): 1-9.
(  0) 0) |
| [7] |
Mafra M R, Fassani F L, Zanoelo E F, et al. Influence of Swirl Number and Fuel Equivalence Ratio on NO Emission in an Experimental LPG-Fired Chamber[J]. Applied Thermal Engineering, 2010, 30(8): 928-934.
(  0) 0) |
| [8] |
Zhou L X, Wang F, Zhang J. Simulation of Swirling Combustion and NO Formation Using a USM Turbulence-Chemistry Model[J]. Fuel, 2003, 82(13): 1579-1586. DOI:10.1016/S0016-2361(03)00089-9
(  0) 0) |
| [9] |
Shi L, Fu Z, Shen Y, et al. LES of Swirl Angle on Combustion Dynamic and NOx Formation in a Hybrid Industrial Combustor[J]. International Journal of Heat & Technology, 2016, 34(2): 197-206.
(  0) 0) |
| [10] |
Fu Y, Cai J, Jeng S M, et al. Confinement Effects on the Swirling Flow of a Counter-Rotating Swirl Cup[R]. ASME GT 2005-68622.
(  0) 0) |
| [11] |
Duwig C, Fuchs L, Lacarelle A, et al. Study of the Vortex Breakdown in a Conical Swirler Using LDV, LES and POD[R]. ASME GT 2007-27006.
(  0) 0) |
| [12] |
Stopper U, Meier W, Sadanandan R, et al. Experimental Study of Industrial Gas Turbine Flames Including Quantification of Pressure Influence on Flow Field, Fuel/Air Premixing and Flame Shape[J]. Combustion and Flame, 2013, 160: 2103-2118. DOI:10.1016/j.combustflame.2013.04.005
(  0) 0) |
| [13] |
Bulat G, Jones W P, Marquis A J. NO and CO Formation in an Industrial Gas-Turbine Combustion Chamber Using LES with the Eulerian Sub-Grid PDF Method[J]. Combustion and Flame, 2014, 161(7): 1804-1825. DOI:10.1016/j.combustflame.2013.12.028
(  0) 0) |
| [14] |
Bulat G, Jones W P, Marquis A J. Large Eddy Simulation of an Industrial Gas-Turbine Combustion Chamber Using the Sub-Grid PDF Method[J]. Proceedings of the Combustion Institute, 2013, 34(2): 3155-3164. DOI:10.1016/j.proci.2012.07.031
(  0) 0) |
| [15] |
Gicquel L Y M, Staffelbach G, Poinsot T. Large Eddy Simulations of Gaseous Flames in Gas Turbine Combustion Chambers[J]. Progress in Energy and Combustion Science, 2012, 38(6): 782-817. DOI:10.1016/j.pecs.2012.04.004
(  0) 0) |
| [16] |
Syred N. A Review of Oscillation Mechanisms and the Role of the Precessing Vortex Core (PVC) in Swirl Combustion Systems[J]. Progress in Energy and Combustion Science, 2006, 32(2): 93-161. DOI:10.1016/j.pecs.2005.10.002
(  0) 0) |
| [17] |
Kexin Liu, Victoria Sanderson. The Influence of Changes in Fuel Calorific Value to Combustion Performance for Siemens SGT-300 Dry Low Emission Combustion System[J]. Fuel, 2013, 103: 239-246. DOI:10.1016/j.fuel.2012.07.068
(  0) 0) |
| [18] |
Stöhr M, Boxx I, Carter C D, et al. Experimental Study of Vortex-Flame Interaction in a Gas Turbine Model Combustor[J]. Combustion and Flame, 2012, 159(8): 2636-2649. DOI:10.1016/j.combustflame.2012.03.020
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

