现代高性能的燃气涡轮发动机中, 燃烧室出口的温度日渐提高, 涡轮叶片的热防护问题也越来越严峻。目前, 涡轮转子叶片的冷却技术大致可分为两大类:用来阻隔高温燃气与叶片表面换热的外部冷却措施, 以及用来强化冷却空气与叶片内表面换热的内部冷却措施[1]。在叶片外部, 主要采用气膜冷却和隔热涂层等技术。而在叶片内部, 在不同的位置采用不同但有效的冷却形式[2, 3]。叶片前缘的高热负荷要求具有最强的冷却措施, 一般采用具有很高冷却效率的冲击冷却结构; 叶片中部通常采用带肋片扰流的蛇形冷却通道以增加换热面积; 叶片尾缘区域由于扁平结构及有限的内部空间, 一般采用柱肋冷却结构, 既可以加强通道换热, 同时可有效提高此区域的支撑强度。近些年, 关于旋转叶片内部冷却技术的研究在国内外已有一定的讨论和总结[4, 5]。他们认为涡轮叶片的冷却问题是制约发动机性能提升的重要因素, 有必要在更大参数范围进行实验和数值计算研究。
涡轮叶片中部的内部冷却通道一般被简化为旋转的矩形通道。在叶片中部靠近尾缘区域, 由于叶片外形限制而呈现展向扁平化, 一般具有较大的宽高比(AR≥4)。在旋转大宽高比矩形通道的冷却研究中, Griffith等[6, 7](Ro≤0.3)采用铜块加热法研究了带45°肋和凹槽强化换热的AR=4矩形通道下的换热特性。研究发现大宽高比的窄通道换热要强于方通道和AR=2矩形通道, 且后缘面换热受旋转数的影响强于前缘面。随后, Wright等[8, 9](Ro≤0.3)比较了肋的布置形式及通道入口的几何形式对AR=4通道内换热分布的影响。他们发现入口突扩会导致入口段3~4倍水力直径范围内有更高的换热系数, 同时旋转会削弱这种入口效应的影响。Zhou等[10] (Ro≤0.6)研究了AR=4光滑矩形通道内的换热特性。通过与方通道的换热特性比较, 他们发现旋转在低雷诺数下对换热有增强效应。Huh和Lei等[11, 12]对AR=2:1通道在大旋转数下进行了肋间距及传热特性的研究, 并总结了换热系数与旋转数及浮力数之间的影响关系。在带肋通道中, 赵曙等[13]和陈豪等[14]研究了旋转对通道内换热的影响, 结果表明在带肋通道中旋转的影响被削弱。
虽然旋转大宽高比通道已有一定的研究, 但其展向换热特性在大旋转数下表现出更多的差异特性, 在大旋转数下展向与流向的换热特性仍有待进一步研究。本文针对宽高比为AR=4的光滑矩形通道, 通过旋转高压实验技术[15, 16], 扩大实验旋转数至1.23, 研究不同雷诺数、不同转速下大宽高比通道内的换热特性。大旋转数下换热的研究有利于发动机设计人员在更大范围内选择设计优化空间, 并为地面燃气轮机的旋转换热提供一定的参考。
2 实验设备及实验模型 2.1 旋转换热实验平台旋转换热实验平台结构如图 1所示, 包含动力模块、流路模块、实验件模块及数采模块。实验台动力通过一台大功率电机提供旋转动力, 并通过电控程序调节转速。流路模块包含高压气源、双通道动静转换接头及轴心的软管通道。高压冷气经过过滤和稳压之后流经热式质量流量计实时采集, 通过旋转接头入流端流进轴心的进气软管, 再连接实验件的入口端。实验件的出口端连接轴心的出气软管, 出口空气通过旋转接头出流端接入出口背压调节阀, 最终排入大气中。实验件放置在旋转臂上, 并在旋转臂的另一端放置配重块。实验件中的加热电流和数采模块用电由直流稳压电源提供, 经滑环引电器接入。实验所测试的温度数据在旋转模块的恒温腔中经数采系统转化为数字信号后, 由滑环引电器引出并传送到计算机中进行处理, 最终获得通道内的温度分布及换热系数分布。
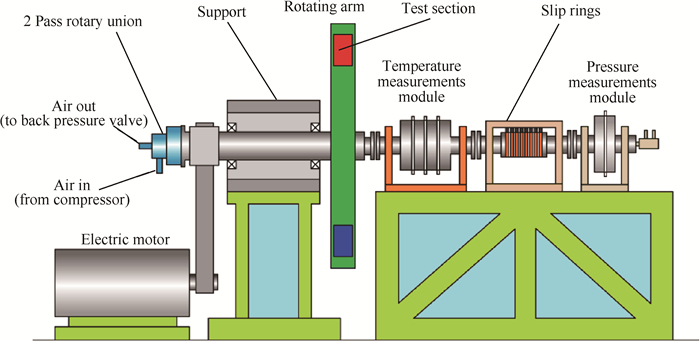
|
Fig. 1 Rotating facility |
如图 2所示, 实验模型为双流程的矩形光滑冷却通道, 矩形通道的第一流程截面为54mm×13mm的加热通道(宽高比AR≈4:1), 第二流程截面为10mm×20mm的非加热出流通道。两个通道连接孔(转弯段)为22mm×13mm的矩形短通道。第一流程通道的水力直径为20.9mm, 两个长边所对应的面为加热面, 两个短边对应的面为非加热面。加热面通过24(8×3)个22mm×16mm光滑壁面紫铜块与绝缘骨架拼接而成。通道的加热段长度为230mm, 加热段入口处距离旋转轴心为350mm, 因此通道平均旋转半径与水力直径的比值为22.2。在加热段之前设置有63mm长度的矩形截面的非加热段, 该矩形截面为34.5mm×13mm, 在加热段入口形成一定的流动突扩效应。

|
Fig. 2 Schematic of test model (mm) |
在通道的流向方向, 根据铜块测点位置, 约定为P1~P8等8个位置, 其对应的无量纲位置参数为X/Dh=0.8~10.2;在展向方向, 根据铜块位置分为内侧(Inner)、中部(Mid-span)及外侧(Outer)等三个区域。通道安装角度定义为该双流程通道对称截面与旋转前进方向之间的夹角, 为了更直观地观察旋转效应, 本文中实验的通道安装角度均为β=90°。
2.3 实验方法本实验的加热方式为电热膜(由镍铬电阻丝制成)加热, 通过绝缘导热硅胶将电热膜粘贴在铜块背面, 并在加热膜背面的铜块凹槽内填满绝热材料。由于每个铜块背面的加热膜的电阻值偏差很小(8Ω±0.2Ω), 且采用串联加热方式, 故本实验的加热壁面条件近似为等热流边界。在铜块背面凸台设有直径1.2mm的盲孔, 孔内填充绝缘导热硅脂, 并在孔内埋设热电偶用以测温。由于紫铜的导热系数很高, 热电偶所测温度可视为测点位置处壁面的平均温度, 实验测试方法介绍参考文献[14, 15]。
局部热损失测试实验在气体流量为零, 通道内塞满绝热岩棉的条件下进行。依据不同加热量及转速下的实验数据, 得到相应实验工况下各铜块的热损失系数, 用于热损失修正。由于提高通道内压力可以在不降低雷诺数的情况下达到高旋转数, 使得通道热损失占总加热量的比例大大降低, 在本文所有实验工况中最大不超过18%。
3 数据处理方法 3.1 无量纲参数计算在旋转通道中, 等角速度旋转坐标系下的流体湍流控制方程组在文献[17, 18]中已有详细的推导和讨论, 本文在此不再赘述。本文采用局部平均的无量纲换热Nu数描述通道内的换热特性
| $ Nu = \frac{{h{D_{\rm{h}}}}}{\lambda } = \frac{{{Q_{{\rm{net}}}}}}{{{A_{{\rm{Cu}}}}\left( {{T_{\rm{w}}}-{T_{\rm{b}}}} \right)}}\frac{{{D_{\rm{h}}}}}{\lambda } $ | (1) |
式中Tw为通道局部平均壁温, Tb为通道径向流通截面的局部主流平均温度, Dh为通道的水力直径, ACu为通道壁面铜块的换热面积, h为壁面对流换热系数, Qnet为铜块壁面的净换热热流, 由电热膜加热功率减去估算的铜块热损失获得。
局部主流平均温度采用能量平衡法计算
| $ {T_{\rm{b}}} = {T_{{\rm{in}}}} + \frac{{\sum {{Q_{{\rm{net}}}}} }}{{\dot m{C_p}}} $ | (2) |
式中Tin为通道进口冷气温度,
在旋转的对流换热通道中, 通常采用雷诺数Re和旋转数Ro分别描述其流动与旋转的影响, 采用平均温比TR表征壁面的加热强度。文中这三个工况参数均定义在加热段通道的进口截面(即X=0位置)。
| $ \mathit{Re = }\frac{{{\rho _{{\rm{in}}}}{U_{{\rm{in}}}}{D_{\rm{h}}}}}{\mu } $ | (3) |
| $ Ro = \frac{{\mathit\Omega {D_{\rm{h}}}}}{{{U_{{\rm{in}}}}}} $ | (4) |
| $ TR = \frac{{{{\bar T}_{\rm{w}}}-{T_{{\rm{in}}}}}}{{{{\bar T}_{\rm{w}}}}} $ | (5) |
式中Uin为加热段通道进口截面处的流体平均速度, Ω为通道的旋转角速度, Tw为通道的整体平均壁温。
在换热结果的讨论中, 通常采用充分发展光滑圆管的换热经验关系式对Nu数进一步无量纲化(Nu/Nu0)或者Nu数的转静比(Nu/Nus)
| $ \frac{{Nu}}{{N{u_0}}} = \frac{{Nu}}{{0.023\mathit{R}{\mathit{e}^{0.8}}\mathit{P}{\mathit{r}^{0.4}}}} $ | (6) |
通过误差传递原理[19]计算可得, 不同实验工况下雷诺数的最大相对误差为±2.20%, 旋转数最大相对误差为±3.4%。局部努塞尔数误差在不同实验工况下和不同通道位置处有明显差异, 在Re=2×104时, 通道局部努塞尔数相对误差不超过±9%;在Re=1×104时, 通道局部努塞尔数的相对误差最大不超过±16%。
3.3 实验工况范围真实发动机工作工况范围为Re=1×104~5×104, Ro=0.1~0.4[1]。本实验为了尽量覆盖该范围采用了高压旋转测试技术。通过提高旋转通道内气体压力, 在通道流量和水力直径不变(即雷诺数不变)的条件下, 由于气体密度随着压力的提高而增大, 气流速度相应地降低; 在转速一定的情况下, 导致旋转数增大, 从而可以在不降低雷诺数和增加转速的情况下达到较高的旋转数, 实现高雷诺数和匹配的高旋转数。根据旋转通道下的相似理论应用[20], 在实验中保证了旋转通道内主要的三个无量纲参数(Re, Ro, TR)即可保证较好的换热结果匹配, 本实验工况如表 1所示。值得注意的是本实验的Ro数最大达到1.23, 可在更大范围内提供旋转换热的实验数据参考。
|
|
Table 1 Boundary and test conditions |
在静止通道的内换热中, Re数通常起着主导作用。但在旋转通道中, Ro数的影响不可忽略, 甚至在大旋转数下起着重要的作用。Ro数是衡量哥氏力与惯性力的强弱对比。哥氏力的引入导致了径向出流通道后缘面附近的流体流速增大, 同时截面二次流的冷流体冲击后缘面, 两者共同作用导致了后缘面换热相比于静止情况大幅增强; 而前缘面的情况正好相反, 换热受到削弱。但在大旋转数下, 受到强哥氏力和浮升力耦合的影响, 前缘面附近的流体可能会出现逆流现象, 从而使得前缘面的换热反而获得强化。
4.1 旋转对通道沿程换热分布的影响 4.1.1 通道沿程换热分布图 3给出了Re=2×104时转速从0r/min到800r/min四个转速工况下的通道沿程Nu/Nu0分布。在静止情况下(0r/min), 该矩形通道具有明显的展向和流向换热分布不均。内侧区域在入口段换热最强, 沿程不断下降, 到通道顶部区域换热为展向最弱; 而外侧区域则刚好相反, 在入口段换热最差, 沿程换热不断增强, 到顶部出流孔附近换热达到展向最强; 中部区域换热水平介于这两者之间, 其换热先小幅下降后上升。同时, 由于几何结构上的对称性, 静止情况下的前后缘面换热基本相同。这种展向之间的换热分布与突扩进口及顶部侧向出流的流动结构息息相关。在通道入口段附近, 外侧区域会形成一个台阶后驻涡, 流动强度最弱, 故换热最低。在通道顶部出流段, 流动在内侧会形成滞止涡, 造成内侧区域的冷却不足, 故内侧壁面换热下降。同时, 由于展向内外侧沿程换热趋势相反, 在靠近出流孔位置(P7, X/Dh=8.9), 观察到一个展向的换热交叉点。在该位置附近, 流动横截面的速度型近似展向分布对称, 故该位置展向换热差异最小。

|
Fig. 3 Channel Nu/Nu0 distribution for 0~800r/min cases (Re=2×104) |
旋转情况下, 当Ro数较小时(如Ro= 0.15), 后缘面换热普遍强于前缘面换热, 在出流孔附近换热均大幅增强。后缘面展向三个区域换热差异明显, 内侧区域仍为整个通道的最高换热水平, 中部区域换热与之接近; 而前缘面展向换热差异大幅减小, 中部区域换热水平与外侧区域相近, 为整个通道的最低换热水平。在较大旋转数下(如Ro≥0.60), 前后缘换热差异进一步扩大。对于后缘面, 通道中段展向换热差异相比小旋转数扩大; 而前缘面的通道中段展向之间的换热差异进一步缩小, 处于整个通道的最低换热水平。
4.1.2 通道不同展向位置的沿程换热分布为了进一步观察旋转对于通道内展向和流动的换热影响, 图 4给出多个旋转数下在同一个展向位置处的沿程Nu/Nu0分布。图中可以清楚地观察到, 随着Ro数的增大, 前后缘面不同展向位置受到旋转的影响各不相同。对于后缘面, 旋转数越大, 三个展向位置的沿程换热均越来越强。而旋转对于前缘面的影响则较为复杂:在展向外侧区域, 旋转小幅强化了该区沿程换热水平; 而旋转在中部区域的影响非常有限, 换热水平与静止情况下相近; 内侧区域所受的影响最为复杂, 旋转削弱了通道入口段及中段的换热水平, 但出流段附近的换热受旋转的影响明显增强。
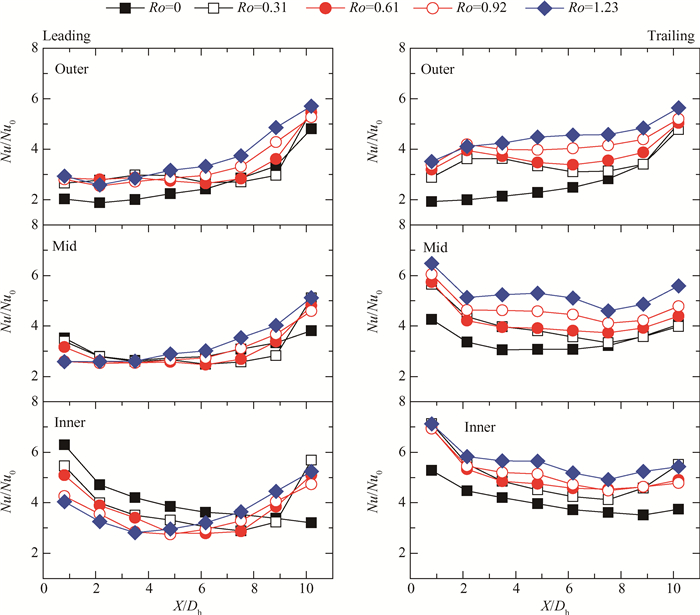
|
Fig. 4 Nu/Nu0 distribution for different span-wise locations (Re=1×104) |
同时, 旋转对于前缘面和后缘面外侧区域的沿程方向影响差异颇大。在外侧区域的入口段(X/Dh < 4), 旋转数的小幅增大导致换热大幅增强, 增幅可达50%~90%, 而继续增大旋转数则换热水平上升有限。这是由于该区域处于通道入口突扩段, 旋转的引入优化了该区域的流动, 但哥氏力的增强并未进一步强化该区域的流动强度。在外侧区域的沿程中段及出流段, 旋转的影响则随着旋转数的增大稳步提升, 增幅在20%~50%。
4.2 大旋转数下通道各点的换热特性 4.2.1 通道外侧旋转的通道内换热的影响是通过在旋转中引入的旋转哥氏力对流动的影响来实现的。但在大宽高比的通道内不同展向和流向位置处所受到的哥氏力强度并不一样, 因此有必要对各个局部位置的换热展开更加详细的分析。局部点换热的旋转数效应一般通过Nu数的转静比(Nu/Nus)来观察。图 5给出了通道展向外侧区域的沿程8个无量纲位置处Nu/Nus与旋转数的关系。
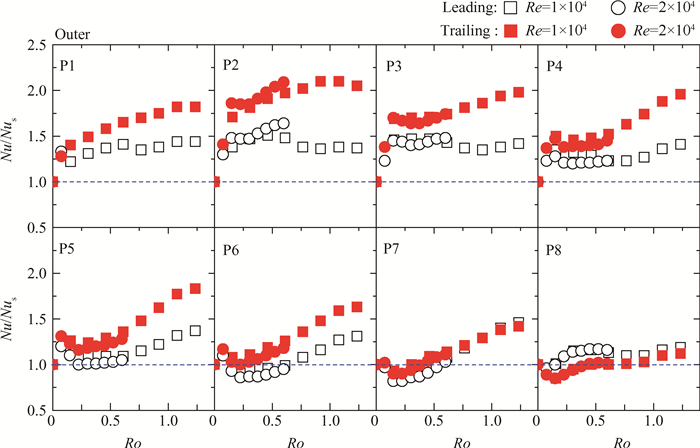
|
Fig. 5 Regional Nu/Nus distributions for outer section |
在通道入口段区域(P1~P3), 旋转数的影响如沿程观察的趋势一致:在Ro数从0到0.2的增大过程中, 该区域的前后缘换热急剧增大50%~80%;在Ro数超过0.2以后, 其换热则增幅缓慢。这说明通道突扩段之后的流动死区在低旋转数下对旋转极为敏感, 但高旋转数下所受影响有限。在通道中段区域(P4~P6), 旋转数的影响与入口段有所不同:小旋转数下换热急速上升, 但随着Ro数增大换热略有下降, 且越往下游方向该下降幅度越大; 随着Ro数进一步增大, 换热开始明显增强, 局部换热强化可达40%~100%。通道出流段(P7~P8)受到出流效应的强烈影响, 旋转对于该区域的影响相对最弱, 且该区域的前后缘换热差异相比通道内其他区域最小。
4.2.2 通道中部通道展向中部的换热趋势在一定程度上反应了通道的平均换热水平。如图 6所示, 旋转对于中部区域换热的影响与常规的方通道相近:旋转强化了后缘面的换热, 而削弱了前缘面的换热。由于通道的大宽高比结构, 哥氏力的作用流程相对较短, 前后缘面之间的冷热流体对流强度较弱。因此, 对于后缘面的换热强化程度, 最高在50%~70%;对于前缘面的换热削弱程度, 最大在20%左右, 所受的旋转效应相比方形通道小[16, 21]。另外一方面, 由于旋转对于中部区域的前后缘面换热截然不同的影响, 其前后缘面的换热差异也是随之扩大。

|
Fig. 6 Regional Nu/Nus distributions for Mid-span section |
在沿程的不同位置, 旋转的影响也略有不同。除了靠近通道入口位置处(P1), 通道的入口段和中段(P2~P6), 前缘面和后缘面的换热随着Ro的增大, 经历了先下降后上升的趋势, 且两个面的趋势大致相同。同时, 两个面具有相同的转折点(即临界旋转数), 且该转折点随着流向位置的增大而减小。在通道出流段(P7~P8), 该区的流动受到强烈的出流效应的主导作用, 旋转效应大幅削弱。
4.2.3 通道内侧受旋转的影响, 内侧区域前后缘换热差异最大。旋转对后缘面换热表现出明显的积极影响, 而对前缘面换热则是明显弱化作用, 如图 7所示。在后缘面的入口段(P1~P3), 旋转对换热的影响与中部区域一样, 在较大Ro数下, 换热随着Ro的增大而先减小后增大。而前缘面换热则随着Ro数的增大呈现减弱的趋势, 最大削弱幅度可达40%。在通道中段(P4~P6), 后缘面换热随着Ro数的增大而单调增强, 不再有减弱的趋势, 但最大的增强幅度为50%左右。在前缘面观察到明显的临界旋转数, 这与中部区域的趋势一样。当Ro小于临界旋转数时, Nu/Nus随着Ro数的增大而减小; 当Ro大于该临界值时, 则刚好相反, Nu/Nus不断增大。在流向上, 该临界旋转数随着X/Dh的增大而减小, 这与方通道中观察的现象一致。在通道出流段(P7~P8), 由于该区域在静止情况下存在一个滞止涡, 而旋转情况下反而会压缩该滞止涡的影响范围, 故旋转在该区域的影响反而相比中部和外侧区域要强一些。
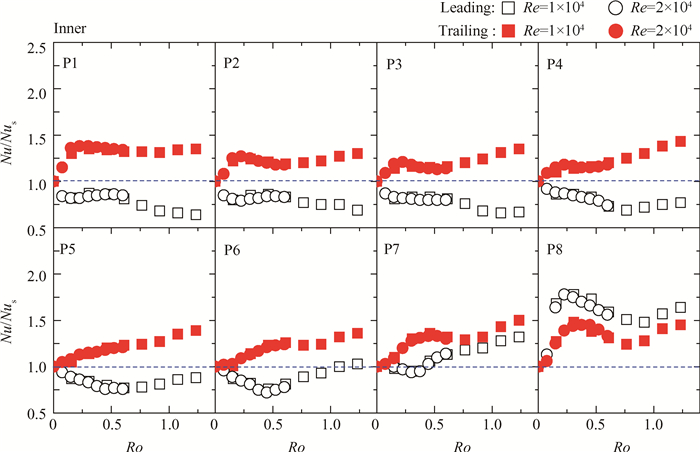
|
Fig. 7 Regional Nu/Nus distributions for inner section |
通过上述的局部换热分析, 在展向不同位置处, 旋转的效应差别很大。因此, 通过对展向三个位置的换热Nu/Nus进行平均, 可以观察旋转对于流向不同位置的前后缘换热的影响, 如图 8所示。对于后缘面, 随着Ro数增大, 沿程换热的增强幅度下降。如在入口段(P1~P3), 低旋转数下(Ro>0.2)的平均换热强度即可达静止状态下的1.5倍以上; 而在通道中下游, 仅在高旋转数下(Ro>1.0)的旋转换热强度较大。对于前缘面, 旋转对于展向不同位置处的换热有增强作用(外侧), 也有削弱作用(中部与内侧)。但对其平均影响, 通道沿程的前半段的Nu/Nus基本上处于1.0左右水平, 即与静止情况的平均换热水平相当。这说明旋转改变了前缘面展向不同位置处的换热分布, 但对其平均换热水平影响不大。而对于通道的后半段, 随着旋转数的增大, 前缘面的换热则表现出典型的先减弱后增强的换热趋势, 但增强减弱的幅度相比方通道要小得多。在通道出流段附近, 旋转对于平均换热起着积极的作用, 主要是由于旋转压缩了该区域的滞止涡, 改善了当地的流动, 故而改善了换热。
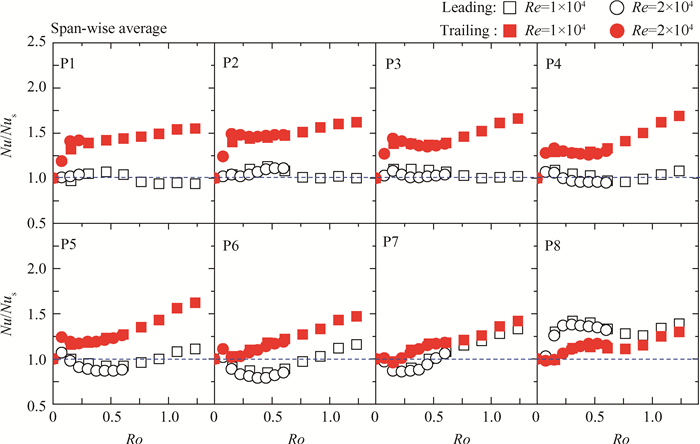
|
Fig. 8 Span-wise average Nu/Nus distributions |
另一方面, 虽然旋转对于通道沿程不同位置的影响差别大, 但展向三个位置的不同影响也可以通过流向换热的平均来观察, 如图 9所示。由于外侧区域在入口段受到突扩的影响, 出口段受到出流效应的影响, 旋转的引入显著改善了这两处的换热。因此对于整个外侧区域, 无论是前缘面还是后缘面, 旋转都起到了增强换热的作用。但是哥氏力引起的二次流作用依然存在, 旋转对于外侧后缘面的增强作用强于前缘面。旋转对于中部及内侧区域的影响趋势相近, 是典型地强化后缘面换热, 而削弱前缘面换热。在低旋转数和大旋转数下, 旋转对于中部后缘面的作用更强。
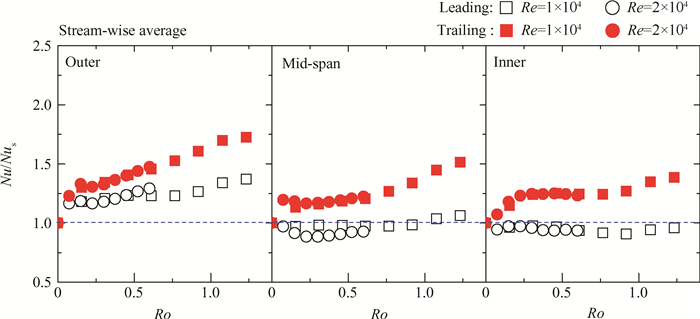
|
Fig. 9 Stream-wise average Nu/Nus distributions |
本文针对AR=4:1矩形通道实验模型, 通过旋转高压技术提高旋转数, 在Re=1×104~2×104, Ro=0~1.23内研究了大宽高比矩形通道的换热特性, 结论如下:
(1) 静止下的大宽高比通道表现出非常强的展向换热不均, 内侧换热沿程下降, 外侧换热沿程增强, 但旋转的引入大幅削弱了这种展向换热差异, 对低半径区的外侧换热可提高50%~90%。
(2) 旋转同时强化外侧区域前缘面和后缘面换热, 但在较小旋转数下会削弱中部及内侧区域前缘面的换热, 且在通道中段位置存在一个对应最低换热值的临界旋转数(Roc=0.2~ 0.5)。
(3) 高旋转数下(Ro≥0.6), 除内侧区域前缘面外, 通道其他位置处的前缘面和后缘面换热均受到强化和改善, 最高可达静止的2倍水平。
(4) 旋转下的通道前半段的前缘面展向平均换热与静止情况相当, 而前缘面后半段则随旋转数增大先减弱后增强。流向平均下, 旋转显著改善了的外侧前后缘面换热, 最高强化幅度可达70%以上。
| [1] |
Han J C. Fundamental Gas Turbine Heat Transfer[J]. Journal of Thermal Science and Engineering Applications, 2013, 5(2).
(  0) 0) |
| [2] |
阚瑞, 迟重然, 杨力, 等. 燃气轮机高温叶片内部冷却技术概述[J]. 热力透平, 2013, 42(4): 260-264. (  0) 0) |
| [3] |
刘钊, 杨星, 丰镇平. 燃气轮机透平叶片传热和冷却研究:内部冷却[J]. 热力透平, 2013, 42(4): 265-275. (  0) 0) |
| [4] |
倪萌, 朱惠人, 裘云, 等. 航空发动机涡轮叶片冷却技术综述[J]. 燃气轮机技术, 2006, 18(4): 25-33. (  0) 0) |
| [5] |
Han J C. Turbine Blade Cooling Studies at Texas A & M University:1980-2004[J]. Journal of Thermophysics and Heat Transfer, 2006, 20(2): 161-187. DOI:10.2514/1.15403
(  0) 0) |
| [6] |
Griffith T S, Al-Hadhrami L, Han J C. Heat Transfer in Rotating Rectangular Cooling Channels (AR=4) with Angled Ribs[J]. Journal of Heat Transfer, 2002, 124(4): 617-625. DOI:10.1115/1.1471525
(  0) 0) |
| [7] |
Griffith T S, Al-Hadhrami L, Han J C. Heat Transfer in Rotating Rectangular Cooling Channels (AR=4) with Dimples[J]. Journal of Turbomachinery, 2003, 125(3): 555-563. DOI:10.1115/1.1571850
(  0) 0) |
| [8] |
Wright L M, Fu W L, Han J C. Thermal Performance of Angled, V-shaped, and W-Shaped Rib Turbulators in Rotating Rectangular Cooling Channels (AR=4: 1)[R]. ASME 2004-GT-885.
(  0) 0) |
| [9] |
Wright L M, Fu W L, Han J C. Influence of Entrance Geometry on Heat Transfer in Rotating Rectangular Cooling Channels (AR=4:1) with Angled Ribs[J]. Journal of Heat Transfer, 2005, 127(4): 378-387. DOI:10.1115/1.1860564
(  0) 0) |
| [10] |
Zhou F, Lagrone J, Acharya S. Internal Cooling in 4:1 AR Passages at High Rotation Numbers[J]. Journal of Heat Transfer, 2007, 129(12): 1666-1675. DOI:10.1115/1.2767676
(  0) 0) |
| [11] |
Huh M, Lei J, Liu Y H, et al. High Rotation Number Effects on Heat Transfer in a Rectangular (AR=2:1) Two-Pass Channel[J]. Journal of Turbomachinery, 2011, 133.
(  0) 0) |
| [12] |
Lei J, Huh M, Han J C. Effect of Rib Spacing on Heat Transfer in a Two Pass Rectangular Channel (AR=2:1) at High Rotation Numbers[J]. Journal of Heat Transfer, 2012, 134(9): 1-9.
(  0) 0) |
| [13] |
赵曙, 朱惠人, 郭涛, 等. 旋转带肋回转通道换热实验研究[J]. 推进技术, 2015, 36(6): 899-906. (ZHAO Shu, ZHU Hui-ren, GUO Tao, et al. Experimental Investigation of Heat Transfer for Rotating Internal Cooling Channels with Rib Turbulators[J]. Journal of Propulsion Technology, 2015, 36(6): 899-906.)
(  0) 0) |
| [14] |
陈豪, 邓宏武, 李洋, 等. 高旋转数下45°斜肋回转通道平均换热特性研究[J]. 推进技术, 2015, 36(9): 1339-1346. (CHEN Hao, DENG Hong-wu, LI Yang, et al. Heat Transfer in Rotating Two-Pass Square Duct with 45° Ribbed Walls under High Rotation Numbers[J]. Journal of Propulsion Technology, 2015, 36(9): 1339-1346.)
(  0) 0) |
| [15] |
程俊华, 倪彬, 邓宏武, 等. 高旋转数内冷通道换热实验技术及验证[J]. 航空动力学报, 2014, 29(8): 1817-1823. (  0) 0) |
| [16] |
邓宏武, 程俊华, 陈豪, 等. 高旋转数下光滑回转通道的换热特性[J]. 北京航空航天大学学报, 2014, 40(5): 701-706. (  0) 0) |
| [17] |
Dutta S, Andrews M J, Han J C. Prediction of Turbulent Heat Transfer in Rotating Smooth Square Ducts[J]. International Journal of Heat and Mass Transfer, 1996, 39(12): 2505-2514. DOI:10.1016/0017-9310(95)00319-3
(  0) 0) |
| [18] |
曹玉璋, 陶智, 徐国强, 等. 航空发动机传热学[M]. 北京: 北京航空航天大学出版社, 2005.
(  0) 0) |
| [19] |
Moffat R J. Describing the Uncertainties in Experimental Results[J]. Experimental Thermal and Fluid Science, 1988, 1(1): 3-17. DOI:10.1016/0894-1777(88)90043-X
(  0) 0) |
| [20] |
Xu G, Li Y, Deng H, et al. The Application of Similarity Theory for Heat Transfer Investigation in Rotational Internal Cooling Channel[J]. International Journal of Heat and Mass Transfer, 2015, 85(1): 98-109.
(  0) 0) |
| [21] |
Deng H, Qiu L, Tao Z, et al. Heat Transfer Study in Rotating Smooth Square U-Duct at High Rotation Numbers[J]. International Journal of Heat and Mass Transfer, 2013, 66: 733-744. DOI:10.1016/j.ijheatmasstransfer.2013.07.080
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

