现代燃气涡轮入口温度不断提高, 使得高压涡轮工作环境更加恶劣, 对动叶叶顶采用恰当的结构或冷却方式能够有效控制泄漏流动并改善换热。涡轮凹槽叶顶是控制间隙泄漏流动的典型方式, 针对叶顶凹槽间隙气膜冷却进行传热机理研究, 探讨影响传热效果的冷却参数的合理设定, 对改善叶顶冷却效率具有十分重要的意义。
早期Metzger[1]通过实验研究了壁面静止的平面间隙和凹槽间隙内部换热情况, 发现凹槽深度与宽度比, 间隙尺寸与宽度比会对壁面Nu数产生较大影响。Goldstein等[2~4]对主流与冷气动量比和密度比、主流Re数、冷气吹风比、冷却孔形状和角度对气膜冷却的影响展开了大量研究, 验证了气膜冷却参数对传热效果有较大的影响。Kim等[5]提出了四种叶顶不同气膜冷却模型, 并展开了相应的实验研究发现, 吹风比对不同模型产生较大影响, 吹风比提高能有效提高平面叶顶圆柱孔的气膜冷却效率, 降低了压力侧孔的气膜冷却效率; 对凹槽叶顶气膜冷却角度等参数对换热的影响并未考虑。Wang等[6]对跨声速条件平面及凹槽间隙冷气喷射对泄漏流动分析表明, 平面叶顶冷气喷射对泄漏流控制作用优于凹槽冷气喷射, 但未对凹槽间隙模型换热进行详细分析。虞跨海等[7]研究了叶顶结构和叶顶间隙对涡轮气动和传热的影响, 在相同间隙条件下, 凹槽射流叶片能够获得最佳的气动性能和较低的叶顶温度。Ma等[8]研究表明, 叶顶泄漏流和叶顶冷却气体相互作用会对叶顶换热产生较大影响。Zhou等[9]对跨声速平面和凹槽叶顶气膜冷却的气热性能分析表明, 凹槽叶顶气膜冷却能够获得较平面叶顶更高的冷却效率, 并降低凹槽叶顶热负荷。平面叶顶中, 泄漏流体在叶顶压力侧出现分离及再附, 泄漏流动再附使得叶顶换热系数显著增加。周凯等[10]对跨声速平面叶顶气膜冷却进行研究, 大部分冷却气体随间隙流向下游, 使得叶顶气膜冷却表现并不理想。Newton等[11]对叶栅平面叶顶气膜冷却换热进行研究发现, 叶顶靠近压力侧泄漏流再附区域换热系数最大, 并研究了不同冷却孔位置对换热的影响, 发现冷气孔布置在叶顶再附区上游的分离泡区域时, 冷却气体能有效覆盖在叶顶表面, 减少叶顶热流量。
对凹槽叶顶, 特别是在靠近前缘部分, 叶片厚度相对较大, 凹槽底面会受到泄漏流冲击导致局部换热系数过高[9, 12, 13], 因此该区域承受的温度往往相对较高。Yang等[12]研究了凹槽叶顶底面受到冲击时, 冷气孔布置对凹槽叶顶气膜冷却性能的影响, 将冷气孔布置在附着线上时, 气膜冷却效率最大, 将冷气孔布置在附着线靠压力侧位置时冷气覆盖更加均匀。李军等[14]采用数值计算, 进一步研究了GE E3动叶凹槽叶顶气膜冷却孔布置在凹槽底面再附线上的非定常气膜冷却性能, 并研究了吹风比对叶顶气膜冷却性能的影响, 随着吹风比增加, 气膜冷却效率先增加, 当吹风比过大时, 冷气脱离凹槽底面, 气膜冷却效率迅速降低。Arisi等[15]对两种出口Ma数的跨声速叶栅肋条叶顶气膜冷却展开试验和数值研究, 肋条叶顶峰值换热区域位于受泄漏流冲击的凹槽底面, 随着出口Ma数增加, 冲击区域换热系数增大, 凹槽内部漩涡强度增加使得气膜冷却效率下降。随着凹槽叶顶几何结构的变化及受非定常流动的影响, 凹槽底面再附线位置发生变化。对受泄漏流冲击的凹槽间隙模型气膜冷却展开研究, 为凹槽叶尖气膜冷却设计提供参考。此外, 考虑到动叶叶顶换热同时会受固体域导热的影响, 结合流固耦合对叶顶凹槽气膜冷却的综合研究势在必行, 且相关研究工作开展也较少。
本文在以往研究的基础上, 结合三维气热耦合计算, 探讨了凹槽间隙底面受到泄漏流冲击的流动特性, 详细研究了吹风比、冷却孔相对位置和冷却孔角度对凹槽间隙气膜冷却传热的影响, 以实现对涡轮动叶叶顶的高效冷却。
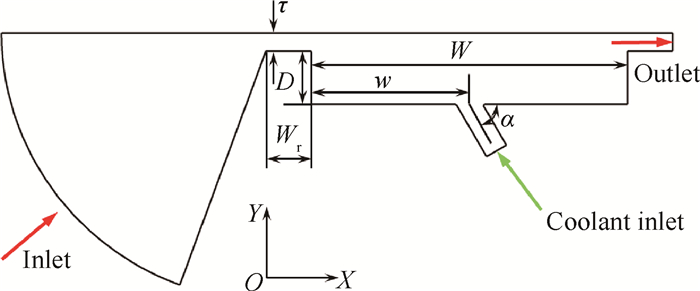
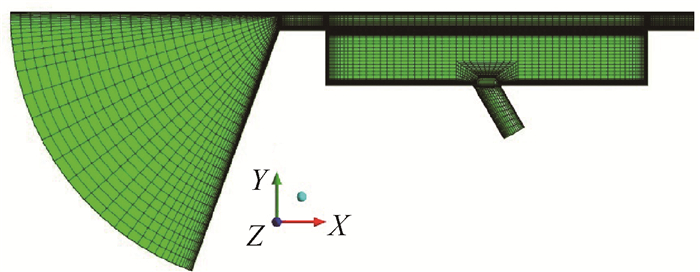
2 计算模型及验证 2.1 凹槽间隙气膜冷却模型研究的凹槽间隙模型如图所示, 间隙尺寸τ, 凹槽深度D, 凹槽宽度W, 肋条宽度Wr, 气膜冷却孔位于凹槽底面并与其成一定角度α, 分析单个气膜孔准三维模型对间隙换热的影响, 具体几何如图 1。图 2所示为计算模型的网格图示, 采用全六面体网格, 并对固体壁面、孔口网格加密。数值验证时单个模型计算网格节点约46万, 网格单元约44万。
|
Fig. 1 Geometric schematic of squealer tip with film cooling |
|
Fig. 2 Computational mesh |
数值模拟计算基于ANSYS CFX 14.5平台, 首先基于Metzger等[1]对未考虑气膜冷却情况的凹槽间隙实验结果, 分别采用SST γ-θ, κ-ω, κ-ε等三种湍流模型进行三维数值模拟计算, 并对数值结果与实验数据进行了对比。图 1中的凹槽几何结构与文献[1]中的实验模型基本结构相同(图 1增加了冷气射流孔), 其中实验模型的几何展向高度为76.2mm, 肋条宽度为9.5mm; 选取具体实验研究的几何结构及边界条件为τ/W=0.10, D/W=0.20, 基于间隙尺寸τ与间隙入口速度的Re=1.5×104, 试验模型入口存在一个70°的楔形角。
图 3对比了凹槽间隙三种湍流模型及实验的Nu分布, 横坐标为壁面沿X方向的无量纲坐标, 壁面Nu的计算公式如(1)所示。计算结果与实验结果的对比情况表明, κ-ε会放大局部位置的湍流强度, 使得数值计算结果偏大。采用SST γ-θ湍流模型得到的数值结果更接近实验Nu数数据点, 即表明该湍流模型能较准确地获得凹槽间隙壁面Nu数分布。因此后续计算均选用SST γ-θ湍流模型, 王志多等[16, 17]的研究也验证了SST γ-θ湍流模型对GE E3动叶叶顶和机匣换热计算的可行性。
| $ Nu = \frac{{{q_{\rm{w}}}\tau }}{{k\left( {{T_{{\rm{in}}}}-{T_{\rm{w}}}} \right)}} $ | (1) |

|
Fig. 3 Comparison of CFD results and test data[1] |
本文主要研究气膜冷却吹风比、冷却孔位置、冷气孔角度对凹槽对叶顶换热特性的影响。表 1和表 2分别展示了气膜冷却参数变化取值和边界条件设置, 其中的吹风比通过改变冷却孔入口速度获得, 文献[13, 18]研究表明壁面相对运动对凹槽叶顶及采用气膜冷却的凹槽状叶顶的泄漏流动及换热影响较大, 而科氏力和离心力对对凹槽叶顶的影响较小, 因此计算域设置成静止, 仅壁面设置一定的速度。采用间隙尺寸τ=0.4mm、凹槽深度D=1.2mm、凹槽宽度W=7mm、肋条宽度1mm、垂直于纸面方向Z厚度5mm, 以近似模拟涡轮叶片几何结构。
|
|
表 1 Various parameter of film cooling in grooved tip |
|
|
Table 2 Boundary condition of film cooling in grooved tip |
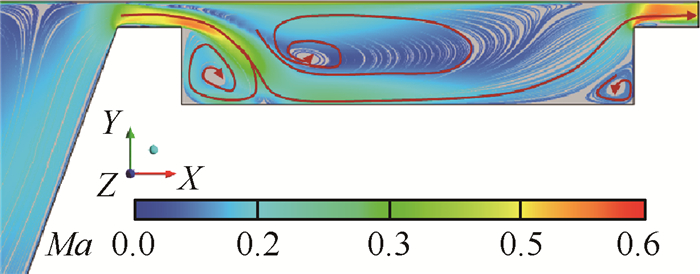
图 4展示了在目前设置边界条件下获得的二维流线图, 从图中可以观察到间隙泄漏流冲击到凹槽底面、并在凹槽内部形成复杂旋涡结构的流动形态, 由于研究模型和数值验证模型几何尺寸发生变化, 对不带冷气孔的数值研究模型进行网格无关性验证, 当网格数大于22万时, 计算结果基本不随网格数变化, 当添加冷却孔后, 网格数略有增加。
|
Fig. 4 2D streamline of squealer tip without film cooling |

|
Fig. 5 Grid independence of Nu number |
图 6给出了在叶顶凹槽底面w/W=0.3位置垂直喷气时, 5种吹风比对凹槽叶顶间隙流动及换热效果的影响, 图 6(a), 6(b), 6(c)分别为吹风比M=0.50, 1.00, 1.50时冷却孔的中分面二维流线、壁面Nu及出口冷气质量分布图, 图 6(d)为第一条肋至出口的凹槽壁面Nu沿Z向平均分布, 其中L表示沿固体壁面流向的长度, 图中虚线区域内表示肋条侧壁面区域。

|
Fig. 6 Effects of blowing ratio on clearance flow and heat transfer in squealer tip |
如图 6(a)所示, 在M=0.50时间隙泄漏流二维流线分布变化不大, 冷却气体在冷却孔出口即被压向两侧, 对冷却孔相同Z向位置第一条肋及下游产生一定冷却效果, 冷却气体随间隙流在第二条肋上方收缩, 收缩位置上下端壁冷却Nu数有所降低。
随着吹风比增加, 间隙泄漏流被冷却气体吹离底面, 并对上壁面产生冲击作用, 同时一部分冷却气体被吹向第一条肋角区, 使得当地的Nu进一步下降, 另一部分冷却气体则直接与间隙泄漏流掺混(如图 6(b))、或在冲击上壁面后与间隙泄漏流掺混(如图 5(c))。冷却气体与泄漏流的直接掺混使得气膜冷却作用效果降低, 且使上端壁产生局部高换热区; 图 6(c)中冷却气体冲击上壁面后与泄漏流掺混使上端壁换热产生明显变化, 在泄漏流冲击位置产局部高Nu区, 而在冷气冲击下游时Nu显著下降。间隙出口冷气质量分布结果显示, 吹风比越大, 出口冷气Z向所占范围越大, 对第二条肋上下壁面Nu越低。
图 6(d)中吹风比增大, 冷却孔上游、第一条肋侧壁面、第二条肋壁面Nu有所下降, 而在冷却孔下游凹槽底面, 除M=1.50外, Nu均有所上升。这表明对于本文所研究条件下的凹槽间隙, 吹风比增加并不一定能降低壁面Nu, 改善换热。
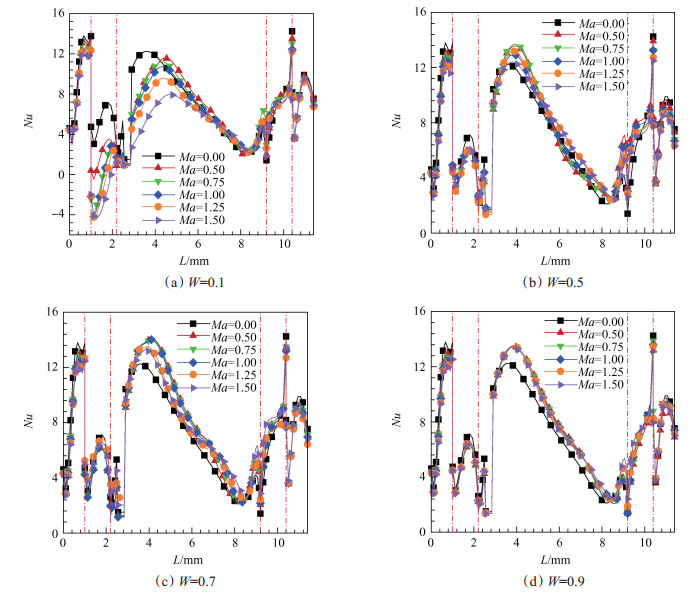
3.2 冷却孔位置对凹槽底面换热的影响由图 7可见, 冷却孔位于凹槽底面冲击位置上游(w/W=0.1)时, 第一条肋侧壁、凹槽底面Nu随吹风比增加显著下降, 在第一条肋侧壁甚至出现Nu为负值, 即气流向壁面传热, 在凹槽底面中部以后, 气膜冷却作用效果下降, 凹槽底面Nu分布趋于均匀。
|
Fig. 7 Effects of hole locations on distribution of Nu |
冷却孔位于凹槽底面冲击位置下游(w/W=0.5, 0.7, 0.9)时, 凹槽底面大部分区域Nu随冷气增加先增大后减小, 但总体上仍大于无气膜冷却(黑色曲线)的条件, 表明冷气并没有有效覆盖凹槽底面、反而增加了对凹槽底面流动的扰动。
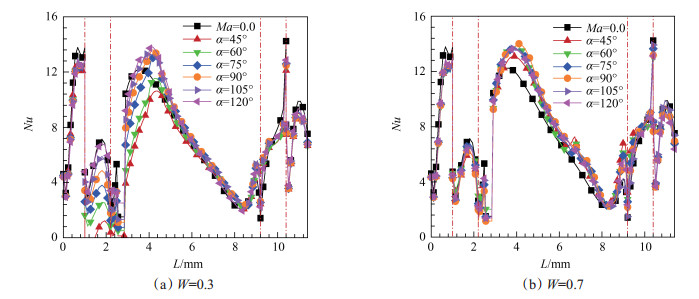
3.3 冷却孔角度对凹槽底面换热的影响图 8为0.3W及0.7W位置的冷却孔角度对壁面Nu分布的影响对比。0.3W冷却孔角度α < 90°时, α越小第一条肋侧壁及冷却孔上游壁面Nu越小, α=45°局部Nu小于0;α>90°时气膜冷却对上述位置仍存在一定冷却效果, 但是导致冷却孔下游Nu显著升高, 两种情况在对下游0.5W位置后Nu的影响均不大。在0.7W冷却孔角度对壁面换热影响均较小, 其总体趋势使得凹槽底面Nu明显增大。
|
Fig. 8 Effects of hole angle on distribution of Nu in grooved tip at 0.3W and 0.7W |
由上述分析可知, 当间隙泄漏流冲击凹槽底面时, 凹槽间隙气膜冷却孔位置及吹风比对凹槽壁面换热产生显著的影响, 当冷却孔位于泄漏流冲击凹槽底面上游时, 冷却孔角度会对凹槽底面换热系数产生显著的影响, 本文所采用的气膜孔布置方法可以为实际凹槽叶顶气膜冷却设计提供参考。
4 凹槽间隙气膜冷却气热耦合计算 4.1 气热耦合计算方案与计算边界为进一步研究三维凹槽叶顶气膜冷却壁面换热的影响, 对E3高压涡轮第一级动叶进行流固耦合分析, 考虑实际实验条件下叶顶凹槽气膜冷却布置的影响, 仅采用简单光滑冷却通道进行分析。分别对四种方案进行研究, 固体域如图 9所示。具体方案说明如表 3所示, 叶顶前缘径向孔表示前缘位置的径向复合冷却孔(蓝色椭圆区域A)。第一条冷却通道复合角度孔, 表示对压力侧肋条和吸力侧肋条进行冲击的冷却孔; 第二条冷却通道径向孔, 为垂直凹槽底面的冷却孔(红色椭圆区域B)。

|
Fig. 9 Schematic of computational geometric model |
|
|
Table 3 Tip cooling schemes |
考虑到几何模型的复杂性, 将几何模型拆分为4部分:主流流体域、第一冷却通道、第二冷却通道, 固体域。对模型进行离散时采用非结构化网格, 主流流体域、第一冷却通道、第二冷却通道流体域采用四面体、六面体、棱柱体混合型网格类型, 流体域固体壁面采用棱柱层模拟附面层流动特性, 其中棱柱层设置13层; 固体域采用四面体和六面体混合网格。总的网格计算单元1420万左右, 计算节点为440万左右, 图 10所示为计算模型的网格图示。

|
Fig. 10 Mesh of computational model |
计算边界条件入口给定总压、总温及湍流度沿叶高分布, 出口给定静压, 冷却通道入口给定总温及流量, 其中四种方案冷气流量均保持不变, 叶片榫头给定第三类边界条件, 即温度和换热系数, 上端壁为绝热边界条件, 计算模型选用SST γ-θ湍流模型。对叶片表面无量纲温度进行分析, 计算公式如(2), 式中Tin, Tw, Tc分别为动叶入口相对总温、壁面温度、冷气入口温度。
| $ \bar T = \frac{{{T_{\rm{w}}}-{T_{\rm{c}}}}}{{{T_{{\rm{in}}}}-{T_{\rm{c}}}}} $ | (2) |
由图 11可见, Case 1方案中叶顶前缘位置没有布置冷却孔, 导致此处无量纲温度超过0.8, 主流燃气泄漏导致压力侧和吸力侧肋条温度均相对较高, 部分冷气从间隙泄漏使得压力侧肋条温度明显低于吸力侧肋条。Case 2在叶片前缘靠近叶顶位置布置三个径向冷却孔, 结果显示叶片前缘位置高温区范围急剧减小, 仅在压力侧肋条前缘位置出现小范围的高温区, 叶顶吸力侧肋条前缘位置温度较低, 吸力侧肋条的中后部温度依旧较高。Case 3在叶顶平面布置与第一条通道和第二条通道相连的冷却孔, 第一条冷却通道冷却孔冲击肋条内侧壁面使得叶顶肋条靠近前缘位置的温度明显降低, 仅在叶顶前缘折转位置无量纲温度相对较高, 叶顶冷气喷射使得压力侧和吸力侧肋条温度均降低, 最大无量纲温度为仅为0.77左右。

|
Fig. 11 Distribution of temperature on blade |
Case 4中同时采用了上述两种方法对叶顶进行冷却, 使得叶顶前缘高温区进一步减小, 但是叶片表面前缘叶顶冷气喷射导致叶顶冷气量减小, 这使得叶顶吸力侧肋条的温度略有上升。结合叶顶凹槽气膜冷却与叶顶前缘径向孔冷却可以实现对叶顶的有效冷却, 使得叶片表面温度更均匀。
用R(T≥T0)表示叶片表面无量纲温度大于T0的面积占整个叶片表面积的百分比函数, 由表 4叶片表面温度参数可见, 在叶顶无冷却时叶片表面最高无量纲温度T达0.868, 当对叶顶进行冷却时, 能够显著降低最大温度, 其中采用Case 4冷却方式时, 最高无量纲温度T仅为0.712, 虽然其叶片表面平均温度未达到最低, 但是其温度分布明显更加均匀, R(T≥0.75)为0, 且R(T≥0.7)仅为0.01%。, 其冷却效果优于其它方案。
|
|
Table 4 Temperature parameters on blade surfaces |
通过本文研究, 得出以下结论:
(1) 凹槽间隙壁面Nu数分布受冷却孔位置影响较大, 冷却孔位于泄漏流冲击凹槽底面上游位置时, 能够有效降低凹槽壁面Nu; 位于冲击位置下游时, 增加了对泄漏流动的扰动使得Nu反而升高。
(2) 吹风比对凹槽间隙换热呈现两种不同的结果, 位于冲击位置上游时, 吹风比增大, 能改善凹槽壁面的换热; 位于冲击位置下游时, 冷气直接或冲击上壁面后与间隙泄漏流掺混均使得换热效果变差。
(3) 冷气充分进入冲击位置上游旋涡时, 能有效覆盖凹槽壁面, 改善叶顶换热; 凹槽间隙气膜冷却中对第二条肋角区位置壁面换热的影响较小。
(4) 对于叶顶前缘及肋条位置的高温区, 仅通过叶顶前缘径向孔冷却无法实现叶顶的有效冷却, 若有效结合叶顶凹槽气膜冷却, 则能够降低叶顶最高温度, 最高无量纲温度仅为0.712, 叶片表面温度更趋均匀。
| [1] |
Metzger D E, Bunker R S, Chyu M K. Cavity Heat Transfer on a Transverse Grooved Wall in a Narrow Flow Channel[J]. Journal of Heat Transfer, 1989, 111(1): 73-79.
(  0) 0) |
| [2] |
Goldstein R J. Film Cooling[J]. Advances in Heat Transfer, 1971, 7: 321-379. DOI:10.1016/S0065-2717(08)70020-0
(  0) 0) |
| [3] |
Goldstein R J, Eckert E R G, Burggraf F. Effects of Hole Geometry and Density on Three-Dimensional Film Cooling[J]. International Journal of Heat and Mass Transfer, 1974, 17(5): 595-607. DOI:10.1016/0017-9310(74)90007-6
(  0) 0) |
| [4] |
Pedersen D R, Eckert E R G, Goldstein R J. Film Cooling with Large Density Differences Between the Mainstream and the Secondary Fluid Measured by the Heat-Mass Transfer Analogy[J]. Journal of Heat Transfer, 1977, 99(4): 620-627. DOI:10.1115/1.3450752
(  0) 0) |
| [5] |
Kim Y W, Metzger D E. Heat Transfer and Effectiveness on Film Cooled Turbine Blade Tip Models[J]. Journal of Turbomachinery, 1995, 117(1): 12-21. DOI:10.1115/1.2835630
(  0) 0) |
| [6] |
Wang Z, Zhang Q, Liu Y, et al. Impact of Cooling Injection on the Transonic Over-Tip Leakage Flow and Squealer Aerothermal Design Optimization[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(6): 062603. DOI:10.1115/1.4029120
(  0) 0) |
| [7] |
虞跨海, 杨茜, 岳珠峰. 高压涡轮冷却叶片叶顶结构气动与传热[J]. 推进技术, 2012, 33(2): 174-178. (YU Kua-hai, YANG Xi, YUE Zhu-feng. Aerodynamic and Heat Transfer of Cooling Blade Tips for High Pressure Turbine[J]. Journal of Propulsion Technology, 2012, 33(2): 174-178.)
(  0) 0) |
| [8] |
Ma H, Zhang Q, He L, et al. Cooling Injection Effect on a Transonic Squealer Tip, Part 2: Analysis of Aerothermal Interaction Physics[R]. ASME GT 2016-57587.
(  0) 0) |
| [9] |
Zhou C. Thermal Performance of Transonic Cooled Tips in a Turbine Cascade[J]. Journal of Propulsion and Power, 2015, 31(5): 1268-1280. DOI:10.2514/1.B35392
(  0) 0) |
| [10] |
周凯, 周超, 钟芳盼. 跨声速叶栅中气膜冷却对平面叶尖流动和传热特性的影响[J]. 航空动力学报, 2013, 28(11): 2440-2447. (  0) 0) |
| [11] |
Newton P J, Lock G D, Krishnababu S K, et al. Aerothermal Investigations of Tip Leakage Flow in Axial Flow Turbines, Part Ⅲ:TIP Cooling[J]. Journal of Turbomachinery, 2008, 131(1): 011008.
(  0) 0) |
| [12] |
Yang D L, Feng Z P, Yu X. Investigation of Film Cooling Effectiveness on Squealer Tip of a Gas Turbine Blade[R]. ASME GT 2009-60280.
(  0) 0) |
| [13] |
杜昆, 宋立明, 李军. 凹槽状叶顶涡轮叶片传热特性的数值研究[J]. 推进技术, 2014, 35(5): 618-623. (DU Kun, SONG Li-ming, LI Jun. Numerical Investigations on Heat Transfer Characteristics of Turbine Blade with Squealer Tip[J]. Journal of Propulsion Technology, 2014, 35(5): 618-623.)
(  0) 0) |
| [14] |
李军, 王金山, 蒋勇, 等. 凹槽状动叶顶部非定常气膜冷却性能的研究[J]. 西安交通大学学报, 2010, 44(5): 5-10. DOI:10.7652/xjtuxb201005002 (  0) 0) |
| [15] |
Arisi A, Phillips J, Ng W F, et al. An Experimental and Numerical Study on the Aerothermal Characteristics of a Ribbed Transonic Squealer-Tip Turbine Blade with Purge Flow[R]. ASME GT 2016-43073.
(  0) 0) |
| [16] |
王志多, 刘兆方, 丰镇平. 不同湍流模型对燃气透平静叶及动叶叶顶传热预测精度的研究[J]. 工程热物理学报, 2015, 36(9): 1894-1897. (  0) 0) |
| [17] |
Wang Z D, Liu Z F, Feng Z P. Influence of Mainstream Turbulence Intensity on Heat Transfer Characteristics of a High Pressure Turbine Stage with Inlet Hot Streak[J]. Journal of Turbomachinery, 2015, 138(4).
(  0) 0) |
| [18] |
Yang D L, Yu X B, Feng Z P. Investigation of Leakage Flow and Heat Transfer in a Gas Turbine Blade Tip with Emphasis on the Effect of Rotation[J]. Journal of Turbomachinery, 2010, 132(4).
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

