1 引言

资源短缺和日益严重的环境问题使得节能减排成为能源行业共同追求的目标, 而燃烧作为重要的能源转换方式, 发展相应的高效低排的新式燃烧装置近年来备受关注。在不同的燃烧形式中, 预混燃烧方式特别是贫燃预混, 因为其燃烧温度分布均匀、污染物(尤其是热力型NO_x)排放低等优势, 在新型燃气轮机和航空发动机中应用广泛^[1]。但是在实际工况中, 反应物通常是非均匀的, 因此燃烧形式可能属于分层燃烧。相比于贫燃预混燃烧, 分层燃烧可以拓宽燃烧极限、增强燃烧稳定性, 受到国际学者的广泛关注^[2]。数值模拟可以为分析燃烧工况、优化燃烧器设计等提供指导意见, 发展更精确的模拟手段显得越来越重要。大涡模拟(LES)通过过滤操作, 将直接求解的大尺度结构和采用模型封闭的小尺度脉动分开考虑, 权衡了计算效率和准确性的要求, 在湍流燃烧的数值模拟中得到广泛应用。

但是在预混或者分层燃烧中, 火焰厚度通常很薄, LES的网格难以捕捉, 为了解决这个问题, 诸多学者提出了适用于预混燃烧的亚格子燃烧模型, 如加厚火焰面模型(ATF)^[3]、火焰面密度模型(FSD)^[4]、G方程模型(level-set)^[5]、过滤建表模型(F-TACLES)^[6]、概率密度函数模型(PDF)^[7]、条件矩封闭模型(CMC)^[8]等。在预混燃烧中, 亚格子燃烧模型需要正确描述其传播特性和火焰厚度, 其中火焰面密度模型可以保证火焰传播速度的正确性, 通过反应进度变量表征燃烧发生在火焰前锋上, 该方法的实现既可以通过引入代数表达式(即代数火焰面密度模型), 也可通过求解附加输运方程(即输运火焰面密度模型), Ma等^{[9, 10]}分别对代数火焰面密度模型和输运火焰面密度模型进行了详细的比较。相比于代数火焰面密度模型, 输运火焰面密度模型虽然更贴近实际工况, 但是由于其输运方程中未封闭量过多且难以模化, 其广泛应用还难以实现。而代数火焰面密度模型则在预混和分层燃烧中得到了推广与应用, Marincola等^[11]和Butz等^[12]分别将其应用到Darmstadt分层燃烧器和TECFLAM分层旋流燃烧器中, 得到了很好的预测结果。但是火焰面密度模型忽略了火焰内部的详细组分信息, 这对细致分析燃烧现象产生了影响。化学热力学建表结合假定概率密度函数方法^[13], 通过将流动与化学反应解耦, 采用少数的建表标量表征详细的化学反应过程, 但是其很难正确反映火焰传播特性。为了发挥两种模型的优点, Lecocq等^[14]采用两种方法将上述模型进行耦合, 并成功模拟了PRECCINSTA燃烧器的实验工况, 结果表明耦合模型可以准确定位反应区位置, 同时能够正确预测火焰前锋内的化学反应过程。

剑桥分层旋流燃烧器由Sweeney等^[15]设计并进行实验, 为描述流动中拟序结构^{[16, 17]}、发展燃烧模型、分析燃烧现象提供了丰富的数据。Proch等^[18]发展了分层条件下加厚火焰面模型耦合化学热力学建表方法的亚格子燃烧模型, 并成功测试了无旋条件下预混、中等分层、强分层工况。Nambully等^[19]采用过滤的层流火焰面模型模拟了与Proch等^[18]同样的实验工况, 指出亚格子燃烧模型中考虑热损及差异扩散的重要性。Mercier等^[20]采用过滤建表模型, 比较了静态皱褶因子模型和动态皱褶因子模型的区别以及考虑热损的亚格子燃烧模型的表现。Brauner等^[21]采用概率密度函数模型, 验证了欧拉概率密度函数模型在预混、分层燃烧中的应用。总体上说, 分层燃烧现象复杂, 更精细的燃烧模型仍有待发展。

本文通过火焰面密度模型描述分层燃烧现象, 结合化学热力学建表方法确定组分信息, 采用大涡模拟分析剑桥分层燃烧工况, 介绍了剑桥分层旋流燃烧器及所选定的实验工况, 推导了分层条件下的大涡模拟控制方程, 给出其中未封闭项的模化方法, 介绍了本文所采用的网格条件及数值方法, 给出数值模拟结果及分层燃烧机制分析。

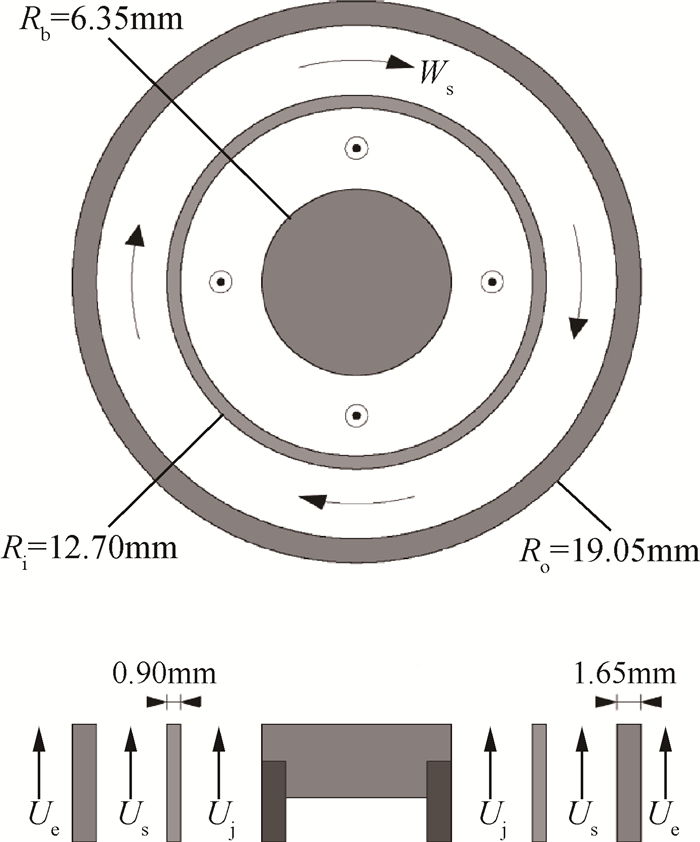
2 剑桥分层旋流燃烧器简介

图 1为剑桥分层旋流燃烧器(SwB)出口处的平面示意图, 其由R_b=6.35mm的中心钝体, R_i=12.70mm, 壁厚为0.90mm的内管以及R_o=19.05mm、壁厚为1.65mm的外管组成。中心钝体与内管及内管与外管间分别形成径向宽度为5.45mm, 4.70mm的环形通道, 各自通入平均轴向速度为U_j的常温常压甲烷空气射流与平均轴向速度为U_s的常温常压甲烷空气旋流。除此之外, 直径为196.80mm的风洞提供平均轴向速度为U_co的空气伴流, 以避免周围环境对实验的影响。基于平均轴向速度和特征尺寸定义射流雷诺数Re_j和旋流雷诺数Re_s。本文选取无旋、中等分层条件的SwB5作为研究对象, 具体实验工况见表 1, 表中φ_j, φ_s和φ_co分别表示射流通道、旋流通道和伴流对应的预混气体当量比。

3 数学物理模型

湍流与火焰之间存在复杂的相互作用, 按照各自的特征时间尺度(即湍流Kolmogorov时间尺度和化学反应时间尺度)确定的无量纲准则数Ka, 可将湍流燃烧机制大致分为火焰面(Flamelet)机制和分布式反应(Distributed Reaction)机制。通常认为在火焰面机制下, 火焰内部结构不受湍流涡旋的影响, 当地火焰结构与层流火焰类似, 湍流对火焰的影响体现在火焰前锋的形变^[22]。除了PDF、CMC等模型外, 大多数模型的适用范围均处于火焰面机制, 包括本文采用的火焰面密度模型。

3.1 火焰面密度模型

为了描述燃料在空间上的非均匀性, 分层燃烧引入混合物分数Z表征燃料在空间上的分布, 按照Bilger的定义式^[23], 混合物分数在纯空气和纯燃料条件下分别为0和1。同预混燃烧一样, 分层燃烧引入反应进度变量作为描述燃烧过程的物理量。在火焰面密度模型中, 反应进度变量通常表示成某种燃料质量分数Y_F的函数形式, 即可以表示为

$ c = \left( {{Y_{\rm{F}}} - Y_{\rm{F}}^{\rm{u}}\left( Z \right)} \right)/\left( {Y_{\rm{F}}^{\rm{b}}\left( Z \right) - Y_{\rm{F}}^{\rm{u}}\left( Z \right)} \right) $

(1)

式中上标u, b分别表示未燃状态和已燃状态。

由反应进度变量的通用方程^[24]、式(1)以及关系式Y_F(Z)=ZY_F⁰(式中上标0表示纯燃料流中某种燃料质量分数), 分层燃烧的反应进度变量输运方程如下

$ \begin{array}{l} \frac{{\partial \left( {\rho c} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}c} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( {\rho D\frac{{\partial c}}{{\partial {x_i}}}} \right) + {\omega _{\rm{c}}} + \\ \frac{2}{{ZY_{\rm{F}}^0 - Y_{\rm{F}}^{\rm{b}}\left( Z \right)}}\left( {Y_{\rm{F}}^0 - \frac{{{\rm{d}}Y_{\rm{F}}^{\rm{b}}\left( Z \right)}}{{{\rm{d}}Z}}} \right)\rho D\frac{{\partial c}}{{\partial {x_i}}} \cdot \frac{{\partial Z}}{{\partial {x_i}}} - \\ \frac{c}{{ZY_{\rm{F}}^0 - Y_{\rm{F}}^{\rm{b}}\left( Z \right)}} \times \frac{{{{\rm{d}}^2}Y_{\rm{F}}^{\rm{b}}\left( Z \right)}}{{{\rm{d}}{z^2}}}\rho D\frac{{\partial Z}}{{\partial {x_i}}} \cdot \frac{{\partial Z}}{{\partial {x_i}}} \end{array} $

(2)

在贫燃状态下, 近似假定燃料充分燃烧, 即Y_F^b≈0, 则上式右端最后一项可以忽略^[11]。将上式进行简化并过滤可得

$ \begin{array}{l} \frac{{\partial \left( {\bar \rho \tilde c} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho \widetilde {{u_i}}\tilde c} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \tilde D\frac{{\partial \tilde c}}{{\partial {x_i}}}} \right) + \widetilde {{\omega _c}} + \\ \frac{{\partial \left( {\bar \rho \widetilde {{u_i}}\tilde c - \overline {\rho {u_i}c} } \right)}}{{\partial {x_i}}} + \overline {\frac{{2\rho D}}{Z}\frac{{\partial c}}{{\partial {x_i}}}\frac{{\partial Z}}{{\partial {x_i}}}} \end{array} $

(3)

相比于预混燃烧中反应进度变量的输运方程, 方程(3)右端多出一项, 即$\overline {\frac{{2\rho D}}{Z}\frac{{\partial c}}{{\partial {x_i}}}\frac{{\partial Z}}{{\partial {x_i}}}} $, 该项表示由于燃料空间非均匀性产生的交叉标量耗散率^[24]。对于交叉标量耗散率的模化国际学者仍在探讨, 但是一般认为, 与源项相比, 其量级较小, 可以直接采用可解尺度的物理量近似表示

$ \overline {\frac{{2\rho D}}{Z}\frac{{\partial c}}{{\partial {x_i}}}\frac{{\partial Z}}{{\partial {x_i}}}} = \frac{2}{{\tilde Z}}\bar \rho \left( {\tilde D + \widetilde {{D_{\rm{t}}}}} \right)\frac{{\partial \tilde c}}{{\partial {x_i}}}\frac{{\partial \tilde Z}}{{\partial {x_i}}} $

(4)

式中$\widetilde {{D_{\rm{t}}}}$为湍流扩散系数, 由Germano动态过程确定^[25]。式(3)中亚格子标量通量项($\overline {\rho {u_i}c}-\bar \rho \widetilde {{u_i}}\tilde c$)采用涡扩散模型模化^[1], 而Ma等^{[9, 26]}和Butz等^[12]将化学反应源项表示成通用火焰面密度的形式,

$ {{\tilde \omega }_{\rm{c}}} = {\rho _0}{S_{\rm{L}}}\sum {_{{\rm{gen}}}} $

(5)

式中ρ₀为未燃气密度, S_L为无拉伸的层流火焰传播速度, 其对所采用的化学反应机理敏感, ∑_gen为通用火焰面密度。按照Muppala等^[27]的模化方法, 通用火焰面密度可以表示成

$ \sum {_{{\rm{gen}}}} = \mathit{\boldsymbol{ \boldsymbol{\varXi} }}\left| {\nabla \tilde c} \right| $

(6)

式中$\left| {\nabla \tilde c} \right|$为Favre平均的反应进度变量梯度的范数, 其表征火焰前锋出现在空间某处x的概率与火焰刷厚度的比值^{[9, 27]}。Ξ为皱褶因子, 表征由湍流涡旋作用引起的火焰面面积变化, 其形式如下^[27]

$ \mathit{\boldsymbol{ \boldsymbol{\varXi} }} = 1 + \frac{{0.46}}{{Le}}\mathit{Re}_\mathit{\Delta }^{0.25}{\left( {\frac{{{{u'}_\mathit{\Delta }}}}{{{S_{\rm{L}}}}}} \right)^{0.3}}{\left( {\frac{{\bar p}}{{{p_0}}}} \right)^{0.2}},\mathit{R}{\mathit{e}_\mathit{\Delta }} = \frac{{{{u'}_\mathit{\Delta }}\mathit{\Delta }}}{\nu } $

(7)

式中Le为刘易斯数, 此处取1.0。p, p₀, Δ, ν分别为过滤压力、参考压力、网格尺度、运动粘度。亚格子脉动速度u′_Δ通过Smagorinsky模型模化

$ {u'_\Delta } = \frac{{{\nu _{\rm{t}}}}}{{{C_{\rm{s}}}\Delta }},{\nu _t} = {\left( {{C_{\rm{s}}}\Delta } \right)^2}\left| {\frac{1}{2}\left( {\frac{{\partial {{\tilde u}_j}}}{{\partial {x_i}}} + \frac{{\partial {{\tilde u}_i}}}{{\partial {x_j}}}} \right)} \right| $

(8)

模型系数C_s由Germano动态过程确定^[25]。

按照上述过程模化, 此时, ${\tilde c}$的输运方程为

$ \begin{array}{l} \frac{{\partial \left( {\bar \rho \tilde c} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho \widetilde {{u_i}}\tilde c} \right)}}{{\partial {x_i}}} = \\ \frac{\partial }{{\partial {x_i}}}\left[ {\bar \rho \left( {\tilde D + \widetilde {{D_{\rm{t}}}}} \right)\frac{{\partial \tilde c}}{{\partial {x_i}}}} \right] + {\rho _0}{S_{\rm{L}}}\mathit{\boldsymbol{ \boldsymbol{\varXi} }}\left| {\nabla \tilde c} \right| + \frac{2}{{\tilde Z}}\bar \rho \left( {\tilde D + \widetilde {{D_{\rm{t}}}}} \right)\frac{{\partial \tilde c}}{{\partial {x_i}}}\frac{{\partial \tilde Z}}{{\partial {x_i}}} \end{array} $

(9)

通常火焰面密度模型忽略了火焰内部的详细组分信息, 为了弥补这个不足, 有必要将其与化学热力学建表方法进行耦合。

3.2 化学热力学建表方法和假定概率密度函数模型

化学热力学建表方法求解简化的层流火焰方程, 采用少数建表标量反映详细的化学反应过程。由于剑桥分层燃烧的燃烧机制满足火焰面的基础假设, 本文通过FlameMaster程序^[28]求解不同当量比下一维自由传播层流预混火焰, 获得一系列包含组分、温度、化学反应源项等化学热力学信息φ的层流火焰数据库。上述化学热力学信息可以表示成当量比和空间坐标的函数, 即φ=φ(φ, x)。而当量比与混合物分数之间有如下关系

$ \phi = \frac{Z}{{1 - Z}}\frac{{1 - {Z_{{\rm{st}}}}}}{{{Z_{{\rm{st}}}}}} $

(10)

根据SwB5的燃烧工况, 式中化学当量混合物分数Z_st=0.054, 甲烷的燃烧极限设定为0.026≤Z≤0.093^[18], 区间外的化学热力学信息采用混合物分数方向上插值得到, 则化学热力学信息φ可以映射成φ=φ(Z, x)。采用反应进度变量替换非输运变量的空间坐标, 反应进度变量与空间坐标一一对应, 则层流化学热力学信息可以映射成φ=φ(Z, Y_c)。为了解决Z与Yc之间不独立, 通常引入归一化的反应进度变量c=(Y_c-Y_cmin)/(Y_ceq-Y_cmin)替换Y_c, 其中Y_ceq, Y_cmin分别表示给定混合物分数下Y_c的最大值与最小值, 则层流化学热力学信息最终可以表示成φ=φ(Z, c)。

反应进度变量没有统一的形式, 通常将其表示成重要组分或重要组分的线性组合的函数^[29], 考虑到采用重要组分的线性组合得到的归一化反应进度变量c的输运方程中存在诸多不封闭项, 而且很难进行模化, 国际学者通常采用某种重要组分定义反应进度变量^[11]。本文探讨基于Y_c1=CH₄和Y_c2=CO+CO₂+H₂O+H₂得到的归一化反应进度变量c₁和c₂在实验工况覆盖的贫燃(φ=0.5)及化学当量比(φ=1.0)下的表现。

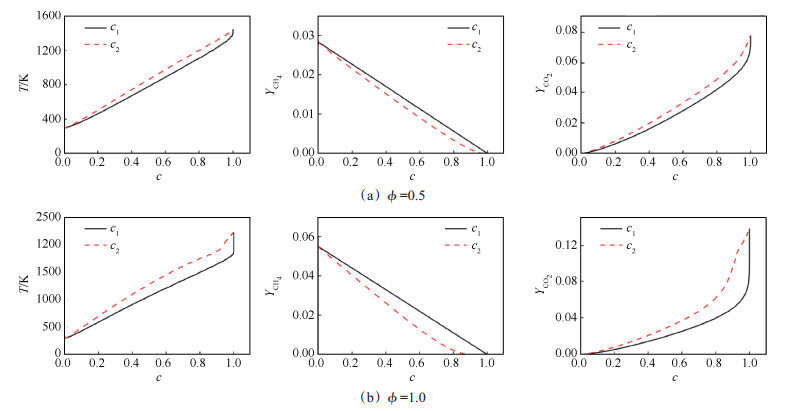
图 2比较了化学热力学信息在归一化反应进度变量c空间上的分布, 横坐标为c, 纵坐标为化学热力学信息(温度、组分等)。相比c₂而言, 在c=1附近, 采用c₁得到的化学热力学信息梯度较大, 尤其在化学当量比工况, 这可能会在查表过程中引入稍大的插值误差。但总体上, 采用c₁可以较好地描述详细化学反应过程。

通过假定概率密度函数考虑湍流涡旋对火焰结构的影响, 对层流化学热力学信息φ积分可得到湍流化学热力学信息${\tilde \varphi }$

$ \tilde \varphi = \iint {\varphi \left( {Z,c} \right)\tilde p\left( {Z,c} \right){\rm{d}}Z{\rm{d}}c} $

(11)

式中$\tilde p\left( {Z, c} \right)$为混合物分数和反应进度变量的假定联合概率密度函数。由于混合物分数和归一化的反应进度变量近似统计独立, 联合概率密度函数可以简化成二者概率密度函数乘积的形式, 即$\tilde p\left( {Z, c} \right) = \tilde p\left( Z \right) \times \tilde p\left( c \right)$。

虽然假定概率密度函数没有统一的形式, 但是通常认为采用Beta函数是合适的^{[1, 30]}, Beta函数的形式如下^[31]

$ p\left( f \right) = \frac{{{f^{a - 1}}{{\left( {1 - f} \right)}^{b - 1}}}}{{\int_0^1 {{f^{a - 1}}{{\left( {1 - f} \right)}^{b - 1}}{\rm{d}}f} }} $

(12)

$ a = \tilde f\left( {\frac{{\tilde f\left( {1 - \tilde f} \right)}}{{\widetilde {{{f''}^2}}}} - 1} \right) $

(13)

$ b = \left( {1 - \tilde f} \right)\left( {\frac{{\tilde f\left( {1 - \tilde f} \right)}}{{\widetilde {{{f''}^2}}}} - 1} \right) $

(14)

式中$\tilde f, \widetilde {{{f''}^2}}$分别表示物理量的期望与方差。

假定混合物分数与反应进度变量的概率密度函数均为Beta函数, 由式(11)可得到湍流化学热力学信息$\tilde \varphi = \tilde \varphi \left( {\tilde Z, \widetilde {{{Z''}^2}}, \tilde c, \widetilde {{{c''}^2}}} \right)$。通过求解混合物分数、归一化反应进度变量以及各自方差的输运方程, 可以确定相应的湍流化学热力学信息。

3.3 大涡模拟控制方程

本文采用Favre过滤的Navier-Stokes方程求解流场, 其中动量方程中的亚格子应力项采用动态Smagorinsky模型模化。除此之外, 分别求解Favre过滤的混合物分数、归一化反应进度变量以及相应方差的输运方程描述燃烧场。按照Domingo等采用的推导方法^[32], 相关方程如下

$ \frac{{\partial \left( {\bar \rho \tilde Z} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho \widetilde {{u_i}}\tilde Z} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \tilde D\frac{{\partial \tilde Z}}{{\partial {x_i}}}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \widetilde {{u_i}}\tilde Z - \bar \rho \widetilde {{u_i}Z}} \right) $

(15)

$ \begin{array}{l} \frac{{\partial \left( {\bar \rho \widetilde {{{Z''}^2}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho \widetilde {{u_i}}\widetilde {{{Z''}^2}}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \tilde D\frac{{\partial \widetilde {{{Z''}^2}}}}{{\partial {x_i}}}} \right) + \\ \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \widetilde {{u_i}}\widetilde {{{Z''}^2}} - \bar \rho \widetilde {{u_i}{{Z''}^2}}} \right) + 2\left( {\bar \rho \widetilde {{u_i}}\tilde Z - \bar \rho \widetilde {{u_i}Z}} \right)\frac{{\partial \tilde Z}}{{\partial {x_i}}} - \bar \rho \tilde \chi _Z^{{\rm{res}}} \end{array} $

(16)

$ \begin{array}{l} \frac{{\partial \left( {\bar \rho \tilde c} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho \widetilde {{u_i}}\tilde c} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \tilde D\frac{{\partial \tilde c}}{{\partial {x_i}}}} \right) + \\ \widetilde {{\omega _{\rm{c}}}} + \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \widetilde {{u_i}}\tilde c - \bar \rho \widetilde {{u_i}c}} \right) + \overline {\frac{{2\rho D}}{Z}\frac{{\partial c}}{{\partial {x_i}}}\frac{{\partial Z}}{{\partial {x_i}}}} \end{array} $

(17)

$ \begin{array}{l} \frac{{\partial \left( {\bar \rho \widetilde {{{c''}^2}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar \rho \widetilde {{u_i}}\widetilde {{{c''}^2}}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \tilde D\frac{{\partial \widetilde {{{c''}^2}}}}{{\partial {x_i}}}} \right) + \\ 2\left( {\widetilde {c{\omega _c}} - \tilde c\widetilde {{\omega _c}}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\bar \rho \widetilde {{u_i}}\widetilde {{{c''}^2}} - \bar \rho \widetilde {{u_i}{{c''}^2}}} \right) + \\ 2\left( {\bar \rho \widetilde {{u_i}}\tilde c - \bar \rho \widetilde {{u_i}c}} \right)\frac{{\partial \tilde c}}{{\partial {x_i}}} - \bar \rho \chi _c^{res} + {\left( {\widetilde {{{c''}^2}}} \right)^{1/2}}\overline {\frac{{2\rho D}}{Z}\frac{{\partial c}}{{\partial {x_i}}}\frac{{\partial Z}}{{\partial {x_i}}}} \end{array} $

(18)

方程(15)~(18)包含很多未封闭项, 其中亚格子标量通量项$\tau _{\tilde \psi }^{{\rm{res}}}\left( {\tau _{\tilde \psi }^{{\rm{res}}} = \bar \rho {{\tilde u}_i}\tilde \psi-\bar \rho \widetilde {{u_i}\psi }} \right)$采用涡扩散模型模化^[1]。亚格子标量耗散率$\tilde \chi _Z^{{\rm{res}}}, \tilde \chi _c^{{\rm{res}}}$采用线性松弛假设模化^[33], 即$\tilde \chi _\psi ^{{\rm{res}}} = \frac{{{C_{\chi \psi }}{C_\varepsilon }}}{{{C_{\rm{u}}}S{c_{\rm{t}}}}}\frac{{{v_{\rm{t}}}}}{{{\Delta ^2}}}\widetilde {{{\psi ''}^2}}$, 其中C_χψ=2.0, C_ε/C_u=2.0, Sc_t=0.4。反应进度变量方差方程中源项通过查取湍流化学热力学表确定。

本文采用GRI3.0机理^[34](53个组分, 325个基元反应)构建湍流化学热力学信息。综合考虑计算精度和内存的要求, 湍流化学热力学表$\tilde \varphi \left( {\tilde Z, \widetilde {{{Z''}^2}}, \tilde c, \widetilde {{{c''}^2}}} \right) $在相应坐标方向上依次包含150, 25, 150, 25个节点, 其在${\tilde Z}$, ${\tilde c}$方向上为均匀分布, 而在相应的方差方向上呈抛物线型分布。

4 数值方法

本文采用时间、空间上的交错网格, 通过有限差分方法求解圆柱坐标系下的大涡模拟控制方程。其中, 非稳态项采用二阶半隐式离散方法, 动量方程中的对流项采用动能守恒的二阶中心差分格式, 标量方程中的对流项采用三阶WENO格式, 扩散项采用二阶中心差分格式, 以综合考虑数值耗散及计算精度的要求。

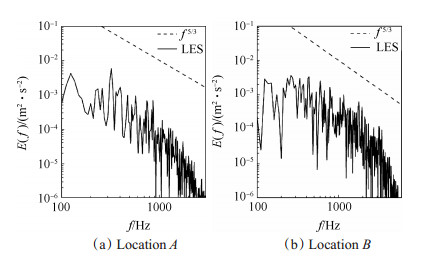
圆柱体计算域轴向、径向尺寸分别为240mm、80mm, 以尽量减小边界条件对计算的影响。轴向、径向采用186×197个非均匀网格, 在射流出口和剪切层附近加密, 周向采用32个均匀网格, 网格总数约为1.17×10⁶个, 最小网格尺寸为0.1mm, 可以满足大涡模拟在燃烧问题中的应用^[30]。为进一步验证网格精度, 图 3给出了冷态场中点A(x=10mm, r=12mm)、点B(x=20mm, r=12mm)处的湍流能谱。点A, B均位于中心射流与环流的剪切层内, 通过与-5/3 Kolmogorov幂次定律比较, 表明该网格可以正确反映惯性子区流场特征。固壁处采用无滑移条件, 出口边界采用对流出口条件。瞬时速度场通过平均速度叠加白噪声确定, 其中射流、旋流入口平均速度均采用^[17]次幂分布^[16], 伴流入口平均速度采用实验中的体积流速。计算过程中动态调节时间步长, 以保证CFL数小于0.5。燃烧场经过10个Flow-timeτ(τ=L_xU_j, L_x为计算域轴向长度)充分发展, 为保证统计结果的有效性, 统计过程持续10个Flow-time。

5 结果与讨论 5.1 流场结构

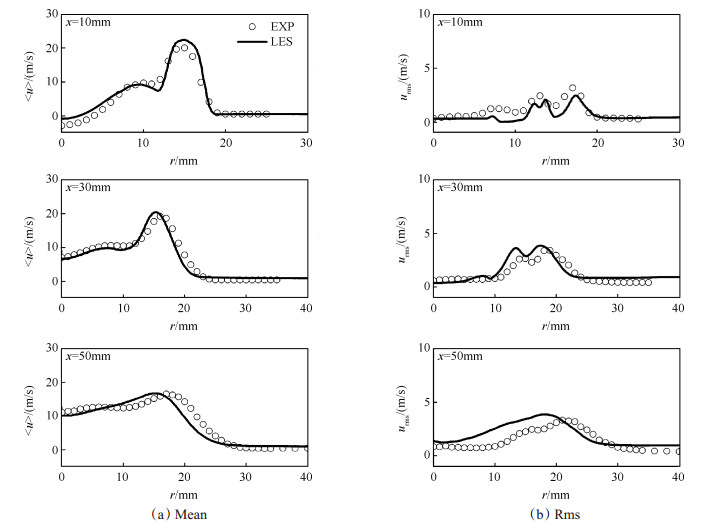
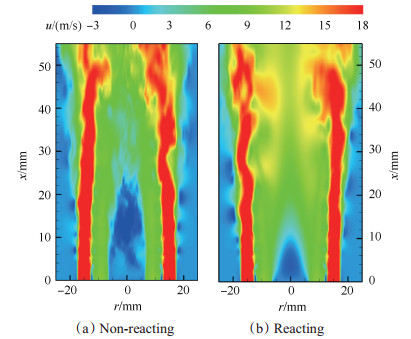
图 4给出了SwB5在轴向位置x为10, 30, 50mm处Favre平均轴向速度及其脉动的径向分布, 其中黑色空心圆表示Zhou等^[35]采用LDA测量的实验值。由图可以看出, 大涡模拟结果与实验值符合较好, 表明所采用的网格可以分辨流场结构。在x=10mm截面上, 大涡模拟预测的回流区速度略小, Proch等^[18]及Nambully等^[19]得到了相似的模拟结果。由于动量交换和热膨胀, 钝体后形成的回流区在下游逐渐消失, 在x=30, 50mm截面上均不存在回流区。图 4中轴向速度脉动的峰值与速度剪切层有关, 下游速度脉动的偏差可能与入口条件有关。图 5分别给出了冷态、燃烧场的轴向速度瞬时分布云图。相比于冷态场, 由于燃烧引起的热膨胀及涡耗散增加导致的再层流化现象, 燃烧场的湍流脉动减弱, 钝体后的回流区接近稳态。

为了进一步分析湍流涡旋对火焰结构的影响, 本文采用Q准则^[36]识别流场中的涡结构。Q准则为速度梯度张量的二次不变量, 形式如下,

$ Q = \left( {{\mathit{\Omega }_{ij}}{\mathit{\Omega }_{ij}} - {S_{ij}}{S_{ij}}} \right)/2 $

(19)

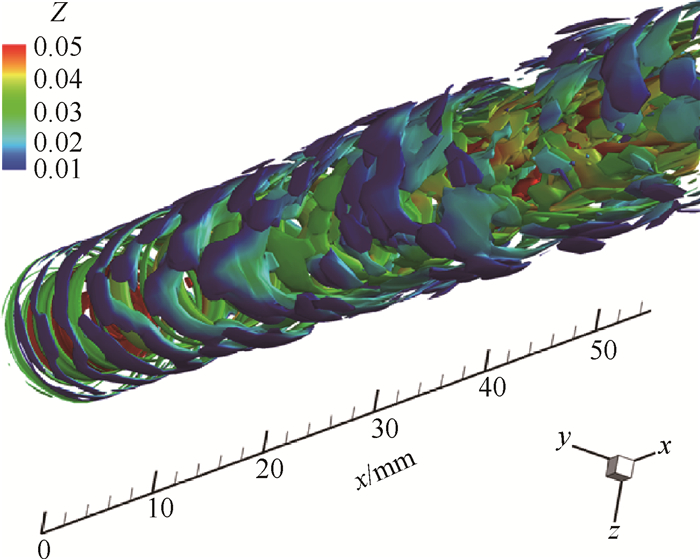
式中S_ij=(u_{i, j}+u_{j, i})/2, Ω_ij=(u_{i, j}-u_{j, i})/2分别表示速度梯度张量的对称部分和反对称部分。Q值表征流体的转动速率Ω_ijΩ_ij与应变率S_ijS_ij之间的量级关系, Q>0表示流体的转动速率占主导, 即该条件下流体中主要由涡结构构成, 所以可采用正Q值表征涡结构。图 6显示了燃烧场Q=2×10⁵s^-2的等值面, 并使用混合物分数着色, 从图中可以看出, 由于中心射流和旋流、旋流和伴流之间速度梯度的剪切作用, 导致流动发生Kelvin-Helmholtz不稳定性, 管口附近形成环状涡结构。这种涡结构有利于改善燃料间的混合特性, 而在流场下游, 环状涡结构逐渐破碎形成随机分布的小涡, 同时伴随着混合物分数的间歇性。

5.2 统计结果

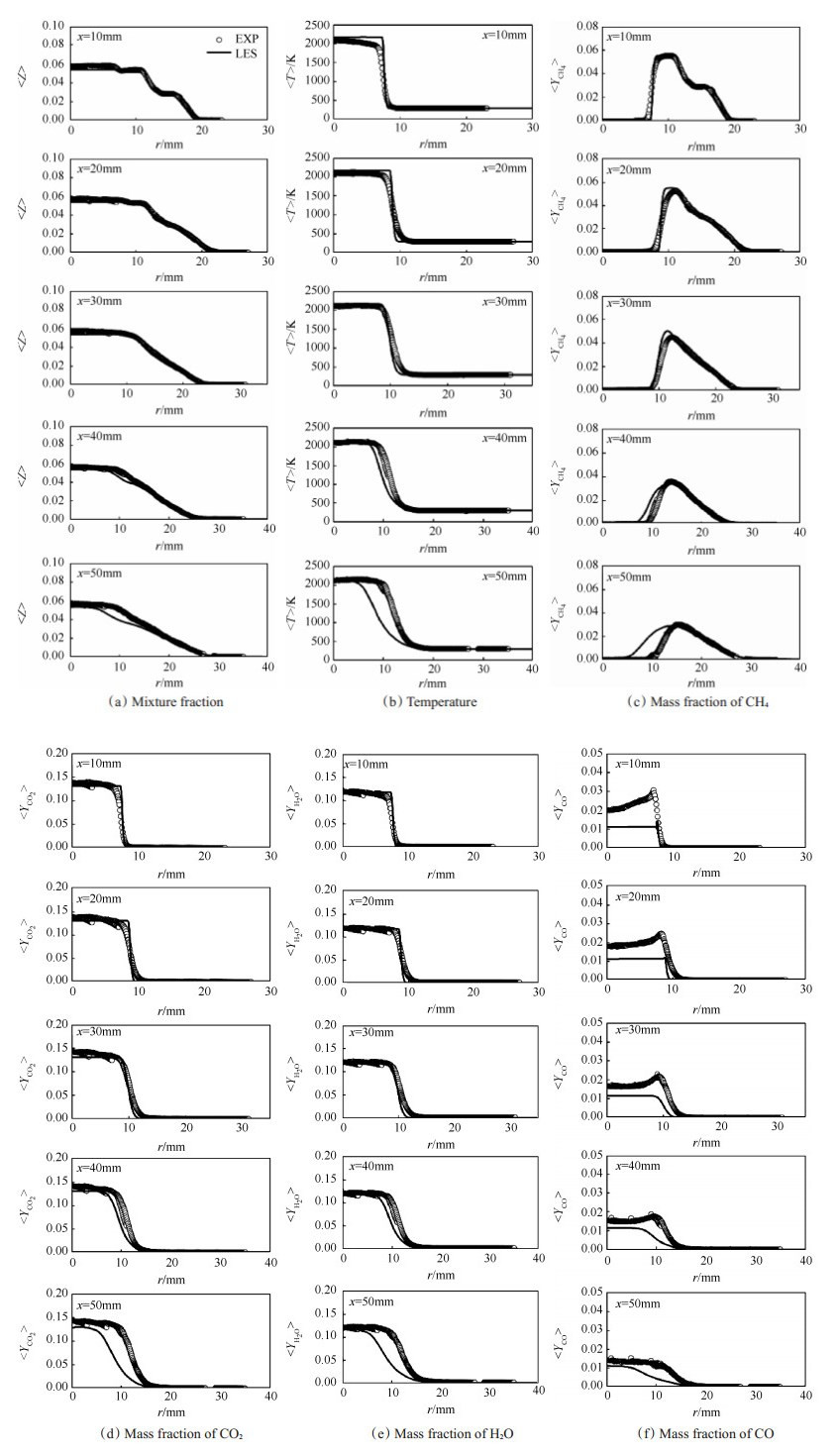
图 7给出了SwB5在轴向位置x为10, 20, 30, 40, 50mm处混合物分数、温度和主要组分的Favre平均径向分布。在x=10mm截面上, 除CO外, 其余物理量均与实验值符合较好。相比实验值, 由于未考虑钝体热损的影响, 大涡模拟预测的温度稍高, 这与Proch等^[18]及Nambully等^[19]的结果一致。组分CH₄的两次阶跃分别对应着旋流入口和射流入口。相比大涡模拟结果, Z的实验值显示出三次阶跃, 径向r < 6mm之前的阶跃可能是钝体后组分的差异扩散导致^[19]。在x=20mm和x=30mm截面上, 混合物分数的模拟结果总体较好, 温度、大组分结果略有偏差, 温度及大组分的偏差体现在火焰前锋厚度预测失准。由于火焰面密度模型倾向于预测完全燃烧状态, 中间组分CO偏差较大。下游x=40, 50mm截面上, 大涡模拟结果与实验值存在一定的偏差, 主要体现在火焰传播速度预测偏小, 这与所采用的皱褶因子模型有关, 而混合物分数的偏差主要由于分层入口条件导致。总体上, 上游的大涡模拟结果与实验较吻合, 而下游存在一定的偏差, 不同的燃烧模型均难以预测中间组分CO信息, 分层条件下CO生成机制有待探讨。

5.3 分层燃烧的燃烧机制

分层燃烧可以看成一类特殊的部分预混燃烧形式, 其火焰前锋沿着一系列当量比方向传播^[37]。分层燃烧的燃烧机制可采用火焰因子^[38]表征, 其形式如下

$ {G_{{\rm{FO}}}} = \nabla {Y_{{\rm{C}}{{\rm{H}}_4}}} \cdot \nabla {Y_{{{\rm{O}}_2}}} $

(20)

反应区内火焰因子取正值时表征预混机制, 取负值时表征非预混机制, 等于零时表征该区域未燃烧。

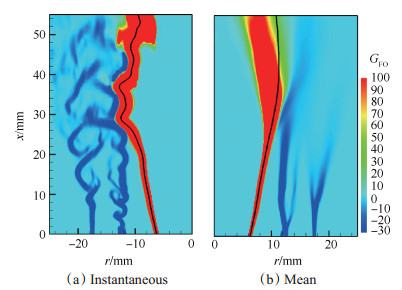
为了证明预混机制在分层燃烧中占主导, 图 8给出了SwB5的火焰因子瞬时和统计云图, 图中黑线为c=0.5等值线, 用以标记反应区。由图可知, 反应区内火焰因子为正值, 即SwB5的燃烧机制由预混燃烧主导。

6 结论

本文采用火焰面密度模型描述燃烧过程, 结合化学热力学建表方法确定组分信息, 通过大涡模拟分析分层燃烧现象, 得到以下结论:

(1) 基于一维自由传播层流预混火焰构建的化学热力学表可以很好地描述分层燃烧中主要标量信息, 弥补了传统火焰面密度模型忽略火焰内部详细组分信息的不足。

(2) 由于燃烧引起的热膨胀及涡耗散增加导致的再层流化现象, 燃烧场的湍流脉动减弱, 钝体后的回流区接近稳态。

(3) 瞬时、统计火焰因子云图表征SwB5的燃烧机制由预混燃烧主导。

(4) 总体上, 大涡模拟结果与实验值在流场上游符合较好, 而在下游存在一定偏差, 这可能与所采用的皱褶因子模型低估了湍流对火焰的形变作用有关, 其他皱褶因子模型在分层燃烧中的表现有待测试。在现有模型的基础上, 可以进一步引入热损及差异扩散的影响, 以提升模拟精度。