2. 西安航天动力研究所 液体火箭发动机技术重点实验室, 陕西 西安 710100;
3. 航天推进技术研究院, 陕西 西安 710100
2. Key Laboratory for Liquid Rocket Engine Technology, Xi'an Aerospace Propulsion Institute, Xi'an 710100, China;
3. China Academy of Aerospace Liquid Propulsion Technology, Xi'an 710100, China
喷嘴的雾化过程和雾化特性研究长期以来都是喷雾燃烧领域基础研究的热点和难点。其中旋流式雾化器产生的锥形液膜由于雾化性能好、稳定燃烧范围宽、结构简单、运行可靠等优点[1]被广泛应用。因此, 通过数值模拟的手段进一步细致地研究旋流液膜的雾化过程及雾化场的结构特征, 对提高喷嘴的雾化性能和设计水平具有重要意义; 获得全雾化场的液滴粒径空间分布, 可为后续的蒸发、混合、燃烧过程计算提供有效的初边值条件。
目前关于锥形液膜破碎理论分析较少, 因为它比平面液膜破碎更加复杂, 主要借助平面液膜破碎理论进行分析。York和Squire等对平面液膜破碎过程进行了理论分析, 认为气液界面处波的形成与增长是导致液膜破碎的重要原因[2, 3]。随着以光学技术为代表的先进可视化测量技术迅速发展, 可以对雾化场进行无接触干扰的动态测试, 极大地促进了锥形液膜的研究。Fraser等应用高速摄影技术展示了液膜破碎过程细节[4]。Youngbin Yoon等实验拍摄了锥形液膜破碎过程图像[5]。Loustalan Paul W等实验研究了锥形液膜破碎机理, 使用高速转鼓相机和铜蒸汽激光获得了雾化区域的细节图像, 并使用“Void fraction”图像分析技术, 清楚地看到连续雾锥上形成了孔洞的细节[6]。岳明等应用PIV激光粒子图像测速仪对锥形液膜的破碎过程进行了实验研究[7]。刘娟等运用高速阴影拍摄了锥形液膜破碎过程图像, 得到液膜破碎长度、液膜锥角[8]。目前液膜雾化破碎过程研究主要还依靠实验, 但实验测量由于受到复杂的实验系统、测量设备、模拟实验工质及难以实现复杂的真实工作条件等的限制, 进一步深入地研究单因素影响及获得流场全部细节参数受到一定的局限。然而数值模拟则不受这些限制, 目前虽然由于涉及多相多尺度流动问题, 锥形液膜雾化过程数值模拟还是难点, 但前人在这方面做了一些探索研究。岳明等对离心式喷嘴喷出的锥形液膜做了空间不稳定性分析, 导出了无粘锥形液膜的色散方程, 并进行了数值求解和分析研究[9]。徐让书等采用VOF和LES对锥形液膜破碎过程进行了CFD模拟, 捕获了清晰的气液相界面以及液膜的不稳定波和初级破碎现象[10]。刘娟采用VOF和LES方法, 获得了离心式喷嘴锥形液膜一次破碎过程的结果[11]。Olivier Desjardins等基于DNS/LES和改进的守恒Level Set方法, 清楚显示了离心式喷嘴出口形成的锥形液膜[12]。
近年来Stéphane Popinet基于四叉树/八叉树的自适应网格(AMR)和VOF方法开发了一种新的开源软件Gerris, 在处理多相流问题中有着很大的优势, 可以精确地描述雾化过程, 是研究雾化机理的有力工具。国外一些研究人员已将Gerris很好地运用于直射流和互击射流雾化过程研究, 并得到了实验验证。Ma Dong-Jun等使用Gerris对射流撞击的雾化形式进行了高精度的数值模拟研究[13]。Xiaodong Chen和Vigor Yang等基于四叉树/八叉树的自适应网格和VOF方法, 采用Gerris对撞击式射流雾化特性及雾化破碎过程进行了高分辨率的数值模拟计算, 得到了非常好的可视化效果[14, 15]。国内李佳楠使用Gerris对直流互击式喷注单元雾化特性进行了准直接数值模拟, 探讨了撞击波的形成机理, 分析了雾场液滴的尺寸分布规律, 撞击夹角、孔径比、射流速度、动量比对雾化特性的影响规律, 计算精度较高[16]。然而目前在国内外公开发表的资料中, 还没看到将Gerris运用于旋流式锥形液膜雾化过程的计算。
本文基于Gerris的特点建立了合理的计算模型, 从研究最多的直射流入手, 对其加以周向的旋转速度, 以此为典型算例计算并与文献中的实验结果对比。在此基础上, 将Gerris用于空心的旋流式锥形液膜雾化过程仿真, 与目前具有代表性的其他仿真手段的计算结果进行了比较, 与实验拍摄的雾化过程进行对比验证, 考证计算方法的准确性, 为后续将该方法用于离心式喷嘴全流场雾化过程的数值模拟奠定基础。
2 数学物理模型 2.1 数值方法Gerris采用的数值方法Popinet在2003年发表的文章中作了详细的描述, 下面对Gerris采用的数值方法做一个总结性的描述。Gerris求解的是不可压、变密度、带有表面张力的N-S方程[17]。
| $ \left\{ \begin{array}{l} \rho \left( {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \nabla \mathit{\boldsymbol{u}}} \right) =-\nabla p + \nabla \cdot \left( {2\mu \mathit{\boldsymbol{D}}} \right) + \sigma \kappa {\delta _{\rm{s}}}\mathit{\boldsymbol{n}}\\ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{u}}} \right) = 0\\ \nabla \cdot \mathit{\boldsymbol{u = }}{\rm{0}} \end{array} \right. $ | (1) |
式中u=(u, v, w)为流体速度; ρ≡ρ(x, t)为流体密度; μ≡μ(x, t)为动力粘度; D为应变张量,
对于两相流动, 引入第一相的体积分数c(x, t)来定义密度和粘度,
| $ \left\{ \begin{array}{l} \rho \left( c \right) \equiv c{p_1} + \left( {1-c} \right){\rho _2}\\ \mu \left( c \right) \equiv c{\mu _1} + \left( {1-c} \right){\mu _2} \end{array} \right. $ | (2) |
式中ρ1, ρ2和μ1, μ2分别是第一相和第二相的密度和粘度。
将密度的连续方程用体积分数的连续方程替换
| $ \frac{{\partial c}}{{\partial t}} + \nabla \cdot \left( {c\mathit{\boldsymbol{u}}} \right) = 0 $ | (3) |
在Gerris中体积分数/密度和压力采用时间交错离散格式, 使用经典的时间分裂投影法进行简化, 达到时间二阶精度。使用四叉树/八叉树进行离散, 使得自适应加密算法可简易灵活地实现, 在不损失计算精度的情况下显著降低了计算量, 非常适合处理多尺度流动问题。使用Godunov动量差分格式, 基于四叉树/八叉树的多尺度求解器可以有效求解压力泊松方程, 达到空间二阶精度。使用分段线性的VOF几何重构方法进行自适应网格界面捕捉, 非常适合应用于包含破碎、聚合现象的雾化过程计算。通过将表面张力转化为某一区域连续的体积力并结合高度函数曲率估计实现表面张力的精确求解。采用单调集成大涡模拟MILES(又称隐式大涡模拟ILES)近似模拟亚格子SGS(SubGrid-Scale)的能量传递, 这是由于数值计算不可避免地有数值耗散, 这种数值耗散的效果与亚格子应力的作用类似, Boris在1992年系统提出并分析了MILES方法[18]。所以Gerris使用的网格自适应过程相当于是一个滤波的过程, 对于大于最小网格尺度的涡结构进行直接数值模拟DNS, 而小于最小网格尺度的涡结构由数值粘性模拟其耗散过程。
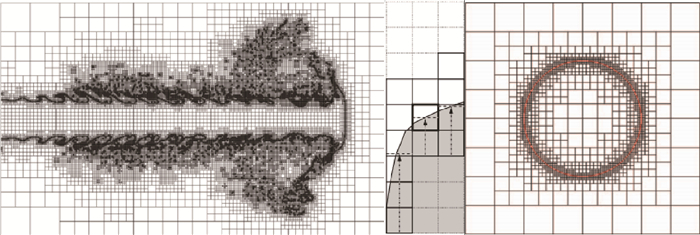
特别说明Gerris对于小液滴的处理方法:Gerris采用自适应网格技术和VOF相界面捕捉技术对两相界面界面进行捕捉, 能够捕捉到小液滴, 如图 1所示[19~21]。这主要是由于使用自适应网格加密算法可以根据流场参数变化对局部网格进行动态加密或粗化, 对两相界面处进行细化加密时, 网格可以自动加密到液滴的尺度量级, 再结合分段线性的VOF方法就可以将相界面比较精确地捕捉到, 自然可以捕捉到小液滴。
|
Fig. 1 Adaptive mesh refinement process of droplets captured based on a piecewise-linear geometrical VOF |
以前的研究对于直射流的较多, 由于初边值条件易于给定, 基于Gerris计算直射流雾化过程的仿真计算已有过研究, 并取得了不错的计算效果。但对于旋流雾化过程未见报道, 本文在直射流的基础上通过外加旋转速度作为典型算例来进行仿真计算, 一方面是为了探索建立一种从直射流过渡到旋流式雾化过程的数值仿真方法, 另一方面也是基于文献中的实验结果对仿真结果进行验证, 以验证建立的计算方法的准确性。
在带旋转流动的射流雾化过程仿真计算的基础上, 再将建立的旋流式液膜雾化过程仿真方法进一步拓展到空心的旋流式锥形液膜雾化过程, 因为空心的旋流式锥形液膜更接近真实的离心式喷嘴形成的锥形液膜。通过对空心的旋流式锥形液膜雾化过程的研究, 可以为离心式喷嘴的雾化过程及雾化特性研究提供更直接的参考。
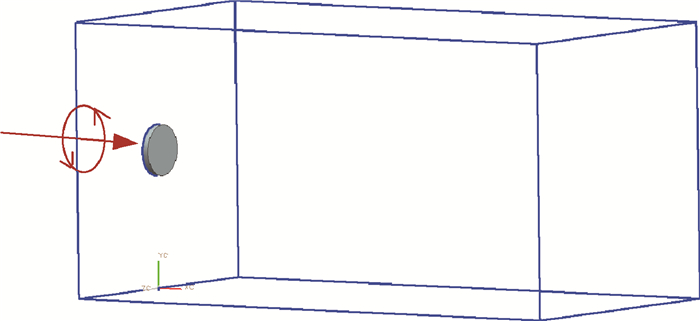
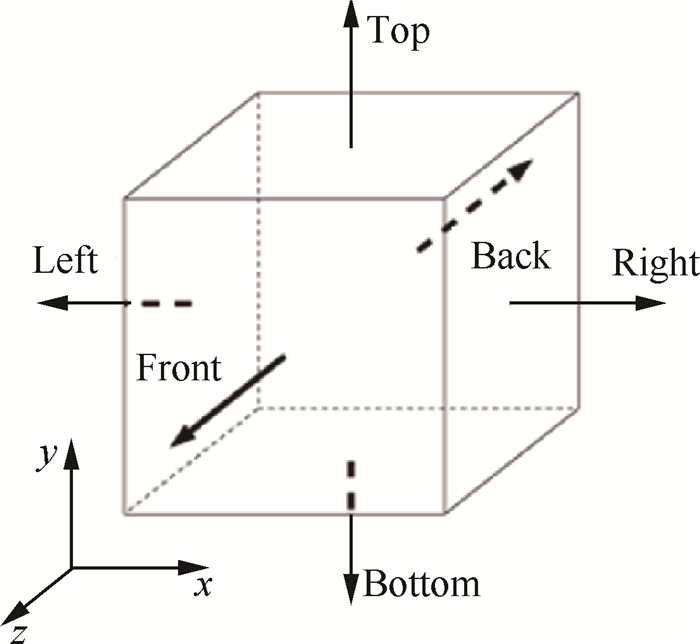
2.2.1 带旋转流动的射流三维雾化过程本算例为一加周向旋转速度的直射流雾化过程, 图 2为计算域的示意图。Gerris中计算域均由L×L×L的基本结构Box构成, 如图 3所示, 本算例由两个2个Box沿流向串联拼接组成, 即计算域为2L×L×L。计算域左端面为入口, 采用速度入口边界; 其余面为出口, 采用Outflow边界。第一相为液相, 第二相为气相。计算域的L=8mm, 最高网格等级采用Level=10加密, 最小网格约7.8μm。网格自适应函数设置为体积分数梯度, 即网格会实时根据流场中计算的体积分数梯度大小进行自适应加密或粗化。详细参数如表 1所示。
|
Fig. 2 Sketch map of computation zone of jet injector with rotational velocity |
|
Fig. 3 Box structure and definition of spatial directions |
|
|
Table 1 Computational parameters of jet injector with rotational velocity |
初始速度的入口边界设置如下, 其中射流的轴向速度为ux, 旋转速度可分解为互相垂直的uy和uz, 以便于在Gerris中进行设置, 三个方向速度分量的具体设置详见公式(4)。α为周向旋转速度和轴向速度的比值, 表征的是旋流度, 在本算例中取0.75。对应的雷诺数为Re=2Rρlux/μl=104, 旋流韦伯数为We=fρux2R/σ≈103。
| $ \left\{ \begin{array}{l} {u_x} = u = 20\;{\rm{if}}\;{\mathit{y}^{\rm{2}}}{\rm{ + }}{{\rm{z}}^{\rm{2}}} \le {\mathit{R}^{\rm{2}}}\\ {u_x} = 0\;{\rm{if}}\;{y^2} + {z^2} > {R^2}\\ {u_y} = v = \alpha u\sin \left[ {\arctan \left( {z/y} \right)} \right]\\ {u_z} = w = - \alpha u\;\cos \left[ {\arctan \left( {z/y} \right)} \right] \end{array} \right. $ | (4) |
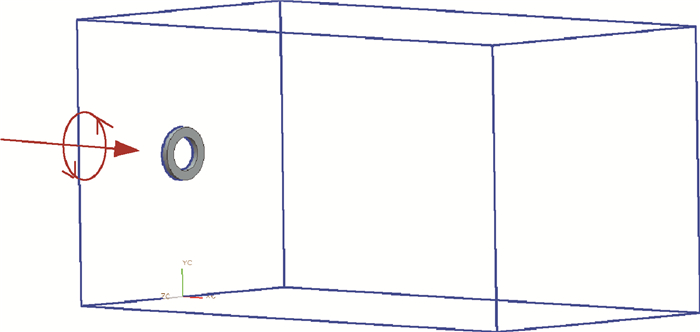
将上述带旋转速度的射流雾化过程仿真方法扩展应用到空心的旋流式锥形液膜雾化过程, 得到一个锥形液膜的三维雾化过程的计算模型, 图 4为计算域的示意图, 本算例类比离心式喷嘴出口的环形液膜, 将入口液相边界设置为空心环形, 增加了内环气相柱。液相为水, 气相为空气, 背压为大气环境。详细参数如表 2所示。
|
Fig. 4 Sketch map of computation zone of conical liquid film |
|
|
Table 2 Computational parameters of conical liquid film |
液相初始速度的入口边界设置如下, 入口边界速度呈环形, 内环和外环半径分别为r和R, 沿周向均匀分布。其中轴向速度为ux, 旋转速度可分解为互相垂直的uy和uz, 三个方向速度分量的具体设置见式(5)。α为周向旋转速度和轴向速度的比值, 表征旋流度, 计算中取1.0。
| $ \left\{ \begin{array}{l} {u_x} = u = 20\;{\rm{if}}\;{r^2} \le {\mathit{y}^{\rm{2}}}{\rm{ + }}{{\rm{z}}^{\rm{2}}} \le {\mathit{R}^{\rm{2}}}\\ {u_x} = 0\;{\rm{if}}\;{y^2} + {z^2} > {R^2}\;{\rm{or}}\;{\mathit{y}^\mathit{2}}\mathit{ + }{\mathit{z}^\mathit{2}}\mathit{ < }{\mathit{r}^\mathit{2}}\\ {u_y} = v = \alpha u\sin \left[ {\arctan \left( {z/y} \right)} \right]\\ {u_z} = w = - \alpha u\;\cos \left[ {\arctan \left( {z/y} \right)} \right] \end{array} \right. $ | (5) |
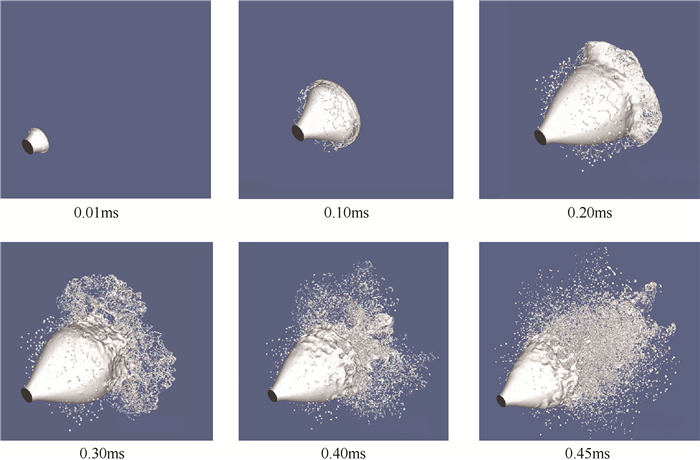
图 5为带旋转流动的直射流的三维雾化过程, 图 6和图 7分别为带旋转流动直射流最终形成的三维雾化场形态和中间截面体积分数云图。从图中可以看出由于旋转速度, 在离心力作用下, 射流中心液体开始分开, 形成一定锥角的液膜, 沿着流向液膜不断变薄, 并在表面出现波动, 且波动幅度不断增大, 连续液膜前缘渐渐断裂破碎, 开始脱落液丝, 进而产生大量液丝和液团, 液丝和大液团又进一步破碎形成液滴。可以发现整个锥形区域内都有大量液滴分布, 其中中间区域液滴速度较大, 且液滴粒径明显较大, 液滴分布较密, 外围液滴速度较小, 慢慢向外运动, 液滴粒径也小许多, 分布密度也小。说明此过程中存在二次雾化现象, 液丝在运动过程中受到气体力和表面张力的作用, 开始断裂形成大液滴, 液滴的形状不规则, 随着进一步收缩破碎成小液滴, 形状渐渐接近球形。
|
Fig. 5 3D spray process of jet injector with rotational velocity |

|
Fig. 6 3D spray field pattern of jet injector with rotational velocity |
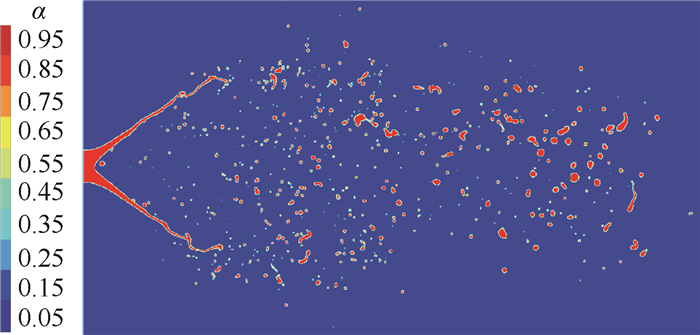
|
Fig. 7 Volume fraction in a median plane |
Gerris可以对全场所有的液滴数目、体积进行统计输出。近似认为每个液滴呈球形, 通过Matlab编程对液滴进行体积换算得到液滴直径, 再通过液滴粒径分段统计处理得到了概率密度分布曲线。图 8(a)和8(b)分别为文献中实验测量和本文计算的液滴粒径概率密度分布曲线, 分别与n=15的卡方分布概率密度曲线进行参考对比。从图中可以看出, 数值计算中捕捉到的液滴数目众多且尺寸变化范围大, 液滴呈两端少、中间多的分布, 与实际雾化过程结果相符。本文计算的分布曲线峰值对应的液滴直径约为14.8μm, 文献中对应的实验结果约为13μm, 绝对值仅相差1.8μm, 相对误差为13.8%, 两者结果符合较好。

|
Fig. 8 PDF distribution curve of droplets diameter |
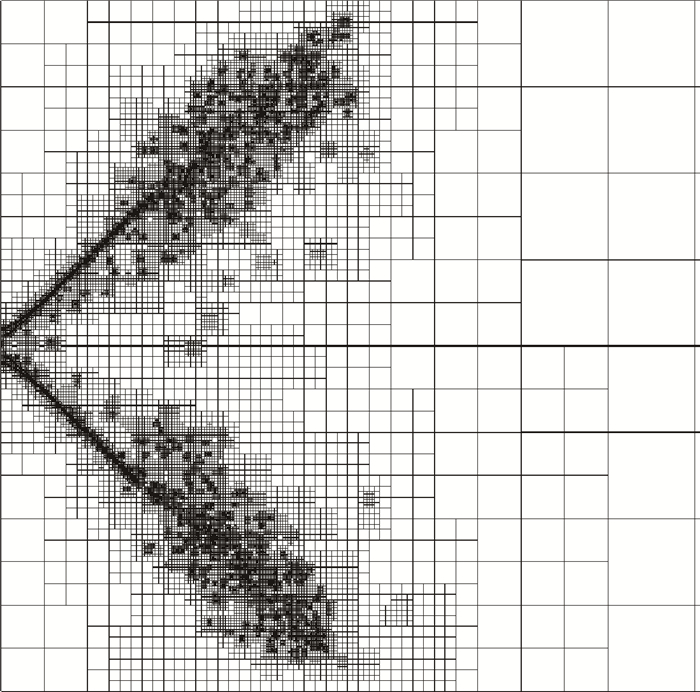
图 9为锥形液膜雾化过程最终生成的自适应网格, 在两相界面处进行了细致加密, 使得锥形液膜和不同尺度的液丝液滴得以有效捕捉, 这是自适应网格的最大优势, 显著降低网格量而不损失计算精度。图 10为中间横截面的体积分数云图和速度矢量图, 从体积分数图 10(a)可以清楚地看到锥形液膜由厚变薄, 逐渐张开锥角。在气液界面剪切力和液相表面张力的共同作用下, 连续液膜断裂, 破碎成液滴, 液滴主要分布在锥形液膜的附近, 锥形液膜中心几乎无液滴, 这与带旋转速度的直射流的液滴空间分布(图 7)显著不同, 这主要是与初始的液膜的形成有关。在速度矢量图 10(b)中可以较为清楚地看到气液界面相互作用的现象, 随着雾锥张开, 液膜表面的扰动不断增大, 会在相界面附近形成许多大大小小的涡, (图 10(b)中用颜色表示体积分数, 可以较为清楚地显示涡相对于两相界面的位置), 这些涡又使得液膜表面的扰动进一步加剧, 直至液膜破碎成液滴。这里引用Olivier Desjardins关于表面张力在液膜破碎形成液滴的过程中所起作用的说法, 在液膜表面波动不大时, 表面张力起着阻碍液膜表面变形的作用, 然而在液膜表面波动很剧烈并快要断裂时, 表面张力起着促进液膜波动、液丝断裂收缩形成液滴的作用[12]。这在三维雾化场结构图 11中液丝液滴的生成及运动变形可以体现出, 液膜表面一开始由于表面张力的阻碍作用难以破碎, 随着气液界面剪切力的持续作用, 使得液膜表面波动加剧, 液膜破碎成液丝、液滴; 而在液丝、液滴进一步运动过程中会在表面张力作用下收缩变形, 使得液丝在颈部收缩断裂, 变形收缩成近球形, 在一定程度上可以印证Olivier Desjardins的观点。
|
Fig. 9 Adaptive mesh of capturing phase interface |
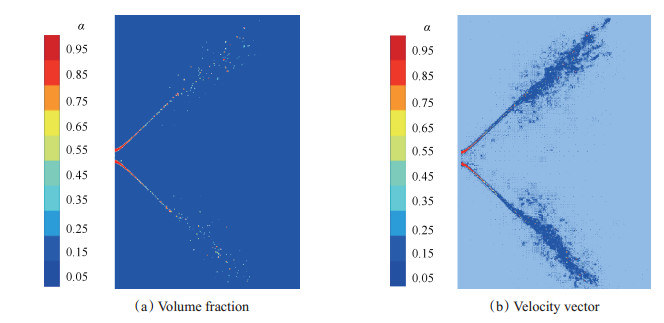
|
Fig. 10 Parameters in a median plane |

|
Fig. 11 3D spray field pattern of conical liquid sheet |
从图 11三维雾化场中可以清楚地看到锥形液膜, 连续的液膜上会形成表面扰动波, 逐渐增长, 达到一定程度后, 液膜上出现孔洞, 前缘开始脱落形成液丝, 液丝又进一步破碎成液滴, 而且可以看到液滴随着轴向距离增加在渐渐减小, 径向同样, 外围液滴较小, 小液滴速度也较小, 说明在此过程中大液滴经过二次雾化形成更小的液滴。另外还可以看到尽管进口边界给定的条件是周向一致的, 然而从上面的图中看到, 在周向液膜破碎位置、液滴粒径及速度分布并不是完全均匀的, 具有一定的随机性, 在实际的喷雾实验中这一现象也是存在, 符合客观事实。
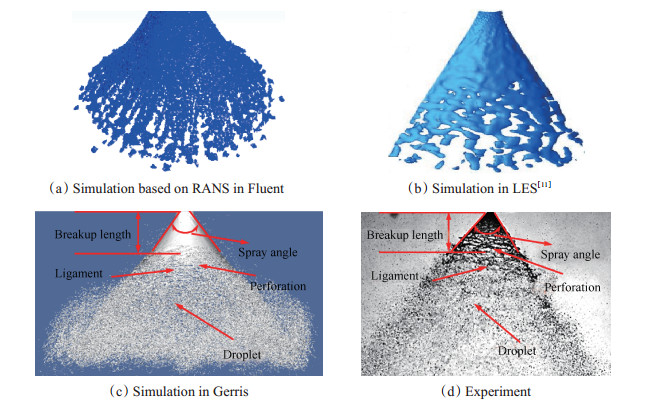
图 12(a)和图 12(b)分别为使用Fluent中的RANS湍流模型网格划分非常精细的计算结果和使用LES计算的结果, 可以看出, 计算只能获得喷雾场的宏观结构特征, 捕捉到大块的液团和少量的大液滴。Fluent由于使用基本均匀一致的网格, 即使局部网格加密, 计算量也将异常大, 难以适应雾化过程瞬时变化的多尺度问题求解, 因而计算效果不佳。而图 12(c)和图 12(d)分别为Gerris数值计算和实验拍摄的锥形液膜雾化过程, 捕捉到液膜锥角、液膜破碎长度、液丝和液滴等结构, 两者基本吻合。可见, Gerris对雾化过程的细节捕捉能力优于Fluent等其他仿真手段, 同时也表明基于Gerris软件建立的计算方法是准确可靠的, 可以得到与实验基本吻合的锥形液膜雾化场细节结构。
|
Fig. 12 Snapshot of the conical liquid sheet spray process |
基于Gerris采用的自适应网格技术和VOF方法, 建立了一种模拟旋流液膜雾化破碎过程的数值方法, 得到的主要结论如下:
(1) 基于Gerris建立的旋流液膜计算模型, 对其雾化破碎过程计算得很细致, 能够逼真地展示旋流液膜破碎成液丝、液丝进一步破碎成液滴的全过程, 能细致地捕捉到雾化过程中的细节特征, 与高速摄影拍摄的雾化破碎过程吻合较好, 对比其他仿真方法的结果, 表明Gerris对雾化过程细节捕捉的细腻程度较其他手段具有显著的优势。
(2) Gerris能捕获到全场液滴空间分布, 液滴捕捉的视觉效果近乎逼真; 捕捉到的液滴数目众多且尺寸变化范围大, 液滴粒径分布与实际雾化过程相符, 与文献中实验测量的液滴粒径分布相比, 分布曲线峰值对应的液滴直径的差值为1.8μm, 相对误差为13.8%, 两者结果基本吻合, 表明建立的计算方法具有较高的准确性。
(3) 通过对旋流液膜破碎过程的精细仿真, 存在二次雾化现象, 液丝在运动过程中受到气体力和表面张力的作用, 开始断裂形成大液滴, 液滴的形状也不规则, 随着进一步收缩破碎成小液滴, 形状渐渐接近球形。
(4) 带旋转速度的直射流和空心旋流式锥形液膜的液滴空间分布存在不同, 前者液滴在锥形区域内都有分布, 而后者液滴只分布在锥形液膜两侧的环形区域, 这与初始的液膜的形成有关。
旋流式液膜雾化是一种重要的雾化方式, 在航天动力领域有着重要应用。随着我国新一代大推力运载火箭以及未来重型运载火箭的研制, 离心式喷嘴在其中得到了广泛的应用, 特别是液氧煤油火箭发动机中。离心式喷嘴产生的旋流式锥形液膜是喷雾燃烧领域重要的研究方向, 而且基于本文建立的计算方法得到的仿真结果已经显示出比其他仿真手段更大的优势, 今后会更趋于成熟。下一步会在本文建立的旋流式液膜雾化过程计算方法的基础上不断完善, 进一步开展离心式喷嘴全流场雾化过程和雾化特性的一体化仿真计算, 精细地研究内部流动过程和外部雾化过程, 借助仿真手段的优势深入探究流动参数、结构参数及介质物性参数对雾化特性的影响规律, 并以计算结果为基础, 总结得到离心式喷嘴的雾化特性经验关系式, 形成一种可靠的喷嘴性能设计和评估方法, 逐步替代需要大量人力、物力、财力的实验研究。
致谢 此项工作是在国家超级计算天津中心的“天河一号”超级计算机上完成, 感谢“天河一号”的大力支持。
| [1] |
王成军, 陈海耿, 张宝诚. 双路离心式喷嘴的实验与数值模拟[J]. 工程热物理学报, 2010, 31(10): 1797-1799. (  0) 0) |
| [2] |
York J L, Stubbs H F, Tek M R. The Mechanism of Disintegration of Liquid Sheets[J]. Transactions of ASME, 1953, 75: 1279-1286.
(  0) 0) |
| [3] |
Squire H B. Investigation of the Instability of a Moving Liquid Film[J]. British Journal of Applied Physics, 1953, 4(6): 167-169. DOI:10.1088/0508-3443/4/6/302
(  0) 0) |
| [4] |
Fraser R P. Liquid Fuel Atomization[J]. Symposium (International) on Combustion, 1957, 6(1): 687-701. DOI:10.1016/S0082-0784(57)80096-4
(  0) 0) |
| [5] |
Youngbin Yoon, In-Seuk Jeung. Effects of Ambient Gas Pressure on the Breakup of Sprays in Like-Doublet and Swirl Coaxial Injectors[C]. Istanbul: International Symposium on Energy Conversion Fundamentals, 2004.
(  0) 0) |
| [6] |
Loustalan Paul W, Davy Martin H, Williams Paul A. Experimental Investigation into the Liquid Sheet Break-Up of High-Pressure DISI Swirl Atomizers[C]. Warrendale, PA: SAE International, 2003.
(  0) 0) |
| [7] |
YUE Ming, XU Hang, YANG Mao-lin, et al. Study on Breakup of Conical Liquid Sheet under Varying Flow Conditions[J]. Chinese Journal of Aeronautics, 2003, 16(1): 12-14. DOI:10.1016/S1000-9361(11)60164-7
(  0) 0) |
| [8] |
刘娟, 李清廉, 刘卫东, 等. 离心式喷嘴液膜破碎过程实验[J]. 推进技术, 2011, 32(4): 539-543. (LIU Juan, LI Qing-lian, LIU Wei-dong, et al. Experiment on Liquid Sheet Breakup Process of Pressure Swirl Injector[J]. Journal of Propulsion Technology, 2011, 32(4): 539-543.)
(  0) 0) |
| [9] |
岳明, 徐茂林. 锥形液膜空间稳定性分析[J]. 航空动力学报, 2003, 18(6): 794-798. (  0) 0) |
| [10] |
徐让书, 年帅奇, 牛玲, 等. 离心式喷嘴内部流动与液膜初始破碎的耦合模拟[J]. 沈阳工业大学学报, 2011, 33(6): 661-666. (  0) 0) |
| [11] |
刘娟. 旋转锥形液膜破碎过程实验与仿真研究[D]. 长沙: 国防科学技术大学, 2012.
(  0) 0) |
| [12] |
Olivier Desjardins, McCaslin Jeremy O, Mark Owkes, et al. Direct Numerical and Large-Eddy Simulation of Primary Atomization in Complex Geometries[J]. Atomization and Sprays, 2013, 23(11): 1001-1048. DOI:10.1615/AtomizSpr.v23.i11
(  0) 0) |
| [13] |
Ma Dong-Jun, Chen Xiao-Dong, Prashant Khare, et al. Atomization Patterns and Breakup Characteristics of Liquid Sheets Formed by Two Impinging Jets[R]. AIAA 2011-97.
(  0) 0) |
| [14] |
Xiaodong Chen, Dongjun Ma, Vigor Yang, et al. High-Fidelity Simulations of Impinging Jet Atomization[J]. Atomization and Sprays, 2013, 23(12): 1079-1101. DOI:10.1615/AtomizSpr.v23.i12
(  0) 0) |
| [15] |
Xiaodong Chen, Dongjun Ma, Vigor Yang. Mechanism Study of Impact Wave in Impinging Jets Atomization [R]. AIAA 2012-1089.
(  0) 0) |
| [16] |
李佳楠, 费俊, 杨卫东, 等. 直流互击式喷注单元雾化特性准直接数值模拟[J]. 推进技术, 2016, 37(4): 713-725. (LI Jia-nan, FEI Jun, YANG Wei-dong, et al. Quasi-Direct Numerical Simulation on Atomization Characteristics of Impinging Jets Injector[J]. Journal of Propulsion Technology, 2016, 37(4): 713-725.)
(  0) 0) |
| [17] |
Daniel Fuster, Anne Bagué, Stéphane Popinet, et al. Simulation of Primary Atomization with an Octree Adaptive Mesh Refinement and VOF Method[J]. International Journal of Multiphase Flow, 2009, 35(6): 550-565. DOI:10.1016/j.ijmultiphaseflow.2009.02.014
(  0) 0) |
| [18] |
阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望[J]. 力学进展, 2011, 41(5): 562-589. DOI:10.6052/1000-0992-2011-5-lxjzJ2010-082 (  0) 0) |
| [19] |
Mehravaran K. Direct Simulation of Primary Atomization in Moderate-Speed Diesel Fuel Injection[J]. International Journal of Materials, Mechanics and Manufacturing, 2013, 1(2): 207-209.
(  0) 0) |
| [20] |
Stéphane Popinet. An Accurate Adaptive Solver for Surface-Tension-Driven Interfacial Flows[J]. Journal of Computational Physics, 2009, 228(16): 5838-5866. DOI:10.1016/j.jcp.2009.04.042
(  0) 0) |
| [21] |
Shahriar Afkhami, Yuriko Renardy. A Volume-of-Fluid Formulation for the Study of Co-Flowing Fluids Governed by the Hele-Shaw Equations[J]. Physics of Fluids, 2013, 25(8): 0820011-0820019.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


