轻质量、小体积的新型热气自增压系统有利于增加推进系统的安全性和可靠性,对应用于航天器轨道调节和姿态控制等的小推力发动机系统提供了新的可选方案。差动活塞式热气自增压系统是液体工质热气自增压系统的一种[1],其利用单组元肼类工质通过催化分解来产生热增压气体,并具有正反馈、自增压和自锁功能。该增压系统工作状态的变化,对姿轨控动力系统的性能有重要影响。
在过去针对液体姿轨控发动机或空间推进系统静态特性研究中,陈杰引入图论理论提出了一种发动机系统动力平衡的通用算法[2],针对空间推进系统推导了系统液路和气路通用积分形式方程,给出了不同部件以压力为自变量表示流量的部件静态数学模型[3];蒋志坚等[4]给出了一种面向对象的空间推进系统通用静态仿真方法;李家文等[5]提出了在动态模型基础上建立和求解空间推进系统静态特性仿真模型的方法;李晓瑾等[6]运用变尺度牛顿迭代法计算了典型双组元姿轨控发动机的静态特性;陈朝等[7]采用了模块化方法对空间轨道转移飞行器推进系统进行静态研究。已开展的有关差动活塞式热气自增压系统的研究涉及了Maybee J C[1],Whitehead J C[8~10],Ly⁃ don M M等[11]对系统原理和试验研究、刘洌等[12]对液体姿轨控发动机增压系统方案选择中液体热气自增压与固体热气自增压以及冷气增压的研究对比以及方忠坚等[13]对系统参数设计方法的研究等。这些研究多集中于姿轨控发动机系统静态特性和差动活塞式热气自增压系统方案、设计及试验等方面,而差动活塞式热气自增压系统静态特性研究工作的文献资料还未见到,因此有必要通过开展差动活塞式热气自增压系统静态特性研究,以获得其主要部件重要参数对系统工作参数的影响规律,为系统参数的设计和性能评估提供可靠的依据。
本文将采用集中参数法,根据系统平衡的参数计算方法,以液体姿轨控发动机差动活塞式热气自增压系统静态工作过程中流量、压力、力、位移等物理量满足的平衡条件,通过补充各组件流量方程,构建系统的静态特性计算模型,给出系统自锁后状态的计算方法,编制仿真程序,研究系统参数变化的影响规律。
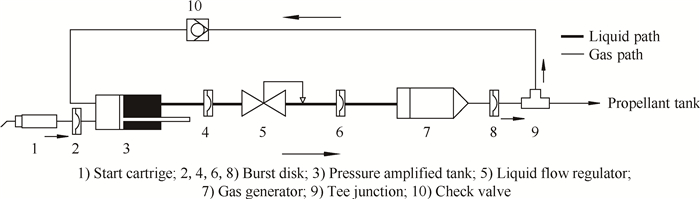
2 系统静态特性计算模型液体姿轨控发动机差动活塞式热气自增压系统静态工作点由系统内介质的压力平衡、流量平衡和热力平衡以及结构的受力平衡和位移平衡等关系确定。压力、流量、力、位移、热力学等五者的平衡,构成了系统静态特性计算准则。本节给出差动活塞式热气自增压系统平衡方程、补充方程、系统静态模型、计算方法和流程,以及系统自锁后压力状态计算模型。系统示意图如图 1所示,其详细工作原理见文献[13]。
|
Fig. 1 Schematic diagram of the differential piston warm gas self-pressurization system |
热气自增压系统压力放大贮箱采用差动活塞式结构,活塞两端分别为气体腔和液体腔。在压力放大贮箱工作过程中,活塞受力运动而产生位移,因此气体腔长度的增加量和液体腔长度的减小量相等,满足以下位移平衡方程
| $ \frac{{{q_{{\rm{m\_g}}}}}}{{{\rho _{\rm{g}}}{A_{\rm{g}}}}} = \frac{{{q_{{\rm{m\_l}}}}}}{{{\rho _{\rm{l}}}{A_{\rm{l}}}}} $ | (1) |
式中qm_g,qm_l分别为气体腔和液体腔质量流量;Ag,Al分别为气体腔和液体腔截面积;ρg, ρl为气体密度和液体密度。
2.2 受力平衡热气自增压系统中存在两个动件:压力放大贮箱活塞和流量调节器阀芯。在系统稳态工作过程中,压力放大贮箱活塞保持匀速运动状态,流量调节器阀芯保持恒定开度,活塞和阀芯均处于受力平衡状态。
活塞受力平衡方程[13]
| $ {\rho _{\rm{g}}}{A_{\rm{g}}} - {\rho _{\rm{l}}}{A_{\rm{l}}} - {p_{\rm{a}}}\left( {{A_{\rm{g}}} - {A_{\rm{l}}}} \right) - {F_{\rm{f}}} = 0 $ | (2) |
阀芯受力平衡方程[13]
| $ {p_{{\rm{reg1}}}}{A_{\rm{i}}} + {p_{{\rm{reg2}}}}{A_{\rm{o}}} - K\left( {{x_{{\rm{off}}}} - h} \right) - {p_{\rm{a}}}{A_{{\rm{oa}}}} = 0 $ | (3) |
式中pg,pl,pa分别为压力放大贮箱气体腔压力、液体腔压力和环境压力;Ff为活塞所受滑动摩擦力,根据压力放大贮箱冷流试验结果取Ff =2kN;h,K,xoff为流量调节器的开度、弹簧刚度和阀门关闭时阀芯位移(阀门原始开度);preg1,preg1分别为流量调节器入口腔和出口腔压力;Ai,Ao,Aoa为入口腔阀芯受力面积、出口腔阀芯等效受力面积和膜片受环境压力作用的等效面积。
2.3 流量平衡根据图 1所示系统的特点,系统可以划分为三条流路。从压力放大贮箱液体腔经过液体管道、流量调节器、燃气发生器一直到三通的流路为第一条流路;从三通经过气体管道、单向阀进入压力放大贮箱气体腔的流路为第二条流路;最后一条为从三通经过气体管道进入下游推进剂贮箱的流路。
在系统稳态工作过程中,每条流路中流经各组件的质量流量是相等的,故系统中只存在三个独立的流量变量。三个流量变量在三通气体管道处产生联系,满足流量平衡方程,即
| $ {q_{{\rm{m\_main}}}} = {q_{\rm{m}}} + {q_{{\rm{m\_self}}}} $ | (4) |
式中qm_main为第一条流路即主流路流量;qm_self为从三通流向压力放大贮箱气体腔流路的流量,即自增压流量;qm为通往下游贮箱的增压气体流量,即增压流量。
2.4 压力平衡每一元件(包括管道),其入口压力pin,出口压力pout和压降Δp满足如下平衡关系
| $ {p_{{\rm{in}}}} - {p_{{\rm{out}}}} = \Delta p $ | (5) |
对于相连两元件,上游元件1出口压力p1out等于下游元件2的入口压力p2in,即
| $ {p_{{\rm{1out}}}} = {p_{{\rm{2in}}}} $ | (6) |
当给定下游推进剂贮箱所需增压压力时,沿着流路通过以上压力平衡方程可以确定系统各结点压力。计算时为减少变量数从而减少方程数量并简化方程组,对于相连元件,上游元件出口与下游元件入口均取接点处同一压力值。
2.5 热力平衡对于肼、水组成的肼类工质,在系统工作过程中,其进入燃气发生器后,经催化剂床催化分解产生一系列化学反应,生成高温、高压的氨、氮、氢、水混合气体。其中化学反应主要包括肼催化分解反应和氨解离平衡反应。
肼完全催化分解式为
| $ {{\rm{N}}_2}{{\rm{H}}_4}\xrightarrow{{{\rm{catalysis}}}}\frac{4}{3}{\rm{N}}{{\rm{H}}_3} + \frac{1}{3}{{\rm{N}}_2} $ | (7) |
氨解离平衡反应式为
| $ {\rm{N}}{{\rm{H}}_3} \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over {\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} \frac{1}{2}{{\rm{N}}_2} + \frac{3}{2}{{\rm{H}}_2} $ | (8) |
设工质中肼和水的摩尔数比为a:c,氨的解离度为y(取值范围为0.5~0.55),则催化分解式为
| $ \begin{array}{*{20}{c}} {a{{\rm{N}}_2}{{\rm{H}}_4} + c{{\rm{H}}_2}{\rm{O}}\xrightarrow{{{\rm{catalysis}}}}\frac{{4a}}{3}\left( {1 - y} \right){\rm{N}}{{\rm{H}}_3} + \frac{a}{3}\left( {2y + 1} \right){{\rm{N}}_2} + } \\ {2ay{{\rm{H}}_2} + c{{\rm{H}}_2}{\rm{O}}} \end{array} $ | (9) |
燃气发生器稳态工作过程中处于热力平衡状态,因此可根据文献[14]中的热力计算方法利用燃烧室压力(取其设计值,为下游推进剂贮箱额定工作压力与燃气发生器和推进剂贮箱间管路压降之和)、工质中肼和水的质量百分数以及氨的解离度,依据上述化学反应关系进行燃气发生器热力计算,得到燃气温度、气体常数、组分摩尔分数等参数,最终确定系统静态仿真过程中所需的燃气粘性系数和密度等,这些参数在静态仿真过程中近似认为不发生变化。为简单起见,认为催化效率是100%。
2.6 补充关系以上建立了系统各平衡关系,但对于系统流量和压力,需找出两者之间的联系,才能构筑封闭的系统静态特性计算方程组。对于各组件,其压力和流量从流阻方程中构成联系,因此,流阻方程经过转化,可以得到各组件的流量方程。
燃气发生器毛细管质量流量方程
| $ {q_{{\rm{m\_main}}}} = {\left( {{H_{{\rm{cpl}}}} + \frac{{0.3164{l_{{\rm{cpl}}}}}}{{\mathit{Re}_{{\rm{cpl}}}^{0.25}{d_{{\rm{cpl}}}}}}} \right)^{ - 0.5}}{N_{{\rm{cpl}}}}{A_{{\rm{cpl}}}}\sqrt {2{\rho _{\rm{l}}}\left( {{p_{{\rm{cpl1}}}} - {p_{{\rm{cpl2}}}}} \right)} $ | (10) |
式中pcpl1,pcpl2为毛细管入口压力、出口压力;Recpl为毛细管雷诺数;Ncpl,lcpl,dcpl,Acpl,Hcpl为毛细管数量、毛细管长度、毛细管内径、单根毛细管流通面积、流阻系数,取Hcpl=1.5 [14]。
燃气发生器催化剂床质量流量方程
| $ {q_{{\rm{m\_main}}}} = \frac{{{A_{{\rm{cb}}}}\sqrt {2{\rho _{\rm{g}}}\left( {{p_{{\rm{cb}}}} - {p_{{\rm{cpl2}}}}} \right)} }}{{\sqrt {2{L_{{\rm{cb}}}}\left[ {{A_{\rm{c}}}\frac{{{\mu _{{\rm{cb}}}}}}{{{v_{{\rm{cb}}}}{\rho _{\rm{g}}}d_{\rm{p}}^2}}\frac{{{{\left( {1 - \varepsilon } \right)}^2}}}{{{\varepsilon ^3}}} + {B_{\rm{c}}}\frac{1}{{{d_{\rm{p}}}}}\frac{{1 - \varepsilon }}{{{\varepsilon ^3}}}} \right]} }} $ | (11) |
式中pcb为催化剂床出口压力(燃气发生器室压),Acb,Lcb分别为催化剂床截面积、床长,dp为催化剂颗粒直径,ε为孔隙率,μcb,vcb分别为催化剂床流体动力粘度、表观速度,经验常数Ac =180,Bc =1.80 [15]。
流量调节器质量流量方程
| $ {q_{{\rm{m\_main}}}} = {C_{{\rm{d\_reg}}}}{\rm{ \mathsf{ π} }}{d_{{\rm{reg}}}}h\sqrt {2{\rho _{\rm{l}}}\left( {{p_{{\rm{reg1}}}} - {p_{{\rm{reg2}}}}} \right)} $ | (12) |
式中Cd_reg为阀芯流量系数,dreg为阀芯入口直径。
管道质量流量方程
| $ {q_{{\rm{m\_pipe}}}} = \sqrt {\frac{{{D_{{\rm{pipe}}}}}}{{{f_{{\rm{pipe}}}}{l_{{\rm{pipe}}}}}}} {A_{{\rm{pipe}}}}\sqrt {2{\rho _{{\rm{pipe}}}}\left( {{p_{{\rm{pipe1}}}} - {p_{{\rm{pipe2}}}}} \right)} $ | (13) |
式中qm_pipe,ppipe1,ppipe2为管道质量流量、管道入口压力和出口压力;ρpipe为管道内流体密度;Apipe,Dpipe,fpipe,lpipe为管道截面积、水力直径、流阻系数、管道长度;管道质量流量等于其所在流路质量流量。
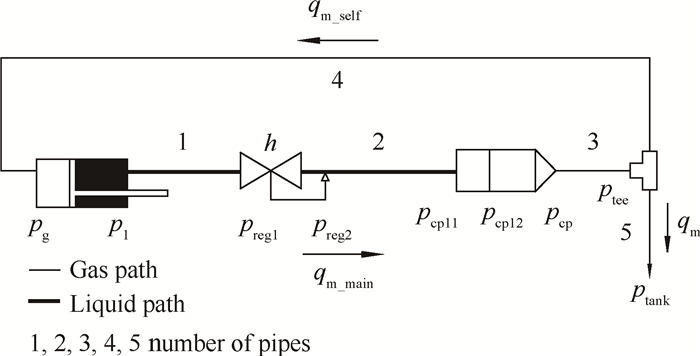
2.7 系统模型建立系统静态模型时,起动药盒不计入系统。系统流路上膜片阀在系统起动完成后均已破裂打开,自增压气路上的单向阀在系统稳态工作过程中也处于打开状态,因此在进行系统静态特性计算时,可略去膜片阀压降,将单向阀压降作为已知局部压降取为0.1MPa归入系统流路。系统的静态模型如图 2所示,由压力放大贮箱、流量调节器、燃气发生器、三通、5根管道等9个元件组成。
|
Fig. 2 Static model of the differential piston warm gas selfpressurization system |
把上述平衡方程和补充方程整合得到系统静态模型方程组为
| $ \left\{ \begin{array}{l} {q_{{\rm{m\_main}}}} - {C_{{\rm{d\_1}}}}{A_{{\rm{pipe\_1}}}}\sqrt {2{\rho _{\rm{l}}}\left( {{p_{\rm{l}}} - {p_{{\rm{reg1}}}}} \right)} = 0\\ {q_{{\rm{m\_main}}}} - {C_{{\rm{d\_reg}}}}{\rm{ \mathsf{ π} }}{d_{{\rm{reg}}}}h\sqrt {2{\rho _{\rm{l}}}\left( {{p_{{\rm{reg1}}}} - {p_{{\rm{reg2}}}}} \right)} = 0\\ {q_{{\rm{m\_main}}}} - {C_{{\rm{d\_2}}}}{A_{{\rm{pipe\_2}}}}\sqrt {2{\rho _{\rm{l}}}\left( {{p_{{\rm{reg2}}}} - {p_{{\rm{cpl1}}}}} \right)} = 0\\ {q_{{\rm{m\_main}}}} - {C_{{\rm{d\_cpl}}}}{N_{{\rm{cpl}}}}{A_{{\rm{cpl}}}}\sqrt {2{\rho _{\rm{l}}}\left( {{p_{{\rm{cpl1}}}} - {p_{{\rm{cpl2}}}}} \right)} = 0\\ {q_{{\rm{m\_main}}}} - {C_{{\rm{d\_cb}}}}{A_{{\rm{cb}}}}\sqrt {2{\rho _{\rm{g}}}\left( {{p_{{\rm{cpl2}}}} - {p_{{\rm{cb}}}}} \right)} = 0\\ {q_{{\rm{m\_main}}}} - {C_{{\rm{d\_3}}}}{A_{{\rm{pipe\_3}}}}\sqrt {2{\rho _{\rm{g}}}\left( {{p_{{\rm{cb}}}} - {p_{{\rm{tee}}}}} \right)} = 0\\ {q_{{\rm{m\_self}}}} - {C_{{\rm{d\_4}}}}{A_{{\rm{pipe\_4}}}}\sqrt {2{\rho _{\rm{g}}}\left( {{p_{{\rm{tee}}}} - {p_{\rm{g}}}} \right)} = 0\\ {q_{\rm{m}}} - {C_{{\rm{d\_5}}}}{A_{{\rm{pipe\_5}}}}\sqrt {2{\rho _{\rm{g}}}\left( {{p_{{\rm{tee}}}} - {p_{{\rm{tank}}}}} \right)} = 0\\ {q_{{\rm{m\_main}}}} - {q_{\rm{m}}} - {q_{{\rm{m\_self}}}} = 0\\ \frac{{{q_{{\rm{m\_self}}}}}}{{{\rho _{\rm{g}}}{A_{\rm{g}}}}} - \frac{{{q_{{\rm{m\_main}}}}}}{{{\rho _{\rm{l}}}{A_{\rm{l}}}}} = 0\\ {\rho _{\rm{g}}}{A_{\rm{g}}} - {\rho _{\rm{l}}}{A_{\rm{l}}} - {p_{\rm{a}}}\left( {{A_{\rm{g}}} - {A_{\rm{l}}}} \right) - {F_{\rm{f}}} = 0\\ {p_{{\rm{reg1}}}}{A_{\rm{i}}} + {p_{{\rm{reg2}}}}{A_{\rm{o}}} - K\left( {{x_{{\rm{off}}}} - h} \right) - {p_{\rm{a}}}{A_{{\rm{oa}}}} = 0 \end{array} \right. $ | (14) |
式中
| $ {C_{{\rm{d\_cpl}}}} = {\left[ {{H_{{\rm{cpl}}}} + 0.3164{l_{{\rm{cpl}}}}/\left( {\mathit{Re}_{{\rm{cpl}}}^{0.25}{d_{{\rm{cpl}}}}} \right)} \right]^{ - 0.5}} $ | (15) |
| $ {C_{{\rm{d\_cb}}}} = {\left[ {2{L_{{\rm{cb}}}}\left( {A\frac{{{\mu _{{\rm{cb}}}}}}{{{v_{{\rm{cb}}}}{\rho _{\rm{g}}}d_{\rm{p}}^2}}\frac{{{{\left( {1 - \varepsilon } \right)}^2}}}{{{\varepsilon ^3}}} + B\frac{1}{{{d_{\rm{p}}}}}\frac{{1 - \varepsilon }}{{{\varepsilon ^3}}}} \right)} \right]^{ - 0.5}} $ | (16) |
式(14)中有pg,pl,preg1,preg2,pcpl1,pcpl2,pcb,ptee,qm_main,qm_self,qm,h共12个待求系统工作状态参数。
2.8 计算方法由式(14)可把热气自增压系统静态特性数学模型统一表达如下
| $ {f_i}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{C}}} \right) = 0,\;\;i = 1,2, \cdots ,n $ | (17) |
式中X为未知量,包括热气自增压系统质量流量、压力、流量调节器开度等状态参数;C为常量,主要含有系统组件结构、特性等参数,如压力放大贮箱气体腔内径、流量系数等;n为方程数或待求变量数,n =12。
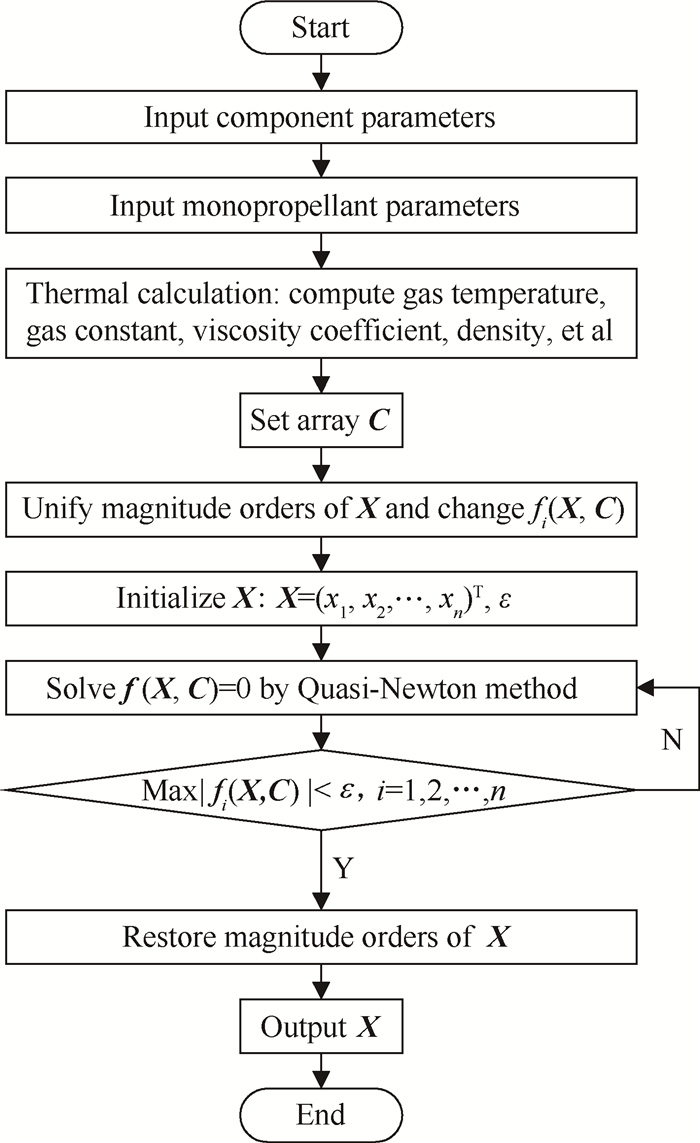
本文主要研究系统结构、特性参数(C)对系统状态参数(X)的影响规律。系统静态特性数学方程组为非线性方程组,采用拟牛顿法对其进行仿真求解。系统静态仿真过程如图 3所示。
|
Fig. 3 Flow chart of static characteristic simulation |
因系统流量、压力和流量调节器开度等变量的数值数量级不一致,差距很大,因此在方程组求解前应对各变量数量级进行统一处理,以避免在方程组求解时产生不收敛情况。如图 3所示,即将各不同量级变量乘以各自对应的系数使其变为同一数量级数值,再在各自变量所在方程中的相应位置除以各自系数以消除量级变化带来的影响,求解完毕还原变量数量级即为求解结果。
2.9 系统自锁后状态计算模型当系统起动充填完毕或下游发动机工作一段时间关闭后,增压系统连同推进剂贮箱会在一定时间内达到自锁状态,在该状态下从流量调节器出口腔到燃气发生器再到气体管道以及压力放大贮箱气体腔和下游推进剂贮箱均稳定在自锁气体压力下,压力放大贮箱液体腔和流量调节器入口腔稳定在自锁液体压力下。假定系统自锁过程是准稳态推进的,应用压力放大贮箱活塞受力平衡方程和流量调节器阀芯受力平衡方程,即可计算自锁状态的自锁气体压力pg_off和自锁液体压力pl_off,计算方程见文献[13],影响自锁状态的主要参数包括Ag,Al,Ff,pa,Ai,Ao,K,xoff,Aoa等,它们作为计算的输入条件。
3 仿真结果与讨论根据上述仿真模型,对图 2所示的差动活塞式热气自增压系统进行实例仿真分析。该系统工质采用肼70,下游发动机贮箱压力额定值为6.9MPa,系统详细设计参数参见文献[13],本文研究的关键参数列于表 1中,dg,dl,Kp分别为压力放大贮箱气体腔内径、液体腔内径和压力放大比。
|
|
Table 1 Known system parameters |
下游推进剂贮箱压力为额定增压压力时计算所得系统静态工作点及其与设计值的对比情况如表 2所示。表中计算值为系统设计状态下的稳态工作点参数,除流量调节器开度外,参数偏差均小于3%,如系统额定增压流量设计值为30.000g/s,本文计算值为29.497g/s,计算偏差为-1.68%。
|
|
Table 2 Comparison of simulation and design values at nominal conditions |
流量调节器开度的计算偏差为-14.25%,稍微偏大,是因为在系统设计过程中采取了对流量调节器入口腔与出口腔取相等压力变化(关闭状态和额定状态下的压力差值)的简化处理。
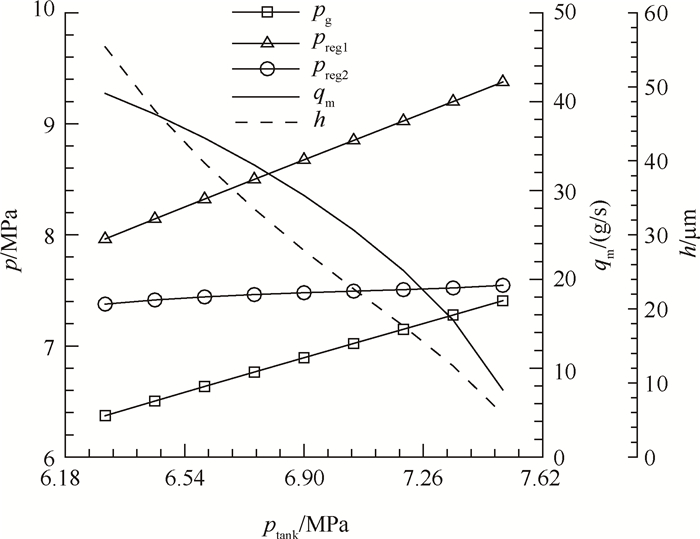
3.2 系统参数对工作状态的影响图 4为系统工作状态参数随推进剂贮箱压力变化规律。随着下游贮箱压力的增大,流量调节器入口腔压力增大,出口腔压力变化很小,流量调节器压降增大;流量调节器开度和增压流量均随推进剂贮箱压力的增大而减小,当推进剂贮箱压力从6.3MPa增大到7.5MPa时,增压流量从42g/s减小到8g/s。可见,增压流量对推进剂贮箱压力的变化比较敏感,其朝着抑制推进剂贮箱压力变化的方向而变化,起到调节和稳定推进剂贮箱压力的作用。
|
Fig. 4 System state parameters versus propellant tank pressure |
图 5为热气自增压系统工作状态参数随系统参数的变化规律。图 5(a)~(c)分别为系统状态参数随压力放大贮箱气体腔内径、液体腔内径和活塞摩擦力的变化规律。随着气体腔(液体腔)内径的增大,流量调节器入口腔压力增大(减小),调节器开度减小(增大),增压流量先增大后减小,流量调节器出口腔压力和压力放大贮箱气体腔压力变化很小。在偏离气体腔(液体腔)内径设计值朝着使压力放大贮箱压力放大比减小的方向变化时,系统增压流量和流量调节器开度均加速变化;反之,系统增压流量和流量调节器开度变化较平缓。当压力放大比在设计值附近[-7.3%,+9.6%](对应压力放大比为[1.138,1.346])的区间变化时,系统稳态工作增压流量偏差保持在[-5%,0%]内(对应增压流量为28.5~30.0g/ s)。当压力放大比小于设计值且压力放大贮箱气体腔(液体腔)内径朝着使压力放大比减小的方向变化时,系统增压气体流量加速减小,增压能力急剧降低。随着压力放大贮箱活塞摩擦力的增大,流量调节器入口腔压力和压降减小,流量调节器开度和系统增压流量在小范围内呈现增大的变化趋势。

|
Fig. 5 System state parameters versus system parameters |
燃气发生器毛细管参数的变化主要对系统增压流量和流量调节器开度造成影响。增压流量和流量调节器开度随毛细管内径的增大而增大,如图 5(d)所示;随毛细管长度的增大而减小,如图 5(e)所示。其内径与长度相比,毛细管内径的变化对系统状态参数的影响作用更大。
从图 5(f)和图 5(g)可以看出,随着流量调节器出口腔(或入口腔)阀芯受力面积的增加,流量调节器出口腔压力、开度和增压流量均减小,但上述参数随流量调节器入口腔阀芯受力面积变化的影响小于随流量调节器出口腔阀芯受力面积变化的影响,即系统状态参数对流量调节器出口腔阀芯受力面积的变化更为敏感。
图 5(h)和图 5(i)分别为系统状态参数随流量调节器弹簧刚度和流量调节器原始开度的变化规律。随着流量调节器弹簧刚度(或原始开度)的增大,图示主要状态参数均增大,且流量调节器出口端压力、流量调节器开度和增压流量均较大幅度的增加。因此,流量调节器弹簧刚度和原始开度的变化对系统状态的影响较大。
3.3 系统参数对自锁压力的影响系统主要参数变化时所引起的系统自锁压力变化规律如图 6所示。

|
Fig. 6 Influences on self-locking pressures of the pressurization system from system parameter variations |
图 6(a)~(c)分别为系统自锁随压力放大贮箱气体腔内径、液体腔内径以及活塞摩擦力的变化规律。随着压力放大贮箱气体腔内径的增大,自锁液体压力增大,自锁气体压力减小;随着液体腔内径或活塞摩擦力的增大,自锁液体压力减小,自锁气体压力增大。上述自锁气体压力的变化均相对较小。
图 6(d)~(g)分别为系统自锁压力随流量调节器出口腔阀芯受力面积、入口腔阀芯受力面积、弹簧刚度和原始开度的变化规律。系统自锁液体压力和自锁气体压力均随入口腔和出口腔阀芯受力面积的增大而减小。随着流量调节器弹簧刚度或原始开度的增大,系统自锁液体压力和自锁气体压力均增大。自锁气体压力随流量调节器参数变化的影响较大。
从上述结果可以看出,压力放大贮箱参数的变化对自锁液体压力有明显影响,但其对流量调节器下游自锁气体压力的影响比较微弱。流量调节器参数的变化对自锁液体压力和自锁气体压力均有较大的影响作用。由文献[13]知,系统自锁气体压力值即为下游推进剂贮箱的压力上偏差(最大工作压力),因此为满足推进剂贮箱在其允许的压力范围内工作,需严格保证流量调节器参数的精度。
4 结论本文构建了液体姿轨控发动机差动活塞式热气自增压系统的静态特性计算模型,编制了仿真程序,研究了主要系统参数对系统状态的影响规律,结果表明:
(1)增压气体流量对下游推进剂贮箱压力的变化比较敏感,随着推进剂贮箱压力的变化,增压气体流量朝着推进剂贮箱压力变化相反的方向而变化,起到调节和稳定推进剂贮箱压力的作用。
(2)燃气发生器毛细管参数的变化主要对系统增压气体流量造成影响,增压气体流量随毛细管内径的增大而增大,随毛细管长度的增大而减小;其内径与长度相比,毛细管内径的变化对系统状态参数的影响作用更大。
(3)当压力放大比在设计值附近[-7.3%,+9.6%]的区间变化时,系统稳态工作增压流量偏差保持在[-5%,0%]内;当压力放大比小于设计值且压力放大贮箱内径朝着使压力放大比减小的方向变化时,系统增压气体流量加速减小,增压能力急剧降低。
(4)流量调节器下游压力和增压气体流量随弹簧刚度和原始开度的增大而增大;随入口腔和出口腔阀芯受力面积的增大而减小。较入口腔阀芯受力面积变化的影响而言,系统状态参数对流量调节器出口腔阀芯受力面积的变化更为敏感。流量调节器结构参数的微小变化都会引起增压气体流量的较大变化,因此调节器结构参数是系统的关键设计参数。
(5)系统自锁气体压力(即推进剂贮箱最大工作压力)受流量调节器参数影响较大。为满足推进剂贮箱在其允许的压力范围内工作,需严格保证流量调节器参数的精度。
| [1] |
Maybee J C, David J K. A Novel Design Warm Gas Pressurization System[R]. AIAA 98-4014.
(  0) 0) |
| [2] |
陈杰. 液体火箭发动机系统动力平衡参数通用计算方法[J]. 上海航天, 1991(4): 1-5. (  0) 0) |
| [3] |
陈杰. 液体推进剂空间推进系统静态数学模型[J]. 上海航天, 1999(2): 11-15. (  0) 0) |
| [4] |
蒋志坚, 张黎辉, 李家文. 空间推进系统静态特性通用仿真研究[J]. 推进技术, 2003, 24(5): 448-451. (JIANG Zhi-jian, ZHANG Li-hui, LI Jia-wen. Versatile Numerical Simulation on Static Characteristics of Space Propulsion Systems[J]. Journal of Propulsion Technology, 2003, 24(5): 448-451.)
(  0) 0) |
| [5] |
李家文, 张黎辉, 张雪梅, 等. 空间推进系统静动态仿真软件研究[J]. 推进技术, 2004, 25(2): 148-151. (LI Jia-wen, ZHANG Li-hui, ZHANG Xue-mei, et al. Simulation Software for the Static and Dynamic Characteristics of Space Propulsion System[J]. Journal of Propulsion Technology, 2004, 25(2): 148-151.)
(  0) 0) |
| [6] |
李晓瑾, 辛坤. 姿控发动机静态特性分析[J]. 火箭推进, 2003, 29(4): 24-29. (  0) 0) |
| [7] |
陈朝, 黄敏超. 空间轨道转移飞行器推进系统静态仿真分析[J]. 火箭推进, 2007, 33(6): 22-27. (  0) 0) |
| [8] |
Whitehead J C. Hydrogen Peroxide Propulsion for Smaller Satellites[R]. SSC 98-Ⅷ-1.
(  0) 0) |
| [9] |
Whitehead J C, Dittman M D, Ledebuhr A G. Progress Toward Hydrogen Peroxide Micropropulsion[R]. SSC 99-Ⅻ-5.
(  0) 0) |
| [10] |
Whitehead J C. Self-Pressurizing HTP Feed Systems [C]. USA: Second International Hydrogen Peroxide Propulsion Conference, 1999.
(  0) 0) |
| [11] |
Lydon M M, Polidor 2Lt M. Hydrogen Peroxide SelfPressurizing Storage Tank Test and Analysis[R]. AIAA 2004-4201.
(  0) 0) |
| [12] |
LIU Lie, LIANG Guo-zhu. Optimization Selection of Regulated Pressurization System Schemes for Liquid Attitude and Divert Propulsion Systems[J]. Procedia Engineering, 2015, 99: 1247-1251. DOI:10.1016/j.proeng.2014.12.655
(  0) 0) |
| [13] |
方忠坚, 刘洌, 梁国柱. 差动活塞式燃气自增压系统参数设计方法[J]. 北京航空航天大学学报, 2017, 43(1): 61-70. (  0) 0) |
| [14] |
周汉申. 单组元液体火箭发动机设计与研究[M]. 北京: 中国宇航出版社, 2009.
(  0) 0) |
| [15] |
MacDonald I F, El-Sayed M S, Mow K, et al. Flow Through Porous Media-the Ergun Equation Revised[J]. Ind. Eng. Chem. Fundamen, 1979, 18(3): 199-208. DOI:10.1021/i160071a001
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

