在压气机叶片两侧压差和动叶与机匣相对运动的共同作用下,一部分流体将穿过叶片与机匣间的间隙,在叶栅通道内形成叶顶间隙流,此流动为一种典型的二次流动[1]。这种靠近叶顶区域的二次流动通常以叶顶泄漏涡的形式存在。叶顶间隙流不仅能够造成泄漏损失,使得压气机效率降低,而且可能导致堵塞,从而降低压气机的压缩能力和稳定工作范围[2]。泄漏涡会产生周期性的波动以及涡的破碎[3],这种非定常流动会使得间隙涡占据流场中更大的区域,引起堵塞加剧[4],降低压气机的稳定裕度[5, 6],同时也降低了叶顶附近的气动载荷[7]。
随着计算能力的提高,大涡模拟(LES)技术逐渐应用于叶顶间隙流、分离泡、转逆以及再附着等压气机内部复杂流动的研究[8]。大涡模拟(LES)通过对N-S方程组进行直接求解获得大尺度高强度漩涡结构,同时通过亚网格尺度的近似模型计算小尺度低强度漩涡结构对大尺度高强度漩涡的影响[8]。大涡模拟(LES)对大尺度湍流结构的求解能够细致地刻画流动的非定常特征,其计算精度高于RANS湍流模型,一系列研究结果表明大涡模拟(LES)能够应用于叶顶区域泄漏涡的模拟并且精度满足工程需求[8]。
对于孤立转子,叶顶间隙流是否发生非定常波动的重要条件是叶顶泄漏涡形成的低压带是否造成相邻叶片的卸载[9]。低压带与相邻叶片压力面的碰撞将会导致二次泄漏流动的产生,同时也会造成叶片两侧压差的突变,破坏叶片力与叶片亏损力之间原有的静态平衡并使得流场建立起新的动态平衡,导致叶顶间隙流发生非定常波动[9]。后来林峰教授对此提出在失速先兆前易于捕捉非定常性的观点[10, 11],以及叶顶泄漏流轨迹与叶片前额线平齐时出现突尖型失速先兆的结论[12]。由于叶顶泄漏涡的非定常波动以及叶顶泄漏涡破碎引起的非定常波动都属于自激振动[9],所以存在相应频率下的稳定振荡模态。
为了分析泄漏涡在不同频率下的波动规律,本文采用大涡模拟(LES)数值计算方法求解低速孤立压气机叶栅非定常流场,并通过动力学模态分解(DMD)技术[13]对x/c=1.0677弦长处S3截面叶顶二次流速度场进行模态分析。动力学模态分解(DMD)基于大量离散流场样本,当样本足够多时,可以在样本间建立起一个线性关系。在时-空速度场中通过最小二乘法得到相邻两个时刻间的最优线性算子[14]。通过建立这个算子,动力学模态分解(DMD)可以基于这个映射的特征值和特征向量获取整个流场系统中的动力信息,在数据内部实现对整个系统的动力特性预估[15, 16]。相比快速傅立叶变换(FFT),动力学模态分解(DMD)技术提供了从复杂流场中提取单一频率拟序结构的能力,能够判断流场中某一频率波动在时间推进过程中是否中性稳定,并且能够得到各阶动态模态,为分析叶顶间隙流提供了可信的后处理手段。
本文通过求解x/c=1.0677弦长处S3截面叶顶二次流速度场动力学模态,对叶顶泄漏涡非定常波动的规律进行探讨和分析。
2 研究对象和数值方法针对美国空军大学的平面叶栅实验模型(图 1),计算中叶片采用的叶型(NACA64-A905),参数如表 1所示[17]。取文献[17]中τ=0.02相对间隙高度的实验结果作为参考,其中τ = τ/c为叶顶间隙高度与叶片弦长之比,即弦长c为衡量间隙的特征尺寸。通过设置移动上端壁边界条件(76.6m/s方向与实际叶片运动方向相反)模拟压气机转子与机匣间的相对运动。采用商用软件FLUENT对流场进行数值模拟[8]。压力速度耦合求解采用SIMPLEC算法,湍流模型采用大涡模拟(LES)方式,时间步长为2μs,约为一个工作周期的1/160。全场采用六面体结构化网格,叶片表面边界层采用O型网格进行处理,叶顶间隙处网格采用二次嵌套的H型网格进行处理,第一层网格无量纲高度y+<5,网格结构如图 1所示。叶片左右舷设置为周期性边界,进口边界给定速度38.3m/s,参考压力为一个标准大气压,出口边界为自由出流。
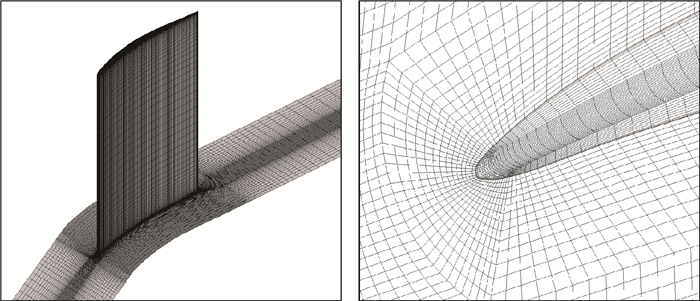
|
Fig. 1 Sketch of calculation grid |
|
|
Table 1 Main parameter of cascade |
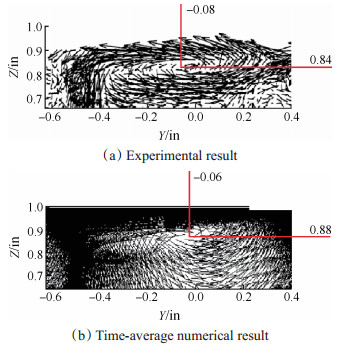
为验证数值计算的有效性,参考文献[1],对距离叶片前缘x/c=1.0677弦长处S3截面叶顶二次流非定常速度场进行采集,采集时间间隔为10μs,采集数量为1000个时间步,并将二次流速度场的时间平均计算结果与文献[17]中实验结果进行对比。如图 2所示(图中红线用于指示涡心的位置坐标),数值计算较好地模拟出了泄漏涡的位置及作用范围,这表明所采用的建模方案以及数值计算方法能够对移动端壁条件下的压气机叶栅叶顶间隙流动进行较为准确的模拟。
|
Fig. 2 Comparison between experimental and timeaveraged numerical results in section S3 at x/c=1.0677 chord length |
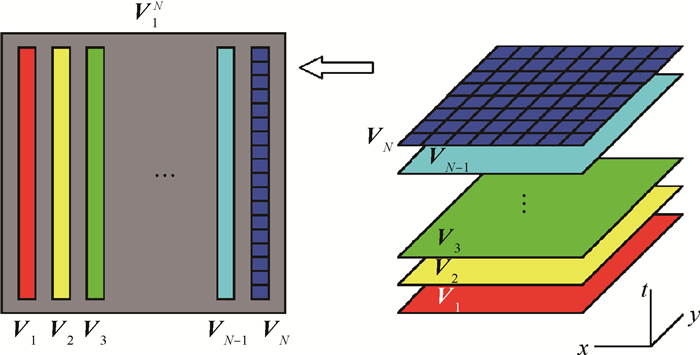
设某一非定常流动的时-空速度场可以表示为矩阵V1N =[v1, v2, ……, vN-1, vN],列向量vi表示第i时间层上流场参数的空间分布,如图 3所示。
|
Fig. 3 Formation of the temporal-spatial matrix |
假设存在一线性变换矩阵A连接相邻两时间层上的流场信息,即
| $ {{\mathit{\boldsymbol{v}}}_{i+1}}=\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{v}}}_{i}} $ | (1) |
若流动是线性系统,A是恒定值;若流动是非线性系统,A为恒定的假设表示对此系统的线性正切近似[15]。DMD的目标是得到系统矩阵A的特征值与特征向量。然而,矩阵A只能从流场的内在动力学机制中获得,所以DMD采用A的伴随矩阵S作为矩阵A的低维近似。
随着采集时间层的增加,向量序列逐渐趋向于线性化,能够更加精确地用之前的向量线性表示最后的向量,即
| $ {{\mathit{\boldsymbol{v}}}_{N}}={{\mathit{\boldsymbol{v}}}_{1}}{{a}_{1}}+{{\mathit{\boldsymbol{v}}}_{2}}{{a}_{2}}+\cdots +{{\mathit{\boldsymbol{v}}}_{N-1}}{{a}_{N-1}}+\mathit{\boldsymbol{r}} $ | (2) |
矩阵形式为
| $ {{\mathit{\boldsymbol{v}}}_{N}}=\mathit{\boldsymbol{V}}_{1}^{N-1}\mathit{\boldsymbol{a}}+\mathit{\boldsymbol{r}} $ | (3) |
其中aT =[a1, a2, …, aN-1]可通过求解极小最小二乘解得到,r为误差向量。
由于系统矩阵能够连接两时间层上的流场信息,所以能够将时-空流场沿时间方向平移
| $ \mathit{\boldsymbol{V}}_{2}^{N}=\left[{{\mathit{\boldsymbol{v}}}_{2}}, {{\mathit{\boldsymbol{v}}}_{3}}, \ldots, {{\mathit{\boldsymbol{v}}}_{N}} \right]=\left[\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{v}}}_{1}}, \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{v}}}_{2}}, \ldots, \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{v}}}_{N-1}} \right]\mathit{\boldsymbol{AV}}_{1}^{N-1} $ | (4) |
由于可以用v1, v2, ……, vN -1线性表示vN,所以列向量aT =[a1, a2, …, aN-1]同样能够将时-空流场沿时间方向平移,将其写成矩阵形式
| $ \mathit{\boldsymbol{AV}}_{1}^{N-1}=\mathit{\boldsymbol{V}}_{2}^{N}=\mathit{\boldsymbol{V}}_{1}^{N-1}\mathit{\boldsymbol{S}}+\mathit{\boldsymbol{re}}_{N-1}^{\rm{T}} $ | (5) |
其中
| $ \mathit{\boldsymbol{S}}=\left( \begin{matrix} 0&{}&{}&{}&{{a}_{1}} \\ 1&0&{}&{}&{{a}_{2}} \\ {}&\ddots &\ddots &{}&\vdots \\ {}&{}&1&0&{{a}_{N-2}} \\ {}&{}&{}&1&{{a}_{N-1}} \\ \end{matrix} \right) $ | (6) |
这里提供了一种无需事先知道流动控制方程,而是从流场一种或者几种物理参数沿时间历程的变化得到系统矩阵A的低维近似方法,伴随矩阵S的特征值包含了系统的时间推进特性,其中
| $ \mathit{\boldsymbol{A}}=\mathit{\boldsymbol{V}}_{2}^{N}\mathit{\boldsymbol{V}}_{1}^{N-1+} $ | (7) |
| $ \mathit{\boldsymbol{S}}=\mathit{\boldsymbol{V}}_{1}^{N-1+}\mathit{\boldsymbol{V}}_{2}^{N} $ | (8) |
| $ \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{p}}_i} = \mathit{\boldsymbol{SV}}_1^{N - 1 + }{\mathit{\boldsymbol{\phi }}_\mathit{i}} = \mathit{\boldsymbol{V}}_1^{N - 1 + }\mathit{\boldsymbol{V}}_2^N{\mathit{\boldsymbol{\phi}}_\mathit{i}} = \mathit{\boldsymbol{V}}_1^{N - 1 + }{\mathit{\boldsymbol{\lambda }}_i}{\mathit{\boldsymbol{\phi}}_\mathit{i}} = {\mathit{\boldsymbol{\lambda }}_i}{\mathit{\boldsymbol{p}}_\mathit{i}} $ | (9) |
所以,将时-空流场矩阵V1N -1投影到矩阵S的特征向量pi上,即可得到流场沿时间推进的空间模态
| $ {\mathit{\boldsymbol{\phi }}_\mathit{i}} = \mathit{\boldsymbol{V}}_1^{N - 1}{\mathit{\boldsymbol{p}}_\mathit{i}} $ | (10) |
通过对V1N -1矩阵进行QR分解可以得到伴随矩阵S。这种基于伴随矩阵S的分解方法在数学上是完全成立的:S = R-1QHV2N。但是,为了得到更加精确的低频动力学模态,需要更长的时间历程,这将产生更多的列向量vi。如果矩阵V1N -1不能保证列满秩,QR分解不仅不唯一,而且上三角矩阵R不能保证可逆,这将直接导致不能得到伴随矩阵S。所以本文采用更加稳定的方法,通过奇异值分解(SVD)求解时-空流场矩阵V1N -1的Moore-Penrose广义逆的方法求解极小二范数最小二乘解,从而通过得到的列向量aT=[a1, a2, …, aN-1]构建出伴随矩阵S,即
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{V}}_1^{N - 1 + }\mathit{\boldsymbol{V}}_2^N $ | (11) |
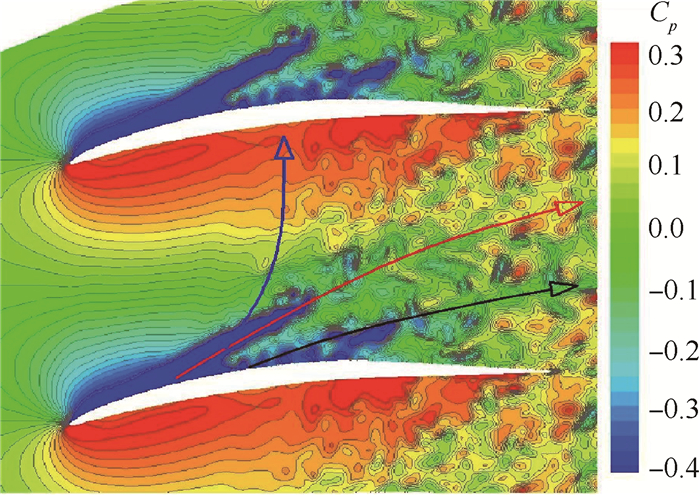
图 4显示了某时刻下叶顶区域98%叶高S1截面静压系数分布。可以看出叶顶泄漏涡轨迹在向下游发展过程中(红线所示),虽然没有和相邻叶片压力面发生碰撞,但是叶顶泄漏涡轨迹形成的低压带却和相邻叶片压力面碰撞(蓝线所示),并造成相邻叶片卸载。同时,低压带的碰撞造成了二次泄漏流的发生(黑线所示)。由于相邻叶片卸载[9],说明叶顶间隙流动处于非定常波动状态。
|
Fig. 4 Static pressure distribution in section S1 at y/h=98% blade height |
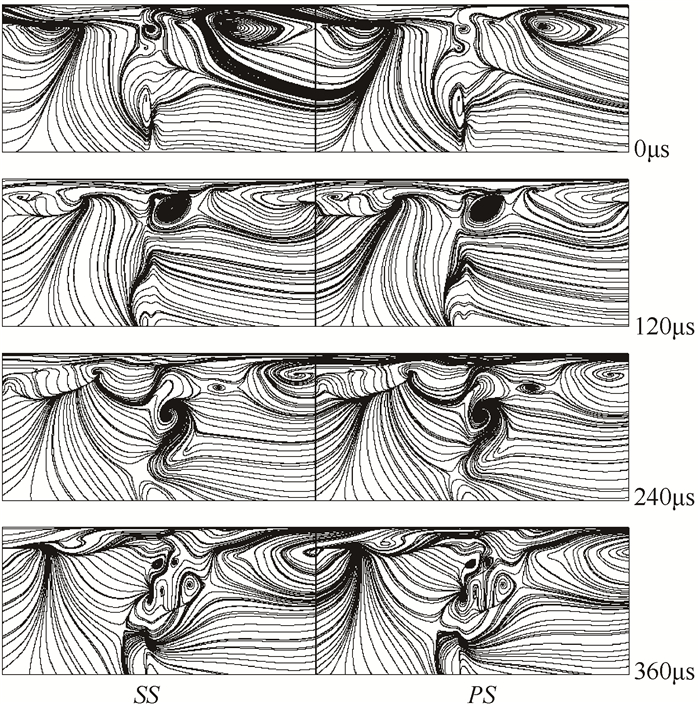
图 5显示了每间隔60个计算时间步长x/c= 1.0677弦长处叶顶S3截面二次流流线。从图中可以看出,二次流动的结构是较为复杂的非定常流动。文献[9]指出,叶顶二次流包含了泄漏涡在叶片压力面与吸力面之间周期的运动,同时泄漏涡表现出一定的不稳定性,在靠近叶片压力面时通常会退化为一结点,除此之外还包含了大量较小空间尺度漩涡与泄漏涡的合并与分裂以及与叶片尾迹涡的相互干扰。通常情况下,流动现象是不同频率下流动结构相互作用的结果,不同时间尺度的脉动包含不同空间尺度的流场结构。由于原始流场包含的频率将不止一个,所以很难分析流场的波动规律。动力学模态分解(DMD),能够把单一频率的流场信息抽取出来,帮助分析不同频率下的叶顶二次流规律。
|
Fig. 5 Stream line in section S3 |
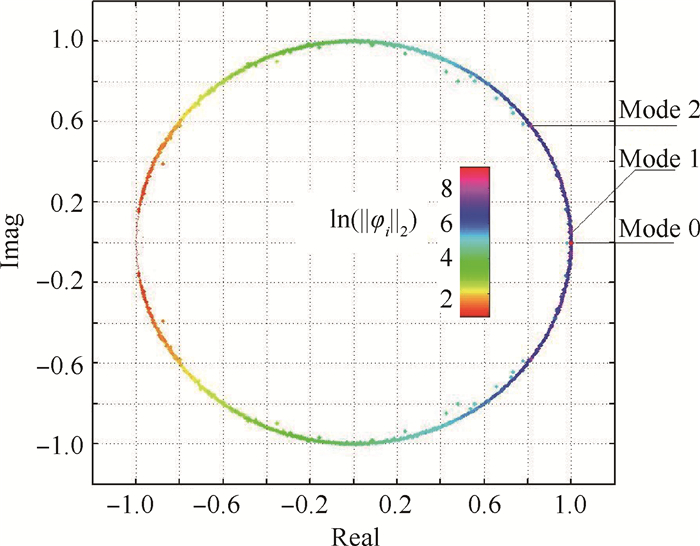
对上述数值模拟数据,选取1001个连续的速度场用于DMD分析,时间间隔为5个计算时间步:ΔT= 10μs;1001个瞬时速度场构成的时-空速度场矩阵会相应产生1000×1000的伴随矩阵S。S矩阵的特征值在复平面上的分布如图 6所示,大部分的特征值都分布在单位圆附近,这表明分解后的大部分模态位于吸引集周围,同时说明这些模态在时间上中性稳定。图 6中圆圈的大小和颜色代表了对数化相关系数的大小,相关系数用来衡量各阶模态在原流场中的相关程度。相关系数的定义为模态ϕi = V1N -1 pi的二范数,由于各阶模态是复数域上的列向量,所以二范数定义为根号下列向量ϕi的共轭转置再乘以列向量ϕi:
| $ {\left\| {{\mathit{\boldsymbol{\phi}}_\mathit{i}}} \right\|_2} = \sqrt {\mathit{\boldsymbol{\phi}}_i^{\rm{H}}{\mathit{\boldsymbol{\phi}}_\mathit{i}}} $ | (12) |
|
Fig. 6 Eigenvalue distribution of adjoint matrix S |
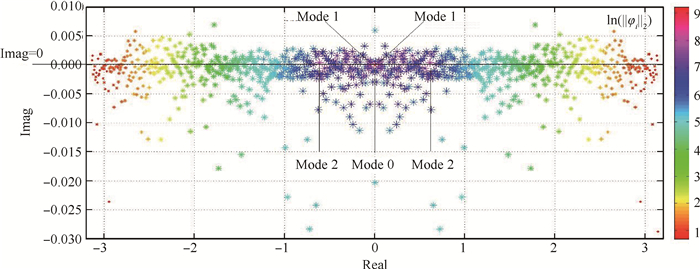
特征值取自然对数:ωi = ln(λi) = ωr(i) + iωi(i),ωi的虚部表征对应模态的相速度,包含模态的频率信息;ωi的实部表征对应模态沿时间增长衰减的趋势。图 7中大部分对数化特征值都落在零线附近也说明绝大多数的模态在时间上中性稳定。
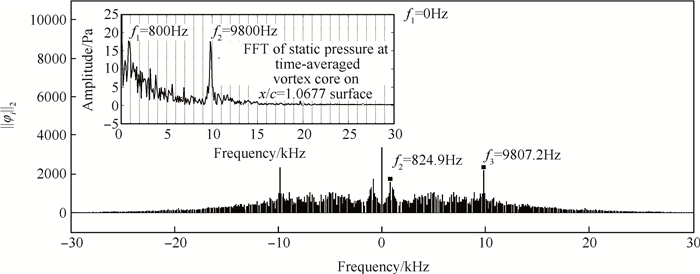
图 8显示了各阶模态的相关系数与频率之间的关系,横坐标ωi(i)/2πΔT为对应模态的频率,纵坐标为各模态相关系数。图中频率为f0 = 0Hz,f1 = 824.9Hz,f2 = 9.8072kHz的三个模态在相关系数上出现峰值,利用弦长和进口速度对自然波动频率无量纲化后得到的叶顶二次流速度场无量纲频率为St1=0.8,St2=9.6;同时在图 7中这三阶模态都位于直线Imag=0轴的附近,这说明三阶模态分别在时间上中性稳定。图 8另外给出了x/c=1.0677弦长处S3截面叶顶时均二次流速度场泄漏涡涡心位置静压脉动的快速傅立叶变换结果,从图中可以观察到在频率为f1 = 800Hz,f2 = 9.8kHz处静压脉动出现明显的峰值;这与S3截面叶顶二次流速度场动力学模态分解得到的结果在频率上基本一致,在幅值上趋势大致相同。通过将DMD与FFT结果进行对比,说明原流场中的两个频率是客观存在的。
|
Fig. 7 Distribution of logarithmic eigenvalue |
|
Fig. 8 Coefficient associate and amplitude of static pressure with corresponding frequencies |
另外,图 8中相关系数和频率的关系是关于Frequency=0轴对称的,这是由于伴随矩阵S的特征值是成对共轭的,它们所对应的特征向量在复数域上也是成对共轭的,并且都存在相同的二范数。对于某一个特征值,对应的特征向量有无数多个,它们的集合构成了在此特征值虚部对应频率下的低维近似非定常流动。
同时,在本实例中机匣上端壁对流场的作用为唯一的非振荡均匀剪切主动力,孤立叶栅模型所构成的开口非线性系统内部产生了沿时间上中性稳定的振荡模态,所以动力学模态分解结果印证了这种非定常的二次流动处于自持振荡状态(Self-sus⁃ tained oscillation)[9]。
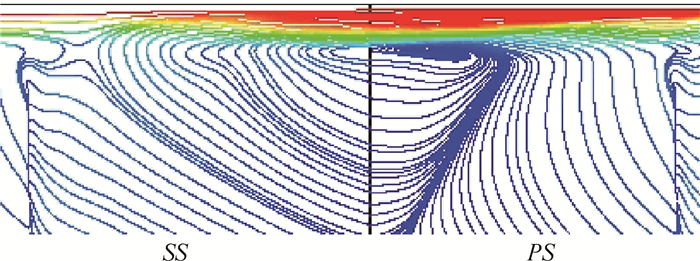
4.4 零阶模态图 9显示了S3截面的0阶速度模态,由于这一模态所对应的特征值为实数,所以这阶模态的频率为零,即是时均的。从流线图中可以明显看出,由于上端壁的移动和叶片两侧压差作用所形成的泄漏涡。实际上可以把0阶模态看作叶顶二次流速度场的基本结构,在这个基本结构上附加着不同形态、频率的二次流速度场振荡模态,这种不同频率动力学模态的线性叠加构成了线性低维近似的实际流场。这一过程为流场的重构。定义ai(t)= e(ωr + iωi)t为流场的重构系数,并运用公式
| $ \mathit{\boldsymbol{V}}_1^{N - 1}\left( {x, y, t} \right) = \sum\limits_{i = 1}^{N - 1} {{a_i}\left( t \right){\mathit{\boldsymbol{\phi }}_\mathit{i}}\left( {x, \mathit{y}} \right)} $ | (13) |
|
Fig. 9 Simplified zero mode |
对所关注的高相关系数模态进行重构[15]。
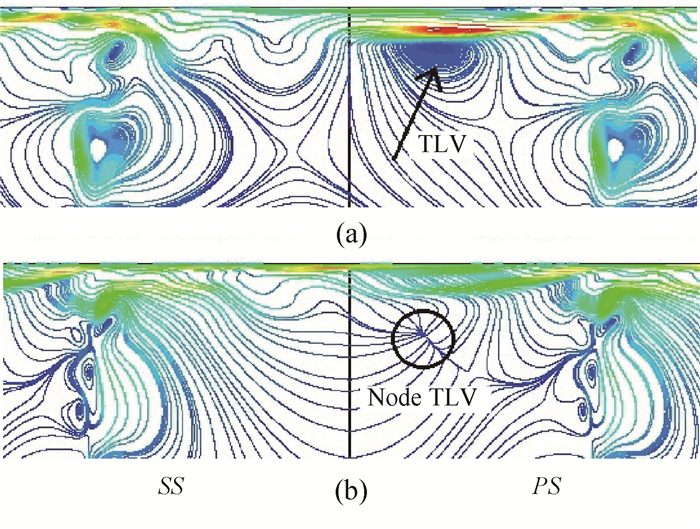
4.5 一阶模态图 10给出了频率f1 = 824.9Hz的两个相位下的1阶速度场模态。可以看出,叶栅通道内存在不稳定的漩涡,并且随着相位的变化逐渐退化为结点。同时在叶片尾缘位置也出现了位置大小和个数随相位周期变化的漩涡[9]。
|
Fig. 10 Simplified 1st mode |
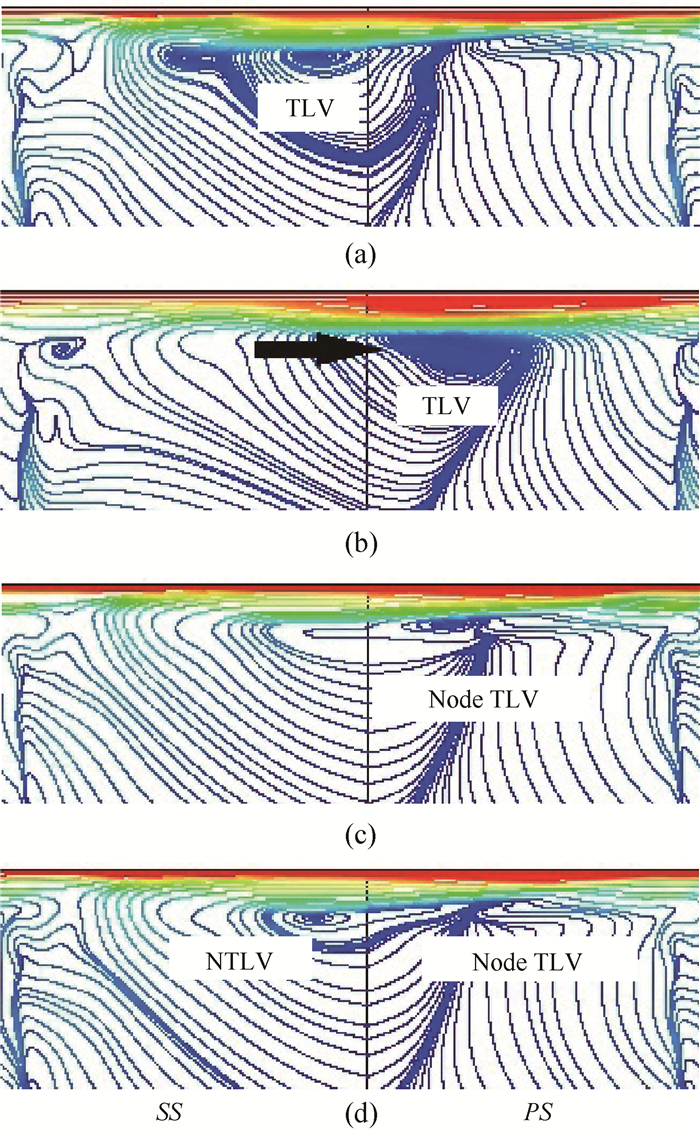
由于单独模态难以观测泄漏涡的振荡规律,通过重构公式,将1阶模态叠加到0阶时均模态上,能够更直观地还原泄漏涡在此频率下的振荡规律。各相位二次流流线如图 11所示。可以看出刚开始在叶片吸力面出现较为稳定的泄漏涡(TLV),随着相位的变化,泄漏涡向叶片压力面运动并逐渐不稳定,当移动到叶片压力面附近时开始退化,最终泄漏涡的螺旋结点退化为一结点。同时在叶片吸力面附近将产生新的稳定泄漏涡(NTLV),完成一个周期的运动。0阶与1阶模态的叠加说明频率为f1 = 824.9Hz的二次流振荡主要表现为泄漏涡的低频周期性生成与退化。
|
Fig. 11 Superposition of 1stand zero mode |
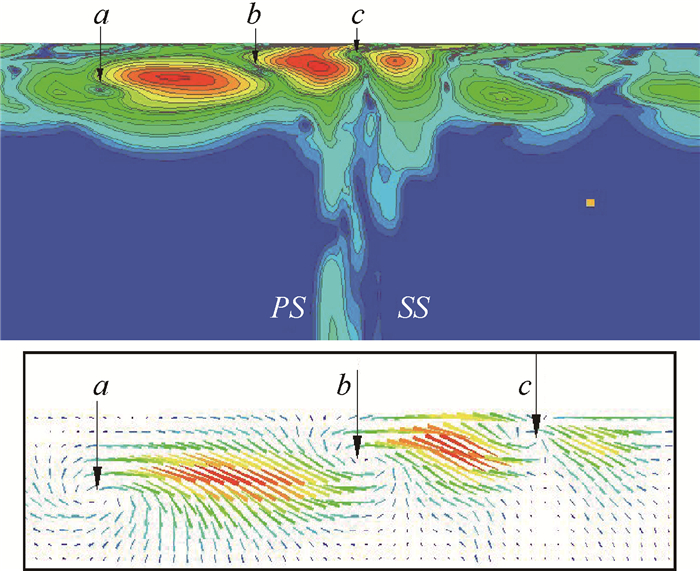
图 12给出了较高频率f2 = 9807.2Hz的一个相位下的2阶速度场模态,从图中可以看出,在靠近移动端壁处存在一系列空间尺度较小且沿叶栅周向排列的漩涡;可以观察到在叶片压力面一侧,随着小尺度漩涡向压力面移动,速度振荡的幅值是逐渐增加的;当漩涡越过叶顶间隙,出现在叶片吸力面一侧时,速度振荡幅值迅速减弱。这种小尺度的涡结构可能是由于移动上端壁带动附近流体产生剪切层的不稳定造成的。由于剪切层内流体运动方向是从叶片吸力面向压力面移动,所以叶片压力面存在的逆压力梯度和叶片顶部的刮削阻挡作用可能加剧了这种不稳定,使得振荡幅值在压力面一侧增加。这种移动端壁剪切层内的涡运动提高了与叶顶端部低能流体的掺混能力,使得叶顶通道内的低速气体微团得到激励,从而能够延缓转子叶顶失速;同时这种漩涡运动与叶顶主流的相互作用也附加了一定的流动损失,降低了压气机转子的效率[7]。
|
Fig. 12 Simplified 2nd mode |
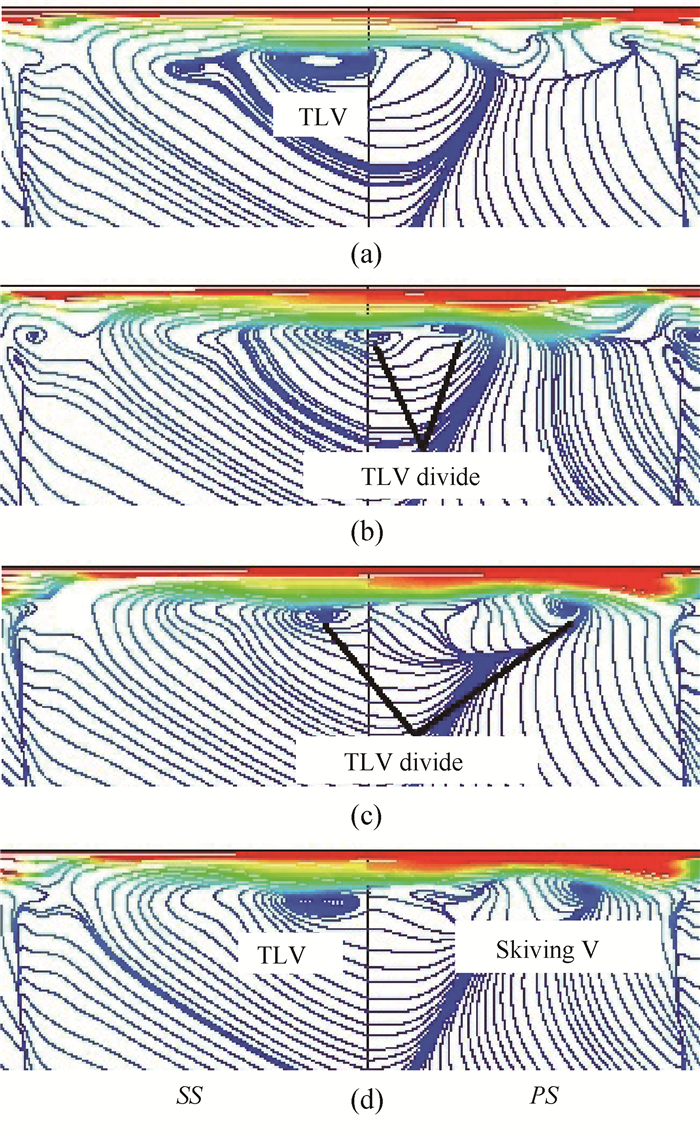
类比1阶模态,通过重构公式,将2阶模态叠加到0阶时均模态上,各相位二次流流线如图 13所示。可以看出随着相位的变化,泄漏涡在叶栅通道内没有出现退化为结点的现象,而是在较小的范围内沿压力面与吸力面方向高频振荡;同时在靠近叶片压力面时出现了涡的分裂,由一个涡变成两个涡。分裂后靠近压力面一侧的漩涡继续向叶片压力面方向移动,并逐渐演化成刮削涡;靠近吸力面一侧的漩涡向叶片吸力面方向移动,从而开始下一个周期的循环。通过对2阶模态进行分析,说明频率为f2 = 9807.2Hz的高频二次流波动主要表现在泄漏涡的高频振荡与分裂。
|
Fig. 13 Superposition of 2nd and zero mode |
图 14再次挑选了某两时刻下原始速度场中x/c= 1.0677弦长处S3截面叶顶二次流流线图,用于与动力学模态分析的结果进行对比。虽然从原流场中很难归纳出二次流的波动规律,但是在某时刻下原始流场仍能够表现出与动力学模态分析结果非常相似的流线结构。从图 14(a)中可以看出在某时刻下泄漏涡在靠近压力面一侧时已经退化成结点形式,这与0,1阶模态叠加结果中d相位流线图相似。同时图 14(b)显示出在某时刻下泄漏涡的分裂,这与0,2阶模态叠加结果中d相位流线图相似。通过原始流场与动力学模态进行对比,验证了动力学模态结果的可信性,同时也说明在此工况下,泄漏涡的生成退化以及振荡分裂是x/c=1.0677弦长处S3截面叶顶二次流速度场非定常运动的主要特征。

|
Fig. 14 Stream line in section S3 |
通过大涡模拟(LES)对低速孤立压气机叶栅进行数值模拟,并运用动力学模态分解(DMD)技术对x/c=1.0677弦长处S3截面叶顶二次流速度场进行分析,结论如下:
(1)低速孤立压气机叶栅x/c=1.0677弦长处S3截面叶顶二次流速度场包含f1 = 824.9Hz,f2 = 9807.2Hz两阶模态。
(2)频率为f1 = 824.9Hz的二次流振荡主要表现在泄漏涡的低频周期性生成与退化。
(3)频率为f2 = 9807.2Hz的二次流振荡是由叶顶移动端壁形成剪切层内的不稳定造成的,主要表现在泄漏涡的振荡与分裂。
致谢 感谢大连海事大学钟兢军教授和韩少冰老师在计算模型方面提供的帮助。
| [1] |
韩少冰, 钟兢军, 严红明. 端壁相对运动对压气机叶栅间隙流场影响的数值模拟[J]. 动力工程学报, 2011, 31(4): 257-262. (  0) 0) |
| [2] |
Wisler D C. Loss Reduction in Axial-Flow Compressors Through Low-Speed Model Testing[J]. Journal of Engineering for Gas Turbines & Power, 1984, 107(2): 90-90.
(  0) 0) |
| [3] |
邓向阳, 张宏武, 朱俊强, 等. 压气机非定常叶顶间隙流的数值模拟研究[J]. 工程热物理学报, 2006, 27(2): 229-231. (  0) 0) |
| [4] |
吴艳辉, 楚武利, 刘志伟. 移动壁对压气机叶栅间隙流动的影响[J]. 航空动力学报, 2006, 21(1): 112-118. (  0) 0) |
| [5] |
王维, 楚武利, 张皓光. 叶顶喷气对高负荷轴流压气机性能的非定常影响机理[J]. 推进技术, 2014, 35(7): 905-913. (WANG Wei, CHU WU-li, ZHANG Hao-guang. Mechanism of Unsteady Influence of Tip Injection on a High-Loaded Axial Compressor Performance[J]. Journal of Propulsion Technology, 2014, 35(7): 905-913.)
(  0) 0) |
| [6] |
张皓光, 楚武利, 吴艳辉, 等. 轴向倾斜缝机匣处理影响压气机性能的机理[J]. 推进技术, 2010, 31(5): 555-561. (ZHANG Hao-guang, CHU Wu-li, WU Yan-hui, et al. Investigation of the Flow Mechanisms of Affecting Compressor Performance with Axial Skewed Slots Casing Treatment[J]. Journal of Propulsion Technology, 2010, 31(5): 555-561.)
(  0) 0) |
| [7] |
陈一, 王建明, 马驰, 等. 一种叶顶叶栅结构对压气机间隙流动的影响[J]. 航空动力学报, 2016, 31(7): 1712-1718. (  0) 0) |
| [8] |
赵龙. 低速轴流压气机转子流场非定常波动的大涡模拟[D]. 北京: 中国科学院研究生院(工程热物理研究所), 2014. http://cdmd.cnki.com.cn/Article/CDMD-80135-1014315615.htm
(  0) 0) |
| [9] |
邓向阳. 压气机叶顶间隙流的数值模拟研究[D]. 北京: 中国科学院工程热物理研究所, 2006. http://cdmd.cnki.com.cn/Article/CDMD-80135-2006089358.htm
(  0) 0) |
| [10] |
Zhang H, Deng X, Lin F, et al. A Study on the Mechanism of Tip Leakage Flow Unsteadiness in an Isolated Compressor Rotor[C]. Barcelona: ASME Turbo Expo 2006: Power for Land, Sea, and Air, 2006: 435-445.
(  0) 0) |
| [11] |
Du J, Lin F, Chen J, et al. Flow Structures in the Tip Region for a Transonic Compressor Rotor[J]. Journal of Turbomachinery, 2013, 135(3): 2561-2572.
(  0) 0) |
| [12] |
耿少娟, 林峰, 张宏武, 等. 低速单转子轴流压气机突尖型失速特征[J]. 工程热物理学报, 2010(6): 929-932. (  0) 0) |
| [13] |
Schmid P J. Dynamic Mode Decomposition of Numerical and Experimental Data[J]. Journal of Fluid Mechanics, 2008, 656(10): 5-28.
(  0) 0) |
| [14] |
唐湛棋. 强扰动作用于边界层的PIV实验研究[D]. 天津: 天津大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10056-1015020023.htm
(  0) 0) |
| [15] |
Pan C, Yu D, Wang J. Dynamical Mode Decomposition of Gurney Flap Wake Flow[J]. Theoretical and Applied Mechanics Letters, 2011, 1(1): 42-46.
(  0) 0) |
| [16] |
Tang Z Q, Jiang N. Dynamic Mode Decomposition of Hairpin Vortices Generated by a Hemisphere Protuberance[J]. Science China Physics Mechanics & Astronomy, 2011, 55(1): 118-124.
(  0) 0) |
| [17] |
Mcmullan R J. Influence of Tip Clearance on the Flowfield in a Compressor Cascade with a Moving Endwall [D]. Ohio: Air Force Institute of Technology, 1996.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

