2. 陕西省人工影响天气办公室研发中心,陕西 西安 710014
2. Weather Modification Office of Shaanxi Province, Xi' an 710014, China
30cm离子推力器是我国针对新一代大型桁架式卫星平台所研制的高功率、大推力离子推力器[1], 其所使用的阴极包括空心阴极(或称主阴极)和中和器阴极。为了满足30cm离子推力器的工作性能参数要求, 我国设计并研制了20A发射电流空心阴极(供气流量约为2.96 Pa∙L∙s-1)以作为30cm离子推力器气体放电的初级电子供给器件。空心阴极的放电区域可分为发射体区、阴极顶小孔区(小孔柱段区域)和阴极羽流区, 其中中性Xe气原子进入阴极管后, 首先在发射体区被电离并产生高密度等离子体, 随后等离子体中的大量电子在触持极和发射体区等离子体鞘层间电场作用下, 从发射体区被抽取出进入小孔区, 并在小孔区与中性原子继续发生电离产生新增的二次电子, 因此小孔区相比发射体区和羽流区具有最高的电子电流密度。若将阴极小孔径向截面假设为电流截面, 则阴极小孔的尺寸和构型设计决定了最终进入放电室的阴极发射电流大小, 因此研究小孔区等离子体特性对阴极小孔的设计和电流发射能力预估具有重要意义。
2002年美国Katz等[2]对早期研制的NSTAR离子推力器BaW阴极(发射电流为3.26A, 供气流率为5.92Pa∙L∙s-1)发射体区和孔区等离子体特性参数进行了计算, 计算模型采用Katz [3]在1996年建立的空间站空心阴极接触器等离子体特性一维流体计算模型。在假设孔区中性气体密度为均匀分布的基础上, 将电子的运动行为假设为流体, 研究结果显示BaW阴极孔区等离子体密度峰值出现在柱段孔区轴线中心处, 孔区两端的等离子体密度则相对较低, 孔区入口处和中心区域电子温度分别约1.1eV和1.5eV, 而进入放电室的电子温度则上升至约2eV, 电子温度计算结果与Malik等[4]试验测试结果符合性较好。Katz等通过统计计算认为NSTAR离子推力器BaW阴极发射的总电子数中约有1/3是在小孔区产生, 并且小孔区尺寸设计对发射电流的产生具有决定性影响。根据计算得到的孔区离子电流密度对孔区壁面的腐蚀效应进行预测, 预测结果与1999年Polk等[5]进行的NSTAR离子推力器BaW阴极8200h寿命试验结果进行了比对, 证明了采用理论分析孔区腐蚀趋势与试验结果的一致性。2005年美国Jameson等[6]对NSTAR离子推力器TH15空心阴极(发射电流为13A, 孔区柱段直径为1mm)小孔区等离子体特性研究中发现, 中性气体在由发射体区进入孔区后, 压强降低至约400Pa左右, 在假设孔区气体温度为2000K后, 采用等离子体扩散零维模型计算得到孔区轴向平均电子温度约为2.3eV, 并且孔区电子温度沿轴线变化不超过1eV, 计算结果与2.2~ 2.3eV的试验测量结果一致, 证明采用等离子体扩散零维模型具有较高的精度并可用于孔区电子温度的预估。根据一维离子连续性方程计算得到孔区等离子体密度约在1×1022~6×1022 /m3范围内, 且密度峰值发生在小孔直段约0.4mm处。
国内对于空心阴极内部等离子体特性研究较少, 研究工作主要包括上海空间推进研究所对霍尔推力器BaW空心阴极的试验研究[7], 以及兰州空间技术物理研究所针对离子推力器LaB6空心阴极的一些计算和试验研究[8, 9]。本文对我国研制的30cm离子推力器20A发射电流LaB6空心阴极采用数值模拟结合有限元分析和试验验证的方法, 对我国20A发射电流空心阴极小孔区的等离子体特性参数(包括Xe原子密度分布、电子温度及电子和离子电流密度等)进行计算, 并根据结果对目前20A发射电流空心阴极小孔的设计尺寸进行评估。
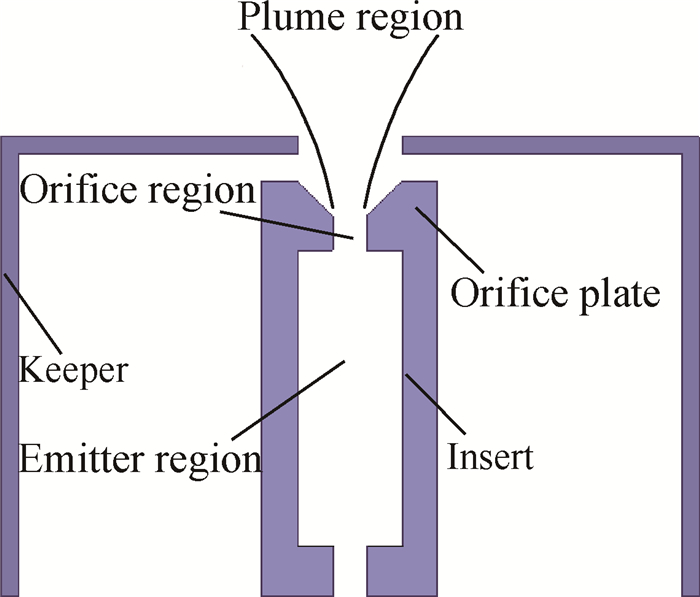
2 阴极小孔区Xe原子密度20A发射电流空心阴极发射体区和小孔区的结构示意图如下图 1所示, 其中小孔直径为1mm, 小孔柱段长度为2mm, 小孔电离区域主要指阴极小孔柱段区域(小孔锥段区域属于阴极羽流放电区)。中性Xe气通过气体分配、气路绝缘以及石墨屏蔽套缓冲后进入阴极管, 首先在发射体区发生自持放电并产生高密度等离子体, 在电场作用下, 发射体区等离子体向阴极孔区运动, 并在孔区形成高电子电流密度,因此电离效应在孔区非常显著。为后续进行孔区等离子体相关参数的计算, 首先需考虑阴极小孔区Xe原子密度分布特性。
|
Fig. 1 Structure of 20A emission current hollow cathode |
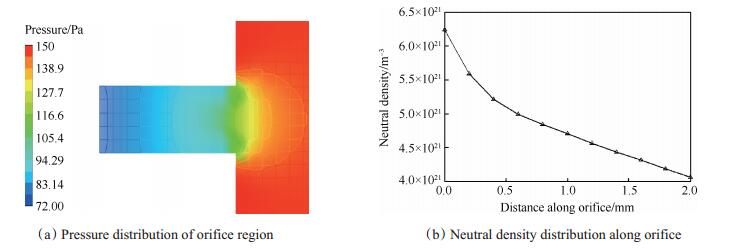
发射电流为20A的空心阴极,其供气流量为2.96Pa∙L∙s-1, 流量计出口压强约为450Pa, 根据作者前期计算得到的空心阴极气路管道流导以及Xe气通过空心阴极小孔的流率、压强关系式[10], 得到阴极管入口压强为260.5Pa, 阴极顶小孔处压强为76Pa。在确定阴极供气管路中的Xe气流动为黏滞流后, 并假设气流在供气管路中均为稳定性流动, 根据Fluent得到阴极小孔区域的压强如图 2 (a)所示。
|
Fig. 2 Pressure and neutral density distribution in cathode orifice region |
根据小孔区中性Xe原子密度n0的表述形式(式(1)),n0由孔区压强pd和中性Xe原子温度Tn的比值决定, 由于Xe原子与小孔区壁面不断碰撞并发生能量交换, 因此可认为Xe原子温度Tn与小孔区壁面温度(采用红外光学测量温度约1800K左右)一致。
| $ {{n}_{0}}=\text{ }9.6\text{ }\times \text{ }{{10}^{24}}{{p}_{\text{d}}}/{{T}_{\text{n}}} $ | (1) |
根据图 2(a)得到的小孔区压强分布, 并假设小孔区不同径向截面的压强基本相等, 得到小孔区轴线方向(阴极顶小孔入口至出口)的中性原子密度分布如图 2(b)所示。从图中结果来看, 20A发射电流空心阴极孔区的中性原子密度基本在4×1021~6×1021/m3, 分布较为均匀且越靠近小孔出口区域的原子密度较低, 这主要是由于阴极小孔的结构特点所造成的。
3 阴极小孔区电子温度获得阴极小孔区中性原子密度分布后, 首先需对小孔区的等离子体产生过程进行研究, 并获得孔区电子温度分布特性。本文采用Jameson等[6]给出的基于等离子体双极扩散机制的阴极小孔区零维(0-D)等离子体扩散方程进行等离子体产生过程描述,方程形式为
| $ {{\left( \frac{r}{{{\lambda }_{01}}} \right)}^{2}}{{n}_{0}}{{\sigma }_{\text{i}}}\left( {{T}_{\text{e}}} \right)\sqrt{\frac{8k{{T}_{\text{e}}}}{\text{ }\!\!\pi\!\!\text{ }m}}\text{ }-D=\text{ }0 $ | (2) |
式中r为阴极小孔半径, Te为电子温度,m为电子质量,D为双极扩散系数[11] (由电子温度、离子温度、离子速度、碰撞截面及原子密度共同决定),λ01为离子扩散方程零阶贝塞尔函数的初始零点,k为Boltzmann常数,σi(Te)为小孔区不同位置的电子温度对应的电离碰撞截面, 根据Bond, Rapp等[12, 13]的研究结果, 碰撞截面σi(Te)可表示为
| $ {{\sigma }_{\text{i}}}\left( {{T}_{\text{e}}} \right)=\text{ }{{({{k}_{1}}\text{ln }\Delta v+{{k}_{2}})}^{2}}\times \text{ }{{10}^{-20}} $ | (3) |
式中k1,k2为碰撞参数,Δv为离子与原子的相对速度(计算中近似以离子热速度代替)。对于λ01的求解, 在将离子扩散方程以柱坐标描述后, 并将等离子体密度n采用径向分布函数f (r)和轴向分布函数g(z)分离变量后得到
| $ \frac{1}{f}\frac{{{\partial }^{2}}f}{{{\partial }^{2}}r}+\frac{1}{rf}\frac{\partial f}{\partial r}+C_{1}^{2}+{{\alpha }^{2}}=-\text{ }\frac{1}{g}\frac{{{\partial }^{2}}g}{{{\partial }^{2}}z}+{{\alpha }^{2}}=\text{ }0 $ | (4) |
式中C1和α均为方程系数, 采用贝塞尔函数的第一种形式, 可得到零阶贝塞尔函数的初始零点λ01表述形式
| $ \frac{r}{{{\lambda }_{01}}}=\sqrt{C_{1}^{2}+{{\alpha }^{2}}} $ | (5) |
从图 2分析结果来看, 由于小孔区存在较为明显的气体压强梯度, 并且在轴向方向梯度差异较大, 而在径向梯度差异较小, 因此可以预测阴极小孔区的电子温度分布将会出现明显差异性。国外在采用零维等离子体扩散方程进行阴极小孔区电子温度描述时, 是将中性气体压强(即原子密度分布)设置为均匀值[2], 从而得到小孔区电子温度、等离子体密度的计算平均值。为更好地描述小孔区电子温度分布的区域性, 本文对20A发射电流空心阴极的小孔区压强分别进行径向(r方向)和轴向(z方向)二阶多项式拟合, 其中z方向取点10个, 步长为0.2mm,r方向取点10个, 步长为0.05mm。拟合后代入式(2), 并将式(4)和式(5)计算得到的λ01, 以及式(3)计算得到的电离碰撞截面代入式(2), 得到径向和轴向电子温度如表 1所示。
|
|
Table 1 Electron temperature radial and axial calculation results in orifice region |
如表 1所示, 30cm离子推力器空心阴极小孔区轴向(z方向)平均电子温度约为2.66eV, 径向(r方向)平均电子温度为2.2eV。该结果与Goebel等[14]采用零维扩散方程计算得到的NSTAR离子推力器空心阴极小孔区平均电子温度为2.3eV的结果基本一致(由于NSTAR离子推力器TH15空心阴极工作点为13A, 孔区温度2000K, 小孔直径1mm, 中性原子密度在1021量级, 我国30cm离子推力器空心阴极工作点为15A, 孔区温度1800K, 小孔直径1mm, 并且原子密度与TH15在同一量级, 因此具有一定可比性)。
从表 1径向电子温度分布结果来看, 越靠近中心区域, 电子温度越高, 而从轴向电子温度分布结果来看, 阴极顶小孔入口处的电子温度较低, 靠近阴极顶小孔出口方向的电子温度相对较高。从作者前期的研究结果来看[15], 电子温度沿阴极顶小孔区轴线的变化特性与发射体区沿轴线方向的电子温度变化特性是一致的, 其中阴极发射体区电子温度在靠近小孔区域最高, 约为1.7eV, 越靠近石墨屏蔽套电子温度越低, 且基本保持在1.5eV左右。也就是说, 在空心阴极的内部放电区域(包括发射体区和小孔区),电子(包括原初电子和二次电子)沿轴线从放电产生后直到从触持极孔引出, 一直处于能量上升阶段。但在发射体区域电子温度升高幅度较小, 约在0.2~ 0.5eV, 而小孔区是电子温度上升的主要区域, 增幅在1~2eV。这一结论通过美国NSTAR离子推力器TH15空心阴极发射体区(发射体直径为3.6mm)和小孔区的电子温度计算和测量结果可得到验证[6],NSTAR离子推力器TH15空心阴极发射体区电子温度分布在1.5~2eV, 进入小孔区后, 电子温度从2eV (入口处)升高至约3eV(出口处)。造成发射体区和小孔区电子温度不均匀现象的原因是多方面的, 其中在发射体区认为由于电场作用不是很明显, 而发射体区等离子体密度高于小孔区域, 因此在发射体区等离子体之间强烈的相互碰撞以及不断的电离过程会导致发射体表面的等离子体鞘层电势降低, 因此发射体区电子温度相对较低, 且分布较为均匀。从阴极的使用寿命来说, 发射体区电子温度的降低有利于减弱过强的电离碰撞效应和等离子振荡现象, 避免产生大量高能一价或二价Xe离子并降低高能离子对发射体的溅射作用, 从而延长发射体工作寿命。
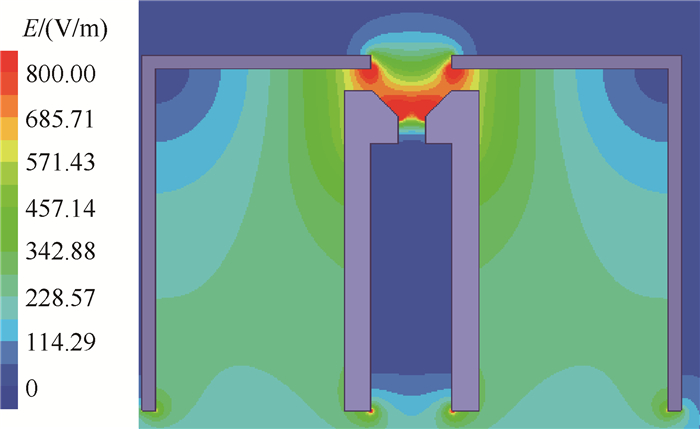
对于小孔区的电子温度分布特性, 认为由于小孔区中性原子密度明显降低, 粒子间的相互碰撞作用进一步减弱, 双极扩散系数D则越大引起小孔区电子温度相对发射体区的较大幅度提升, 其次小孔区电场作用也是重要影响因素。采用Ansoft电磁场仿真软件对20A发射电流空心阴极小孔区的静电场仿真结果来看, 如图 3所示, 小孔区电场强度沿轴向和径向是逐渐增强的, 因此造成表 1所示小孔区电子温度的分布结果。
|
Fig. 3 Electric field distribution in orifice region |
阴极小孔区等离子体密度分布对于研究孔区电子电流密度以及离子电流密度分布属于关键参数, 而对于孔区等离子体密度分布国外Jameson, Polk等[6, 16]分别给出了等离子体扩散零维模型以及一维模型[2] (即一维离子连续性方程)两种计算方法, 由于零维模型仅能粗略反映阴极孔区的等离子体平均参数,并且精确性较差, 因此本文采用一维模型进行孔区等离子体密度计算, 一维离子连续性方程为
| $ \text{ }\!\!\pi\!\!\text{ }{{r}^{2}}\left( -\frac{\partial n}{\partial t}+\frac{\partial {{v}_{\text{i}}}{{n}_{0}}}{\partial z} \right)-\text{ }2\text{ }\!\!\pi\!\!\text{ }r{{v}_{\text{wall}}}n=\text{ }0 $ | (6) |
式中
| $ {{V}_{\text{r}}}=\frac{{{2.4}^{2}}}{2r{{\sigma }_{\text{CEX}}}{{n}_{0}}{{v}_{\text{scat}}}}\frac{e}{M}({{T}_{\text{i}}}+{{T}_{\text{e}}}) $ | (7) |
式中σCEX为交换电荷碰撞截面[4](约为10-18/m2),M为离子质量,Ti为离子温度,vscat为离子轰击至阴极小孔壁面的散射速度。散射速度vscat与离子热速度vth、离子平均速度vi、中性原子速度v0相关, 其表述形式为
| $ {{v}_{0}}=-\frac{{{r}^{2}}}{8\zeta }\frac{\text{d}p}{\text{d}z} $ | (8) |
式中ζ为由温度决定的中性气体黏滞系数, 根据Katz等[11]的研究结论, 该系数与阴极小孔边界处气体的相对温度Tr(Tr = Tn/289.7)有密切关系, 根据图 2给出的压强分布pd, 可得到20A发射电流阴极小孔区中性原子速度v0约在0.8~45m/s内, 且越靠近孔区壁面原子速度v0越低。
离子热速度vth可表述为
将式(7)、式(8)计算得到的v0,vwall,
|
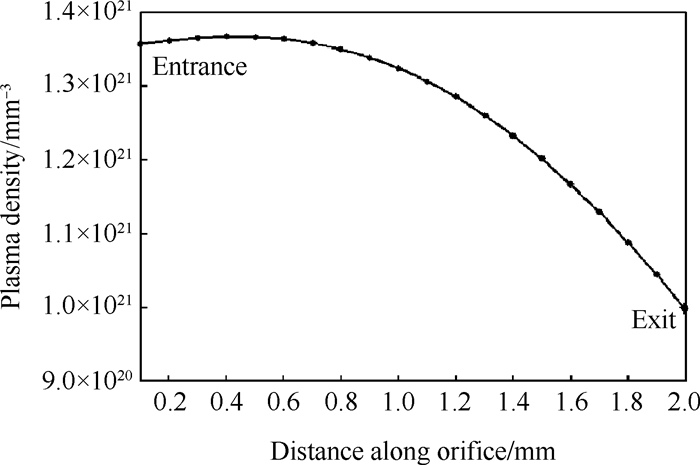
Fig. 4 Plasma density distribution in orifice region |
从图 4计算结果来看, 我国20A发射电流阴极等离子体密度峰值出现在靠近小孔入口约0.4~0.6mm的范围, 越靠近出口, 等离子体密度降低越明显。造成此现象的原因主要是中性原子密度沿轴线方向逐渐降低, 而根据式(6)离子连续性方程表述形式, 孔区中性原子密度n0的下降会导致电离效率以及等离子产生率的降低, 因此造成图 4所示阴极小孔区等离子体密度的分布特性。
5 电子电流密度以及离子电流密度由于阴极小孔区产生的电子电流是阴极发射电流的重要组成部分, 而孔区电子电流与孔径设计存在密切关系, 因此估算电子电流大小对小孔的尺寸以及阴极电流引出能力的设计具有重要意义, 而获得孔区离子电流的密度分布则可以预估空心阴极小孔的主要溅射腐蚀区域和寿命。本文对孔区电子电流密度Je计算采用一维电子连续性方程进行求解,其表述形式为
| $ \text{ }\!\!\pi\!\!\text{ }{{r}^{2}}\left( e\frac{\partial n}{\partial t} \right)+\frac{\partial {{J}_{\text{e}}}}{\partial z}=\text{ }0 $ | (9) |
根据电流定义, 若将小孔区径向截面作为电子通量截面, 则式(9)说明小孔区(从小孔入口至小孔出口)增加的电子电流主要是由小孔区放电等离子体电离所产生的, 并且根据Katz等[2]针对NSTAR离子推力器空心阴极的计算结果, 小孔区新增电子电流大小约为空心阴极总发射电流的1/3。对于式(9)的求解, 将阴极小孔区的等离子体产生率
|
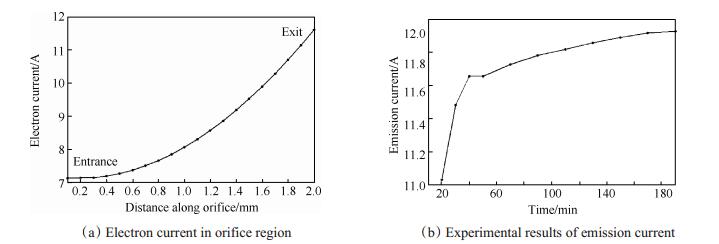
Fig. 5 Electron current calculation results and emission current experimental results |
从图 5(a)计算结果来看, 小孔区入口处(对应发射体放电区域的出口)电子电流约为7.2A, 而出口处的电子电流约为11.6A, 孔区新增电子电流约占20A空心阴极总发射电流(进入放电室)的36%。分析来看, 造成图 5(a)结果的原因主要是由于孔区较高的电离强度, 会对进入小孔区的电子电流形成增益效应, 并且增益效应的程度完全是由小孔区的电离强度决定。考虑到影响电离强度的内部因素, 也可以认为电子电流的增益是由孔区的中性原子密度、气体温度、小孔直径以及电子温度等参数共同决定。
目前对于阴极小孔入口处的电子电流无法通过试验手段进行验证, 但对于阴极小孔出口处的电子电流(即阴极发射电流)可以根据推力器实测电性能参数获得, 根据放电室电流平衡关系[18]即Ie = Id -Ib -Ik,发射电流Ie等于放电电流Id减去推力器束流Ib以及阴极触持电流Ik, 通过对我国研制的30cm离子推力器工作电性能实测参数的计算, 得到阴极发射电流如图 5 (b)所示。
从图 5 (b)来看, 在180min工作时间内, 推力器主阴极发射电流是逐渐升高并趋于稳定, 在前40min内发射电流的升高主要是由于栅极的热启动过程所引起的栅极间距变化, 导致束流值Ib的波动, 其次离子推力器的束流Ib持续下降并最终稳定的特性也是造成后续工作时间内, 阴极发射电流Ie不断升高并最终稳定的原因。根据图 5(b)所示试验结果, 30cm离子推力器工作稳定后的空心阴极发射电流基本维持在11~12A, 与图 5(a)计算得到的阴极小孔区出口处电子电流为11.6A的结果一致。
我国30cm离子推力器空心阴极的小孔设计采用的是A型孔加热模式小孔, 因此小孔具有较大的长径比。小孔长度和直径属于阴极关键设计参数,其对发射电流具有明显影响, 而发射电流会直接决定束流大小, 从而影响推力器所产生的推力值和比冲值。根据Mikelides等[19]的研究结果, 小孔孔径设计越大, 会造成孔区中性原子密度及等离子体密度降低, 并且等离子体电阻加热效应越弱, 从而导致发射电流较低。对于本文所研究的20A发射电流空心阴极小孔, 若保持流率等输入参数不变仅将孔径改为1.2mm, 出口处发射电流粗略预估将降低至8~ 9A, 结果说明目前20A发射电流阴极的小孔尺寸设计满足电流发射能力要求, 并且计算结果与试验结果具有较好的一致性。
在阴极放电成功后, 小孔区内离子在电场作用下加速向小孔壁面运动, 并且部分离子轰击至壁面后会与鞘层电子结合, 部分离子则形成离子电流, 因此离子的轰击溅射作用是造成阴极小孔区腐蚀的重要因素。根据国外研究结果[20], 离子对小孔壁面的腐蚀会在阴极寿命初期造成明显影响, 并且孔区腐蚀最为严重区域为离子电流密度最高处, 因此获得离子电流密度分布可以进行孔区壁面腐蚀区域和腐蚀程度的预估。
对于离子电流密度的计算, 可通过稳态离子和电子的能量方程以及动量方程进行计算, 在忽略中性原子的动量项后, 离子电流密度和电子电流密度关系如式(10)所示[21]。
| $ {{J}_{\text{i}}}=\frac{m{{\nu }_{\text{en}}}}{M{{\nu }_{\text{in}}}(1\text{ }+{{\nu }_{\text{ie}}}/{{\nu }_{\text{in}}})}{{J}_{\text{e}}}-\frac{\nabla (nk{{T}_{\text{i}}}+nk/{{T}_{\text{e}}})}{M{{v}_{\text{in}}}\left( 1+{{\nu }_{\text{ie}}}/{{\nu }_{\text{in}}} \right)} $ | (10) |
式中νei和νen分别为电子和离子以及电子和原子的碰撞频率[22],νie 为离子和电子的碰撞频率[12, 13]。代入式(9)得到的电子电流密度Je以及等离子体密度等相关参数后, 采用数值计算得到20A发射电流阴极孔区离子电流密度如图 6 (a)所示。
|
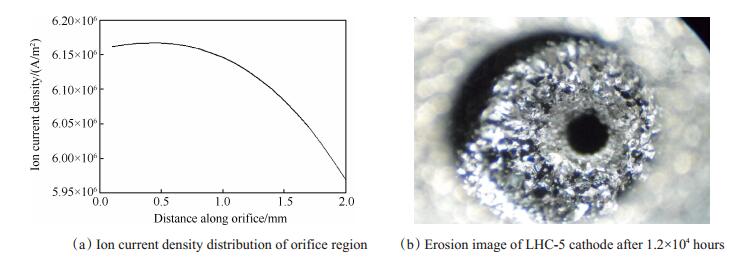
Fig. 6 Ion current density distribution and erosion of LHC-5 cathode after 1.2×104 hours |
从图 6(a)结果来看, 阴极小孔区内的离子电流密度分布较为均匀, 离子电流密度峰值出现在距离小孔入口0.5mm处, 约为6.16×106A/m2, 并且入口处的离子密度整体高于出口处离子密度, 这主要由于当距离沿孔区入口向出口发生变化时, 等离子体电阻率逐渐降低, 导致孔区轴向等离子电势逐渐上升,因此越朝向小孔出口, 离子能量越高且与孔区壁面的溅射作用越为明显, 从而造成离子密度越低。综合来看, 可认为小孔区的离子溅射腐蚀效应是越靠近小孔出口越强, 因此长时间工作的阴极, 其孔区的腐蚀特点应是靠近出口处的孔径在离子腐蚀作用下不断扩张, 并且在扩张到一定程度后, 由于直径的增加, 引起等离子密度、中性原子密度、孔区等离子轴向电势的逐渐降低, 从而使得离子能量降低并最终使离子对小孔壁的腐蚀率降低至可忽略程度, 孔区出口处被腐蚀后的直径将不会再发生变化。目前对于离子电流密度造成的孔区出口处腐蚀深度, 以及阴极工作时间与腐蚀深度的关系, 尚未有理论计算依据, 上述分析仅属于理论预测, 但可以通过完成寿命试验后的阴极小孔区变化结果与理论预测溅射腐蚀趋势进行比对。
由于目前20A发射电流阴极寿命试验正在进行,无法取得试验结果, 本文以我国研制的5A发射电流空心阴极(型号为LHC-5)进行理论预测溅射腐蚀趋势的比对。如图 6(b)所示, 5A发射电流空心阴极在经过1.2×104h后, 其小孔出口区域出现了一定的离子溅射腐蚀。从图中可明显看到小孔出口处直径由于离子溅射作用发生了扩张, 并且在2.1×104h的寿命试验结束后, 通过比对发现阴极孔区的腐蚀情况与1.2× 104h的腐蚀情况基本无变化, 阴极孔区腐蚀情况的寿命试验结果与理论分析预测结果趋势是一致的。
6 结论本文通过对我国研制的20A发射电流空心阴极开展小孔区等离子体特性分析研究, 得出以下结论:
(1) 20A发射电流空心阴极孔区的中性原子密度基本在4×1021~6×1021/m3, 并且越靠近小孔出口区域的原子密度越低。
(2) 采用等离子体零维扩散模型得到阴极小孔区轴向平均电子温度约为2.66eV, 径向平均电子温度为2.2eV, 并且阴极顶小孔入口处轴向电子温度较低, 阴极顶小孔出口处(触持极孔方向)电子温度相对较高, 小孔区是电子温度上升的主要区域, 入口至出口的电子温度增幅在1~2eV。
(3) 采用数值计算方法, 得到小孔区域壁面离子径向平均漂移速度约在0.7~1.64m/s, 平均漂移速度远远低于离子热速度以及中性原子速度, 通过离子连续性方程得到20A发射电流阴极孔区内, 等离子体密度约在1×1021~1.4×1021/m3。越靠近出口, 等离子体密度降低越明显。
(4) 通过电子连续性方程, 得到小孔区入口处的电子电流约为7.2A, 而出口处的电子电流大小约为11.6A, 电子电流增益系数约60%。离子电流密度峰值为6.16×106 A/m2, 且阴极小孔区内的离子电流密度分布较为均匀, 小孔入口处的离子密度整体高于出口处离子密度。
(5) 通过理论分析认为, 长时间工作的阴极, 其孔区的腐蚀特点是靠近出口处的直径在离子腐蚀作用下不断的扩张, 并且在扩张到一定程度后, 离子能量降低并最终使离子对小孔的腐蚀率降低至可忽略程度, 孔区出口处被腐蚀后的直径将不会再发生变化, 理论分析腐蚀趋势与我国研制的LHC-5阴极小孔区寿命试验腐蚀情况基本一致。
由于缺乏相关试验手段, 本文计算得到的孔区等离子体特性参数目前只有部分能够进行试验验证, 后续将继续进行相关的试验方法研究和进一步验证。
| [1] |
孙明明, 张天平, 王亮, 等. 30cm口径离子推力器栅极组件热应力及热形变计算模拟[J]. 推进技术, 2016, 37(7): 1393-1400. (SUN Ming-ming, ZHANG Tian-ping, WANG Liang, et al. Thermal Stress and Thermal Deformation Analysis of Grids Assembly for 30cm Diameter Ion Thruster[J]. Journal of Propulsion Technology, 2016, 37(7): 1393-1400.)
(  0) 0) |
| [2] |
Katz I, Anderson J, Polk J, et al. A Model of Hollow Cathode Plasma Chemistry[R]. AIAA 2002-4241.
(  0) 0) |
| [3] |
Katz I. Model of Plasma Contactor Performance[J]. Journal of Spacecraft and Rockets, 1997, 34(6): 824-828. DOI:10.2514/2.3294
(  0) 0) |
| [4] |
Malik A, Montarde P, Haines M, et al. Spectroscopic Measurements of Xenon Plasma in a Hollow Cathode[J]. Journal of Applied Physics, 2000, 33(3): 2037-2048.
(  0) 0) |
| [5] |
Polk J, Anderson J, Brophy J, et al. An Overview of the Results from an 8200-Hour Wear Test of the NSTAR Ion Thruster[R]. AIAA 99-2446.
(  0) 0) |
| [6] |
Jameson K, Goebel D, Watkins R. Hollow Cathode and Keeper Region Plasma Measurements[R]. AIAA 2005-3667.
(  0) 0) |
| [7] |
张岩, 康小录, 乔彩霞. 钡钨空心阴极放电等离子体特性实验研究[J]. 火箭推进, 2014, 40(5): 55-60. (  0) 0) |
| [8] |
孙明明, 顾左, 郭宁, 等. 离子推力器空心阴极热特性模拟分析[J]. 强激光与粒子束, 2010, 22(5): 1149-1152. (  0) 0) |
| [9] |
郭宁, 唐福俊, 李文峰. 空间用空心阴极研究进展[J]. 推进技术, 2012, 33(1): 155-160. (GUO Ning, TANG Fu-jun, LI Wen-feng. Advances in Spaceborne Hollow Cathode[J]. Journal of Propulsion Technology, 2012, 33(1): 155-160.)
(  0) 0) |
| [10] |
孙明明, 张天平, 吴先明. 20cm离子推力器放电室流场计算模拟[J]. 强激光与粒子束, 2015, 27(5). (  0) 0) |
| [11] |
Katz I, Anderson J, Polk J, et al. One Dimensional Hollow Cathode Model[J]. Journal of Propulsion and Power, 2003, 19(4): 595-600. DOI:10.2514/2.6146
(  0) 0) |
| [12] |
Bond Latham. Ion Thruster Extraction Grid Design and Erosion Modeling Using Computer Simulation[R]. AIAA 95-2923.
(  0) 0) |
| [13] |
Rapp D Francis. Charge Exchange Between Gaseous Ions and Atoms[J]. Journal of Chemical Physics, 1962, 37(11): 2631-2645. DOI:10.1063/1.1733066
(  0) 0) |
| [14] |
Goebel D, Jameson K, Watkins R, et al. Hollow Cath ode and Keeper-Region Plasma Measurements Using Ul tra-Fast Miniature Scanning Probes[R]. AIAA 2004-3430.
(  0) 0) |
| [15] |
孙明明, 张天平, 龙建飞. 30cm离子推力器空心阴极发射体区等离子体特性研究[J]. 推进技术, 2017, 38(12). (SUN Ming-ming, ZHANG Tian-ping, LONG Jian-fei. Plasma Characteristics in Hollow Cathode Emitter Region of 30cm Diameter Ion Thruter[J]. Jour nal of Propulsion Technology, 2017, 38(12).)
(  0) 0) |
| [16] |
Polk J, Grubisic A, Taheri N, et al. Emitter Tempera ture Distributions in the NSTAR Discharge Hollow Cath ode[R]. AIAA 2005-4398.
(  0) 0) |
| [17] |
Mikelides I, Katz I, Goebel D, et al. Plasma Processes Inside Orificed Hollow Cathode[J]. Physics of Plas mas, 2006, 13(5).
(  0) 0) |
| [18] |
Matossian J, Beattie J. Model for Computing Volume Averaged Plasma Properties in Electron-Bombardment Ion Thruster[J]. Journal of Propulsion and Power, 1989, 5(1): 188-196.
(  0) 0) |
| [19] |
Mikelides I, Katz I, Goebel D, et al. Theoretical Model of a Hollow Cathode Plasma for the Assessment of Insert and Keeper Lifetimes[R]. AIAA 2005-4234.
(  0) 0) |
| [20] |
Rawlins V, Sovey J, Anderson J, et al. NSTAR Flight Thruster Qualification Testing[R]. AIAA 98-3936.
(  0) 0) |
| [21] |
Mikelides I, Katz I, Goebel D, et al. Hollow Cathode Theory and Modeling: A Two-Dimensional Model of the Emitter Region[J]. Journal of Propulsion and Power, 2005, 98(10).
(  0) 0) |
| [22] |
Book D. NRL Plasma Formulary[M]. Washington D C: Naval Research Laboratory, 1987, 402-410.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

