2. 中国航发沈阳发动机研究所,辽宁 沈阳 110015
2. AECC Shenyang Engine Institute, Shenyang 110015, China
随着航空发动机技术、性能要求的不断提升,气体泄漏问题已经成为航空发动机领域研究热点[1~4]。航空发动机的密封结构要承受高环境温度、高密封压差以及剧烈振动等多种载荷[5]。密封环又是密封结构的重要部件,只有充分掌握密封环的密封特性,才能更好地设计各种密封参数,达到气体密封要求[6, 7]。
金属密封环主要有O形环、C形环、E形环、Ω形环、W形环等。金属O形密封环是最普通的一种密封元件,它结构简单、装拆方便、成本低廉,应用广泛,且具有自紧密封功能[8, 9]。尽管O形环的密封机理比较简单,但是材料和尺寸选择、沟槽设计、安装及使用都必须符合一定的要求,才能取得良好和可靠的密封效果。1996年美国挑战者号航天飞机的空难事件正是O形环失效引起的[10]。近森德重[11]通过实验数据分析了O形环与接触面间的接触压力。合肥通用机械研究所[12, 13]实验研究了O形环在不同内压和压缩量下的密封特性。彭向和[14]对O形环的压扁与回弹进行了分析并进行实验对比,实验结果和分析数据基本吻合。余伟炜[15]通过实验证实,轴向尺寸和温度对O形环回弹量的影响很小。李亚明[16]通过实验得到了O形环密封比压与紧密系数的关系图,并且分析了镀银对密封性能的影响。金属C形密封环的密封机理和主要特性类似于金属O形环,但柔软性更好,需要的压缩载荷更低,同样压缩20%所需要的压缩载荷只有O形环的50%[17]。Tsujikawa H[18]等实验测试了不同镀层材料下C形环的泄漏量。LIU Ying[19]等分析了压缩量对弹簧自紧式C形环重复利用次数的影响。左国[20]对C形环进行实验研究,结果表明回弹量与压扁度呈正比关系。文献[17]指出,E形金属密封环提供了较低的压缩预载荷,比O形环和C形环更大的回弹性。因此,它们可用于当运行中法兰出现某些分离以及高压和高温场合。吕英[21]研制出一种E形双面密封环,实验表明这种密封环可在压缩量不足的情况下,通过气体压力实现自动密封补偿。金属Ω形环常用于温度、压力波动较大,介质为易燃易爆,不经常拆卸的场合[22]。上海炼油厂在国产高压换热器上采用Ω形密封环,并在设计压力下安全运行了两年[23]。航空发动机用密封环的文献较少,文献[24, 25]进行了详细研究。龚雪婷[25]通过实验测得W形密封环压缩量为0.3mm,气体压力为4MPa时的泄漏量。Sarawate N[26]等通过高温实验台得到了W形密封环在不同压缩量下的密封性能。
本文研究的组合式弹性片金属密封环结构在国产某新机上首次采用,其中的弹性片属于一种特殊的金属密封环。因此,研究其密封特性具有重要价值。本文采取实验与理论相结合的方法对其密封机理进行了分析,研究了腔室气体压力和弹性片压缩量对弹性片密封结构泄漏率和泄漏面积的影响,可对发动机密封结构设计提供理论依据。
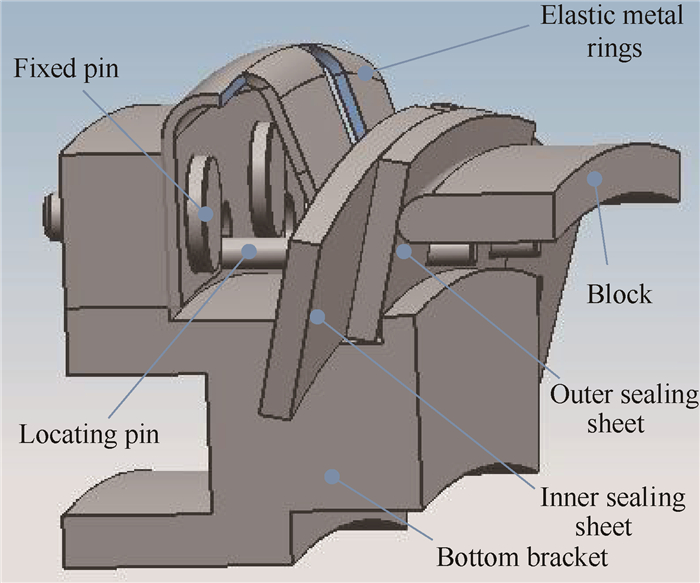
2 组合式弹性片金属密封环结构分析 2.1 组合式弹性片金属密封环结构组合式弹性片金属密封环结构是航空发动机涡轮高压区重要的密封结构,其一周共有27组相同的密封结构:由27个弹性片、27个外封严片、27个内封严片、54个固定销钉、54个定位销钉、1个顶块、1个底托组合而成。内封严片与弹性片接触,外封严片和内封严片相互搭接,如图 1所示。
|
Fig. 1 Structure of the composited elastic metal sealing rings |
组合式弹性片金属密封环在上腔室结构中的位置如图 2所示。弹性片密封结构使用高温合金制造,其它部分使用碳钢。实验中假设上腔室的所有气体均通过弹性片密封结构向大气泄漏,即忽略上腔室通过安装边向下腔室和大气的泄漏。

|
Fig. 2 Upper chamber structure |
弹性片是由镍基材料制成的特殊的金属密封环,是一种轴向自紧式静密封元件,在腔室气体压力和弹性片压缩量共同作用下,依靠自身的弹性变形,产生相应的弹性力作用到封严片,依靠封严片的变形,使封严片与顶块之间完全贴合,产生很高的线密封比压,达到预期的密封效果,否则会产生顶块与封严片处的接触泄漏和定位销钉处的通道泄漏(由于封严片的孔直径比定位销钉直径大)。当压缩量较小或者腔室压力很低的情况下,封严片与顶块并未完全贴合,此时接触泄漏和通道泄漏共存;而当压缩量和腔室压力增加到一定值时,顶块与封严片完全接触并压紧,此时泄漏方式为通道泄漏。
3 组合式弹性片金属密封环密封特性实验研究 3.1 实验原理和装置实验装置系统图如图 3所示,实验装置实物图如图 4所示,空气经压缩机压缩至1MPa后进入缓冲罐,然后通过流量计,通入实验件上压力腔室内。上腔室内压力p可由压力表和压力传感器测量,压力表可以直接监测上腔室压力,压力传感器可以测量上腔室压力并将数据传送给数据采集仪。其中压力表可与进气阀门配合使用调节上腔室内压力。

|
Fig. 3 Schematic diagram of the experimental process |

|
Fig. 4 Experimental device |
此方案的测量原理是,若腔室内压力p数值稳定,则通过腔室泄漏的流量Q与气体管道上流量计测量得到的流量数值相同。因此,在相同弹性片压缩量下,通过调整气流流量,得到腔室不同的压力等级p,即可得到泄漏量Q与压力p的关系。通过调整垫圈初始厚度来增加弹性片压缩量ΔS,从而得到不同弹性片压缩量下,泄漏量Q与压力p的关系。每种情况下进行二次或三次重复性实验,取其平均值进行数据分析。
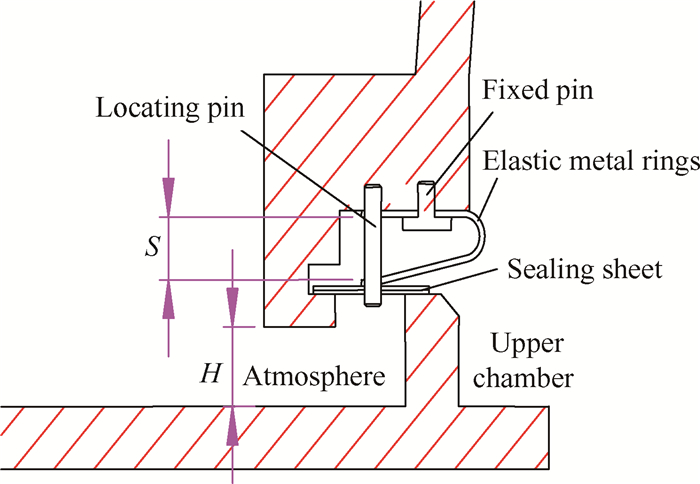
3.2 实验参数确定弹性片密封结构如图 5所示。固定销钉将弹性片固定在上腔盖上,封严片在弹性片的作用下紧搭在两外沿上,将高压区和外界大气分隔,并通过定位销钉进行定位,使其只能沿定位销钉上下移动。其中S表示弹性片两边外端的距离,H表示上下两构件之间的相对距离,实验件装配好之后,S值无法直接测量,所以可以通过测量H值间接计算ΔS。
|
Fig. 5 Elastic metal sealing structure |
测量H的工具为激光位移传感器和千分尺。激光位移传感器和千分尺的测量点示意图和实物图如图 6所示。四个测量点均匀分布,其中一点布置激光位移传感器,其主要作用是监测螺栓预紧时H值的变化量,从而能够简单方便地将H调节至设定值。另外,每次通过螺栓预紧调节H值之后,需要利用千分尺测量四个测试点处的H值以确认四点H都达到设定值。如果有偏差,需要重新调节直至四点都调节至设定H值。

|
Fig. 6 Arrangement of measuring points |
考虑到上腔室能承受的最大压力以及所能提供的最大气源流量,腔室内最大压力可以维持在0.5MPa。所以最终确定测量0.05,0.10,0.15,0.20,0.25,0.30,0.35,0.40,0.45,0.50MPa腔室压力下弹性片密封结构的泄漏率Q。
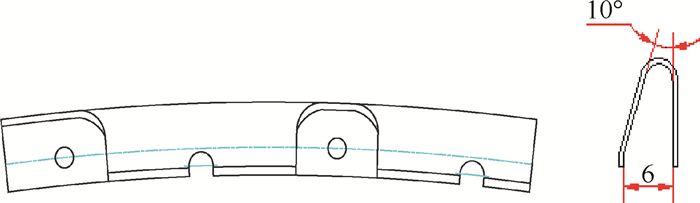
3.2.2 压缩量弹性片如图 7所示。初始无压缩时两边夹角为10°,两边外端距离为6mm。改变弹性片压缩量ΔS即改变两边夹角和两边外端距离。实验中通过上法兰安装边上垫圈的初始厚度和压紧程度来控制H,进而得到ΔS。
|
Fig. 7 Elastic metal rings |
通过计算得出弹性片夹角与压缩量ΔS,压缩量ΔS与垫圈初始厚度的关系,如表 1,表 2所示。
|
|
Table 1 Relationship between angle and compression deformation ΔS |
|
|
Table 2 Relationship between initial thickness of gasket and compression deformation ΔS |
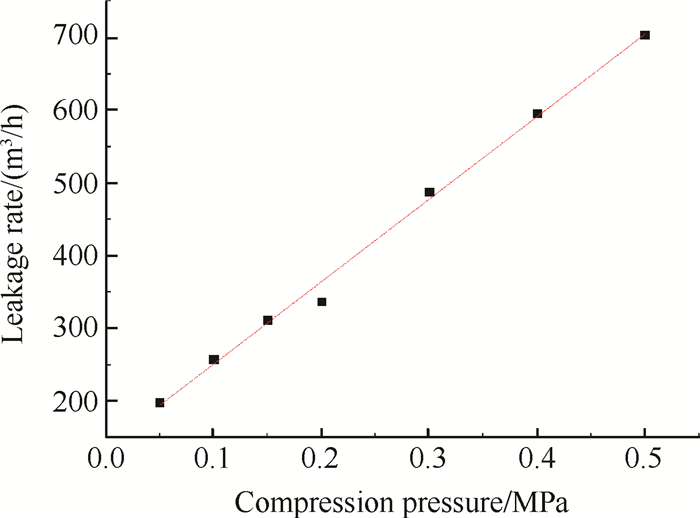
实验研究了不同压缩量下腔室内压力(表压)与泄漏率(已转换为常压下数值,下同)的关系。图 8为通过最小二乘法拟合得到的压缩量为0.4mm (弹性片夹角为8°)时腔室压力(0.05~0.50MPa)与泄漏率的关系。可见,泄漏率随腔室压力的增大而线性增加。
|
Fig. 8 Leakage rate at different chamber pressure when the compression deformation is 0.4mm |
表 3为不同压缩量ΔS情况下,泄漏率Q与腔室压力p的拟合关系式。
|
|
Table 3 Least-squares fit of Q with p under different compression deformation ΔS |
根据气体流动临界条件判定公式,当p>0.09MPa时,气体流速等于当地声速,此时气体流速不会随p的增大而增大。如果泄漏通道面积变化不大,单位时间内气体在不同p情况下泄漏的体积流量不变。如果将各压力情况下的体积流量都换算到大气压情况下的体积流量,那么理论上常压泄漏体积流量随着p的增大而线性增大。
考虑到实际发动机对应的腔位置气体压力约为1MPa,而在现实条件下无法完成该压力下的实验,故需通过拟合方程计算出1MPa腔室压力下的泄漏率,结果如表 4所示。可以看出,在1.0MPa腔室压力下,最大泄漏率Q为1400m3/h,出现在0.1mm压缩量(压缩角为9.5°)情况下;最小泄漏率Q约为1220m3/h,出现在0.6~1.2mm压缩量(压缩角为4°~7°)之间。实验测得最大泄漏率为1400m3/h,即1810kg/h。
|
|
Table 4 Leakage rate Q at different compression deformation ΔS when the chamber pressure is 1MPa |
实验研究了腔室压力为0.05~0.50MPa下,弹性片压缩量与泄漏率的关系,如图 9所示。

|
Fig. 9 Leakage rate at different compression deformation when the chamber pressure varies from 0.05 to 0.5MPa |
在0.05MPa,0.10MPa腔室压力下,Q随量ΔS增大线性减小。分析认为:当p≤0.10MPa时,较小的压力对改善弹性片结构密封效果的作用非常小,弹性片压缩量对改善密封性能效果显著。
当腔室压力在0.15~0.50MPa时,Q随ΔS的增大先减小后趋于不变。分析认为,当p≥0.15MPa时,腔室压力使弹性片结构有一定的密封效果,压力越大密封效果越好。同时,压力越大弹性片压缩量的增大对密封性的改善效果不显著。尤其在弹性片压缩量较大时,继续增大压缩量对密封性基本没有影响,说明腔室压力p越大,弹性片压缩量ΔS对泄漏率Q影响越小。
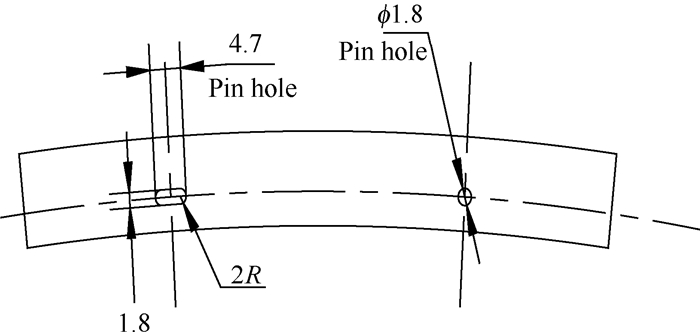
4.3 组合式弹性片金属密封环密封泄漏面积特性分析 4.3.1 泄漏面积分析在1.2mm压缩量、0.05MPa腔室压力下,弹性片结构处仍有150m3/h的泄漏率。说明弹性片结构处此时存在有较大的通道泄漏面积。封严片主要尺寸如图 10所示,因此可估算出通道泄漏面积A1。
|
Fig. 10 Sealing sheet |
当不考虑外封严片作用时,内封严片通道泄漏面积是通道泄漏面积A1的最大值,如式(1)所示
| $ \begin{array}{l} {A_1} \le {\rm{ \mathit{ π} }} \cdot R_1^2 + \frac{1}{2}{\rm{ \mathit{ π} }} \cdot R_1^2 + 2{R_1} \cdot L + \frac{1}{2}{\rm{ \mathit{ π} }} \cdot R_1^2-2{\rm{ \mathit{ π} }} \cdot R_0^2 = \\ 2{\rm{ \mathit{ π} }} \cdot R_1^2 + 2{R_1} \cdot L-2{\rm{ \mathit{ π} }} \cdot R_0^2 \end{array} $ | (1) |
式中R1为定位销钉孔半径0.9mm;R0为定位销钉半径0.8mm;L为定位长销钉孔宽4.7mm。通道泄漏面积为
| $ \begin{array}{l} A \le {\rm{ }}27{A_1} = {\rm{ }}27{\rm{ }} \times (2{\rm{ }} \times {\rm{ }}3.14{\rm{ }} \times {\rm{ }}{0.9^2} + {\rm{ }}2{\rm{ }} \times {\rm{ }}0.9{\rm{ }} \times {\rm{ }}4.7{\rm{ }}-\\ 2{\rm{ }} \times {\rm{ }}3.14{\rm{ }} \times {\rm{ }}{0.8^2}) = 230{\rm{ m}}{{\rm{m}}^2} \end{array} $ |
总泄漏面积A计算方法可参考GB150-2011《压力容器》标准附录B中相关公式,即
| $ {p_{{\rm{trans}}}} = {p_{{\rm{atm}}}}{\left( {\frac{{k + 1}}{2}} \right)^{\frac{k}{{k-1}}}} $ | (2) |
式中ptrans为声速向亚声速转换压力,MPa;patm为大气压力,0.103MPa;k为气体绝热系数,1.4。
由式(2)计算得到的转换压力ptrans为0.195MPa (绝对压力),表压为0.094MPa。如果腔室压力p未达到转换压力ptrans,则按照公式(3)进行计算
| $ A = \frac{{{W_{\rm{s}}}}}{{55.84K \cdot {p_{\rm{d}}}\sqrt {\frac{M}{{ZT}}\frac{k}{{k- 1}}\left[{{{(\frac{{{p_0}}}{{{p_{\rm{d}}}}})}^{2{\rm{/}}k}}-{{(\frac{{{p_0}}}{{{p_{\rm{d}}}}})}^{\frac{{k + 1}}{k}}}} \right]} }} $ | (3) |
否则按照公式(4)进行计算。
| $ A = \frac{{{W_{\rm{s}}}}}{{7.6 \times {{10}^{-2}}CK \cdot {p_{\rm{d}}}\sqrt {M/ZT} }} $ | (4) |
式中A为总泄漏面积,mm2;Ws为质量泄漏率,kg/h;C为气体特性系数;K为泄放系数;pd为腔室绝对压力,MPa;M为气体摩尔质量,g/mol;Z为气体压缩系数;T为腔室内绝对温度,K;k为绝热指数。
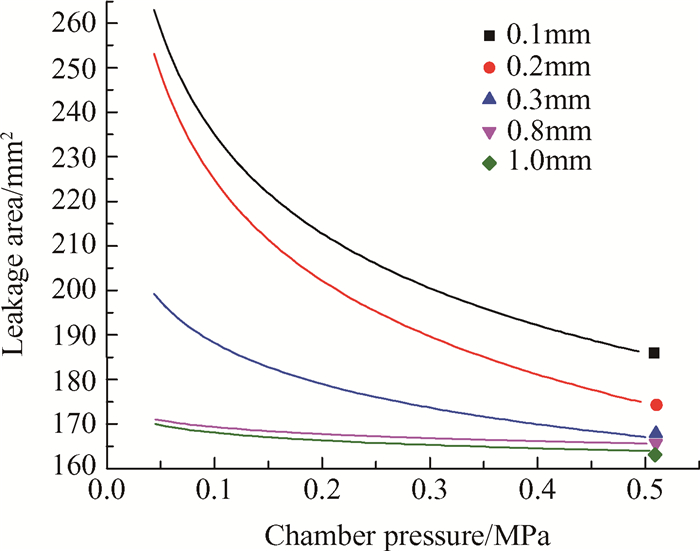
根据公式(3),(4)和实验数据,可以计算出各压缩量和各腔室压力情况下弹性片结构处的总泄漏面积A。不同压缩量下,泄漏面积随腔室压力变化如图 11所示。
|
Fig. 11 Leakage area varies with chamber pressure at different compression deformation |
从图 11中可以看出,增大弹性片压缩量ΔS和腔室压力p都有利于减小泄漏面积A。当压缩量分别为0.1mm,0.2mm和0.3mm时,A均在p=0.05MPa时达到最大值,分别为264mm2,254mm2,199mm2。A随p的增大先减小后趋于不变,p=0.50MPa时,A分别为190mm2,176mm2,169mm2。当压缩量为0.8mm和1.0mm时,p对A基本没有影响,A维持在一个稳定的值169mm2 < 230mm2,满足上述的理论计算。说明此时腔室内泄漏方式为通道泄漏,而169mm2即是通道泄漏面积。
由总泄漏面积A和通道泄漏面积A1可得出接触泄漏面积A2,如图 12所示。

|
Fig. 12 Contact leakage area varies with chamber pressure p at different compression deformation ΔS |
由图 12可知,接触泄漏面积随着压缩量或腔室压力的增大而减小。当压缩量较小的时候,腔室压力的增大对密封性能的改善效果显著;当压缩量大于0.8mm和腔室压力大于0.4MPa时,接触泄漏面积微乎其微,与理论分析吻合。
5 结论通过本文研究,得到以下结论:
(1) 弹性片压缩量在0.1~1.2mm,腔室压力在0.05~1MPa时,不同弹性片压缩量情况下,弹性片结构处泄漏率均随压力增大线性增大。当腔室压力达到1MPa情况下,弹性片结构处最大泄漏率为1400m3/h,最小泄漏率为1220m3/h。
(2) 当腔室压力小于等于0.10MPa时,泄漏率随弹性片压缩量增大线性减小。腔室压力大于等于0.15MPa时,泄漏率随弹性片压缩量增大先减小后趋于不变。
(3) 在压缩量较小或者腔室压力很低的情况下,封严片与顶块并未完全贴合,此时接触泄漏和通道泄漏共存;当压缩量和腔室压力增加到一定值时,顶块与封严片完全接触并压紧,此时泄漏方式为通道泄漏。可见增大弹性片压缩量和腔室压力都有利于减小泄漏面积。
(4) 压缩量增大到0.80mm和腔室压力增大到0.40MPa时,继续增大压缩量或腔室压力对减小泄漏面积作用不大,泄漏面积会稳定在169mm2,即为通道泄漏面积。
| [1] |
李钰洁, 刘永葆, 贺星. 间隙变化对新型涡轮密封气动性能影响的数值分析[J]. 推进技术, 2015, 36(8): 1179-1185. (LI Yu-jie, LIU Yong-bao, HE Xing. Numerical Simulation for Effect of Clearance Change of a Novel Seal on Aerodynamic Performance of Gas Turbine[J]. Journal of Propulsion Technology, 2015, 36(8): 1179-1185.)
(  0) 0) |
| [2] |
李钰洁, 刘永葆, 贺星. 基于气动性能优化的涡轮叶顶新型密封构型研究[J]. 推进技术, 2015, 36(5): 696-702. (LI Yu-jie, LIU Yong-bao, HE Xing. Study Optimization Research on a Novel Turbine Blade Tip Seal Configuration Based on Aerodynamic Performance[J]. Journal of Propulsion Technology, 2015, 36(5): 696-702.)
(  0) 0) |
| [3] |
徐旭, 康顺, 谭春青, 等. 涡喷发动机涡轮密封舱小气路流场数值计算[J]. 推进技术, 2000, 21(2): 29-32. (XU Xu, KANG Shun, TAN Chun-qing, et al. Numerical Simulation on Viscous Flow in the Secondary Flow Path of a Turbine Sealed Cabin[J]. Journal of Propulsion Technology, 2000, 21(2): 29-32.)
(  0) 0) |
| [4] |
李伟, 乔渭阳, 许开富, 等. 涡轮叶尖迷宫式密封对泄漏流场影响的数值模拟[J]. 推进技术, 2009, 30(1): 88-94. (LI Wei, QIAO Wei-yang, XU Kai-fu, et al. Numerical Simulation of Labyrinth Seal on Tip Leakage Flow in Partially and Fully Shrouded Axial Turbine[J]. Journal of Propulsion Technology, 2009, 30(1): 88-94.)
(  0) 0) |
| [5] |
胡广阳. 航空发动机密封技术研究[J]. 航空发动机, 2012, 38(3): 1-4. (  0) 0) |
| [6] |
李玉婷, 廖日东, 辛婷, 等. 低温U形金属密封环密封性能有限元分析[J]. 润滑与密封, 2014, 39(7): 60-66. (  0) 0) |
| [7] |
刘艳梅, 孙扬, 宋鸿达. 某涡喷发动机密封环研制[J]. 推进技术, 1999, 20(6): 45-47. (LIU Yan-mei, SUN Yang, SONG Hong-da. Study of Seal Ring of Turbojet Engine[J]. Journal of Propulsion Technology, 1999, 20(6): 45-47.)
(  0) 0) |
| [8] |
黄迷梅. 液压气动密封与泄漏防治[M]. 北京: 机械工业出版社, 2003.
(  0) 0) |
| [9] |
近森徳重, 河原由夫共. 密封装置[M]. 东京: 幸书房, 1975.
(  0) 0) |
| [10] |
Müller H K, Nau B S. Fluid Sealing Technology : Principles and Applications[M]. ew York: Marcel Dekker, Inc., 1998.
(  0) 0) |
| [11] |
近森德重. 密封元件O形密封圈[M]. 北京: 机械工业出版社, 1976.
(  0) 0) |
| [12] |
合肥通用机械研究所高压密封课程组. 金属O形环基础试验[J]. 化工与通用机械, 1978(2): 19-25. (  0) 0) |
| [13] |
合肥通用机械研究所高压密封课程组. 高温高压金属O形环密封试验研究[J]. 化工与通用机械, 1978(2): 14-18. (  0) 0) |
| [14] |
彭向和, 高芝晖, 曾祥国. O形密封环的弹塑性大变形和循环松弛分析[J]. 重庆大学学报:自然科学版, 1998, 21(2): 46-50. (  0) 0) |
| [15] |
余伟炜, 蔡力勋, 叶裕明, 等. Inconel718金属O形环回弹特性研究[J]. 工程力学, 2006, 23(6): 142-147. (  0) 0) |
| [16] |
李亚明, 文联奎, 赵正修. 不锈钢O形环垫的密封性能试验研究[J]. 中国石油大学学报自然科学版, 1994, 18(6): 80-85. (  0) 0) |
| [17] |
蔡仁良. 流体密封技术:原理与工程应用[M]. 北京: 化学工业出版社, 2013.
(  0) 0) |
| [18] |
Tsujikawa H, Maruoka S, Koeda M, et al. Preliminary Studies on Large Metal-Sealed Gate Valves for the International Thermonuclear Experimental Reactor (ITER)[J]. Vacuum, 1996, 47(6): 639-646.
(  0) 0) |
| [19] |
Liu Y, Zhou K, Huang W F, et al. Numerical and Experimental Analysis of the Reusability of Spring Energized Metal C Rings[J]. Science China Technological Sciences, 2014, 57(8): 1670-1676. DOI:10.1007/s11431-014-5584-3
(  0) 0) |
| [20] |
左国, 郝守信, 尹小龙. 先进压水堆C形环研究[J]. 核动力工程, 2002, 23(2): 107-112. (  0) 0) |
| [21] |
吕英, 伊松年, 朱丽平, 等. 制动管系用E形双面主动密封法兰密封圈的研制[J]. 铁道车辆, 2009, 47(10): 11-14. DOI:10.3969/j.issn.1002-7602.2009.10.003 (  0) 0) |
| [22] |
陈晔, 顾伯勤, 冯秀. Ω形密封环的应力分析[J]. 南京工业大学学报(自科版), 2002, 24(6): 44-47. (  0) 0) |
| [23] |
顾雪东. 高压换热器的Ω形环密封结构[J]. 压力容器, 2000, 17(6): 25-26. (  0) 0) |
| [24] |
邢敏杰. 航空发动机中W形金属密封环密封性能及泄漏研究[D]. 北京: 北京理工大学, 2015.
(  0) 0) |
| [25] |
龚雪婷. 航空发动机用W形金属密封环特性研究[D]. 北京: 北京化工大学, 2011.
(  0) 0) |
| [26] |
Sarawate N, Wolfe C, Sezer I, et al. Characterization of Metallic W-Seals for Inner to Outer Shroud Sealing in Industrial Gas Turbines[C]. Copenhagen: Turbine Technical Conference and Exposition. American Society of Mechanical Engineers, 2012: 1855-1862.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

