2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
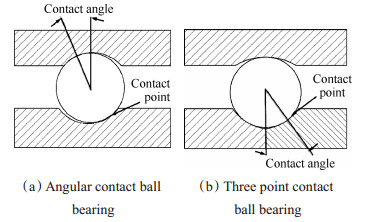
三点接触球轴承由于其可综合承受双轴向载荷、径向载荷和扭转载荷,同时在结构布置和复杂度上优于传统背靠背的双排角接触球轴承,被广泛应用于透平旋转机械的支承结构中。随着旋转机械转速的不断提高,轴承支承特性对整个轴承—转子系统的刚度、振动以及稳定性的影响越来越显著[1],准确分析轴承的刚度特性对于提高转子动力学性能具有重要的理论意义。三点接触球轴承作为燃气轮机和航空发动机转子系统中广泛采用的支承形式,其支承特性对于转子动力学性能具有重要影响。三点接触球轴承的结构设计与动力学特性与一般的角接触球轴承存在较大区别。如图 1所示,三点接触球轴承结构紧凑,内圈分半,滚道为双圆弧曲线,能同时承受较大的径向载荷与轴向载荷,能起到一对角接触球轴承的作用;同时,由于其采用整体保持架,具有较高的速度特性。
|
Fig. 1 Distinguish between angular contact ball bearing and three point contact ball bearing |
对于多点接触球轴承的研究,国内外学者多针对应用选型进行了定性讨论,还有学者采用Hertz接触理论分析了轴承的静态受力,得到了一些经验公式,而对于复杂载荷作用下轴承的刚度特性并没有深入研究[2~5]。Leblanc A,Guo Y等[6, 7]采用了解析模型与分析准则对四点接触球轴承进行了理论分析,并将所得结果与Kraus J[8]的四点接触球轴承分析程序结果进行对比,结果表明如果将四点接触球轴承作为两个角接触球轴承的叠加,求解径向力与力矩时将会出现较大误差。徐荣瑜等[9~11]对三点、四点接触球轴承模型结构进行了详细的分析,指出了三点接触球轴承与普通角接触球轴承的区别,并提出了三点接触球轴承的应用场合与设计要求,但对三点接触球轴承的刚度特性并没有开展研究。平丽浩和姚廷强等[12, 13]基于有限元分析方法,利用Workbench建立四点接触球轴承非线性接触模型,并分析了四点接触球轴承的受力与变形情况,结果表明轴承的受力情况与Hertz接触理论分析结果相近,比较符合轴承的实际受力情况,但没有建立轴承的刚度模型。
对采用三点接球轴承的透平机组而言,在整个运行工况范围内,三点接触球轴承往往受到的轴向力较大且存在变化。轴向力的作用会改变三点接触球轴承滚珠与内、外滚道的接触和受力关系,进而影响轴承的刚度特性。对于这种受力复杂的轴承,以往的研究成果并不能获得较为准确的刚度特性,进而无法准确分析其转子动力学特性。
本文针对某型船用燃气轮机动力涡轮后支承三点接触球轴承,采用结构力学理论与Hertz接触理论系统分析了三点接触球轴承结构特征以及载荷与变形协调关系,并通过有限元分析软件建立了考虑轴向力影响的三点接触球轴承刚度计算模型,重点分析了横向力、内圈转速、滚动体个数与垫片角等因素对考虑轴向力影响的三点接触球轴承刚度特性的影响规律。
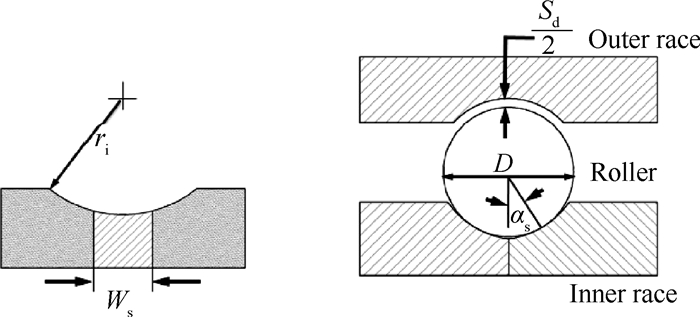
2 三点接触球轴承力学模型 2.1 三点接触球轴承结构模型三点接触球轴承的内圈在磨削时,两半内圈之间加有垫片,垫片的宽度与垫片角有关,如图 2所示。当移去垫片并将双半内圈靠紧后就形成垫片角。垫片的宽度可表示为
|
Fig. 2 Structural model of three point contact ball bearing[14] |
| $ {W_{\rm{s}}} = \left( {2{f_{\rm{i}}} - 1} \right)D\sin {a_{\rm{s}}} $ | (1) |
式中
| $ {f_{\rm{i}}} = {r_{\rm{i}}}/D $ |
ri为切削之前内圈半径,D为滚动体直径,as为垫片角。
三点接触轴承的接触角可以表示为
| $ {a^{\rm{o}}} = {\cos ^{ - 1}}\left( {10 - \frac{{{S_{\rm{d}}}}}{{2BD}} - \frac{{\left( {2{f_{\rm{i}}} - 1} \right)\left( {1 - \cos {a_{\rm{s}}}} \right)}}{{2B}}} \right) $ | (2) |
式中Sd为初始游隙,D为径向游隙;B = fi + fo -1为轴承总曲率;fo = ro/D。
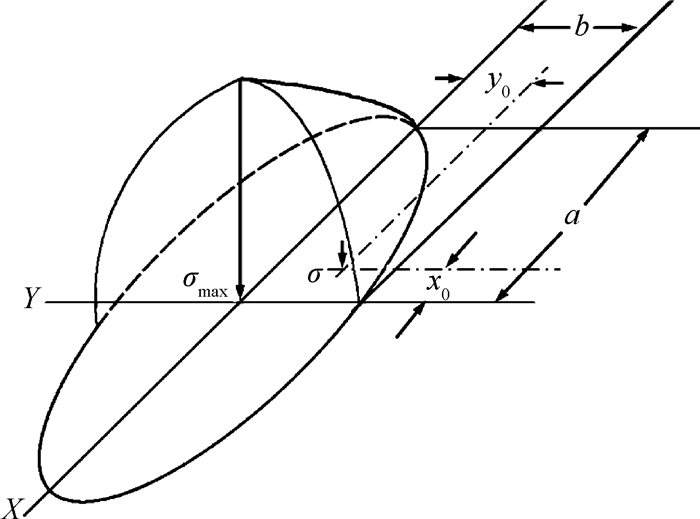
2.2 滚动体Hertz接触分析轴承在高速运转时,内外圈接触角会发生变化。根据Hertz接触理论,随着载荷的增加,接触面积不断增大,点接触变为面接触,并且接触部位的变形达到峰值,轴承的刚度表现为非线性特性。Hertz弹性接触理论可以用来分析滚动轴承的接触应力与应变[15]。在计算过程中需做以下假设:(1)接触区域仅存在弹性变形并服从Hooke定律。(2)接触面平滑连接。(3)不计除了离心力之外的其他惯性力。(4)忽略润滑油膜对轴承刚度的影响。(5)轴承几何形状是理想的,轴承运转时不考虑内外圈、滚动体的陀螺运动与偏斜。点接触变形情况如图 3所示。
|
Fig. 3 Hertz point contact model |
接触体曲率和半径为
| $ \sum r = {r_{11}} + {r_{12}} + {r_{21}} + {r_{22}} $ | (3) |
接触体曲率差半径为
| $ F\left( r \right) = \frac{{\left( {{r_{11}} - {r_{12}}} \right) + \left( {{r_{21}} - {r_{22}}} \right)}}{{\sum \rho }} $ | (4) |
椭圆接触区域长半轴,短半轴分别为
| $ a = {\left( {\frac{{2{\kappa ^2}E}}{{\rm{ \mathsf{ π} }}}} \right)^{\frac{1}{3}}}{\left[ {\frac{{3F}}{{2\sum \rho }}\left( {\frac{{\left( {1 - \xi _1^2} \right)}}{{{E_1}}} + \frac{{\left( {1 - \xi _{11}^2} \right)}}{{{E_{11}}}}} \right)} \right]^{\frac{1}{3}}} $ | (5) |
| $ b = {\left( {\frac{{2E}}{{{\rm{ \mathsf{ π} }}\kappa }}} \right)^{\frac{1}{3}}}{\left[ {\frac{{3F}}{{2\sum \rho }}\left( {\frac{{\left( {1 - \xi _1^2} \right)}}{{{E_1}}} + \frac{{\left( {1 - \xi _{11}^2} \right)}}{{{E_{11}}}}} \right)} \right]^{\frac{1}{3}}} $ | (6) |
对于椭圆接触区域,最大压应力出现在几何中心,其大小为
| $ {{\sigma _{\max }} = \frac{{3F}}{{2{\rm{\pi }}ab}}} $ | (7) |
接触区域内其余点的法向应力为
| $ {\sigma = \frac{{3F}}{{2{\rm{\pi }}ab}}{{\left[ {1 - {{\left( {\frac{x}{a}} \right)}^2} - {{\left( {\frac{y}{b}} \right)}^2}} \right]}^{\frac{1}{2}}}} $ | (8) |
式中ξ为接触体材料泊松比;E为接触体材料弹性模量;r11,r12,r21,r22分别表示接触两物体之间,某一物体在基准平面内的曲率半径;曲率ρ为曲率半径的倒数,表征物体表面的凹凸度;F为接触面法向外载荷。
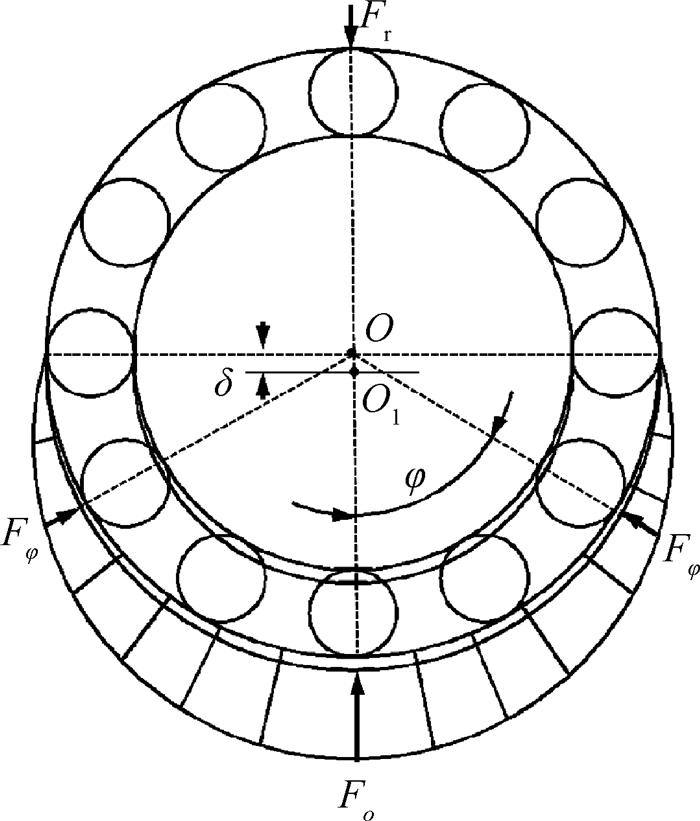
2.3 载荷与变形协调关系对于图 4所示的三点接触球轴承,在不考虑轴向力的作用下,任意角度位置滚动体的径向位移[16~18]为
|
Fig. 4 Load distribution of rolling bearing |
| $ {\delta _j} = {\delta _{\max }}\left[ {1 - \frac{1}{{2e}}\left( {1 - \cos \varphi } \right)} \right] $ | (9) |
式中
| $ e = \frac{1}{2}\left( {1 - \frac{{{P_{\rm{d}}}}}{{2{\delta _{\rm{r}}}}}} \right) $ |
式中Pd = Sd +(2fi -1)(1 -cosas)。δr是φ = 0°处套圈的径向移动量。由此可以得到由径向游隙确定的负荷区域的角度范围为
| $ \varphi = {\cos ^{ - 1}}\left( {\frac{{{P_{\rm{d}}}}}{{2{\delta _{\rm{r}}}}}} \right) $ | (10) |
当游隙为0时,φ = 90°。
对于滚子—滚道接触,力和变形的协调关系为
| $ F = K{\delta ^n} $ | (11) |
由此可以得到第j个滚动体的接触力为
| $ {F_j} = {\left( {\frac{{{\delta _j}}}{{{\delta _{\max }}}}} \right)^n}{F_{\max }} $ | (12) |
将式(9),(11)代入上式,得
| $ {F_j} = {F_{\max }}{\left[ {1 - \frac{1}{{2e}}\left( {1 - \cos \varphi } \right)} \right]^n} $ | (13) |
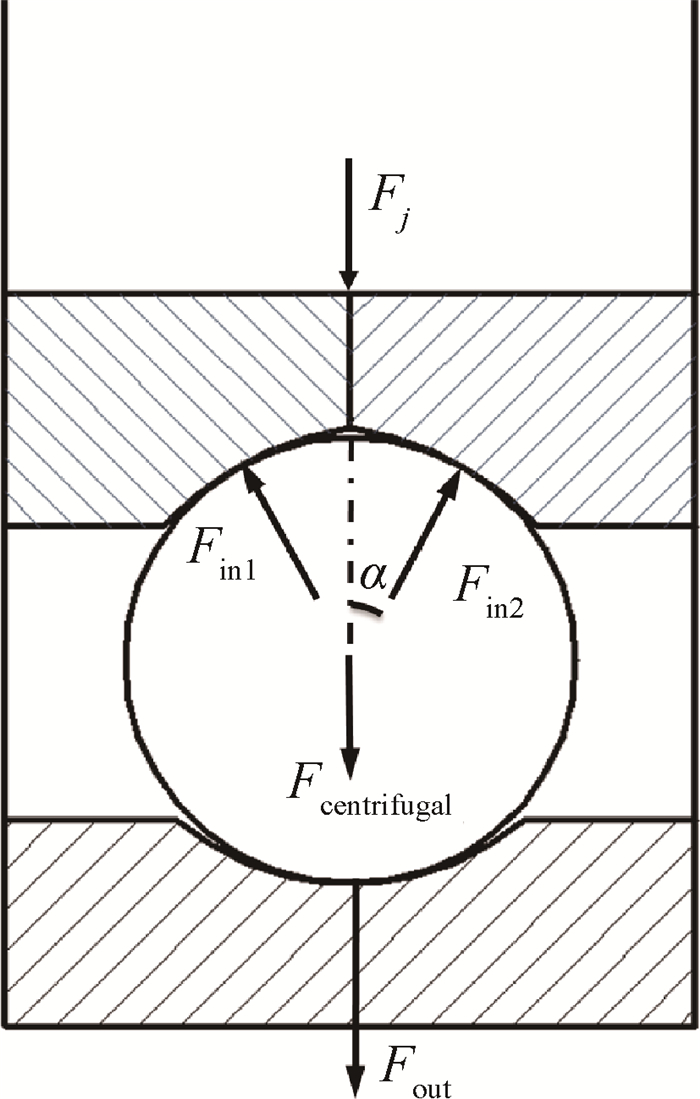
由上边的理论推导,可以得到图 5为三点接触球轴承单个滚动体与内圈的接触力为
|
Fig. 5 Load distribution of a roller |
| $ {F_{{\rm{in}}1}} = {F_{{\rm{in2}}}} = {F_j}\cos \alpha $ | (14) |
个滚动体与外圈的接触力为
| $ {F_{{\rm{out}}}} = {F_j} + {F_{{\rm{centrifugal}}}} = {F_j} + m{w^2}r $ | (15) |
式中m为滚动体质量,w为滚动体公转角速度,r为滚动体公转半径。
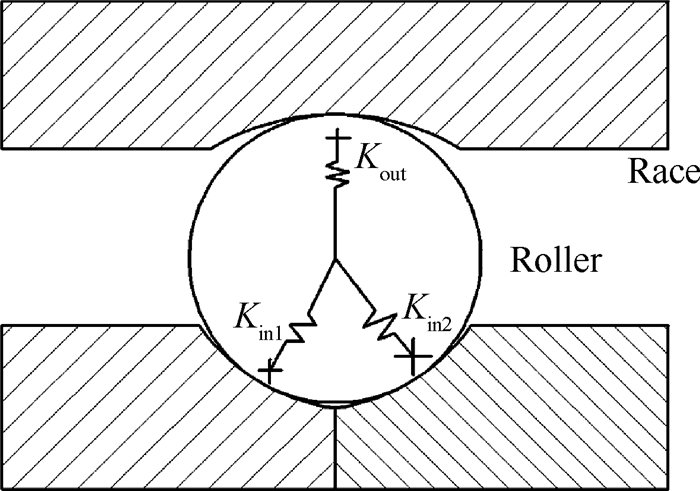
3 静态刚度模型图 6为三点接触球轴承的等效刚度示意图。当横向载荷作用于滚动轴承内圈时,轴承发生变形。滚动体与滚道内圈接触区域形成等效刚度Kin1和Kin2,滚动体与滚道外圈接触区域形成等效刚度Kout。则三点接触球轴承单个滚动体等效刚度模型可以表示为
|
Fig. 6 Stiffness model of roller-race single contact |
| $ {K_j} = \frac{{\partial {F_j}}}{{\partial {\delta _j}}} = {\left[ {\frac{1}{{\frac{{\partial {F_{{\rm{in1}}}}}}{{\partial {\delta _{{\rm{in1}}}}}} + \frac{{\partial {F_{{\rm{in2}}}}}}{{\partial {\delta _{{\rm{in2}}}}}}}} + \frac{1}{{\frac{{\partial {F_{{\rm{out}}}}}}{{\partial {\delta _{{\rm{out}}}}}}}}} \right]^{ - 1}} = {\left[ {\frac{1}{{{K_{{\rm{in1}}}} + {K_{{\rm{in2}}}}}} + \frac{1}{{{K_{{\rm{out}}}}}}} \right]^{ - 1}} $ | (16) |
式中Fj为接触点受到的载荷,δj为载荷作用下的变形量,Kin1,Kin2,Kout分别为三个接触点的等效刚度。
结合单个滚动体静态刚度模型和单个滚动体的载荷变形协调关系,整个三点接触球轴承的向静态刚度表达式为
| $ {K_{\rm{r}}} = \sum\limits_{j = 1}^{{n_1}} {{{\left[ {{{\left( {{a_1}F_{j\left( {{\rm{in1}}} \right)}^{{a_2}}{D^{{a_3}}} + {a_1}F_{j\left( {{\rm{in2}}} \right)}^{{a_2}}{D^{{a_3}}}} \right)}^{ - 1}} + {{\left( {{a_1}F_{j\left( {{\rm{out}}} \right)}^{{a_2}}{D^{{a_3}}}} \right)}^{ - 1}}} \right]}^{ - 1}}} $ | (17) |
式中a1,a2,a3为轴承刚度计算过程中刚度系数,Fj(in1),Fj(in2),Fj(out)为三点接触球轴承接触点受到的载荷大小,n1为载荷作用下受载滚动体的个数。
对于式(17)的刚度表达式,只适用于求解仅受横向力作用的三点接触球轴承静态横向刚度。当轴承受到轴向力作用时,三点接触球轴承的接触角会发生变化,然而建立接触角和轴向力的解析关系非常困难[14],因此需要通过数值解法来分析轴向力对轴承刚度特性的影响
4 三点接触球轴承有限元分析方法 4.1 有限元模型以某型船用燃气轮机动力涡轮后支承三点接触球轴承为研究对象,根据三点接触球轴承基本结构参数,采用商业软件UG对轴承建模。轴承的具体参数如表 1所示,三维模型如图 7所示。

|
Fig. 7 3D model of three point contact ball bearing |
|
|
Table 1 Geometric parameters of a ball bearing |
利用Workbench中Mesh模块分别对轴承外圈、内圈与滚动体进行建模,生成的网格如图 8所示。根据接触面尺寸大小并采用软件内嵌Refinemen方法对接触域进行网格加密,并采用默认的单元类型10节点的四面体单元Solid187对轴承进行网格划分,该单元有10个节点,每个节点有3个自由度。在进行网格无关性验证后,最终确定外圈网格尺寸为2.6mm,内圈网格尺寸为2.4mm,滚动体网格尺寸为2mm,总的网格节点数为194144。

|
Fig. 8 Mesh of bearing |
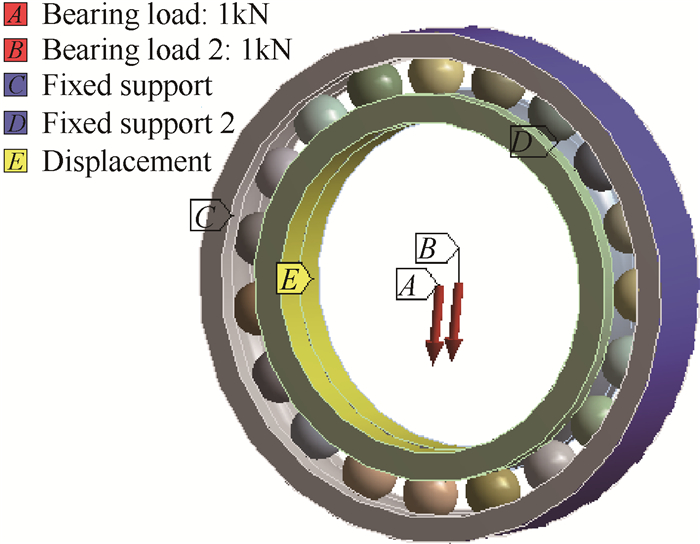
由图 9可见,根据三点接触球轴承的实际工况,轴承内圈采用Bearing load加载轴承受到的横向力,内圈左侧加载轴承受到的轴向力;设置外圈与滚动体表面、滚动体表面与内圈均为摩擦接触,摩擦系数为0.2;对于三点接触球轴承模型,包括太多的接触对配合,而所有的滚动球体仅依靠接触关系实现约束,因此在非线性计算中极难收敛。求解时采用纯罚函数法,同时选择合适的法向接触刚度系数和求解区域网格系数使计算收敛,得到轴承的变形量,并根据载荷与变形量的关系求解三点接触球轴承的轴向刚度与横向刚度。
|
Fig. 9 Load and constraint |
表 2给出了在轴向力为0时,有限元方法和第3节解析解法的横向刚度计算结果对比。结果表明:在不考虑轴向力影响时,解析解法与有限元方法的计算结果比较接近,偏差约为6.7%。
|
|
Table 2 Finite element solution compare with analytic solution |
然而,滚动轴承的刚度除取决于轴承的结构参数外,还受其运行工况的影响。本文在考虑轴向力影响的情况下,采用有限元方法重点分析横向力、滚动体个数、转速、垫片角等因素对三点接触球轴承的横向刚度与轴向刚度的影响。
该型燃气轮机在额定工况工作时,其轴向力约为7.5kN,横向力约为1kN,求得三点接触球轴承横向刚度Kro = 5.3149 × 108N/m,轴向刚度Kao = 3.44 × 109N/m。本文后续的分析结果均以此工况为基准,给出刚度变化的百分比。百分比定义式为:(某工况刚度值-额定工况刚度值) /额定工况刚度值。
图 10,11为三点接触球轴承在额定工况工作下有限元分析结果,并提取轴承横向变形与轴向变形,根据载荷与变形量的关系求解三点接触球轴承的横向刚度与轴向刚度。

|
Fig. 10 Lateral deformation of rated condition |
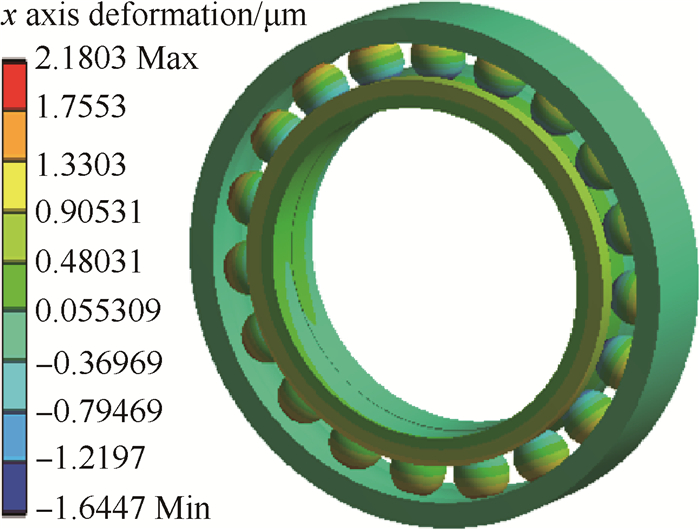
|
Fig. 11 Axial deformation of rated condition |
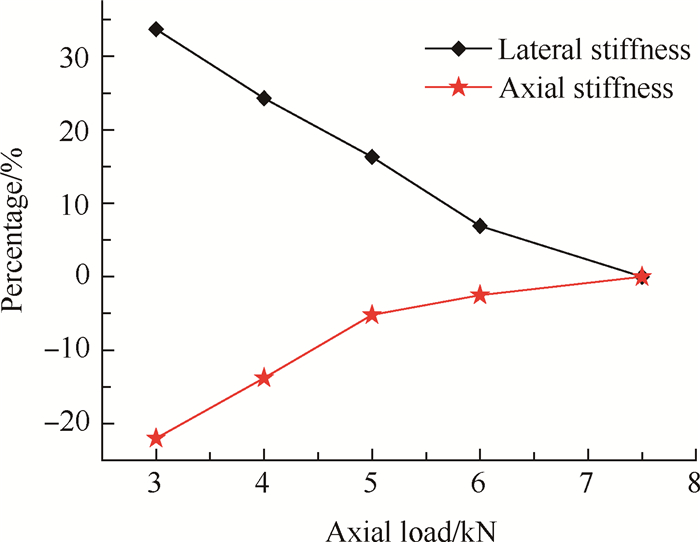
图 12给出了不同轴向力作用下,该三点接触球轴承横向刚度和轴向刚度的变化百分比。
|
Fig. 12 Effects of axial load on stiffness |
结果表明:三点接触球轴承横向刚度随着轴向力增大而减小,轴向刚度随着轴向力增加而增大。本文分析的船用燃气轮机动力涡轮后支承轴承采用定位预紧方式,轴向力作用使预紧力增大,导致接触角增大,这是使横向刚度减小、轴向刚度增大的根本原因。
由于轴向力对轴承刚度的影响较大,在分析其它因素对三点接触球轴承刚度影响时,有必要将轴承受到的轴向力考虑其中。
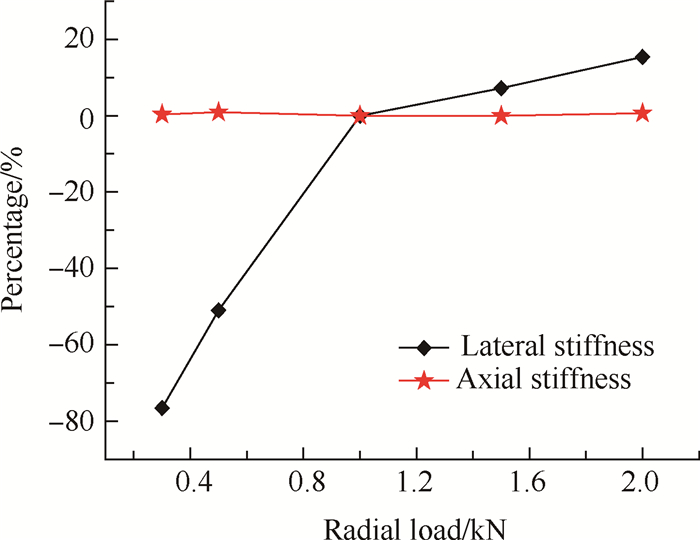
5.2 变横向力对轴承刚度的影响图 13为三点接触球轴承横向刚度与轴向刚度随着横向力变化的百分比。横向刚度随着载荷的增大而增大,而轴向刚度变化不大。研究的三点接触球轴承滚动体个数相对比较多,在横向力的变化下,轴向变形相对较小,所以横向载荷对轴向刚度影响不明显。
|
Fig. 13 Effects of lateral load on stiffness |
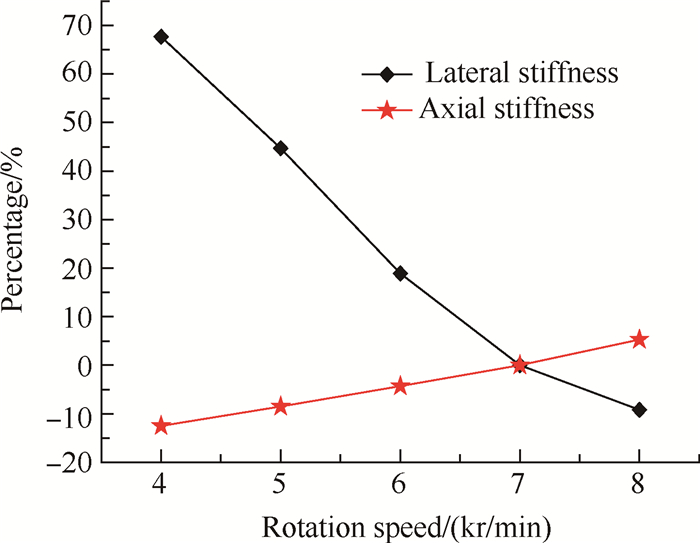
图 14为三点接触球轴承横向刚度与轴向刚度随着转速变化的百分比。考虑轴向力影响的三点接触球轴承,横向刚度随着内圈转速的增大而减小,轴向刚度随着内圈转速的增大而增大。其原因在于当轴承内圈转速增加时,会导致轴承接触角变大,从而造成横向刚度减小,轴向刚度增大。
|
Fig. 14 Effects of rotation speed on stiffness |
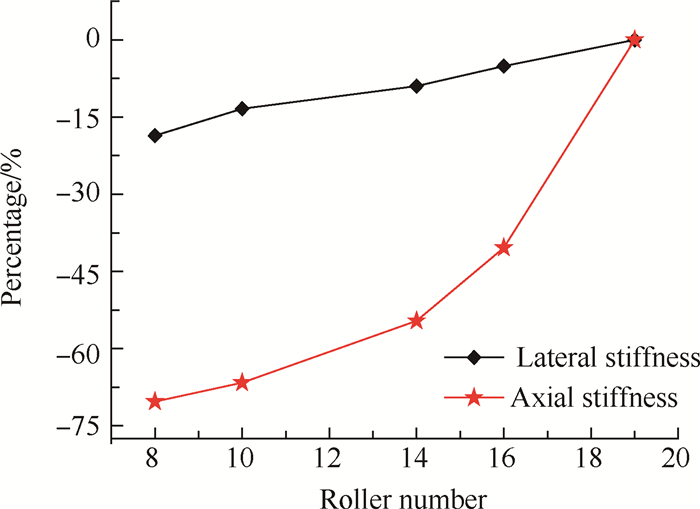
滚动体个数作为轴承结构的一个重要参数,对轴承刚度的影响较大。图 15为三点接触球轴承轴向刚度与横向刚度随着滚动体个数变化的百分比。随着滚动体个数的增多,轴向刚度和横向刚度均增大,轴向刚度的变化更为显著。这是因为当滚动体个数增加时,轴承的整体抵抗变形能力增强,轴承刚度增大。
|
Fig. 15 Effects of roller number on stiffness |
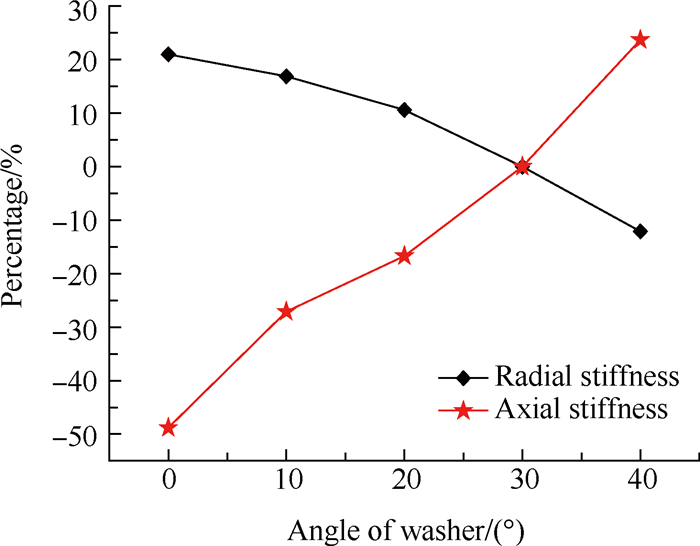
垫片角是三点接触球轴承区别于其它类滚动轴承的一个重要结构参数,其对轴承刚度的影响必须考虑。图 16为轴承刚度随着垫片角变化的百分比。轴承横向刚度随着垫片角增大而减小,轴向刚度随着垫片角增大而增大。垫片角的大小最终影响的是轴承在不同工况下的接触角大小,会使轴承的受力特征发生明显变化,从而影响轴承的刚度。
|
Fig. 16 Effects of washer angle on stiffness |
本文构建了三点接触球轴承结构模型、受力模型与刚度模型,在理论分析的基础上,采用有限元方法研究了在考虑轴向力影响的前提下,三点接触球轴承静态刚度随运行工况和结构参数的变化规律,并获得了如下结论:
(1) 对于三点接触球轴承,轴向力对轴承的刚度影响显著,在诸如轴向力较大的燃气轮机轴承选型及轴承刚度特性分析中必须考虑轴向力的影响。
(2) 考虑轴向力影响的三点接触球轴承,横向刚度受横向载荷、内圈转速、滚动体个数和垫片角影响均比较大;而轴向刚度只对内圈转速、滚动体个数和垫片角的变化敏感,横向载荷影响不明显。
在下一步的工作中,结合轴承实际运行情况,考虑研究轴承的装配关系与游隙对轴承刚度的影响规律,同时开展相关的实验研究。
| [1] |
王海飞, 陈果. 含滚动轴承径向游隙的航空发动机整机振动响应特征分析[J]. 推进技术, 2016, 37(5): 945-959. (WANG Hai-fei, CHEN Guo. Characteristics Analysis of Aero-Engine Whole Vibration Response with Rolling Bearing Radial Clearance[J]. Journal of Propulsion Technology, 2016, 37(5): 945-959.)
(  0) 0) |
| [2] |
蒋云帆, 廖明夫. 航空发动机高压转子前轴承刚度特性分析[J]. 推进技术, 2014, 35(8): 1123-1130. (JIANG Yun-fan, LIAO Ming-fu. Stiffness Characteristics Analysis on High-Pressure Rotor Front Bearing of Aero-Engine[J]. Journal of Propulsion Technology, 2014, 35(8): 1123-1130.)
(  0) 0) |
| [3] |
Hertz H. On the Contact of Elastic Solids[J]. Math, 1881, 92: 156-171.
(  0) 0) |
| [4] |
Halpin J D, Tran A N. An Analytical Model of FourPoint Contact Rolling Element Ball Bearings[J]. Journal of Tribology, 2016, 138(4): 1-13.
(  0) 0) |
| [5] |
Jones A B. The Mathematical Theory of Rolling-Element Bearings, Mechanical Design and Systems Handbook[M]. New York: McGraw-Hill, 1964.
(  0) 0) |
| [6] |
Leblanc A, Nelias D. Ball Motion and Sliding Friction in a Four-Contact-Point Ball Bearing[J]. Journal of Tribology, 2007, 129(4): 801-808. DOI:10.1115/1.2768079
(  0) 0) |
| [7] |
Guo Y, Parker R G. Stiffness Matrix Calculation of Rolling Element Bearings Using a Finite Element/Contact Mechanics Model[J]. Mechanism & Machine Theory, 2012, 51(5): 32-45.
(  0) 0) |
| [8] |
Kraus J, Blech J J, Braun S G. In Situ Determination of Rolling Bearing Stiffness and Damping by Modal Analysis[J]. Journal of Vibration & Acoustics, 1987, 109(3): 235-240.
(  0) 0) |
| [9] |
徐荣瑜, 何剑. 三点, 四点接触球轴承设计与应用[J]. 轴承, 1998(12): 2-5. (  0) 0) |
| [10] |
Dougdag M, Ouali M, Boucherit H, et al. An Experimental Testing of a Simplified Model of a Ball Bearing: Stiffness Calculation and Defect Simulation[J]. Meccanica, 2012, 47(2): 335-354. DOI:10.1007/s11012-011-9434-0
(  0) 0) |
| [11] |
Wock M, Spachtholz G. 3-and 4-Contact Point Spindle Bearings-a New Approach for High Speed Spindle Systems[J]. CIRP Annals-Manufacturing Technology, 2003, 52(1): 311-316. DOI:10.1016/S0007-8506(07)60591-5
(  0) 0) |
| [12] |
平丽浩, 王长武, 李良军. 四点接触球轴承的接触问题研究[J]. 南京理工大学学报(自然科学版), 2007, 31(4): 458-461. (  0) 0) |
| [13] |
姚廷强, 黄亚宇, 王立华. 圆柱滚子轴承多体接触动力学研究[J]. 振动与冲击, 2015(7): 15-23. (  0) 0) |
| [14] |
Harris T A, Park U, Kotzalas M N, et al. Rolling Bearing Analysis[M]. Boca Raton: Crc Press, 2006.
(  0) 0) |
| [15] |
You Hui-yuan. Contact Analysis on Large Negative Clearance Four-Point Contact Ball Bearing[J]. Procedia Engineering, 2012, 37(1): 174-178.
(  0) 0) |
| [16] |
Harris T A, Kotzalas M N. Advanced Concepts of Bearing Technology[M]. Abingdon: Taylor & Francis, 2006.
(  0) 0) |
| [17] |
Nelias D. Analysis of Ball Bearings with 2, 3 or 4 Contact Points[J]. Tribology Transactions, 2008, 51(3): 372-380. DOI:10.1080/10402000801888887
(  0) 0) |
| [18] |
Hernot X, Sartor M, Guillot J. Calculation of the Stiffness Matrix of Angular Contact Ball Bearings by Using the Analytical Approach[J]. Journal of Mechanical Design, 2000, 122(1): 83-90. DOI:10.1115/1.533548
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

