组合循环发动机可有效克服超燃冲压发动机在低马赫数下难以启动的缺陷,近年来得到广泛的关注与研究[1, 2]。高效气气掺混是组合循环发动机关键技术之一,其物理实质为富燃燃气与超声速空气来流形成的可压缩反应混合层。但由于发动机内部气流速度快并受其物理尺寸限制,驻留时间极短[3]。而超声速混合层的增长也受压缩性[4]和化学反应释热[5]的抑制。因此开展超声速混合层混合增强技术的研究,具有重要的工程指导意义。
超声速混合层对初边值条件极其敏感,线性稳定性理论研究表明,混合层中大尺度展向涡结构受不稳定扰动波的控制[6]。基于此理论,提出了强迫扰动诱导混合增强技术,即主动混合增强技术。该技术主要通过主动施加外部强迫激励,在发动机内并不容易实现,目前多停留在实验室或数值研究阶段。Mclaughlin[7]开展超声速混合增强的实验研究时,在入口施加电火花激励。孙明波等[8]采用大涡模拟数值研究入流周期性温度激励下的二维超声速混合层时发现,周期性温度激励对混合增强非常有利,激励的频率、幅值对混合效果有重要影响。曹伟等[9]数值研究了在二维超声速混合层入口引入T-S波和在低速侧加入流向振荡两种不同激励方式下流动的演化,结果表明,引入流向振荡对混合增强效果更为明显。Weisbrot[10]和Zhou[11]分别在混合层上游边界层内施加振动片激励,Ashish等[12]等将介质阻挡放电等离子激励应用到混合增强中去,但这些实验研究仅在低速条件下开展,未涉及超声速。其中张冬冬等[13, 14]在研究隔板强迫振动的超声速混合层流场结构与掺混特性时发现,强迫振动能够诱导产生大尺度的不稳定涡结构,高频振动更利于混合效率的提高。但是隔板的振动需要外部强迫激振,在工程应用中难以实现。
为克服强迫振动诱导混合增强难以工程实现的缺点,提出隔板的自激振动诱导混合增强的新技术。该技术基于流固耦合原理,超声速气流与隔板通过两相的接触面相互作用,一方面气动力做功使隔板发生弹性变形存储变形能,而振动反作用于流场即对流场产生激励。其中隔板的作用相当于“俘能器”(Energy harvesting device),可实现整个系统能量形式的转化。隔板振动对混合层流场的激励存在最优频率带,可以激发混合层的最大增长率,因此设计适用的隔板,提供最优频率的不稳定扰动,是该技术的关键。本文采用平板开凹腔的隔板构型,凹腔本身具有声学的自激振荡特性,主要表现为压力的高频波动,可激发隔板产生自激振动。
本文采用非接触式微小振动测量系统对隔板自激振动的位移实时测量,系统研究了凹腔隔板的自激振动特性。首先采用大涡模拟方法解释了隔板自激振动的原因,然后对自激振动特性的影响因素如约束条件,隔板构型参数长深比、后缘倾角等进行详细分析。
2 实验系统与方法 2.1 混合层风洞与实验模型本文沿用了易仕和等[15]吸气式层流化低噪声的超声速混合层风洞设计方案,设计如图 1(a)。喷管段为两个马赫数不同的二维型面喷管,中间由平板隔开,如图 1(b)。稳定段上游的总压调节器可调节喷管上侧入口总压,使得在喷管出口处上下侧静压匹配,在实验段产生压力匹配的混合层流场。喷管型面以B-spline[16]样条曲线的特征线方法进行设计,精度较高,尽可能减小喷管出口的边界层厚度,改善实验段的流场品质。采用皮托测压对喷管进行校准得其实际入口来流参数如表 1,此时静压仅相差1 %,可以认为已达到静压匹配。试验件与喷管段隔板一体化设计,隔板喷管段为厚1mm的平板,试验段内隔板可视为左侧固支的悬臂板结构,其设计及尺寸如图 1(c)所示,材料参数见表 2。记板件D4K5θ60即凹腔深度D= 4 mm,长深比为K = 5,后缘倾角θ = 60°,下文中均采用此记法,在所有实验中保持凹腔深度固定不变。图中所示固定杆一方面防止悬臂板变形失稳,另一方面可通过调节固定杆与悬臂板之间的缝隙来精确的改变约束条件。如图 1(b),(d)所示,试验段上开贯穿螺纹孔,四支螺杆由外部旋入试验段内。限位尺寸由螺杆的上下升降实现,升降距离用千分尺精确测量。

|
Fig. 1 Schematic of the supersonic mixing layer tunnel and test model |
|
|
Table 1 Parameters of incoming flow |
|
|
Table 2 Material parameters of test models |
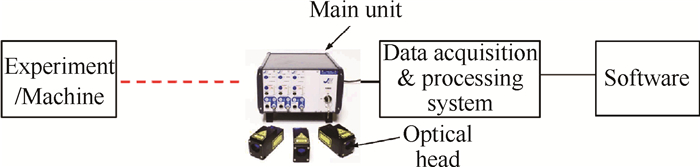
由于超声速混合层的感受性,初边值条件对流场产生很大影响,传统的接触式测量手段如在被测物上粘贴应变片、加速度传感器等不仅会对流场产生较大扰动,且在混合层风洞中难以实现。本文使用意大利Julight公司生产的VSM4000-L-EXT非接触式微小振动测量系统,该设备的工作原理参见文献[17],位移测量误差为1%。可对相对粗糙的漫反射材料实现精确的振动位移测量,其系统组成如图 2所示。在振动测试时,将激光探头发射出的光束与被测实验件保持垂直。在不同工况的实验中分别保持测试点位置一致。
|
Fig. 2 Contactless laser vibrometer |
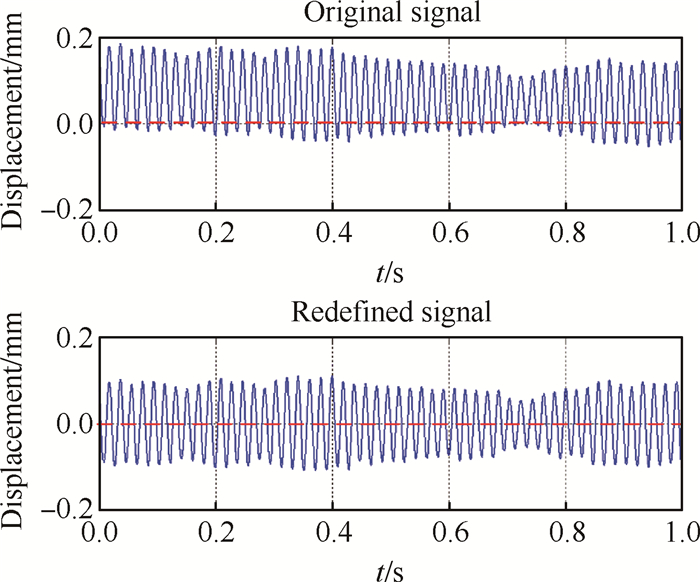
微小振动测量系统在风洞实验室工作时,会受到环境中各种外界环境因素的干扰。为提高信噪比和数据精度,首先采用最小二乘法[18]消除多项式趋势项。如图 3,消除多项式趋势项后,偏离0基准线的趋势被改变,位移量围绕基线上下波动。其次采用五点三次平滑法[19]对测试数据进行平滑处理。然后通过带通滤波器对数据进行滤波,消除测试信号中的噪声和虚假成分,提高信噪比。最后采用快速傅里叶变换(FFT)将时域信号转化为功率谱函数(PSD,Power Spectrum Densities)获得数据中含有的频率成分。上述预处理过程均由MATLAB编制程序完成。
|
Fig. 3 Comparison of before and after eliminating polynomial trend item |
测试得到的隔板位移的时间历程表现出随机振动的特性,因此需采用数据的统计特征来反映隔板振动的一些性质。本文采用位移方差来表征响应幅值的波动情况,另一方面位移方差也可在一定程度上反映隔板疲劳损伤的强弱程度,其表达式为
| $ {A_{{\rm{std}}}}\left( z \right) = \left( {\frac{1}{T}\int_0^T {{{\left[{y\left( {z, t} \right)-\overline {y\left( {z, t} \right)} } \right]}^2}} } \right) $ | (1) |
以位移的均方根(RSM)值代替有效位移,均方根值常用来计算一组振动数据的平均值,其计算公式为
| $ RSM = \sqrt {\frac{{\sum\limits_{i = 1}^n {x_i^2} }}{n}} = \sqrt {\frac{{x_1^2 + x_2^2 + \cdots x_n^2}}{n}} $ | (2) |
为了获得凹腔隔板所受的气动力,以D4K5板为例,采用大涡模拟[20]得到隔板上下表面压强的面积分加权平均值,由式(3)得出
| $ \bar P = \frac{1}{A}\int {p{\rm{d}}A} = \frac{1}{A}\sum {{p_i}\left| {{A_i}} \right|} $ | (3) |
则驱动隔板振动的动力来源ΔP满足
| $ \Delta \bar P = {\bar P_{{\rm{up}}}}-{\bar P_{{\rm{down}}}} $ | (4) |
式中Pup,Pdown分布为上下表面面积分加权平均值。整个计算区域尺寸为140×51×30mm (x× y× z),y向尺寸与风洞试验段保持一致,在x,z方向简化处理。图 4为其流向二维剖面,被隔板分为上下两部分,隔板尺寸详见图 1(c),网格数量为Nx × Ny × Nz = 201×301×31,在隔板及凹腔壁面附近进行加密,本文中y+ =0.85,计算区域上下壁面位置不是计算考虑的重点,不做加密处理。z方向网格均匀分布。针对亚格子应力项,采用Yoshizawa一方程亚格子模型进行封闭。控制方程的对流项采用五阶WENO格式求解,粘性项采用四阶中心差分格式,时间推进采用三阶Runge-Kutta方法,CFL设定为0.5。需要特别指出的是,本文使用的数值方法对超声速凹腔流动的预测能力在先前的研究中已经得到验证[21]。

|
Fig. 4 Schematic of computational zone |
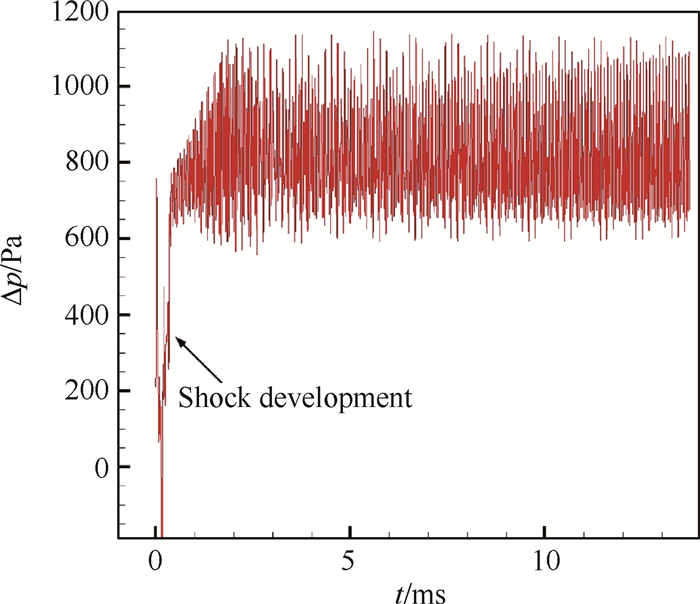
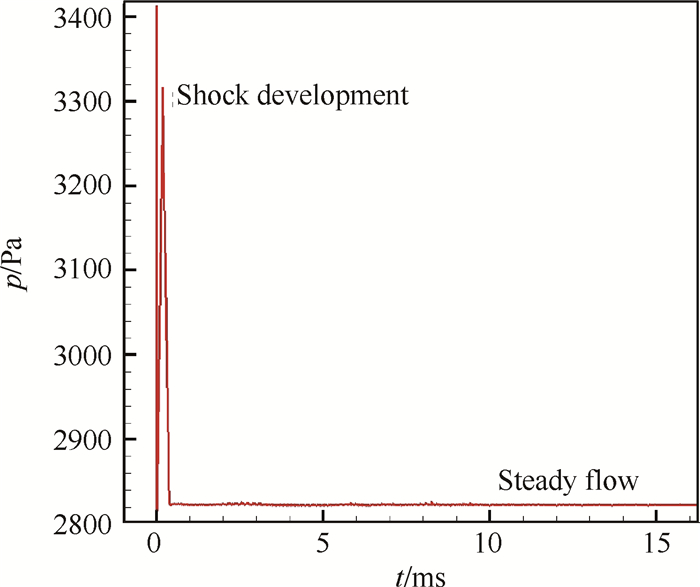
图 5为隔板上下表面平均压力差随时间的变化,描述了气流进入、向下游推进到稳定流动的全过程。由图 6可知下表面压力趋于波动极小的无波动状态。在图 5,图 6中靠近0时刻出现的压力波动是超声速气流进入流道形成正激波,激波向下游推移所致。隔板凹腔的声学自激振荡使上表面出现压力波动,是隔板自激振动的直接原因,导致上下表面出现压力差波动,进而使隔板自激振动。
|
Fig. 5 Fluctuation of pressure difference between upper and lower plate |
|
Fig. 6 Time history of facet-average pressure on lower plate |
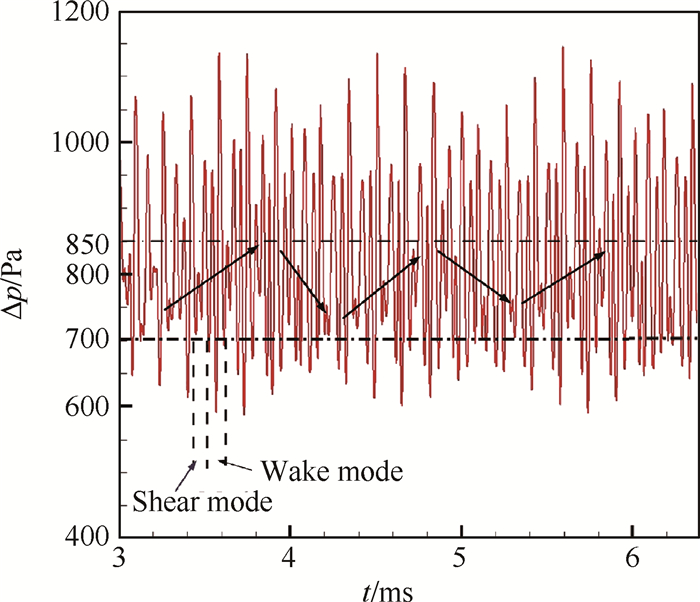
从压力差的时间历程线条的疏密和幅值的大小可知,压力差的波动模式存在能量不同的模态,整体表现与“拍”现象类似。凹腔剪切层的失稳位置表现为间歇效应,撞击后壁面的强度并非始终一致。汪洪波[22]指出超声速凹腔剪切层流动存在着混合剪切层/尾迹振荡模式。图 7为3~6.4ms的压力差的时间历程。尾迹振荡模式需要很多能量,当不能从自由流中获取足够能量时就会转换成剪切层模式,交替出现。剪切层模式历时时间短,振荡幅值小,振荡范围仅在700~850Pa。在剪切层模式中逐渐吸收能量,步步抬升,达到尾迹振荡模式的最大值,该过程也伴随着剪切层模式振荡压力的提高,如图中箭头所指的演变趋势。而后进入衰减过程尾迹振荡模式逐步降低至最低值,然后进行下一个振荡周期。尾迹振荡模式强度逐步升高又衰减的过程与“拍”现象类似。由图 7可知剪切层模式振荡压力的变化往往滞后于尾迹模式。
|
Fig. 7 Fluctuation of pressure difference between upper and lower plate from 3 to 6.4ms |
隔板的瞬态结构动力学方程可表达为
| $ \mathit{\boldsymbol{m}}\ddot x + \mathit{\boldsymbol{c}}\dot x + \mathit{\boldsymbol{k}}x = \mathit{\boldsymbol{F}} $ | (5) |
式中m是质量矩阵,c是阻尼矩阵,k是刚度矩阵,F表示外载荷向量。质量分布与隔板的材料与构型有关,刚度和阻尼矩阵与材料类型有关。就外载荷向量而言,其主要来源为凹腔声学自激振荡产生的压力波动,而自激振荡强度与凹腔构型参数如长深比、后缘倾角和来流条件等有关[23]。此外局部约束条件对系统固有模态产生影响,进而影响响应模态。下文通过实验手段分析了约束条件及凹腔构型参数长深比、后缘倾角对自激振动特性的影响。
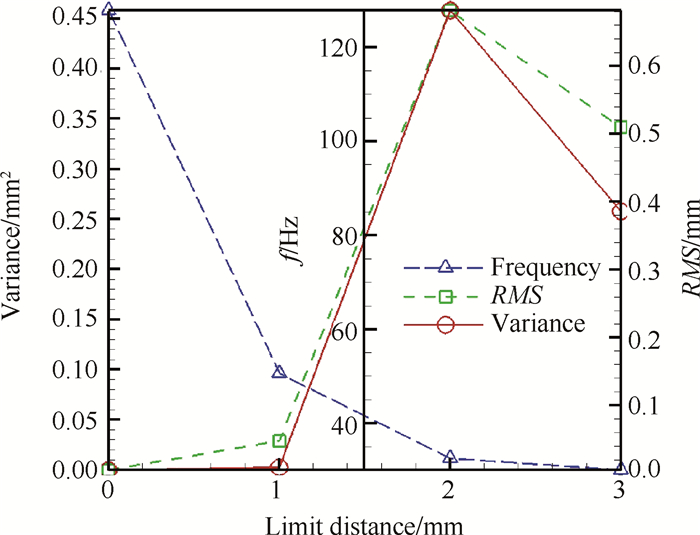
3.2.1 约束条件的影响通过螺杆旋进的方式可以精确地控制悬臂板与固定杆之间的间隙大小,来控制振动限制位移。隔板的约束形式左端为固支,右端为自由,简支和振动位置限制三种约束条件。以D4K3为测试对象,开展了0,1,2,3mm四种限位尺寸下的实验研究。结果表明,均方根、方差与限位尺寸呈正相关,而与频率呈负相关,如图 8。与限位尺寸为3mm相比,0mm的限位尺寸振动频率提高了324.63%,振动频率出现了大幅增长。当限位尺寸由1mm增加为2mm时,均方根剧烈增加,这时振动频率接近隔板的固有频率。限位尺寸直接改变了长悬臂板的约束条件,导致振动过程中振幅的限制性变大,波动性小。从能量的角度来讲,动能到变形能的转换不可能是无限制的,在弹性变形范围内,达到一定程度的变形后会出现回弹,在总能量一定时,振动幅值的减小会造成振动频率的增加。
|
Fig. 8 Distribution of variance, RSM and frequency with different limit distance |
本文设计了凹腔长深比K=0, 1, 3, 5, 7五种工况,本工况及下文中的实验均在限位尺寸为0mm时进行的。记无凹腔时K=0,此时自激振动的频率最大,出现了两阶模态,如图 9所示,两阶模态幅值相差不大,但幅值相对较小,有效位移(RSM)不足尾缘厚度的千分之一。随着K的增加,频率一直呈下降趋势,如图 10所示,与K=1时相比,K=7的频率降低了19.36%。与改变约束条件相比,该变化幅度较小。凹腔的振动幅值与方差在K从0增长到1时呈下降趋势,而后随K的增加呈增长趋势。

|
Fig. 9 Displacement time history and response frequency of the 5mm self-excited plate |

|
Fig. 10 Distribution of variance, RMS and frequency with different length depth ratio |
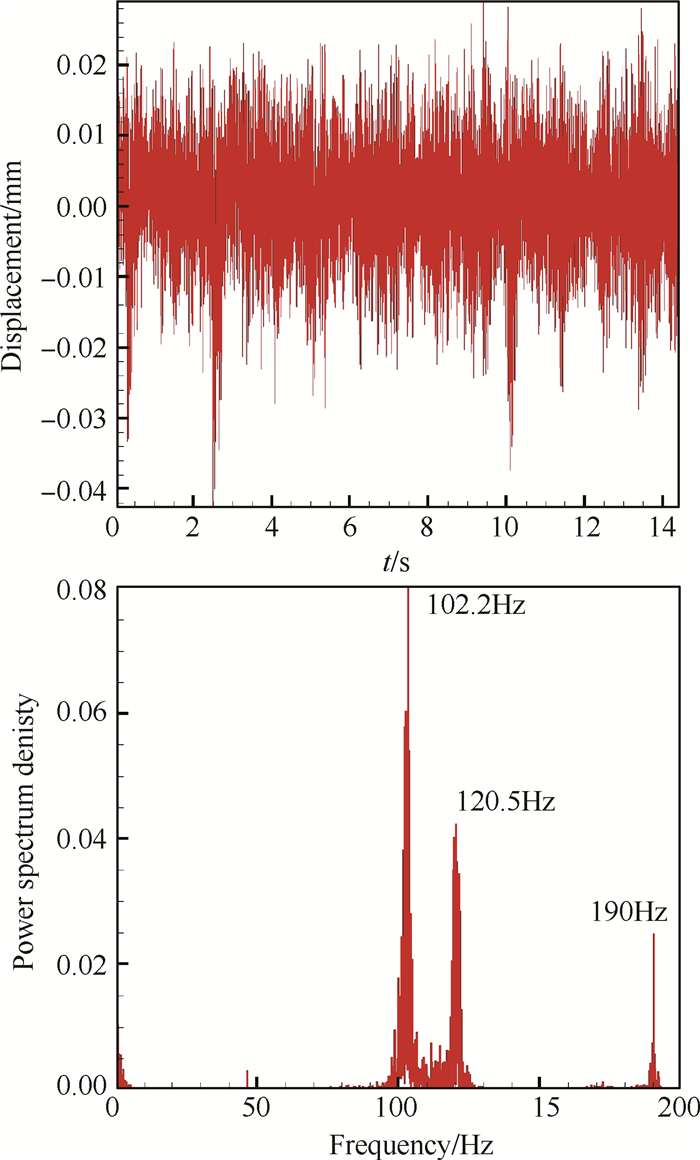
在K=0时,不存在因凹腔声学的自激振荡引起的不稳定压力波动。平板压力波动来源有两种可能,一是湍流的压力脉动,二是在板件尾部主流的涡脱落引起的压力波动。由于实验过程中流场品质及试验件长度的影响,超声速流动发生转捩进入湍流状态,出现高频压力脉动,作用在隔板上引起振动。这种解释也可从1mm铝平板自激振动的实验结果中得到证实,如图 11所示,该板件的振动同样表现多阶模态,而主频相对较低,有效振幅达到了0.018mm,较5mm厚平板明显增长,主要原因是1mm铝平板的弹性模量与刚度值较小。在该工况中板厚仅为1mm,尾缘没有涡脱落现象,这证实了上述湍流脉动引起板件振动。
|
Fig. 11 Displacement time history and response frequency of the 1mm self-excited vibration plate |
当K从0开始增加的过程中,流致振动的作用力存在两种模式的转换。在K = 1时,凹腔被边界层淹没并且凹腔较小,凹腔不稳定性在激励隔板振动方面表现的并不明显。与K = 0时一致,压力波动的主要来源为湍流脉动。随着K的增加,由凹腔不稳定性引起的压力波动开始发挥作用,突出表现为有效振幅与方差的增长。
3.2.3 凹腔后缘倾角对隔板自激振动特性的影响为了研究凹腔后缘倾角对隔板自激振动特性的影响,选用D4K7θ90, D4K7θ60, D4K7θ30三种不同后缘倾角的板件进行风洞实验,后缘倾角的改变如图 12所示,

|
Fig. 12 Change of cavity ramp angle |
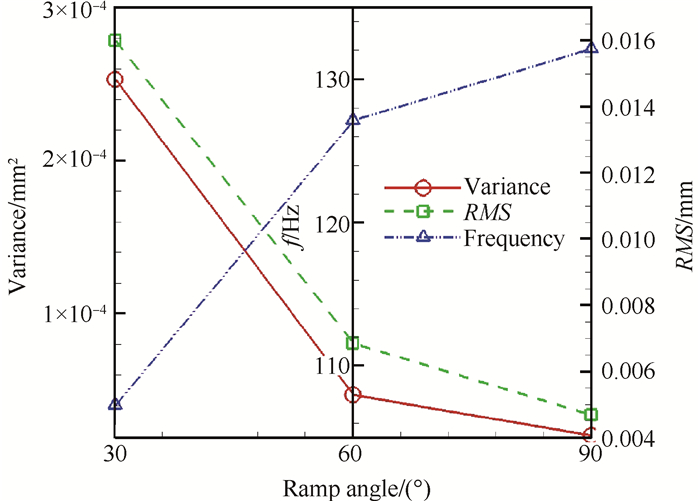
对实验数据分析可知,如图 13所示,后缘倾角从30°增加至90°时,有效振幅降低70.75%,而频率增长了23.15%,与改变约束条件相比,增长幅度较小。测试得到的振动信号在经过前处理后,均以单一模态为主,没有出现多阶模态。隔板自激振动特性与凹腔的声学自激振荡强度密切相关,后缘倾角的减小使剪切层更深入地潜入凹腔内部,与后壁相互作用时,更多的能量被反射出凹腔,凹腔剪切层趋于稳定,声学振荡减弱,振动频率降低。
|
Fig. 13 Distribution of variance, RMS and frequency with different cavity ramp angle |
需要指出的是,隔板高频振动对超声速混合层的激励作用最为明显[24],混合增强的效果显著,相比较而言,隔板振动有效幅值的增加对混合增强的效果并不显著。Grimshaw[25]在波涡理论中指出,扰动波的幅值在0.1%h时即可诱导产生流场的拟序结构,触发扰动波与拟序结构的相互作用。Pittard[26]也指出,当结构振幅比湍流边界层粘性底层厚度大时,即可对流场结构产生扰动,而当其小于湍流边界层的粘性底层厚度时,可忽略结构振动对流场的影响。因此自激振动混合增强技术对频率的要求远高于振幅。在本文的实验研究中,自激振动频率较低,最高频率仅有250Hz,且此时为5 mm厚平板的测试结果,其振动有效幅值,频率均难以起到较好的混合增强的效果。实验研究已经表明,凹腔构型参数如凹腔长深比、后缘倾角对自激振动特性的影响较小,频率难以大幅提高,而改变隔板的约束条件,可以大幅增加自激振动的响应频率,是未来优化设计的一个重要方向。
4 结论本文开展了超声速平行来流条件下,凹腔隔板的自激振动特性的系统研究,得到以下结论:
(1)凹腔的声学自激振荡使隔板上表面产生压力波动,而下表面为平面趋向于无压力波动;隔板上下表面的压力差是其自激振动的直接原因,压力差波动表现出的“拍”现象,与凹腔剪切层失稳位置的间歇效应和声学自激振荡的模式变换有关。
(2)隔板的约束条件以及凹腔的构型参数长深比、后缘倾角对隔板的自激振动特性有重要影响。振动频率与限位尺寸呈负相关,与限位尺寸为3mm相比,0mm限位尺寸时振动频率提高了324.63%,频率大幅提高;随着长深比的增加,频率呈下降趋势,与K = 1时相比,K = 7的频率降低了19.36%,变化幅度较小;隔板自激振动频率与凹腔后缘倾角呈正相关,当后缘倾角从30°增加至90°时,频率增长了23.15%。
(3)自激振动混合增强技术对频率的要求远高于振幅,改变凹腔长深比、后缘倾角难以大幅提高频率,而改变的约束条件可大幅提高自激振动的频率,是未来优化一个重要方向。
| [1] |
Kato K, Kudo T, Kudo K, et al. Experimental Study of Combined Cycle Engine Combustor in Scramjet-Mode [R]. AIAA 2005-3316.
(  0) 0) |
| [2] |
刘兴洲. 中国超燃冲压发动机研究回顾[J]. 推进技术, 2008, 29(4): 385-395. (LIU Xing-zhou. Review of Scramjet Research in China[J]. Journal of Propulsion Technology, 2008, 29(4): 385-395.)
(  0) 0) |
| [3] |
何国强, 秦飞, 魏祥庚, 等. 火箭冲压组合发动机燃烧的若干基础问题研究[J]. 实验流体力学, 2016, 30(1): 1-14. (  0) 0) |
| [4] |
Papamashcou D, Rosh k A. Observation of Supersonic Free Shear Layer[R]. AIAA 86-0162.
(  0) 0) |
| [5] |
Mahle I, Foysi H, Sarkar S. On the Turbulence Structure in Inert and Reacting Compressible Mixing Layers[J]. Journal of Fluid Mechanics, 2007, 593: 171-180.
(  0) 0) |
| [6] |
Michalke A. Vortex Formation in a Free Boundary Layer According to Stability Theory[J]. Journal of Fluid Mechanics, 1965, 23: 371-383.
(  0) 0) |
| [7] |
Mclaughlin D K, Martens S, Kinzie K W. An Experimental Investigation of Large Scale Instabilities in a Low Reynolds Number Two-Stream Supersonic Shear Layer [R]. AIAA 92-0177.
(  0) 0) |
| [8] |
孙明波, 王振国, 梁剑寒. 入口周期性温度激励下的二维超声速混合层混合增强[J]. 宇航学报, 2008, 29(2): 444-448. (  0) 0) |
| [9] |
曹伟, 周恒. 二维超音速混合层增强混合的研究[J]. 中国科学(A辑), 2002, 3(2): 150-157. (  0) 0) |
| [10] |
Weisbrot I, Wygnanski I. On Coherent Structures in a Highly Excited Mixing Layer[J]. Journal of Fluid Mechanics, 1988, 195: 137-159. DOI:10.1017/S0022112088002356
(  0) 0) |
| [11] |
Zhou M D, Wygnanski I. The Response of a Mixing Layer Formed between Parallel Streams to a Concomitant Excitation at Two Frequencies[J]. Journal of Fluid Mechanics, 2001, 441: 139-168.
(  0) 0) |
| [12] |
Ashish S, Jesse L. Active Control of a Turbulent Mixing Layer Using Puslsed Laser and an ns-DBD Plasma Actuator[R]. AIAA 2016-0455.
(  0) 0) |
| [13] |
Tan J, Zhang D, Lv L. Flow Characteristics of Supersonic Mixing Layer under Forced Vibration[C]. Glasgow: Proceedings of the AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2015.
(  0) 0) |
| [14] |
张冬冬, 谭建国, 吕良. 超声速混合层在强迫振动下流场结构的实验研究[J]. 推进技术, 2016, 37(4): 601-607. (ZHANG Dong-dong, TAN Jian-guo, LV Liang. An Experimental Study on Flow Structure of a Supersonic Mixing Layer Influenced by Forced Vibration[J]. Journal of Propulsion Technology, 2016, 37(4): 601-607.)
(  0) 0) |
| [15] |
易仕和, 赵玉新, 田立丰, 等. 超声速流场NPLS精细测试技术及典型应用[M]. 北京: 国防工业出版社, 2013.
(  0) 0) |
| [16] |
易仕和, 赵玉新, 何霖, 等. 超声速与高超声速喷管设计[M]. 北京: 国防工业出版社, 2013.
(  0) 0) |
| [17] |
Giuliani G, Bozzipietra S, Donati S. Self-Mixing Laser Diode Vibrometer[J]. Measurement Science & Technology, 2003, 14(1): 24-32.
(  0) 0) |
| [18] |
龙源, 谢全民, 钟明寿, 等. 爆破震动测试信号预处理分析中趋势项去除方法研究[J]. 工程力学, 2012, 29(10): 63-68. (  0) 0) |
| [19] |
肖立波, 任建亭, 杨海峰. 振动信号预处理方法研究及其MATLAB实现[J]. 计算机仿真, 2010, 27(8): 330-337. (  0) 0) |
| [20] |
孙明波. 超声速来流稳焰凹腔的流动及火焰稳定机制研究[D]. 长沙: 国防科技大学, 2008.
(  0) 0) |
| [21] |
孙明波, 耿辉, 梁剑寒, 等. 超声速来流稳焰凹腔上游气体燃料横向喷注的流动混合特征[J]. 推进技术, 2008, 29(3): 306-311. (SUN Ming-bo, GENG Hui, LIANG Jian-han, et al. Mixing Characteristics of Gaseous Fuel Injection Upstream of a Flameholding Cavity in Supersonic Flow[J]. Journal of Propulsion Technology, 2008, 29(3): 306-311.)
(  0) 0) |
| [22] |
Wang H, Sun M, Qin N, et al. Characteristics of Oscillations in Supersonic Open Cavity Flows[J]. Flow, Turbulence and Combustion, 2013, 90(1): 121-142. DOI:10.1007/s10494-012-9434-8
(  0) 0) |
| [23] |
Heller H H, Bliss D B. The Physical Mechanism of Flow Induced Pressure Fluctuations in Cavities and Concepts for Their Suppression[R]. AIAA 75-491.
(  0) 0) |
| [24] |
冯军红. 超声速混合层增长特性及混合增强机理研究[D]. 长沙: 国防科技大学, 2016.
(  0) 0) |
| [25] |
Grimshaw R. Wave Action and Wave-Mean Flow Interaction, with Application to Stratified Shear Flows[J]. Annual Review Fluid Mechanics, 1984(16): 11-44.
(  0) 0) |
| [26] |
Pittard M T, Blotter J D. Numerical Modeling of LES Based Turbulent Flow Induced Vibration[C]. Washington: International Mechanical Engineering Congress and Exposition, 2003.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

