固体火箭发动机较液体火箭发动机,具有体积小,结构简单、机动性好以及成本低等优点,广泛应用于各型弹箭武器。从弹箭武器多年的发展历程来看,固体发动机的结构完整性直接影响着武器系统的可靠性和安全性。端羟基聚丁二烯复合固体推进剂(HTPB)作为一种常用的固体火箭推进剂,其力学行为的研究对固体火箭发动机结构完整性的分析具有重要的意义。
HTPB推进剂是高刚度颗粒填充基体形成的颗粒增强复合材料。由于基体是低度交联的高聚物材料,推进剂整体表现出粘弹性特征。同时,由于颗粒与基体之间的“脱湿”以及基体内微裂纹和空穴等损伤的影响,材料又表现出非线性特征。为了准确描述固体推进剂材料的非线性力学特征,众多学者从宏观和细观的角度对固体推进剂材料进行了本构研究。Schapery[1~3]等基于伪应变和伪应变能建立了粘弹性损伤模型。Ozupek[4]等基于实验观测结果,从唯象学角度出发,建立了能够反映材料体积膨胀和应力软化的本构模型。Jung [5]等在Simo [6]粘弹性本构模型的基础上,直接引入两个标量损伤内变量,建立了一个粘弹性脱湿损伤模型。Abdel-Tawab[7, 8]等基于不可逆热力学,巧妙地利用叠加原理,建立了一个通过有效应力和有效应变表征的损伤模型。彭威[9]基于弹性裂纹扩展准则建立了一个固体推进剂微裂纹损伤模型。阳建红[10]等直接用有效应力替代蠕变本构模型中的真实应力并考虑老化的影响,建立了一个粘弹性老化损伤本模型。此外,姚东[11]、王哲君[12]和杨龙[13]等也进行了相关的研究。细观方面,Chen[14, 15]等用空穴替代脱湿的颗粒,基于等效夹杂理论,建立了颗粒完全脱湿和部分脱湿的粘弹性细观损伤模型。Tan[16]等在颗粒与基体间引入了内聚力模型,建立了模拟颗粒界面脱湿过程的损伤模型。Tohgo [17]等将材料视为由基体、完全粘结颗粒、空穴和部分脱湿颗粒组成的四相复合材料,建立了一个增量型细观损伤模型。细观模型弥补了宏观模型难以反映材料损伤细节的缺点,但随之产生的问题是计算效率的降低。因此,有学者尝试将两种方法结合起来,建立一种宏细观相结合的损伤本构模型,典型的如Jung[18]模型和彭威[9]模型。Jung[18]模型的特点是其损伤演化方程是基于细观颗粒脱湿能量守恒原理建立的,因此模型能够有效地反映材料脱湿颗粒分数的变化。然而该模型是在Simo[6]粘弹性模型上,直接用有效模量替代无损模量得到的,并不是经严格热力学推导获得。
为了建立一个完全服从不可逆热力学的粘弹性损伤本构模型,文章直接从不可逆热力学出发,在Abdel-Tawab[7, 8]等研究的基础上,通过重新定义宏观损伤效应张量和引入细观损伤效应函数,选取相对微裂纹密度为损伤内变量,建立了一个严格满足热力学耗散不等式的,宏细观相结合的蠕变型损伤本构模型。数值结果表明,文中建立的模型能够有效地反映固体推进剂材料的非线性损伤行为。
2 粘弹性损伤模型 2.1 热力学本构粘弹性材料的Gibbs比自由能可以表示为
| $ \phi = \phi \left( {{\mathit{\boldsymbol{\sigma }}_{ij}},{\gamma _r},{\omega _{ij}},T} \right) $ | (1) |
式中σij为应力张量,γr为粘性内变量,ωij为损伤内变量,T为温度。
材料的变形过程必须满足热力学熵不等式
| $ - \dot \phi - {\varepsilon _{ij}}{{\mathit{\boldsymbol{\dot \sigma }}}_{ij}} - S\dot T - \frac{{{\mathit{\boldsymbol{h}}_i}{T_{,i}}}}{T} \ge 0 $ | (2) |
式中εij为应变张量,S为熵,hi为热流矢量,T, i = ∂T/∂xi是空间坐标xi方向的温度梯度。
将式(1)代入式(2),有
| $ {\varepsilon _{ij}} = - \frac{{\partial \phi }}{{\partial {\sigma _{ij}}}} $ | (3) |
| $ S = - \frac{{\partial \phi }}{{\partial T}} $ | (4) |
| $ {\mathit{\Gamma }_r}{{\dot \gamma }_r} + {Y_{ij}}{{\dot \omega }_{ij}} - \frac{{{h_i}{T_{,i}}}}{T} \ge 0 $ | (5) |
式中Γr和Yij分别是与内变量γr和ωij对偶的热力学力,表示为
| $ {\mathit{\Gamma }_r} = - \frac{{\partial \phi }}{{\partial {\gamma _r}}} $ | (6) |
| $ {Y_{ij}} = - \frac{{\partial \phi }}{{\partial {\omega _{ij}}}} $ | (7) |
假定粘性耗散、损伤耗散和热耗散互不耦合,则式(5)可以进一步分解为
| $ {\mathit{\Gamma }_r}{{\dot \gamma }_r} \ge 0;\;\;\;{Y_{ij}}{{\dot \omega }_{ij}} \ge 0;\;\;\; - \frac{{{h_i}{T_{,i}}}}{T} \ge 0 $ | (8) |
在一定的应力和损伤下,材料的热力学状态逐渐由非平衡态向其平衡态过渡。与此对应,粘性内变量γr逐渐向其平衡态γre过渡,因而假定[8]
| $ \gamma _r^{\rm{e}} = \gamma _r^{\rm{e}}\left( {{\sigma _{ij}},{\omega _{ij}}} \right) $ | (9) |
对于小变形问题,γr和γer均为小量。将Gibbs比自由能在平衡态展开并略去高阶项,有
| $ \phi = {\phi _{\rm{e}}} + \frac{1}{2}{\phi _{{\rm{rq}}}}\left( {{\gamma _r} - \gamma _r^{\rm{e}}} \right)\left( {{\gamma _{\rm{q}}} - \gamma _{\rm{q}}^{\rm{e}}} \right) $ | (10) |
式中ϕe = ϕe(σij, ωij, T)为平衡态的Gibbs比自由能,ϕrq为对称矩阵,表示为
| $ {\boldsymbol{\phi} _{{\rm{rq}}}} = {\left( {\frac{{{\partial ^2}\phi }}{{\partial {\gamma _r}\partial {\gamma _{\rm{q}}}}}} \right)_{\rm{e}}} $ |
下标e表示在平衡态时的偏导值。
假设粘性热力学对偶力Γr与粘性热力学流
| $ {\mathit{\Gamma }_r} = {a_{\rm{T}}}\left( T \right)\mathit{\boldsymbol{a}}_{{\rm{rq}}}^{\rm{o}}{{\dot \gamma }_{\rm{q}}} $ | (11) |
式中aT为恒正的标量函数,arqo为对称半正定矩阵。
将式(10)和式(6)代入式(11),有
| $ \boldsymbol{a}_{{\rm{rq}}}^{\rm{o}}\frac{{{\rm{d}}{\gamma _{\rm{q}}}}}{{d\xi }} + {\boldsymbol{\phi} _{{\rm{rq}}}}{\gamma _{\rm{q}}} = {\boldsymbol{\phi} _{{\rm{rq}}}}\gamma _{\rm{q}}^{\rm{e}} $ | (12) |
式中ξ为缩减时间,定义为
| $ \xi = \int_0^t {\frac{{{\rm{d}}t'}}{{{a_{\rm{T}}}\left[ {T\left( {t'} \right)} \right]}}} $ | (13) |
注意到式(12)中的系数均为对称矩阵,可以利用坐标变换进行解耦,有
| $ A_r^{\rm{o}}\frac{{{\rm{d}}{{\hat \gamma }_r}}}{{{\rm{d}}\xi }} + {\mathit{\Phi }_r}{{\hat \gamma }_r} = {\mathit{\Phi }_r}\hat \gamma _r^e\left( {r\;不求和} \right) $ | (14) |
式中
求解式(14)有
| $ {{\hat \gamma }_r} = \hat \gamma _r^e\left( {1 - {e^{ - \xi /{\tau _r}}}} \right)\left( {r\;不求和} \right) $ | (15) |
式中τr为迟滞时间,定义为τr = Aro/Φr。
正则坐标下式(10)简化为
| $ \phi = {\phi _{\rm{e}}} + \frac{1}{2}\sum\limits_r {{\mathit{\Phi }_r}{{\left( {{{\hat \gamma }_r} - \hat \gamma _r^e} \right)}^2}} $ | (16) |
将式(16)和式(15)代入式(3),整理得
| $ {\varepsilon _{ij}} = - \frac{{\partial {\phi _0}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{ij}}}} + \sum\limits_r {\left( {1 - {{\rm{e}}^{ - \xi /{\tau _r}}}} \right)\frac{{\partial {\mathit{\Lambda }_r}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{ij}}}}} $ | (17) |
式中
在一定的损伤和应力下,材料的Gibbs比自由能ϕe可以表示为
| $ {\phi _{\rm{e}}} = - \mathit{\boldsymbol{\alpha }}_{ij}^{\rm{o}}{\mathit{\boldsymbol{\sigma }}_{ij}}\Delta T - \frac{1}{2}\mathit{\boldsymbol{\tilde S}}_{ijkl}^{\rm{e}}{\mathit{\boldsymbol{\sigma }}_{ij}}{\mathit{\boldsymbol{\sigma }}_{kl}} $ | (18) |
式中αijo = αijo(ωij)为热膨胀张量,ΔT = T -Tref为相对于参考态Tref的温度差,
| $ \mathit{\boldsymbol{\tilde S}}_{ijkl}^{\rm{e}} = \mathit{\boldsymbol{S}}_{ijmn}^{\rm{e}}{\mathit{\boldsymbol{Q}}_{mnkl}}\left( {{\omega _{ij}}} \right) $ | (19) |
式中Sijmne为无损材料平衡态的柔度张量,Qmnkl(ωij)为引入的宏观损伤效应张量,并且有Qmnkl(0) = Imnkl,Imnkl为单位四阶张量。
材料损伤的尺度远大于高分子链蠕动变形的尺度,损伤对粘性内变量及其平衡态具有相同的影响,则
| $ {\mathit{\Lambda }_r} = \frac{1}{2}\mathit{\boldsymbol{\tilde S}}_{ijkl}^{\rm{r}} + {\mathit{\boldsymbol{\sigma }}_{ij}}{\sigma _{kl}}\;\;\;\forall r $ | (20) |
式中ΔSijmnr为瞬态有效柔度张量,定义为
| $ \Delta \mathit{\boldsymbol{\tilde S}}_{ijkl}^{\rm{r}} = \Delta \mathit{\boldsymbol{S}}_{ijmn}^{\rm{r}}{\mathit{\boldsymbol{P}}_{mnkl}}\left( {{\omega _{ij}}} \right) $ | (21) |
式中ΔSijmnr为无损材料的瞬态柔度张量,Pmnkl(ωij)为引入的宏观损伤效应张量,同样有Pmnkl(0) = Imnkl。
将式(18)和式(20)代入式(17),得
| $ {\varepsilon _{ij}} = \varepsilon _{ij}^{\rm{e}} + \varepsilon _{ij}^v $ | (22) |
式中εije和εijv分别为弹性应变和瞬态应变,表示为
| $ \varepsilon _{ij}^{\rm{e}} = - \frac{{\partial {\phi _0}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{ij}}}} = \alpha _{ij}^{\rm{o}}\Delta T + \left[ {\mathit{\boldsymbol{S}}_{ijmn}^{\rm{e}}{\mathit{\boldsymbol{Q}}_{mnkl}} - \sum\limits_r {\Delta \mathit{\boldsymbol{S}}_{ijmn}^{\rm{r}}{\mathit{\boldsymbol{P}}_{mnkl}}} } \right]{\sigma _{kl}} $ |
| $ \varepsilon _{ij}^{\rm{v}} = \sum\limits_r {\left( {1 - {{\rm{e}}^{ - \xi /{\tau _r}}}} \right)\frac{{\partial {\mathit{\Lambda }_r}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{ij}}}}} = \sum\limits_r {\Delta \mathit{\boldsymbol{S}}_{ijmn}^{\rm{r}}\left( {1 - {{\rm{e}}^{ - \xi /{\tau _r}}}} \right){\mathit{\boldsymbol{P}}_{mnkl}}{\sigma _{kl}}} $ |
Jung[5]实验表明,不同损伤程度下材料的松弛模量在双对数坐标中纵向相差一个平移量,则令
| $ {\mathit{\boldsymbol{Q}}_{mnkl}} = {\mathit{\boldsymbol{P}}_{mnkl}} $ | (23) |
则蠕变响应式(22)改写为
| $ {\varepsilon _{ij}} = \alpha _{ij}^o\Delta T + {\mathit{\boldsymbol{S}}_{ijmn}}{\mathit{\boldsymbol{P}}_{mnkl}}{\sigma _{kl}} $ | (24) |
式中
引入有效应力
| $ {{\mathit{\boldsymbol{\tilde \sigma }}}_{ij}} = {\mathit{\boldsymbol{P}}_{ijkl}}{\mathit{\boldsymbol{\sigma }}_{kl}} $ | (25) |
则式(24)又可以表示为
| $ {\varepsilon _{ij}} = \alpha _{ij}^{\rm{o}}\Delta T + {\mathit{\boldsymbol{S}}_{ijkl}}{{\tilde \sigma }_{kl}} $ | (26) |
注意式(26)是在一定的应力和损伤下获得的,对于变化的应力和损伤,利用叠加原理有
| $ {\varepsilon _{ij}} = \alpha _{ij}^{\rm{o}}\left( {{\omega _{ij}}} \right)\Delta T + \int_{{0^ - }}^t {{\mathit{\boldsymbol{S}}_{ijkl}}\left( {\xi - \xi '} \right)\frac{{\partial {{\tilde \sigma }_{kl}}}}{{\partial \tau }}{\rm{d}}\tau } $ | (27) |
式(27)即为粘弹性损伤本构方程。该方程在形式上与线性粘弹性本构方程相似,差别仅在于用有效应力代替真实应力。同时注意到,损伤是通过有效应力引入的,因此该方程实际上考虑了损伤历史的影响。另一方面,由上述推导过程可见,从不可逆热力学的角度来衡量,通过有效应力引入损伤,要比直接用有效柔度张量替代无损柔度张量更为合理。这一结果与早期Schapery[19]建立的粘弹性损伤模型在形式上相似。此外,式(27)是一个广泛的粘弹性损伤本构方程,只要选择合适的宏观损伤效应张量,该方程可以表征不同形式的损伤。
将式(15),(16),(18)和(20)代入式(7),得损伤对偶热力学力为
| $ {Y_{{\rm{ab}}}} = \frac{1}{2}\left[ {\mathit{\boldsymbol{S}}_{ijmn}^{\rm{o}} + \sum\limits_r {\left( {2\frac{{{{\hat \gamma }_r}}}{{\hat \gamma _r^e}} - {{\left( {\frac{{{{\hat \gamma }_r}}}{{\hat \gamma _r^e}}} \right)}^2}} \right)\Delta \mathit{\boldsymbol{S}}_{ijmn}^r} } \right]\frac{{\partial {\mathit{\boldsymbol{P}}_{mnkl}}}}{{\partial {\omega _{{\rm{ab}}}}}}{\sigma _{ij}}{\sigma _{kl}} $ | (28) |
式中
根据有效柔度的定义式(19),反解得宏观损伤效应张量为
| $ {\mathit{\boldsymbol{P}}_{mnkl}} = {\mathit{\boldsymbol{C}}_{mnij}}{{\mathit{\boldsymbol{\tilde S}}}_{ijmn}} $ | (29) |
式中Cmnij = Sijmn-1为无损材料的刚度张量。前文指出,损伤对材料的平衡模量和瞬态模量具有相同的影响。因此在式(29)中取材料为弹性材料,从而可以避免复杂的粘弹性均匀化问题[20~22]。
假设材料初始状态是各向同性的,其柔度张量用矩阵可以表示为
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {1/E}&{ - v/E}&{ - v/E}&0&0&0\\ { - v/E}&{1/E}&{ - v/E}&0&0&0\\ { - v/E}&{ - v/E}&{1/E}&0&0&0\\ 0&0&0&{1/G}&0&0\\ 0&0&0&0&{1/G}&0\\ 0&0&0&0&0&{1/G} \end{array}} \right] $ | (30) |
式中E,v和G分别为杨氏模量、泊松比和剪切模量。
假设材料为正交各向异性损伤,取损伤主方向为坐标轴方向,则损伤内变量可以表示为
| $ \mathit{\boldsymbol{\omega }} = \left[ {\begin{array}{*{20}{c}} {{\omega _1}}&0&0\\ 0&{{\omega _2}}&0\\ 0&0&{{\omega _3}} \end{array}} \right] $ | (31) |
通常损伤会改变材料的对称性,为了描述这一过程,引入细观标量损伤效应函数,将材料损伤后的柔度张量表示为
| $ \mathit{\boldsymbol{\tilde S}} = \left[ {\begin{array}{*{20}{c}} {{f_1}/E}&{ - v{f_4}/E}&{ - v{f_5}/E}&0&0&0\\ { - v{f_4}/E}&{{f_2}/E}&{ - v{f_6}/E}&0&0&0\\ { - v{f_5}/E}&{ - v{f_6}/E}&{{f_3}/E}&0&0&0\\ 0&0&0&{{f_7}/G}&0&0\\ 0&0&0&0&{{f_8}/G}&0\\ 0&0&0&0&0&{{f_9}/G} \end{array}} \right] $ | (32) |
式中fi = fi(ω1, ω2, ω3) (i = 1, 2, ..., 9)是九个细观标量损伤效应函数,它们是损伤变量的单调增函数,分别用于描述损伤对材料九个柔度系数的影响,并且有fi(0, 0, 0) = 1 (i = 1, 2, ..., 9)。
将式(30)和式(32)代入式(29),得宏观损伤效应张量为
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&0\\ 0&\mathit{\boldsymbol{B}} \end{array}} \right] $ | (33) |
式中
| $ \mathit{\boldsymbol{A}} = \frac{1}{{\left( {1 + v} \right)\left( {1 - 2v} \right)}} \cdot \\ \left[ {\begin{array}{*{20}{c}} {\left( {1 - v} \right){f_1} - {v^2}\left( {{f_4} + {f_5}} \right)}&{v\left( {{f_2} - \left( {1 - v} \right){f_4} - v{f_6}} \right)}&{v\left( {{f_3} - \left( {1 - v} \right){f_5} - v{f_6}} \right)}\\ {v\left( {{f_1} - \left( {1 - v} \right){f_4} - v{f_5}} \right)}&{\left( {1 - v} \right){f_2} - {v^2}\left( {{f_4} + {f_6}} \right)}&{v\left( {{f_3} - v{f_5} - \left( {1 - v} \right){f_6}} \right)}\\ {v\left( {{f_1} - v{f_4} - \left( {1 - v} \right){f_5}} \right)}&{v\left( {{f_2} - v{f_4} - \left( {1 - v} \right){f_6}} \right)}&{\left( {1 - v} \right){f_3} - {v^2}\left( {{f_5} + {f_6}} \right)} \end{array}} \right]\;\;\;\;\\ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{f_7}}&0&0\\ 0&{{f_8}}&0\\ 0&0&{{f_9}} \end{array}} \right] $ |
由上式不难验证当ωij = 0时,有Pmnkl = Imnkl。
另一方面,正交各向异性材料的柔度张量可以表示为
| $ \mathit{\boldsymbol{\tilde S}} = \left[ {\begin{array}{*{20}{c}} {1/{{\tilde E}_1}}&{ - {{\tilde v}_{21}}/{{\tilde E}_2}}&{ - {{\tilde v}_{31}}/{{\tilde E}_3}}&0&0&0\\ { - {{\tilde v}_{12}}/{{\tilde E}_1}}&{1/{{\tilde E}_2}}&{ - {{\tilde v}_{32}}/{{\tilde E}_3}}&0&0&0\\ { - {{\tilde v}_{13}}/{{\tilde E}_1}}&{ - {{\tilde v}_{23}}/{{\tilde E}_2}}&{1/{{\tilde E}_3}}&0&0&0\\ 0&0&0&{1/{{\tilde G}_{12}}}&0&0\\ 0&0&0&0&{1/{{\tilde G}_{13}}}&0\\ 0&0&0&0&0&{1/{{\tilde G}_{23}}} \end{array}} \right] $ | (34) |
式中,
| $ \left\{ \begin{array}{l} \frac{{{{\tilde E}_r}}}{E} = \frac{1}{{1 + \frac{{16}}{3}\left( {1 - {v^2}} \right){\eta _r}}}\;\;\;\;\;\;\;\;\left( {r = 1,2,3} \right)\\ \frac{{{{\tilde G}_{rs}}}}{G} = \frac{1}{{1 + \frac{{16}}{3}\frac{{1 - v}}{{2 - v}}\left( {{\eta _r} + {\eta _s}} \right)}}\;\;\;\left( {r \ne s;r,s = 1,2,3} \right)\\ \frac{{{{\tilde v}_{rs}}}}{v} = \frac{1}{{1 + \frac{{16}}{3}\left( {1 - {v^2}} \right){\eta _r}}}\;\;\;\;\;\;\;\;\;\;\left( {r \ne s;r,s = 1,2,3} \right) \end{array} \right. $ | (35) |
式中ηr = Nrar3 (r = 1, 2, 3)是沿三个正交方向分布的微裂纹的密度,Nr和ar分别为单位体积内r方向上的微裂纹数和微裂纹的平均尺寸。
定义损伤内变量为相对微裂纹密度,即
| $ {\omega _i} = \frac{{{\eta _i}}}{{\eta _i^{\rm{c}}}}\left( {i = 1,2,3} \right) $ | (36) |
式中ηic为材料断裂时的临界微裂纹密度。
将式(35)代入式(34),化简后与式(32)比较,得细观损伤效应函数为
| $ \left\{ \begin{array}{l} {f_i}\left( {{\omega _1},{\omega _2},{\omega _3}} \right) = 1 + \frac{{16}}{3}\left( {1 - {v^2}} \right){\omega _i}\eta _i^{\rm{c}}\;\;\;\;\left( {i = 1,2,3} \right)\\ {f_i}\left( {{\omega _1},{\omega _2},{\omega _3}} \right) = 1\;\;\;\;\left( {i = 4,5,6} \right)\\ {f_7}\left( {{\omega _1},{\omega _2},{\omega _3}} \right) = 1 + \frac{{16}}{3}\frac{{1 - v}}{{2 - v}}\left( {{\omega _1}\eta _1^{\rm{c}} + {\omega _2}\eta _2^{\rm{c}}} \right)\\ {f_8}\left( {{\omega _1},{\omega _2},{\omega _3}} \right) = 1 + \frac{{16}}{3}\frac{{1 - v}}{{2 - v}}\left( {{\omega _1}\eta _1^{\rm{c}} + {\omega _3}\eta _3^{\rm{c}}} \right)\\ {f_9}\left( {{\omega _1},{\omega _2},{\omega _3}} \right) = 1 + \frac{{16}}{3}\frac{{1 - v}}{{2 - v}}\left( {{\omega _2}\eta _2^{\rm{c}} + {\omega _3}\eta _3^{\rm{c}}} \right) \end{array} \right. $ | (37) |
对于横观各向同性损伤,假设损伤主轴为x方向(ω1 ≠ 0, ω2 = ω3 = 0),有
| $ \left\{ \begin{array}{l} {f_1}\left( {{\omega _1},0,0} \right) = 1 + \frac{{16}}{3}\left( {1 - {v^2}} \right){\omega _1}\eta _1^{\rm{c}}\\ {f_i}\left( {{\omega _1},0,0} \right) = 1\;\;\;\;\;\left( {i = 2,3,6,9} \right)\\ {f_4}\left( {{\omega _1},0,0} \right) = {f_5}\left( {{\omega _1},0,0} \right) = 1 + \frac{{16\left( {1 - 2v} \right)\left( {{v^2} - 1} \right)}}{{3v\left( {2 - v} \right)}}{\omega _1}\eta _1^{\rm{c}}\\ {f_7}\left( {{\omega _1},0,0} \right) = {f_8}\left( {{\omega _1},0,0} \right) = 1 + \frac{{16}}{3}\frac{{1 - v}}{{2 - v}}{\omega _1}\eta _1^{\rm{c}} \end{array} \right. $ | (38) |
对于各向同性损伤,有
| $ \left\{ \begin{array}{l} {f_i}\left( \omega \right) = 1 + \frac{{16\left( {1 - {v^2}} \right)\left( {10 - 3v} \right)}}{{45\left( {2 - v} \right)}}\omega {\eta ^{\rm{c}}}\;\;\;\left( {i = 1,2,3} \right)\\ {f_i}\left( \omega \right) = 1 + \frac{{16\left( {1 - {v^2}} \right)}}{{45\left( {2 - v} \right)}}\omega {\eta ^{\rm{c}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {i = 4,5,6} \right)\\ {f_i}\left( \omega \right) = 1 + \frac{{32\left( {1 - v} \right)\left( {5 - v} \right)}}{{45\left( {2 - v} \right)}}\omega {\eta ^{\rm{c}}}\;\;\;\;\;\;\;\;\;\left( {i = 7,8,9} \right) \end{array} \right. $ | (39) |
将式(37),(38)或(39)代入式(33)即得到正交各向异性损伤、横观各向同性损伤或各向同性损伤的宏观损伤效应张量,再将此宏观损伤效应张量代入本构方程式(27),即得到正交各向异性损伤、横观各向同性损伤或各向同性损伤的粘弹性本构方程。
需要注意的是,除各向同性损伤外,式(33)定义的宏观损伤效应张量不为完全对称张量,这与经典损伤力学中的损伤效应张量不同。为了阐明本构方程式(27)的物理意义,以单轴拉伸下材料发生横观各向同性损伤为例进行说明。任取一不为零的损伤状态,不妨取ω1 = 0.2, ω2 = ω3 = 0,泊松比v = 0.498,将式(38)代入式(33),有
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} 68.5561\\ 67.0221\\ 67.0221\\ 0\\ 0\\ 0 \end{array}&\begin{array}{l} 0.1790\\ 1.1775\\ 0.1775\\ 0\\ 0\\ 0 \end{array}&\begin{array}{l} 0.1790\\ 0.1775\\ 0.1775\\ 0\\ 0\\ 0 \end{array}&\begin{array}{l} 0\\ 0\\ 0\\ 1.3565\\ 0\\ 0 \end{array}&\begin{array}{l} 0\\ 0\\ 0\\ 0\\ 1.3565\\ 0 \end{array}&\begin{array}{l} 0\\ 0\\ 0\\ 0\\ 0\\ 1 \end{array} \end{array}} \right] $ | (40) |
采用Voigt记法,则真实应力状态可以表示为{σ1, 0, 0, 0, 0, 0}T,根据有效应力定义式(25),有
| $ \mathit{\boldsymbol{\tilde \sigma }} = {\left\{ {68.5561{\sigma _1},67.0221{\sigma _1},67.0221{\sigma _1},0,0,0} \right\}^{\rm{T}}} $ | (41) |
由式(41)可见,三个主方向上的有效应力均不为零。这表明,对于单轴拉伸导致的横贯各向同性损伤而言,本构方程(27)中采用式(25)定义的有效应力来表征损伤的影响,实际上是在有效应力空间用各向同性材料的三轴加载来模拟真实应力空间横观各向同性材料的单轴加载。对于其它各向异性损伤,不难得出类似的结论。
2.3 损伤演化Schapery[24]在研究粘弹性材料的断裂问题时,提出了一个简化的裂纹扩展模型
| $ \dot a = k{\mathit{\Pi }^\alpha } $ | (42) |
式中a为裂纹长度,Π = -∂Φ/∂S为裂纹扩展时的能量释放率,Φ为材料的势能,S为裂纹扩展面积,α是与材料蠕变/松弛性能相关的参数,k是一个包含材料蠕变、裂尖失效区以及失效区内应力分布等信息的组合参数。
基于式(42),Park[25]提出了一个幂型损伤演化模型
| $ {S_m} = {A_m}{\left( { - \frac{{\partial W}}{{\partial {S_m}}}} \right)^{{\alpha _m}}} $ | (43) |
式中αm为材料参数,Sm为损伤内变量,下标m表示损伤内变量的数目,W为伪应变能,-∂W/∂S为能量释放率。系数Am通常是损伤内变量Sm的函数,具体的形式取决于损伤内变量Sm的定义。
文献[9, 26, 27]研究指出,对于颗粒填充的高聚物材料,微裂纹首先在颗粒/基体界面的极点形成,并迅速扩展至一定角度。因此简化起见,忽略界面裂纹的萌生过程,假定裂纹一旦形成便迅速扩展到一定尺寸,并且这个尺寸与颗粒的粒径尺寸密切相关。考虑到颗粒尺寸的分布特性,取其平均尺寸作为萌生微裂纹的参考尺寸。同时,考虑到颗粒/基体界面的粘结强度通常小于基体材料的断裂强度,以及材料的高填充性,可以认为材料的损伤主要是微裂纹数目的增加,并且当微裂纹数目增加到一定程度时,微裂纹迅速侨联形成宏观裂纹,材料发生断裂破坏。因此,对于各向同性损伤有
| $ \dot \omega = \frac{{\dot N{a^3}}}{{{\eta _{\rm{c}}}}} $ | (44) |
在式(43)中令损伤内变量Sm为微裂纹的总长度,即Sm = Na,则有
| $ \begin{array}{l} \dot N = \frac{{A\left( {Na} \right)}}{a}{\left( { - \frac{{\partial W}}{{\partial Na}}} \right)^\alpha } = \frac{{A\left( {Na} \right)}}{{{a^{1 + \alpha }}}}{\left( { - \frac{{\partial W}}{{\partial \omega }}} \right)^\alpha }{\left( {\frac{{\partial \omega }}{{\partial N}}} \right)^\alpha } = \\ \;\;\;\;\;\;A\left( {Na} \right)\frac{{{a^{2\alpha - 1}}}}{{\eta _{\rm{c}}^\alpha }}{\left( { - \frac{{\partial W}}{{\partial \omega }}} \right)^\alpha } \end{array} $ | (45) |
另一方面,根据式(42)有
| $ \dot Na = k{\left( { - \frac{{\partial \mathit{\Phi }}}{{\partial S}}} \right)^\alpha }{\left( {\frac{{\partial \mathit{S}}}{{\partial \left( {Na} \right)}}} \right)^\alpha } = k{\left( {\pi a} \right)^\alpha }{\mathit{\Pi }^\alpha } $ | (46) |
令-∂W/∂ω = Π,对比式(45)和(46),有
| $ A\left( {Na} \right) = \frac{{k{{\left( {\pi a{\eta _{\rm{c}}}} \right)}^\alpha }}}{{{a^{2\alpha }}}} = k{\left( {\frac{{\pi {\eta _{\rm{c}}}}}{a}} \right)^\alpha } $ | (47) |
将式(47)和式(45)代入式(44),得
| $ \dot \omega = \frac{k}{{{\eta _{\rm{c}}}}}{\pi ^\alpha }{a^{\alpha + 2}}{\left( { - \frac{{\partial W}}{{\partial \omega }}} \right)^\alpha } = \frac{k}{{{\eta _{\rm{c}}}}}{\pi ^\alpha }{a^{\alpha + 2}}{Y^\alpha } $ | (48) |
式(48)即微裂纹的损伤演化方程,将其式代入式(8)的第二个小式,不难验证其满足损伤耗散不等式。
3 模型验证为了验证模型的有效性,借助UMAT子程序接口,将其嵌入Abaqus软件,采用文献[5]的松弛模量建立模型,计算不同温度和应变率下的应力响应,并与文中的实验数据进行对比。
3.1 材料参数利用Park[28]等的转换方法,将文献[5]中20℃时的松弛模量转换为蠕变柔量,有
| $ S\left( t \right) = {S_0} + \sum\limits_{r = 1}^{10} {{S_r}\left( {1 - {{\rm{e}}^{ - t/{\tau _r}}}} \right)} $ | (49) |
式中τr = 8 × 10r -8s (r = 1, 2, ..., 10),S0 = 7.2kPa,其余参数见表 1。
|
|
Table 1 Retardation strengths(kPa) |
时温等效因子为[5]
| $ \lg \left( {{a_T}} \right) = - \frac{{6.12\left( {T - 20} \right)}}{{171.44 + T - 20}} $ | (50) |
取临界裂纹密度ηc为1,初始泊松比为0.498。
3.2 结果与讨论不同温度和应变率下,计算结果如图 1所示。图中实线为计算结果,离散点为实验数据。
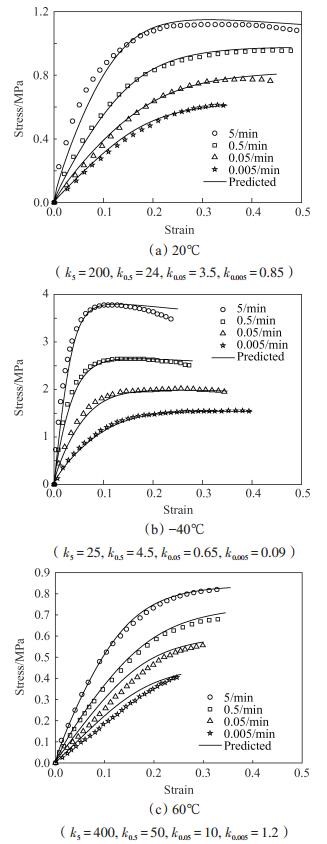
|
Fig. 1 Comparisons of the predicted and test datas at different temperature and strain rate(α = 1.3, c = 0.54) |
从图 1可以看出,当临界裂纹密度ηc取1,幂指数α与平均微裂纹尺寸c取常数,参数k随温度和应变率变化时,计算结果与实验数据具有较好的一致性,这表明文中建立的模型能够有效地反映材料的粘弹性损伤行为。
Park[25]在建立损伤模型式(43)时,建议幂指数αm根据加载控制条件(应力控制或位移控制)取1 +1/n或1/n,其中n为双对数坐标中材料松弛模量曲线斜率的绝对值。对于固体推进剂类满足时温等效原理的粘弹性材料,不同温度下材料的松弛模量曲线在双对数坐标中近似平行,因此幂指数α与温度无关。同时,根据Jung[5]的研究结果,损伤不影响材料的松弛速率,则幂指数α又与材料的损伤程度无关。注意到决定材料损伤程度的两大因素为温度和加载速率,故α与加载应变率无关。鉴于以上两点考虑,幂指数α可作为一个材料常数;根据前文假设,平均微裂纹尺寸c是一个与填充颗粒平均尺寸相关物理量,显然是一个与温度和加载速率无关的常量;对于参数k,Schapery指出该参数会随着温度、老化或其它加载条件的变化而变化[29],从拟合结果来看,其随着温度的升高和应变率的增加而增大。对于粘弹性材料而言,通常降低温度与增大应变率对材料的力学性能具有相当的影响。而参数k的变化并不满足这一规律,究其原因,主要是该参数本身是一个包含多个基本力学性能参数的复杂表达式,其变化规律并不似单一的基本力学性能参数(如松弛模量),具有简单的时温等效特性,这还需要更深入的研究。
4 结论通过本文研究,得出以下结论:
(1)基于不可逆热力学的推导过程表明,为获得蠕变型损伤本构方程,直接在无损线性蠕变型本构方程中,通过有效应力替代真实应力,要比有效柔度张量替代无损柔度张量更为合理。
(2)除各向同性损伤外,宏观损伤效应张量为非完全对称张量。对于单轴加载情形而言,宏观损伤效应张量的非完全对称性揭示了在有效应力空间,用各向同性材料多轴加载来模拟真实应力空间各向异性性材料单轴加载的物理本质。
(3)基于Schapery微裂纹扩展模型建立的损伤演化方程能够有效地反映材料损伤的温度依赖性和率相关性。幂指数α和平均微裂纹尺寸c可作为材料常数,参数k随着温度和应变率的增大而增大。
| [1] |
Park S W, Schapery R A. A Viscoelastic Constitutive Model for Particulate Composites with Growing Damage[J]. International Journal of Solids and Structures, 1997, 34(8): 931-947. DOI:10.1016/S0020-7683(96)00066-2
(  0) 0) |
| [2] |
Hinterhoelzl R M, Schapery R A. FEM Implementation of a Three-Dimensional Viscoelastic Constitutive Model for Particulate Composites with Damage Growth[J]. Mechanics of Time-Dependent Materials, 2004, 8(1): 65-94. DOI:10.1023/B:MTDM.0000027683.06097.76
(  0) 0) |
| [3] |
Ha K, Schapery R A. A Three-Dimensional Viscoelastic Constitutive Model for Particulate Composites with Growing Damage and Its Experimental Validation[J]. International Journal of Solids and Structures, 1998, 35(26): 3497-3517.
(  0) 0) |
| [4] |
Ozupek S, Becker E B. Constitutive Equations for Solid Propellants[J]. Journal of Engineering Materials and Technology, 1997, 119(2): 125-132. DOI:10.1115/1.2805983
(  0) 0) |
| [5] |
Jung G D, Youn S K. A Nonlinear Viscoelastic Constitutive Model of Solid Propellant[J]. International Journal of Solids and Structures, 1999, 36(25): 3755-3777. DOI:10.1016/S0020-7683(98)00175-9
(  0) 0) |
| [6] |
Simo J C. On a Fully Three-Dimensional Finite-Strain Viscoelastic Damage Model: Formulation and Computational Aspects[J]. Computer Methods in Applied Mechanics and Engineering, 1987, 60(2): 153-173. DOI:10.1016/0045-7825(87)90107-1
(  0) 0) |
| [7] |
Abdel-Tawab K, Weitsman Y J. A Strain-Based Formulation for the Coupled Viscoelastic/Damage Behavior[J]. Journal of Applied Mechanics, 2001, 68(2): 304-311. DOI:10.1115/1.1348013
(  0) 0) |
| [8] |
Abdel-Tawab K, Weitsman Y J. A Coupled Viscoelasticity/Damage Model with Application to Swirl-Mat Com posites[J]. International Journal of Damage Mechanics, 1998, 7(4): 351-380. DOI:10.1177/105678959800700403
(  0) 0) |
| [9] |
彭威. 复合固体推进剂粘弹损伤本构模型的细观力学研究[D]. 湖南: 国防科学技术大学, 2001.
(  0) 0) |
| [10] |
阳建红, 俞茂宏, 侯根良, 等. HTPB复合固体推进剂含损伤和老化本构研究[J]. 推进技术, 2002, 23(6): 509-512. (YANG Jian-hong, YU Mao-hong, HOU Gen-liang, et al. Research on the Constitutive Equations of HTPB Composite Solid Propellant with Damage and Aging[J]. Journal of Propulsion Technology, 2002, 23(6): 509-512.)
(  0) 0) |
| [11] |
姚东, 张光喜, 高波. 考虑应力状态的HTPB/AP推进剂含损伤热-粘弹性本构方程[J]. 固体火箭技术, 2014, 37(4): 496-499. (  0) 0) |
| [12] |
王哲君, 强洪夫, 王广, 等. 中应变率下HTPB推进剂压缩力学性能和本构模型研究[J]. 推进技术, 2016, 37(4): 776-782. (WANG Zhe-jun, QIANG Hong-fu, WANG Guang, et al. Mechanical Properties and Constitutive Model for HTPB Propellant under Intermediate Strain Rate Compression[J]. Journal of Propulsion Technology, 2016, 37(4): 776-782.)
(  0) 0) |
| [13] |
杨龙, 谢侃, 裴江峰, 等. HTPB推进剂拉伸力学行为的应变速率相关超弹本构模型[J]. 推进技术, 2017, 38(3): 687-694. (YANG Long, XIE Kan, PEI Jiang-feng, et al. A Strain-Rate-Dependent Hyperelastic Constitutive Model for Tensile Mechanical Behavior of HTPB Propellant[J]. Journal of Propulsion Technology, 2017, 38(3): 687-694.)
(  0) 0) |
| [14] |
Chen J K, Huang Z P, Mai Y W. Constitutive Relation of Particulate-Reinforced Viscoelastic Composite Materials with Debonded Microvoids[J]. Acta Materialia, 2003, 51(12): 3375-3384. DOI:10.1016/S1359-6454(03)00120-4
(  0) 0) |
| [15] |
Chen J K, Huang Z P, Mai Y W. A Constitutive Theory of Particulate-Reinforced Viscoelastic Materials with Partially Debonded Microvoids[J]. Computational Materials Science, 2008, 41(3): 334-343. DOI:10.1016/j.commatsci.2007.04.013
(  0) 0) |
| [16] |
Tan H, Huang Y, Liu C. The Viscoelastic Composite with Interface Debonding[J]. Composites Science and Technology, 2008, 68(15-16): 3145-3149. DOI:10.1016/j.compscitech.2008.07.014
(  0) 0) |
| [17] |
Tohgo K, Itoh Y, Shimamura Y. A Constitutive Model of Particulate-Reinforced Composites Taking Account of Particle Size Effects and Damage Evolution[J]. Composites Part A: Applied Science and Manufacturing, 2010, 41(2): 313-321. DOI:10.1016/j.compositesa.2009.10.023
(  0) 0) |
| [18] |
Jung G D, Youn S K, Kim B K. A Three-dimensional Nonlinear Viscoelastic Constitutive Model of Solid Propellant[J]. International Journal of Solids and Structures, 2000, 37(34): 4715-4732. DOI:10.1016/S0020-7683(99)00180-8
(  0) 0) |
| [19] |
Schapery R A A. On Viscoelastic Deformation and Failure Behavior of Composite Materials with Distributed Flaws[J]. Advances in Aerospace Structures and Materials, 1981(1): 5-20.
(  0) 0) |
| [20] |
Sanahuja J. Effective Behaviour of Ageing Linear Viscoelastic Composites: Homogenization Approach[J]. International Journal of Solids and Structures, 2013, 50(19): 2846-2856. DOI:10.1016/j.ijsolstr.2013.04.023
(  0) 0) |
| [21] |
Lavergne F, Sab K, Sanahuja J, et al. Homogenization Schemes for Aging Linear Viscoelastic Matrix-Inclusion Composite Materials with Elongated Inclusions[J]. International Journal of Solids and Structures, 2016, 80: 545-560. DOI:10.1016/j.ijsolstr.2015.10.014
(  0) 0) |
| [22] |
El Kouri M, Bakkali A, Azrar L. Mathematical Modeling of the Overall Time-Dependent Behavior of NonAgeing Viscoelastic Reinforced Composites[J]. Applied Mathematical Modelling, 2016, 40(7): 4302-4322.
(  0) 0) |
| [23] |
赵爱红, 虞吉林. 含正交排列夹杂和缺陷材料的等效弹性模量和损伤[J]. 力学学报, 1999, 31(4): 475-483. (  0) 0) |
| [24] |
Schapery R A. Simplifications in the Behavior of Viscoelastic Composites with Growing Damage[M]. New York: Springer, 1990, 193-214.
(  0) 0) |
| [25] |
Park S W. Development of a Nonlinear Thermo-Viscoelastic Constitutive Equation for Particulate Composites with Growing Damage[D]. Austin: University of Texas at Austin, 1994.
(  0) 0) |
| [26] |
Huang N C, Korobeinik M Y. Interfacial Debonding of a Spherical Inclusion Embedded in an Infinite Medium under Remote Stress[J]. International Journal of Fracture, 2001, 107(1): 11-30. DOI:10.1023/A:1026500321333
(  0) 0) |
| [27] |
García I G, Mantič V, Graciani E. A Model for the Prediction of Debond Onset in Spherical-Particle-Reinforced Composites under Tension. Application of a Coupled Stress and Energy Criterion[J]. Composites Science and Technology, 2015, 106: 60-67. DOI:10.1016/j.compscitech.2014.10.010
(  0) 0) |
| [28] |
Park S W, Schapery R A. Methods of Interconversion Between Linear Viscoelastic Material Functions, Part I: a Numerical Method Based on Prony Series[J]. International Journal of Solids and Structures, 1998, 36(11): 1653-1675.
(  0) 0) |
| [29] |
Schapery R A. A Theory of Crack Initiation and Growth in Viscoelastic Media, Part Ⅱ: Approximate Methods of Analysis[J]. International Journal of Fracture, 1975, 11(1): 141-59. DOI:10.1007/BF00034721
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

