2. 南京航空航天大学 能源与动力学院,江苏 南京 210016
2. College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
波箔型动压气体轴承被认为是小型发动机等高速透平机械的理想转子支撑机构[1],它利用轴面带动楔形间隙内气体形成动压压缩效应提供承载力,利用弹性箔片组合增强自适应稳定性[2]。从该型轴承的工作原理不难看出,轴承间隙内的流动状态及流固耦合作用决定了轴承主要性能。由于轴承转子转速高、转静子间间隙小,间隙内流动常处于过渡流状态,转静子与润滑气膜作用面存在界面滑移[3, 4]。学者已关注到流固耦合界面的滑移效应对轴承性能存在较大影响。Gans最早利用矩方法从线性玻尔兹曼方程出发,推导获得了努森数Kn变化下的润滑方程,并证明了边界滑移对动压轴承性能存在影响[3]。Fukuis [4],Mitsuya[5]等在考虑流固表面作用系数下,发展了动压轴承性能计算的1.5阶边界滑移速度模型,并通过与试验数据对比,验证了模型改进的有效性。Lee[6],Ma[7]等分别利用一阶和二阶边界滑移速度模型对轴承静特性变化规律进行了研究,结果表明二阶及高阶边界滑移速度模型仅为数学上的推导,缺乏物理意义,结果准确性低。黄海[8]、周建斌[9]等则利用该模型对滑移影响下间隙内流动特征变化进行了数值模拟研究,获得了有滑移条件下的气膜压力、承载力随轴承数、长径比等参数变化规律。Guo等[10]则考虑周向变截面的楔形气膜间隙内周向局部滑移状态不一致而改进了计算方法,利用局部边界滑移速度模型对轴承性能进行了数值模拟,得到了气膜间隙内周向滑移状态存在明显差异、大偏心率条件下局部滑移对轴承性能影响大的结论。前述研究中大都认为转静子间隙两侧流固边界滑移状态一致。然而,随着轴面硬化处理工艺、轴面涂层以及箔片内面固体润滑涂层的逐步改进,轴面侧和箔片侧的流固耦合表面协调系数差异增大,轴面侧和箔片侧滑移状态也明显存在不一致性[11]。王丽丽[12]的动压轴承流场测量试验和数值模拟结果就验证了该结论。然而,轴面侧与箔片侧滑移状态的不一致对轴承性能带来的影响在前人的研究中较少涉及。随着动压轴承应用领域的推广和其精细化设计要求的逐步提高,掌握流固耦合边界不同滑移状态及滑移相关参数对轴承性能的影响机制,显然对转轴和动压轴承箔片的关键参数设计至关重要。
本文以典型波箔型动压气体轴承(径向)为研究对象,针对轴面侧和箔片侧流固耦合边界不同滑移状态,分别建立极限剪应力滑移流模型下的气膜压力方程和弹性气膜厚度方程,利用牛顿迭代法进行耦合求解。数值研究不同边界滑移状态时轴承静特性随滑移相关参数的变化规律,以期获得不同边界滑移状态及其相关轴承参数对轴承静特性的影响规律。
2 研究模型波箔型动压气体轴承(径向)结构的截面如图 1(a)所示。轴承结构由壳体、波纹箔片及平箔片组成。波纹箔片和平箔片的前缘点焊在轴承壳体上,后缘为自由端,波纹箔片为平箔片提供支承,平箔片表面为复合耐磨固体润滑涂层,轴径表面作耐磨硬化处理。柱坐标系下轴承壳体内圆圆心O′与轴心O连线的最大气膜厚度处为θ零点,轴向为z向。轴承半径间隙为c,c = R′ -R,其中R′为平箔片内表面周向圆半径,R为轴颈半径,e为偏心距。图 1(b)为轴承周向展开局部示意图,本文数值研究中将柱坐标系转化为直角坐标系,周向展开为x向,径向为y向,轴向依然为z向[7, 9],图中还标识了轴承主要参数。本文所研究的典型轴承主要参数如表 1所示。

|
Fig. 1 Sketch map of bearing |
|
|
Table 1 Parameters of bearing |
为研究不同边界滑移状态对轴承性能的影响,以轴承周向展开模型为对象,根据轴面侧和箔片侧切应力边界条件和N-S方程[12, 13],可得不同滑移状态下的润滑气膜可压流动雷诺方程[13, 14],式(1)两侧均无滑移状态,式(2)为轴面侧滑移而箔片侧无滑移状态,式(3)为箔片侧滑移而轴面侧无滑移状态,式(4)为两侧均滑移状态。
| $ \frac{\partial }{{\partial x}}\left( {p{h^3}\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {p{h^3}\frac{{\partial p}}{{\partial z}}} \right) = 6\mu \omega R\frac{{\partial \left( {ph} \right)}}{{\partial x}} $ | (1) |
| $ \frac{\partial }{{\partial x}}\left( {p{h^3}\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {p{h^3}\frac{{\partial p}}{{\partial z}}} \right) =-3{\tau _x}h\frac{{\partial \left( {ph} \right)}}{{\partial x}}-3{\tau _z}h\frac{{\partial \left( {ph} \right)}}{{\partial z}} $ | (2) |
| $ \begin{array}{l} \frac{\partial }{{\partial x}}\left( {p{h^3}\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {p{h^3}\frac{{\partial p}}{{\partial z}}} \right) = 3\omega R\mu \frac{{\partial \left( {ph} \right)}}{{\partial x}} + \\ 3{{\tau '}_x}h\frac{{\partial \left( {ph} \right)}}{{\partial x}} + 3{{\tau '}_z}h\frac{{\partial \left( {ph} \right)}}{{\partial z}} \end{array} $ | (3) |
| $ \begin{array}{l} \frac{\partial }{{\partial x}}\left( {p{h^3}\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {p{h^3}\frac{{\partial p}}{{\partial z}}} \right) = 2\left( {{{\tau '}_x}-{\tau _x}} \right) \cdot \\ h\frac{{\partial \left( {ph} \right)}}{{\partial x}} + 2\left( {{{\tau '}_z}-{\tau _z}} \right)h\frac{{\partial \left( {ph} \right)}}{{\partial z}} \end{array} $ | (4) |
式中h为润滑气膜厚度(m),μ为润滑气体的动力粘度(Pa·s),p为气膜压力(Pa),ω为轴颈角速度(rad/s),其值为120πN,N为轴颈转速(r/min),R为轴颈半径(m)。
局部气膜厚度h随气膜压力作用下的箔片变形量变化而变化,本文采用的波箔型动压轴承气膜厚度方程如式(5)所示[2, 11]
| $ h = c\left( {1 + \varepsilon \cos \theta } \right) + \frac{{2{p_0} \cdot s}}{{cE}}{\left( {\frac{l}{{{t_{\rm{B}}}}}} \right)^3}\left( {1-{\nu ^2}} \right)\left( {p-{p_0}} \right) $ | (5) |
式中p0为大气压力,此处取1.01 × 105Pa。ε为偏心率,c为名义半径间隙(m),E为波箔片弹性模量(Pa),ν为波箔片泊松比,s为波箔片单位长度(m),2l为波箔片波纹长度(m),tB为波箔片厚度(m)。
本文忽略小气膜厚度内y向的切应力,考虑了x向和z向的存在滑移速度,其切应力分量τx,τz,τ'x,τ'z在轴面侧和箔片侧产生滑移时,等于x向和z向的极限切应力分量值,其表达式如式(6)所示。其中τd为轴面侧极限切应力,τu为箔片侧极限切应力。考虑轴面为金属硬化表面,箔片侧为固体润滑无机耐磨涂层,根据极限切应力模型[12, 14]和相关试验测量的无量纲数据[15, 16],本文采用的极限切应力如式(7)所示。假设滑移发生前后各向切应力分量比例一致。
| $ \left\{ \begin{array}{l} {\tau _x} = {\tau _{\rm{d}}}\cos \beta \\ {\tau _z} = {\tau _{\rm{d}}}\sin \beta \\ {{\tau '}_x} = {\tau _{\rm{u}}}\cos \beta '\\ {{\tau '}_z} = {\tau _{\rm{u}}}\sin \beta ' \end{array} \right. $ | (6) |
式中β或β'为
| $ \left\{ \begin{array}{l} {\tau _{\rm{d}}} = 0.82\omega R\mu /c'\\ {\tau _{\rm{u}}} = 0.38\omega R\mu /c' \end{array} \right. $ | (7) |
式中c'为当地实际间隙。
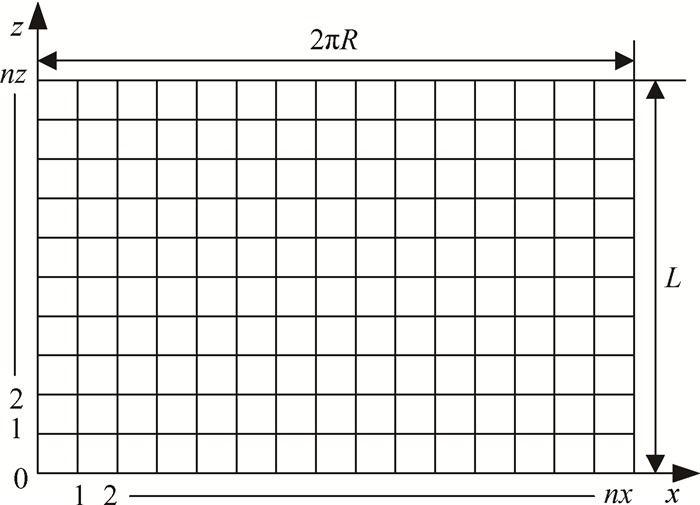
3.2 网格和边界条件流体域建立二维网格模型如图 2所示,对z方向(轴承长度方向)进行nz等分,对x方向的圆周长度进行nx等分,因此,z方向轴承长度有nz+1个节点,x方向圆周长度有nx+1个节点。定义求解域为(0:nx,0:nz)。
|
Fig. 2 Grid of gas film |
边界条件定义如下:轴承两端气膜压力均等于大气压力,即p(x, 0) = p0,p(x, nz) = p0。在圆周方向p(0, z) = p(nx, z)。
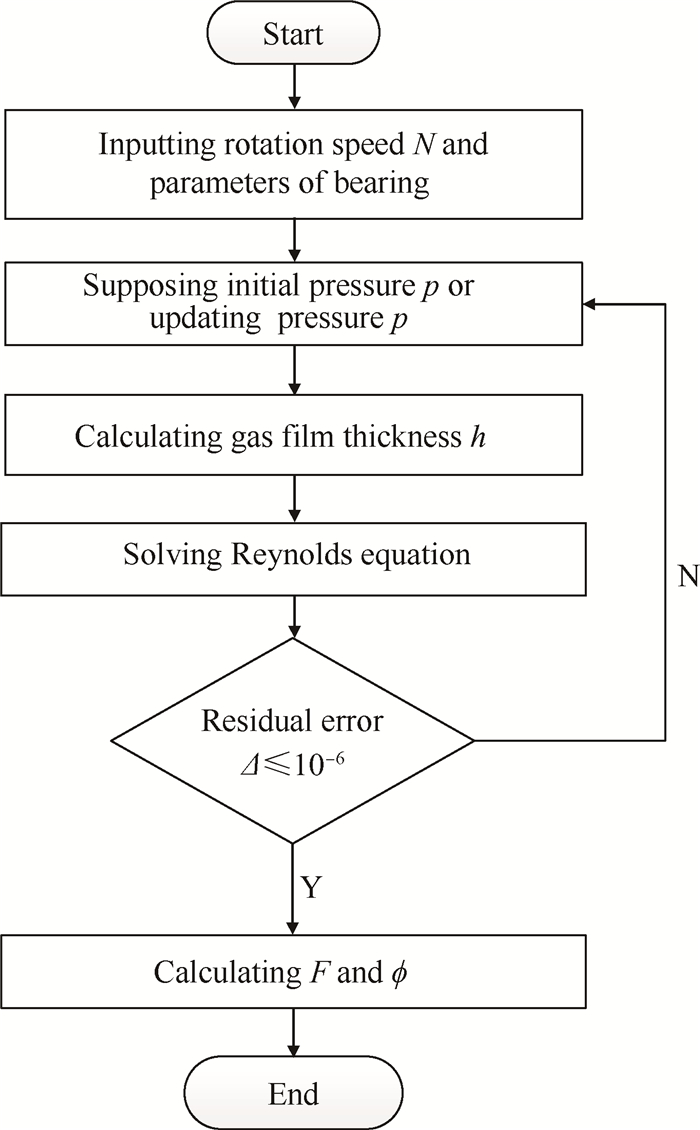
3.3 数值计算方法及验证数值计算流程如图 3所示,本文采用中心差分方法进行偏微分方程离散,采用超松弛迭代法进行收敛求解[13]。迭代中同步计算气膜压力下的箔片变形和气膜厚度,气膜压力和气膜厚度进行耦合迭代,迭代计算残差小于10-6,如式(8)所示[13, 17]。通过迭代计算获得求解域内所有节点的气膜压力分布和气膜厚度分布,根据式(9),式(10)可求出表征轴承静特性的承载力和偏位角[6, 8]。
|
Fig. 3 Method of numerical calculation |
| $ \Delta = \sqrt {\sum\limits_{i = 2}^{nx-1} {\sum\limits_{j = 2}^{nz-1} {{{\left( {\frac{{p_{i, j}^{k + 1}-p_{i, j}^k}}{{p_{i, j}^k}}} \right)}^2}} } } \le {10^{ - 6}} $ | (8) |
| $ \left\{ \begin{array}{l} {F_x} = \int_0^L {\int_0^{2\pi } {\left( {p-{p_0}} \right)} } \sin \theta {\rm{d}}\theta {\rm{d}}z\\ {F_y} =-\int_0^L {\int_0^{2\pi } {\left( {p-{p_0}} \right)\cos \theta {\rm{d}}\theta {\rm{d}}z} } \\ F = \sqrt {F_x^2 + F_y^2} \end{array} \right. $ | (9) |
| $ \phi = \arctan \left( {{F_x}/{F_y}} \right) $ | (10) |
式中pi, jk表示迭代的第k步第(i,j)坐标节点的气膜压力值(Pa),F为承载力(N),ϕ为偏位角(°)。
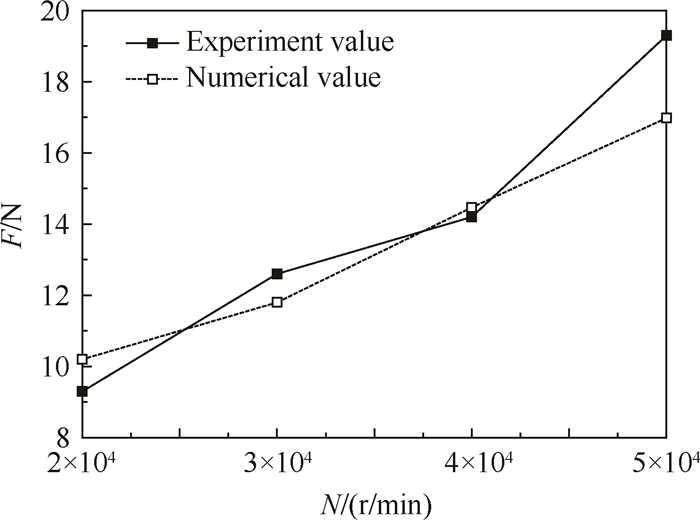
两侧均考虑滑移与轴承实际情况相符合,通过与本文轴承参数相近的文献试验数据,对两侧均考虑滑移下的数值模型进行验证[18]。数值计算中保证箔片状态及偏心率(约0.45~0.53)、转速等参数与文献相同。对比结果如图 4所示,承载力计算与试验规律一致,最大偏差约为2N(约10%),二者吻合较好。这表明本文的计算方法及极限切应力模型可行。
|
Fig. 4 Comparison of numerical and experimental results |
努森数Kn决定流动状态,当0.001 < Kn < 0.1时,属于滑移流状态。根据本文研究参数范围可得该波箔型动压气体轴承间隙内流动努森数Kn范围约为2.1 × 10-3 ~ 3.5 × 10-2,属于滑移流状态。局部是否会产生滑移取决于局部流动状态、流道尺寸、边界状态等因素。将流体域轴面侧和箔片侧不同滑移状态划分为4种情况:(1)两侧均无滑移;(2)仅轴面侧滑移;(3)仅箔片侧滑移;(4)两侧均滑移。与滑移状态相关的参数如表 2所示,其中转速和偏心率决定流动速度和局部尺寸分布,气体动力粘度主要影响流固耦合边界切应力。
|
|
Table 2 Changing range of parameters |
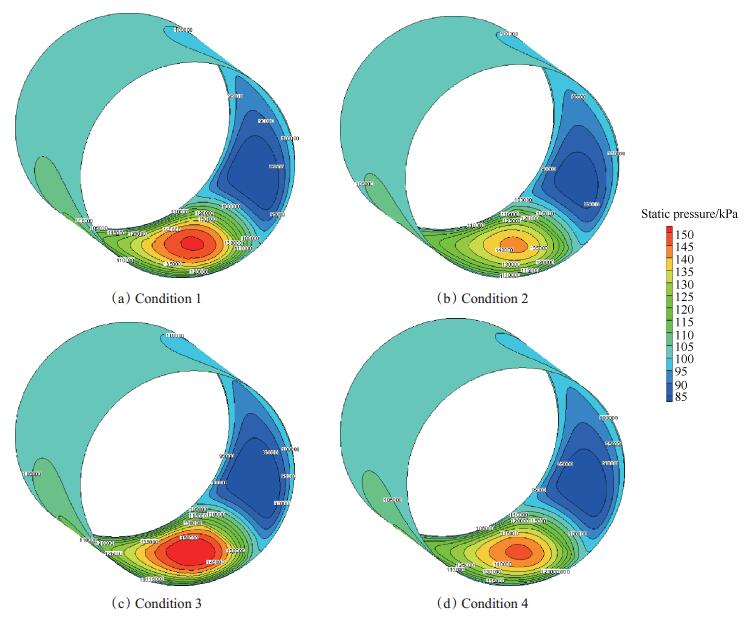
图 5给出了在上述四种滑移状态下气膜静压分布情况,图中ε=0.9,N=50kr/min,c=50μm。图 5分别对应4种不同边界滑移状态。从单个图上可以看出,轴承长度中截面处压力最大,往两端压力逐渐减小,气膜压力分布存在负压区,压力大小及其分布状态与文献[8, 10]研究结果一致,进一步说明本文的计算方法可行。下文分析中,所有边界滑移状态均与两侧不考虑滑移的状态1相比进行分析。状态2仅考虑轴面侧滑移时,最高压力值明显降低,由约0.15MPa降低至0.14MPa,且高压区面积明显减小,低压区压力略有减小。状态3仅考虑箔片侧滑移时,高压区面积大幅增大,低压区受影响较小。状态4考虑两侧均存在滑移时,由0.15MPa降低至0.145MPa,高压区面积减小,同样低压区受影响较小。以上状态主要是因为:在轴面侧流固边界粘性剪切力的作用下,高速旋转轴面带动轴承小间隙内润滑气体产生周向流动,楔形结构的局部小间隙处,动压作用下气体被压缩压力升高,局部大间隙处气体膨胀压力下降,从而形成周向压差和承载力,气体流速越高动压压缩效果越强。因此,当轴面侧达到极限切应力产生滑移时,润滑气体产生与转动方向相反的滑移速度,导致动压压缩效果和最高压力均会下降;而箔片侧产生滑移时则降低了箔片对周向流动的摩阻损失,使动压压缩效果和最高压力增强。高压区位于小气膜厚度处剪应力大,受滑移的影响较大,气膜压力变化较大;而低压区和负压区处于大气膜厚度处剪应力较小,受滑移的影响较小,气膜压力变化较小。总之,轴面侧边界滑移会降低动压压缩效果。箔片侧滑移增强动压压缩效果。
|
Fig. 5 Comparison with gas film pressure contours under different boundary sliding condition |
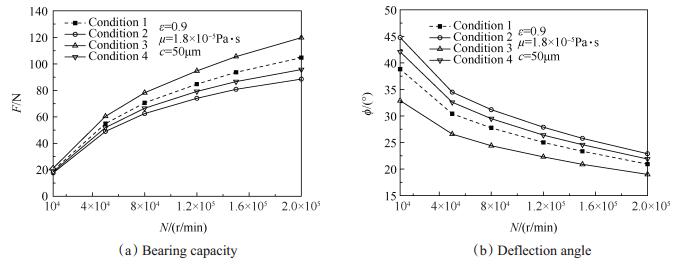
图 6为不同边界滑移状态下轴承静特性随转速N变化规律。图 6(a)为不同边界滑移状态下轴承承载力F随转速N变化规律。承载力表征了轴承承担转子重力负载的能力。从图上可以看出,低转速时边界滑移对承载力的影响较小,随着转速的提高不同滑移状态与不考虑边界滑移的状态1相比承载力差异逐渐增大。状态1的承载力由20N逐渐增大到约100N。状态2承载力低于状态1,随着转速的提高差异幅度逐渐增至约20%。状态3承载力高于状态1,随着转速的提高差异幅度逐渐增至约20%。状态4承载力低于状态1高于状态2,随着转速的提高差异幅度逐渐增至约10%。图 6(b)为不同边界滑移状态下轴承偏位角ϕ随转速N变化规律。偏位角ϕ表征了重力作用线与轴偏心线间的角度,如图 1(a)所示。该角度越大轴偏心转动越容易受到干扰,越不稳定。从图中可以看出,低转速时边界滑移对偏位角的影响较大[2],随着转速的提高不同滑移状态与状态1相比偏位角差异逐渐减小。状态1的偏位角由38°逐渐减小到24°。状态2偏位角高于状态1,差异幅度随着转速的提高由约7°减小到约3°。状态3的偏位角低于状态1,差异幅度随着转速的提高由约6°减小到约3°。状态4的偏位角高于状态1,差异幅度随着转速的提高由约4°减小到约2°。以上规律主要是因为,轴面侧的边界滑移使得动压压缩效果下降,从而使得周向压差下降,承载能力下降,而箔片侧边界滑移使得摩阻损失减小,动压压缩效果增强,从而使得承载力提升。转速越高边界滑移对周向压差影响程度越大,对承载力的影响也越大。边界滑移主要影响的是高压区压力,从而主要影响y向分力大小,因此轴面侧滑移会使y向分力减小偏位角增大,箔片侧滑移会使得y向分力增大偏位角减小。并且低转速时承载力较小偏位角较大,y向分力较小,其变化对偏位角影响比例较大,高速时承载力较大偏位角较小,y向分力较大,其变化对偏位角影响比例较小,因此随着转速的提高,滑移对偏位角的影响越来越小。
|
Fig. 6 Variation of static characteristics of bearing with rotation speed N under different boundary sliding condition |
图 7为不同边界滑移状态下轴承静特性随半径间隙c的变化规律。图 7(a)为不同边界滑移状态下轴承承载力F随半径间隙c的变化规律。从图中可以看出,随着半径间隙c由20μm逐渐增大到200μm,各状态下承载力逐渐减小,由64~90N降低到约5N。小间隙时(20μm)边界滑移对轴承承载力影响较大,与状态1相比,状态2承载力低10%,状态3承载力高约13%,状态4低约5%。随着间隙逐渐增大到120~200μm时,边界滑移对承载力的影响可以忽略。图 7(b)为不同边界滑移状态下轴承偏位角ϕ随半径间隙c的变化规律,随着半径间隙逐渐增大,各状态下偏位角逐渐增大,由约26°逐渐增大到42°~60°。小间隙时边界滑移对轴承偏位角影响较小。大间隙时(200μm),边界滑移对偏位角影响较大,与状态1相比,状态2偏位角高约10°,状态3偏位角低约8°,状态4高约5°。产生上述规律的主要原因是:半径间隙较小时,周向流道流通尺度较小切应力较大,此时滑移速度较大,因而小间隙下滑移对承载力影响较大。随着间隙的增大,边界滑移逐渐减弱,因此对承载力的影响也减小。小间隙时,承载力较大偏位角较小y向分力较大,其变化对偏位角的影响比例较小。而大间隙时,承载力较小,偏位角较大,y向分力较小,其变化对偏位角的影响比例较大,因此小间隙时滑移对偏位角影响小,大间隙时影响大。

|
Fig. 7 Variation of static characteristics of bearing with radius gap c under different boundary sliding condition |
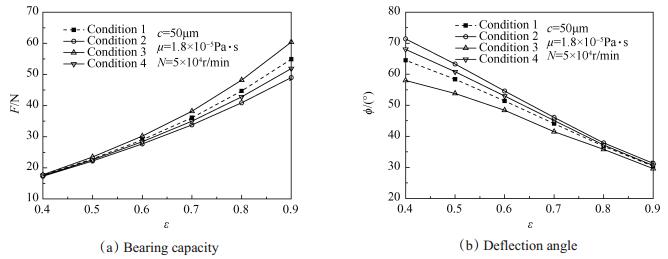
图 8为不同边界滑移状态下轴承静特性随偏心率ε变化规律。图 8(a)为不同边界滑移状态下轴承承载力F随偏心率ε的变化规律。从图中可以看出,随着偏心率ε由0.4逐渐增大到0.9,各状态下承载力逐渐增大,由约17N逐渐增大到约48~60N。小偏心率(ε =0.4)时,边界滑移对轴承承载力影响可以忽略。大偏心率时(ε=0.9),边界滑移对轴承承载力影响较大,与状态1相比,状态2低约12%,状态3高约10%,状态4低约5%。图 8(b)为不同边界滑移状态下轴承偏位角ϕ随偏心率ε的变化规律。从图中可以看出,随偏心率的逐渐增大各状态偏位角逐渐减小,从58°~71°减小到约33°。小偏心率时(ε=0.4)偏位角受影响较大,与状态1相比较,状态2的偏位角高约9°,状态3偏位角低约8°,状态4偏位角高约3°。随着偏心率的逐渐增大,偏位角受边界滑移的影响逐渐减小,大偏心率(ε=0.9)时,偏位角受影响较小,可忽略不计。上述规律主要是因为:如图 1(a)所示,当偏心率增大时,最小气膜厚度减小,最大气膜厚度增大,动压压缩效果和压差增强,使得承载力增加。当偏心率较小时,小气膜厚度处的局部流道尺寸较大,切应力和滑移速度降低,滑移对其高压区压力影响较小,因此小偏心率时滑移对承载力的影响较小。当偏心率逐渐增大时,最小气膜厚度处的流道尺寸减小,径向速度梯度增大,切应力和滑移速度增大,滑移对承载力的影响逐渐增大。偏位角的变化规律原因同前述相似。
|
Fig. 8 Variation of static characteristics of bearing with eccentricity ε under different boundary sliding condition |
图 9为不同边界滑移状态下轴承静特性随润滑气体动力粘度μ的变化规律。图 9(a)为不同边界滑移状态下轴承承载力F随润滑气体动力粘度μ变化规律。从图中可以看出,随着润滑气体动力粘度μ由0.42逐渐增大到4.46,各状态下承载力逐渐增大,由约20N逐渐增大到约62~100N。小动力粘度(μ = 0.42)时,边界滑移对轴承承载力影响可以忽略。大动力粘度时(μ = 4.46),边界滑移对轴承承载力影响较大,与状态1相比,状态2低约30%,状态3高约25%,状态4低约15%。图 9(b)为不同边界滑移状态下轴承偏位角ϕ随动力粘度μ的变化规律。从图中可以看出,随动力粘度的逐渐增大,各状态偏位角逐渐减小,从33°~44°减小到约23°~28°。小动力粘度时(μ =0.42)偏位角受滑移影响较大,与状态1相比较,状态2的偏位角高约8°,状态3偏位角低约10°,状态4偏位角高约6°。随着动力粘度的逐渐增大,偏位角受边界滑移的影响逐渐减小,各滑移状态下差异在5°以内。上述规律主要是因为:当动力粘度逐渐增大时,轴面带动润滑气体的动压压缩效果增强,使得承载力普遍增加。当动力粘度较小时,切应力较小滑移速度较小,因此滑移对承载力的影响较小。随着动力粘度的增大,粘性切应力逐渐增大,滑移速度逐渐增大,滑移对承载力的影响增大。偏位角的变化规律原因同前述相似。

|
Fig. 9 Variation of static characteristics of bearing with gas dynamic viscosity μ under different boundary sliding condition |
本文建立了波箔型动压气体轴承(径向)不同边界滑移状态雷诺方程,耦合弹性气膜厚度方程进行迭代求解,研究了不同边界滑移状态下滑移相关参数变化对轴承静特性的影响规律。在本文研究参数范围内,主要结论如下:
(1)边界滑移主要影响小气膜厚度处的高气膜压力区域,轴面侧滑移使得高压区气膜压力下降约0.1MPa且面积减小,箔片侧滑移使得高压区面积增大。两侧均考虑滑移时,对高压区的影响介于前二者之间。
(2)轴面侧滑移使得承载力下降、偏位角增大,对轴承静特性不利。箔片侧滑移使得承载力提高、偏位角减小,对提高轴承静特性有利。两种情况承载力最大影响幅度达到20%,偏位角达到10°。在本文的极限切应力条件下,两侧均考虑滑移时轴承承载力降低、偏位角增大。
(3)随转速N,偏心率e和润滑气体动力粘度μ的增大,切应力逐渐增大,边界滑移对承载力的影响逐渐增大,对偏位角的影响逐渐减小。随轴承间隙c的逐渐增大,切应力逐渐减小,边界滑移对承载力的影响逐渐减小,对偏位角的影响逐渐增大。
边界滑移状态通过调节供气压力、固体界面状态等实现,可开展相关试验研究,获得环境状态变化和界面状态变化对轴承性能的影响。
| [1] |
张广辉, 刘占生. 旋转冲压发动机高速动静混合气体轴承性能分析[J]. 推进技术, 2009, 30(5): 610-617. (ZHANG Guang-hui, LIU Zhan-sheng. Performance Analysis of High-Speed Hybrid Gas Bearings for Rotating Ram Jet[J]. Journal of Propulsion Technology, 2009, 30(5): 610-617.)
(  0) 0) |
| [2] |
虞烈, 刘恒. 轴承-转子系统动力学[M]. 西安: 西安交通大学出版社, 2001.
(  0) 0) |
| [3] |
Gans R F. Lubrication Theory at Arbitrary Knudsen Number[J]. Journal of Tribology, 1985, 107(3): 43l-433.
(  0) 0) |
| [4] |
Fukuis, Kaneko R. Analysis of Ultra-Thin Gas Film Lubrication Based on Linearized Boltzmann Equation: First Report Derivation of a Generalized Lubrication Equation Including Thermal Creep Flow[J]. Journal of Tribology, 1988, 110: 253-262. DOI:10.1115/1.3261594
(  0) 0) |
| [5] |
Mitsuya Y. Modified Reynolds Equation for Ultra-Thin Film Gas Lubrication Suing 1.5-Order Slip-Flow Model and Considering Surface Accommodation Coefficient[J]. Journal of Tribology, 1993, 115(2): 289-294. DOI:10.1115/1.2921004
(  0) 0) |
| [6] |
Lee Y B, Kwak H D, Kim C H, et al. Numerical Prediction of Slip Flow Effect on Gas-Lubricated Journal Bearings for MEMS/MST-Based Micro-Rotating Machinery[J]. Tribology International, 2005, 38: 89-96. DOI:10.1016/j.triboint.2004.01.003
(  0) 0) |
| [7] |
Ma G J, Wu C W, Zhou P. Wall Slip and Hydrodynam ics of Two-Dimensional Journal Bearing[J]. Tribology International, 2007, 40: 1056-1066. DOI:10.1016/j.triboint.2006.10.003
(  0) 0) |
| [8] |
黄海, 孟光, 赵三星. 二阶滑移边界对微型气浮轴承稳态性能的影响[J]. 力学学报, 2006, 38(5): 668-673. (  0) 0) |
| [9] |
周健斌, 孟光, 张文明. 微机电系统径向气体轴承特性研究[J]. 振动与冲击, 2007, 26(9): 30-33. (  0) 0) |
| [10] |
Guo F, Wong P L. Full and Partial Boundary Slippage Effect on Squeeze Film Bearings[J]. Tribology International, 2010, 43: 997-1004. DOI:10.1016/j.triboint.2009.12.059
(  0) 0) |
| [11] |
方华, 常海萍, 张镜洋, 等. 润滑气体及箔片材料对动压轴承动特性的影响分析[J]. 推进技术, 2014, 35(8): 1116-1122. (FANG Hua, CHANG Hai-ping, ZHANG Jing-yang, et al. Analysis of Lubrication Gas and Elastic Foil for Gas Foil Bearing Dynamic Characteristics[J]. Journal of Propulsion Technology, 2014, 35(8): 1116-1122.)
(  0) 0) |
| [12] |
王丽丽. 高速滑动轴承的边界滑移及空穴机理研究[D]. 济南: 山东大学, 2012.
(  0) 0) |
| [13] |
Carpino M, Talmage G. A Fully Coupled Finite Element Formulation for Elastically Supported Foil Journal Bearings[J]. Tribology Transactions, 2003, 46: 560-565. DOI:10.1080/10402000308982664
(  0) 0) |
| [14] |
吴成伟, 马国军, 周平. 流体流动的边界滑移问题进展[J]. 力学进展, 2008, 38(3): 266-277. (  0) 0) |
| [15] |
Spikes H A. The Half-Wetted Bearing, Part 1: Extended Reynolds Equation[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2003, 217: 1-14.
(  0) 0) |
| [16] |
Spikes H A. The Half-Wetted Bearing, Part 2: Potential Application in Low Load Contacts[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2003, 217: 15-26. DOI:10.1243/135065003321164776
(  0) 0) |
| [17] |
Rao TVVLN. Theoretical Prediction of Journal Bearing Stability Characteristics Based on the Extent of the SlipRegion on the Bearing Surface[J]. Tribology Transactions, 2009, 52(6): 750-758. DOI:10.1080/10402000903097387
(  0) 0) |
| [18] |
Lez S L, Arghir M, Frene J. Static and Dynamic Characterization of a Bump-Type Foil Bearing Structure[J]. Journal of Tribology, 2007, 129(1): 75-83. DOI:10.1115/1.2390717
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

