热力学指出提高涡轮前温度可以提高燃气涡轮发动机性能,实践中涡轮前温度不断提高正是燃气涡轮发动机技术发展趋势,如空客A380装配的Trent 900民用航空发动机起飞状态涡轮前温度已经高达1850K[1],远超过用于制造涡轮叶片的镍基单晶高温合金材料的工作最大许用温度1370K[2]。20世纪50,60年代发展起来的自压气机提取较低温度空气用于冷却涡轮叶片的设计,已经成为航空发动机高压涡轮设计所必须的一项技术。
为提高冷却效果,航空发动机制造厂商以及众多学者已经对涡轮叶片内部对流换热、外部气膜冷却设计技术开展了广泛而深入的研究[3],正是涡轮冷却设计技术的发展结合材料性能的提升推动了涡轮前温度水平的不断提高。
然而另一方面,冷却射流与主流掺混造成的流动损失会抵消涡轮前温度提升带来的性能收益。尽管有学者自涡轮冷却设计技术提出初始就开始关注并构建用于涡轮气动方案设计中冷却射流掺混损失预测的理论模型和计算方法[4~6],但和人们对于提高冷却设计换热效果的研究工作相比,冷却射流损失所吸引的注意要少很多。涡轮前温度的不断提高要求用于冷却的空气流量比例越来越大,冷却掺混损失对于涡轮性能的影响也变的不容忽视,MacAr⁃ thur[7]和Horlock等[8]提出,基于当前材料技术条件,进一步提高涡轮前温度可能实际导致整机循环效率下降。
为预测气冷叶片中冷却射流掺混损失,Hartsel[4]于20世纪70年代提出了一种单排射流孔条件下掺混损失模型,冷却射流与部分主流在壁面附近所谓“掺混层”中等压条件下掺混,“掺混层”之外的流场被称为“未受影响主流”,理论推导得出一种冷却射流掺混损失预测方法;Hartsel提出的掺混模型被后续研究者广泛采用,Ito等[9]和Day等[10]试验研究指出Hartsel冷却掺混损失预测值显示了和试验数据较好的符合性;Bohn等[11]采用与Hartsel相似的掺混模型构造了一种冷却损失预测方法并成功应用于其气冷涡轮通流设计程序;Hong等[12]研究了叶片表面不同区域单排射流孔对叶栅性能的影响,发现吸力面射流对叶栅性能影响最大,压力面射流影响最小;国内学者也针对气冷叶片冷却射流对叶栅性能的影响规律开展了试验与数值研究,乔渭阳等[13]试验研究了在叶片表面不同位置气膜孔喷气情况下冷气流量变化对涡轮叶栅性能和流场结构的影响,指出叶栅损失随前缘气膜孔喷气流量增大而单调增大,而叶片压力面和吸力面气膜孔喷气对涡轮叶栅损失影响规律比较复杂;曾军等[14]对叶片尾缘全劈缝冷气喷射条件下涡轮叶栅流场和气动性能进行了平面叶栅试验与数值研究,发现在较小冷气流量下,尾缘全劈缝冷气喷射使叶栅能量损失降低,尾缘冷气喷射减小尾迹亏损,降低了尾迹掺混损失;孙大伟等[15]试验研究了尾缘半劈缝和全劈缝两种不同冷气喷射结构对叶栅性能的影响,研究发现在相同条件下半劈缝冷气喷射结构叶栅出口的总压损失系数小于全劈缝结构;侯伟涛等[16]对典型高压涡轮叶型平面叶栅压力面气膜冷却对叶栅性能的影响开展了数值研究,发现叶栅能量损失系数随冷气入射角度并非单调变化,而是存在最佳冷气入射角度。
气冷涡轮中冷却射流掺混损失研究工作中包括掺混模型的构建和损失预测方法的提出普遍针对简化的单排气膜孔射流情况,在实际气冷叶片多排射流孔存在条件下,多排冷却射流相互作用对叶栅性能影响规律有待研究。
针对此问题,本文选择包含叶身多排气膜孔和尾缘劈缝冷却结构的典型高压涡轮气冷叶片为研究对象,通过比较分析,对叶身表面不同区域冷却射流相互作用情况下叶栅性能变化规律开展了平面叶栅数值研究,并将冷却掺混损失数值计算结果与Hartsel模型预测值进行了对比,根据研究结果对冷气掺混损失预测方法进行评估,期望通过进一步的研究工作获得适用于气冷涡轮设计的冷气掺混损失预测方法。
2 研究内容及研究方法 2.1 研究内容本文所开展工作主要目的在于研究高压涡轮气冷叶片表面不同区域气膜冷却射流相互作用条件下的叶栅性能,根据研究结果评估气冷涡轮设计中常用的Hartsel模型冷气掺混损失预测方法,完善设计体系提高设计质量。
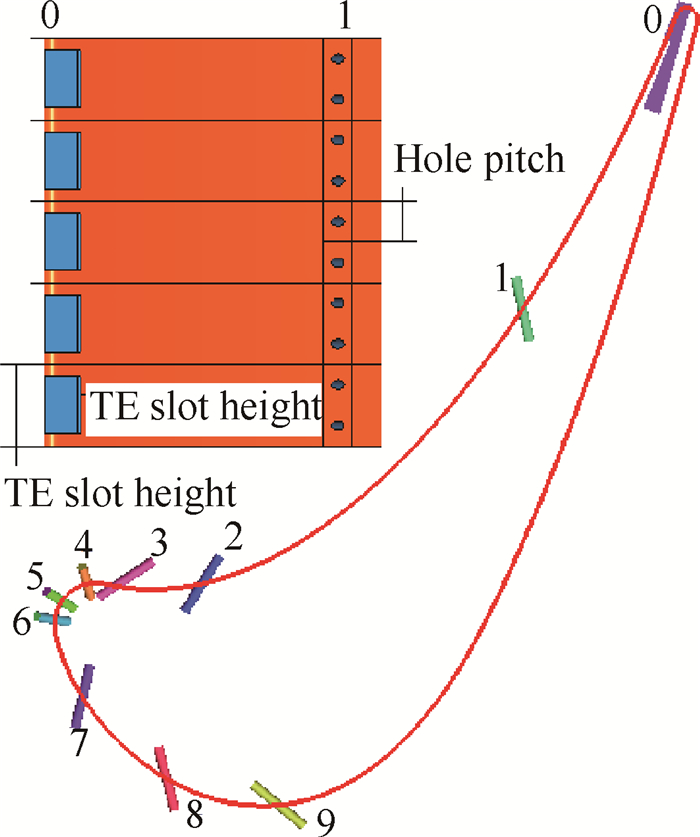
2.1.1 研究对象根据研究目的确定首先开展带冷气的平面叶栅数值研究,研究对象选择典型高压涡轮气冷叶片叶型。图 1给出了研究对象基本叶型及表面气膜孔排布、尾缘劈缝结构形式。叶型表面共布置9排气膜孔(圆孔),按照研究思路分成压力侧(Pressure Side,PS)、前缘(Leading Edge,LE)和吸力侧(Suction Side,SS)3个冷却射流区域,其中标号1~3排孔位于压力侧、标号4~6排孔位于前缘、标号7~9排孔位于吸力侧。尾缘(Trailing Edge,TE)采用压力面半劈缝冷却结构。叶型和气膜孔的主要参数如表 1,表 2所示。
|
Fig. 1 Blade profile and cooling geometry |
|
|
Table 1 Blade design parameters |
|
|
Table 2 Cooling holes geometry |
根据研究目的和研究对象,确定按照以下思路开展研究工作:
(1)研究基准算例无冷却射流情况叶栅性能及流场状况,利用冷气掺混损失模型预测各路冷却射流损失。
(2)采用两种分析办法研究叶片表面不同区域冷却射流对叶栅性能的影响:
(a)研究叶片表面不同区域(尾缘、前缘、压力侧和吸力侧)冷却射流独自作用对叶栅性能的影响,通过与基本算例对比,剥离不同区域冷却射流独自作用所带来的叶栅性能的变化。
(b)按照尾缘劈缝、前缘气膜、压力面气膜、吸力面气膜的顺序,在基本算例基础上逐步添加各区域冷却射流(研究算例复杂程度逐渐提高),研究冷却射流相互作用条件下对叶栅性能的影响,通过各算例之间的对比,逐步剥离不同区域冷却射流所带来的叶栅性能的变化。
(c)对比两种办法分析结果,总结气冷叶片表面不同区域气膜冷却射流之间相互作用对叶栅性能的影响规律。
(3)对比分析冷却射流损失数值研究计算结果与损失模型预测值。
2.2 研究方法本文采用求解定常RANS方程的办法,数值研究叶片表面不同区域冷却射流之间相互作用对叶栅性能的影响。
数值研究中计算域范围、网格划分拓扑结构、边界条件、湍流模型及工质属性等设定方法参考文献[17]。作者曾对两套跨声速平面叶栅开展试验研究[17],并对比试验与数值计算结果校核确定数值模拟方法,数值计算结果与试验数据叶片表面等熵马赫数、尾迹分布及总压损失统计结果取得了较好的符合性。
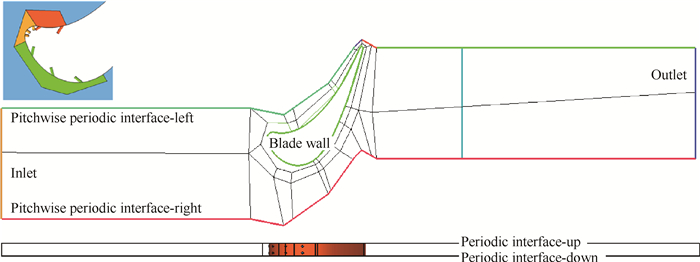
2.2.1 计算域和网格划分计算域和网格划分拓扑结构如图 2所示。计算域进口至叶片前缘(进口段)距离2倍弦长,出口至叶片尾缘(出口段)距离2.5倍弦长;叶片栅距方向采用平移周期性交接面设置将研究范围简化为单个叶栅通道;沿叶高方向尾缘劈缝与气膜孔按周期性排布,单个尾缘劈缝布置周期范围对应两个气膜孔布置周期,因此叶高方向亦采用平移周期性交接面设置将研究范围进一步简化为单个尾缘劈缝周期范围。
|
Fig. 2 Simulation domain and mesh topology |
计算采用分块结构化网格,拓扑结构划分如下:进出口延伸段及叶栅通道主流区域采用H型网格,叶片周围、气膜孔附近和射流通道内部采用O型网格;尾缘劈缝和气膜孔区域单独分块,通过交接面方式与主流连通。采用这种拓扑结构,避免了冷却射流出口与主流区域之间交接面的存在,消除了由于交接面的引入而带来的网格节点之间插值运算导致的数值误差,能够更准确的捕捉到气膜冷却射流与叶片表面边界层之间的相互作用。
2.2.2 边界条件和湍流模型边界条件设置如下:计算域进口边界为均匀进气条件,给定总压、总温和进气方向,出口边界给定截面平均静压,表 3给出了主流边界条件;冷却射流进口按照与主流进口流量比例给定质量流量、总温和进气方向,表 4给出了冷却射流边界条件;叶片表面、冷却射流孔尾缘劈缝壁面设置绝热无滑移边界;叶栅通道栅距方向两侧采用平移周期性边界;叶高方向两侧采用平移周期性边界。
|
|
Table 3 Boundary conditions |
|
|
Table 4 Cooling massflow ratio |
数值模拟中湍流模型参考文献[17]选择SST模型,求解采用理想气体工质,考虑定压比热容、动力粘性系数随温度变化情况。收敛标准设定为均方根残差小于1×10-5。
3 计算结果及分析叶栅性能一般用热力学效率或能量损失系数度量,这两个参数之和为1。叶栅热力学效率定义为出口实际动能与等熵条件下出口理想动能之比,公式(1)给出了能量损失系数ξ的计算方法;对于气冷叶片,能量损失系数定义须考虑各路冷却射流的影响(见公式(2))。
| $ \xi = 1 - \frac{{1 - {{\left( {\frac{{{p_2}}}{{{p_{{\rm{t2}}}}}}} \right)}^{\frac{{k - 1}}{k}}}}}{{1 - {{\left( {\frac{{{p_2}}}{{{p_{{\rm{t1}}}}}}} \right)}^{\frac{{k - 1}}{k}}}}} $ | (1) |
| $ \xi = 1 - \frac{{\left( {1 + \sum\limits_{i = 1}^n {\frac{{{W_{{\rm{c}}i}}}}{{{W_1}}}\frac{{{T_{{\rm{tc}}i}}}}{{{T_{{\rm{t1}}}}}}} } \right)\left[{1-{{\left( {\frac{{{p_2}}}{{{p_{{\rm{t2}}}}}}} \right)}^{\frac{{k-1}}{k}}}} \right]}}{{1 - {{\left( {\frac{{{p_2}}}{{{p_{{\rm{t1}}}}}}} \right)}^{\frac{{k - 1}}{k}}}{\rm{ + }}\sum\limits_{i = 1}^n {\frac{{{W_{{\rm{c}}i}}}}{{{W_1}}}\frac{{{T_{{\rm{tc}}i}}}}{{{T_{{\rm{t1}}}}}}} \left[{1-{{\left( {\frac{{{p_2}}}{{{p_{{\rm{tc}}i}}}}} \right)}^{\frac{{k-1}}{k}}}} \right]}} $ | (2) |
式中下标1,2分别代表叶栅进口和出口截面,ptci, Ttci和Wci分别为某一路冷却射流总压、总温和射流流量。
需要指出的是,气冷叶片能量损失系数计算中冷却射流相关参数需采用冷却射流供气流动参数,而不是接近射流出口位置流动参数,即能量损失系数定义考虑了冷却气在叶片内部复杂冷却结构流动过程中所产生的流动损失。
在实际发动机环境中冷却射流供气条件(总压ptc、总温Ttc)通常由整机循环参数决定。对于固定的冷却射流供气压力气冷叶片效率取决于叶栅出口总压,气冷叶片效率预测等同于预测叶栅通道中壁面边界层、尾缘阻塞及冷却射流与主流掺混所带来的叶栅前后总压变化Δpt。因此,气冷叶栅性能还可以采用总压损失系数Yp来评价。
| $ {Y_p} = \frac{{\Delta p}}{{{p_{\rm{t}}}}} $ | (3) |
基于以上分析,本文采用能量损失系数ξ(公式(2))和总压损失系数Yp(公式(3))两个参数评估气冷叶栅性能。研究算例气冷叶片能量损失系数ξ计算中冷却射流供气压力为主流进口压力1.12倍;叶栅出口数据分析选择尾缘下游0.4倍轴向弦长位置截面。
3.1 冷却射流损失理论模型预测结果 3.1.1 基本叶栅流场由于壁面边界层的存在,求解RANS方程数值计算方法中湍流模型、壁面函数的引入,数值模拟中研究算例网格规模、网格划分细节如壁面Y+值选取会对计算结果产生一定影响。为尽量避免网格因素对研究结果的干扰,选择基准算例首先进行了网格敏感性分析。
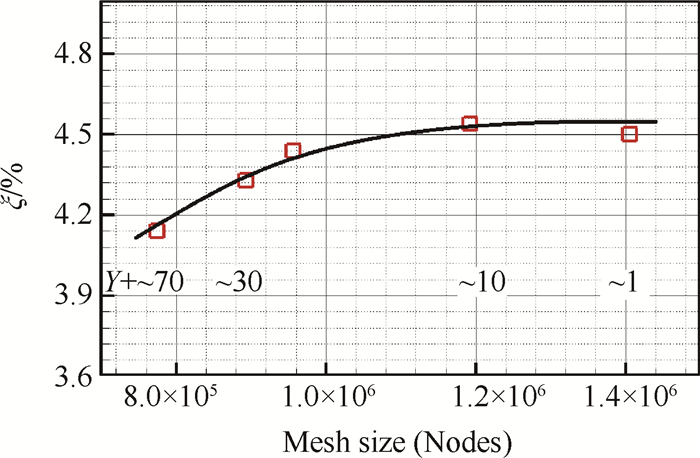
图 3给出了叶栅能量损失系数随网格规模(对应不同壁面Y+值)变化趋势。分析可以发现,随着网格规模增加,数值计算结果叶栅能量损失系数逐渐增大;当Y+大于30之后,能量损失系数增大趋势明显放缓,Y+从20减小到1左右能量损失系数变化范围仅0.1%。因此,之后数值研究中Y+值选取10左右。对应叶片表面O网格第一层网格厚度约为0.01μm,增长比例1.12;吸力面靠近尾缘边界层内包含网格节点数目为30左右;各气膜冷却射流通道内采用O型网格划分,截面网格节点数目约300;由于周期性交界面的采用,网格节点总数大大减少。
|
Fig. 3 Mesh refinement analysis |
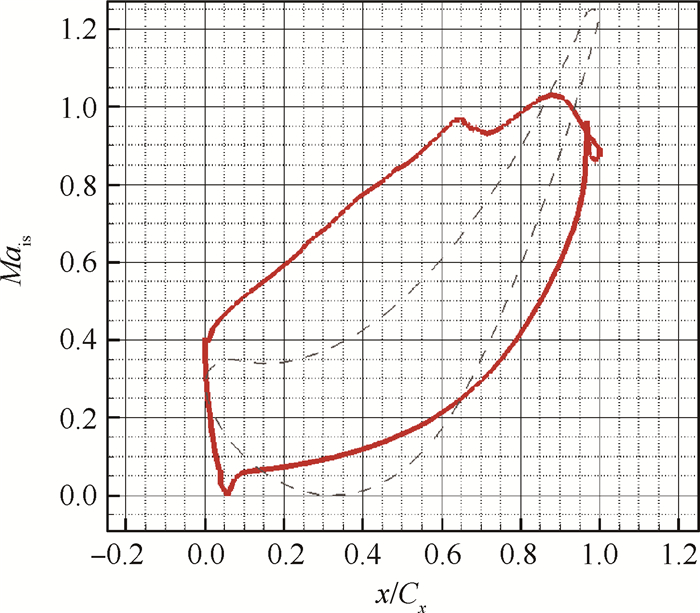
基于以上分析结果,首先对基本叶栅流场开展了数值研究。数值计算结果显示,基准算例(无冷却射流)总压损失系数Yp为2.62%,能量损失系数ξ为4.58%。图 4给出了基准算例叶片表面等墒马赫数分布情况。
|
Fig. 4 Blade isentropic Mach number distribution |
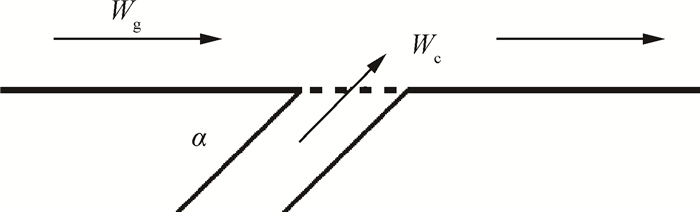
为了预测冷却射流与主流掺混对叶栅性能的影响,Hartsel提出了一种掺混模型,冷却射流和主流而不是边界层以一维的方式掺混,对叶片压力分布不产生任何作用。在此情况下,冷却射流与主流掺混损失独立于叶型损失、尾缘损失及端壁损失,可以和其他各类损失叠加,Hartsel通过试验证实了这种简化假设的合理性。
在此基础上对一维劈缝简化模型(见图 5)应用Shapiro提出的“影响系数”方法理论推导得出了冷却射流与主流掺混所带来的总压损失
| $ {Y_p} = \frac{{\Delta p_{\rm{t}}}}{{{p_{\rm{t}}}}} = \frac{{\gamma Ma_{\rm{g}}^2}}{2}\frac{{{W_{\rm{c}}}}}{{{W_{\rm{g}}}}}\left[{1 + \frac{{{T_{{\rm{tc}}}}}}{{{T_{{\rm{tg}}}}}}-\frac{{2{V_{\rm{c}}}}}{{{V_{\rm{g}}}}}\cos \alpha } \right] $ | (4) |
|
Fig. 5 One-dimensional mixing model |
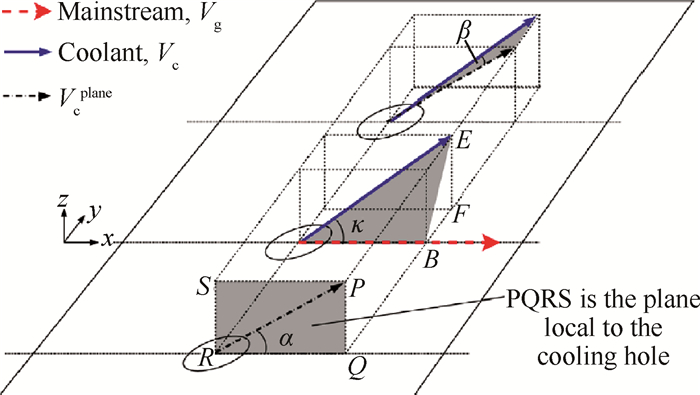
Hartsel根据一维劈缝简化模型得出的结论不适用于以空间复合角度入射的冷却射流与主流的掺混情况,Lim等[18]通过控制体分析指出,将一维劈缝简化模型中射流倾斜角度α替换为射流孔出口当地主流与射流矢量方向夹角,即可将Hartsel所得出结论试验范围推广。
如图 6所示,角度κ与射流倾斜角(Inclination angle)α及射流偏航角(Yaw angle)β射之间存在以下关系
| $ \cos \kappa = \cos \alpha \cdot \cos \beta $ | (5) |
|
Fig. 6 Flow angle definition[18] |
因此,以空间复合角度入射的冷却射流与主流的掺混所带来的总压损失为
| $ {Y_p} = \frac{{\gamma Ma_{\rm{g}}^2}}{2}\frac{{{W_{\rm{c}}}}}{{{W_{\rm{g}}}}}\left[{1 + \frac{{{T_{{\rm{tc}}}}}}{{{T_{{\rm{tg}}}}}}-\frac{{2{V_{\rm{c}}}}}{{{V_{\rm{g}}}}}\cos \alpha \cdot \cos \beta } \right] $ | (6) |
这个公式揭示出影响掺混损失的主要因素在于冷却气入射当地马赫数、冷却流量比、温度比、速度比以及入射角度,以其简便的形式非常适用于在气冷涡轮气动方案一维和二维设计阶段,但需要指出的是这个冷却掺混损失计算公式基于均匀主流与单个位置射流掺混模型得到,对于实际气冷叶片多排冷却射流相互作用条件下的适用情况还需要研究验证。
本文研究对象中多排气膜孔以空间复合角度入射主流,因此冷却射流掺混损失采用经Lim等[18]修正后的Hartsel预测方法(公式(6))。在气冷叶栅数值研究前,本文首先对研究对象各排冷却射流掺混损失进行了评估。公式(6)中各参数按照以下办法确定:基准算例数值计算显示叶栅进出口静温差39.7K,比热比变化小于0.1%,因此比热比参数取常数1.40;根据各排冷却射流在叶片上所处位置结合叶片表面等墒马赫数分布(见图 3)确定了射流入射当地主流马赫数;冷却射流与主流总温比由边界条件确定,本文研究算例中冷却射流与主流总温相同,因此总温比参数为1;冷却射流与主流速度比由公式(7)和(8)确定,公式(7)根据各冷却射流流量可以得到射流在出口位置马赫数Mac,其中射流静压psc与主流当地静压一致;射流角度由射流孔几何参数确定(见表 2)。表 5给出了各排孔冷却射流掺混总压损失Yp预测结果及相关参数,将Hartsel所提出的冷却掺混损失与其他损失类型之间的损失叠加假设推广至多排孔冷却射流条件下各排孔射流所引入损失的情况,各区域多排孔冷却掺混损失预测结果为该区域各排孔损失预测值之和。
| $ {W_{\rm{c}}} = {M_{\rm{c}}}\sqrt {1 + \frac{{{\gamma _{\rm{c}}} - 1}}{2}M_{\rm{c}}^2} \sqrt {\frac{{{\gamma _{\rm{c}}}}}{{{R_{\rm{c}}}{T_{{\rm{tc}}}}}}} {p_{{\rm{sc}}}}{A_{\rm{c}}} $ | (7) |
| $ \frac{{{V_{\rm{c}}}}}{{{V_{\rm{g}}}}} = \sqrt {\frac{{{\gamma _{\rm{c}}}{R_{\rm{c}}}{T_{{\rm{tc}}}}}}{{{\gamma _{\rm{g}}}{R_{\rm{g}}}{T_{{\rm{tg}}}}}}} \frac{{M{a_{\rm{c}}}}}{{M{a_{\rm{g}}}}}\sqrt {\frac{{1 + \left[{\left( {{\gamma _{\rm{g}}}-1} \right)/2} \right]Ma_{\rm{g}}^2}}{{1 + \left[{\left( {{\gamma _{\rm{c}}}-1} \right)/2} \right]Ma_{\rm{c}}^2}}} $ | (8) |
|
|
Table 5 Predicted coolant mixing loss |
根据表 5损失评估结果分析,可以发现不同区域冷却射流对叶栅性能影响程度的差异,尾缘劈缝与吸力面冷却射流对叶栅性能影响较大,前缘区域次之,压力面冷却射流对叶栅性能影响较小,Hong等[12]研究结论与此一致。
需要指出的是,损失预测结果显示压力面3排气膜孔(编号1~3)所引入的总压损失为负值,即冷却射流没有导致叶栅总压损失增大,反而略有降低。分析原因在于:根据损失预测公式,编号2和3的两排气膜孔所引入的总压损失为负值,此两排孔以45°倾斜角入射主流,射流与主流速度比显著高于其余各排孔(第4排孔入射倾斜角为90°,在损失预测公式中速度比参数值没有影响)。相比较与主流掺混所带来的总压损失,高动量的冷却射流所引入的总压提高效果更大,因此基于总压损失系数定义方法,预测结果显示为负值。
3.2 冷却射流损失数值计算结果 3.2.1 各区域冷却射流独自作用按照既定研究思路,首先对叶片表面不同区域冷却射流独自作用情况叶栅性能变化开展了研究。表 6给出了基准算例和各区域冷却射流独自作用算例总压损失Yp和能量损失ξ两种损失系数计算结果。通过对比基准算例,剥离得到了不同区域冷却射流各自所导致的损失系数变化ΔYp和Δξ。
|
|
Table 6 Loss coefficient(separated cooling) |
分析发现:由于定义不同,不同区域冷却射流独立作用研究算例两种损失系数具体数值有区别,但各区域冷却射流所引入的总压损失ΔYp之间的比较能反映出不同区域冷却射流对叶栅性能影响程度的差异与数值研究前损失预测结果(见表 5)相一致,即尾缘劈缝与吸力面冷却射流对叶栅性能影响较大,前缘区域次之,压力面冷却射流对叶栅性能影响较小。值得一提的是,数值计算结果也显示出压力面冷却射流所引入的总压损失系数Yp为负值,与数值研究前损失预测结果一致。
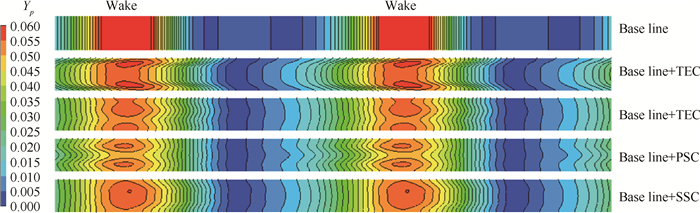
图 7显示了叶栅尾缘下游0.4倍轴向弦长位置处总压损失系数Yp云图。可以看出,和基准算例相比,冷却射流与主流的掺混作用导致栅后尾迹范围明显增大,尾迹核心损失有所降低。尾迹核心区域损失反映出各区域冷却射流与主流掺混作用的影响,如尾缘劈缝射流离开矩形出口后角区位置与主流掺混、压力面射流与主流掺混在尾迹区域表现出两个明显的损失核心。
|
Fig. 7 Total pressure loss(Yp)contour(trailing edge downstream 0.4Cx,separated cooling region) |
在上一节不同区域冷却射流独自作对叶栅性能影响研究基础上,进一步研究了各区域冷却射流相互作用情况叶栅性能的变化。
按照尾缘劈缝、前缘气膜、压力面气膜、吸力面气膜的顺序,在基本算例基础上逐步添加各区域冷却射流(算例复杂程度逐渐提高)确定带冷气研究算例。
表 7给出了基准算例和各区域冷却射流相互作用算例总压损失Yp和能量损失ξ两种损失系数计算结果。对比基准算例,剥离得到了各算例总的冷却射流所带来的损失系数变化ΔYp和Δξ;对比带冷气各算例,进一步剥离得到了叶片各区域冷却射流相互作用情况下,不同区域射流各自所带来的损失系数变化ΔYp ′和Δξ′,分析可以得出与各区域射流独立作用一致的结论。
|
|
Table 7 Loss coefficient(accumulated cooling) |
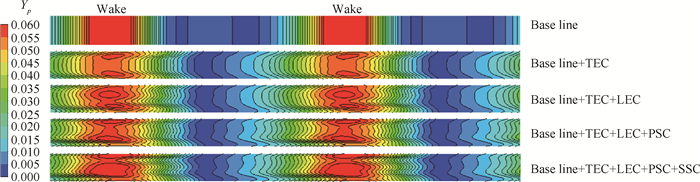
图 8显示了各冷却区域射流相互作用情况下叶栅尾缘下游0.4倍轴向弦长位置处总压损失系数Yp云图。和基准算例相比,冷却射流与主流的掺混作用导致栅后尾迹范围明显增大,随着射流出流位置的增多,尾迹核心高损失区域范围逐渐变大。
|
Fig. 8 Total pressure loss(Yp)contour(trailing edge downstream 0.4Cx, accumulated cooling region) |
至此,采用两种分析办法数值研究分别得到了叶片表面不同区域冷却射流对叶栅性能的影响,表 8列出了两种损失系数的比较情况。
|
|
Table 8 Loss coefficient comparison for different cases |
可以发现,两种数值研究方法计算结果分析所得各区域冷却射流引入的损失系数比较相差非常小,总压损失系数差别小于0.005%,能量损失系数差别小于0.049%,即各区域冷却射流相互作用情况下每一部分所引入的流动损失与各自独立所用情况基本相同。
由此得出结论:气冷叶片表面多排冷却射流之间与主流掺混引入的流动损失相互独立,具有简单的可叠加性质。
表 9给出了各区域冷却射流引入总压损失数值研究计算结果与理论模型预测值的比较。可以发现,和数值计算结果相比,总压损失系数预测结果偏高,尤其对于尾缘和吸力面区域较高主流马赫数情况,预测值分别为计算结果的4倍和2倍;前缘和压力面预测值和计算结果符合性较好。
|
|
Table 9 Total pressure loss comparison |
基于这种差异,分析认为Hartsel冷气掺混损失模型不能直接应用于涡轮气动一维与二维设计阶段。
5 结论本文选择包含叶身多排气膜孔和尾缘劈缝冷却结构的典型高压涡轮气冷叶片为研究对象,对叶身表面不同区域冷却射流相互作用情况下叶栅性能变化规律开展了平面叶栅数值研究,得出了如下结论:
(1)气冷叶片表面多排冷却射流共同作用情况下,各排冷却射流与主流掺混引入的流动损失相互独立,具有简单的可叠加性质,将Hartsel所提出的冷却掺混损失与其他损失类型之间的损失叠加假设推广至多排孔冷却射流条件下各排孔射流引入损失的情况,并经过初步数值研究,验证了其合理性,该结论有待进一步的试验验证。
(2)叶片表面各区域冷却射流出流对叶栅性能影响程度有所不同,尾缘劈缝与吸力面冷却射流对叶栅性能影响较大,前缘区域次之,压力面冷却射流对叶栅性能影响较小。
(3)和数值计算结果相比,总压损失系数预测值偏高,尤其对于尾缘和吸力面主流马赫数较大的区域,预测值分别为计算结果的4倍和2倍,而前缘和压力面预测值和计算结果符合性较好,因此在气冷涡轮气动方案一维与二维设计中不能直接应用Hartsel冷气掺混损失模型。
本文的研究工作尚未得出在气冷涡轮设计中适用的冷却射流掺混损失模型,需要开展进一步的研究工作总结规律、归纳修正办法,并对修正方法开展试验验证。
| [1] |
Rolls-Royce. The Jet Engine[M]. UK: Key Publishing Limited, 2005.
(  0) 0) |
| [2] |
Young J B, Wilcock R C. Modeling the Air-Cooled Gas Turbine: Part 1-General Thermodynamics[J]. ASME Journal of Turbomachinery, 2002, 124(2): 207-213. DOI:10.1115/1.1415037
(  0) 0) |
| [3] |
Lakshminarayana B. Fluid Dynamics and Heat Transfer of Turbomachinery[M]. New York: Wiley, 1995.
(  0) 0) |
| [4] |
Hartsel J E. Prediction of Effects of Mass-Transfer Cooling on the Blade-Row Efficiency of Turbine Airfoils[R]. AIAA 72-11.
(  0) 0) |
| [5] |
Hartsel J E. An Experimental Investigation of the Effects of Massive Film-Cooling on the Aerodynamics of a Turbine Airfoil[D]. Ohio: The Ohio State University, 1970.
(  0) 0) |
| [6] |
Shapiro A. The Dynamics and Thermodynamics of Compressible Fluid Flow: Volume I[M]. New York: Ronald Press, 1953.
(  0) 0) |
| [7] |
MacArthur C D. Advanced Aero-Engine Turbine Technologies and Their Application to Industrial Gas Turbines[R]. ISABE 99-7151.
(  0) 0) |
| [8] |
Horlock J H, Watson D T, Jones T V. Limitations on Gas Turbine Performance Imposed by Large Turbine Cooling Flows[J]. Journal of Engineering for Gas Turbines & Power, 2000, 123(3): 487-494.
(  0) 0) |
| [9] |
Ito S, Eckert E R G, Goldstein R J. Aerodynamic Loss in a Gas Turbine Stage with Film Cooling[J]. Journal of Engineering for Power Transactions of the ASME, 1980, 102(4): 964-970. DOI:10.1115/1.3230368
(  0) 0) |
| [10] |
Day C R B, Oldfield M L G, Lock G D. Aerodynamics Performance of an Annular Cascade of Film Cooled Nozzle Guide Vanes Under Engine Representative Conditions[J]. Experiments in Fluids, 2000, 29(2): 117-129. DOI:10.1007/s003489900062
(  0) 0) |
| [11] |
Bohn D, Kim T S. Aerodynamic Loss Prediction of Axial Flow Turbine Blade Rows with Coolant Injection[J]. Journal of Power & Energy, 1999, 213(2): 93-101.
(  0) 0) |
| [12] |
Hong Y, Fu C, Cunzhong G, et al. Investigation of Cooling-Air Injection on the Flow Field within a Linear Turbine Cascade[R]. ASME 97-GT-520.
(  0) 0) |
| [13] |
乔渭阳, 曾军, 曾文演, 等. 气膜孔喷气对涡轮气动性能影响的实验研究[J]. 推进技术, 2007, 28(1): 14-19. (QIAO Wei-yang, ZENG Jun, ZENG Wenyan, et al. Experimental Studies for the Aerodynamic Loss in Gas Turbine with Film Cooling[J]. Journal of Propulsion Technology, 2007, 28(1): 14-19.)
(  0) 0) |
| [14] |
曾军, 乔渭阳, 孙大伟, 等. 带尾缘劈缝冷气喷射的涡轮叶栅性能实验及计算[J]. 推进技术, 2008, 29(6): 710-715. (ZENG Jun, QIAO Wei-yang, SUN Da-wei, et al. Numerical Simulation and Experiment for Turbine Cascade with Trailing Edge Coolant Injection[J]. Journal of Propulsion Technology, 2008, 29(6): 710-715.)
(  0) 0) |
| [15] |
孙大伟, 乔渭阳, 曾军, 等. 尾缘喷气方式对涡轮叶栅气动性能的影响[J]. 推进技术, 2007, 28(6): 641-646. (SUN Da-wei, QIAO Wei-yang, ZENG Jun, et al. Aerodynamic Effect of Turbine Blade Trailing Edge Ejection on Turbine Cascade[J]. Journal of Propulsion Technology, 2007, 28(6): 641-646.)
(  0) 0) |
| [16] |
侯伟涛, 乔渭阳, 罗华玲. 压力面气膜冷却数值模拟[J]. 推进技术, 2009, 30(3): 318-322. (HOU Weitao, QIAO Wei-yang, LUO Hua-ling. Numerical Simulation of the Pressure Side Film Cooling[J]. Journal of Propulsion Technology, 2009, 30(3): 318-322.)
(  0) 0) |
| [17] |
侯伟涛. 跨声速涡轮非定常流动机理及设计技术研究[D]. 西安: 西北工业大学, 2011.
(  0) 0) |
| [18] |
Lim C H, Pullan G, Northall J. Estimating the Loss Associated with Film Cooling for a Turbine Stage[J]. Journal of Turbomachinery, 2010, 134(2): 206-210.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

