实现高超声速飞行的两种方式为高超声速吸气类及高超声速滑翔类飞行器。吸气类如高超声速吸气式武器概念(Hypersonic Air-breathing Weapon Concept,HAWC),目的是在现有高超声速技术的基础上,对关键技术进行研发和验证,从而形成对设防目标快速打击的能力,其中的关键技术包括高效的高超声速先进气动布局。滑翔类如战术助推滑翔系统(TBG),目的是发展和演示战术级空射高超声速助推滑翔系统所需关键技术,包括高升阻比构型及热防护系统。由此可见,高性能高超声速吸气类/滑翔类飞行器均离不开满足工程需求的先进气动布局方案。
乘波体作为一种典型的气动外形,非常适合作为高超声速飞行器机体,所有前缘均有附体激波[1],高升阻比的显著特点使之成为国内外的研究热点。Nonweiler在1959年首次提出乘波体的设计概念[2],并实现了平面斜激波流场构造“∧”型高超声速乘波飞行器。Jones等[3]在1968年将直锥轴对称流动应用于乘波体的设计,并提出锥导乘波体的概念。Corda [4]将最小阻力锥作为乘波体设计的基准流场,得到了比传统构型具有更高升阻比特性的乘波体。而Mangin等[5]利用“钝头”轴对称流场设计的乘波体具有很好的容积特性。
1990年,Sobieczky等[6]提出了密切锥导乘波体(Osculating Cone,OC)的设计方法,极大地丰富了流线追踪技术在乘波体设计中的应用。研究表明[7~9],三维超声速流动可以在二阶精度范围内利用当地密切平面内的轴对称流动来近似而不需要考虑横向流动的影响。在密切锥导乘波体设计理论的基础上,Patrick提出了[10]密切“指数律体(Power law body)”基准流场生成乘波体(Osculating Flowfield,OF)的方法,并指出这种方法获得的乘波体在容积率及力矩特性上有所改进。文献[11]发展了基于钝椭圆锥/组合锥流场及流线追踪技术的乘波体设计方法,研究表明,基准流场的性能对乘波体的性能具有决定作用。
利用密切技术,文献[12]开展了基于内锥流场的乘波体设计方法研究,为了提高乘波体压缩量,改善其容积特性。文献[13, 14]提出了密切曲面锥方法(Osculating Curved Cone,OCC),研究结果表明利用密切曲面锥流场生成的OCC乘波体改善了上述问题。
为了进一步拓展提高乘波体压缩量及容积特性的方法和途径,测试多种基准流场下的乘波体特性,在不同约束条件下获得最优乘波体构型,本文在OCC方法[13]的基础上,通过理论分析及数值模拟,对密切凸、凹激波外锥流场生成OCS乘波体的技术可行性及有效性展开了初步分析与研究。
2 曲激波外锥设计及密切方法 2.1 曲激波外锥设计外凸、凹激波外锥流场利用特征线方法(MOC)设计[15],MOC方法具有快速高效的特点。外锥流场的特征线过程涉及内点、固定边界点(固定壁面、固定壁面流动参数)、外部激波点的计算。
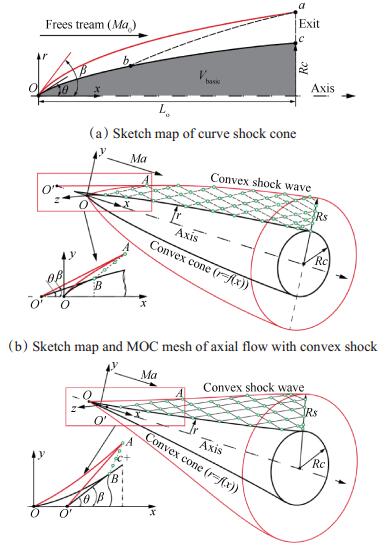
根据特征线特征网格特点,曲激波外锥流场可分为两大部分:弯曲激波锥头流场oab及曲面压缩流场abc,如图 1(a)所示。曲外锥母线obc(r=f(x))的特征线解法在文献[16~18]中有详细的阐述,凸、凹激波外锥的前缘点初值线处理方法及特征网格如图 1(b),(c)所示。编制的设计程序可用于计算:(1)设计状态和非设计状态的无粘轴对称内外锥流场;(2)设计状态和非设计状态的无粘二维流场。设计程序识别的固定边界条件包含:固定壁面、流动参数(p,Ma)沿物理壁面的分布以及两类边界条件的组合。特征线流场及网格的流线追踪技术见参考文献[19]。
|
Fig. 1 Outer cone flow-field with convex/concave shock |
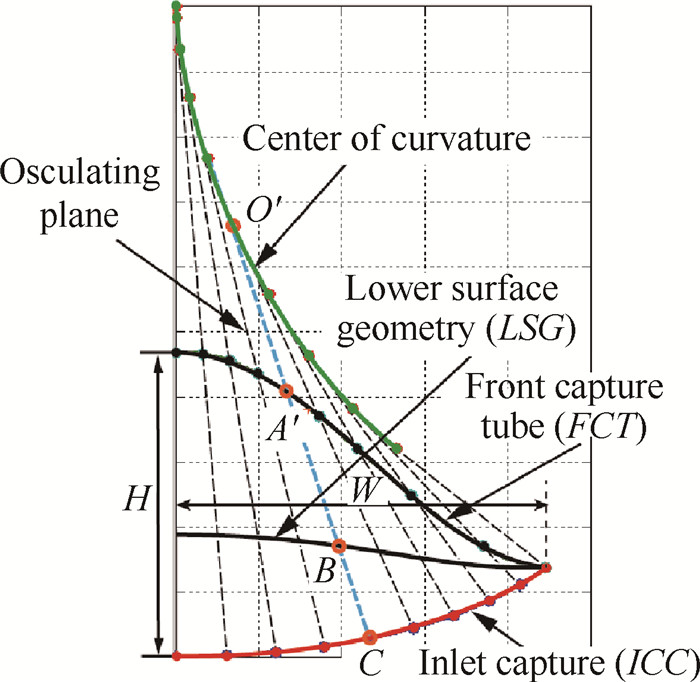
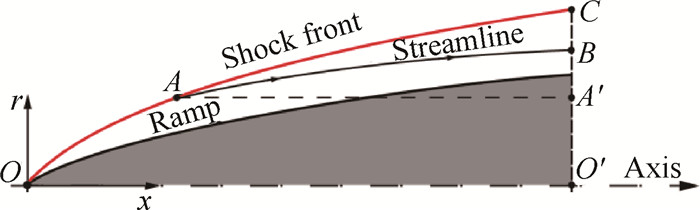
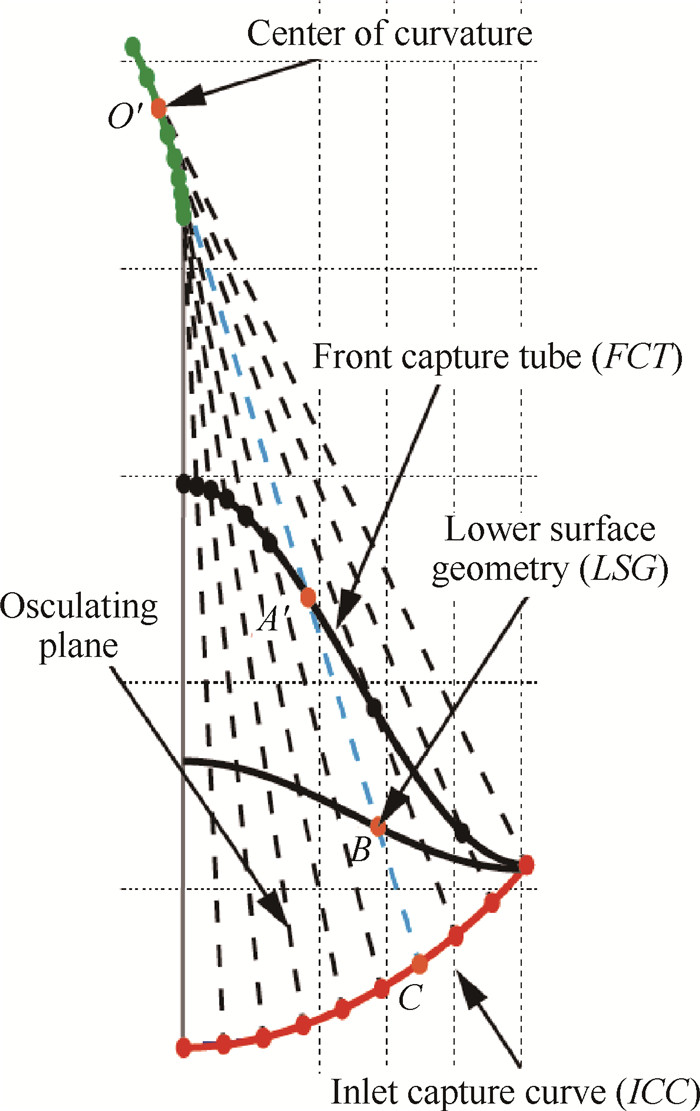
根据定义的ICC曲线,获得ICC曲线的曲率中心位置(O′)及曲率半径(O′C),如图 2所示,ICC曲线上C点及其对应的曲率中心位置,可生成过FCT曲线(交点为A′)的密切平面O′A′BC。根据曲率半径的相对大小,将基准流场进行缩放,确保缩放后基准流场半径(O′C)与密切面的曲率半径一致。沿前缘激波OAC(如图 3所示)与A′同半径的A点向流场下游追踪,并终于B点,由此获得该密切平面内的流线AB,按照同样的处理方法,扫略ICC曲线上所有的特征点,获得一系列密切平面内的流线,利用曲面放样的方法即可获得密切乘波体的下表面。根据乘波体的几何特征,定义乘波体宽度为2W,高度为H,如图 2所示。
|
Fig. 2 Design method of OCS wave-rider at exit plane |
|
Fig. 3 Design method of OCS wave-rider at osculating plane O'A'BC |
从上述方法可看出,当曲率半径O′C为常值且曲率中心交于一点时,获得的乘波体为完全的流线追踪乘波体,性能完全继承基准流场;当曲率半径O′C为变量或者曲率中心不在同一位置时,获得的乘波体为近似的流线追踪乘波体,性能基本能够继承基准流场。
基于流线追踪及密切技术的乘波体的基本性能主要取决于基准内外锥流场的压缩特性。而基于直激波内外锥的乘波体优化空间主要体现在:锥角,乘波体前缘型状(FCT),后缘激波形状参数(ICC)的选择。存在优化空间小,难以针对约束条件获得最优的几何构型。
本文尝试在任意弯曲激波外锥流场中引入密切技术,并针对两种曲率中心分布,利用课题组自主开发的AHL3D软件验证密切弯曲激波乘波体技术的可行性及有效性。软件的无粘流场数值计算采用三维欧拉方程作为基本控制方程,基于结构网格的有限体积法及AUSMPW +对流通流格式,并利用MUSCL插值方法获得具有二阶精度的流场信息。
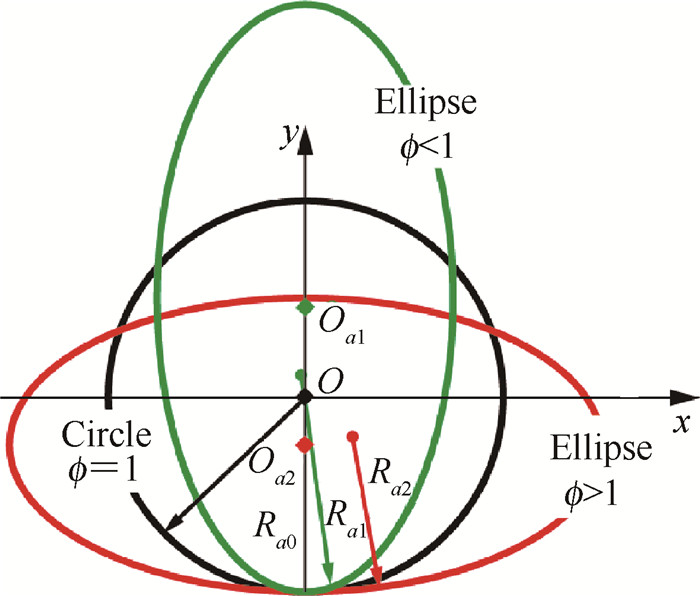
设定超椭圆方程作为本文研究的ICC曲线,定义如式(1)所示,其中n为超椭圆指数,ϕ为椭圆xy轴之比。图 4为超椭圆方程典型n值时的图形样式,结合外锥激波曲线的特点,选择n=2的超椭圆方程定义密切外锥乘波体的ICC曲线(激波形状)是合理的。

|
Fig. 4 Hyper-elliptic curve under different exponent(n) |
| $ \begin{array}{l} x = {k_{{\rm{scale}}}}\phi \cos {\left( \theta \right)^n}\\ y = {k_{{\rm{scale}}}}\cos {\left( \theta \right)^n} \end{array} $ | (1) |
如图 5所示,假定θ = -π/2时,曲线的曲率
|
Fig. 5 Sketch map of ICC curve at different ϕ |
|
Fig. 6 OCS wave-rider at exit plane while ϕ < 1 |
本节基于凸激波外锥流场,设计了容积率及宽度相同的两种激波形状(ϕ > 1及ϕ < 1)的乘波体构型。针对这两种构型,开展了密切技术在凸激波外锥流场中应用的可行性验证。
凸激波外锥无量纲流场固定壁面采用Von Karman曲线[20],由公式(2),(3)确定,其中L0/Rc = 5。
| $ \omega = {\rm{arc}}\cos \left( {1 - \frac{{2x}}{{{L_0}}}} \right) $ | (2) |
| $ r = f\left( x \right) = \frac{{{R_{\rm{c}}}}}{{\sqrt {\rm{ \mathit{ π} }} }}\sqrt {\omega - \frac{{\sin \left( {2\omega } \right)}}{2}} $ | (3) |
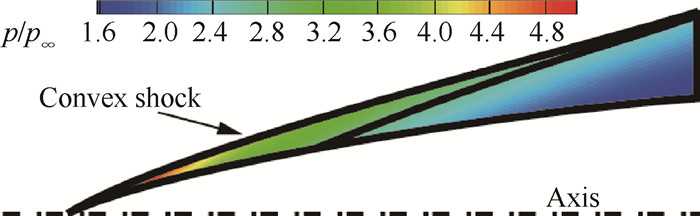
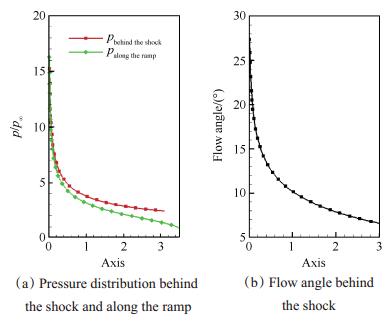
基准流场的设计马赫数Ma∞ = 6,来流压力p∞ = 2511.18Pa,静温T∞ = 221.649K,对应25km标准大气。利用2.1节的外锥流场计算方法,得到的凸激波外锥流场如图 7所示,图 8(a)为该外锥流场凸激波面、壁面的压力分布,图 8(b)为凸激波面上流动角沿轴向的变化趋势。可以看出凸激波面上压力均高于同轴向位置的物面,且波后气流角在锥头位置变化剧烈。
|
Fig. 7 Pressure contour of convex shock flow-field |
|
Fig. 8 Information of convex shock flow-field |
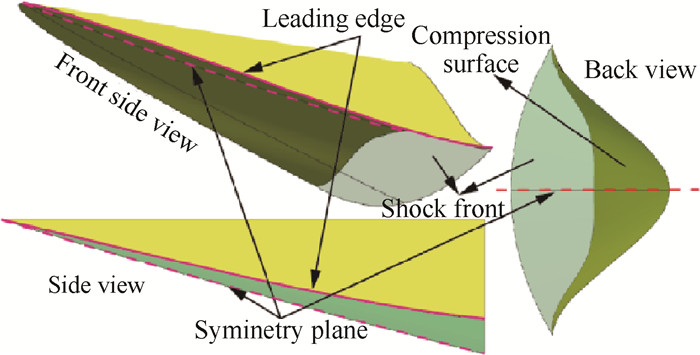
ϕ < 1的密切凸激波外锥乘波体设计参数的选择:ICC曲线的长短轴之比ϕ =0.5,θ = 0.25π,乘波体宽140mm,高度H=80mm。FCT曲线为首尾两坐标点及斜率控制的三次曲线。生成的乘波体(以下称为Config A)的三维视图如图 9所示。
|
Fig. 9 Three dimensional view of Config A |
图 10(a),10(b)给出了密切面前缘位置的初始压缩角及部分特征密切面内流线上压力沿流向的变化趋势。从图中可以看出:流线上的压力沿流向单调递减,即dp/dx < 0;靠近对称面的流线(Z越小)上的初始压缩角越大,起始压力越高;在同一x位置,越靠近对称面压力越低,即dp/dz > 0。
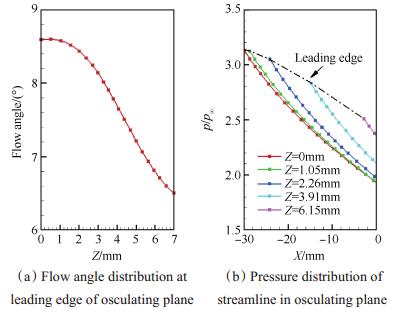
|
Fig. 10 Flow parameter distribution of Config A based on MOC method |
图 11(a)~(d)给出了Config A的理论解(MOC)与数值解(CFD)的流场信息。从图 11(a)的流场压力云图可见,数值解与理论设计的压力分布,激波面形状均符合较好,达到了乘波效果。图 11(b)中的对称面及尾部横向(LSG)压力分布也可以看出,数值解与理论解几乎完全重合。
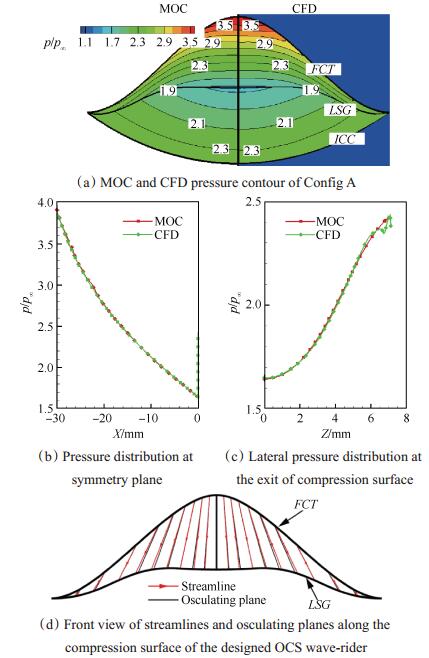
|
Fig. 11 Flow-field information of Config A derived from theoretical and numerical method |
值得注意,乘波压缩面上的实际流线走向与密切平面并不完全重合,如图 11(c)所示:密切面在靠近对称面时,流线有一定程度的向内偏转;密切面远离对称面时,流线有向外偏转的趋势。这是由密切技术的理论近似引起的。文献[7]给出了改善密切锥乘波体各密切面横向压力梯度的设计方法,结果表明在Ma>3的情况下,密切面之间的横向压力梯度对基于密切技术设计乘波体影响不大。
3.2 ICC曲线ϕ > 1的密切乘波体ϕ > 1的密切凸激波外锥乘波体设计参数的选择:ICC曲线的长短轴之比ϕ =2,θ = 0.25π,乘波体宽140mm,高度H=80mm。FCT曲线为首尾两坐标点及斜率控制的三次曲线。生成的乘波体((以下称为Config B))的三维视图如图 12所示。
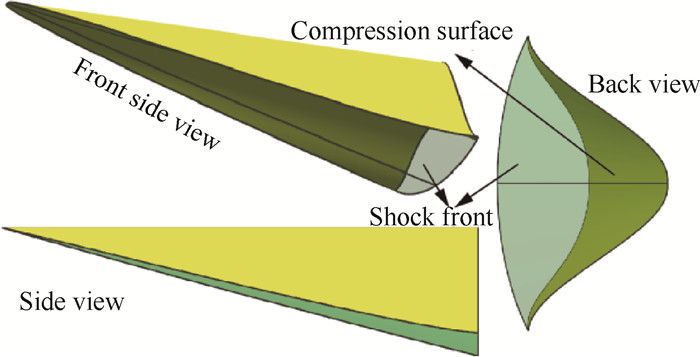
|
Fig. 12 Three dimensional view of Config B |
图 13(a)~(d)给出了Config B理论与数值解得到的流场信息。从图 13(a)可见,流场的压力分布,激波面的形状均很好地验证了该构型的乘波特性。与Config A相比,虽然数值解与理论解得到的对称面压力分布几乎完全重合,但两种方法下的尾部横向(LSG)压力在Z=2~6mm存在最大4.0%的偏差,且MOC理论解比数值解偏低。
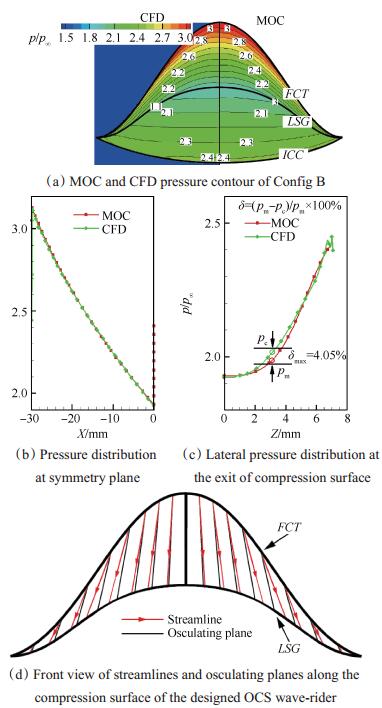
|
Fig. 13 Flow-field information of Config B derived from theoretical and numerical method |
流线与密切平面的相对位置和Config A不同,如图 13(b)所示,流线与密切平面相比存在向外偏转,且密切面远离对称面一侧流线偏转更为明显。
3.3 小结表 1给出了基于凸激波外锥流场设计的密切乘波体(Config A & B)的升阻特性。从表 1可看出,定义偏差等于100%×(数值解-理论解)/理论解,则乘波体升力,阻力及升阻比的数值解与理论解偏差能够控制在5%以内,且乘波体ICC曲线ϕ > 1时,这种偏差明显大于ICC曲线ϕ < 1的乘波体构型。
|
|
Table 1 Lift and drag characteristic of convex OCS waverider |
综合上述结论可以看出:在超椭圆ICC曲线约束下(ϕ > 1及ϕ < 1),基于凸激波外锥流场的密切乘波体尽管压缩面上实际流线与设计的密切平面存在偏差,但压缩面,出口(LSG与ICC之间的封闭区域),对称面及尾部横向(LSG)的压力分布、升力、阻力及升阻比的数值解与理论解均符合较好。说明利用密切及流线追踪技术在凸激波外锥流场内生成乘波体的设计方法是合理可行的。
4 密切技术在凹激波外锥流场中的应用凹激波外锥无量纲流场固定条件以壁面马赫数线性分布(式(4))作为约束条件为例,其中L0/Rc = 5。
| $ Ma = kx + M{a_\infty } $ | (4) |
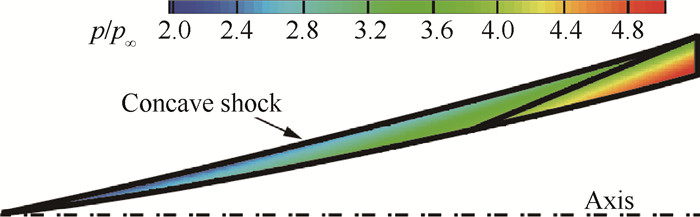
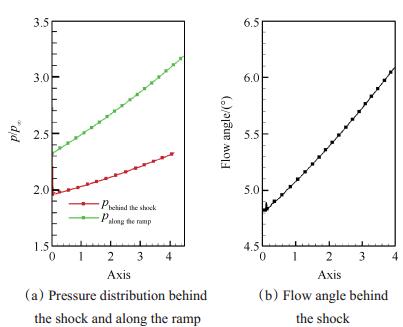
按照第2节的来流条件,计算得到的凹激波外锥流场如图 14所示,图 15(a)给出了该外锥流场凹激波面、壁面的压力分布,图 15(b)为凹激波面流动角沿轴向的分布。可以看出与凸激波外锥流场不同,凹激波面压力均低于同位置的物面压力,且波后气流角在轴向有近似线性增加的趋势。
|
Fig. 14 Pressure contour of concave shock flow-field |
|
Fig. 15 Information of concave shock flow-field |
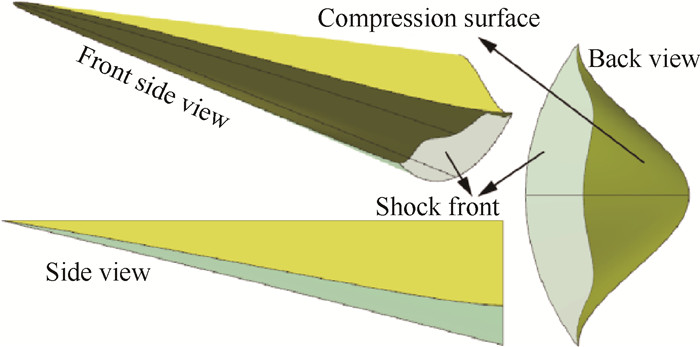
ϕ < 1的密切凹激波外锥乘波体设计参数的选择:ICC曲线的长短轴之比ϕ =0.5,θ = 0.25π,乘波体宽140mm,高度H=80mm。FCT曲线为首尾两坐标点及斜率控制的三次曲线。生成的乘波体(Config C)的三维视图如图 16所示。
|
Fig. 16 Three dimensional view of Config C |
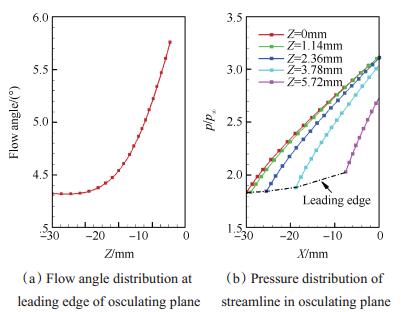
图 17(a),(b)给出了Config C密切面前缘位置的初始压缩角,及部分特征密切面内流线上压力沿流向的变化趋势。与凸激波外锥流场相反:流线上的压力沿流向单调递增,即dp/dx > 0;前缘线上越靠近对称面的起始压力越低;在同一x位置,越靠近对称面压力越高,即dp/dz < 0。
|
Fig. 17 Flow parameter distribution of Config C based on MOC method |
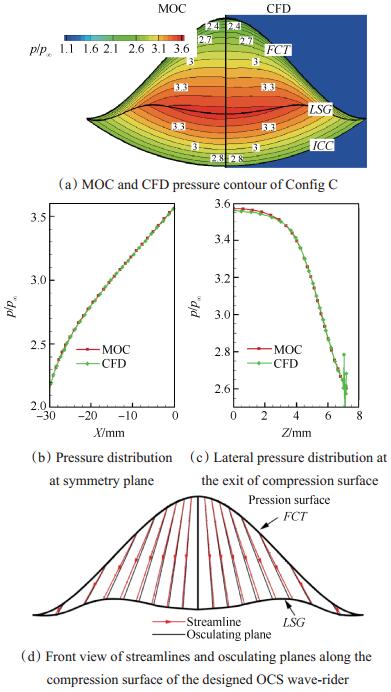
如图 18(a)压力云图所示,Config C乘波体理论与数值解压力云图在乘波面及出口均吻合较好,激波面位置、形状也与设计基本一致,达到了很好的乘波效果。这点在图 18(b)所示的对称面及尾部横向(LSG)压力分布也可以看出。
|
Fig. 18 Flow-field information of Config C derived from theoretical and numerical method |
从图 18(c)的流线与密切平面的相对位置示意图可以看出,实际流线与密切平面相比仍有略微向外偏转。但这样的流线偏转并未对Config C乘波体的流场参数及激波面形状产生显著影响。
4.2 ICC曲线ϕ > 1的密切乘波体ϕ > 1的密切凹激波外锥乘波体设计参数的选择:ICC曲线的长短轴之比ϕ = 2,θ = 0.25π,乘波体宽140mm,高度H=80mm。FCT曲线为首尾两坐标点及斜率控制的三次曲线。生成的乘波体(Config D)的三维视图如图 19所示。

|
Fig. 19 Three dimensional view of Config D |
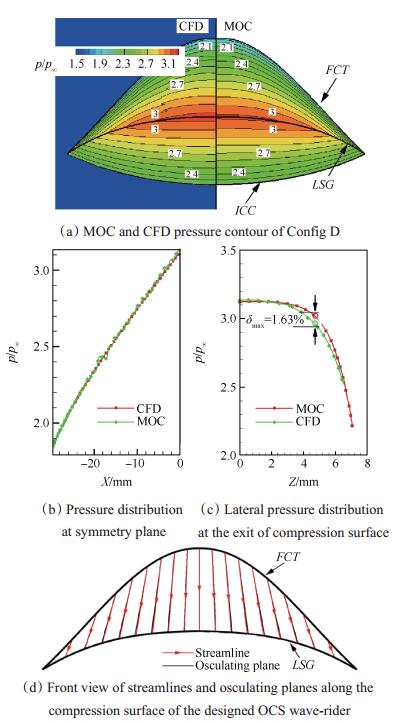
图 20(a)~(d)给出了理论与数值解得到的流场信息。从图 20(a)给出的流场压力云图来看,数值解得到的乘波压缩面及出口压力分布,激波面形状均与理论设计相符,具备较好的乘波效果。理论与数值解得到的对称面压力完全重合,如图 20(b)所示。图 20(c)所示的乘波体尾部的横向压力在Z=3~6mm,理论解略低于数值解,且最大误差约为1.6%,但总体分布基本一致。
|
Fig. 20 Flow-field information of Config D derived from theoretical and numerical method |
从与其他三种构型不同,图 20(d)示意的流线走向与密切平面相比有很小的向内偏转趋势,但几乎完全重合。
4.3 小结表 2给出了基于凹激波外锥流场设计的密切乘波体(Config C & D)的升阻特性。从表 1可看出,乘波体升力、阻力及升阻比的数值解与MOC理论解偏差能够控制在1%以内,且乘波体ICC曲线ϕ > 1时,这种偏差大于ICC曲线ϕ < 1的乘波体构型。综合四种构型的流场及升阻特性可知,Config A具有更高的升阻比,因此是一种相对较优的方案。
|
|
Table 2 Lift and drag characteristic of concave OCS waverider |
综合上所述,尽管乘波体压缩面上实际流线并未与设计的密切平面完全匹配,但在压缩面,出口(LSG与ICC之间的封闭区域),对称面及尾部横向位置的压力分布,理论设计与数值模拟的结果均具有较好的一致性,说明利用密切及流线追踪技术在凹激波外锥流场内生成乘波体的设计方法是合理可行的。
5 结论本文对密切技术在基于弯曲激波外锥流场的乘波体设计中的应用及有效性开展了研究工作,具体针对n=2时,ϕ < 1及ϕ > 1两种超椭圆ICC波形,完成了密切技术在凸/凹激波外锥流场中应用的可行性验证。结果表明:
(1)在本文预置的约束条件下,乘波体整个流场的压力分布、激波面形状均与设计吻合较好,说明利用密切技术在弯曲激波外锥流场中获得乘波体的方法是可行的。
(2)四种构型对称面内压力的理论与数值解均符合非常好,ϕ = 0.5时,乘波体尾部的横向压力分布也基本一致,ϕ = 2时,Config B乘波体尾部的横向压力在理论与数值解的偏差约4%,而Config D乘波体尾部的横向压力偏差在1.6%左右。
(3)四种构型的乘波体乘波压缩面上的实际流线与密切平面的相对位置关系各有特点:Config A靠近对称面附近的流线与密切平面相比向内偏转,远离对称面的流线向外偏转,Config B & C流线与密切平面相比向外偏转,Config D流线向内偏转。
(4)相同容积率及宽度的约束条件下,基于凸激波外锥流场的乘波体具有更高的升阻比,而基于椭圆轴之比ϕ < 1的激波型线的密切乘波体的理论解与无粘数值解的偏差也更小。
对上述四种构型的研究可以看出,在横向压力梯度dp/dz > 0或者dp/dz < 0的约束条件下,流线与密切平面的相对位置均出现了向内、向外偏转现象,这说明横向压力梯度并非流线与密切平面出现偏差的唯一原因,还需要进一步开展研究。
| [1] |
Lunan D. Wave-Rider, a Revised Chronology[R]. AIAA 2015-3529.
(  0) 0) |
| [2] |
Nonweiler T R F. Aerodynamic Problems of Manned Space Vehicles[J]. Journal of the Royal Aeronautical Society, 1959, 63: 521-528. DOI:10.1017/S0368393100071662
(  0) 0) |
| [3] |
Jones J G, Moore K C, Pike J, et al. A Method for De-signing Lifting Configurations for High Supersonic Speeds, Using Axisymmetric Flow Fields[J]. Inge-nieur-Archive, 1968, 37: 56-72. DOI:10.1007/BF00532683
(  0) 0) |
| [4] |
Corda S. Viscous Optimized Hypersonic Wave-Rider Designed from Flows over Cones and Minimum Drag Bodies[D]. College Park: University of Maryland, 1988. https://www.researchgate.net/publication/33877062_Viscous_optimized_hypersonic_waveriders_designed_from_flows_over_cones_and_minimum_drag_bodies
(  0) 0) |
| [5] |
Mangin B, Benay R, Chanetz B, et al. Optimization of Viscous Wave-Riders Derived from Axisymmetric Pow-er-Law Blunt Body Flows[J]. Journal of Spacecraft and Rockets, 2006, 43(5): 990-998. DOI:10.2514/1.20079
(  0) 0) |
| [6] |
Sobiezczky H, Dougherty F C, Jones K. Hypersonic Wave-Rider Design from Given Shock Waves[C]. Maryland: First International Wave-Rider Symposium, 1990. http://www.researchgate.net/publication/23840521_Hypersonic_waverider_design_from_given_shock_waves
(  0) 0) |
| [7] |
Chauffour M L, Lewis M J. Corrected Wave-Rider De-sign for Inlet Applications[R]. AIAA 2004-0511. http://arc.aiaa.org/doi/abs/10.2514/6.2004-3405
(  0) 0) |
| [8] |
Chauffour M L. Shock-Based Wave-Rider Design with Pressure Corrections, and Computational Simulations[D]. College Park: University of Maryland, 2004. http://arc.aiaa.org/doi/abs/10.2514/1.13027
(  0) 0) |
| [9] |
Lewis M J, Chauffour M L. Shock-Based Wave-Rider Designed with Pressure Gradient Corrections and Com-putational Simulations[J]. Journal of Aircraft, 2005, 42(5): 1350-1352. DOI:10.2514/1.13027
(  0) 0) |
| [10] |
Patrick E Rodi. The Osculating Flow-Field Method of Wave-Rider Geometry[R]. AIAA 2005-0511. http://arc.aiaa.org/doi/abs/10.2514/6.2005-511
(  0) 0) |
| [11] |
Liu C Z, Bai P, Chen B Y, et al. Rapid Design and Op-timization of Wave-Rider from 3D Flow[R]. AIAA 2016-3288.
(  0) 0) |
| [12] |
HE Xu-zhao, NI Hong-li. Osculating Inward Turning Cone Design Methods and Performance Analysis[J]. ACTA SINICA, 2011, 43(5): 879-985.
(  0) 0) |
| [13] |
贺旭照, 倪鸿礼. 密切曲面锥乘波体-设计方法及性能分析[J]. 力学学报, 2011, 43(6): 1077-1082. DOI:10.6052/0459-1879-2011-6-lxxb2010-502 (  0) 0) |
| [14] |
He X Z, Le J L, Wu Y C. Design of a Curved Cone De-rived Wave-Rider Fore-Body[R]. AIAA 2009-7423. http://arc.aiaa.org/doi/abs/10.2514/6.2009-7423
(  0) 0) |
| [15] |
Maurice J Zucrow, Joe D Hoffman. Gas Dynamics Volume(Ⅱ)[M]. American: Library of Congress Catalog-ing, 1976.
(  0) 0) |
| [16] |
卫锋, 贺旭照, 贺元元, 等. 三维内转式进气道双激波基准流场的设计方法[J]. 推进技术, 2015, 36(3): 358-364. (WEI Feng, HE Xu-zhao, HE Yuanyuan, et al. Design Method of Dual-Shock Wave Basic Flow-Field for Inward Turning Inlet[J]. Journal of Pro-pulsion Technology, 2015, 36(3): 358-364.)
(  0) 0) |
| [17] |
卫锋, 贺旭照, 陈军, 等. 微修形异型转圆内转式进气道的设计与试验研究[J]. 推进技术, 2017, 38(6): 1218-1225. (WEI Feng, HE Xu-zhao, CHEN Jun, et al. Design and Experiment Study of Minimized Shape Transformation Inward Turning Inlet with Abnor-mity Entrance to Circle Exit[J]. Journal of Propulsion Technology, 2017, 38(6): 1218-1225.)
(  0) 0) |
| [18] |
周正, 贺旭照, 卫锋, 等. 密切曲内锥乘波前体进气道低马赫数性能试验研究[J]. 推进技术, 2016, 37(8): 1456-1460. (ZHOU Zheng, HE Xu-zhao, WEI Feng, et al. Experimental Studies of Osculating In-ward Turning Cone Wave-Rider Fore-Body Inlet(OIC-WI)at Low Mach Number Conditions[J]. Journal of Propulsion Technology, 2016, 37(8): 1456-1460.)
(  0) 0) |
| [19] |
卫锋. 基于特征线理论的流线追踪内转向进气道设计方法研究[D]. 长沙: 国防科学技术大学, 2012: 65-70. http://cdmd.cnki.com.cn/Article/CDMD-90002-1014047904.htm
(  0) 0) |
| [20] |
Nielsen J N. Missile Aerodynamics[M]. New York: Mc-Graw-Hill Book Co. Inc., 1960, 280-293.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


