疲劳破坏是航空发动机轮盘常见的失效形式,多发生在榫槽、喉道、螺栓孔等结构不连续处[1, 2],或者盘心等大危险体积处[3],因而航空发动机轮盘的疲劳破坏多存在缺口效应及体积效应。疲劳缺口效应和体积效应很早就为疲劳试验所发现。文献[4~6]在研究缺口疲劳强度极限时发现缺口疲劳缺口系数Kf随缺口半径而变化。Buch[7]在钢棒的疲劳试验中发现疲劳强度极限随着光棒直径的增加而单调下降,且下降趋势逐渐变缓,疲劳强度极限在所研究的尺寸范围内最大下降了20%。目前,常见的疲劳试验结果多由标准光滑试棒得到,因此应用其进行轮盘等具有缺口的大型构件的疲劳寿命预估时需要考虑缺口及危险体积的影响。
传统的名义应力法和局部应力应变法均属于典型的“点方法”寿命模型,工程应用较广泛,但其仅以最危险点处的应力/应变参量来代表构件危险区域的损伤,在缺口应力集中较严重或者危险体积较大时疲劳寿命预估精度明显降低。临界距离法近年来颇受学者们的青睐,该理论主要分为“点法”[4]、“线法”[5]、“面法”[8]以及“体法”[9]等,其核心参数为临界距离。然而从目前的研究结果来看,临界距离的选取各有千秋,主要原因在于临界距离的影响因素较多,不仅与应力集中、应力比有关,同时也随着疲劳寿命的变化而变化[10]。Shirani等[11]对由EN-GJS-400-18-LT球墨铸铁材料制成的、直径分别为21mm和50mm的试验件进行了高周疲劳试验,验证了疲劳寿命服从Weibull分布假设,且利用基于最弱环理论的Weibull体方法建立了应力和失效概率的关系。可利用此Weibull体方法分析具有不同应力梯度和危险体积的双缺口构件的失效概率[12, 13],并在Weibull体方法的基础上发展了A*模型和V*模型,以分别考虑大应力区的危险表面积和危险体积对失效概率的影响[14]。但上述方法均仅能求得特定寿命下构件的失效概率,而无法求取其他失效概率下的疲劳寿命。国内的研究人员也对缺口效应和体积效应进行了较为深入的研究,并取得了一定的研究成果。应力场强法[15]通过对缺口破坏区内的应力加权得到当量应力,以此作为疲劳破坏的判据参数,其本质上是临界距离法中“体法”的一种。陆山等提出的应力体方法[16]和应变体方法[3]作为一种有效考虑体积效应的方法,通过单元细化思想和Weibull最弱环理论得到危险部位的概率寿命。但其假设疲劳寿命服从对数正态分布假设,在预估高可靠度概率寿命时存在理论缺陷。刘香等[17]通过引入应力梯度影响因子和尺寸影响因子考虑应力梯度和体积效应对疲劳寿命的影响。但其应力梯度影响因子仅从弹性结果得到,在弹塑性条件下是否适用还未知。
本文基于“等概率寿命,等损伤”的核心思想提出了可以有效考虑缺口效应和体积效应的等效体积概率寿命体方法。该方法采用考虑平均应力效应的修正Walker模型,以及疲劳寿命服从Weibull分布的假设,将轮盘危险区域内任意应力、应力比下的小子块根据损伤相等的原则转化为最危险点处的等效体积并累加,结合Weibull最弱环理论即可求得轮盘任意可靠度下的概率寿命。
2 修正Walker模型平均应力(或应力比)对疲劳寿命有明显的影响[18, 19]。材料手册中大部分材料仅有R=0.05(或R=0.1)和R=-1时的试验数据,仅少数材料还有R=0.5时的疲劳试验结果,但在实际工程中大部分构件危险部位的应力比都不能恰好处于材料手册中试验数据所对应的应力比[20]。很多学者已提出了考虑平均应力影响的疲劳寿命模型。从最终结果来看,Goodman模型预估结果偏保守,而Morrow模型则偏危险,SWT模型因未考虑材料因素精度一般[18]。Walker模型则未考虑平均应力效应随最大应力而变化的现象,从而对部分材料寿命预估精度明显降低。修正Walker模型在Walker模型的基础上考虑了最大应力对平均应力效应的影响,表达式为
| ${\sigma _{{\rm{mw}}}} = {\sigma _{{\rm{max}}}}{\left( {\frac{{1 - R}}{2}} \right)^{m + n{\rm{lg}}{\sigma _{{\rm{max}}}}}}$ | (1) |
式中σmax为危险部位最大应力,R为对应的应力比,m和n为与试验数据相关的拟合参数,σmw为考虑平均应力效应的修正Walker等效应力。因此,修正Walker模型的应力-寿命的关系可由式(2)表示,其中b,k1,k2和k3均可由不同应力比下的试验数据通过多元线性拟合得到。对比式(1)和式(2)可知m=k2/k1,n=k3/k1。可以看出,修正Walker模型将不同应力比下的试验数据用统一的形式进行描述,同时考虑了材料和最大应力对平均应力效应的影响。
| $\begin{array}{*{20}{l}} {{\rm{lg}}{N_{\rm{f}}} = b + {k_1}{\rm{lg}}{\sigma _{{\rm{max}}}} + {k_2}{\rm{lg}}\left( {\frac{{1 - R}}{2}} \right) + }\\ {{k_3}{\rm{lg}}{\sigma _{{\rm{max}}}}{\rm{lg}}\left( {\frac{{1 - R}}{2}} \right)} \end{array}$ | (2) |
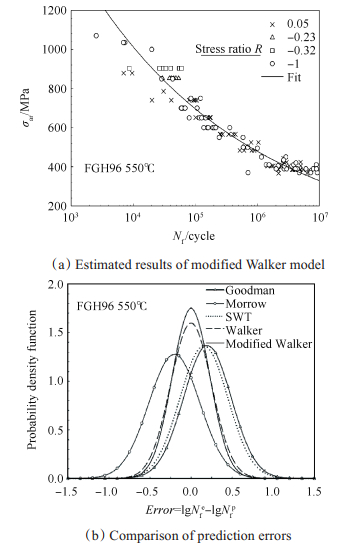
由涡轮盘常用的粉末高温合金FGH96材料在550℃时的试验数据[20]所得到的修正Walker模型结果以及与其它常用平均应力修正模型的误差分析对比如图 1所示。从图 1(a)可以看出,各应力比下的试验数据均匀分布在修正Walker模型拟合曲线两侧,且集中性很好;结合图 1(b)的误差对比,可以看出对于550℃的FGH96材料,修正Walker模型具有较高的疲劳寿命预估精度,Walker模型的精度稍差,SWT模型和Goodman模型的结果偏保守,而Morrow模型的结果偏危险。
|
Fig. 1 Estimated results of modified Walker model for FGH96 superalloy at 550℃ |
指定应力水平下的疲劳寿命是一个随机量,通常可以用对数正态分布或者Weibull分布描述[21]。对数正态分布假设应用于计算中间概率寿命时具有一定的精度,但其在计算大可靠度(亦即小失效概率)情形时存在明显的理论缺陷。这是因为对于对数正态分布,只有当对数安全寿命趋于负无穷大时,亦即疲劳寿命为零时,可靠度才可以等于100%,显然这不符合实际情况[22]。三参数Weibull分布中引入了最小寿命N0作为100%可靠度时对应的疲劳寿命,弥补了对数正态分布的理论缺陷。采用Weibull分布理论,在极高可靠度范围(99.99%~100%)内所给出的安全寿命或最小安全寿命是比较符合实际情况的[22],其概率密度函数可表示为
| $\begin{array}{*{20}{c}} {f\left( N \right) = \frac{b}{{{N_{\rm{a}}} - {N_0}}}{{\left[ {\frac{{N - {N_0}}}{{{N_{\rm{a}}} - {N_0}}}} \right]}^{b - 1}}{\rm{exp}}\left\{ { - {{\left[ {\frac{{N - {N_0}}}{{{N_{\rm{a}}} - {N_0}}}} \right]}^b}} \right\}}\\ {({N_0} < N < \infty )} \end{array}$ | (3) |
式中N0为最小寿命,Na为特征寿命,b为形状参数。
本文假设在不同载荷水平下,疲劳寿命均服从三参数Weibull分布。为了进一步研究在不同应力水平下疲劳寿命分散性的规律,对550℃时FGH96材料在各组应力水平下的疲劳试验数据均分别进行Weibull分布参数估计。工程中一般假设相同材料在不同载荷下疲劳寿命分布相似[21, 23],因此可认为FGH96材料Weibull分布的形状参数b为定值。采用试验数据的子样平均值、子样中值和子样标准差分别作为各Weibull分布对应值的点估计量[22],寻找使得所有载荷水平下Weibull分布的均值、中值以及标准差与对应的点估计量的误差绝对值之和最小(如式(4)所示)时的b,该b即为FGH96材料在550℃时的形状参数,此时所有应力水平下拟合所得Weibull分布均与试验结果的真实分布最为接近。进而根据形状参数b可以确定每组试验结果的Weibull分布所对应的N0, i和Na, i。
| $ \begin{array}{c} \min \sum\limits_{i = 1}^n {\left\{ {\left| {\frac{{{N_{0,i}} + \left( {{N_{a,i}} - {N_{0,i}}} \right)\mathit{\Gamma }\left( {1 + {}^{1}\!\!\diagup\!\!{}_{b}\;} \right)}}{{{{\overline X }_i}}} - 1} \right|} \right.} + \\ \left| {2\exp \left\{ { - {{\left[ {\frac{{{N_{50{\rm{\% ,}}i}} - {N_{0,i}}}}{{{N_{a,i}} - {N_{0,i}}}}} \right]}^b}} \right\} - 1} \right| + \\ \left. {\left| {\frac{{\left( {{N_{a,i}} - {N_{0,i}}} \right){{\left[ {\mathit{\Gamma }\left( {1 + {}^{2}\!\!\diagup\!\!{}_{b}\;} \right) - {\mathit{\Gamma }^2}\left( {1 + {}^{1}\!\!\diagup\!\!{}_{b}\;} \right)} \right]}^{1/2}}}}{{{\rm{std}}\left( {{X_i}} \right)}} - 1} \right|} \right\} \end{array} $ | (4) |
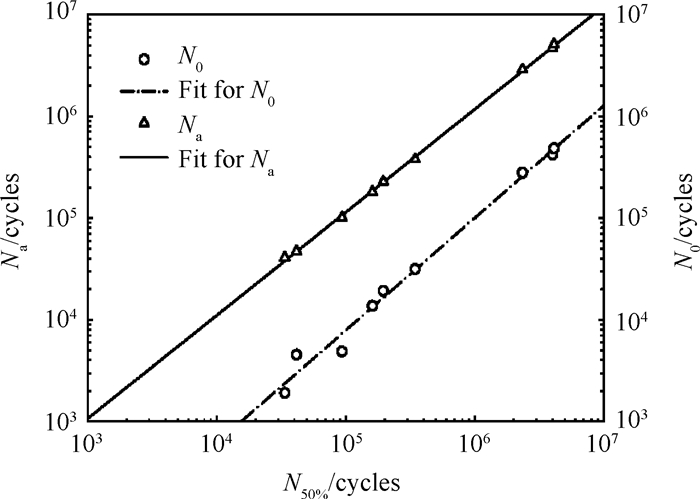
研究发现,不同载荷水平下Weibull分布的最小寿命N0, i和特征寿命Na, i均与对应的中位寿命N50%, i在双对数坐标系下呈线性关系,如图 2所示。
|
Fig. 2 Plot of minimum parameter N0 and scale parameter Na of Weibull distributions versus median life N50% for different stress levels of FGH96 superalloy at 550℃ |
可以看出,由FGH96材料各应力水平下试验数据估计所得Weibull分布的最小寿命和特征寿命基本都在其与中位寿命的线性回归线附近,且不难发现,两条回归线的斜率基本都为1。因此,可以得到中位寿命与最小寿命、特征寿命的关系如下
| ${\rm{lg}}{N_0} = {k_0} \cdot {\rm{lg}}{N_{50{\rm{\% }}}} + {d_0}$ | (5) |
| ${\rm{lg}}{N_{\rm{a}}} = {k_{\rm{a}}} \cdot {\rm{lg}}{N_{50{\rm{\% }}}} + {d_{\rm{a}}}$ | (6) |
式中k0和d0表示最小寿命N0与中位寿命N50%回归线的斜率和截距;ka和da则表示特征寿命Na与中位寿命N50%在双对数坐标系下回归线的斜率和截距。由于k0和ka均十分接近1,从而式(5)和式(6)可表示为
| ${N_0} = {\beta _0}{N_{50{\rm{\% }}}}$ | (7) |
| ${N_{\rm{a}}} = {\beta _{\rm{a}}}{N_{50{\rm{\% }}}}$ | (8) |
式中β0=10d0,βa=10da。
从式(7)和式(8)可以看出,当由不同载荷水平下的疲劳试验数据分别确定了最小寿命和特征寿命与中位寿命的关系后,便可得到任意载荷下疲劳寿命的Weibull分布。
4 等效体积概率寿命分析方法等效体积转换的核心思想是:当两个构件的概率寿命相同时,则认为这两个构件内所包含的损伤相等,危险体积等效。基于此思想,结合修正Walker模型、Weibull分布假设和最弱环理论[24],可将任意应力、应力比下的危险体积转换为特定应力、应力比下的等效体积。该特定应力、应力比分别被称为目标应力σt和目标应力比Rt,由σt和Rt计算所得疲劳寿命为目标寿命Nf, t。对于应力集中现象不十分严重的构件,可将最危险点附近不同应力下的危险体积转换为最危险点处应力、应力比下的等效体积。当应力梯度很大时(如尖锐的三角形缺口等情形),也可将95%的峰值应力作为目标应力。
尽管缺口附近多存在应力梯度,但总可以将其危险区域内的单元进行细化而得到内部应力比较均匀的小子块。对于任意一个小子块,可根据其应力、应力比结合式(2)中的修正Walker应力寿命模型求出危险体积等于参考体积时的中位寿命
| ${N_{{\rm{f}}, i}}\left( {{V_0}, {p_{{\rm{f}} - 50{\rm{\% }}}}} \right) = f\left( {{\sigma _i}, {R_i}} \right)$ | (9) |
式中V0为参考体积,pf-50%表示失效概率为50%,σi,Ri为任意小子块的应力、应力比。需要说明的是,参考体积V0是名义载荷与目标应力、目标应力比相同的标准应力疲劳试验件(多为光滑漏斗棒)的等效体积。进而根据计算所得中位寿命结合式(3)、式(7)和式(8)所得到的疲劳寿命的Weibull分布可求出各小子块疲劳寿命为目标寿命、危险体积为参考体积时的失效概率
| ${p_{\rm{f}}}\left( {{N_{{\rm{f}}, {\rm{t}}}}, {V_0}} \right) = f\left( {{N_{{\rm{f}}, i}}\left( {{V_0}, {p_{{\rm{f}} - 50{\rm{\% }}}}} \right), {\beta _0}, {\beta _{\rm{a}}}, b} \right)$ | (10) |
然后通过Weibull最弱环理论可知,该小子块在疲劳寿命为目标寿命时的失效概率
| ${{p}_{\text{f}}}\left( {{N}_{\text{f},\text{t}}},{{V}_{i}} \right)=1-{{(1-{{p}_{\text{f}}}({{N}_{\text{f},\text{t}}},{{V}_{0}}))}^{{}^{{{V}_{i}}}\!\!\diagup\!\!{}_{{{V}_{0}}}\;}} $ | (11) |
根据等效体积的基本思想,目标应力、应力比下危险体积为Veq, i时与小子块概率寿命相等,该Veq, i即为小子块对应的等效体积。根据疲劳寿命的Weibull分布、Weibull最弱环理论和式(11)可得,等效体积的计算公式为
| $ \begin{array}{*{20}{l}} {{V_{{\rm{eq}}, i}} = \frac{{{V_i}}}{{{\rm{ln}}2}}{{\left[ {\frac{{{N_{{\rm{f}}, t}} - {N_0}\left( {{N_{{\rm{f}}, i}}} \right)}}{{{N_{\rm{a}}}\left( {{N_{{\rm{f}}, i}}} \right) - {N_0}\left( {{N_{{\rm{f}}, i}}} \right)}}} \right]}^b} = }\\ {\;\;\;\;\;\;\;\;\;\frac{{{V_i}}}{{{\rm{ln}}2}}{{\left[ {\frac{{{N_{{\rm{f}}, {\rm{t}}}}/{N_{{\rm{f}}, i}} - {\beta _0}}}{{{\beta _a} - {\beta _0}}}} \right]}^b}} \end{array} $ | (12) |
从式(12)可以看出,当子单元的应力、应力比及危险体积确定后,其在目标应力和应力比下的等效体积也随之确定。将危险区域内所有小子块的等效体积累加,利用Weibull最弱环理论即可求得该构件在任意失效概率下的疲劳寿命,如式(13)所示,其中pf为失效概率,Nf为概率寿命,Veq为等效体积之和。
| $ \begin{array}{*{20}{l}} {{N_{\rm{f}}}\left( {{p_{\rm{f}}}} \right) = {N_{{\rm{f}}, {\rm{t}}}}\left[ {{\beta _0} + \left( {{\beta _{\rm{a}}} - {\beta _0}} \right){{\left( {{\rm{ln}}\frac{1}{{1 - {p_{\rm{f}}}}}} \right)}^{\frac{1}{b}}}} \right]\cdot}\\ {{{[{\beta _0} + \left( {{\beta _{\rm{a}}} - {\beta _0}} \right){{\left( {\frac{{{V_{{\rm{eq}}}}}}{{{V_0}}}{\rm{ln}}2} \right)}^{\frac{1}{b}}}]}^{ - 1}}} \end{array} $ | (13) |
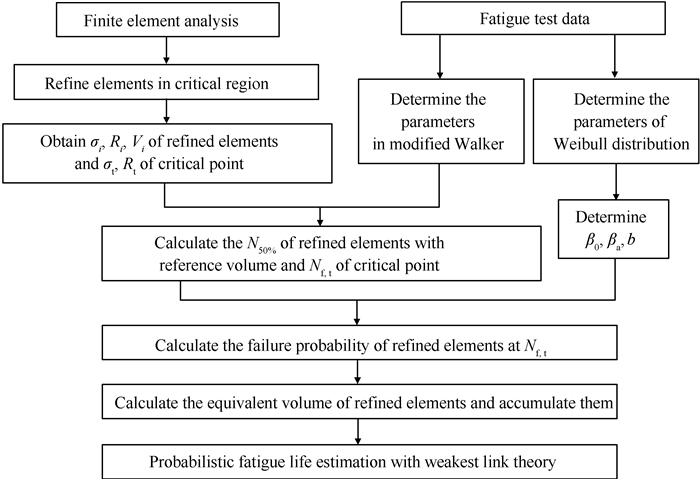
等效体积概率寿命分析方法的流程如图 3所示。
|
Fig. 3 Flow chart of equivalent volumetric method for probabilistic fatigue life prediction |
螺栓孔处因存在明显的应力集中,且载荷较大,从而成为涡轮盘常见的疲劳破坏部位之一。涡轮盘螺栓孔模拟试件是根据涡轮盘螺栓孔处的疲劳特征所设计的模拟试件[25],可用来进行较大子样下的高温疲劳试验,以弥补真实涡轮盘疲劳试验数据的不足。
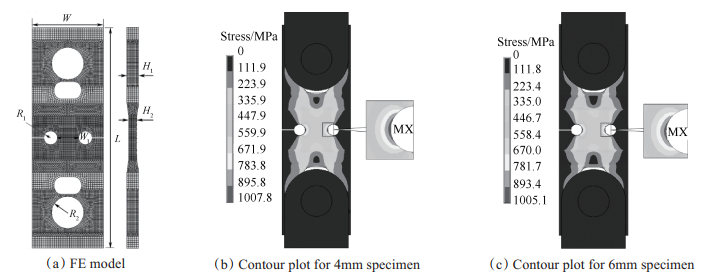
对4mm和6mm厚涡轮盘螺栓孔模拟试件进行疲劳概率寿命分析,结合实例详细阐述等效体积概率寿命分析方法,并对该方法的疲劳概率寿命预估精度进行验证。两种厚度的模拟试件均采用粉末高温合金FGH96材料,相关材料参数见表 1。模拟试件和加载接头通过销钉连接,为了保证加载销钉孔处具有足够的强度储备,对模拟试件加载段进行了局部加厚。两种模拟试件的主要尺寸见表 2,有限元模型分网及修正Walker等效应力云图如图 4所示。
|
|
Table 1 Material properties of FGH96 superalloy at 550℃ |
|
|
Table 2 Main parameters for simulated bolt-holespecimens (mm) |
|
Fig. 4 FE model and modified Walker stress for two specimens |
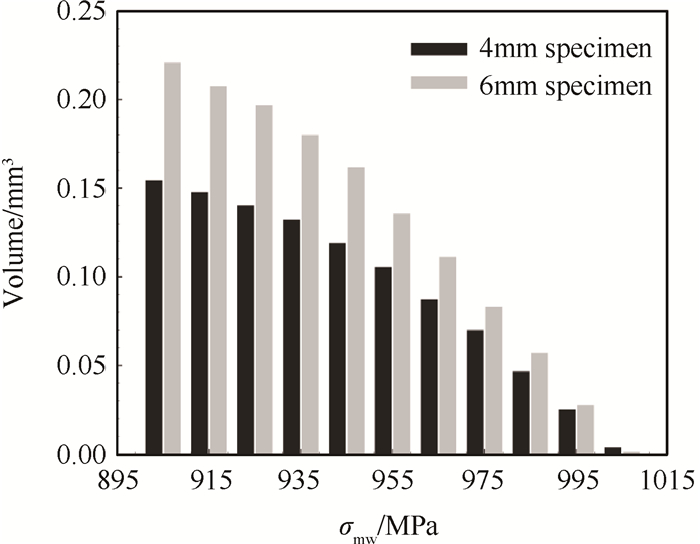
从有限元计算结果来看,两种模拟试件的最大应力点均出现在孔边,其中4mm厚模拟试件的最大等效应力为1157.5MPa,应力比为-0.514,从而最大修正Walker应力为1007.8MPa;而6mm厚试件的最大等效应力为1154.3,应力比为-0.522,最大修正Walker应力为1005.1MPa,且两个孔边均存在较明显的应力集中。两种厚度的模拟试件最危险点附近的相同修正Walker等效应力水平下的危险体积对比如图 5所示。需要说明的是,图 5中的危险体积累积结果为经过细化的内部应力较均匀的小子块的体积累积结果(小子块内最大应力差不超过10MPa)。可以看出,两种模拟试件大应力区的危险体积均较小,随着应力的减小,危险体积逐渐增大,这符合典型的应力集中情形下的应力分布规律。同时,除了在大应力区4mm试件的危险体积稍大于6mm试件外,在距危险点较远区域6mm试件的危险体积明显大于4mm试件,表现出明显的体积效应。
|
Fig. 5 Comparison of detrimental volume in large stress regions of the two specimens |
550℃时FGH96材料的修正Walker模型应力-寿命关系可由式(14)表示。
| $ \begin{array}{*{20}{l}} {{\rm{lg}}{N_{\rm{f}}} = - 7.3753{\rm{lg}}{\sigma _{{\rm{max}}}} - 19.2257{\rm{lg}}\left( {\frac{{1 - R}}{2}} \right) + }\\ {5.0847{\rm{lg}}{\sigma _{{\rm{max}}}}{\rm{lg}}\left( {\frac{{1 - R}}{2}} \right) + 26.0912} \end{array} $ | (14) |
根据第2节所述方法对FGH96材料550℃时不同应力水平下的试验数据进行处理,得到β0=0.09,βa=1.1,b=3.64。从而FGH96材料在不同应力水平下疲劳寿命的Weibull分布可表示为式(15),其中Np为任意失效概率下的疲劳寿命。
| $ \begin{array}{*{20}{l}} {f\left( {{N_{\rm{p}}}} \right) = \frac{{3.64}}{{1.01{N_{50{\rm{\% }}}}}}{{\left[ {\frac{{{N_{\rm{p}}}/{N_{50{\rm{\% }}}} - 0.09}}{{1.01}}} \right]}^{2.64}}\cdot}\\ {{\rm{exp}}\left\{ { - {{\left[ {\frac{{{N_{\rm{p}}}/{N_{50{\rm{\% }}}} - 0.09}}{{1.01}}} \right]}^{3.64}}} \right\}} \end{array} $ | (15) |
对于存在应力集中的构件,随着与最危险点距离的增大,应力和应力比均减小,减小的幅度与应力集中的程度有关。在进行等效体积法概率寿命预估时,对两种模拟试件均选取最危险点应力的90%作为应力阈值,大于应力阈值的单元参与单元细化、等效体积转换以及概率寿命计算,小于应力阈值的单元不予考虑。这是因为应力阈值处的应力和应力比已经比较小,由式(1)可以看出,此时修正Walker等效应力明显减小,从而等效体积明显减小。如4mm试件的应力阈值所对应的修正Walker等效应力仅为765MPa,此时将其转换为以最危险点为目标的等效体积仅为原体积的0.1%左右,可以忽略。
为了对比两种模拟试件的等效体积,以4mm试件最危险点处的应力和应力比为目标进行转换。对于4mm试件,参与转换的应力阈值以上的危险体积为16.39mm3,转换后的等效体积为1.39mm3;6mm试件参与转换的体积为22.33mm3,转换后的等效体积为1.74mm3。可以看出,尽管6mm试件试验段的总体积是4mm试件的1.5倍,但无论在转换前还是转换后,6mm试件的危险体积均小于4mm试件危险体积的1.5倍。因此,在工程实际中,危险体积的关系不能简单地根据几何拓扑关系来推断。
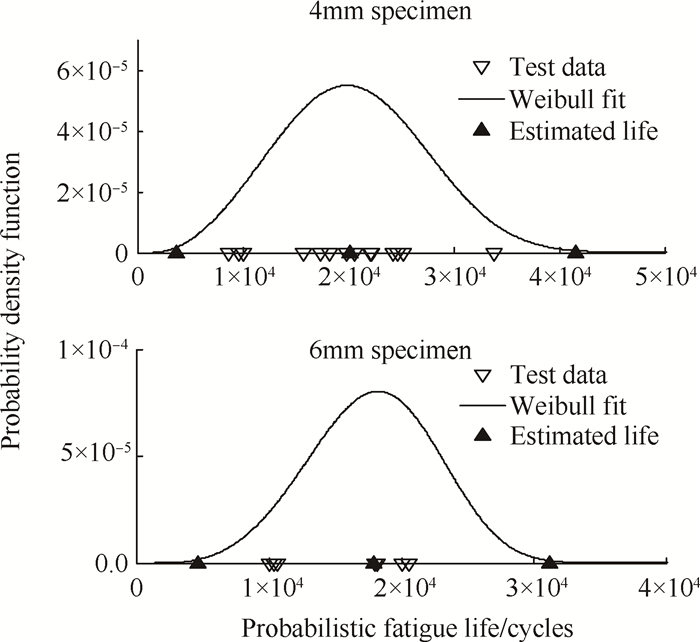
对两种模拟试件在550℃下进行高温疲劳试验,采用正弦波进行加载控制,载荷比R=0.05。其中4mm模拟试件共进行疲劳试验14件,6mm厚模拟试件共进行疲劳试验7件。根据两种模拟试件的试验结果分别进行疲劳寿命的三参数Weibull分布拟合,两种模拟试件的试验结果以及相应的Weibull分布拟合结果如图 6所示。采用等效体积概率寿命体方法分别预估两种模拟试件的疲劳概率寿命,结果如图 6和表 3所示。同时,表 3也列出了两种模拟试件由试验结果的Weibull分布所推断的概率寿命以及应力体方法计算所得概率寿命。
|
Fig. 6 Comparison of estimated probabilistic fatigue life versus fatigue test data |
|
|
Table 3 Comparison of estimated probabilistic fatigue life versus experimental results for the two specimens |
通过对比不难发现,等效体积概率寿命体方法的预估结果偏保守,在低可靠度时预估寿命小于试验结果,误差在-30%左右;而在中高可靠度时的预估寿命虽然仍小于试验结果,但精度有所提高,与试验结果最大误差仅为-23.2%。应力体方法在低可靠度时的预估寿命明显偏危险,而在高可靠度时的预估结果又太保守,最大误差为-44.4%。同时,无论是试验结果,还是等效体积法或应力体方法,均体现出一定的体积效应,即6mm试件的疲劳概率寿命基本都比4mm试件的小。
6 结论本文基于“等概率寿命,等损伤”的基本思想,结合修正Walker模型和Weibull统一分布模型以及最弱环理论,建立了等效体积概率寿命体方法并通过试验验证,获得了如下结论:
(1) 对FGH96材料考虑平均应力效应随最大应力变化的现象,得到了比常用平均应力修正模型精度更高的结果。
(2) 通过对不同应力水平下的FGH96试件疲劳试验结果研究表明,最小寿命和特征寿命在双对数坐标下随中位寿命呈线性规律变化。
(3) 采用等效体积概率寿命体方法对4mm和6mm两种厚度的螺栓孔模拟试件进行了概率寿命预估,并与试验结果及应力体方法预估结果进行对比。结果显示等效体积法的预估结果偏保守,最大误差在30%左右,且在中高可靠度时的预估精度较高,最大误差仅有-23.2%;应力体方法在低可靠度时的预估结果偏危险,而在高可靠度时的预估结果又偏保守。
(4) 总体来看,等效体积概率寿命体方法的预估精度高于应力体方法,而两种方法在低可靠度时的预估精度均有待进一步提高。
| [1] |
李骏, 宋友辉, 刘汉斌, 等. 涡轮叶片-榫头-轮盘的蠕变与低循环疲劳寿命预测[J]. 推进技术, 2015, 36(11): 1699-1704. (LI Jun, SONG You-hui, LIU Han-bin, et al. Creep and Low Cycle Fatigue Life Prediction for Turbine Blade-Tenon-Disk Structure[J]. Journal of Propulsion Technology, 2015, 36(11): 1699-1704.)
(  0) 0) |
| [2] |
牟园伟, 陆山. 轮盘低周疲劳概率寿命预估模型[J]. 推进技术, 2012, 33(2): 288-292. (MOU Yuan-wei, LU Shan. Low Cycle Fatigue Probabilistic Life Prediction Models for Fan Disk[J]. Journal of Propulsion Technology, 2012, 33(2): 288-292.)
(  0) 0) |
| [3] |
唐俊星.含夹杂粉末盘概率寿命三维仿真方法与应用[D].西安: 西北工业大学, 2008.
(  0) 0) |
| [4] |
Peterson R E. Stress Concentration Factors[M]. New York: John Wiley & Sons, 1974.
(  0) 0) |
| [5] |
Neuber H. Theory of Notch Stresses[M]. Virginia: USAEC Office of Technical Information, 1961.
(  0) 0) |
| [6] |
Kuhn P, Hardran H F. An Engineering Method for Estimating Notch-Size Effect in Fatigue Tests of Steel[R]. NACA-TN-2805, 1952. https://www.researchgate.net/publication/290813397_An_engineering_method_for_estimating_notch-size_effect_in_fatigue_tests_on_steel
(  0) 0) |
| [7] |
Buch A. Evaluation of Size Effect in Fatigue Tests on Unnotched Specimens and Components[J]. Archiv Furdas Eisenhuttenwesen, 1972, 43(4): 885-900.
(  0) 0) |
| [8] |
Sheppard S D. Field Effects in Fatigue Crack Initiation: Long Life Fatigue Strength[J]. Journal of Mechanical Design, Transaction of the ASME, 1991, 113(2): 188-194. DOI:10.1115/1.2912768
(  0) 0) |
| [9] |
Bellett D, Taylor D, Marco S, et al. The Fatigue Behavior of Three-Dimensional Stress Concentrations[J]. International Journal of Fatigue, 2005, 27(3): 207-221. DOI:10.1016/j.ijfatigue.2004.07.006
(  0) 0) |
| [10] |
辛朋朋, 胡绪腾, 宋迎东. 基于临界距离理论的TC4合金缺口试样低循环疲劳寿命预测[J]. 航空动力学报, 2012, 27(5): 1105-1112. (  0) 0) |
| [11] |
Shirani M, Harkegard G. Fatigue Life Distribution and Size Effect in Ductile Cast Iron for Wind Turbine Components[J]. Engineering Failure Analysis, 2011, 18(1): 12-24.
(  0) 0) |
| [12] |
Daniel S, Marten O. An Investigation of the Prediction Accuracy for Volume Based HCF Models Using Scaled Geometries and Scaled Loading[J]. International Journal of Fatigue, 2016, 82(2): 317-324.
(  0) 0) |
| [13] |
Kristoffer K, Marten O. A Study of the Volume Effect and Scatter at the Fatigue Limit–Experimental and Computations for a New Specimen with Separated Notches[J]. International Journal of Fatigue, 2011, 33(3): 363-371. DOI:10.1016/j.ijfatigue.2010.09.012
(  0) 0) |
| [14] |
Kristoffer K, Marten O. A Investigation of a Fatigue Model with Two Competing Failure Mechanisms[J]. International Journal of Fatigue, 2014, 64(7): 131-139.
(  0) 0) |
| [15] |
Yao W X. Stress Field Intensity Approach for Prediction Fatigue Life[J]. International Journal of Fatigue, 1993, 15(3): 234-245.
(  0) 0) |
| [16] |
陆山, 张鸿, 唐俊星, 等. 考虑尺寸效应的轮盘应力疲劳概率寿命分析方法[J]. 航空动力学报, 2011, 26(9): 2039-2043. (  0) 0) |
| [17] |
刘香, 王延荣, 田爱梅, 等. 考虑尺寸效应的缺口疲劳寿命预测方法[J]. 航空动力学报, 2017, 32(2): 429-437. (  0) 0) |
| [18] |
Dowling N E, Calhoun C A, Arcari A. Mean Stress Effects in Stress-Life Fatigue and the Walker Equation[J]. Fatigue & Fracture of Engineering Materials & Structures, 2008, 32(3): 163-179.
(  0) 0) |
| [19] |
苏运来, 陆山. 适用于任意应变比的应变寿命新模型[J]. 推进技术, 2018, 39(1): 169-175. (SU Yun-lai, LU Shan. A New Strain-Life Model Accounting for Effects of Various Strain Ratios[J]. Journal of Propulsion Technology, 2018, 39(1): 169-175.)
(  0) 0) |
| [20] |
苏运来, 陆山, 杨茂, 等. 任意应力比下涡轮盘的塑性应变能寿命模型[J]. 航空动力学报, 2017, 32(4): 828-834. (  0) 0) |
| [21] |
谢里阳, 任俊刚, 吴宁祥, 等. 复杂结构部件概率疲劳寿命预测方法与模型[J]. 航空学报, 2015, 36(8): 2688-2695. (  0) 0) |
| [22] |
高振同, 熊俊江. 疲劳可靠性[M]. 北京: 北京航空航天大学, 2000: 74-75.
(  0) 0) |
| [23] |
奚蔚, 姚卫星. 缺口件疲劳寿命分布预测的有效应力法[J]. 固体力学学报, 2013, 34(2): 205-212. (  0) 0) |
| [24] |
Weibull W. A Statistical Distribution Function of Wide Applicability[J]. ASME Journal of Applied Mechanics, 1951, 18(3): 293-297.
(  0) 0) |
| [25] |
陆山, 王春光, 陈军. 任意最大应力梯度路径轮盘模拟试件设计方法[J]. 航空动力学报, 2010, 25(9): 2000-2005. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


