2. Department of Mechanical Engineering,Institute of Engineering,Lalitpur 44700,Nepal
2. Department of Mechanical Engineering, Institute of Engineering, Lalitpur 44700, Nepal
当前空天飞行器技术是航空航天领域的研究热点,其中一个重要方向是发展高性能、宽马赫数的推进动力系统。传统的超燃冲压发动机在高飞行速度下往往存在推力不足、热效率低等问题[1],这些缺点限制了空天飞行器的进一步发展,然而爆轰模式的推进系统能够很好地解决这一问题。
与热扩散效应主导的燃烧现象相比,爆轰的燃烧速率更快,效率更高,近似于等容燃烧[2, 3],这些优点使爆轰波拥有很好的应用前景。爆轰波在高速推进系统中的运用可分为三种[4~7]:(1)脉冲爆轰发动机;(2)斜爆轰发动机;(3)旋转爆轰发动机。其中斜爆轰发动机由于点火方式简单,结构紧凑等优势,逐渐受到广泛关注。
实现斜爆轰推进的首要问题是控制斜爆轰波在楔面上的稳定起爆,这要求对斜爆轰波的生成和发展机理进行深入研究。作为一种超声速燃烧现象,斜爆轰波的形成和发展过程中夹杂着复杂的化学动力学和气动力学效应。早期Silva等[8]通过详细化学反应模型模拟了斜爆轰波生成的过程,发现诱导反应时间在激波-爆轰波的转变过程中起着重要作用,当诱导反应时间相对总反应时间越小,激波向爆轰波的过渡越平滑。Choi等[9]通过单步化学反应模型研究了活化能对斜爆轰波结构的影响,发现在相同的网格尺度下,高活化能趋于激发不稳定的波面结构,而低活化能下,斜爆轰波面较平滑。董刚等[10]则着重研究了不同来流温度下的斜爆轰波结构,得出在初始温度较高时,爆轰波阵面较平滑,而初始温度较低时,爆轰波呈现出较明显的三波点结构,且温度越低,三波点数量越多,排列越紧密。此外,Liu等[11]还研究了斜爆轰波生成过程中三波点向上游移动的过程,通过R-H分析得出三波点附近的压力大于斜爆轰波的脱体压力是造成这种移动的原因,并且当来流马赫数降低时,移动会变得剧烈。
在众多机理性研究中,斜爆轰波的诱导过程是一个重要的研究方向,相关工作也已开展多年。试验和数值模拟均表明[12~14],在上游斜激波和下游燃烧波之间存在一段诱导区域,该区域对下游气体的化学反应和能量释放起着重要作用。Fusina等[15]运用详细化学反应模型,研究了诱导区内的原子团生成过程,发现HO2原子团在诱导区内的链分支反应中起着先导作用。Viguier等[16]和Desbordes等[17]通过实验和数值模拟,研究了不同反应物下的爆轰波结构,得出激波-爆轰波的诱导过程主要由诱导区的反应时间所控制。Liu等[18]则研究了诱导区末端的CJ爆轰波的反射形态,发现随马赫数增加,CJ爆轰波在楔面处的反射会呈现马赫反射、正规反射和无反射三种形态。
目前对斜爆轰波诱导区特性的研究主要集中在诱导区长度和诱导区的过渡形式(斜激波-斜爆轰波)。诱导区长度的评判标准就研究目的的不同而有所变化。熊姹等[19]采用OH原子团浓度可以作为测量诱导区长度的标准,研究了不同化学反应机制下的诱导过程,发现多步反应能够很好地捕捉爆轰波的ZND结构。Wang等[20]将诱导区温度达到稳态ZND结构的最终温度作为诱导区结束的标准,结合CVC(定容燃烧)理论,比较了诱导区的理论长度和数值模拟长度,证明这是种预测诱导区长度的有效方法。Teng等[21]以反应温度提高10%作为诱导区结束的标准,研究了压力和马赫数对诱导区特性的影响,发现诱导区的过渡形式与马赫数联系较强而与压力联系较弱,诱导区长度近似与马赫数成正比而与压力成反比。通常诱导区的过渡形式有平滑型和突变型两种,其具体形式同样依赖于来流的化学和气动参数。Hui等[22]研究了马赫数、活化能和放热量对过渡形式的影响,发现斜激波与斜爆轰波之间的夹角大小可以用来判诱导区的过渡形式。
之前的研究多集中于来流的气动参数对斜爆轰波诱导区特性的影响,对化学参数的影响关注较少。在斜爆轰燃烧室的运行过程中,上游燃料掺混的不均匀会导致燃烧室入口来流当量比的变化,这种改变会对斜爆轰波的诱导区特性造成很大影响。Zhang等[23]通过数值模拟得到了诱导区长度变化的U型曲线,但其未深入研究造成这种变化的原因。鉴于此,本文通过数值模拟研究来流当量比的变化对斜爆轰波诱导区特性的影响,并结合CVC理论[20, 21],比较诱导区的理论长度和模拟长度,探索诱导区特性变化的内在机制。
2 控制方程与数值方法本文选取二维非稳态无粘可压欧拉方程来构建数学模型。采用开源CFD软件OpenFOAM进行运算[24],控制方程如下:
连续方程
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot\left( \mathit{\boldsymbol{\varphi }} \right) = 0$ | (1) |
动量方程
| $\frac{{\partial \rho \mathit{\boldsymbol{U}}}}{{\partial t}} + \left( {\mathit{\boldsymbol{\varphi }}\cdot\nabla } \right)\mathit{\boldsymbol{U}} = - \nabla p$ | (2) |
能量方程
| $\frac{{\partial \left( {\rho E} \right)}}{{\partial t}} + \nabla \cdot\left( {\mathit{\boldsymbol{\varphi }}H} \right) = 0$ | (3) |
组份方程
| $\frac{{\partial \rho {Y_i}}}{{\partial t}} + \nabla \cdot\left( {\mathit{\boldsymbol{\varphi }}{Y_i}} \right) = {\omega _i}{W_i}$ | (4) |
理想气体状态方程
| $p = \rho RT\sum\limits_i {} \frac{{{Y_i}}}{{{W_i}}}$ | (5) |
这里,
本文采用的化学动力模型为H2/Air11组份[O2,O,H2,H,OH,H2O,HO2,H2O2,N2,N,NO]23步可逆反应模型[25],反应速率及摩尔生成速率由CHEMKIN计算而得。数值方法采用了AUSM+通量离散格式[20]。每步迭代中采用黎曼外推法从各网格值推导各网格中心面左右面通量值,在标量梯度的计算中采用压力梯度项用以限制数据变化范围。进口边界处来流参数保持不变,各组分的质量分数根据来流工况调整。壁面和出口边界处采用零梯度条件。
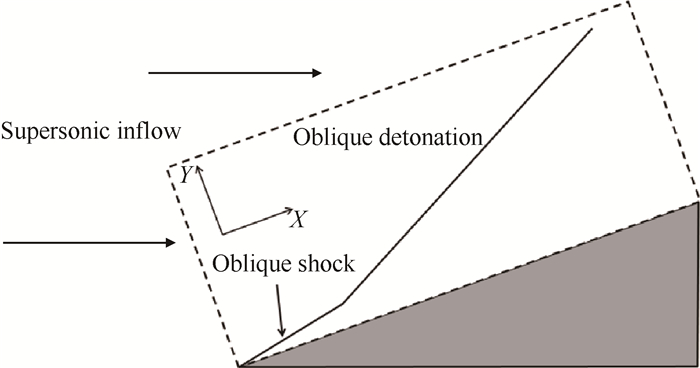
3 计算区域与网格划分方法本文采用了150mm×75mm的计算域,反应物为均匀的H2/Air混气,进口来流Ma数为6,温度为800K,压强为35kPa,斜楔角为16°。图 1展示了计算域区域及斜爆轰波的基本结构。以左边界和上边界为进口端,来流参数在进口端均匀分布,N2摩尔数为3.76不变,当量比等于H2/O2的摩尔比。
|
Fig. 1 Sketch of oblique detonation waves and computational domain |
本文中研究对象为诱导区长度和过渡形式,所选用的网格需要能够完整、清晰、准确地体现诱导区的结构。采用均匀结构化网格,选取两种尺寸的网格作比较,最小尺寸分别为20μm×20μm和40μm×40μm。设定进口来流当量比为1,图 2显示了该条件下两种网格划分下的压力分布,可看出在40μm下斜爆轰波的结构已经清晰、完整,除了下游局部高压区,上游的诱导区结构与20μm下无明显区别。

|
Fig. 2 Results from the grid resolution study for H2:O2:N2=2:1:3.76 showing pressure contours |
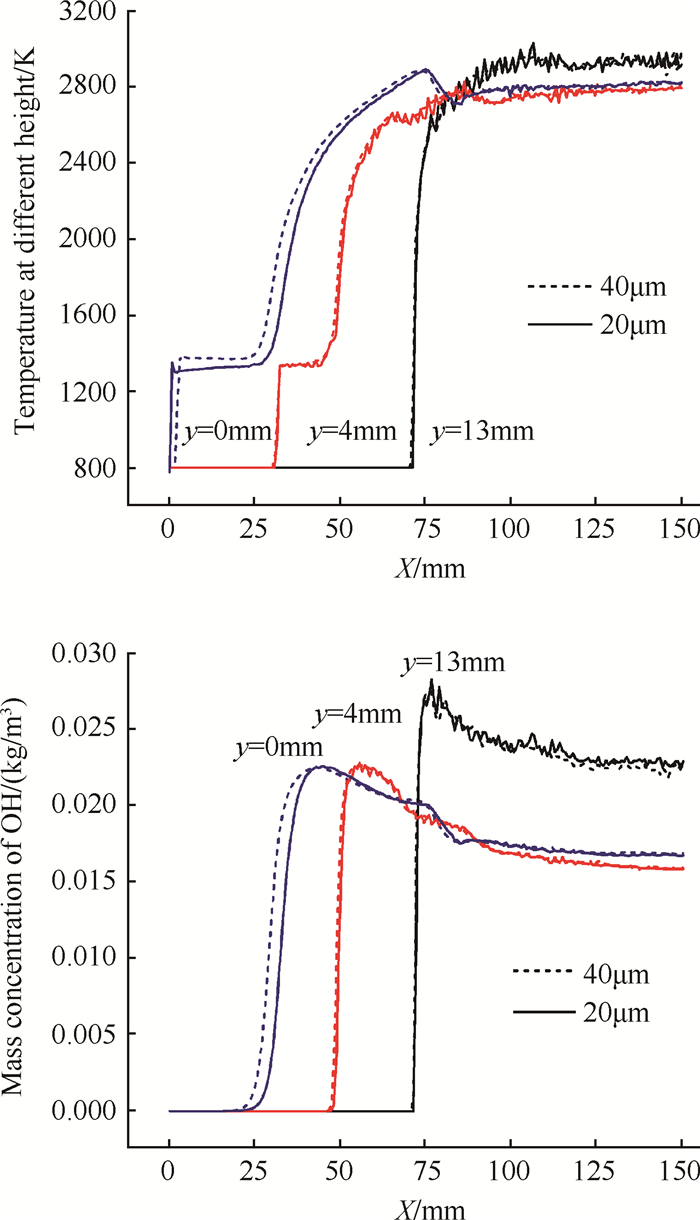
图 3为不同高度上温度和OH自由基质量浓度的分布情况。由图 3可看出,40μm和20μm两种网格尺度下的数值结果在变化趋势上是基本吻合的,只有y=0mm上,数值结果有略微偏差,这种偏差在文献[21]也出现了,是斜爆轰波的内部不稳定性造成的结果,对研究诱导区特性并不会带来实质性的影响。此外观察诱导区内(y=0mm,y=4mm)的数值变化可知,40μm下参数变化平滑稳定,数值结果已基本收敛,20μm下存在一定的数值波动,这表明斜爆轰波的内部不稳定性逐步显现。本文的研究对象为斜爆轰波诱导区,需要网格能够清晰完整地体现诱导区长度和过渡形式,而并不需要过密网格来捕捉这种不稳定性,综合考虑下,40μm是合适的选择。
|
Fig. 3 Results from the grid resolution study for H2:O2:N2=2:1:3.76, showing the temperature and specie profiles along different y-line locations |
CVC理论假设,在贴近楔面处反应物完全燃烧,压缩波强度很弱,楔面处的反应近似于定容燃烧。这种方法被证明是一种有效的定性分析方法[20, 21]。本研究借鉴此方法,由于本文采用的动力学模型、模拟采用的工况和计算域等因素的不同,采用稳态ZND结构的最终温度或者反应温度提升10%作为诱导区结束的判断标准会产生较大的误差,达到两倍以上,所以需要寻找合适于本研究的诱导区长度测量方法。
来流的温度为800K,压力为35kPa,马赫数为6,斜楔角为16°,采用理想气体的激波关系式,可以得到气流经过斜激波后的温度及To和压力po。在定容燃烧模型中采用To和po为初始温度和压力,得到不同当量比下温度和时间的变化关系。最终反应平衡温度为T1,认为当温度T=T1-0.01%×(T1-To)时反应已完成,此时间为理论反应完成时间tcvc。已知进口端的各组分含量、速度和楔面角度,通过理想气体的激波关系式可得出激波后诱导区内的气体速度V,V与tcvc的乘积即为诱导区长度的理论值Lcvc(Theoretical initiation length)。
在数值模拟结果中,沿壁面以楔面顶点到温度最大值处的距离为诱导区长度的模拟值Lnum(Numerical initiation length)。将两种诱导区长度进行对比,结果如表 1所示。表 1中理论值与模拟值之间的误差在33%以内,因此认为本文所采用的方法能够作为定性分析的手段。
|
|
Table 1 Comparison of numerical and theoretical initiation length |
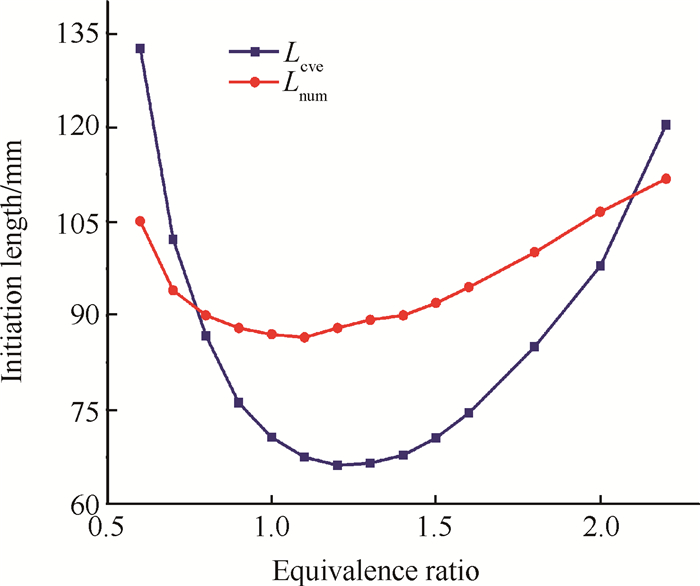
在保证来流中N2摩尔数不变的情况下改变当量比,得到诱导区长度随时间的变化曲线,如图 4所示,从图中可看出,随当量比增加Lcvc和Lnum都呈现先降后升的变化形式。
|
Fig. 4 Numerical and theoretical initiation length dependent on fuel–air equivalence ratio, at p=35kPa |
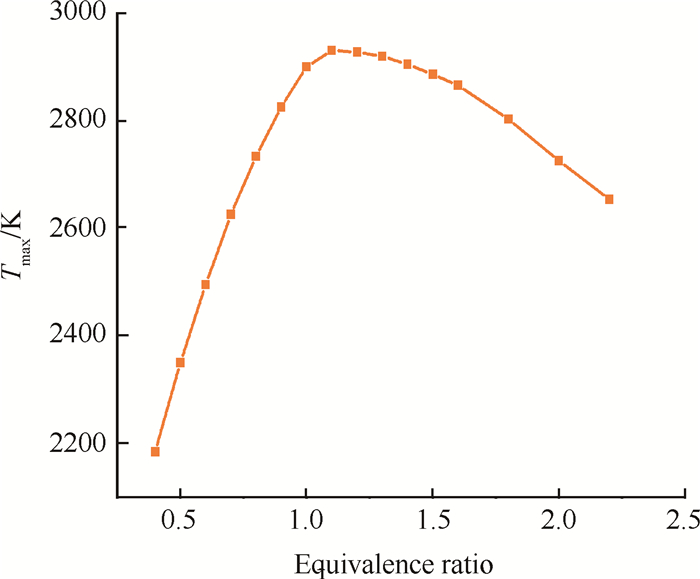
理论分析和实验表明[26],当量比的变化能够影响反应进程的发展。图 5给出了数值模拟中,诱导区沿楔面的最大温度Tmax随当量比的变化趋势。由图 5可知,当量比小于1.1时,增大当量比会促进诱导区内的化学反应,提高诱导区内的反应温度,但当量比大于等于1.1时,继续增大当量比会抑止反应发展,导致反应温度降低。诱导区长度大小主要取决于诱导区内的反应时间[12, 13],因此温度越高,反应越迅速,诱导区长度也越短,这与图 4中诱导区长度随当量比呈U型曲线变化的现象是一致的。
|
Fig. 5 Maximum temperature dependent on fuel–air equivalence ratio along y=0mm, at p=35kPa |
由于采用定容假设,Lcvc仅仅与当量比相关。在图 4中Lcvc和Lnum的最小值所对应的临界当量比分别为1.2和1.1,在临界当量比两侧,Lnum的变化幅度和速率要远小于Lcvc。这种现象暗示了斜爆轰波的诱导过程除了化学因素在影响外,还有其他因素起着重要作用。
CVC理论假设,诱导区内在贴近楔面处温度和压力均匀分布,诱导反应完全由化学反应主导,但斜爆轰波的诱导过程并非如此,其中存在复杂的气动力学效应。以往的研究大多侧重于Ma数、温度等因素对斜爆轰波结构的影响,对压力的关注较少,但Lu和Ng等[26, 27]的研究表明,压力在爆轰现象中起到了重要作用,由于第二爆炸极限效应的影响,存在一定临界压力,低于该临界值时,升高压力能够促进反应速率,但超过临界值,高压会使反应整体变得迟滞。Teng等[28]比较了诱导区长度与来流压力的相对关系,发现在进口压力较低时,诱导区长度的模拟值和理论值吻合较好,压力升高时,模拟值值会大大偏离理论值,他将这种现象解释为诱导区内反应主导因素由化学动力学效应向气动力学效应转变的结果,这与Lu和Ng的结果是一致的。
为进一步探索气动力学效应对诱导区反应的影响,本文在其他参数不变的情况下,分别将进口来流的压力降低到20kPa和提升到50kPa,使用相同方法测量诱导区长度的理论值与模拟值。
图 6显示了两种压力下Lcvc和Lnum随当量比的变化曲线。从图 6可看出,尽管进口压力升高,Lnum仍然能沿CVC理论所预测的U型曲线变化,但压力较高时,Lnum的变化幅度较小,曲线较平缓,而压力较低时,Lnum的变化幅度较大,变化速率较快,曲线也更趋近于理论所预测的轨迹。

|
Fig. 6 Numerical and theoretical initiation length dependent on fuel–air equivalence ratio at different pressure |
为进一步定量分析,本文对比了不同进口压力下诱导区长度随当量比的变化范围和幅度,如表 2所示。在表 2中,随着进口压力升高,诱导区长度的理论值和模拟值都相应减小,这说明升高压力对诱导区长度起抑止作用。此外,在三种压力下,理论值的变化幅度很接近,但模拟值的变化幅度却迅速减小,这表明在爆轰环境下,压力升高也能够抑止诱导区长度的剧烈变化。
|
|
Table 2 Comparison of the changing range and scope of numerical and theoretical initiation length |
综上所述,诱导区长度随当量比的变化轨迹会被进口压力影响,高压时诱导区内的气动力学效应较强,阻止了诱导区长度的剧烈变化;低压时气动力学效应减弱,诱导区内化学动力学效应占据主导地位,诱导区长度随理论值呈U型曲线变化。
5.2 当量比对诱导区过渡形式的影响前人的研究表明Ma数和活化能可以影响诱导区的过渡形式[21, 22, 28],但并没有考虑当量比的影响。
图 7给出了不同当量比下流场内的温度和压力分布,可看出随着当量比增大,诱导区的过渡形式呈现出由平滑型变为突变型,之后再变回平滑型的变化规律。当量比小于0.6或大于2.5时,诱导区的过渡为一条平滑的曲线,诱导区末端不存在明显的三波点,并且压力分布较均匀,如图 7(a)、(f)所示。0.6和2.5可视为诱导区过渡形式转变的临界值。

|
Fig. 7 Temperature(up)and pressure(down)contours at different fuel–air equivalence ratio |
从图 7(b)中可看出,在当量比等于0.6时,初步形成了λ型结构[28],这标志着三波点的形成,此时诱导区末端形成了较强的压缩波,压缩波与斜激波相互作用,这种作用改变了诱导区的过渡形态,使其由平滑型转变为突变型。进一步增大当量比,这种λ型结构会得到加强,如图 7(c)所示。然而这种变化趋势并不是不变的,在当量比逐渐接近2.5时,诱导区末端的压缩波强度渐渐减小,λ型结构减弱,如图 7(d)、(e)所示。在图 7(f)中,λ型结构已完全消失,诱导区的过渡重新变回了平滑的曲线。
为进一步定量分析诱导区末端压缩波强度的变化情况,分别取斜楔面上的一条直线(y=0mm)和穿过诱导区的一条直线(y=7mm),可以得到诱导区末端压力峰值随当量比的变化曲线,如图 8所示。从图 8中可看出,随当量比增大,压缩波的强度呈现出先增大后变小的变化形式,这与图 7中诱导区过渡形式呈现的平滑型—突变型—平滑型的变化形式相对应,即当量比在一定范围内(对于本文,该范围为0.6~2.5),诱导区末端形成强压缩波,压缩波与斜激波作用形成突变型的过渡形态,而在该范围以外,压缩波强度较弱,过渡形态变为平滑型。

|
Fig. 8 Maximum pressure dependent on fuel–air equivalence ratio, along y=7mm and y=0mm |
以上分析表明:诱导区末端的压缩波强度是影响诱导区过渡形式的决定性因素。
6 结论本文通过改变H2/O2摩尔比,模拟了当量比变化对斜爆轰波诱导区诱导长度和过渡形式的影响,并结合定容燃烧(CVC)理论分析了诱导区特性变化的内在机制。结果表明:
(1) 诱导区末端的温度是影响诱导区长度的关键因素。当量比的变化能够影响诱导区内的反应进程,随着当量比增大,诱导区末端温度存在先上升后下降的过程,这导致诱导区长度呈U形曲线变化。
(2) 诱导区末端的压缩波强度是影响诱导区的过渡形式的决定性因素。诱导区末端的压缩波与斜激波相互作用,改变了诱导区的过渡形式。定量分析发现,当量比存在一定范围(对于本文,该范围为0.6~2.5),在该范围内过渡形式为突变型,反之为平滑型。
(3) 诱导区内的化学动力学效应和气动力学效应共同主导了诱导区长度的变化。结合CVC理论,对比不同进口压力下诱导区长度的理论值和模拟值的变化曲线得出:在当量比增大的过程中,由于化学动力学效应的作用,诱导区长度的模拟值能够和理论值保持相同的变化趋势,均沿U型曲线变化;由于气动力学效应的作用,诱导区长度变化幅度较小,变化速率也并不会像理论值那样剧烈。
致谢: 感谢国家自然科学基金资助。
| [1] |
姜宗林. 关于吸气式高超声速推进技术研究的思考[J]. 力学进展, 2009, 39(4): 398-405. DOI:10.3321/j.issn:1000-0992.2009.04.003 (  0) 0) |
| [2] |
Dunlap R. A Preliminary Study of the Application of Steady-State Detonative Combustion to a Reaction Engine[J]. Jet Propulsion, 1957, 28(7): 158-160.
(  0) 0) |
| [3] |
Hertzberg A, Bruckner A P, Bogdanoff D W. Ram Accelerator-A New Chemical Method for Accelerating Projectiles to Ultrahigh Velocities[J]. AIAA Journal, 2015, 26(2): 195-203.
(  0) 0) |
| [4] |
马丹花, 翁春生. 爆震管内扰流片对爆震波影响的数值分析[J]. 推进技术, 2011, 32(3). (MA Dan-hua, WENG Chun-sheng. Numerical Investigation of Two-Phase Detonation with the Osbstacles[J]. Journal of Propulsion Technology, 2011, 32(3).)
(  0) 0) |
| [5] |
陈巍, 范玮, 李建玲, 等. 脉冲爆震火箭发动机高频实验研究[J]. 推进技术, 2011, 32(3): 443-446. (CHEN Wei, FAN Wei, LI Jian-ling, et al. Experiments on High Frequency Pulse Detonation Rocket Engine[J]. Journal of Propulsion Technology, 2011, 32(3): 443-446.)
(  0) 0) |
| [6] |
刘世杰, 覃慧, 林志勇, 等. 连续旋转爆震波细致结构及自持机理[J]. 推进技术, 2011, 32(3): 431-436. (LIU Shi-jie, QIN Hui, LIN Zhi-yong, et al. Detailed Structure and Propagating Mechanism Research on Continuous Rotating Detonation Wave[J]. Journal of Propulsion Technology, 2011, 32(3): 431-436.)
(  0) 0) |
| [7] |
归明月, 范宝春. 尖劈诱导的斜爆轰波的精细结构及其影响因素[J]. 推进技术, 2012, 33(3): 490-494. (GUI Ming-yue, FAN Bao-chun. Fine Structure and Its Influence Factor of Wedge-Induced Oblique Detonation Waves[J]. Journal of Propulsion Technology, 2012, 33(3): 490-494.)
(  0) 0) |
| [8] |
Silva L F F D, Deshaies B. Stabilization of an Oblique Detonation Wave by a Wedge: a Parametric Numerical Study[J]. Combustion & Flame, 2000, 121(1–2): 152-166.
(  0) 0) |
| [9] |
Choi J Y, Kim D W, Jeung I S, et al. Cell-Like Structure of Unstable Oblique Detonation Wave from High-Resolution Numerical Simulation[J]. Proceedings of the Combustion Institute, 2007, 31(2): 2473-2480. DOI:10.1016/j.proci.2006.07.173
(  0) 0) |
| [10] |
董刚, 范宝春. 来流温度影响驻定爆轰波结构和性能的数值研究[J]. 高压物理学报, 2011, 25(3): 193-199. (  0) 0) |
| [11] |
Liu Y, Wu D, Yao S, et al. Analytical and Numerical Investigations of Wedge-Induced Oblique Detonation Waves at Low Inflow Mach Number[J]. Combustion Science & Technology, 2015, 187(6): 843-856.
(  0) 0) |
| [12] |
Powers J M, Stewart D S. Approximate Solutions for Oblique Detonations in the Hypersonic Limit[J]. AIAA Journal, 1992, 30(3): 726-736. DOI:10.2514/3.10978
(  0) 0) |
| [13] |
Ashford S A, Emanuel G. Wave Angle for Oblique Detonation Waves[J]. Shock Waves, 1994, 3(4): 327-329. DOI:10.1007/BF01415831
(  0) 0) |
| [14] |
Morris C I, Kamel M R, Hanson R K. Shock-Induced Combustion in High-Speed Wedge Flows[J]. Symposium on Combustion, 1998, 27(2): 2157-2164. DOI:10.1016/S0082-0784(98)80064-7
(  0) 0) |
| [15] |
Fusina G, Sislian J P, Parent B. Formation and Stability of Near Chapman-Jouguet Standing Oblique Detonation Waves[J]. AIAA Journal, 2012, 43(7): 1591-1604.
(  0) 0) |
| [16] |
Viguier C, Gourara A, Desbordes D. Three-Dimensional Structure of Stabilization of Oblique Detonation Wave in Hypersonic Flow[J]. Symposium on Combustion, 1998, 27(2): 2207-2214. DOI:10.1016/S0082-0784(98)80069-6
(  0) 0) |
| [17] |
Desbordes D, Hamada L, Guerraud C. Supersonic H2-Air Combustions behind Oblique Shock Waves[J]. Shock Waves, 1995, 4(6): 339-345. DOI:10.1007/BF01413876
(  0) 0) |
| [18] |
Liu Y, Liu Y S, Wu D, et al. Structure of an Oblique Detonation Wave Induced by a Wedge[J]. Shock Waves, 2016, 26(2): 161-168. DOI:10.1007/s00193-015-0600-5
(  0) 0) |
| [19] |
熊姹, 严传俊, 邱华. 不同化学反应机理对爆震波模拟的影响[J]. 燃烧科学与技术, 2008, 14(4): 355-360. DOI:10.3321/j.issn:1006-8740.2008.04.013 (  0) 0) |
| [20] |
Wang T, Zhang Y, Teng H, et al. Numerical Study of Oblique Detonation Wave Initiation in a Stoichiometric Hydrogen-Air Mixture[J]. Physics of Fluids, 2015, 27(9).
(  0) 0) |
| [21] |
Teng H, Ng H D, Jiang Z. Initiation Characteristics of Wedge-Induced Oblique Detonation Waves in a Stoichiometric Hydrogen-Air Mixture[J]. Proceedings of the Combustion Institute, 2016, 36(2): 2735-2742.
(  0) 0) |
| [22] |
Hui T H, Lin J Z. On the Transition Pattern of the Oblique Detonation Structure[J]. Journal of Fluid Mechanics, 2012, 713(6): 659-669.
(  0) 0) |
| [23] |
Zhang Y, Gong J, Wang T. Numerical Study on Initiation of Oblique Detonations in Hydrogen–Air Mixtures with Various Equivalence Ratios[J]. Aerospace Science & Technology, 2016, 49: 130-134.
(  0) 0) |
| [24] |
Bhattrai S, Hao T. Numerical Study of Shcramjet Combustor Characteristic Control Techniques[J]. Frontiers in Aerospace Engineering, 2013, 2(3): 189-198.
(  0) 0) |
| [25] |
Kee R J, Rupley F M, Meeks E, et al. CHEMKIN-Ⅲ: A Fortran Chemical Kinetics Package for the Analysis of Gas Phase Chemical and Plasma Kinetics, Sandia National Laboratories Report[J]. Sandia Report, 1991, 96(3): 142-6.
(  0) 0) |
| [26] |
Lu T, Law C, Ju Y. Some Aspects of Chemical Kinetics in Chapman-Jouguet Detonation: Induction Length Analysis[J]. Biomedical Chromatography, 2003, 17(2-3): 126-132. DOI:10.1002/(ISSN)1099-0801
(  0) 0) |
| [27] |
Ng H D, Ju Y, Lee J H S. Assessment of Detonation Hazards in High-Pressure Hydrogen Storage from Chemical Sensitivity Analysis[J]. International Journal of Hydrogen Energy, 2007, 32(1): 93-99. DOI:10.1016/j.ijhydene.2006.03.012
(  0) 0) |
| [28] |
Teng H, Zhang Y, Jiang Z. Numerical Investigation on the Induction Zone Structure of the Oblique Detonation Waves[J]. Computers & Fluids, 2014, 95(3): 127-131.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


