2. 中国科学院大学 航空宇航学院,北京 100049;
3. 西安交通大学 能源与动力工程学院,陕西 西安 710049;
4. 中国科学院轻型动力重点实验室,北京 100190
2. School of Aeronautics and Astronautics, University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
4. Key Laboratory of Light-Duty Gas-Turbine, Chinese Academy of Sciences, Beijing 100190, China
高推重比是目前世界先进航空发动机发展的重要指标之一,而航空发动机的压缩部件占其重量和长度的1/3以上,因此,提升级载荷实现压气机减级减重,是提高推重比的重要技术途径之一。其中,对转技术是高负荷压气机发展的一个重要方向,但级载荷的提升、以及静叶排的取消,使得高负荷对转压气机级间非定常干涉现象如尾迹-激波干涉等变得更加剧烈。
轴向间隙作为影响压气机级间非定常干涉的关键参数之一,长久以来一直是国内外学者关注的重点。Valkov等[1],Sirakov等[2]通过数值模拟研究发现:对于亚声速压气机,轴向间隙的减小,总压比和效率都相应地有一定程度的提升,这与Smith[3]和Mikolajczak[4]的实验结论一致;Smith[5, 6],Tan[7],Valkov等[1, 8],Adamczyk[9]认为这是尾迹在下游转子通道中的恢复,减小了与主流的掺混损失。对于高马赫数、高负荷压气机,Gorrell等[10~12]通过数值模拟、实验研究发现,轴向间隙的减小,总压比、效率、堵塞流量都相应地减小的原因是由于轴向间隙较小时,一方面,下游转子外伸激波在上游导叶尾缘改变方向,变成正激波从而产生额外的损失;另一方面,下游转子外伸激波较强,上游转子尾迹脱落涡自身涡量值会增大,带来损失,Kenneth等[13]也得到相同的结论。此外,Estevadeordal等[14]通过PIV实验发现,高负荷压气机尾迹脱落涡受到下游转子外伸激波的干涉,导致脱落频率固定即存在“锁相”。这使得上游转子尾迹涡脱落时,相对下游转子的周向位置固定。为此,针对轴向间隙变化对高负荷压气机级间非定常干涉及气动性能影响的机理,有必要从尾迹脱落涡的级间迁移路径变化着手开展研究。
关于尾迹脱落涡级间迁移路径影响因素的研究,Zachcial等[15]通过二维非定常数值模拟得出,转速和轴向间隙的变化可以改变尾迹脱落涡进入下游转子的位置而上游静子的栅距变化却不能;Botros[16]通过对上游为无偏折导叶、下游为转子的压气机,进行二维数值模拟发现,对于给定的进口马赫数和叶片几何,尾迹在下游转子通道中的迁移轨迹取决于尾迹在轴向间隙内输运的时间与下游转子转过一个通道的时间的比值。对于给定的叶片几何、来流马赫数,在同一轴向间隙下,尾迹脱落涡进入下游转子时,相对下游转子的周向位置不变;不同迁移路径下,压气机的压比、效率等不一样。
对于高负荷对转压气机而言,一方面由于上游转子叶片的气流折转使尾迹脱落涡存在周向分速度;另一方面,上游转子自身旋转使得尾迹脱落涡具有较大的周向牵引速度。两者相结合,对上游转子尾迹涡进入下游转子通道的周向位置会产生显著影响,也即对尾迹脱落涡级间迁移的轨迹产生重要影响。针对高负荷对转压气机,国内西北工业大学的张恒铭等[17, 18]分析了上游转子尾迹对压气机性能影响的原因,但对上游转子尾迹涡级间迁移影响因素的研究还不足。
为此,通过非定常数值模拟研究,旨在揭示轴向间隙对高负荷对转压气机上游转子尾迹脱落涡级间迁移的影响,并结合理论分析与数学推导,建立上游转子尾迹脱落涡在下游转子通道中迁移轨迹的无量纲准则关系式。并基于该关系式,结合通流计算与激波模型,在设计阶段预估上游转子尾迹脱落涡的迁移轨迹,为非定常设计提供理论支撑依据。
2 研究方法及研究对象 2.1 非线性谐波法雷诺平均的N-S方程中的守恒变量,可以解耦成时均项与周期性扰动项,即
| $ U\left( \mathit{\boldsymbol{r}},t \right)=\bar{U}\left( \mathit{\boldsymbol{r}} \right)+\mathop{\sum }^{}{U}'\left( \mathit{\boldsymbol{r}},t \right) $ | (1) |
式中U是时均项,U'是周期性扰动项。
每一个周期性扰动项又可以分解成有限阶数N的傅里叶级数,则有
| $ {U}'\left( \mathit{\boldsymbol{r}},t \right)=\sum\limits_{k=1}^{N}{\left[ {{{\tilde{U}}}_{k}}\left( \mathit{\boldsymbol{r}} \right){{\text{e}}^{\text{j}{{\omega }_{k}}t}}+{{{\tilde{U}}}_{-k}}\left( \mathit{\boldsymbol{r}} \right){{\text{e}}^{\text{j}{{\omega }_{k}}t}} \right]} $ | (2) |
将式(2)和式(1)代入雷诺平均N-S方程,经过时间平均和简化,得到守恒型的方程组,再将其写成有限体积法形式的方程组,则有
| $ \frac{\partial U}{\partial t}V+\overset{{}}\sum\limits_{\Delta S}\,\left( {{F}_{\text{C}}}-{{F}_{\text{V}}} \right)\cdot n\text{ }\!\!\Delta\!\!\text{ }S=QV $ | (3) |
式中FC为离散的对流项,FV离散的粘性项,V为网格单元体积,ΔS为面积,Q为源项(包括科氏力和离心力项)。
将式(3)投射到频域,则可进行频域上的定常求解,将定常求解的结果进行时域重构,则可得到时域上的非定常结果。
非线性谐波法[19](NLH)不受上下游叶排叶片数的限制,只需计算单通道就可得到较精确的解。因此,大大地减小了计算量,便于非定常求解应用于工程实际。
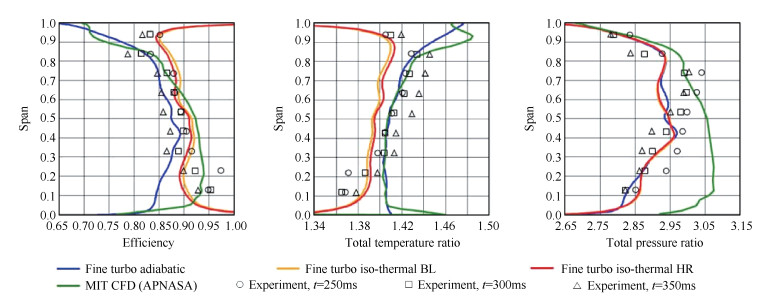
非线性谐波法可通过控制扰动源数目和傅里叶阶数来控制求解精度。理论上阶数N取无穷大可以得到精确的非定常解,但阶数的增加对计算资源的需求也随之增加。辛辛那提大学的Knapke等[20]以MIT对转压气机为研究对象、西北工业大学的刘波等[21]以西北工业大学两级对转压气机为研究对象,分别对比分析了非线性谐波法求解的结果和实验得出的结果,得出3阶非线性谐波法获得的整体性能与实验结果吻合较好,分别如图 1,表 1所示。
|
Fig. 1 Spanwise exit profiles of efficiency, total temperature ratio and total pressure ratio for comparison among the FINETM/Turbo simulations, MIT simulations and the experiment[20] |
|
|
Table 1 Comparison of the performance parameters[21] |
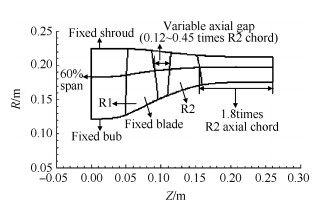
为规避端壁、叶顶泄漏流等的影响,以某高负荷对转压气机60%叶高的叶型为基础,沿流向截取0.1mm的等厚薄层作为研究对象,如图 2所示。该研究对象相关的参数见表 2。
|
Fig. 2 Relationship of coordinates |
|
|
Table 2 2D compressor parameters |
为了研究轴向间隙对上游转子尾迹脱落涡级间迁移的影响,保持流道、上游转子、相对叶高的叶型几何、薄层高度固定不变,通过改变下游转子的轴向位置来改变上下游转子之间的轴向间隙,相关的坐标关系如图 2所示。
表 3列出了所要研究的轴向间隙变化范围,并以下游转子弦长对其进行了无量纲化,为后文叙述方便,将不同的轴向间隙进行了编号。
|
|
表 3 Gap at 60% span(fraction of R2 chord) |
非定常数值模拟采用了有限体积法,对流项采用中心差分格式,时间推进采用4阶龙格库塔格式,湍流模型采用S-A模型,入口边界条件给定总温288.15K,总压101330Pa,轴向进气,出口边界条件给定平均静压,选用绝热无滑移壁面条件,工质选用理想气体,上下端壁设成镜像对称。定常计算时,动-动交界面设成一维无反射类型;非定常计算时,用定常结果作为初场以加快收敛。
计算网格采用HOH多块结构化网格,近壁面y+ < 5。网格无关性验证计算结果如表 4所示,网格数变化前后,总压比、效率、质量流量变化的误差最大值小于0.1%,则认为满足网格无关性要求。因此,为节约计算成本,采用网格数约为14万进行非定常数值模拟研究,计算网格示意图,如图 3所示。此时,沿叶展方向布置2个节点,第一、二排叶片网格数均约7万,总共约14万网格点。当改变轴向间隙时,采用相同的拓扑结构,并且适当地改变上下游转子轴向间隙内沿流向的网格数,保证整体网格密度基本一致。改变轴向间隙的同时,保证出口计算域长度为1.8倍下游转子60%叶高的轴向弦长。
|
|
Table 4 Grid independency solutions |

|
Fig. 3 2D mesh |
为了选取合理的谐波阶次,在保证计算精度的前提下尽量节约计算成本。分别选取7,8,9阶谐波阶次进行非定常数值模拟。
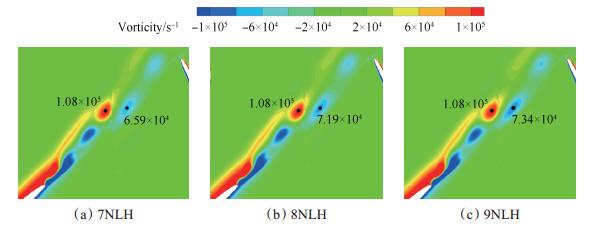
对比分析动-动交界面上下游相同位置处涡量值可知(如图 4所示),在谐波阶次分别为7,8,9时,动-动交界面上游位置涡量的大小相等而下游位置涡量的变化差异随阶次提高而逐渐减小,7,8阶时相差9.1%而8,9阶时相差2%左右。因此,在保证数值模拟精度的前提下,为了节约计算成本,采用8阶次的非线性谐波法进行非定常数值模拟研究。
|
Fig. 4 Radial Vorticity at different harmonics |
为了揭示轴向间隙对上游转子尾迹脱落涡在下游转子通道中迁移轨迹的影响规律,选取表 3的轴向间隙变化范围,进行非定常数值模拟。
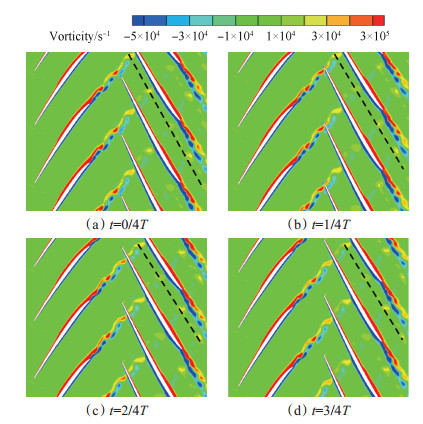
通过对比分析一个周期内不同时刻的涡量云图可知(如图 5所示):对于给定的叶型几何、来流马赫数,在同一轴向间隙下,上游转子尾迹脱落涡到达下游转子通道入口时的周向位置不变,因此使得上游转子尾迹脱落涡在下游转子通道中的迁移轨迹保持不变。
|
Fig. 5 Trajectory at 25% R2 chord |
通过对比分析不同轴向间隙下的涡量云图可知(如图 6所示):a轴向间隙下,尾迹脱落涡沿下游转子压力面迁移;b轴向间隙下,尾迹脱落涡沿下游转子通道中间迁移;c轴向间隙下,尾迹脱落涡沿下游转子吸力面迁移。由此可见,随着轴向间隙的增加,上游转子尾迹脱落涡在下游转子通道中的迁移路径由下游转子压力面逐渐向吸力面偏移;而随着轴向间隙进一步增大(如图 6中d,e,f轴向间隙),尾迹脱落涡迁移路径将重复之前的变化,进而导致不同轴向间隙下,可能存在相同的迁移路径。
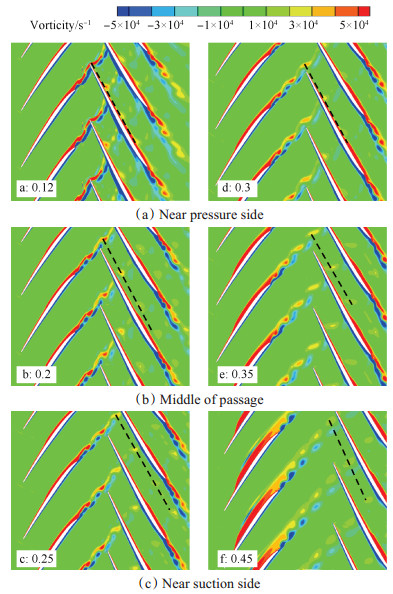
|
Fig. 6 Trajectories at different gap in transient time |
考虑到尾迹脱落涡迁移路径的变化会对压气机的压比、效率产生影响,为了在高负荷对转压气机设计阶段合理选择轴向间隙大小,进而控制尾迹脱落涡的迁移路径,需进一步开展上游转子尾迹脱落涡在下游转子通道中迁移轨迹的影响因素的研究。
4 尾迹脱落涡级间迁移的影响因素 4.1 上游转子尾迹脱落涡脱落频率分析为了探究高负荷对转压气机尾迹脱落涡迁移路径的影响因素,首先需要澄清上游转子尾迹涡脱落频率的特点及与下游转子压力势场之间的关系。
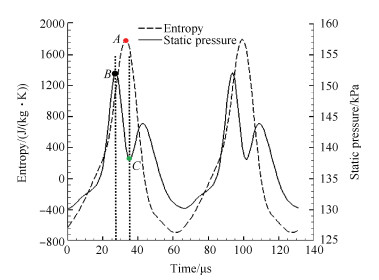
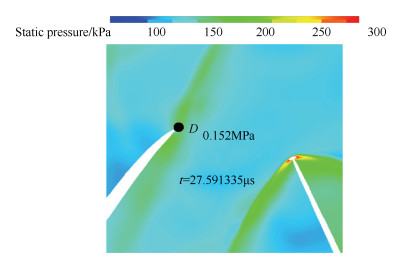
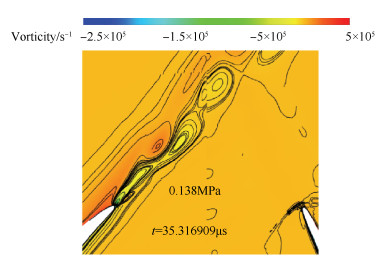
图 7中熵、静压随时间变化的曲线是通过在上游转子尾缘附近布置数值监测点(如图 8中点D所示)得到的。从中可以看出,上游转子尾缘附近熵值与静压值呈现明显的周期性波动,熵的极大值点A对应上游转子尾迹脱落涡涡核附近的熵值;静压变化曲线中的B点对应下游转子外伸激波的波后静压值(如图 8所示),C点对应上游转子尾迹脱落涡涡核附近的静压(如图 9所示)。
|
Fig. 7 Entropy and static pressure varying by time near R1 trialing edge |
|
Fig. 8 Static pressure near R1 trailing edge when shock wave is arriving |
|
Fig. 9 Static pressure value near R1 trailing edge with radial vorticity lines when wake vortex is forming |
为了更直观地分析上游转子尾迹涡的脱落频率,将图 7熵、静压随时间变化曲线进行傅里叶变换,得到相应的频谱图,如图 10所示。
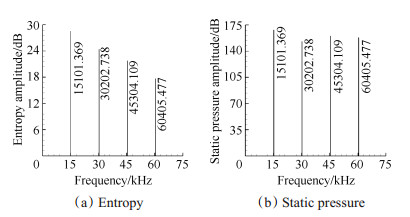
|
Fig. 10 Spectrum near R1 trailing edge |
对于对转压气机,定义RBPF(下游转子叶片相对于上游转子叶片的通过频率)公式为
| $ RBPF=\frac{{{n}_{1}}}{60}\cdot {{N}_{1}}+\frac{{{n}_{2}}}{60}\cdot {{N}_{2}} $ | (4) |
式中n1为上游转子转速大小,N1为上游转子叶片数,n2为上游转子转速大小,N2为上游转子叶片数。
考虑到上游转子转速大小为18310.8r/min,叶片数27;下游转子转速大小为15247.8r/min,叶片数27。将已知参数代入式(4),计算得到RBPF=15101.37Hz。
由图 10可知,熵、静压变化的频率与RBPF成倍数关系,表明上游转子尾迹涡的脱落频率与下游转子外伸激波扫掠上游转子尾缘的频率一致。且从图 7中B点与C点的时序位置可以看出,上游转子尾迹涡的脱落是由于下游转子外伸激波的扫掠而导致的。
4.2 上游转子尾迹脱落涡级间迁移无量纲准则关系式通过前文的分析可知,上游转子尾迹涡的脱落与下游转子外伸激波的扫掠相关。为此,在给定的几何、工况及轴向间隙下,上游转子尾迹涡脱落时,尾迹脱落涡相对于下游转子前缘的周向位置固定。
因此,在给定的几何、工况及轴向间隙下,上游转子尾迹脱落涡到达下游转子额线时的周向位移由以下两个参数的比值来表征(初始时刻t=0选取下游转子外伸激波扫掠上游转子尾缘的时刻,参照叶片选取该外伸激波所属的下游转子叶片):上游转子尾迹脱落涡到达下游转子额线时,相对于参照叶片的周向位移S与下游转子栅距W的比值。详细地推导如下:
为了简化上游转子尾迹脱落涡在级间轴向间隙内迁移的问题,选取上游转子为参照物。图 11将上游转子尾迹脱落涡级间迁移所涉及的影响因素进行了示意。
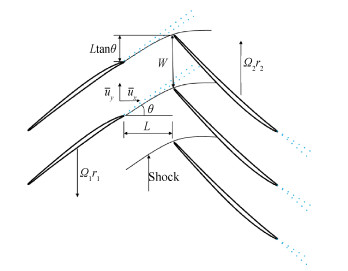
|
Fig. 11 Relative position of R1and R2 at time=0 |
假设级间的主流平均速度近似不变,则上游转子尾迹脱落涡在级间轴向间隙内输运的时间为
| $ {{t}_{\text{convect}}}=\frac{L}{{{{\bar{u}}}_{x}}} $ | (5) |
式中L为上下游转子间轴向间隙,ux为级间主流平均相对速度的轴向分速度,tconvect 为轴向间隙内输运时间。
初始时刻,下游转子外伸激波扫掠上游转子尾缘时,下游转子前缘相对上游转子尾缘的周向位移为
| $ {{S}_{\text{shock}\_\text{impact}}}=L\text{tan}\theta $ | (6) |
式中θ为下游转子外伸激波与轴向的夹角。
由于上游转子叶型偏折的影响,上游转子尾迹脱落涡完成级间输运时相对上游转子尾缘运动的周向位移为
| $ {{S}_{{{{\bar{u}}}_{y}}}}={{{\bar{u}}}_{y}}{{t}_{\text{convect}}} $ | (7) |
式中uy为级间主流平均相对速度的切向分速度。
在上游转子尾迹脱落涡级间输运的时间内,下游转子相对上游转子转过的周向位移为
| $ {{S}_{{{R}_{1}}+{{R}_{2}}}}=\left( {{\mathit{\Omega }}_{1}}{{r}_{1}}+{{\mathit{\Omega }}_{2}}{{r}_{2}} \right){{t}_{\text{convect}}} $ | (8) |
式中Ω1为上游转子角速度,r1为上游转子半径,Ω2为下游转子角速度,r2为下游转子半径。
上游转子尾迹脱落涡到达下游转子额线时,相对于参照叶片的周向位置为
| $ S={{S}_{{{R}_{1}}+{{R}_{2}}}}+{{S}_{\text{shock}\_\text{impact}}}-{{S}_{{{{\bar{u}}}_{y}}}} $ | (9) |
将式(5),(6),(8)代入式(9)得到S,并与下游转子栅距做比值,则可得到高负荷对转压气机上游转子尾迹脱落涡级间迁移的无量纲准则关系式为
| $ {{B}_{5}}=\frac{L}{W}\left( \frac{{{\Omega }_{1}}{{r}_{1}}+{{\Omega }_{2}}{{r}_{2}}-{{{\bar{u}}}_{y}}}{{{{\bar{u}}}_{x}}}+\text{tan}\theta \right) $ | (10) |
式中W为下游转子栅距。
由以上公式可知,对于高负荷对转压气机,上游转子尾迹脱落涡级间迁移路径与上下游转子的初相位置无关。同时,当上游叶排为静子且无偏折时,式(10)与Botros[16]静-动干涉下所取得的上游导叶尾迹脱落涡级间迁移无量纲准则关系式(11)一致。
| $ {{B}_{3}}=\frac{L}{W}\left( \frac{{\mathit{\Omega }} r}{{{u}_{x}}}+\text{tan}\theta \right) $ | (11) |
为了在设计阶段合理选择轴向间隙大小,进而控制尾迹脱落涡的迁移路径,可基于上文得到的高负荷对转压气机尾迹脱落涡级间迁移无量纲准则关系式,并结合一维预估、通流计算与激波模型,对尾迹脱落涡的迁移路径进行预估。
如图 12所示,经过一维预估得到以下参数:轴向间隙L=0.021m;上游转子尾缘处旋转半径r1=0.191m;下游转子前缘处旋转半径r2=0.193m,下游转子栅距W=0.045m;上游转子转速n1=18310.8r/min;下游转子转速n2=15247.8r/min。
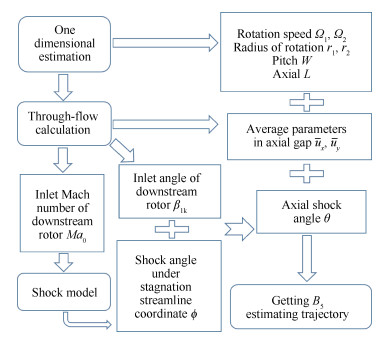
|
Fig. 12 Procedure of predicting the trajectory |
采用S2通流计算得到60%叶高轴向间隙内部分参数:下游转子来流马赫数Ma0=1.4;下游转子前缘进口几何角β1k =66.01°;轴向间隙、进出口速度及其平均值(如表 5所示)。
|
|
Table 5 Parameters of S2 calculation at axial gap |
依据通流计算得到的下游转子来流马赫数、前缘进口几何角,采用Moeckel[22]提出的双曲线逼近脱体激波模型,可预估得到滞止流线坐标系下的激波角。然而,式(7)中的角度θ为下游转子外伸激波与轴向的夹角。因此,需要进行简单的坐标变换,如图 13所示。滞止流线坐标下,脱体激波渐近线角度为
| $ \phi =\sqrt{Ma_{0}^{2}-1} $ | (12) |
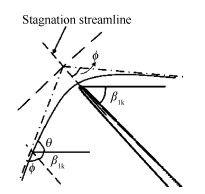
|
Fig. 13 Relationship of angles |
式中ϕ为渐进线角度(弧度),Ma0为来流马赫数。
将通流计算所得的下游转子来流马赫数代入式(12),计算出对应的渐近线角度为56.14°。由于下游转子外伸激波在靠近上游转子尾缘时,与渐近线基本平行,因此,可近似采用渐近线角度,预估滞止流线坐标系下的激波角。对于前缘较薄、无预压缩的超声速叶栅,在设计工况下,滞止流线与轴向的夹角,与下游转子前缘进口几何角近似。则近似可以得出下游转子外伸激波与轴向的夹角表达式
| $ \theta =180-{{\beta }_{1\text{k}}}-\phi $ | (13) |
将渐近线角度、前缘几何角代入式(13),则可得激波角为θ=57.85°,见图 13。
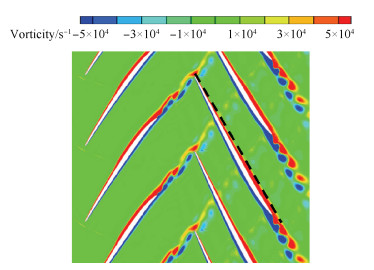
将以上已知参数代入式(11),则有B5=1.9。说明上游转子尾迹脱落涡到达下游转子额线时,相对于参照叶片的周向位置为1.9倍的下游转子栅距,即上游转子尾迹脱落涡在下游转子通道中迁移的轨迹为靠近压力面。
图 14为设计轴向间隙下,设计点的非定常数值模拟结果。对其进行分析,得到上游转子尾迹脱落涡到达下游转子额线时,相对于参照叶片的周向位置为1.967倍的下游转子栅距,预估值与数值模拟计算值相对误差为3.5%。
|
Fig. 14 Unsteady numerical simulation result at design axial gap and under design condition |
针对不同轴向间隙,开展高负荷对转压气机尾迹脱落涡级间迁移影响因素研究,所取得的主要结论如下:
(1)对于给定的叶型与工况,同一轴向间隙下,上游转子尾迹脱落涡到达下游转子通道入口时的周向位置不变;随着轴向间隙增大,尾迹脱落涡迁移路径由下游转子压力面逐渐向吸力面偏移。
(2)上游转子尾迹涡的脱落频率与下游转子外伸激波扫掠上游转子尾缘的频率一致。
(3)高负荷对转压气机上游转子尾迹脱落涡,在下游转子通道中的迁移轨迹与上下游转子的初相位置无关。
(4)通过理论分析与数学推导,建立了高负荷对转压气机尾迹脱落涡级间迁移无量纲准则关系式,表明尾迹脱落涡的迁移路径与轴向间隙、下游转子栅距、上下游转子转速、下游转子外伸激波角度、级间主流平均相对速度大小与方向有关。
(5)基于建立的尾迹脱落涡级间迁移路径无量纲准则关系式,结合一维预估、通流计算及简单激波模型,在设计阶段预估上游转子尾迹脱落涡到达下游转子入口时,相对参照叶片的周向位置,预估值与数值模拟计算值相对误差为3.5%,较为准确,进而可为高负荷对转压气机设计阶段合理选择轴向间隙以控制尾迹脱落涡迁移路径提供参考。
致谢: 感谢国家自然科学基金重大项目和国家重点研发计划资助。
| [1] |
Valkov T V, Tan C S. Effect of Upstream Rotor Vortical Disturbances on the Time-Average Performance of Axial Compressorm Stators, Part 2: Rotor Tip Vortex / Streamwise Vortex-Stator Blade Interactions[J]. Journal of Turbomachinery, 1998, 121(3): 387-397.
(  0) 0) |
| [2] |
Sirakov B T, Tan C S. Effect of Unsteady Stator WakeRotor Double-Leakage Tip Clearance Flow Interaction on Time-Average Compressor Performance[J]. Journal of Turbomachinery, 2003, 125(3): 465-474.
(  0) 0) |
| [3] |
Smith L H. Casing Boundary Layers in Multistage Axial Flow Compressors[C]. Switzerland: Proceeding of the Symposium on Flow Research on Blading, 1970: 275 – 304.
(  0) 0) |
| [4] |
Mikolajczak A A. The Practical Importance of Unsteady Flow[R]. AGARD CP-177,1976
(  0) 0) |
| [5] |
Smith L H. Wake Dispersion in Turbomachines[J]. Journal of Basic Engineering, 1996, 88(3): 688-690.
(  0) 0) |
| [6] |
Smith L H. Wake Ingestion Propulsion Benefit[J]. Journal of Propulsion & Power, 1993, 9(1): 74-82.
(  0) 0) |
| [7] |
Tan C S. Internal Flow-Concepts and Applications[D]. Cambridge: Cambridge University Press, 2007.
(  0) 0) |
| [8] |
Valkov T, Tan C. Effects of Upstream Rotor Vortical Disturbances on Time-Average Performance of Axial Compressor Stator, Part 1: Framework of Technical Approach and Rotor Wakes-Stator Blade Interaction Interaction[J]. Journal of Turbomachinery, 1999, 121(3): 377-386.
(  0) 0) |
| [9] |
Adamczyk J J. Wake Mixing in Axial Flow Compressors [R]. ASME GT 1996-29.
(  0) 0) |
| [10] |
Steven E Gorrell, Theodore H Okiishi, William W Copenhaver. Stator-Rotor Interactions in a Transonic Com pressor, Part 1: Effect of Blade-Row Spacing on Performance[R]. Journal of Turbomachinery, 2003, 125 (2): 328-335.
(  0) 0) |
| [11] |
Gorrell S E, Okiishi T H, Copenhaver W W. Stator-Rotor Interactions in a Transonic Compressor, Part 2: Description of a Loss-Producing Mechanism[J]. Journal of Turbomachinery, 2003, 125(2): 336-345. DOI:10.1115/1.1540120
(  0) 0) |
| [12] |
Gorrell S E, Car D, Puterbaugh S L, et al. An Investigation of Wake-Shock Interactions in a Transonic Compressor with Digital Particle Image Velocimetry and TimeAccurate Computational Fluid Dynamics[J]. Journal of Turbomachinery, 2005, 128(4): 616-626.
(  0) 0) |
| [13] |
Clark K P, Gorrell S E. Analysis and Prediction of Shock-Induced Vortex Circulation in Transonic Com pressors[J]. Journal of Turbomachinery, 2015, 137(12).
(  0) 0) |
| [14] |
Estevadeordal J, Gogineni S, Goss L, et al. Study of Wake-Blade Interactions in a Transonic Compressor Using Flow Visualization and DPIV[J]. Journal of Fluids Engineering, 2002, 124(1): 166-175. DOI:10.1115/1.1429638
(  0) 0) |
| [15] |
Zachial A, Nurnberger D. A Numerical Study on the Influence of Vane-Blade Spacing on a Compressor Stage at Sub-and Trasonic Operating Conditions[R]. ASME GT 2003-38020.
(  0) 0) |
| [16] |
Botros B. Impact of Unsteady Flow Processes on the Performance of a High Speed Axial Flow Compressor[D]. Massachusetts: Massachusetts Institute of Technology, 2008.
(  0) 0) |
| [17] |
张恒铭, 黄秀全. 高负荷对转压气机中尾迹传播机制研究[J]. 推进技术, 2015, 36(10): 1479-1486. (ZHANG Heng-ming, HUANG Xiu-quan. Investigation of Wake Propagation in a Highly Loaded Counter-Rotating Compressor[J]. Journal of Propulsion Technology, 2015, 36(10): 1479-1486.)
(  0) 0) |
| [18] |
张恒铭, 黄秀全, 张翔, 等. 两级对转风扇非定常特性分析[J]. 推进技术, 2016, 37(2): 209-217. (ZHANG Heng-ming, HUANG Xiu-quan, ZHANG Xiang, et al. Unsteady Characteristic Analysis of a TwoStage Counter-Rotating Fan[J]. Journal of Propulsion Technology, 2016, 37(2): 209-217.)
(  0) 0) |
| [19] |
He L. Method of Simulating Unsteady Turbomachinery Flows with Multiple Perturbations[J]. AIAA Journal, 1992, 30(11): 2730-2735. DOI:10.2514/3.11291
(  0) 0) |
| [20] |
Knapke R D, Turner M G. Unsteady Simulations of a Counter-Rotating Aspirated Compressor[R]. ASME GT 2013-95209.
(  0) 0) |
| [21] |
刘波, 王雷, 黄建. 非线性谐波法在双级对转压气机中的进一步校验[J]. 航空动力学报, 2013, 28(6): 1333-1341. (  0) 0) |
| [22] |
Moeckel W E. Approximate Method for Predicting Form and Location of Detached Shock Waves Ahead of Plane or Axially Symmetric Bodies[R]. NACA-TN-1921.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


