近年来,三维内转式进气道作为一种新型高超声速进气道,由于其压缩效率高、浸润面积小、工作马赫数范围广、进出口形状可控等优势,逐渐成为各国研究人员的关注重点。
德国学者Busemann于1942年首先提出了内锥形流场概念,并设计出由一簇汇于一点的等熵压缩波和一道反射激波组成的经典“Busemann进气道”,这种进气道压缩效率很高,但也存在一些不足,譬如压缩面过长,在高马赫数下粘性损失显著;再如纯内压式构型使其在低马赫数下无法自起动。随后Tam等[1, 2]设计了圆形进口流线追踪Busemann进气道,在基准流场内流线追踪出的进气道型面具有天然的唇口侧溢流窗,一定程度上解决了起动问题。随着截面渐变技术的出现,Smart[3]将直接追踪的流线光滑合并为一种矩形进口转椭圆出口的REST内转式进气道,实现了对进出口形状的控制。Tylor等[4]研究了典型渐变函数对截面渐变进气道性能的影响。美国空军实验室Malo-Molina等[5]为减弱多道激波之间的相互干扰,设计出一种新型Jaws进气道,这种进气道在竖直和水平方向上对来流进行压缩的同时,两个方向上激波不会形成交叉反射。
在国内,尤延铖等[6, 7]提出了进出口形状可定制的内乘波进气道设计方法。南向军、李永洲等[8, 9]通过给定参数分布规律反设计出基准流场,并对进气道进行了仿真和试验研究,性能优良。李永洲[10]还以损失部分流量为代价,通过放气减小了出口涡流区大小,并降低了进气道自起动马赫数。朱呈祥等[11]将矩形进出口内乘波式进气道与典型侧压进气道进行了对比。王德鹏等[12]研究了进口形状对内转式进气道起动特性的影响。
无论是直接流线追踪进气道还是截面渐变进气道,由于其三维压缩特性,在真实粘性作用下,其流场会与基准流场有所偏差,且隔离段内常出现“对涡”等流动现象[13, 14],导致出口气流畸变较大,进气道性能下降。
本文通过设置不同的进口和出口宽高比,给出了一种顶压和侧压比例可控的矩形转矩形截面渐变内转式进气道设计方法,实现了对周向截面内不同位置的激波强度和压力分布的控制,减弱了局部激波/附面层相互作用和周向流动强度。随后研究了进出口宽高比的各种组合方式对进气道总压恢复与气流畸变等参数的影响规律,得到了截面渐变内转式进气道进出口宽高比的最优选取范围。
2 进出口宽高比不等的内转式进气道设计方法进出口形状同时可控的内转式进气道设计流程为:(1)设计内锥形基准流场;(2)进/出口型线分别流线追踪;(3)两组流线合并实现截面渐变;(4)粘性修正。
2.1 基准流场设计作为初步研究,选取一种较为成熟的反正切马赫数分布规律设计内收缩基准流场,其函数为
| $ \begin{array}{*{20}{l}} {Ma\left( x \right) = M{a_{\rm{r}}} - }\\ {\left[ {c \cdot {\rm{arctan}}\left( {a\left( {x - b} \right)} \right) + c \cdot {\rm{arctan}}\left( {ab} \right)} \right]} \end{array} $ | (1) |
其中的设计参数a=7.2,b=0.45,c=0.35,此外,基准流场的其它设计参数取值分别为:设计马赫数Mai=6,进口半径Ri=0.25m,前缘压缩角δ=6°,中心体半径Rc=0.1Ri。特征线法反设计出壁面型线后,重新计算得到的流场结构如图 1所示,主要性能参数列于表 1,表中φ,σ,π,Mae分别为流量系数、总压恢复系数、出口压升和出口马赫数,CRT,CRI和L分别为总收缩比、内收缩比和长度。
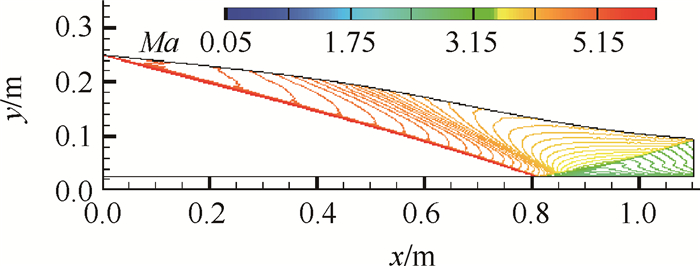
|
Fig. 1 Configuration of the basic flow field |
|
|
Table 1 Geometry and performance parameters of the basic flow field |
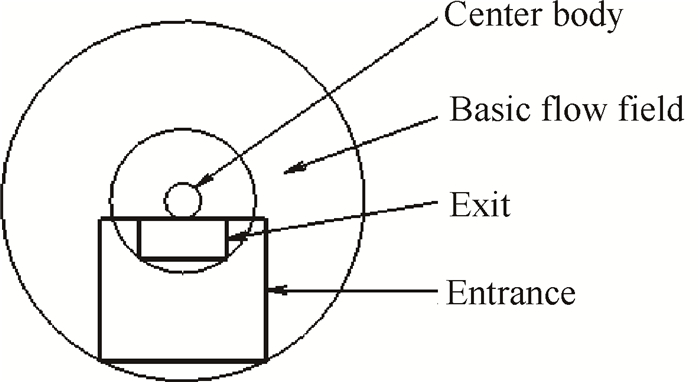
对于要求进出口形状同时可控的内转式进气道,需在基准流场内从进、出口分别向后、向前追踪流线,得到两个流线追踪进气道,如图 2所示。其中,为使两个前后流线追踪进气道匹配,需保证进出口面积合适,具体方法为:先给定矩形出口型线,则进口矩形的面积大小取为与矩形出口向前追踪出的进气道捕获面积相同。
|
Fig. 2 Entrance and exit profile in the basic flow field |
然后将二者对应流线进行合并,本文采用的是一种简便且适应性较广的线性函数,在基准流场柱坐标系下表示为
| $ \left\{ {\begin{array}{*{20}{l}} {r\left( z \right) = k \cdot {r_1}\left( z \right) + \left( {1 - k} \right) \cdot {r_2}\left( z \right)}\\ {\varphi \left( z \right) = k \cdot {\varphi _1}\left( z \right) + \left( {1 - k} \right) \cdot {\varphi _2}\left( z \right)} \end{array}} \right. $ | (2) |
式中下标1,2分别表示进口向后追踪流线和出口向前追踪流线。
对三维流线进行粘性修正难度极大,在此选取一种简单实用的修正方法,采用位移厚度进行边界层修正,其物理意义明显,修正后型面扩大的流通面积正好用于补偿边界层内的低速流。其公式为[15]
| $ \delta \left( x \right) = Ax + Bx{{\rm{e}}^{ - x}} $ | (3) |
式中A,B为系数,与来流马赫数、单位雷诺数等有关。
值得注意的是,若沿每根流线分别进行精确的边界层修正,出口形状将不再是严格矩形,为保证出口形状精确可控,采取整体边界层修正的方法。即在沿流向同一位置上,顶板上每一根流线均向外修正同一个合适的边界层厚度,其大小等于所有流线边界层厚度的平均值
| $ \delta {\rm{ = }}\sum\limits_{i = 1}^N {\left( {{\delta _i} \cdot \Delta {d_i}} \right)} /\sum\limits_{i = 1}^N {\Delta {d_i}} $ | (4) |
侧板和唇口板与之类似。
3 进气道模型依照上述设计方法在同一基准流场内生成了A,B,C,D四组内转式进气道模型,图 3所示为其中一个典型模型示意图。每一组模型在矩形转矩形截面渐变过程中,保持进口矩形的宽高比AR1相等,分别为0.8,1.2,1.6,2.0,出口矩形的宽高比AR2从0.8逐渐增大至2.4。其中,如果进出口宽高比相差过大,截面渐变后部分型面的前缘压缩角可能会减小为负值,此时远前方来流进入进气道后会出现一段膨胀加速过程,这与进气道对气流减速增压的功能相悖,为避免这种情况发生,A组舍去了AR2为2.4的模型,D组舍去了AR1为0.8的模型。此外,定义RAR(Ratio of the aspect ratios)为出口矩形与进口矩形宽高比之比,即
| $ RAR = A{R_2}/A{R_1} $ | (5) |

|
Fig. 3 Inward turning inlet with rectangular entrance and exit of different aspect ratios |
参数RAR用来描述截面渐变过程中选取的进出口宽高比之间的相对大小关系。
在圆形基准流场内选取不同宽高比进出口时,其面积也各不相同,不同捕获面积下进气道的长度没有可比性,为研究进出口宽高比对进气道长度的影响规律,将各模型缩放至同一捕获面积进行比较,即
| $ L' = \sqrt {\frac{{{A_0}}}{A}} \cdot L $ | (6) |
式中A和L分别为进气道的捕获面积和真实长度,L'为缩放后长度。此处以Model A1为基准,A0为其捕获面积,Model A1的进、出口宽高比相等,同为0.8。
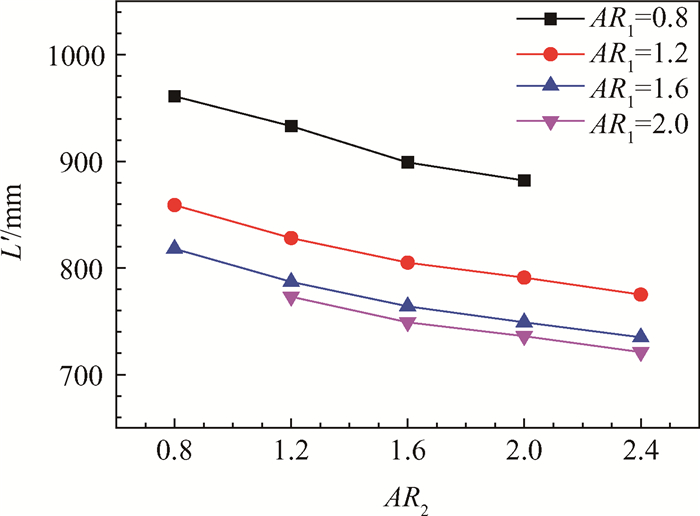
图 4给出了进出口宽高比AR1和AR2对长度L'的影响规律,增大AR1与AR2均能减短进气道长度,在1.2~2.4内,增大进口宽高比AR1可使长度缩短约17%,增大出口宽高比AR2可使长度缩短约9%。所有模型中最短的Model D4相对于Model A1的最大减幅达到25.0%,这对减轻进气道的重量和粘阻是有帮助的。
|
Fig. 4 Changing regulation of inlet lengths with the aspect ratios at the same capture area |
采用ICEM软件划分结构网格,由于模型的对称性,取其一半进行划分和计算,壁面第一层网格高度为0.1,增长因子1.15,总网格量约250万(图 5)。

|
Fig. 5 Mesh of the inward turning inlet |
采用Fluent软件求解,通量差分选取Roe-FDS格式,湍流模型选取k-ε (RNG)方程,均用二阶迎风格式进行离散。使用Sutherland公式计算分子粘性系数,壁面均为绝热无滑移边界,同时使用了压力远场、压力出口及对称面等边界条件。收敛标准为各项残差下降三个数量级并保持稳定,且沿程截面流量守恒。这种数值模拟方法已在文献[16]、[17]的内转式进气道风洞试验中得到验证。
对于设计点Ma6,来流条件设置为静压2.549kPa,静温221.55K。
5 计算结果分析 5.1 进出口宽高比比例对总压恢复系数的影响表 2为四组模型的详细数值计算结果,其中φ,πth,σex和Dex分别为进气道流量系数、喉道压比、出口总压恢复系数和出口流场畸变指数。各模型流量系数均接近于1,喉道压比与基准流场出口压比基本一致,但出口总压恢复系数和气流畸变指数有较大差异。
|
|
Table 2 Performance parameters of different models |
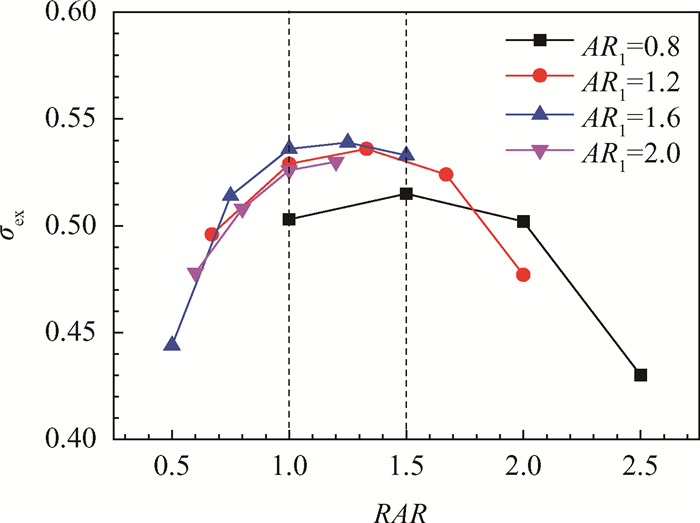
图 6给出了进出口宽高比比例对进气道出口总压恢复系数的影响规律,图中仅AR1=0.8一条曲线位于下部,其它三条近似贴合,并呈抛物线形状。值得注意的是,抛物线的对称轴也即各条曲线的峰值在RAR约等于1.25时取到,总压恢复系数最大值超出最小值25.3%,说明截面渐变过程中选择宽高比相等的进出口并不能使出口总压恢复系数最高。RAR在1~1.5的进气道出口总压恢复均处于较高水平,区间之外则迅速下降。此外,进口宽高比小于1时,也会导致出口总压恢复系数偏低。
|
Fig. 6 Changing regulation of throat and exit total pressure recovery coefficient with RAR |
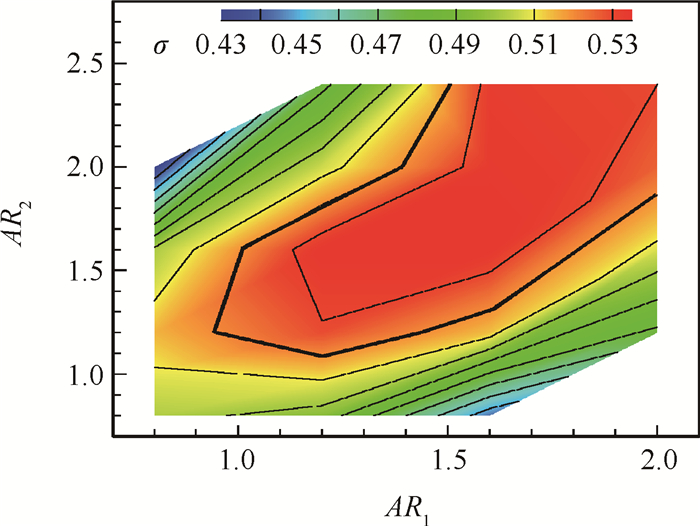
利用已有的18个数据点及内部插值的方法,制成了AR1和AR2分别在0.8~2.0和0.8~2.4的出口总压恢复系数云图(图 7),可作为截面渐变内转式进气道进出口宽高比的选取依据。
|
Fig. 7 Exit total pressure recovery coefficient contour on different combinations of the aspect ratios |
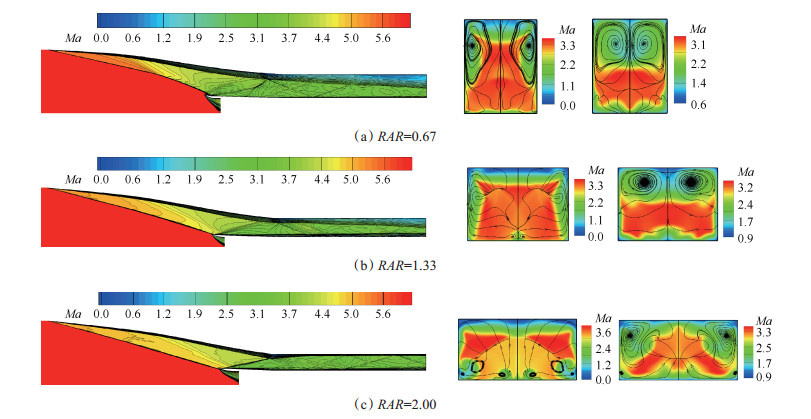
图 8给出了出口与进口宽高比比例RAR分别为小、中、大三种典型情况下的进气道对称面、喉道和出口截面流场结构。RAR较小时,进气道顶向压缩弱于侧向压缩,对称面上前缘激波开始很弱,随后在侧板的作用下逐渐变强,弯曲程度也越来越大,当出口宽高比逐渐变大时,前缘激波弯曲程度越来越小。RAR过小或过大均会导致前缘激波与基准流场差距过大,进而造成总压损失增大。
|
Fig. 8 Flowfield structures of inward turning inlets with different RAR (Left: Mach number contours on symmetry; Right: Mach number contours with surface streamlines on throat and exit) |
可以看出,各模型喉道截面的主流区范围较大,但随后由于横向压力差的存在,隔离段的周向二次流动逐渐发展,至出口截面主流区范围不到一半且具有较大的非均匀性。当RAR较小时,在较强的侧向压缩下侧板肩部边界层较厚并发生了分离,气流沿侧板向顶板上洗、沿顶板向对称面汇聚,最终这些低能流在整个流道靠近顶板一侧占据了一半以上的流通面积。随着进气道出口宽高比逐渐增大到与进口相近,这种对涡现象变得尤为明显。当RAR进一步增大,进气道的侧向压缩更弱,侧板边界层很薄且未发生分离,上洗气流难以通过如此薄的附面层向顶板流动,仅在侧板和顶板分别形成了两处较小的涡流区,同时由于宽度较大,涡流最终未在对称面相遇,相当于减弱了整体对涡流动。
5.2 进出口宽高比比例对出口气流畸变的影响为定量说明气流的非均匀程度,定义参数D作为流场畸变指数[18]
| $ D = \sum \left| {{\rho _i}{u_i} - \overline {\rho u} } \right| \cdot {A_i}/\dot m $ | (7) |
式中
| $ \overline {\rho u} = \sum \left( {{\rho _i}{u_i} \cdot {{\dot m}_i}} \right)/\dot m $ |
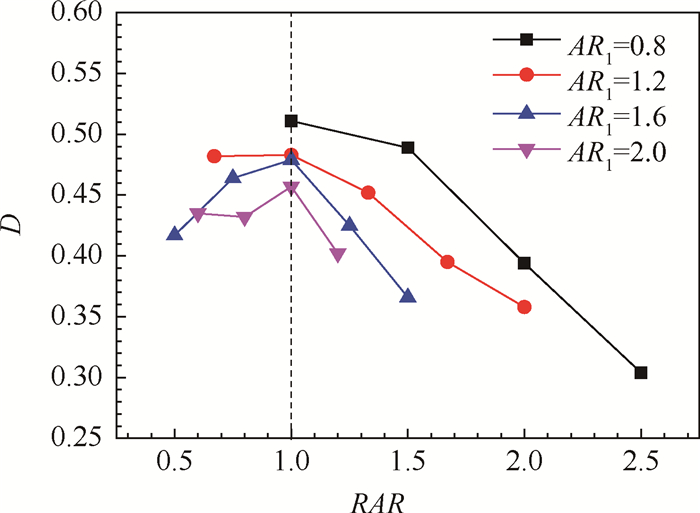
畸变指数D反映了通过截面的动量变化大小,其值越大,说明流动非均匀程度越大。如图 9所示,四组模型具有相似的变化规律,进出口宽高比相等时,出口畸变指数D最大;RAR不等于1时,D显著减小。四组模型最大减幅分别达到40.5%,25.9%,23.6%,12.0%。
|
Fig. 9 Changing regulation of distortion indexes with RAR |
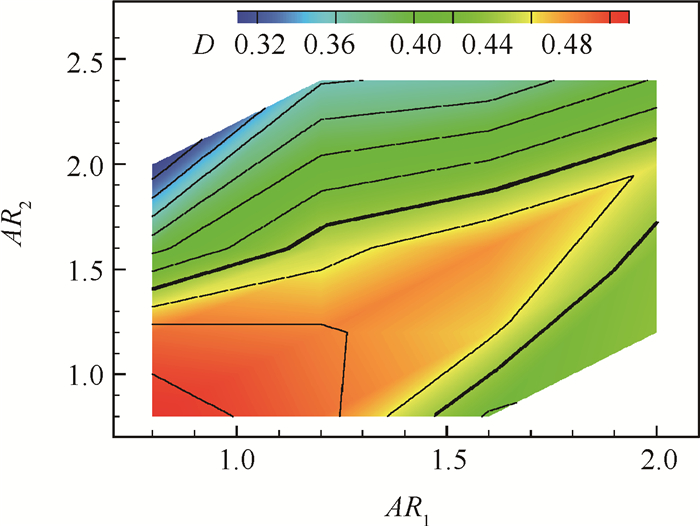
利用已有的18个数据点及内部插值的方法,制成了AR1和AR2分别在0.8~2.0和0.8~2.4的出口气流畸变云图(图 10)。可以看到,增大进口宽高比,并设置出口宽高比与进口不等,可以减小出口气流畸变。原因在于进出口宽高比相等时进气道三维压缩效应最为明显,横向压力梯度最大,涡流必然最严重,而当出口宽高比较小时,进气道构型趋于无顶压的侧压式进气道,当出口宽高比较大时,进气道构型趋于二元进气道,这两种进气道的气流畸变都相对较小。
|
Fig. 10 Exit distortion index contour on different combinations of the aspect ratios |
通过本文研究,得到以下结论:
(1)按照本文所述截面渐变及粘性修正方法,可以得到不同宽高比矩形进出口的截面渐变内转式进气道,进气道能够大致保持基准流场的基本特征,设计点流量系数接近于1。
(2)同一基准流场内,出口与进口宽高比的比值RAR是截面渐变进气道性能的主要影响因素,该比值在1~1.5时,进气道出口总压恢复系数整体较高;该比值不等于1时,进气道出口气流畸变显著减小。
(3)在同一基准流场和捕获面积下,增大进口宽高比能显著缩短进气道长度,增大出口宽高比能小幅缩短进气道长度,进出口宽高比在0.8~2.4内的进气道长度最大减幅达25%。
| [1] |
Tam C J, Baurle R A. Inviscid CFD Analysis of Streamline Traced Hypersonic Inlets at Off-Design Conditions[R]. AIAA 2001-0675. http://arc.aiaa.org/doi/pdf/10.2514/6.2001-675
(  0) 0) |
| [2] |
Tam C J, Baurle R A, Streby G D. Numerical Analysis of Stream-Traced Hypersonic Inlets[R]. AIAA 2003-13. https://www.researchgate.net/publication/267231391_Numerical_Analysis_of_Streamline-Traced_Hypersonic_Inlets
(  0) 0) |
| [3] |
Smart M K. Design of Three-Dimensional Hypersonic Inlets with Rectangular-to-Elliptical Shape Transition[J]. Journal of Power and Propulsion, 1999, 15(3): 408-416. DOI:10.2514/2.5459
(  0) 0) |
| [4] |
Taylor T, Vanwie D. Performance Analysis of Hypersonic Shape-Changing Inlets Derived from Morphing Streamline Traced Flowpaths[R]. AIAA 2008-2635. https://arc.aiaa.org/doi/abs/10.2514/6.2008-2635
(  0) 0) |
| [5] |
Malo-Molina F J, Gaitonde D V, Kutschenreuter P H. Numerical Investigation of an Innovative inward Turning Inlet[R]. AIAA 2005-4871. http://www.researchgate.net/publication/268561409_numerical_investigation_of_an_innovative_inward_turning_inlet
(  0) 0) |
| [6] |
尤延铖, 梁德旺, 黄国平. 一种新型内乘波式进气道初步研究[J]. 推进技术, 2006, 27(3): 252-256. (YOU Yan-cheng, LIANG De-wang, HUANG Guo-ping. Investigation of Internal Waverider Derived Hypersonic Inlet[J]. Journal of Propulsion Technology, 2006, 27(3): 252-256. DOI:10.3321/j.issn:1001-4055.2006.03.015)
(  0) 0) |
| [7] |
尤延铖, 梁德旺. 基于内乘波概念的三维变截面高超声速进气道[J]. 中国科学E缉:技术科学, 2009, 39(8): 1483-1494. (  0) 0) |
| [8] |
南向军, 张堃元, 金志光, 等. 压升规律可控的高超声速内收缩进气道设计[J]. 航空动力学报, 2011, 26(3): 518-523. (  0) 0) |
| [9] |
李永洲, 张堃元, 南向军. 基于马赫数分布规律可控概念的高超声速内收缩进气道设计[J]. 航空动力学报, 2012, 27(11): 2484-2491. (  0) 0) |
| [10] |
李永洲, 张堃元, 张留欢. 抽吸对高超声速内收缩进气道涡流区及起动性能的影响[J]. 航空动力学报, 2016, 31(7): 1630-1637. (  0) 0) |
| [11] |
朱呈祥, 黄国平, 尤延铖, 等. 内乘波式进气道与典型侧压式进气道的性能对比[J]. 推进技术, 2011, 32(2): 151-158. (ZHU Cheng-xiang, HUANG Guo-ping, YOU Yan-cheng, et al. Performance Comparison Between Internal Waverider Inlet and Typical Sidewall Compression Inlet[J]. Journal of Propulsion Technology, 2011, 32(2): 151-158.)
(  0) 0) |
| [12] |
王德鹏, 田方超, 张启帆, 等. 进口形状对内转式进气道的起动特性影响[J]. 航空动力学报, 2015, 30(6): 1400-1406. (  0) 0) |
| [13] |
李永洲.马赫数分布可控的高超声速内收缩进气道及其一体化设计研究[D].南京: 南京航空航天大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10287-1015951706.htm
(  0) 0) |
| [14] |
南向军.压升规律可控的高超声速内收缩进气道设计方法研究[D].南京: 南京航空航天大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10287-1013024016.htm
(  0) 0) |
| [15] |
Travis W Drayna, Ioannis Nompelis, Graham V Cabdler. Hypersonic Inward Turning Inlets: Design and Optimization[R]. AIAA 2006-297. https://www.researchgate.net/publication/269129623_Hypersonic_Inward_Turning_Inlets_Design_and_Optimization?ev=auth_pub
(  0) 0) |
| [16] |
南向军, 张堃元, 金志光, 等. 矩形转圆形高超声速内收缩进气道数值及试验研究[J]. 航空学报, 2011, 32(6): 988-996. (  0) 0) |
| [17] |
李永洲, 张堃元, 孙迪. 马赫数分布可控的方转圆高超声速内收缩进气道实验研究[J]. 航空学报, 2016, 37(10): 2970-2979. (  0) 0) |
| [18] |
Bagaveyev N T, Engbom W A, Bhagwandin V A. Parametric Investigation of Racetrack-to-Circular Cross Section Transition of a Dual-Mode Ramjet Isolator[R]. AIAA 2010-0942. http://www.researchgate.net/publication/269051358_parametric_investigation_of_racetrack-to-circular_cross-section_transition_of_a_dual-mode_ramjet_isolator
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


