涡轴发动机具有重量轻、体积小、功率大、振动小、易于启动、便于维修与操纵等优点,已经作为直升机的主要动力系统得到了广泛的使用。通过几十年的发展,涡轴发动机已成功研制了四代。从发展时间上来看,第一代涡轴发动机于20世纪50年代开始研制,20世纪60年代开始服役;第二代涡轴发动机于20世纪60年代开始研制;第三代代涡轴发动机于20世纪70年代末80年代初研制;第四代涡轴发动机于20世纪80年代以后研制。
第1代~4代的典型涡轴发动机主要技术参数[1]如表 1。从表 1可知,涡轴发展的主要技术规律[2]为:(1)涡轴发动机的循环参数不断提高,如压气机总压比opr从第一代的7提高到第四代的15左右,涡轮前总温T4由第一代的1200K提高到第四代的1600K。这使得发动机的总体性能大大提高,单位功率ps从第一代的150kW/(kg∙s)提高到第四代的300kW/(kg∙s),平均每代单位功率提高50kW/(kg∙s);耗油率SFC由第一代的0.37kg/(kW∙h)降低到第四代的0.27kg/(kW∙h)左右;功重比P/W从第一代的3.675kW/kg增加到第四代的7.35kW/kg。(2)涡轴发动机结构产生了较大变化,如涡轴发动机的压气机结构形式发生了改变,第一代的纯轴流发展到第二代第三代的轴流加离心的组合压气机,第四代则是两级离心的组合压气机的结构形式。
|
|
Table 1 Technical parameters of turboshaft |
目前,美英等国已经开展了第五代涡轴发动机的研究。由于配装T700-701D[3]涡轴发动机的美军UH-60“黑鹰”和AH-64“阿帕奇”直升机在伊拉克和阿富汗战争中显示出作战能力的不足,T700-701D改进潜力有限,因此,美国航空应用技术理事会于2007年启动了先进经济可承受涡轮发动机(AATE)计划,实质是研制第五代涡轴发动机,用于给“阿帕奇”和“黑鹰”换发。该计划的两个验证发动机项目之一便是GE公司的GE3000。据AATE计划透露GE3000需要与T700-701D发动机尺寸相同,质量为204kg,功率为2237kW,且在保持T700-701D发动机质量和良好的可靠性、可维护性、耐久性与可生产性的基础上,将油耗降低25%,功重比提高65%,寿命延长20%,成本降低35%[4, 5]。GE公司透露,为了达到以上目标,在GE3000研制过程中采用了先进的3D气动设计技术、高温陶瓷基复合材料以及增材制造技术。目前关于GE3000的相关结构、性能、部件资料较少,难以对GE3000的真实部件性能与循环参数有一个清楚的了解,对于新技术以及新材料的实际作用效果也难以进行准确的评估。
因此提出了一种基于涡轴发动机性能与尺寸重量相耦合的评估方法,该方法在基于部件法涡轴发动机总体性能与尺寸重量计算模型的基础上,对涡轴发动机的总体性能、总体结构、部件的气动/结构/强度/尺寸以及重量等进行评估。通过该方法对“阿帕奇”和“黑鹰”的动力涡轴发动机T700-701D的换发美国的第五代先进涡轴发动机GE3000进行评估,评估结果与GE公司公布的数据对比分析来验证模型可靠性,并以评估结果来研究第五代涡轴发动机技术参数的发展以及新技术新材料的引入对涡轴发动机总体性能的影响。
2 计算模型研究对象为带组合压气机的单转子燃气发生器和功率前输出的自由涡轮式涡轴发动机,主要部件包括进气道、轴流加离心的组合压气机、燃烧室、燃气涡轮、自由涡轮和尾喷管。
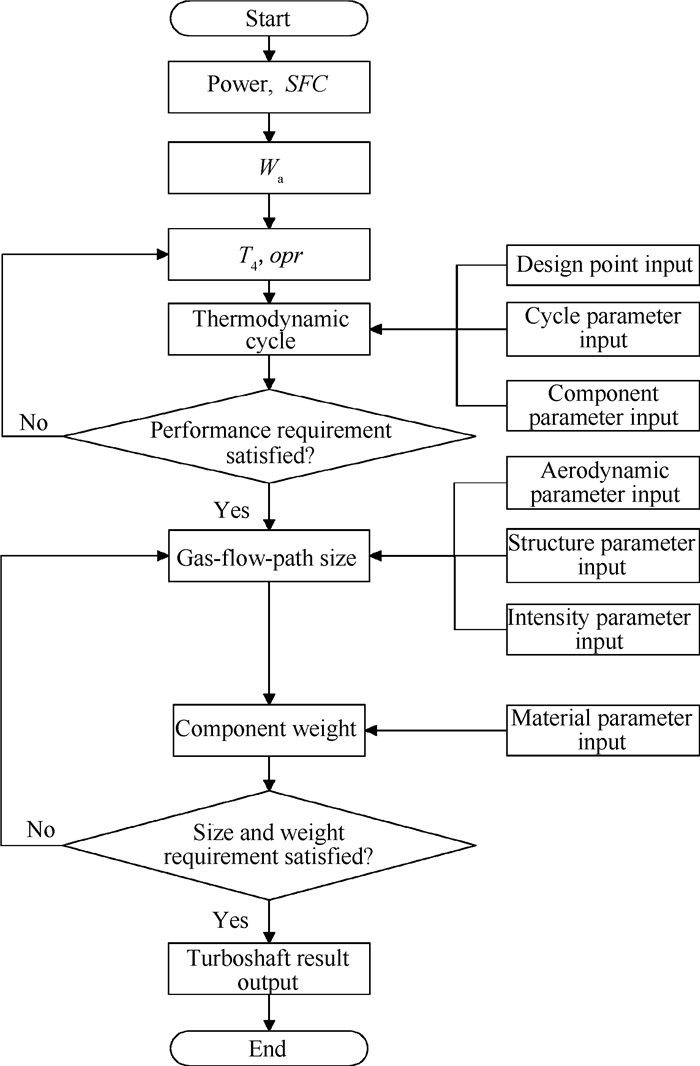
基于涡轴发动机性能与尺寸重量的耦合评估方法流程图如图 1,主要的计算模型包括涡轴发动机的总体性能评估模体、尺寸重量评估模型以及部件性能/气动/结构/强度等的耦合评估模型,主要的思路是根据待评估涡轴发动机的设计年代和设计厂商的设计水平,输入发动机设计点和各部件的性能参数(效率η,总压恢复系数σ等),引用冷气量计算模型[6~8]进行涡轴发动机的循环分析,得到满足涡轴发动机总体性能参数的循环参数(总压比opr,涡轮前温度T4)。在完成涡轴发动机的总体性能计算之后,可以获得发动机各个截面的气动热力参数以及部件的性能参数,将其作为尺寸与重量评估的输入,根据待评估涡轴发动机的剖面图可以得到涡轴发动机转子部件的结构参数(轮毂比HTR,展弦比AR等参数),然后输入各个截面的马赫数,计算出各转子部件的几何尺寸(叶片内径DH,外径DT,弦长CB,叶片数等)、气动(载荷系数)、强度(叶根应力σBP、应力参数An2)以及整机/部件的重量W等参数,如果上述评估过程中出现性能参数、结构参数、以及强度等参数不协调的情况,重新修改部分参数,并进行新一轮的评估计算。
|
Fig. 1 Flow chart of turboshaft assessment |
采用部件法来建立涡轴发动机的性能[9~11]评估模型,选定涡轴发动机的设计点,按照发动机的设计水平给定各个部件的效率和压力损失,根据冷气量的计算模型计算出冷气量百分比Pcblc,进行涡轴发动机的气动热力学循环分析,通过满足发动机的总体性能确定涡轴发动机的总压比opr和涡轮前总温T4,并且计算出各个截面的气动热力学参数和部件性能参数。
2.2 尺寸与重量评估模型发动机尺寸与重量评估模型,是基于部件法的涡轴发动机的几何尺寸以及重量的评估模型[12~19],通过对涡轴发动机的转子部件(轴流压气机、离心压气机、燃气涡轮以及动力涡轮)的尺寸/气动/结构/强度/重量的评估以及非转子部件(主燃烧室、喷管、轴、支撑等)的尺寸流路和重量的评估,获得详细的涡轴发动机技术参数。由于篇幅的原因,这里只对组合压气机的压比分配模型进行进行介绍,详细的涡轴发动机尺寸与重量计算参考文献[12, 13]。
在进行涡轴发动机总体性能评估的时候,轴流加离心的组合压气机是当成一个整体进行评估的,总体性能评估的是组合压气机的总压比opr和等熵效率ηC,但是在进行涡轴发动机尺寸重量计算的时候,需要对轴流加离心的组合压气机进行分压比的计算,分别计算出轴流级和离心级的压比pr和等熵效率η。首先根据组合压气机的总压比opr和等熵效率ηC,计算出组合压气机的功率ηH, C。给定离心压气机的等熵效率ηCc,然后根据轴流级的级数,给定轴流压气机占组合压气机的功率分配比例RAc(一般一级轴流加一级离心的组合压气机,轴流压气机的功率比例约占组合压气机的15%~17%,三级轴流加一级离心的组合压气机,轴流压气机的功率比例约占组合压气机的35%~42%,轴流级多于三级的组合压气机,轴流压气机的功率比例约占组合压气机的45%~55%),然后假定一个轴流压气机的初始压比prAc,由总压比和轴流压气机的初始压比,计算出离心压气机的总压比prCc。通过轴流压气机的功率迭代计算出计算出轴流压气机的等熵效率和出口截面参数,由计算出的离心压气机的总压比prCc效率和效率ηCc计算出离心压气机的功率,构建计算出的离心压气机的功率和和DH, C(1-RAc)的残差方程,通过迭代prAc,使得残差方程收敛。最终通过这样的分压比计算,分别计算出轴流压气机和离心压气机的压比和等熵效率,为轴流压气机和离心压气机的尺寸与重量评估提供输入条件。
在涡轴发动机尺寸与重量的评估过程中,尺寸与重量的关键输入参数主要有轴流压气机占组合压气机的功率分配比例RAc,轴流压气机进口轮毂比HTR以及燃气涡轮和动力涡轮的载荷系数Y*。轴流压气机占组合压气机的功率分配比例RAc直接影响到轴流压气机和离心压气机的压比分配,进而影响轴流压气机和离心压气机的尺寸与重量。轴流压气机的进口轮毂比HTR不仅关系到轴流压气机的尺寸重量、强度以及载荷系数,而且还影响核心机的转速进而影响到离心压气机和燃气涡轮的尺寸重量和强度。燃气涡轮和动力涡轮的载荷系数Y*不仅关系到燃气涡轮和动力涡轮的尺寸影响涡轮的重量,而且也关系到涡轮的等熵效率进而影响涡轮的性能。
2.3 耦合评估模型耦合评估模型是基于转子部件的耦合图来进行研究分析的,转子部件的耦合图引用于参考文献[20]。所谓耦合图,就是连接涡轴发动机性能参数与部件气动/结构/强度参数的“桥梁”,在涡轴发动机性能/气动/结构/部件的耦合评估中起着举足轻重的作用。以下就涡轴发动机主要旋转部件压气机和涡轮的耦合图作详细说明。
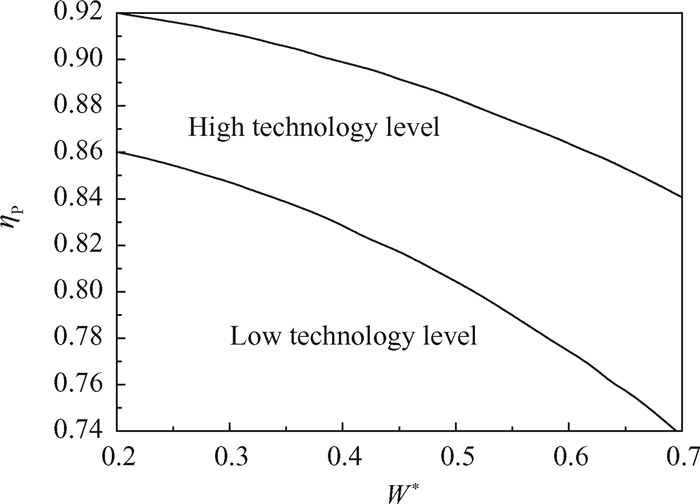
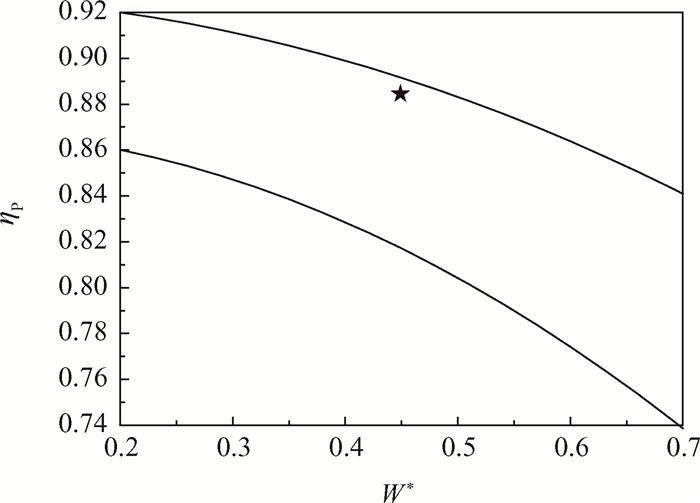
图 2为轴流压气机的耦合图[20],即轴流压气机的平均中径载荷系数W*与多变效率ηP变化关系图。由图可知,随着平均中径载荷系数W*的增加,轴流压气机的多变效率逐渐降低。图中标注了两条技术水平线,分别代表着高技术水平和低技术水平。高技术水平代表更高的多变效率,可以取得更高的等熵效率,体现了压气机更好的性能。低技术水平代表相对较低的多变效率,从而使压气机的等熵效率较低。
|
Fig. 2 Coupling diagram of axial compressor |
轴流压气机的耦合图中主要涉及到两个参数:多变效率ηP和平均中径负荷W*。其中,多变效率的定义为
| $ {\eta _{\rm{P}}} = {\rm{ln}}\left( {{\pi ^{\frac{{k - 1}}{k}}}} \right)/{\rm{ln}}\left( {\frac{{{\pi ^{\frac{{k - 1}}{k} - 1}}}}{{{\eta _{\rm{C}}}}} - 1.0} \right) $ | (1) |
式中ηC为轴流压气机的等熵效率,π为轴流压气机的压比。
轴流压气机载荷系数的定义为
| $ {W^{\rm{*}}} = \frac{{\Delta H}}{{{U_{\rm{M}}}^2Z}} $ | (2) |
式中W*为轴流压气机的平均中径载荷系数,ΔH为轴流压气机单位质量空气的总焓变,近似等于轴流压气机轮缘功,单位为J/kg;UM为轴流压气机进出口截面中径的平均切线速度;Z为轴流压气机的级数。
由以上参数的定义可以知道,多变效率ηP反映了轴流压气机压比π和等熵效率ηC在整个热力过程中的变化关系,在多变效率ηP一定的情况下,等熵效率ηC随着压比π的提高而逐渐下降。平均中径载荷系数W*反映了轴流压气机所承受的气动负荷,与级数Z成反比,由涡轴发动机尺寸与重量计算模型可知,W*还与轴流压气机进口叶尖切线速度、进口轮毂比、流道形式以及进出口轴向马赫数相关。因此,轴流压气机的耦合评估图就把压气机部件性能参数(压比π和等熵效率ηC)、结构参数(轮毂比)、部件参数(级数、叶尖切线速度和马赫数)有机的联系起来了。
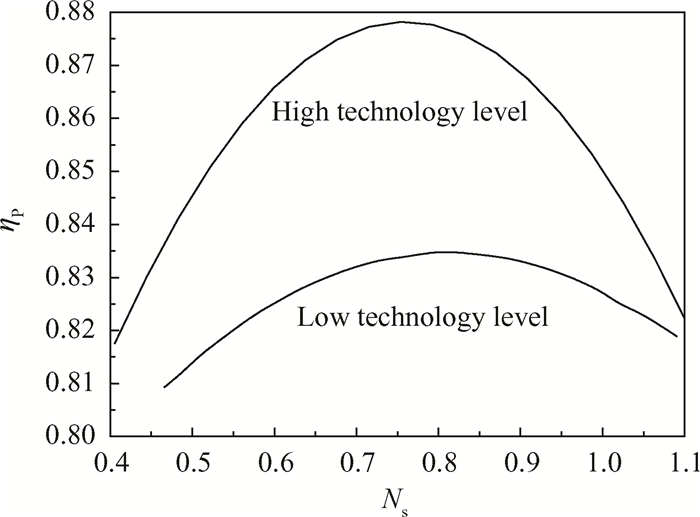
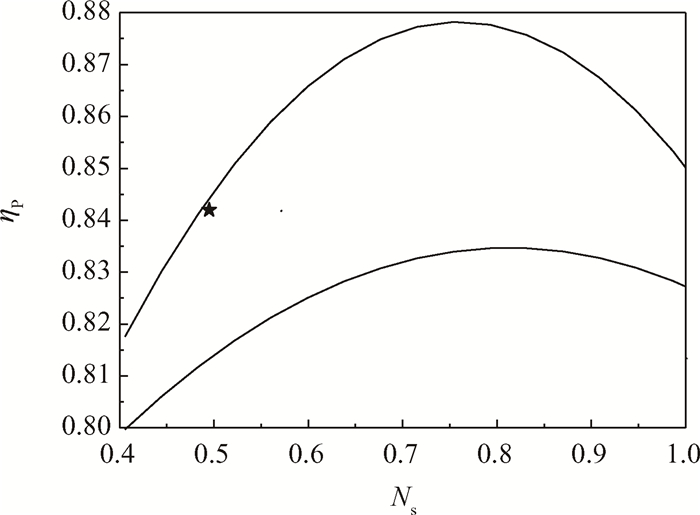
图 3是离心压气机的耦合图[20],横坐标为离心压气机的比转速Ns,纵坐标为离心压气机的多变效率ηP。比转速Ns=N·Q0.5/H0.75表征了离心压气机的流量与加功量的关系,式中Q表示容积流量,H表示等熵焓升,N表示转速。比转速的大小决定了叶轮的大致特点。比转速小的叶轮总宽度和出口宽度都较窄,进出口直径比较小;比转速大的叶轮宽度大,叶轮进出口直径大,大量统计数据表明叶轮多变效率与比转速有直接关系,由图 3也可以看出多变效率在无量纲比转速Ns为0.75~0.8时达到最高。如果比转速太大,可以考虑降低转速,加大尺寸,甚至改用轴流压气机。如果比转速太小,可以提高转速,减小尺寸,甚至改用双级离心。离心压气机的耦合图也标注了两条技术水平线,分别代表高技术水平和低技术水平,它们的意义和轴流压气机相似。
|
Fig. 3 Coupling diagram of centrifugal compressor |
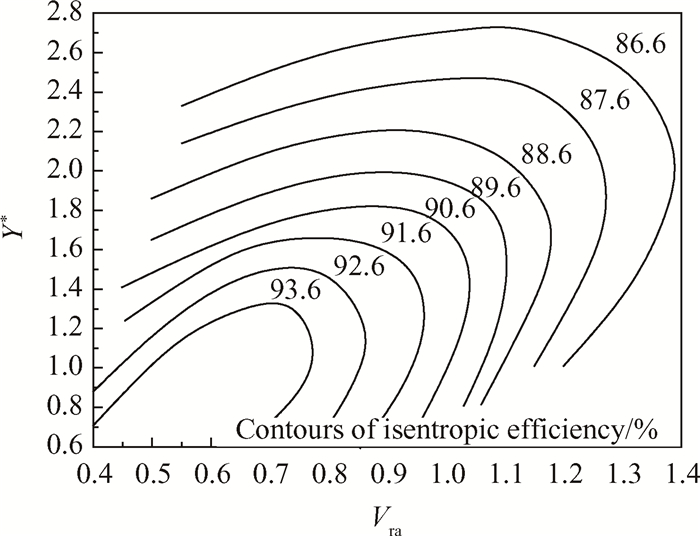
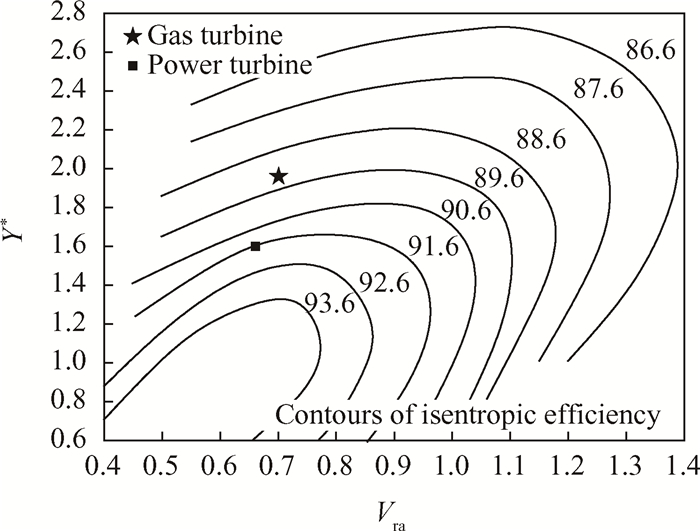
涡轮的耦合图[20]如图 4所示,该图表示涡轮载荷系数Y*,速度系数Vra与涡轮等熵效率ηT的变化关系。
|
Fig. 4 Coupling diagram of the turbine |
速度系数定义为
| $ {V_{{\rm{ra}}}} = \frac{{{V_{\rm{a}}}}}{{{U_{{\rm{M}}, {\rm{o}}}}}} $ | (3) |
式中Va为涡轮出口气流轴向速度,UM, o为涡轮出口中径切线速度,Vra为涡轮出口速度系数。
中径载荷系数定义为
| $ {Y^{\rm{*}}} = {\rm{\Delta }}{H_{\rm{T}}}/\left( {{U_{{\rm{M}}, {\rm{o}}}}^2Z} \right) $ | (4) |
式中由参数的定义可知,涡轮载荷系数Y*,正比于其单位质量的焓变ΔHT,反比于涡轮级数Z和涡轮出口中径切线速度的平方;由发动机总体性能计算模型可知,涡轮冷气量会影响其单位质量的焓变;由发动机尺寸与重量计算模型可知,涡轮出口截面中径切线速度的计算不仅与转子转速有关,还与涡轮出口马赫数相关。这样,涡轮耦合图就将性能参数(涡轮等熵效率和冷气量)、部件参数(级数、转子转速和马赫数)有机的联系起来了。
应用此耦合评估方法对涡轴发动机进行尺寸与重量的评估时,如果有待评估涡轴发动机的结构剖面图,则涡轴发动机各转子部件的结构参数(轮毂比、展弦比等)都是已知的,通过迭代各部件的进出口气动参数以及涡轮的载荷系数Y*,完成发动机各个部件的尺寸重量评估以及在耦合图中的评估,通过此评估方法完成17台国外典型型号的涡轴发动机的尺寸与重量的评估,详见参考文献[21, 22]。如果通过现有已知尺寸重量的发动机评估未知结构剖面的涡轴发动机,依据NASA的文献[12]各参数的取值范围以及已评估发动机的各技术参数通过线性回归处理,根据待评估涡轴发动机的设计年代和设计水平,获取发动机各部件的气动参数输入,通过迭代获取各个部件的尺寸,进而完成各个部件的重量评估以及在耦合图中的评估。
3 算例与分析应用涡轴发动机总体性能评估模型、尺寸与重量评估模型以及耦合评估模型,并编制了相应的计算程序和软件,在UH-60“黑鹰”和AH-64“阿帕奇”直升机配装的现役T700-701D涡轴发动机的基础上,对其换发美国的第五代先进涡轴发动机GE3000进行耦合评估,并且就模型和评估方法的可靠性和准确性进行验证以及新材料新技术的引入对性能的影响进行分析。
3.1 T700-701D涡轴发动机的评估涡轴发动机T700-701D是主要是由进气道(带粒子分离器)、五级轴流加一级离心的组合压气机、折流燃烧室、两级燃气涡轮、两级动力涡轮以及尾喷管组成。根据已有的T700-701D的性能参数、T700-701D的结构图以及部件的材料参数等,应用涡轴发动机的总体性能评估模型、尺寸与重量评估模型以及耦合评估模型对T700-701D进行总体综合评估,这里由于篇幅的原因,只对T700-701D的总体性能参数进行输出,总体性能的评估结果如表 2。
|
|
Table 2 T700-701D performance parameters |
根据GE3000与T700-701D的尺寸大致相等,轴功率提高50%(达到2237kW),耗油率降低25%,功重比提高65%等相关的技术参数,对GE3000进行耦合评估,表 3为GE3000性能的输入参数,表 4~6分别为轴流压气机、离心压气机、涡轮(燃气涡轮以及动力涡轮)的气动、结构以及强度输入参数。
|
|
Table 3 GE3000 performance inputs |
|
|
Table 4 Axial compressor inputs for size & weight |
|
|
Table 5 Centrifugal compressor inputs for size & weight |
|
|
Table 6 Turbine inputs for size & weight |
通过对GE3000涡轴发动机的总体性能和尺寸与重量的耦合评估,获得详细的GE3000涡轴发动机的评估结果,表 7为GE3000的性能评估结果。
|
|
Table 7 Overall performance assessment result |
表 8~10分别为涡轴发动机轴流压气机、离心压气机、涡轮(燃气涡轮以及动力涡轮)的性能/气动/结构/强度/尺寸的重要参数的评估结果。表 11为GE3000的各部件重量评估结果。表 12为GE3000的各个部件的尺寸评估结果,各个部件的尺寸和T700-701D的尺寸对比变化不大,总长和T700-701D基本相等。图 5~图 7分别为轴流压气机、离心压气机以及涡轮(燃气涡轮和动力涡轮)在耦合图中的位置。
|
|
Table 8 Axial compressor assessment result |
|
|
Table 9 Centrifugal compressor assessment result |
|
|
Table 10 Gas turbine assessment result |
|
|
Table 11 GE3000 component weight assessment result |
|
|
Table 12 GE3000 component size assessment result |
|
Fig. 5 GE3000 coupling diagram of axial compressor |
|
Fig. 6 GE3000 coupling diagram of centrifugal compressor |
|
Fig. 7 GE3000 coupling diagram of the turbines |
通过对GE3000涡轴发动机的评估结果与GE公司公布的的参数[4]进行对比可知,GE3000总体性能的的误差小于1.0%,整机重量(功重比)的误差小于2.0%,整机尺寸的误差小于1.0%,说明评估模型和评估方法可行,且精度较高。
3.3 T700-701D与GE3000的对比分析表 13为T700-701D涡轴发动机与GE3000涡轴发动机的的参数对比,GE3000发动机的性能相比T700-701D有大幅提升,主要是采用了高温陶瓷基复合材料、增材制造零部件以及先进的3D气动设计。
|
|
Table 13 Comparison between T700-701D and GE3000 |
由于GE3000采用了先进的3D气动设计,在与T700-701D涡轴发动机尺寸变化不大的情况下,压气机的流通能力体现在发动机的流量从5.36kg/s提高到6.24kg/s,提高了16.4%;五级轴流加一级离心的组合压气机的总压比从17.4提高到25.5,提高了46.6%,压气机的第一级压比pr1从1.489提高到1.743,GE3000的第一级轴流压气机叶尖速度UT达到510m/s,甚至高于高负荷的军用涡扇发动机压气机的第一级叶尖速度;并且转子部件的等熵效率也有不同程度的提高。GE3000涡轴发动机高温高压部件燃烧室和涡轮采用了高温陶瓷基复合材料和增材制造技术,在发动机性能大幅度提高的同时,还能够有效地减轻发动机的重量和提高部件的寿命。
由表 1可知,第四代涡轴发动机的功重比约为7.35kW/kg,由于新材料新技术的使用,从表 12可以看出美国的第五代先进涡轴发动机GE3000的功重比比T700-701D提高了65.9%,达到了10.8045kW/kg,可以预测第五代涡轴发动机的功重比将达到8.82~11.025kW/kg。
4 结论在涡轴发动机总体性能与尺寸重量模型的基础上,发展了一种基于涡轴发动机总体性能、总体结构、部件气动/结构/强度/材料等的耦合评估方法,并利用该方法对T700-701D和美国第五代先进涡轴发动机GE3000进行了评估以及对比分析。结论如下:
(1)与GE公司公布的GE3000的数据对比表明,本模型评估的涡轴发动机总体性能误差小于1.0%,整机重量误差小于2.0%,部件的尺寸和整机尺寸小于1.0%,表明此模型和评估方法可行。
(2)GE3000涡轴发动机压气机通过先进的3D气动设计,使得五级轴流加一级离心的组合压气机的总压比大幅增加,达到25.5,并且效率也有所改善,进而提高发动机整机的总体性能参数。
(3)高温陶瓷基复合材料以及增材制造技术的应用,使得GE3000涡轴发动机的高温高压部件燃烧室和涡轮能承受更高的温度和强度,且能有更轻的重量,进而提升发动机的整机功重比。
(4)GE3000涡轴发动机各部件技术参数的评估结果纳入到涡轴发动机的技术参数数据库中,完善了涡轴发动机的数据库,能够更好地为我国第五代涡轴发动机总体方案设计技术参数的选取提供技术参考。
| [1] |
乞征, 向克胤, 刘彦雪. 涡轴发动机技术发展研究综述[J]. 飞航导弹, 2016(7): 83-86. (  0) 0) |
| [2] |
银越千, 金海良, 陈璇. 涡轴/涡桨发动机压气机流动特点与发展趋势[J]. 航空学报, 2017, 38(9): 35-50. (  0) 0) |
| [3] |
Ahmet Duyar, Zhen Gu, Jonathan S Litt. Simplified Dynamic Model of the T700 Turboshaft Engine[R]. Journal of the American Helicopter Society, 1992, 40(4): 67-70. http://www.ingentaconnect.com/content/ahs/jahs/1995/00000040/00000004/art00005
(  0) 0) |
| [4] |
GE Aviation Press Center. US Army and GE Aviation Sign Cooperative Agreements for Advanced Helicopter Engine Technology Development[EB/OL]. https://www.geaviation.com/press-release/military-engines/us-army-and-ge-aviation-complete-testing-second-ge3000-helicopter, 2014-06-02.
(  0) 0) |
| [5] |
肖蔓. AATE和ITEP计划下的涡轴发动机分阶段研发综述[J]. 航空发动机, 2016, 42(2): 98-102. (  0) 0) |
| [6] |
James W Gauntner. Algorithm for Calculating Turbine Cooling Flow and the Resulting Decrease Inturbine Efficiency[R]. NASA-TM-81453, 1980.
(  0) 0) |
| [7] |
Valerio Lallini, Jan Janikovic. A Calculation Tool of a Turbine Cooling Air Schedule for General Gas Turbine Simulation Algorithms[J]. Journal of Turbomachinery, 2012, 134(4).
(  0) 0) |
| [8] |
唐海龙, 张坤, 郭昆, 等. 涡轴发动机性能非确定性模型校核与应用[J]. 推进技术, 2017, 38(11): 2447-2455. (TANG Hai-long, ZHANG Kun, GUO Kun, et al. Verification of Turbo-Shaft Engine Performance Uncertainty Model and Applications[J]. Journal of Propulsion Technology, 2017, 38(11): 2447-2455.)
(  0) 0) |
| [9] |
赵强, 陈玉春, 王永文, 等. 基于部件法的涡轴发动机性能计算模型研究[J]. 航空工程进展, 2011, 2(3): 2-3. (  0) 0) |
| [10] |
冯海峰.航空涡轴发动机数学建模方法与控制规律研究[D].西安: 西北工业大学硕士论文, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10699-2007057945.htm
(  0) 0) |
| [11] |
寥光煌, 焦洋. 涡轴发动机高精度实时部件级模型研究[J]. 推进技术, 2016, 37(1). (LIAO Guang-huang, JIAO Yang. Research on High Accuracy Real-Time Component-Level Modeling Method for Turbo-Shaft Engine[J]. Journal of Propulsion Technology, 2016, 37(1).)
(  0) 0) |
| [12] |
Onet E, Kless G W. A Method to Estimate Weight and Dimensions of Large and Small Gas Turbine Engines[R]. NASA-CP-159481, 1979. https://ntrs.nasa.gov/search.jsp?R=19790006875
(  0) 0) |
| [13] |
Hale P L. A Method to Estimate Weight and Dimensions of Small Aircraft Propulsion Gas Turbine Engines[R]. AIAA 82-23037.
(  0) 0) |
| [14] |
Michael T Tong. A Computer Code for Gas Turbine Engine Weight and Disk Life Estimation[J]. ASME GT-2002-30500. http://www.researchgate.net/publication/245353515_A_Computer_Code_for_Gas_Turbine_Engine_Weight_and_Disk_Life_Estimation
(  0) 0) |
| [15] |
郭淑芬, 陈军, 赵洪利. 涡喷与涡扇发动机重量估算方法[J]. 航空发动机, 1999(2): 8-10. (  0) 0) |
| [16] |
郭淑芬, 宋慧敏, 王甫君. 涡轴与涡桨发动机特殊部件重量估算[J]. 航空发动机, 1999(2): 8-10. (  0) 0) |
| [17] |
黄志勇. 航空发动机压气机转子重量预估方法研究[J]. 燃气涡轮试验与研究, 2004, 17(4): 24-26. DOI:10.3969/j.issn.1672-2620.2004.04.007 (  0) 0) |
| [18] |
Jack D Mattingly, William H Heiser. Aircraft Engine Design[J]. Aircraft Engine Design, 1987(3).
(  0) 0) |
| [19] |
Stephen A Suhr. Preliminary Turboshaft Engine Design Methodology for Rotorcraft ApplicAtions[D]. Atlanta: Georgia Institute of Technology, 2006.
(  0) 0) |
| [20] |
Walsh P P, Paul F P. Gas Turbine Performance[M]. 2nd Edition. USA: American Society of Mechanical Engineers, 2004.
(  0) 0) |
| [21] |
周新新, 陈玉春, 樊巍, 等. 涡轴发动机技术参数与发展趋势评估[J]. 航空工程进展, 2013, 4(2): 150-157. DOI:10.3969/j.issn.1674-8190.2013.02.003 (  0) 0) |
| [22] |
樊巍.涡轴发动机总体综合设计方法初步研究[D].西安: 西北工业大学, 2014.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


