燃气弹射是一种利用固体火箭发动机产生高速燃气射流,在发射筒内快速建压推动导弹向上运动的航天发射技术[1]。由于传统高温推进剂下发射流场温度高达3000~3500K[2, 3],会对弹体及临近发射单元产生较强的热烧蚀和强冲击效应[4],现多采用低燃温推进剂作为弹射动力原料。Fu[5]和杨育文等[6]分别对固体发动机欠膨胀射流和尾流场的复燃特性进行了数值研究; 在此基础上,胡晓磊等[7]研究发现低燃温推进剂的燃烧产物同样具有强复燃特性,会与发射筒内空气发生剧烈的二次燃烧,造成弹底初始压力冲击和热环境品质劣化; 李恩义等[8]研究发现随着喷管入口总压的上升,弹底压力载荷会再次出现二次冲击波峰。针对此问题,胡晓磊等[9]在发射筒内增加环形腔有效缓解了初始压力冲击,但在弹射后期引起了较大的压力振荡和波动。李仁凤等[10]在发射筒壁面布置障碍物,并用穷举法分析了障碍物高度对压力曲线平滑效果的影响,尽管达到了一定的平滑效果,但引起了较大的冲量损失。两种结构策略均以实验装置的弹底压力曲线平稳性作为评价指标,进行单目标穷举寻优,未耦合考虑初容室长度、导弹出筒性能、弹底热环境以及发射场坪压力载荷的变化,优化结果具有较大的局限性。低燃温弹射内弹道载荷直接影响导弹出筒指标、发射筒强度设计和发射场坪的承载能力分析,而针对该问题的优化设计鲜见报道,建立起多目标响应的优化平台具有重要的工程意义。
相对于传统零维内弹道优化设计,CFD分析能耦合结构尺寸和外形变化,有效捕捉流场细节和运动机理,提高优化设计的导向性和精准度。将CFD实时计算与试验设计、响应面方法以及现代智能算法相结合的多学科优化设计已在诸多领域得到实现[11~14],但燃气弹射内弹道多目标寻优仍然停留在穷举法,搭建多学科策略平台进行优化的报道较少。
本文首先结合动态分层动网格技术,求解二维轴对称多组分N-S方程,分析流场特性;然后提出4块环形隔板递减布置、第5块隔板作为调控和增大导流锥半径的结构方案来平衡内弹道载荷之间的强耦合关系;最后搭建起从试验设计到建立响应面近似数学模型,再到多目标算法组合优化的策略平台,对内弹道多目标进行优化设计。
2 基准数值模型与结构策略 2.1 数值建模第一步是数值模型的网格划分。燃气弹射装置主要由固体燃气发生器、导流锥、发射筒、导弹尾罩、底座以及支撑结构组成。其中,固体燃气发生器与导流锥通过文献[15]的导流架形式连接成整体,导流架通过细长钢结构固定于发射筒壁面,因支撑结构对流场影响较小,三维几何模型简化如图 1所示。其中,P点为实验和数值仿真的监测点。针对弹射装置具有高度轴对称的特点,数值求解采用二维轴对称多组分Navier-Stokes控制方程[16],对1/2轴对称面进行结构化网格划分,如图 2所示。尾罩网格采用动态分层动网格技术实现更新,导弹在燃气推力、重力、摩擦力和气动阻力的作用下运动,摩擦力采用0.02倍弹重进行折算考虑。运动方程参考文献[8],以此编写UDF嵌入FLUENT解算器,通过加载DEFINE_CG_MOTION宏函数,实时赋予动网格速度。

|
Fig. 1 3-D geometric model |
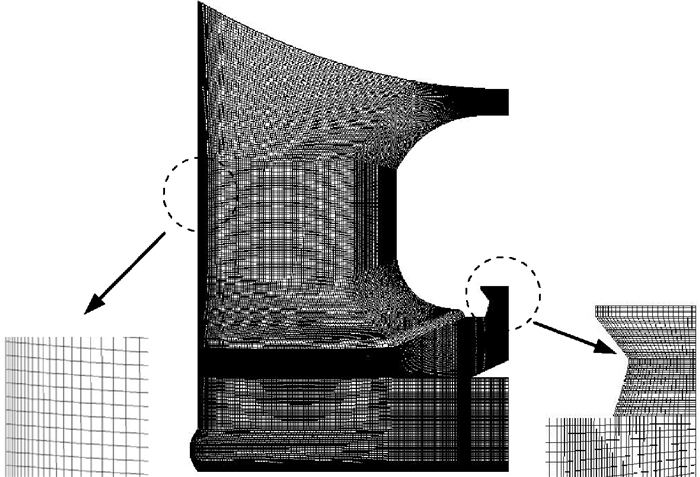
|
Fig. 2 Mesh model |
第二步是确定数值模型的计算方法。燃烧模型、湍流模型及边界条件与文献[10]一致,图 3和表 1分别为喷管入口的总压曲线和燃气组分及其质量分数,采用有限体积法对控制方程进行离散,求解方法采用压强-速度耦合算法,选择稳定性较好、计算速度较快的SIMPLE耦合形式。压力梯度项采用二阶格式离散,动量方程的差分格式均采用二阶迎风格式,湍流输运方程的差分格式采用一阶迎风格式,各项残差收敛精度为1×10-4,计算步长为40μs。
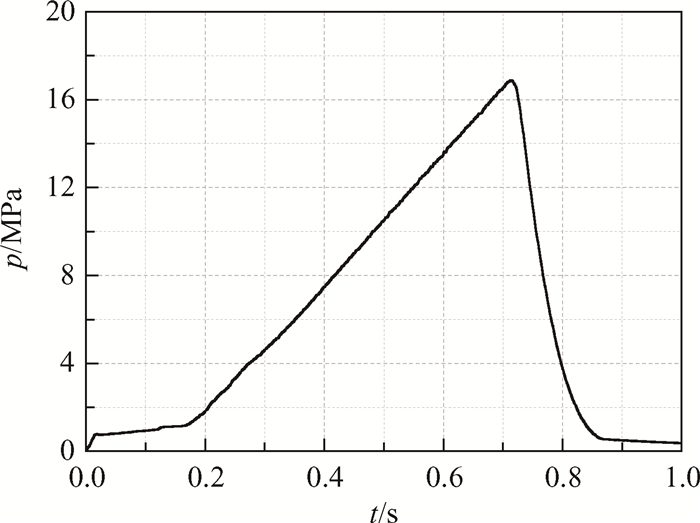
|
Fig. 3 Curve of total pressure |
|
|
Table 1 Species and mass fraction of nozzle inlet |
第三步是验证数值模型的有效性。提取P点的压力和温度载荷曲线与文献[10]中发射实验实测值进行对比,如图 4所示。其中,p0为监测点的压力参考值,T0为监测点的温度参考值,t0为推进剂燃烧完全的时间。从图 4可见,压力与温度的数值曲线与实验曲线吻合较好,趋势基本一致,成功捕捉了压力双峰和温度单峰。实验测得第一个压力峰值为0.83p0,计算值为0.84p0;实验测得第二个压力峰值为0.78p0,计算值为0.79p0;实验测得温度峰值0.94T0,计算值为0.94T0。数值计算结果与实验值峰值最大误差为1.2%,表明数值模型具有较高的可信度。
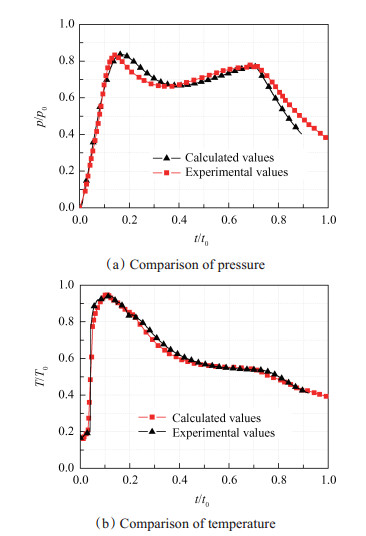
|
Fig. 4 Comparison of calculation and experiment values |
由于压力曲线存在双波峰冲击,对于燃气弹射实验装置,考虑布置4块高度递减的环形隔板,实现燃气与筒内空气的有效隔断,延缓二次燃烧以减小初始冲击,如图 5(a)所示;对于车载导弹武器,发射筒初容段长度越短,装备越紧凑化,机动性能越好。当初容段缩小时,建压速度加快,但氧气量减少,二次燃烧冲击出现减弱,基于此,考虑布置第5块环形隔板进行调控,如图 5(b)所示。由于筒底压力直接决定发射场坪的载荷,为实现广域公路机动发射,应尽可能减小对地压力载荷,而导流锥直接决定燃气入射角度,考虑增大导流锥半径以减小筒底压力。其中,由于装填空间的约束,初容段缩短的极限约为200mm。
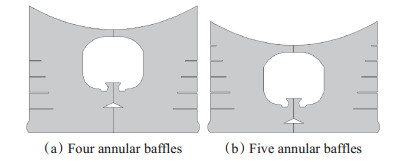
|
Fig. 5 Structure schemes |
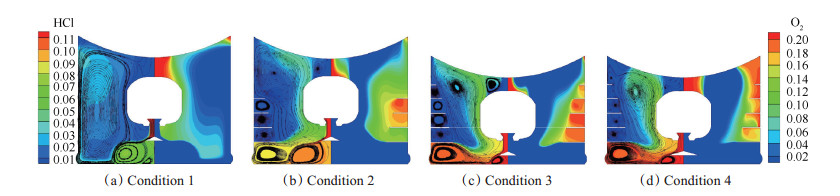
假设实验装置的初容室长度为L,ΔR为相对实验装置导流锥半径的增加量。为分析环形隔板对压力曲线的平滑机理、第5块环形隔板以及导流锥半径对流场的作用,选取4种工况进行对比分析,工况布置如表 2所示,其中第5块环形隔板高度h5为75mm。由于HCl仅存在于燃气组分,其空间分布可以表征燃气的扩散进程;O2质量分数的空间分布可以表征二次燃烧的剧烈程度。图 6为在0.15t0时刻,4种工况的流场云图,其中左侧为流线图和HCl质量分数云图,右侧为O2质量分数云图。图 7(a)~(b)分别为O2质量分数、弹底压力、温度和筒底压力的时程曲线。
|
|
Table 2 Condition arrangements |
|
Fig. 6 Flow field nephograms of 4 kinds of conditions at 0.15t0 |
|
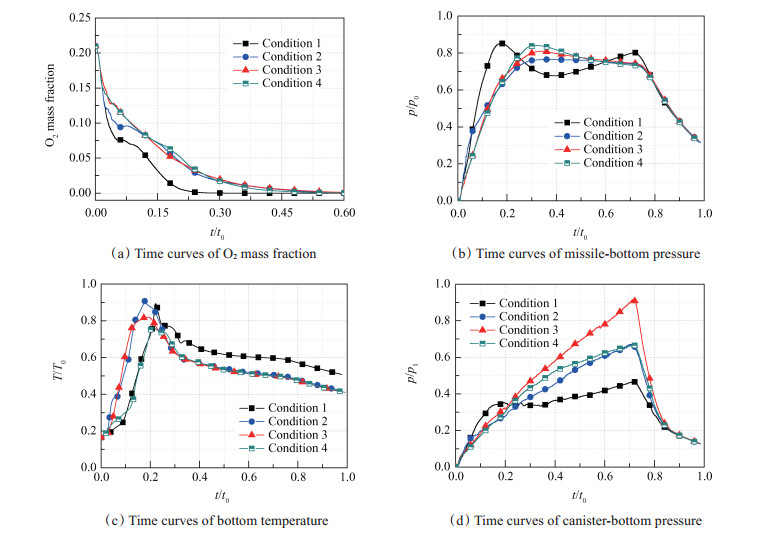
图 7 Time curves of O2 mass fraction and loads |
对比工况1和工况2,结合图 6,图 7(a)和(b)可见,工况2氧气消耗速率明显小于工况1,环形隔板一方面阻挡燃气向上扩散,延缓二次燃烧进程以减小初始压力冲击,另一方面实现燃气与氧气的空间隔断,在弹射中期持续发生二次燃烧增压,以抵消因发射筒容积增加引起的压力快速衰减,从而平滑压力曲线,如图 7(b)所示。由O2质量分数云图可见,布置环形隔板后二次燃烧区域包裹燃烧室并迅速扩散至尾罩,导致工况2温度上升超前于工况1,如图 7(c)所示。增加环形隔板使得燃气在隔板下方聚集,这导致了筒底压力的大幅度上升,如图 7(d)所示。
对比工况2和工况3,由图 6和图 7可见,由于工况2导流锥下方空间大、氧气量多,所以早期氧气消耗速率快于工况3,待下方空间氧气消耗殆尽后,燃气向上扩散受阻,所以在中期二者消耗速率基本保持一致。工况3发射筒容积小而建压迅速,氧气总量少而二次燃烧减弱,所以温度峰值小于工况2,弹底压力峰值大于工况2,这表明容积因素相对二次燃烧占据主导。初容段的减小使得导流锥距离筒底更近,当总压达到峰值时,筒底压力会大幅度上升。
对比工况3和工况4,增加第5块隔板、增大导流锥半径,使得燃气筒底反射点外移,氧气的空间分布改变,二次燃烧规律也相应改变,导致弹底压力峰值的增加。由图 6(d)可见,工况4尾罩底部二次燃烧区域减小,导致温度上升滞后于工况3,如图 7(c)所示。如图 7(d)可见,导流锥半径的增加使得筒底压力大幅度降低。
3.2 多目标优化评价体系综合2.1节对4种工况流场运动机理的分析,在初容室缩短工况下,可以选择h5和ΔR作为寻优的结构参数,由于弹底压力直接决定导弹加速度曲线,为方便给予约束,选用弹底加速度峰值amax,加速度曲线平稳性、筒底压力峰值p1 max以及弹底热环境
Minmize
| $ \left\{ {\begin{array}{*{20}{l}} {{a_{{\rm{max}}}} = {f_1}\left( {{h_5}, \Delta R} \right)}\\ {S = {f_2}\left( {{h_5}, \Delta R} \right)}\\ {{p_{1\ {\rm{max}}}} = {f_3}\left( {{h_5}, \Delta R} \right)}\\ {\int_0^{{t_{\rm{g}}}} {T{\rm{d}}t} = {f_4}\left( {{h_5}, \Delta R} \right)} \end{array}} \right. $ | (1) |
Subject to
| $ \left\{ {\begin{array}{*{20}{l}} {0 \le {h_5} \le 150{\rm{mm}}}\\ {0 \le {\rm{\Delta }}R \le 100{\rm{mm}}}\\ {{a_{{\rm{max}}}} \le {a_0}}\\ {0.8{v_0} \le {v_{\rm{g}}} \le {v_0}}\\ {{p_{1\ {\rm{max}}}} \le \left| {{p_{1\ {\rm{max}}}}} \right|} \end{array}} \right. $ | (2) |
式中tg为导弹出筒时刻,a0为导弹允许的加速度最大值,v0为导弹设计速度最大值。|p1 max|为发射场坪极限承载强度,本文采用高速公路常见的面层、半刚性基层、底基层和土基4层场坪结构,详细结构见文献[17],当发射筒底座单独加载时,0.8182p1接近发射场坪极限承载强度。
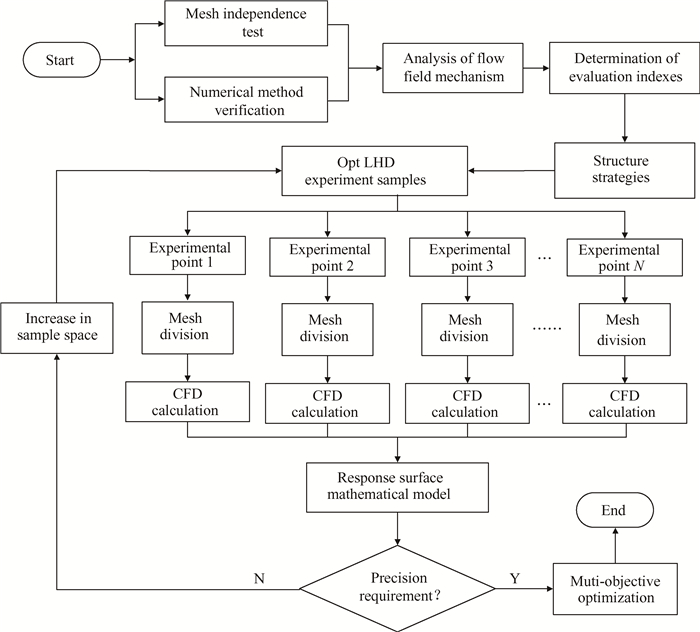
4 内弹道多目标组合优化设计燃气弹射内弹道多目标优化涉及结构设计、网格划分、CFD实时计算、试验方案设计、响应面近似数学模型的选择以及多目标优化算法的确定,是典型的多学科协同问题,搭建策略平台实现流程化设计尤为重要,原理流程如图 8所示。
|
Fig. 8 Flow chart of optimization platform principle |
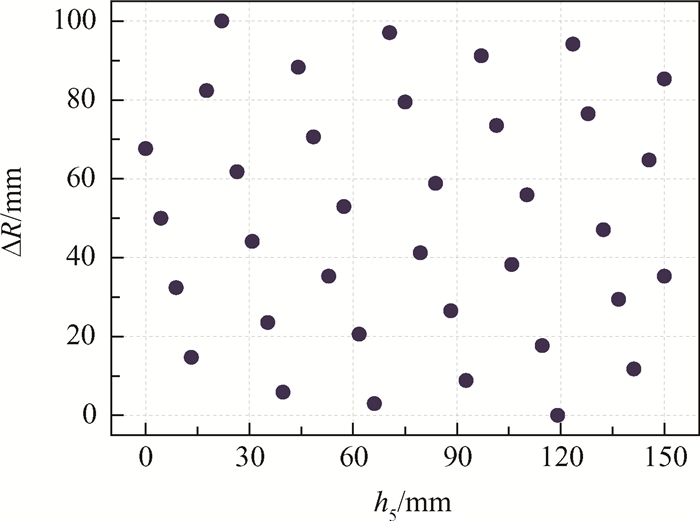
为获取高精度的响应面近似数学模型,因子应当尽量遍历样本空间,这使得计算量过大而难以实现,所以需要利用试验设计(Design of experiment,DOE)的方法,用尽量少的特征样本点拟合出连续响应面。DOE构建样本空间的正交性和充满度直接决定响应面函数拟合精度以及模型的解析能力,优化拉丁超立方设计(Optimal latin hypercube design,Opt LHD)改进了随机拉丁超立方的均匀性,使得因子和响应的拟合更加精准,正交性和充满度得到显著提高。本文采用Opt LHD方法进行两因素试验设计,经过平台多次采样、计算与拟合,最后满足工程精度的样本空间为36抽样点,如图 9所示。
|
Fig. 9 Sample points for two factors |
由于燃气弹射内流场特性受发射筒结构影响较大,使得内弹道评价指标具有强非线性,且弹射过程涉及网格的动态增加,所以传统的穷举法CFD寻优过程会耗费较多的计算机资源。基于此,利用合理的试验设计,建立满足工程精度的响应面近似数学模型,可以较高精度描述样本空间信息,降低“数值噪音”[18],减少寻优过程对CFD的调用次数,提高优化设计效率。本文采用带交叉项的六阶响应面构造近似数学模型,去除一半的交叉项以减少运算量,其函数构造形式为
| $ \begin{array}{l} F\left( X \right) = {a_0} + \sum\limits_{i = 1}^N {{b_i}x_1^i} + \sum\limits_{j = 1}^N {{c_j}x_2^j} + \sum\limits_{j = 1}^{N - 1} {{d_{1j}}{x_1}x_2^j} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^{N - 2} {{d_{2j}}x_1^2x_2^j} + \sum\limits_{j = 1}^{N - 3} {{d_{3j}}x_1^3x_2^j} + \sum\limits_{j = 1}^{N - 4} {{d_{4j}}x_1^4x_2^j} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^{N - 5} {{d_{5j}}x_1^5x_2^j} \end{array} $ | (3) |
式中F(X)为目标函数,即F(X) = [f1, f2, f3, f4],其中,f1为amax,f2为标准差S,f3为p1 max,f4为
对式(1)中各项系数进行最小二乘回归分析求解,使得试验样本值与响应面预测值误差平方和最小,拟合优度一般采用决定系数R2作为评价指标,工程上要求其值大于0.9才能保证模型的准确性[19]。经过平台多次采样计算,近似数学模型达到了理想的工程精度,F (X)向量的R2分别为0.9337,0.9379,0.9892和0.9461,表 3为F (X)向量近似数学模型的各项系数。
|
|
Table 3 Coefficients of the approximate mathematical model |
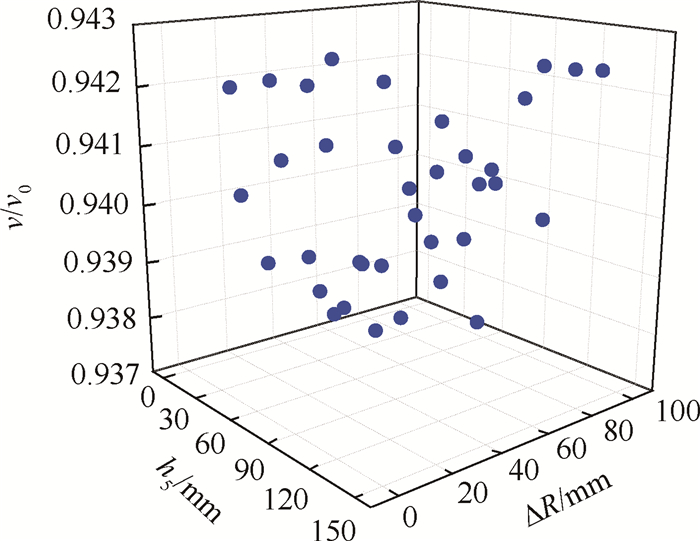
此外,导弹出筒速度vg也是h5和∆R的函数,样本空间如图 10所示,vg在0.937v0~0.943v0波动,对结构参数不构成约束。为验证近似数学模型的有效性,随机抽取3组结构方案进行验证,CFD计算值与预测值误差分析如表 4所示。3组随机误差分析显示,响应面近似数学模型误差较低,满足工程设计精度。
|
Fig. 10 Three-dimensional point chart of missile velocity out of canister |
|
|
Table 4 Error analysis of the approximate mathematical model |
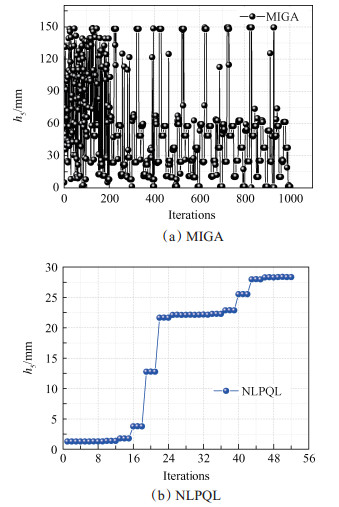
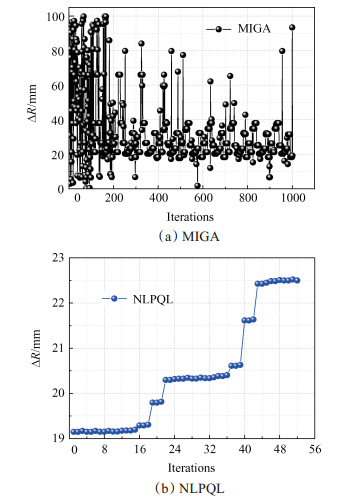
选取基于多岛遗传算法(Multi-island genetic algorithm,MIGA)和序列二次规划算法的组合寻优方案,MIGA算法具有良好的全局搜索能力,能对高度非线性问题进行空间遍历而迅速定位目标区域,NLPQL算法能在目标区域内迅速收敛逼近最优解,寻优精度高。运用组合优化策略对响应面近似数学模型进行寻优,共迭代1052次达到收敛,其中MIGA迭代1000次,NLPQL迭代52次,当h5和ΔR分别为28.35mm和22.5mm时,内弹道性能达到最优。由图 11,12寻优历程可见,MIGA算法主要发挥全局搜索定位功能,在最优解附近呈现震荡特性,而对接的NLPQL算法则迅速捕捉到最优解,充分互补了二者的优势。
|
图 11 Optimization process of h5 |
|
Fig. 12 Optimization process of ΔR |
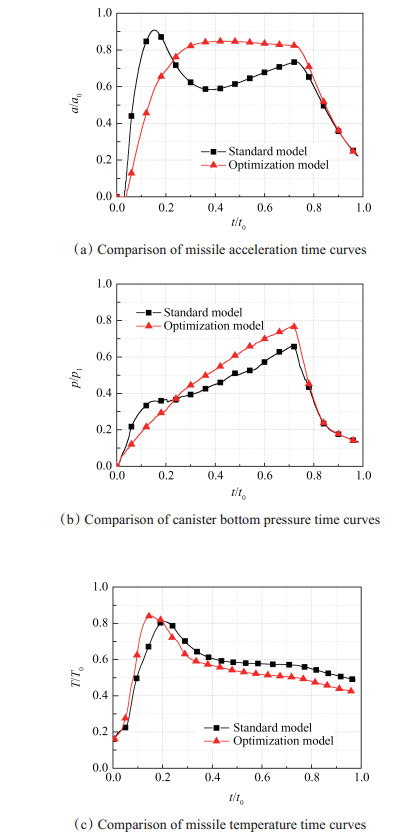
限于文章的篇幅,各评价指标的优化历程没有给出。以工况3为基准模型,表 5给出了优化前、后的设计参数以及优化结果。由表 5可见,CFD计算值与组合优化预测值最大误差为7.0%,满足工程精度,相对于基准模型,加速度峰值减小了6.6%,加速度曲线平稳性增加了79.5%,筒底压力峰值增加了16.2%,弹底热环境品质增加了6.1%。寻优结果表明内弹道优化目标之间存在耦合关系,导弹加速度曲线冲击峰值、平稳性以及弹底热环境品质的改善须以筒底压力增加为代价,一味追求弹底压力冲击平滑度极有可能造成发射场坪过载。图 13(a)~(c)分别为优化前后的导弹加速度、筒底压力和弹底温度时程曲线对比。
|
|
Table 5 Comparison of optimization results |
|
Fig. 13 Time curves of optimization |
由图 13(a)可见,相对于基准模型,优化后的模型导弹加速度曲线品质得到了显著改善。在初容室缩短工况下,化“双峰”曲线为“单峰”曲线,成功解决了初容室过小引起加速度过载的问题,极大改善了车载机动性能;由图 13(b)可见,尽管筒底压力峰值有所上升,但仍然在场坪承载能力之内,压力曲线上升的均匀性更佳;结合图 6和图 13(c)可见,布置隔板后,燃气沿燃烧室壁面包围尾罩的进程要超前于无环形隔板工况,这导致优化模型温度前期上升速率较快,由于良好的隔断效果,使得二次燃烧缓慢发生,改善了弹底的热环境。
5 结论通过本文研究,得出如下结论:
(1)通过分析布置级减环形隔板平滑弹底压力、增大导流锥半径减小筒底压力的流场机理,提出了第5块环形隔板高度和导流锥半径耦合变化的结构方案,能为同类弹射装置内弹道多目标寻优提供参考。
(2)基于优化拉丁超立方试验设计,建立了六阶响应面近似数学模型,避免了传统穷举寻优计算量大的局限性,R2分析和随机抽样误差分析显示,拟合的近似数学模型满足工程精度,可用于内弹道多目标优化设计。
(3)基于响应面近似数学模型,搭建的多岛遗传算法和序列二次规划梯度算法的组合策略,在多目标优化历程中展现了良好的优势互补,能快速定位最优解。
(4)相对于基准模型,优化后的模型加速度峰值减小了6.6%,加速度曲线平稳性增加了79.5%,筒底压力峰值增加了16.2%,弹底热环境品质增加了6.1%。以较小的筒底压力增加为代价,极大地改善了内弹道性能曲线的品质。
致谢: 感谢国家自然科学基金资助。
| [1] |
姜毅, 史少岩, 牛钰森, 等. 发射气体动力学[M]. 北京: 北京理工大学出版社, 2015.
(  0) 0) |
| [2] |
Sourgen F, Haertig J, Rey C, et al. Experimental and Numerical Investigations of Flow Confined in a Vertical Missile Launcher[J]. Journal of Spacecraft and Rockets, 2009, 46(2): 307-317. DOI:10.2514/1.37614
(  0) 0) |
| [3] |
乔野, 聂万胜, 吴高杨, 等. 多喷管液体火箭动力系统尾焰冲击特性研究[J]. 推进技术, 2017, 38(2): 498-503. (QIAO Ye, NIE Wan-sheng, WU Gao-yang, et al. Research on Plume Impact Characteristics of Multi-Nozzle Rocket Propulsion System[J]. Journal of Propulsion Technology, 2017, 38(2): 498-503.)
(  0) 0) |
| [4] |
Hegab A M, Sait H H, Hussain A, et al. Numerical Modeling for the Combustion of Simulated Solid Rocket Motor Propellant[J]. Computers and Fluids, 2014, 89(7): 29-37.
(  0) 0) |
| [5] |
Fu D, Yong Y, Niu Q. Simulation of Underexpanded Supersonic Jet Flows with Chemical Reactions[J]. Chinese Journal of Aeronautics, 2014, 27(3): 505-513. DOI:10.1016/j.cja.2014.04.003
(  0) 0) |
| [6] |
杨育文, 邓康清, 余小波, 等. 高含铝推进剂低压固体火箭发动机尾流场复燃数值模拟与实验研究[J]. 推进技术, 2017, 38(3): 680-686. (YANG Yu-wen, DENG Kang-qing, YU Xiao-bo, et al. Numerical Simulation and Experimental Investigation on Plume Afterburning of Low-Pressure Solid Rocket Motor with Highly Aluminized Propellant[J]. Journal of Propulsion Technology, 2017, 38(3): 680-686.)
(  0) 0) |
| [7] |
胡晓磊, 王辉, 乐贵高, 等. 二次燃烧对燃气弹射载荷和内弹道影响数值研究[J]. 固体火箭技术, 2015, 38(6): 776-781. (  0) 0) |
| [8] |
李恩义, 乐贵高, 马大为, 等. 低温燃气弹射内弹道影响因素的数值研究[J]. 航空动力学报, 2017, 32(6): 1296-1306. (  0) 0) |
| [9] |
胡晓磊, 乐贵高, 马大为, 等. 环形腔对燃气弹射初容室二次燃烧影响数值研究[J]. 兵工学报, 2015, 36(6): 1024-1032. DOI:10.3969/j.issn.1000-1093.2015.06.009 (  0) 0) |
| [10] |
李仁凤, 乐贵高, 马大为, 等. 壁面障碍物对燃气弹射流场和内弹道的影响[J]. 固体火箭技术, 2016, 39(3): 444-450. (  0) 0) |
| [11] |
Navid A, Khalilarya S, Taghavifar H. Comparing Multi-Objective Non-Evolutionary NLPQL and Evolutionary Genetic Algorithm Optimization of a DI Diesel Engine: DOE Estimation and Creating Surrogate Model[J]. Energy Conversion and Management, 2016, 126: 385-399. DOI:10.1016/j.enconman.2016.08.014
(  0) 0) |
| [12] |
朱正, 招启军. 低HSI噪声旋翼桨尖外形优化设计方法[J]. 航空学报, 2015, 36(5): 1442-1452. (  0) 0) |
| [13] |
Li F, Qin Y, Pang Z, et al. Design and Optimization of PSD Housing Using a MIGA-NLPQL Hybrid Strategy Based on a Surrogate Model[J]. Strojniski Vestnik, 2014, 60(7-8): 525-535. DOI:10.5545/sv-jme
(  0) 0) |
| [14] |
Zhang T T, Huang W, Wang Z G, et al. A Study of Airfoil Parameterization, Modeling, and Optimization Based on the Computational Fluid Dynamics Method[J]. Zhejiang University-SCIENCE A(Applied Physics and Engineering), 2016, 17(8): 632-645. DOI:10.1631/jzus.A1500308
(  0) 0) |
| [15] |
胡晓磊, 盛文成, 乐贵高, 等. 车载导弹垂直发射系统双面导流器[J]. 火力与指挥控制, 2013(11): 53-55. DOI:10.3969/j.issn.1002-0640.2013.11.013 (  0) 0) |
| [16] |
Artan H. Simulation of a MILD Combustion Burner Using ILDM Chemistry[J]. Progress in Computational Fluid Dynamics, 2014, 14(4): 233-243. DOI:10.1504/PCFD.2014.063861
(  0) 0) |
| [17] |
王桂娇.某机动导弹发射场坪承载性能研究[D].哈尔滨: 哈尔滨工业大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D592319
(  0) 0) |
| [18] |
Das P K, Zheng Y. Cumulative Formation of Response Surface and Its Use in Reliability Analysis[J]. Probabilistic Engineering Mechanics, 2000, 15(4): 309-315. DOI:10.1016/S0266-8920(99)00030-2
(  0) 0) |
| [19] |
Montgomery D C. Design and Analysis of Experiments[M]. New York: John Wiley and Sons, 2001.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


