水冲压发动机采用水反应金属基燃料体系,燃料燃烧后的富燃燃气在燃烧室与海水剧烈反应放热,结合“超空泡”减阻技术,可使水下航行器实现高达200节的航速,弥补常规水下航行器采用螺旋桨推进时航速较低或采用固体火箭发动机推进时航程较短的不足,受到广泛关注[1, 2]。对于旨在提高比冲的高金属含量水冲压发动机[3],燃料体系氧化剂含量极少,可能导致燃料点火困难、自持燃烧放热不足以维持其持续分解,或少量气相产物不足以将凝聚相金属“吹入”燃烧室等无法启动金属/水稳定持续反应的现象,点火药及进水等参数对高金属含量燃料点火及持续燃烧影响较大[4]。
国内外学者已开展水冲压发动机数值计算研究,韩超等[5, 6]分别在氩气和水蒸汽环境中试验研究了73%镁基水反应金属燃料的燃烧特征。Miller等[7]认为镁在燃烧室环境中可凝结为微米量级的液滴,离散相对发动机内部的流动和燃烧影响较大,计算中不容忽略。李芳等[8]仅考虑镁/水反应,采用颗粒轨道模型数值模拟了水冲压发动机三维、气液两相、湍流流动与燃烧过程,计算将氧化镁以气相处理。上述数值计算均针对给定燃烧室入口条件的稳态工况,未考虑流场与燃料间的传热耦合作用,无法表征燃料的真实燃烧状态,难以反映点火过程中可能存在的熄火或爆炸等现象。高金属含量燃料难以自持燃烧,维持其持续分解反应必须从燃烧室内近燃面处吸收热量,所以以上方法均不适用于高金属含量水冲压发动机数值分析。
本文针对镁(Mg,73wt%)/高氯酸铵(AP,19wt%)/丁羟(HTPB,8wt%)燃料体系,基于N-S方程,将高金属含量燃料和点火药向气相流场的质量、动量和能量输运转化为对应守恒量控制方程在近燃面第一层网格和点火药包覆盖区域网格的源项,将脱离燃面的熔融镁近似为燃烧室入口释放的镁液滴,实现燃料燃烧/点火药燃烧/流场多相湍流燃烧的耦合计算,给出点火过程镁的粒径分布和运动轨迹,计算得到燃面温度-时间曲线和燃速-压强曲线,并以此确定点火性能评判指标,对比黑火药和硼/硝酸钾点火药对燃料燃烧的影响。
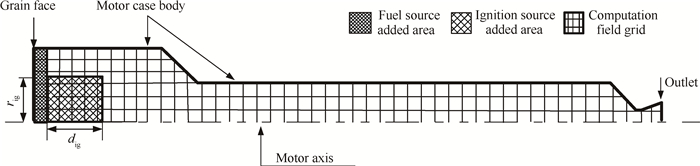
2 物理建模与计算方法采用文献[9]中的试验发动机构型,图 1为二维轴对称模型下的结构及网格划分示意图。采用结构化网格,并在燃面、近壁面、进水孔附近局部加密网格以提高计算精度。一次进水位置距离燃面30mm,进水孔径为1mm,进水指向流场上游、与发动机径向垂线夹角ϕ为45°。

|
Fig. 1 Motor structure and computation grid |
连续相模型采用包含多组份输运和体化学反应的二维轴对称、可压缩、湍流N-S方程组,其守恒形式的控制方程如下
| $ \begin{array}{*{20}{l}} {\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \left( {E - {E_{\rm{ \mathit{ ν} }}}} \right)}}{{\partial x}} + \frac{1}{r}\frac{{\partial r\left( {F - {F_{\rm{ \mathit{ ν} }}}} \right)}}{{\partial r}} = S}\\ { = {S_{\rm{S}}} + {S_{{\rm{Ig}}}} + {S_{\rm{L}}} + {S_{\rm{R}}} + {S_{\rm{H}}}} \end{array} $ | (1) |
式中$\mathit{\boldsymbol{U}} = {(\rho, \rho u, \rho v, {e_{\rm{t}}}, \rho {Y_{\rm{k}}})^{\rm{T}}}$分别对应质量、轴向动量、径向动量、能量和多组份质量等守恒量;E, F, Ev, Fv分别为各守恒量在两个坐标方向的对流通量和扩散通量;S为各守恒量的源项,产生形式包括:燃料向流场输运项SS,点火药向流场输运项SIg,离散相蒸发项SL,气相燃烧反应项SR和轴对称项SH,各项具体计算方法分别在2.1~2.3节中详细说明。
补充完全气体状态方程封闭控制方程组为
| $ P = \rho {R_{\rm{u}}}T\sum\limits_{s = 1}^n {\frac{{{Y_s}}}{{{M_s}}}} $ | (2) |
式中ρ为混合气体密度;Ru为通用气体常数,Ms为各组份的摩尔质量。
2.1 燃料向流场输运源项水冲压发动机燃料燃烧过程中,大部分镁颗粒虽然没有参与燃料自持燃烧,但不能阻止燃面的退移[10];对于由AP和HTPB组成的单元(以下表达为AH),AP和HTPB的质量消耗率之比等于其质量分数之比;且AP分解遵循零级阿累尼乌斯公式。因此,燃料燃烧的线燃速可表达为
| $ r = \frac{{{A_{{\rm{AP}}}}{\rho _{{\rm{AP}}}}{\rm{exp}}\left( { - {E_{{\rm{AP}}}}/R{T_{\rm{S}}}} \right){S_{{\rm{AP}}}}}}{{{\rho _{{\rm{AH}}}}\left( {{S_{{\rm{AP}}}} + {S_{\rm{P}}}} \right)}} \cdot \frac{{\left( {\alpha + \beta } \right)}}{\alpha } $ | (3) |
式中下标AP和P分别代表AP和HTPB,AH为由AP和HTPB组成的单元。AAP和EAp分别为AP热分解的指前因子和活化能,R为通用气体常数,TS为燃面温度,ρ为密度,α和β分别为AP和HTPB的质量百分数,S为组份燃烧面积,由平面几何学确定[11]。以现有试验数据[12]拟合模型中的活化能和指前因子,取EAP和AAP分别为1.56 × 107J/kmol和1950 m/s。
基于课题组自研的水冲压发动机热力计算软件,取燃烧室压强3MPa,喷管出口背压0.1MPa,初始温度300K时,忽略质量分数较少的产物,计算得到燃料燃烧热力学平衡时的主要产物及其质量分数如表 1所示。基于热力计算结果,简化燃料燃烧反应,结合燃速模型,确定各组份的质量流量[10]。
|
|
Table 1 Self-sustained combustion products and corresponding weight fractions |
不考虑燃烧过程中的热辐射及其他能量损失时,单位时间内气相火焰通过热传导反馈至单位燃面面积上的热量与凝聚相反应净放热量之和用于使推进剂由初温T0升高到燃面温度Ts[13]。
当燃面温度低于镁的着火温度时,即Ts < Tm,单位时间燃料向环境的净放热量Q包括:AP和HTPB分解放热和镁的焓变吸热。
| $ \begin{array}{*{20}{l}} {Q = {{\dot m}_{{\rm{AP}}}}\left( {{h_{{\rm{AP}}, {T_{\rm{s}}}}} - {h_{{\rm{AP}}, {T_0}}} + {q_{{\rm{AP}}}}} \right) + }\\ \;\;\;\;\;\;\;{{{\dot m}_{\rm{P}}}\left[ {{h_{{\rm{P}}, {T_{\rm{s}}}}} - {h_{{\rm{P}}, {T_0}}} + {q_{\rm{P}}}} \right] + {{\dot m}_{{\rm{Mg}}}}\left( {{h_{{\rm{Mg}}, {T_{\rm{s}}}}} - {h_{{\rm{Mg}}, {T_0}}}} \right)} \end{array} $ | (4) |
式中${\dot m}$代表组份的质量消耗率,由式(3)确定的燃速及各组份质量分数确定;hr代表组份在温度T下的标准生成焓,由多项式函数确定;q代表各组份的分解热。
当Ts≥Tm后,镁颗粒在氧化气氛中迅速氧化并放热,激励燃料燃烧持续进行。考虑模型的连续性,将过程分为燃料热分解和燃气升温两个步骤:固体AP,HTPB和镁颗粒燃烧并升温至Tm,此后燃烧产物继续升温至燃面温度Ts,凝聚相一侧提供的能量为
| $ \begin{array}{l} Q = {{\dot m}_{{\rm{AP}}}}\left( {{h_{{\rm{AP}},{T_{\rm{m}}}}} - {h_{{\rm{AP}},{T_0}}} + {q_{{\rm{AP}}}}} \right) + {{\dot m}_{\rm{P}}}\left[ {{h_{{\rm{P}},{T_{\rm{m}}}}} - {h_{{\rm{P}},{T_0}}} + {q_{\rm{P}}}} \right] + \\ {{\dot m}_{{\rm{Mg}}}}\left( {{h_{{\rm{Mg}},{T_{\rm{m}}}}} - {h_{{\rm{Mg}},{T_0}}}} \right) + \sum\limits_{i = 0}^5 {{{\dot m}_i}\left( {{h_{i,{T_{\rm{s}}}}} - {h_{i,{T_{\rm{m}}}}} + {q_i}} \right)} \end{array} $ | (5) |
式中i=0, 1, 2…5分别对应燃料燃烧的六种热力计算产物MgO,C,Mg,MgCl2,H2和N2。
综上,燃料向流场的输运项表达式为
| $ {S_{\rm{s}}} = {J_{\rm{s}}}r{A_{{\rm{gr}}}}{\rho _{\rm{s}}}/{V_{{\rm{gr}}}}{(1, r, 0, Q, {Y_0}, \ldots , {Y_5})^{\rm{T}}} $ | (6) |
式中Js为燃料源项开关函数,仅对存在燃料输运的流场网格单元取1;Agr和Vgr分别为网格单元的截面积和体积。
2.2 点火药向流场输运源项点火药的燃气生成速率通常由发动机模拟自由容积试验压强-时间曲线换算得到,呈类抛物线形式。本文采用二次多项式模拟点火药燃气生成速率${\dot m_{{\rm{ig}}}}$,即
| $ {\dot m_{{\rm{ig}}}} = a{t^2} + bt + c $ | (7) |
给定点火器工作时间tigt和点火药质量Mig,求解a, b, c使满足
| $ \begin{array}{*{20}{l}} {{{\dot m}_{{\rm{ig}}}}{|_{t = 0}} = 0}\\ {{{\dot m}_{{\rm{ig}}}}{|_{t = {t_{{\rm{igt}}}}}} = 0}\\ {\int_0^{{t_{{\rm{igt}}}}} {{{\dot m}_{{\rm{ig}}}}{\rm{d}}t = {M_{{\rm{ig}}}}} } \end{array} $ | (8) |
点火药向燃料表面和流场的热量交换方式包括生成燃气和粒子的热传导、对流和热辐射,为简化模型,将三种方式的传热量统一为点火燃气的热值,即
| $ {q_{{\rm{ig}}}} = {\dot m_{{\rm{ig}}}}{Q_{{\rm{ig}}}} $ | (10) |
式中qig为点火燃气的能量生成率,Qig为单位点火药燃烧反应放热值,由点火药性质确定。为简化计算,认为点火药燃气与发动机初始流场气体具有相同的性质。
综上,点火药向流场的输运项可表达为式(11),Jig为点火药源项开关函数,仅对存在点火药能量输运的网格单元取1,η为点火药燃烧产气率。
| $ {\mathit{\boldsymbol{S}}_{{\rm{ig}}}} = {J_{{\rm{ig}}}}{\dot m_{{\rm{ig}}}}/{V_{{\rm{ig}}}}{(\eta , 0, 0, {Q_{{\rm{ig}}}}, 0, \ldots , 1)^{\rm{T}}} $ | (11) |
本文计算基于商业CFD计算平台FLUENT进行自定义函数(UDF)二次开发,离散相蒸发项SL,气相燃烧反应项SR和轴对称项SH由软件内嵌模型计算。其中离散项颗粒采用拉格朗日坐标系下的颗粒轨道模型描述,其向连续相质量、动量和能量的输运由液滴蒸发模型描述;湍流模型选择标准k-ε模型;燃烧模型选择涡耗散模型。
2.4 耦合数值计算方法 2.4.1 源项添加方法燃料表面为热耦合边界[14],燃料着火前按加热表面处理,仅惰性吸热升温,与流场无质量、动量交换;当燃料表面某点温度达到着火温度Tm后,按加质加热表面处理,向流场的质量、动量和能量输运量遵循2.1节所述燃料输运模型,燃面温度取靠近燃料表面第一层网格单元温度。
点火药包是一类无结构强度的点火器,可在数值计算中处理为体积源[15]。假设点火药包为半径rig,厚度dig的圆柱构型,在二维轴对称计算模式下,点火药包的直接覆盖区域为靠近发动机燃面处rig×dig的矩形,见图 2。
|
Fig. 2 Illustration of user-defined sources addition |
假定rig=dig,当点火药质量Mig和点火药密度ρig确定时,即可确定流场中添加点火源项的网格单元范围。由于靠近燃面第一层网格单元温度在计算中用来作为燃面温度,若同时在此区域添加点火能量源项,将导致点火药燃气与药柱表面的换热速率无限大,燃面温度跃变为点火药燃气高温,这与实际物理过程相违背。本文计算将近药柱表面的第二层网格作为点火药源项的添加起点,由于第一层网格高度与点火药厚度相比为小量,可认为该方法与实际点火传热过程一致。2.2节所述点火药源项的开关函数Jig可表示为
| $ {J_{{\rm{ig}}}} = \left\{ {\begin{array}{*{20}{l}} {1\;\;\;\;\;\;\;\;\;{x_1} < x < \left( {{d_{{\rm{ig}}}} + {x_1}} \right)\mathop \cap \nolimits r < {r_{{\rm{ig}}}}\mathop \cap \nolimits t < {t_{{\rm{igt}}}}}\\ {0\;\;\;\;\;\;\;\;\;{\rm{other}}} \end{array}} \right. $ | (12) |
| $ {r_{{\rm{ig}}}} = {d_{{\rm{ig}}}} = \sqrt[3]{{{M_{{\rm{ig}}}}/\pi {\rho _{{\rm{ig}}}}}} $ | (13) |
式中x1为近壁面第一层网格单元中心的轴向坐标,x, r, t分别为网格单元的轴向坐标、径向坐标和流动时间。
2.4.2 边界条件及初始条件药柱表面取绝热壁面边界;发动机中心线取对称轴边界;发动机壁面取无滑移绝热壁面;喷管出口取为压力出口。
忽略点火信号触发的响应时间及点火药着火的延迟时间,以点火器开始向燃烧室喷射高能燃气的时刻作为流场仿真计算的时间零点,初始时刻取发动机内流场压强大气压,温度为300K。发动机初始流场空气中的极少量氧气对燃烧流动影响较小,且发动机工作过程中燃烧室内氧气质量分数非常小,简化认为初始流场发动机内部充斥气体全部为氮气。
3 结果与讨论 3.1 计算分析及模型验证采用上述发动机结构及数值计算方法进行非稳态、多相耦合数值计算。工况设置取点火药为40g黑火药、进水时刻为第60ms,进水量为0.5kg/s,进水角度为垂直于进水孔指向上游45°,进水轴向和径向速度大小均为20m/s,水液滴粒径分布遵循粒径最小值为50μm,最大值为150μm,均值为100μm的R-R分布。图 3为不同时刻镁液滴粒径分布图。图 4为稳态建立时流场温度分布云图。脱离燃面的镁液滴在注水孔附近与进水发生掺混,未蒸发部分受进水剪切在发动机下游集中于轴线附近。注水孔附近进水蒸发吸热并受主流“冲刷”作用形成“C型”低温区,“C型”轮廓外镁/水反应放热,产生高温。

|
Fig. 3 Diameters distribution of Mg droplets |

|
Fig. 4 Temperature contour in final steady state |
水冲压发动机地面直连实验通常通过在进水管路上安装汽蚀文氏管,以解决发动机试车过程中流量不稳定的问题,点火时序为先进水后点火[16]。表 2为数值计算与文献[9]试验的结果对比。其中,表中所列进水量试验值文献中未直接给出,由文献所列燃面燃速及一次水燃比数据推得。试验工况与数值计算工况并不完全一致但接近,试验结果可在一定可信性范围内验证模型。
|
|
Table 2 Comparison between experiment and simulation results |
目前广泛应用的点火药主要包括两大类:为以硝酸钾、硫和木炭为主要构成的黑火药(Black Powder)和以硼(B)和硝酸钾(KNO3)为主要构成的硼类点火药,本小节针对无进水情况下采用相同质量、两种类型点火药点火工况进行计算,定义从点火药开始向外喷射高能热燃气到燃料燃面平均温度首次达到着火温度的时间间隔为点火延迟时间tig,燃烧室压强在到达准稳态前的最大压强作为点火压强峰值pmax,发动机实现稳态工作时的时刻为启动时间ts,稳态燃面温度和燃烧室压强分别记为Tf和pf,通过监测非稳态计算过程中的燃面平均温度-时间曲线和燃烧室压强-时间曲线,确定上述参数值,并将其作为发动机点火性能的评价指标,讨论两类点火药的点火性能,表 3为两类点火药的基本性质及本节算例的点火药参数设置。其中η为点火药燃烧过程中的产气率,tigt,Mig和Qig分别为点火药的质量、燃烧时间和单位质量燃烧放热量。
|
|
Table 3 Ignition powder property[17] and case setup |
图 5为采用40g黑火药点火时,不同时刻燃烧室头部温度云图和燃面温度曲线图。点火启动后,点火能量在燃面被点火药包粘附区域附近局部激发,燃面近发动机轴线位置温度迅速升高。t=1ms时,燃面中心已达到着火温度,燃料部分着火。此后在点火药能量的持续激励下,燃面温度继续增加,t=10ms时,燃面近轴线处温度已接近1100K,燃料剧烈燃烧并释放大量燃气,由于点火药燃气的轴向阻碍和径向剪切作用,燃气脱离燃面后径向偏转,在燃烧室上壁面碰撞分流,形成上、下游两个涡流区从而增强高/低温流体掺混及换热。燃料近轴线位置温度由点火药燃气扩散控制,保持1100K高温,远离轴线位置温度由燃气扩散控制,随径向距离增加燃面温度升高。随扩散深度和掺混程度的增加,t=80ms时,燃面低温区温度升高至满足着火条件,此时燃料全面着火。t=100ms后,点火药工作结束,燃面温度主要受燃气热反馈控制,燃面各处温度趋于一致。t=350ms时,燃料完全着火且燃面温度分布均匀,此时燃处于燃烧平衡状态,燃面温度为940K。

|
Fig. 5 Temperature contours and curves of combustion chamber and grain surface with black powder |
图 6为采用40g硼/硝酸钾点火药点火时,不同时刻燃烧室头部温度云图和燃面温度曲线。

|
Fig. 6 Temperature contours and curves of combustion chamber and grain surface with B/KNO3 powder |
t=1ms时,燃面近发动机轴线位置温度迅速升高,但仍低于燃料的着火温度,燃料整体处于惰性升温阶段。与图 5(a)相比,尽管B/KNO3点火药单位质量热值较大,但由于其密度小且产气量少,点火药包体积较大且体积中心距燃面较远,点火药燃气对于燃面的热反馈较弱,因此t=1ms时仍未着火。t=10ms时,高温点火药燃气已沿径向和轴向扩散一定深度,流场受扰动区域增大,燃面近轴线位置温度升高至1020K,满足着火条件,但距轴线较远位置处仍保持300K低温,此时燃料部分着火,开始向流场输运燃气。t=80ms时,燃料燃烧和点火药掺混燃气扩散深度继续增加,且轴向扩散速度远大于径向,燃面低温区升温速率较慢。t=100ms后,点火药工作结束,扩散高温燃气碰撞燃烧室收敛段壁面,形成局部涡流增强燃烧室上半部分的掺混及换热,燃面低温区温度逐渐提升,着火区域面积增多。t=350ms时,燃料完全着火,燃面温度分布均匀,此时燃料达到燃烧平衡状态,燃面温度为1020K。
综上,本文算例条件设置下,采用40g黑火药和B/KNO3点火药均可实现点火药耗尽后燃料全面、稳定燃烧,燃面着火始于近轴线位置并沿径向扩张。黑火药产气量较大,其对燃气的轴向阻碍和径向剪切有利于增强燃烧室上半部分的掺混换热,燃面低温区升温速率较快;但黑火药单位质量热值较低,燃料平衡燃面温度较低。
3.3 不同点火药对点火性能影响分析图 7为采用两种点火药点火时的燃料燃面平均温度-时间曲线,蓝色点虚线对应于燃料的着火温度885K。采用硼/硝酸钾点火药点火时,燃料燃面温度上升速率较慢,但平衡燃烧温度较高;在点火启动初期由于点火药产气量较小且燃料表面着火区域较小,流场质量通量未满足喉部的壅塞条件,燃烧室压强降低,此后燃面温度缓慢增加,燃料表面着火燃烧面积逐渐增加,当燃气产生质量流量增加到大于出口燃气质量流量时,燃烧室压力逐渐增加直至稳态压力建立。

|
Fig. 7 Average combustion temperature-time curves during ignition |
上述两种点火药的差别可用3.2节所列点火性能评价指标量化,结果如表 4所示。采用硼/硝酸钾点火药点火时可实现较高的燃料燃烧平衡温度,但需以较长的平衡建立时间为代价,实际应用时应考虑以添加堵盖等方式减小点火过渡进程。
|
|
Table 4 Ignition performance comparison between two ignition powders |
(1)基于FLUENT平台,通过自定义函数开发及网格单元源项,实现了一种燃料燃烧/点火药燃烧/流场多相湍流燃烧的耦合计算,可用于计算得到点火过程燃料燃面温度瞬时分布规律,解决高金属含量水冲压发动机燃速实验测量组织难度大的问题。
(2)采用40g黑火药点火、进水流量为0.5kg/s,进水偏离发动机轴线45°指向上游时,燃料平衡燃面温度约为943K,可实现发动机的可靠点火和燃料的稳定燃烧。
(3)硼/硝酸钾点火药与黑火药对流场和燃料燃烧的影响有明显差异。相同质量的硼/硝酸钾点火药与黑火药相比,燃料燃烧平衡温度较高,平衡建立时间也较长。
致谢: 感谢国家自然科学基金资助。
| [1] |
宋伟峰. 超空泡技术将改变海战模式[J]. 舰载武器, 2003(2): 20-22. (  0) 0) |
| [2] |
Kiely D H. Review of Underwater Thermal Propulsion[R]. AIAA 94-2840.
(  0) 0) |
| [3] |
胡凡, 张为华, 江振宇. 金属燃料/水冲压发动机构型试验[J]. 推进技术, 2012, 33(1): 125-130. (HU Fan, ZHANG Wei-hua, JIANG Zhen-yu. Configuration Experiment of Metal Fuel/Water Ramjet[J]. Journal of Propulsion Technology, 2012, 33(1): 125-130.)
(  0) 0) |
| [4] |
Yang Y, He M. Theoretical Investigation of Thermodynamic Performance for a Ramjet Based on a Magnesium-Water Reaction[J]. J. Engineering for the Maritime Environment, 2009, 224: 61-72.
(  0) 0) |
| [5] |
韩超, 夏智勋, 胡建新, 等. 高金属含量水反应金属燃料稳态燃烧模型[J]. 固体火箭技术, 2011, 34(5): 609-613. DOI:10.3969/j.issn.1006-2793.2011.05.015 (  0) 0) |
| [6] |
韩超, 夏智勋, 胡建新, 等. 水反应金属燃料在水蒸气环境下的稳态燃烧特性[J]. 固体火箭技术, 2011, 34(1): 75-78. DOI:10.3969/j.issn.1006-2793.2011.01.017 (  0) 0) |
| [7] |
Miller T F, Herr J D. Green Rocket Propulsion by Reaction of Al and Mg Powders and Water[R]. AIAA 2004-4037.
(  0) 0) |
| [8] |
李芳, 张为华, 王中伟, 等. 水反应金属燃料发动机三维两相燃烧数值模拟[J]. 固体火箭技术, 2007, 30(5): 384-387. DOI:10.3969/j.issn.1006-2793.2007.05.005 (  0) 0) |
| [9] |
韩超.高金属含量镁基燃料水冲压发动机稳态燃烧机理研究[D].长沙: 国防科学技术大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-90002-1012020659.htm
(  0) 0) |
| [10] |
董戈.高金属含量水冲压发动机点火瞬态过程仿真研究[D].长沙: 国防科学技术大学, 2016.
(  0) 0) |
| [11] |
王英红, 李葆萱, 张晓宏, 等. 含硼富燃料推进剂低压燃烧模型[J]. 固体火箭技术, 2006, 29(1): 39-42. DOI:10.3969/j.issn.1006-2793.2006.01.011 (  0) 0) |
| [12] |
张炜, 张为华. 镁基水反应金属燃料[M]. 北京: 国防工业出版社, 2013.
(  0) 0) |
| [13] |
Kuo K K, Summerfield M. Fundamentals of Solid-Propellant Combustion[M]. 北京: 宇航出版社, 1988.
(  0) 0) |
| [14] |
Zhang S, Hu F, Wang D, et al. Numerical Simulations on Unsteady Operation Processes of N2O/HTPB Hybrid Rocket Motor with/without Diaphragm[J]. Acta Astronautica, 2017, 136: 115-124. DOI:10.1016/j.actaastro.2017.03.005
(  0) 0) |
| [15] |
樊超.尾部点火双推力发动机点火过程研究[D].长沙: 国防科学技术大学, 2010.
(  0) 0) |
| [16] |
黄利亚, 夏智勋, 胡建新. 水冲压发动机地面直连试验技术研究[J]. 推进技术, 2009, 30(6): 722-726. (HUANG Li-ya, XIA Zhi-xun, HU Jian-xin. Investigation on Ground Direct-Connect Test Technology for Water Ramjet Engine[J]. Journal of Propulsion Technology, 2009, 30(6): 722-726. DOI:10.3321/j.issn:1001-4055.2009.06.016)
(  0) 0) |
| [17] |
成一, 陈守文. 点火药点火性能的研究[J]. 火工品, 2001(4): 21-22. DOI:10.3969/j.issn.1003-1480.2001.04.006 (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


