随着近年来航天事业的蓬勃发展,越来越多的空间科学测量任务被提出。目前主导的两项空间科学测量任务是地球重力场测量和空间引力波探测[1]。新一代卫星重力技术[2]可以提供全球的高质量重力测量数据,为利用重力场信息研究地球系统动力过程及系统内物质运动和时空分布的可行性提供了保证。近年来已经发射的重力卫星有CHAMP[3](Challenging Minisatellite Payload),GRACE[4](Gravity Recovery and Climate Experiment),GOCE[5~7](Gravity and Steady State Ocean Circulation Explorer)。以上基于卫星的重力场测量均取得良好效果,对于地球科学研究及其它领域里的应用是非常重要的。引力波探测会促进相对论天体物理和相对论宇宙学深入发展,帮助我们了解宇宙的开端和运行机制。目前欧空局开展了LISA[8, 9](Laser Interferometer Space Antenna)计划,并且已经发射了LISA探路者[10]卫星用于验证测试质量自由飞行、无拖曳[11, 12]等关键技术;国内中山大学开展了天琴计划[13],中科院胡文瑞院士等开展了太极计划,这些计划将对中低频段的引力波进行观测。
空间科学测量任务带来的科学意义是巨大的,但是这样的测量任务对航天器试验环境要求非常高,几乎都要求航天器平台的残余扰动力尽可能小。为了保证航天器的高度稳定性,实时补偿非保守力,需要采用无拖曳控制方法设计航天器控制系统。无拖曳控制技术[14]是指通过控制系统的作用,使得推力器实时抵消太空环境对航天器的扰动力,航天器能够实时跟踪内部自由飞行的惯性参考基准——测试质量,最终实现航天器的无拖曳运行。无拖曳控制回路如图 1所示,采用高精度位移测量技术(传感器)测量航天器与测试质量的相对运动,该相对信号作为输入传递至控制系统,控制系统控制微推进器产生相应推力值作用到航天器上,实现控制目标。

|
Fig. 1 Flow chart of drag free control |
目前已经有大量学者针对无拖曳控制系统建模问题进行了研究,美国弗罗里达大学Nguyen等利用3U微小卫星进行了无拖曳卫星的硬件在环仿真[15];斯坦福大学Singh等使用H∞理论进行控制器设计[16];都灵理工大学Canuto则提出了嵌入式控制方法[12],在嵌入式模型中给出了较为完备的模型及控制器的设计方法;伍斯特理工学院Blandino等利用霍尔推力器的数据,基于PID控制方法建立了相应的无拖曳控制系统,针对不同轨道高度的工况进行了仿真分析[17]。国内的主要研究单位是哈尔滨工业大学,哈尔滨工业大学航天学院王玉爽、李传江、马广富利用最优控制、鲁棒控制等控制理论设计了相应的无拖曳控制器[18];张锦绣等围绕自适应控制理论进行无拖曳控制研究[19];国防科学技术大学王涛等基于LQG/LTR控制方法建立了控制器[20]。
以上关于控制系统的研究均取得良好效果,但是无拖曳飞行需求不仅对系统建模及控制提出很高要求,还对其推进系统的工作性能指标也提出了很高的要求。非保守力的大幅快速变化的特点和实时补偿的目标要求推进系统必须具有连续可调范围宽、响应快速、推力分辨率高且噪声低的特点。目前全球各科研机构已成功发射5次无拖曳航天器,每次飞行任务设计中,推进系统的研制和发展都是其中的一项关键研究环节。1972年9月2日,无拖曳控制技术在美国海军TRIAD I航天器[21]上进行了首次测试,该航天器采用冷气推力器作为其推进系统,并且采用传统的开关控制方式,其工作性能良好,完成了技术验证。2004年4月20日,NASA发射了GP-B[22](Gravity Probe B)卫星利用陀螺仪验证广义相对论,该航天器使用了16个氦气推力器(推进剂2440L,采用比例控制方式)作为其推进系统。该型推力器的最高比冲为130s,推力分辨率为0.2mN。随着电推进技术的逐渐发展[23, 24],其技术成熟度和实际应用性能满足了飞行需求,GOCE卫星则采用英国QinetiQ公司的T5考夫曼型离子推力器作为其沿轨方向的推进系统,用于实时补偿卫星的非保守力。该型离子推力器推力范围为0.6~20mN,推力分辨率为12μN,顺利完成了重力场测量任务的飞行要求[7]。LISA探路者则采用冷气推力器(推力范围1~500μN)和胶体推力器(范围5~30μN,分辨率0.1μN)作为其推进系统,验证了LISA卫星所需的关键技术。ESA研制的MicroSCOPE[25]卫星主要科学任务是进行等效原理测试,希望该型卫星的观测精度达到10-15量级。MicroSCOPE在初始任务设计中采用FEEP(Field Effect Electric Thrusters)作为其推进器,在2009年决定使用冷气推力器替代FEEP,最终于2016年4月成功发射。由上述无拖曳航天器的发展进程可知,相较于传统的化学推进系统,电推进系统比冲高、响应快速、推力分辨率高、长寿命的优势逐渐引起了科研人员的注意,随着电推力器技术的进一步发展成熟,在将来发射的LISA和天琴航天器中也将采用电推力器作为其推进系统,电推进将成为航天器无拖曳飞行的主要推进手段。
相较于离子[26]、霍尔推力器[27]等电推力器,会切场推力器是目前国际涌现出的一类新型电推进概念。德国泰雷兹公司(TEDG)于1998年提出了高效多级会切磁场等离子推力器(High Efficiency Multi-Stage Plasma Thruster,HEMPT)的发明专利。2001年,TEDG制造出了第一代原理样机,并进行了实验验证。由于会切场推力器采用永磁铁代替励磁线圈,独特的多级会切磁场位形能够有效约束等离子体,可以大幅提高系统工作稳定性,同时大幅降低了等离子体对壁面的溅射侵蚀,从而有效提高推力器寿命。TEDG对于HEMP的首次测试就发现推力器可以实现1~43mN推力的连续变化[28],并于2007年起开始对HEMP-3050进行寿命测试,结果表明HEMPT-3050在额定工况(阳极电压1000V功率1380W)下工作1200h以后,内尖端陶瓷被腐蚀形成凹槽的深度只有5μm[29]。由此可以预测其工作寿命能够达到数万小时以上。除TEDG之外,麻省理工学院于2007年开展了DCFT[30](Diverging Cusped Field Thruster)的研究,DCFT采用圆锥型放电通道和类似于德国HEMPT的磁场构型,研究人员围绕DCFT推力器的空心羽流问题、电流模式切换问题等物理特性问题进行了大量研究。
会切场推力器大范围工作稳定、弱腐蚀、长寿命、结构简单的工作特性非常符合无拖曳任务的需求,引起了哈尔滨工业大学等离子体推进实验室的注意。该实验室针对重力场测量任务设计了一型会切场推力器样机[31],目前已经围绕该型推力器进行了大量数值仿真以及性能实验验证,结果证明会切场等离子体微推力器可实现推力三个数量级连续变化,有望通过该型推力器实现空间科学测量任务对推进系统的苛刻指标要求,进而辅助空间测量系统完成这些空间试验,实现其科学价值。
综上所述,目前关于无拖曳卫星的研究中已经围绕控制系统设计、推力器的设计及性能验证进行了大量研究,但是针对这两者的研究基本都是独立的,在控制系统研究中仅将推力器视为一个理想的执行机构,尚未考虑推力器各项动态性能对整个控制系统的影响。为了分析航天器无拖曳控制系统的建模方法、评估会切场推力器性能对无拖曳控制系统性能的影响,本文对会切场推力器的工作原理和特点进行简要介绍,介绍了本课题组关于该型推力器的性能实验结果,对无拖曳控制系统的建模方法和流程进行详细描述,给出了模型的仿真结果,分析了推力器推力分辨率、推力器响应时间以及传感器测量误差对闭环系统控制精度的影响。
2 物理建模与计算方法会切场推力器作为一种新型电推力器,加速过程类似于传统的霍尔推力器,依靠通道出口的局部电磁场来加速离子产生推力,但与之不同的是,阴极释放的电子会受会切磁场的约束,由于磁镜效应的影响在通道内部磁尖端处往复螺旋运动,而在非尖端处电子沿近似平行于通道内壁的磁力线运动,这样既能保证电子的有效束缚,提高电离率,同时也会大大降低电子与通道内壁的碰撞频率,这样的电离特点类似于离子推力器。所以会切场推力器综合了霍尔推力器和离子推力器的优势,既能保证出口较高的推力密度,又可减小电子对壁面的侵蚀,大幅提高推力器的使用寿命。
会切场推力器的多级会切位型使得推力器的性能较优,与传统电推力器相比,会切场推力器体现出了腐蚀更低、寿命更长、结构简单、容易小型化等优势。所以本课题组对会切场推力器的性能特性进行了实验验证。图 2为供电电压从300~1100V,氙工质流量0.3~1mg/s变化下的推力、推力分辨率、阳极电流、阳极功率、比冲和阳极效率的实验数据图。图 2(a)的推力性能实验数据说明了在这样的工况变化下该推力器可实现0.37~19.20mN推力的连续变化。在低流量低电压条件下,放电电流达到毫安量级,推力可通过探针测量数据推算,测得最小推力为66μN。根据推力实验数据可计算出供电电压调节1V时推力的分辨率数据如图 2(b)所示,可看出推力分辨率均小于20μN,在部分高电压低流量工况其分辨率可小于5μN。由放电电流数据图 2(c)可知会切场推力器具有较好的恒流特性,在阳极流量恒定时,放电电流随供电电压大幅变化时变动幅值极小,说明推力器的工作稳定性较好。在全部测量工况范围内,推力器消耗功率范围为5~636W(如图 2(d)所示)。由图 2(e)可知推力器比冲随着阳极流量和供电电压的增加而增加,最高可达1959s,而且其增加趋势并未停止,所以在后期实验中可通过进一步增加供电电压来提高比冲和推力,进一步拓宽推力器工作参数范围和应用领域。阳极效率实验数据如图 2(f)所示,在大阳极流量时可达到30%,优于其他同尺寸的小型推力器。上述实验结果证明了会切场推力器具备推力三个数量级连续变化,大范围稳定工作,高推力分辨率的能力,而且整体工作性能较为优异,是适用于重力场测量任务中无拖曳控制要求的。

|
Fig. 2 Experimental data of the cusped field thruster |
由无拖曳控制框图(图 1)可知,控制系统建模主要包含四部分:测试质量与航天器的轨道计算、航天器受到的非保守力计算、控制律设计、推力器模型设计。
2.1 轨道计算由于测试质量在太空自由飞行,不受任何非保守力影响,其运动方程为标准的二体轨道动力学方程
| $ {{\mathit{\boldsymbol{\ddot r}}}_{\rm{t}}}\left( t \right) = - \mu \left( {\frac{{{\mathit{\boldsymbol{r}}_{\rm{t}}}\left( t \right)}}{{{{\left| {{\mathit{\boldsymbol{r}}_{\rm{t}}}\left( t \right)} \right|}^3}}}} \right) + {a_{{\rm{ns}}}} $ | (1) |
式中下标t表示测试质量的相关参数;
除地球引力之外,航天器还会受到各类非保守力的影响,例如大气阻力、光压、推力等,这里只考虑大气阻力和推力的影响,所以航天器轨道方程为
| $ {{\mathit{\boldsymbol{\ddot r}}}_{\rm{c}}}\left( t \right) = - \mu \left( {\frac{{{\mathit{\boldsymbol{r}}_c}\left( t \right)}}{{{{\left| {{\mathit{\boldsymbol{r}}_{\rm{c}}}\left( t \right)} \right|}^3}}}} \right) + {a_{{\rm{ns}}}} + {a_{\rm{d}}}\left( t \right) + u\left( t \right) $ | (2) |
式中下标c表示航天器的相关参数;
由于在近地轨道,大气阻力在各类外界阻力中占比最大,所以本模型只考虑了大气阻力的影响,大气阻力的表达式为[17]
| $ F = - 0.5{C_{\rm{D}}} \cdot {S_{\rm{D}}} \cdot \rho \cdot \mathit{\boldsymbol{\upsilon }} \cdot \left| \mathit{\boldsymbol{\upsilon }} \right| $ | (3) |
式中CD表示无量纲大气阻力系数,取2.2;SD表示航天器迎流面面积;ρ为航天器所在高度的大气密度值,根据MSIS-E-90(Mass Spectrometer - Incoherent Scatter)模型计算[17];υ表示航天器与大气的相对运动速度。
定义新的阻力系数c(t)[32]
| $ c\left( t \right) = \rho \frac{{{C_{\rm{D}}}{S_{\rm{D}}}}}{{2m\left( t \right)}} $ | (4) |
式中m(t)表示航天器的质量,则大气阻力造成的加速度ad(t)为
| $ {a_{\rm{d}}}\left( t \right) = - c\left( t \right) \cdot \mathit{\boldsymbol{\upsilon }}\left( t \right) \cdot \left| {\mathit{\boldsymbol{\upsilon }}\left( t \right)} \right| $ | (5) |
由于在实际飞行中,阻力系数c(t)不是恒定值,且无法实时测量,所以需要设计相应的估计方法对c(t)进行实时估计,采用的估计公式如下[17]
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\tilde c\left( t \right) = - \mathit{\Gamma }{\left( {\gamma {\rm{\Delta }}\mathit{\boldsymbol{\dot r}}\left( t \right) + {\rm{\Delta }}\mathit{\boldsymbol{r}}\left( t \right)} \right)^{\rm{T}}}{{\mathit{\boldsymbol{\dot r}}}_{\rm{c}}}\left( t \right)\left| {{{\mathit{\boldsymbol{\dot r}}}_{\rm{c}}}\left( t \right)} \right| $ | (6) |
式中
|
|
Table 1 System parameter and controller parameter |
由测试质量和航天器的轨道方程可知,二者的加速度差值为
| $ \begin{array}{*{20}{l}} {\Delta \mathit{\boldsymbol{\ddot r}}\left( t \right) = {{\mathit{\boldsymbol{\ddot r}}}_{\rm{c}}}\left( t \right) - {{\mathit{\boldsymbol{\ddot r}}}_{\rm{t}}}\left( t \right) = }\\ \;\;\;\;\;\;\;{\mu \left( {\frac{{{\mathit{\boldsymbol{r}}_{\rm{t}}}\left( t \right)}}{{{{\left| {{\mathit{\boldsymbol{r}}_{\rm{t}}}\left( t \right)} \right|}^3}}} - \frac{{{\mathit{\boldsymbol{r}}_{\rm{c}}}\left( t \right)}}{{{{\left| {{\mathit{\boldsymbol{r}}_{\rm{c}}}\left( t \right)} \right|}^3}}}} \right) + {a_{\rm{d}}}\left( t \right) + u\left( t \right)} \end{array} $ | (7) |
依据反馈线性化和PD控制设计方法[17],控制律设计为
| $ \begin{array}{*{20}{l}} {u\left( t \right) = - \mu \left( {\frac{{{\mathit{\boldsymbol{r}}_{\rm{t}}}\left( t \right)}}{{{{\left| {{\mathit{\boldsymbol{r}}_t}\left( t \right)} \right|}^3}}} - \frac{{{\mathit{\boldsymbol{r}}_{\rm{c}}}\left( t \right)}}{{{{\left| {{\mathit{\boldsymbol{r}}_{\rm{c}}}\left( t \right)} \right|}^3}}}} \right) - \left[ {{K_{\rm{p}}}} \right]{\rm{\Delta }}\mathit{\boldsymbol{r}}\left( t \right) - }\\ \;\;\;\;\;\;\;{\left[ {{K_{\rm{d}}}} \right]{\rm{\Delta }}\mathit{\boldsymbol{\dot r}}\left( t \right) + \tilde c\left( t \right)\mathit{\boldsymbol{\upsilon }}\left( t \right) \cdot \left| {\mathit{\boldsymbol{\upsilon }}\left( t \right)} \right|} \end{array} $ | (8) |
在模型中,上式的航天器和测试质量的位置和速度可由轨道方程计算获得,但是实际运行中航天器实际位置和速度是通过GPS获取,测试质量的实际位置和速度无法直接测量,所以需要使用电容传感器测量测试质量与航天器的相对位移△rm,通过数值方法[17](二阶插值型求导公式)求解相对速度
| $ {\rm{\Delta }}{{\mathit{\boldsymbol{\dot r}}}_{\rm{m}}} = \frac{{\rm{d}}}{{{\rm{d}}t}}{\rm{\Delta }}{\mathit{\boldsymbol{r}}_{\rm{m}}} = \frac{{3{\rm{\Delta }}\mathit{\boldsymbol{r}}_{\rm{m}}^i - 4{\rm{\Delta }}\mathit{\boldsymbol{r}}_{\rm{m}}^{i - 1} + {\rm{\Delta }}\mathit{\boldsymbol{r}}_{\rm{m}}^{i - 2}}}{{2{\rm{\Delta }}t}} $ | (9) |
式中下标m表示对应参数的测量值。在此控制律下,整个闭环系统微分方程为
| $ \begin{array}{*{20}{l}} {{\rm{\Delta }}\mathit{\boldsymbol{\ddot r}}\left( t \right) + \left[ {{K_{\rm{p}}}} \right]{\rm{\Delta }}\mathit{\boldsymbol{r}}\left( t \right) + \left[ {{K_{\rm{d}}}} \right]{\rm{\Delta }}\mathit{\boldsymbol{\dot r}}\left( t \right) = }\\ {\left( {c\left( t \right) - \tilde c\left( t \right)} \right)\mathit{\boldsymbol{\upsilon }}\left( t \right) \cdot \left| {\mathit{\boldsymbol{\upsilon }}\left( t \right)} \right|} \end{array} $ | (10) |
阻力系数c(t)估计无误差时,上式为
| $ {\rm{\Delta }}\mathit{\boldsymbol{\ddot r}}\left( t \right) + \left[ {{K_{\rm{p}}}} \right]{\rm{\Delta }}\mathit{\boldsymbol{r}}\left( t \right) + \left[ {{K_{\rm{d}}}} \right]{\rm{\Delta }}\mathit{\boldsymbol{\dot r}}\left( t \right) = 0 $ | (11) |
设定闭环系统阻尼比为ζ,无阻尼自然频率为ωn,则控制器增益为
| $ {K_{\rm{p}}} = {\omega _{\rm{n}}}^2, {K_{\rm{d}}} = 2\zeta {\omega _{\rm{n}}} $ | (12) |
以上系统参数及控制器增益参数设定值见表 1。
2.4 推力器模型设计推力器建模采用黑箱建模方法,即根据实验测得数据进行拟合获得推力器输入与输出之间的关系。本模型中设定供电电压和阳极流量为模型输入,推力、功率、效率等性能参数为输出,拟合多项式如下
| $ X = A + B{V_{\rm{d}}} + C{V_{\rm{d}}}^2 + D\dot m + E{{\dot m}^2} + F{V_{\rm{d}}}\dot m $ | (13) |
式中X表示推力、功率、效率、放电电流、比冲等性能参数;Vd为推力器供电电压;
在模型中,控制器根据位移误差、速度误差给定推力指令,所以推力器模型需要根据指定的推力指令反算推力器供电电压和阳极流量。
3 结果与讨论仿真设定卫星运行轨道要素为轨道高度250km,轨道偏心率为e=0.001,升交点赤经为Ω=0°,轨道倾角为i=88.5°,近地点幅角为ω=45°。在仿真程序中使用以卫星质心为原点的NTW坐标系。在NTW坐标系中,T轴表示沿轨运动方向,W表示卫星角动量方向,N方向与T,W垂直,并指向轨道外部。仿真代码采用MATLAB文本编写,时间步长为0.5s,仿真总时长为6000s。在每一个仿真时刻都会根据状态误差估算非保守力,根据控制律计算推力指令,计算推力器工作参数及测试质量和卫星的运动方程。在计算完成之后,程序会输出每个仿真步中航天器在NTW坐标系下受到的非保守力、推力器推力以及三轴方向的位移误差和速度误差。
由于本节重点分析推力器参数对闭环控制系统工作性能的影响,所以仿真程序中所采用的系统参数、控制器参数[33]直接在表 1中给出。
3.1 推力器理想状况下的计算结果分析推力器在理想工作状况下认为传感器无测量误差、推力器分辨率无限高、无动态响应延迟。在此设定条件下,航天器运动方向上估算的阻力系数(式(6)估计获得)和实际阻力系数(式(4)计算获得)随轨道周期的变化及二者的差值如图 3所示。航天器在6000s运行时长内的实际输出推力和所受阻力随轨道周期的变化及二者差值如图 4所示。可以看到估算阻力系数与实际值非常吻合,其中阻力系数的最大误差为8.33×10-12km-1,说明阻力参数方法合理。推力器输出推力与阻力的最大差值为284.2μN,为此时推力器推力的2.7%,说明推力器满足了非保守力实时补偿的要求。
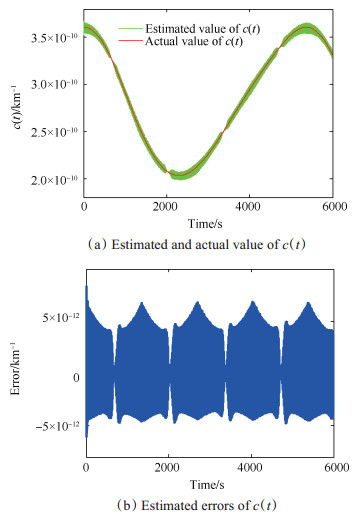
|
Fig. 3 Simulation results of c(t) |
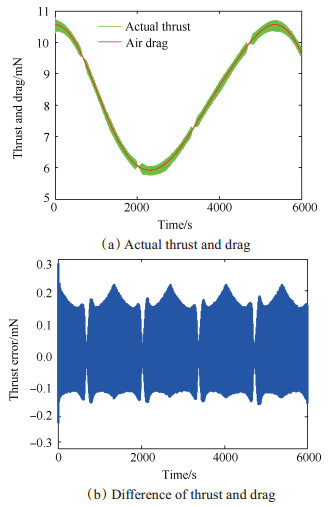
|
Fig. 4 Simulation results of thrust and drag |
图 5和图 6分别显示了航天器和测试质量之间的位置和速度误差,两种误差的量级在N方向和W方向上都是几十个nm,在沿轨T方向上是百nm量级(误差的最大值如表 2所示),这是因为大气阻力是由于航天器与大气的相对运动造成的,而航天器在沿轨方向的相对运动速度远高于其他两个方向,所以大气阻力主要作用于沿轨方向,进而导致T方向的误差幅值大于N,W方向。
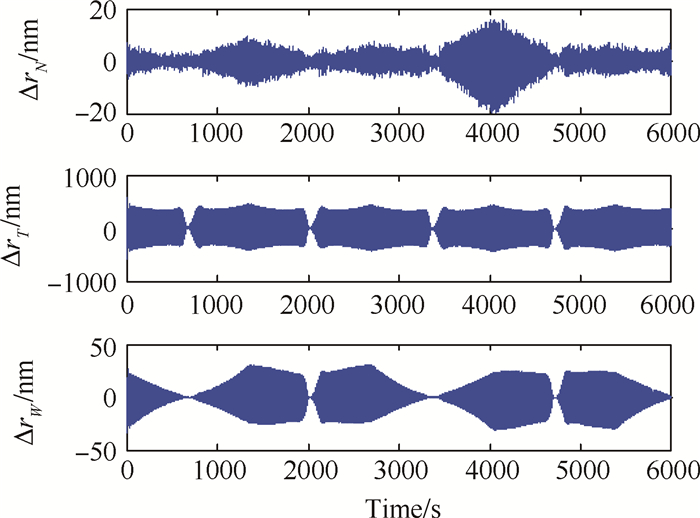
|
Fig. 5 Displacement errors with ideal thruster |
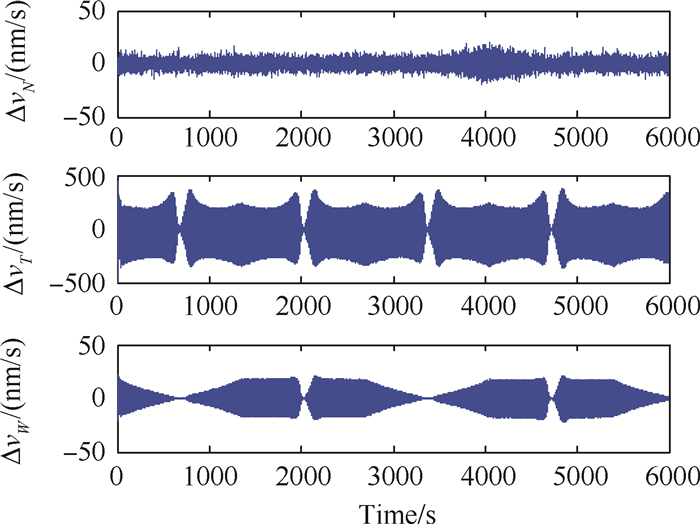
|
Fig. 6 Velocity errors with ideal thruster |
|
|
Table 2 Maximum errors of displacement and velocity with ideal thruster |
推力器在理想状况下设定的推力分辨率为无限高,即推力输出非常精确。但是实际上电推力器由于供电电压和阳极流量调节限制和自身的性能限制,并不能做到推力的连续调节,因此根据实验测得的推力数据设定推力器的推力分辨率为10μN,由于推力、大气阻力、阻力系数等参数的仿真数据图与上节理想推力器条件下的运行结果图极为相似,这里不再列出,只给出闭环系统最终的位移误差和速度误差在各方向的极大值,如表 3所示。
|
|
Table 3 Maximum errors of displacement and velocity in consideration of thrust resolution |
可看出当推力分辨率为10μN时,控制系统的精度并没有明显改变。由于该非保守力模型中只考虑了大气阻力,在250km轨道上大气阻力量级较大,推力器10μN分辨率对其影响极小,但是如果航天器飞行轨道达到万公里量级,非保守力幅值将为微牛级,10μN分辨率则会明显影响控制精度,所以针对超高轨道的无拖曳卫星,推力器的推力分辨率应进一步改善提高。
3.3 推力器响应时间对控制系统的影响在推力器实际运行中,推力指令发生变化时,放电电压和阳极流量需要进行调节,推力器也需要一定的动态响应时间输出相应推力,所以推力输出不可避免地存在延迟。程序中采用0.1s作为推力器的瞬态响应时间。仿真结果如见表 4。
|
|
Table 4 Maximum errors of displacement and velocity in consideration of thruster response delay |
由上表可知,推力器响应延迟导致位移误差、速度误差均大幅增加,其中T方向位移误差增幅为23.5%,速度误差增幅达到30%。说明针对该型推力器,响应延迟成为其性能提升的主要限制因素。不过误差量级仍满足无拖曳飞行的要求。
3.4 传感器存在测量误差状况下的计算结果分析由于实际系统中会受到传感器测控技术的限制,以及数据传输处理等因素的影响,对航天器位置、速度以及测试质量与航天器之间的相对位移测量会存在相应的测量误差。通过查阅相关资料可知,GPS定位位移信号误差±50m,测量的最大速度误差为±10cm/s,电容传感器测得的位移误差为±5nm。模型中设定测量误差分别取各自量的最大值,考虑测量误差后的表达式如下
| $ {\mathit{\boldsymbol{r}}_{\rm{m}}} = {\mathit{\boldsymbol{r}}_{\rm{c}}} + {\mathit{\boldsymbol{\varepsilon }}_{{\rm{pos}}}} $ | (14) |
| $ {\mathit{\boldsymbol{v}}_{\rm{m}}} = {\mathit{\boldsymbol{v}}_{\rm{c}}} + {\mathit{\boldsymbol{\varepsilon }}_{{\rm{vel}}}} $ | (15) |
| $ {\rm{\Delta }}{\mathit{\boldsymbol{r}}_{\rm{m}}} = \left( {{\mathit{\boldsymbol{r}}_{\rm{c}}} - {\mathit{\boldsymbol{r}}_{\rm{t}}}} \right) + {\mathit{\boldsymbol{\varepsilon }}_{{\rm{ \mathit{ δ} r}}}} $ | (16) |
式中rm为考虑测量误差后的航天器位移;vm为考虑测量误差后的航天器速度;△rm为考虑测量误差后的相对位移;ε表示相应物理量测量误差的最大值乘以随机数[-1, 1]。
在考虑推力分辨率和响应时间的基础上,进一步加入测量误差对系统的影响,最终闭环系统的位移误差和速度误差仿真结果如图 7,图 8所示。表 5列出了误差在各方向的极大值。
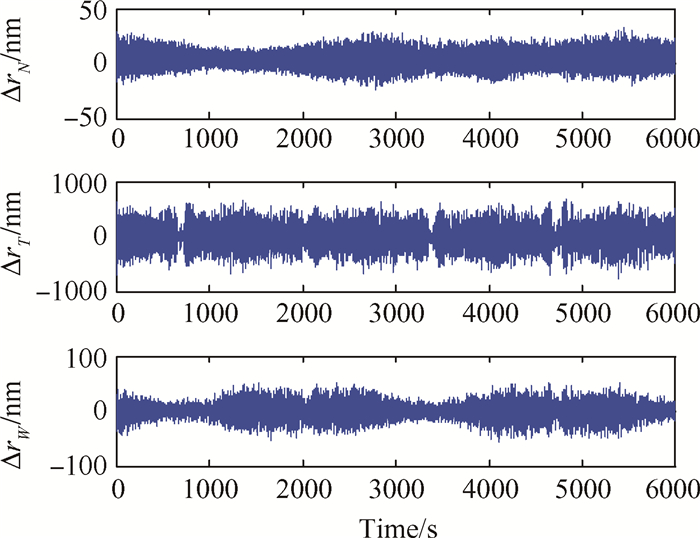
|
Fig. 7 Displacement errors in consideration of measurement errors |
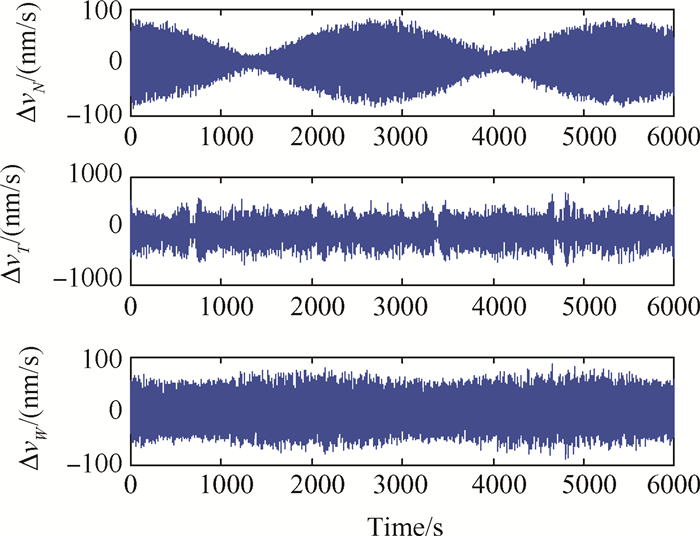
|
Fig. 8 Velocity errors in consideration of measurement errors |
|
|
Table 5 Maximum errors of displacement and velocity in consideration of measurement errors |
由仿真结果可知,由于测量误差的存在导致整个运动过程中位移和速度误差均有小幅增加,所以应尽可能应用更先进的测控技术或者改进控制算法来降低测量误差对整个系统性能的影响。
通过比较表 3和表 5可知,考虑推力器的实际工作特性和传感器的测量误差后,N方向与W方向的位移误差几乎翻倍,速度误差增幅更大,达到理想工况下误差值的4倍;T方向位移误差达到747.51nm,速度误差增加约250nm/s。
4 结论通过本文研究,得到如下结论:
(1)推力分辨率以及传感器的测量误差对系统性能影响较小,但是推力延迟对系统精度影响较大,以T方向为例,位移误差增幅为23.5%,速度误差增幅达到30%,所以响应延迟问题需要在后期的推力器设计和改进中进行进一步的优化。
(2)综合考虑推力器的实际工作特性和传感器的测量误差后,N方向与W方向的位移误差几乎翻倍,速度误差增加4倍;T方向速度误差增加约250nm/s,位移误差增幅29%,达到747.51nm。
(3)从目前的实验和仿真结果来看,会切场推力器是一种非常可行的用于无拖曳控制的微推力器,有望通过进一步改善该型推力器的设计方案,使其性能满足空间科学探测任务的需求。
致谢: 感谢国家自然科学基金资助。
| [1] |
Finn L S. Detection, Measurement and Gravitational Radiation[J]. Physical Review D Particles & Fields, 1992, 46(12): 5236-5249.
(  0) 0) |
| [2] |
宁津生, 王正涛, 超能芳. 国际新一代卫星重力探测计划研究现状与进展[J]. 武汉大学学报(信息科学版), 2016, 41(1): 1-8. (  0) 0) |
| [3] |
Reigber C, Lühr H, Schwintzer P. CHAMP Mission Status[J]. Advances in Space Research, 2002, 30(2): 129-134. DOI:10.1016/S0273-1177(02)00276-4
(  0) 0) |
| [4] |
Loomis B D, Nerem R S, Luthcke S B. Simulation Study of a Follow-on Gravity Mission to GRACE[J]. Journal of Geodesy, 2012, 86(5): 319-335. DOI:10.1007/s00190-011-0521-8
(  0) 0) |
| [5] |
李克行, 彭冬菊, 黄珹, 等. GOCE卫星重力计划及其应用[J]. 天文学进展, 2005, 23(1): 29-39. DOI:10.3969/j.issn.1000-8349.2005.01.003 (  0) 0) |
| [6] |
钟波.基于GOCE卫星重力测量技术确定地球重力场的研究[D].武汉: 武汉大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10486-2010167102.htm
(  0) 0) |
| [7] |
Allasio A, Anselmi A, Catastini G, et al. Goce Mission: Design Phases and in-Flight Experiences[J]. Advances in the Astronautical Sciences, 2010, 137.
(  0) 0) |
| [8] |
Danzmann K. LISA-An ESA Cornerstone Mission for the Detection and Observation of Gravitational Waves[J]. Advances in Space Research, 2003, 32(7): 1233-1242. DOI:10.1016/S0273-1177(03)90323-1
(  0) 0) |
| [9] |
赵艳彬, 王孝东, 孙克新. LISA引力波探测器与关键技术分析[C].哈尔滨: 中国宇航学会深空探测技术专业委员会学术年会, 2010.
(  0) 0) |
| [10] |
Gerndt R, Team E L. LTP-LISA Technology Package: Development Challenges of a Spaceborne Fundamental Physics Experiment[C]. Barcelona: the 7th International LISA Symposium, 2009.
(  0) 0) |
| [11] |
Fichter W, Schleicher A, Bennani S, et al. Closed Loop Performance and Limitations of the LISA Pathfinder Drag-Free Control System[C]. Hilton Head: AIAA Guidance, Navigation and Control Conference and Exhibit, 2007.
(  0) 0) |
| [12] |
Canuto E. Drag-Free and Attitude Control for the GOCE Satellite[J]. Automatica, 2008, 44(7): 1766-1780. DOI:10.1016/j.automatica.2007.11.023
(  0) 0) |
| [13] |
Luo J, Chen L S, Duan H Z, et al. TianQin: a Space-Borne Gravitational Wave Detector[J]. Classical & Quantum Gravity, 2015, 33(3).
(  0) 0) |
| [14] |
胡明, 李洪银, 周泽兵. 无拖曳控制技术及其应用[J]. 载人航天, 2013, 19(2): 61-69. DOI:10.3969/j.issn.1674-5825.2013.02.010 (  0) 0) |
| [15] |
Nguyen A N, Conklin J W. Three-Axis Drag-Free Control and Drag Force Recovery of a Single-Thruster Small Satellite[J]. Journal of Spacecraft & Rockets, 2015, 52(6): 1-11.
(  0) 0) |
| [16] |
Singh S, D'Amico S, Pavone M. High-Fidelity Modeling and Control System Synthesis for a Drag-Free Microsatellite[C]. Munich: International Symposium on Space Flight Dynamics, 2015.
(  0) 0) |
| [17] |
Blandino J J, Marchetti P, Demetriou M A. Electric Propulsion and Controller Design for Drag-Free Spacecraft Operation[J]. Journal of Spacecraft & Rockets, 2015, 45(45): 1303-1315.
(  0) 0) |
| [18] |
王玉爽.无拖曳卫星控制方法研究[D].哈尔滨: 哈尔滨工业大学控制科学与工程, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10213-1012000994.htm
(  0) 0) |
| [19] |
张锦绣, 董晓光, 曹喜滨. 基于无速度测量的无拖曳卫星自适应控制方法[J]. 宇航学报, 2014, 35(4): 447-453. DOI:10.3873/j.issn.1000-1328.2014.04.011 (  0) 0) |
| [20] |
王涛, 张洪波, 汤国建.基于线性化运动方程的无阻力卫星LQG/LTR控制方法[C].南京: 第33届中国控制会议, 2014.
(  0) 0) |
| [21] |
Snyder N J, Williams W M, Denton D L, et al. A Satellite Freed of All but Gravitational Forces: " TRIAD I"[J]. Journal of Spacecraft & Rockets, 1974, 11(9): 637-644.
(  0) 0) |
| [22] |
Bencze W J, Debra D B, Herman L, et al. On-Orbit Performance of the Gravity Probe B Drag-Free Translation Control System[J]. Advances in the Astronautical Sciences, 2006, 125(3).
(  0) 0) |
| [23] |
毛根旺, 韩先伟, 杨涓, 等. 电推进研究的技术状态和发展前景[J]. 推进技术, 2000, 21(5): 1-5. (MAO Gen-wang, HAN Xian-wei, YANG Juan, et al. Research State of Electric Propulsion and Its Development Prospect[J]. Journal of Propulsion Technology, 2000, 21(5): 1-5. DOI:10.3321/j.issn:1001-4055.2000.05.001)
(  0) 0) |
| [24] |
吴汉基, 蒋远大, 张志远. 电推进技术的应用与发展趋势[J]. 推进技术, 2003, 24(5): 385-392. (WU Han-ji, JIANG Yuan-da, ZHANG Zhi-yuan. Application and Development Trend of Electric Propulsion Technology[J]. Journal of Propulsion Technology, 2003, 24(5): 385-392. DOI:10.3321/j.issn:1001-4055.2003.05.001)
(  0) 0) |
| [25] |
Touboul P, Rodrigues M, Métris G, et al. Microscope, Testing the Equivalence Principle in Space[J]. Comptes Rendus De Lacademie Des Sciences, 2001, 2(9): 1271-1286.
(  0) 0) |
| [26] |
郑茂繁, 张天平, 孟伟, 等. 20cm氙离子推力器性能扩展研究[J]. 推进技术, 2015, 36(7): 1116-1120. (ZHENG Mao-fan, ZHANG Tian-ping, MENG Wei, et al. Research of Improvement Performance for 20cm Xenon Ion Thruster[J]. Journal of Propulsion Technology, 2015, 36(7): 1116-1120.)
(  0) 0) |
| [27] |
田立成, 郭宁, 龙建飞, 等. LHT-100霍尔推力器宽功率范围工作实验研究[J]. 推进技术, 2014, 35(9): 1283-1289. (TIAN Li-cheng, GUO Ning, LONG Jian-fei, et al. Experimental Study of LHT-100 Hall Thruster Operation in the Wide Power Range[J]. Journal of Propulsion Technology, 2014, 35(9): 1283-1289.)
(  0) 0) |
| [28] |
Kornfeld G, Koch N, Coustou G, et al. First Test Results of the HEMP Thruster Concept[C]. Toulouse: the 28th International Electric Propulsion Conference, 2003.
(  0) 0) |
| [29] |
Koch N, Schirra M, Weis S, et al. The HEMPT Concept-a Survey on Theoretical Considerations and Experimental Evidences[C]. Wiesbaden: the 32nd International Electric Propulsion Conference, 2011.
(  0) 0) |
| [30] |
Courtney D, Lozano P, Martinezsanchez M. Continued Investigation of Diverging Cusped Field Thruster[C]. Hartford: the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2008.
(  0) 0) |
| [31] |
Liu H, Chen P B, Sun Q Q, et al. Design of a Cusped Field Thruster for Drag-Free Flight[J]. Acta Astronautica, 2016, 126: 35-39. DOI:10.1016/j.actaastro.2016.04.009
(  0) 0) |
| [32] |
Marchetti P, Blandino J, Demetriou M, et al. Electric Propulsion and Controller Design for Drag-Free Spacecraft Operation in Low Earth Orbit[J]. Blood, 2008, 45(6): 1303-1315.
(  0) 0) |
| [33] |
Rock B S, Blandino J J, Demetriou M. Propulsion Requirements for Drag-Free Operation of Spacecraft in Low Earth Orbit[J]. Journal of Spacecraft & Rockets, 2006, 43(3): 594-606.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


