2. 海军工程大学 舰船动力工程军队重点实验室,湖北 武汉 430033
2. Military Key Laboratory for Naval Ship Power Engineering, Naval University of Engineering, Wuhan 430033, China
为适应当代船舶对动力的需求,满足高性能船的航行要求,燃气轮机压气机逐步朝着高效率、高负荷及高稳定性方向发展。性能提升的同时也带来了一系列问题,导致压气机流场结构受到破坏,内部损失明显增大。研究表明,造型后的端壁能够优化压气机的流场结构,减小通道内的二次流损失[1]。实验数据和仿真结果也都表明,不同的端壁造型方法得到的端壁外形及其计算结果差别较大。因此,如何更好地构造非轴对称端壁,使之能最大程度地改善流场结构、提高压气机的气动性能,成为了各国专家学者研究的重点。
20世纪70年代,学者们发现通过对端壁进行造型可以减少流动损失,提出了造型原理及其减少流动损失机理[2~5]。1994年,提出了非轴对称端壁造型技术的概念[6]。1999年三维线性设计系统运用到了非轴对称端壁的造型上,并提出了采用傅里叶级数构造非轴对称端壁[7~9],之后又成功应用在了航空发动机单级高压涡轮Trent 500[10]上。2001年,Nagel对端壁造型进行设计时,又提出了采用衰减函数构造端壁[11]。
李国君等在讨论非轴对称端壁成型时分别提出采用三角函数法和压差法构造端壁[12, 13]。近年来又出现了双控制型线法[14]和脊线法[15],都是根据特定的数学表达式并依据造型的基本原理来生成端壁[16]。随着计算机性能和三维流场求解能力的提升,又发展出非轴对称端壁的优化设计系统。高增珣用NURBS曲线进行端壁设计,并用ISIGHTTM对非轴对称端壁进行优化造型[17]。张鹏等应用人工神经网络和遗传算法,对跨声速轴流压气机[18]和涡轮[19]的端壁进行优化造型,都获得了较好的数值计算结果。
通过对不同非轴对称端壁造型方法的分析,发现造型后的端壁静压分布相比造型前更加均匀,且横向压差减小。设想采用一种方法,直接改变端壁的压力分布,减小吸力面与压力面之间的压力梯度。基于此,本文设计出了一种基于轮毂静压的非轴对称端壁造型方法。
2 物理模型与计算 2.1 研究对象研究对象是NASALewis研究中心设计的独立轴流压气机转子Rotor37,该模型具有高压比、高效率、喘振边界较广的特点[20]。主要参数[21]见表 1。
|
|
Table 1 Rotor 37 design parameters |
网格采用AutoGrid5自动生成,拓扑结构默认为O4H。间隙为蝶形网格,网格节点数17。y+值取1,计算出第一层网格厚度为3μm。
数值计算采用FINE/TURBO模块,选用Spalart-Allmaras(S-A)湍流模型求解相对坐标系下的三维Reynold-Averaged Navier-Stokes(RANS)方程,选取中心差分格式和当地时间步,CFL数为3。进口给定绝对总压、绝对总温沿径向分布[20](图 1)和来流方向,出口给定压力的简单径向平衡方程,壁面采用绝热无滑移条件。
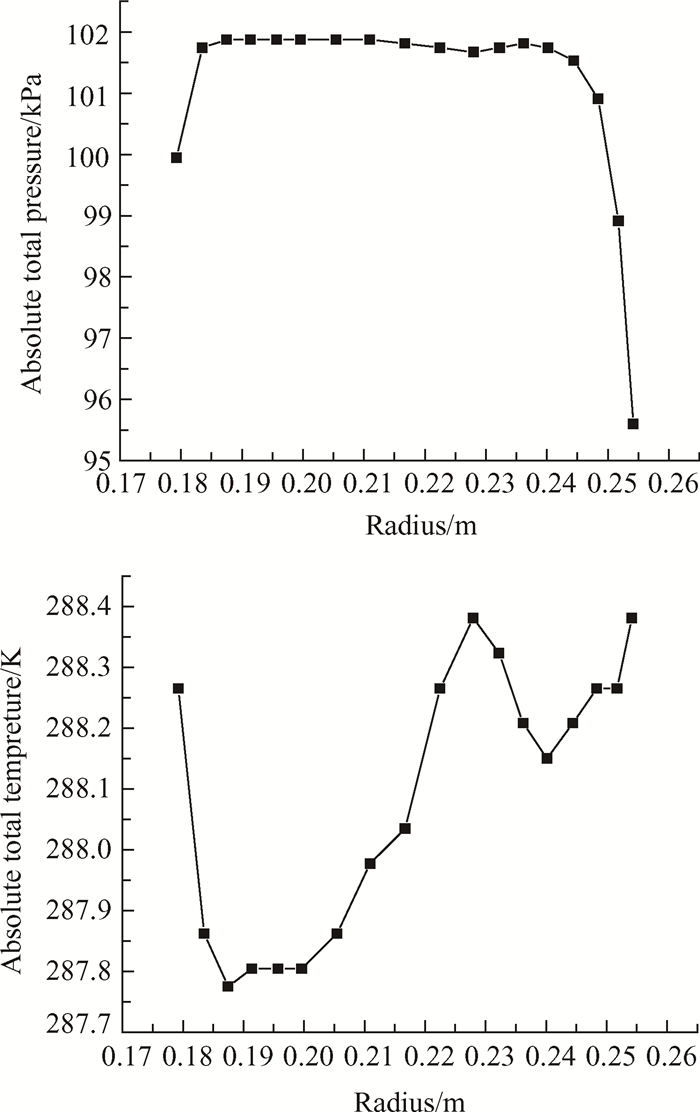
|
Fig. 1 Radial distribution of absolute total pressure and absolute total temperature at the entrance |
进行网格无关性验证如表 2所示,当网格总数达到8.7×105时,网格数的增加对效率已经没有影响,故采用8.7×105网格数。
|
|
Table 2 Grid numbers and associated efficiency |
设计转速下,对比数值计算值与实验数据[22],如图 2所示,可以看到,出口气流角的计算值与实验值的误差在1~5°内,并且走势保持基本一致;压比沿叶高的分布也符合实验结果,计算得到的峰值效率与给定值只相差0.0138,表明采用的数值方法是准确有效的。
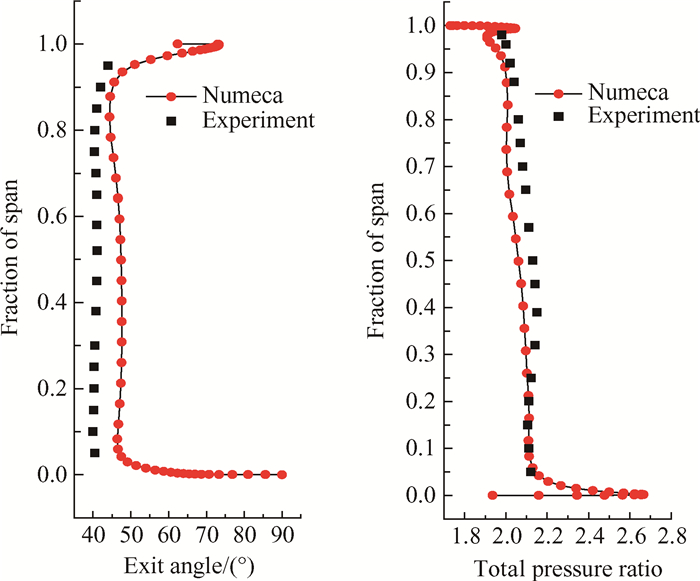
|
Fig. 2 Spanwise distribution of flow angle and total pressure ratio at exit |
本文采用的是一种全新的根据流道内部物理场进行端壁造型的方法。造型的依据是轮毂静压,目的是将轮毂静压的变化反映到端壁的造型上,使端壁造型很好地贴合流道内部物理场的变化。
2.3.1 造型原理为便于表述,原始平面端壁用Plane代替,非轴对称端壁用Non_axi代替。造型的基本思路:用经过处理的静压值表示端壁的造型幅度,得到最初的端壁造型,然后通过多次计算,根据计算得到的端壁静压对其进行反复的调试,最后通过优化,得到最终的非轴对称端壁。
2.3.2 造型过程本文使用AutoBlade模块对Rotor37的轮毂进行造型,基本步骤如下:
(1)数值计算。首先利用FINE/TURBO模块对模型进行数值计算,得到平面端壁的静压分布。如图 3,可以看出,轮毂静压在叶片进口的分布很不均匀,吸力面和压力面的压力梯度较大。
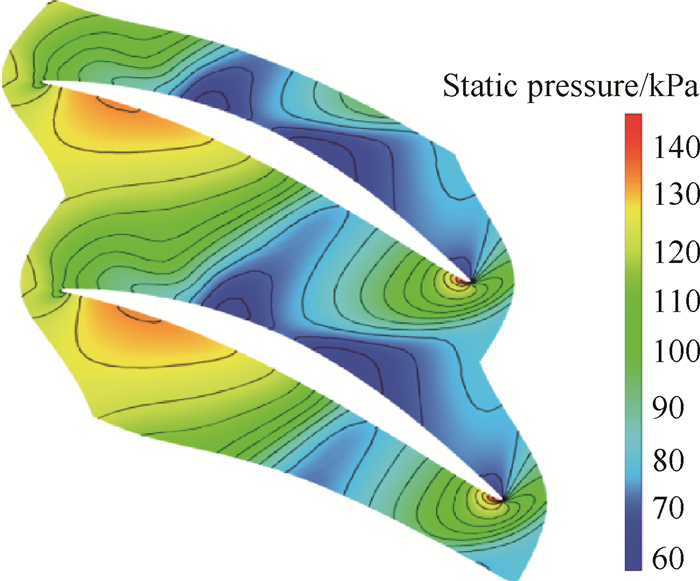
|
Fig. 3 Static pressure distribution on hub |
(2)端壁面划分。在通道内部沿圆周方向截取8条线,截取的线的疏密程度与端壁静压的压力梯度相符,压力梯度大的地方适当加密,如叶片进出口附近。每条线上等间距取9个点,得到共72个不同点处的静压值,点的选取必须保证这些点处的静压值能够准确刻画出端壁面的静压变化情况。端壁划分的示意图如图 4。
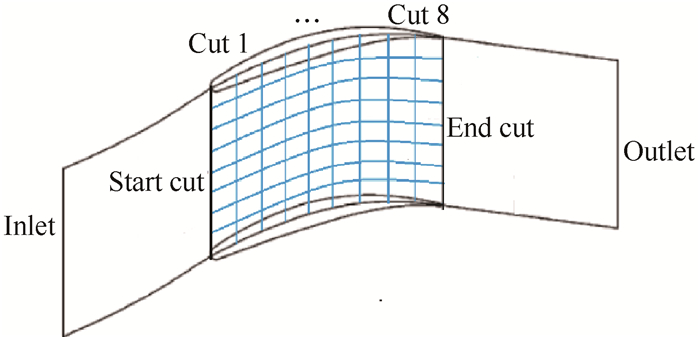
|
Fig. 4 Endwall division |
(3)对静压ps进行处理,获得端壁的扰动量△R。静压的单位为Pa,不能直接作为扰动量来生成非轴对称端壁,应对静压值减小适当的倍数。实际的扰动量与静压的表达式为
| $ {\rm{\Delta }}R = A \times \left( {{p_{\rm{s}}} - {p_{{{\rm{s}}_{\rm{ - }}}{\rm{mid}}}}} \right) \times {10^{ - 7}} $ | (1) |
式中ps为当地静压,ps_mid为每条线中间点处静压,A为幅值,可通过改变A的大小调节整个端壁的幅度,且保证造型幅度不超过叶高的5%。为有效控制质量流量的变化,若直接减小ps作为端壁幅值,生成的端壁相当于在原端壁上增加了一部分,通流大幅面积减小,导致流量也相应减小,本文采用了(ps-ps_mid)来表示端壁幅值,这样的设计既可以保证生成的端壁为经典的非轴对称端壁构型,即在吸力面形成凹面,压力面形成凸面,又可以有效控制质量流量基本不变。
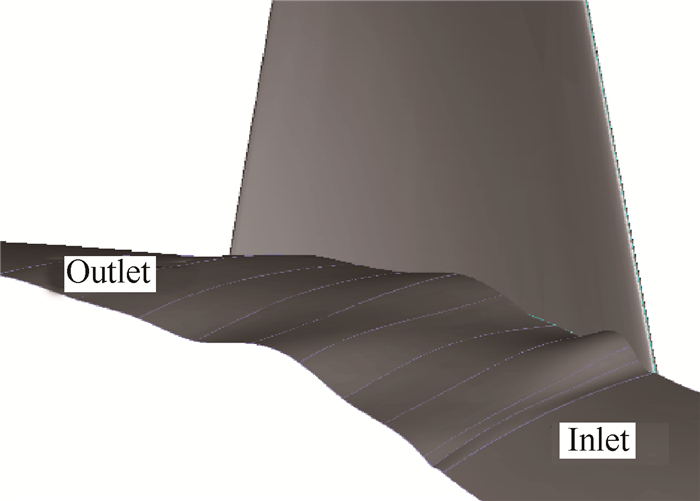
(4)非轴对称端壁生成。端壁的生成在AutoBlade模块中进行。造型的范围限定在叶片进出口之间,起止Cut线分别设置在前尾缘处,以保证叶片通道与进出口延伸段的光滑过度。Cut线的间距与叶片通道划分时截取的线间距保持一致。整个端壁面的设计变量为72个,与壁面划分时得到的静压值的位置一一对应。得到Roto37最初的端壁造型Non_axi0如图 5所示。
|
Fig. 5 Initial non-axisymmetic endwall shape |
(5)非轴对称端壁调试。非轴对称端壁叶片进口处的静压往往变化较大,首先保证在进口延伸段的过渡自然,对进口处的端壁进行调整,得到Non_axi1(图 6为调整前后进口处的造型对比),再根据调试后计算得到的端壁静压分布调整端壁幅值,得到Non_axi2。调试过程遵循:降低低压区的端壁幅值,增大高压区的端壁幅值。从而使低压区静压升高,高压区压力降低,进一步减小了横向压差。

|
Fig. 6 Comparison of adjusted endwall shapes |
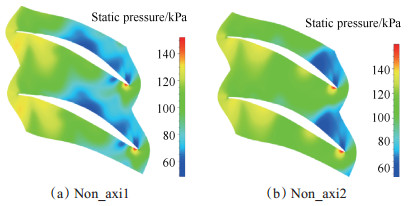
图 7为调试前后端壁静压分布比较。显然,调试后端壁的静压更加均匀,通道中部的低压区消失,低压区面积明显减小。
|
Fig. 7 Contours of non-axisymmetric endwalls |
从造型过程及端壁的调试过程可以看出,基于轮毂静压的造型方法在构造非轴对称端壁方面优势较为明显,它不仅将端壁造型幅度同端壁静压结合起来,而且还能对端壁幅值进行有针对性的修改,使端壁的造型符合流道的压力场分布。可以预见,近轮毂区域通道的横向压差将大幅减小,端壁附面层低能流体与吸力面附面层混合的趋势将被削弱。
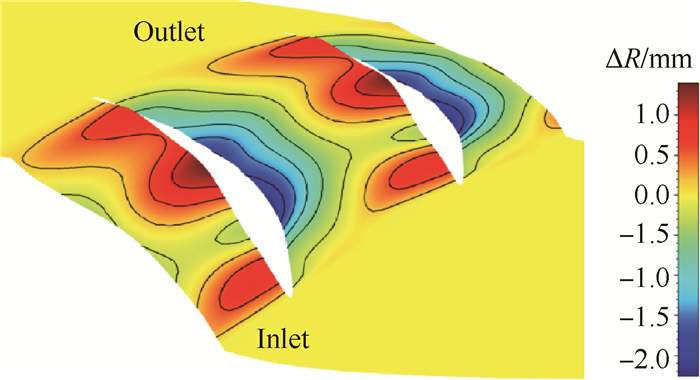
2.4 非轴对称端壁优化为使端壁造型更为合理,采用Design3d优化平台对Non_axi2再次进行优化。样本总数为144个。优化过程利用人工神经网络(Artificial neural network)建立目标函数与设计变量间的联系,通过遗传算法(Genetic algorithms)寻目标函数的最优解。本文的优化目标是:保持质量流量不变,效率最大化。得到最终的端壁Non_axi3幅值云图如图 8所示。
|
Fig. 8 Height contour isolines of optimized non-axisymmetric endwall |
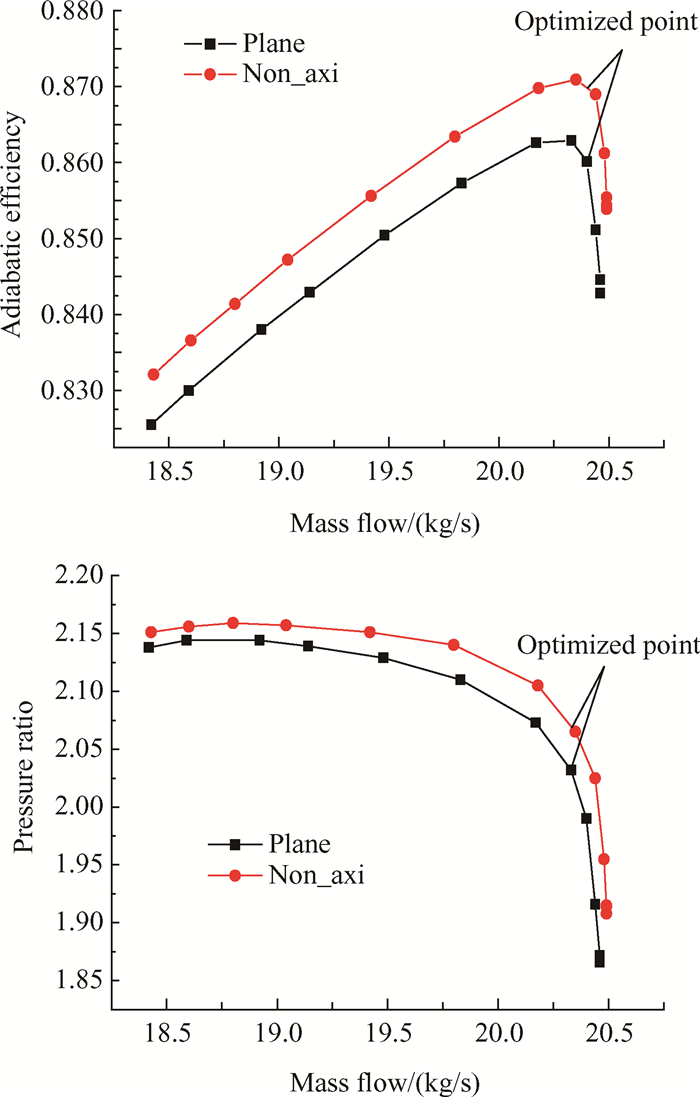
图 9给出了Plane和Non_axi3压气机转子的特性曲线,从整个流量范围来看,造型后的端壁效率、压比都比平面端壁要大。在优化点,绝热效率提高0.88%,压比提高1.47%,堵塞点的流量稍有增加,通流能力一定程度上得到提高,压气机的总体性能得到改善。
|
Fig. 9 Characteristic comparison of the compressor with initial hub and optimized hub |
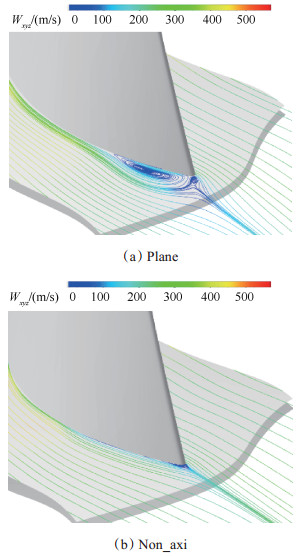
从5%叶高截面的流线分布图(图 10)可以看到,对于平面端壁,气流流经叶片尾缘时,靠近吸力面侧发生分离,并逐步向后发展,并在出口处形成了两个较强的漩涡。优化后,非轴对称端壁的漩涡数量减少为一个,分离的位置也明显后移,且强度和范围都大幅减小。表明优化后的端壁由于减小了附面层吸力面与压力面的横向压差,使离心力与横向压差再度平衡,从而有效地抑制了气流过早分离。
|
Fig. 10 Streamlines of S1 surfaces at 5% blade height |
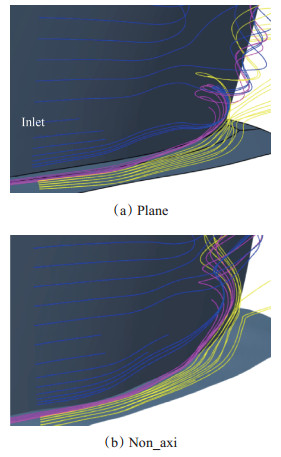
如图 11显示,造型后的端壁吸力侧靠近轮毂处的涡系结构显著减少。这是由于近端壁附近压力梯度的减小,削弱了环壁面附面层低能流体与叶片吸力面附面层的参混,因此在吸力面侧的通道涡得到有效抑制。表明进一步研究发现,40%叶高以上,非轴对称端壁对气流的分离不产生影响。
|
Fig. 11 Streamlines of suction surfaces near hub |
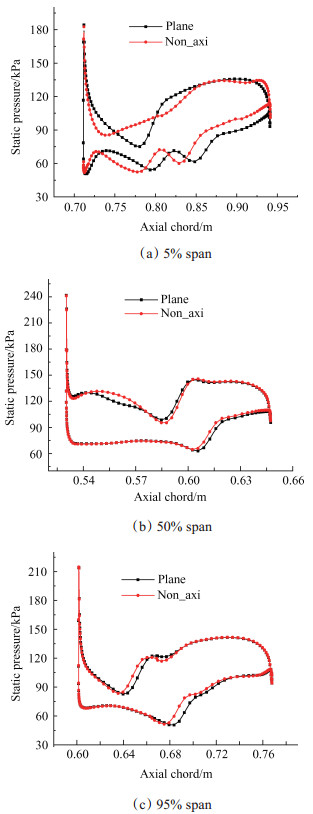
图 12为不同叶高处的静压分布。在50%和95%叶高部分,非轴对称端壁和平面端壁叶片表面的压差基本保持一致。在5%叶高处,靠近前缘的压差明显减小,从一开始就削弱了气流分离。40%轴向弦长往后,叶片表面压差也有明显减小。从整体上看,靠近叶根部位的压差减小较为明显,通道内部静压分布更加均匀。
|
Fig. 12 Radius distribution of blade static pressure |
总压损失系数是评价压气机内部损失的一种主要方式,表达式为
| $ {C_p} = \frac{{{p_{{\rm{t\_inlet}}}} - {p_{\rm{t}}}}}{{\frac{1}{2}{\rho _{{\rm{inlet}}}}{\omega _{{\rm{inlet}}}}^2}} $ | (2) |
式中pt_inlet为进口总压,pt为出口截面总压,ρinlet,ωinlet分别是进口密度和进口相对速度。
如表 3所示,优化后出口截面的平均总压损失系数为0.112,相比平面壁降低了8.94%。
|
|
Table 3 Comparison of average total pressure loss coefficient between plane and non-axi endwall at blade exit |
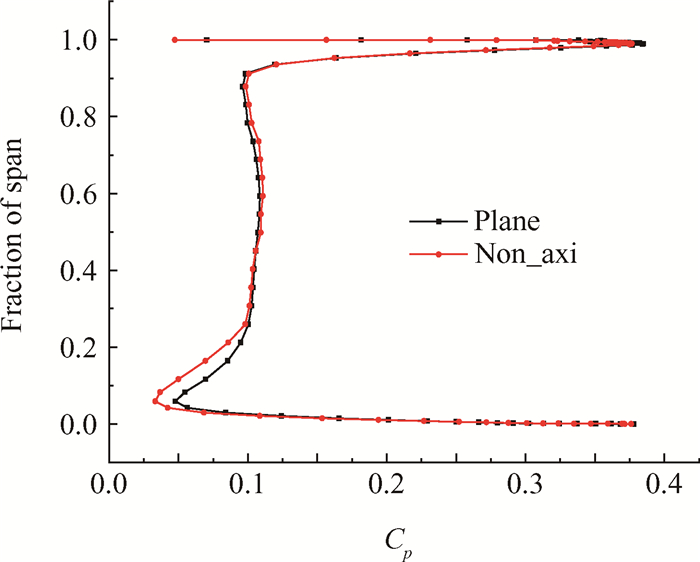
图 13显示了造型前后的总压损失系数在叶片出口处的分布云图。靠近轮毂部分,高损失区显著减小,低损失区域面积扩大;在50%~80%叶高,高损失区的范围略有增加。在图 14中可以看到,从叶根至30%叶高,非轴对称端壁的总压损失系数明显比平面端壁要小,50%~85%叶高,非轴对称端壁的总压损失系数略有增加,但增加幅度较小,这与总压损失系数沿叶高方向的分布相一致。由此可以看出,采用非轴对称端壁能够减小压气机转子靠近轮毂处的压力损失,这是优化后的端壁使压气机转子效率和压比提高的一个重要因素。

|
Fig. 13 Total pressure loss coefficient contours at blade exit |
|
Fig. 14 Radius distribution of total pressure loss at blade exit |
本文基于NUMECA软件,设计出基于轮毂静压的端壁造型方法,分析了造型后端壁对压气机转子的气动性能及流场结构的影响,得到结论如下:
(1)基于轮毂静压构造非轴对称端壁是一种全新的根据叶片通道内部物理场进行端壁造型的方法,它将轮毂静压与端壁造型紧密结合,得到的端壁造型更符合流动规律,且造型过程可以依据静压分布对端壁造型进行有针对性的调整。
(2)造型后的端壁使压气机转子的总体性能得到提升。设计转速下的效率特性线和压比特性线提升较大,其中,优化工况点的压比提高了1.47%,效率提高了0.88%,且出口截面的总压损失系数减小了8.94%。
(3)经过端壁造型的压气机转子,叶片根部的流场结构得到显著优化。端壁的低压区基本消失,通道内压差明显减小;气流分离现象得到抑制,涡系的强度和范围明显减少,并且涡的数量由两个减少到一个。
致谢: 感谢国防创新基金资助。
| [1] |
那振喆, 刘波, 高丽敏. 高压涡轮导叶非轴对称端壁优化设计[J]. 航空工程进展, 2013, 4(3): 319-326. DOI:10.3969/j.issn.1674-8190.2013.03.010 (  0) 0) |
| [2] |
Morris A W H, Hoare R G. Secondary Loss Measurements in a Cascade of Turbine Blades with Meridional Wall Profiling[J]. Mechanical Engineering, 1976, 98(2).
(  0) 0) |
| [3] |
Germain T, Nagel M, Raab I, et al. Improving Efficiency of a High Work Turbine Using Non-Axisymmetric Endwalls PartI: Endwall Design and Performance[R]. ASME 2008 GT-50469.
(  0) 0) |
| [4] |
Boletis E. Effects of Tip Endwall Contouring on the Three-Dimensional Flow Investigation[J]. Journal of Engineering for Gas Turbines and Power, 1985, 107(4): 983-990. DOI:10.1115/1.3239845
(  0) 0) |
| [5] |
Atkins M J. Secondary Losses and Endwall Profiling in a Turbine Cascade[R]. IMech E C 255/87, 1987: 225-226.
(  0) 0) |
| [6] |
Rose M G. Non-Axisymmetric Endwall Profiling in the HP NGVs of an Axial Flow Gas Turbine[R]. ASME 94-GT-249.
(  0) 0) |
| [7] |
Harvey N W, Rose M G, Taylor M D. Non-Axisymmetic Turbine End Wall Design, Part Ⅰ: Three-Dimensional Linear Design System[R]. ASME 99-GT-337.
(  0) 0) |
| [8] |
Hartland J C, Gregory-Smith G, Harvey N W, et al. Non-Axisymmetric Turbine End Wall Design: Part Ⅱ Experimental Validation[R]. ASME 99-GT-338.
(  0) 0) |
| [9] |
Shahpar S, Lapworth B L. A Forward and Inverse Three- Dimensional Linear Design System for Turbomachinery Applications[C]. Athens: 4th ECCOMASS Computational Fluid Dynamics Conference, 1998.
(  0) 0) |
| [10] |
Brennan G, Harvey N W, Rose M G. Improving the Efficiency of the Trent 500-HP Turbine Using Nonaxisymmetric End Walls, Part Ⅰ: Turbine Design[R]. ASME 2001 GT-0505.
(  0) 0) |
| [11] |
Nagel M G, Fottner L, BaierR. Optimization of Three Dimensionally Designed Turbine Blades and Side Walls[R]. ISABE-2001-1058.
(  0) 0) |
| [12] |
李国君, 马晓永, 李军. 非轴对称端壁成型及其对叶栅损失影响的数值研究[J]. 西安交通大学学报, 2005, 39(11): 1169-1172. DOI:10.3321/j.issn:0253-987X.2005.11.002 (  0) 0) |
| [13] |
李国君, 郑金, 李军, 等. 一种新非轴对称端壁成型方法的数值研究[J]. 航空动力学报, 2007, 22(9). (  0) 0) |
| [14] |
孙皓, 宋立明, 李军, 等. 小展弦比叶栅非轴对称端壁造型及气动性能的数值研究[J]. 航空工程进展, 2012, 46(11): 6-11. (  0) 0) |
| [15] |
田兴江, 常海萍, 张镜洋, 等. 基于参数化脊线的非轴对称端壁成型方法[J]. 推进技术, 2017, 38(6): 1294-1301. (TIAN Xing-jiang, CHANG Hai-ping, ZHANG Jing-yang, et al. Non-Axisymmetric Endwall Contouring Method Based on Parameterized Ridge Line[J]. Journal of Propulsion Technology, 2017, 38(6): 1294-1301.)
(  0) 0) |
| [16] |
孙皓, 李军, 李国君, 等.非轴对称端壁造型技术在透平机械中的应用和发展[C].西安: 西安交通大学, 2011.
(  0) 0) |
| [17] |
高增珣, 高学林, 袁新. 透平叶栅非轴对称端壁的气动最优化设计[J]. 工程热物理学报, 2007, 28(4). (  0) 0) |
| [18] |
张鹏, 刘波, 毛晓晨, 等. 三维造型和非轴对称端壁在跨声速压气机中的应用[J]. 推进技术, 2016, 37(2): 250-257. (ZHANG Peng, LU Bo, MAO Xiao-chen, et al. Application of 3D Blading and Non-Axisymmetric Endwall in a Transonic Compressor[J]. Journal of Propulsion Technology, 2016, 37(2): 250-257.)
(  0) 0) |
| [19] |
赵刚剑, 刘波, 那振喆, 等. 采用新型非轴对称端壁优化设计方法提高涡轮性能的数值研究[J]. 推进技术, 2014, 35(5): 597-602. (ZHAO Gang-jian, LIU Bo, NA Zhen-zhe, et al. Improving the Performance of Turbine Based on a New Optimization Design Method[J]. Journal of Propulsion Technology, 2014, 35(5): 597-602.)
(  0) 0) |
| [20] |
Reid L, Moore R D. Design and Overall Performance of Four Highly Loaded, High-Speed Inlet Stages for an Advanced High-Pressure-Ratio Core Compressor[R]. NASA-TP-1337, 1978.
(  0) 0) |
| [21] |
Ali A. A. NASA Rotor 37 CFD Code Validation Glenn-HT Code[R]. AIAA 2009-1060.
(  0) 0) |
| [22] |
赵辛午.基于遗传算法的压气机三维气动优化设计方法研究[D].哈尔滨: 哈尔滨工业大学, 2008.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


