1 引言

随着军事任务多样化需求的不断提高以及高性能战术导弹研制的持续推进，低温条件下的安全性已经成为大多数战术导弹的工作指标，低温和点火压力载荷的叠加使得固体推进剂药柱的结构完整性问题变得更加突出。20世纪80年代前后，美国在开展低温-40℃条件下战术导弹发射时，就已经有部分SRM发生爆炸现象^{[1, 2]}。此后，国内外在进行SRM的研制过程中，也不断有类似现象的发生^{[3, 4]}。美国Aerojet公司通过对大量战术导弹的发射情况进行统计和分析发现，低温点火瞬间战术导弹推进剂药柱结构完整性的破坏是引发SRM失效的主要原因^[5]。这些现象的发生严重滞后了武器型号的定型，且目前所使用战术导弹均经过不同时间贮存，因此，建立低温点火条件下战术导弹SRM老化药柱的强度极限线对于分析药柱结构完整性具有十分重要的指导意义。

固体推进剂是典型的颗粒增强粘弹性材料，其力学性能受到外界温度、加载应变率和老化时间等因素的影响，因此为构建SRM老化药柱强度极限线必须开展不同加载条件下力学性能试验。Jeremic^[6]的研究表明，研究低温条件下1~10²s^-1应变率范围内固体推进剂的力学性能对分析真实低温点火条件下战术导弹SRM药柱的结构完整性具有更重要的意义。

为分析固体推进剂药柱的结构完整性，需要开展大量的力学性能试验，以确定推进剂在不同加载条件下的变形特性。单向恒定应变率条件下的拉压实验简单易行，而且基本上能够表征固体推进剂的力学极限特性。但固体推进剂在使用和贮存过程中，其受力状态是多维的，而且固体推进剂是典型的颗粒增强粘弹性材料，其力学性能明显受到应力（或应变）状态的影响。因此，简单采用一维单轴拉压实验获得的结果评判固体推进剂在多维受力情况下的变形行为时，会带来较大的偏差，因为材料在一维受力和多维受力时的力学行为是不同的。国内外研究表明，在点火建压载荷下，固体推进剂药柱的内孔表面通常是安全系数较低的部位^{[7, 8]}。D’Andrea等^[9]指出，点火建压时固体推进剂药柱内孔表面的受力状态可近似为双轴受拉状态。因此，为有效分析固体推进剂药柱的结构完整性，必须对双轴拉伸应力状态下固体推进剂的力学性能进行研究。

目前针对固体推进剂的双轴强度准则研究仍十分罕见。阳建红等^[10]通过开展准静态加载条件下剪切试验，建立了不同环境压强下NEPE高能推进剂的强度准则，发现NEPE高能推进剂的破坏强度随拉伸速率的增加而不断增大。孟红磊等^[11]通过开展准静态不同拉伸速率的力学试验，基于试验结果构建了双基推进剂考虑累积损伤的强度准则。王哲君等^[12~15]开展了低温动态加载下未老化HTPB推进剂单轴拉压力学性能试验与准双轴拉伸力学试验，并建立了推进剂的双轴强度准则，发现了环境温度和动态加载（1~10²s^-1）对推进剂力学性能有重要影响。

综上所述，目前针对低温动态加载下老化后固体推进剂双轴拉伸试验及强度准则研究还未开展，因此，本文在王哲君等研究基础之上进一步开展老化后HTPB推进剂准双轴拉伸试验，以双剪强度理论为基础，开展低温动态加载下老化后HTPB推进剂强度准则研究，研究结果可以对低温点火条件下战术导弹SRM药柱结构完整性分析提供数据支持。

2 试验

本文以典型战术导弹SRM用固体颗粒（AP/Al）填充质量分数88%的三组元端羟基聚丁二烯（Hydroxyl-Terminated Polybutadience，HTPB）推进剂为研究对象。根据GJB770B-2005《火药试验方法》^[16]制作标准哑铃型试验件，根据王哲君等的研究方法^{[14, 17]}制作板条试验件，参考GJB770B-2005《火药试验方法》^[16]将板条试验件放入防爆油浴烘箱进行油浴70℃热加速老化0d，32d，74d处理。拉伸试验前对推进剂进行低温冷冻24h，并开展25℃，-30℃，-50℃和0.0152m/s，0.152m/s，0.543m/s（应变率分别为0.40s^-1，4.00s^-1和14.29s^-1）拉伸速率下的试验。试验件与试验机的连接以及拉伸方法与王哲君等^{[12, 14]}的试验方法一致。

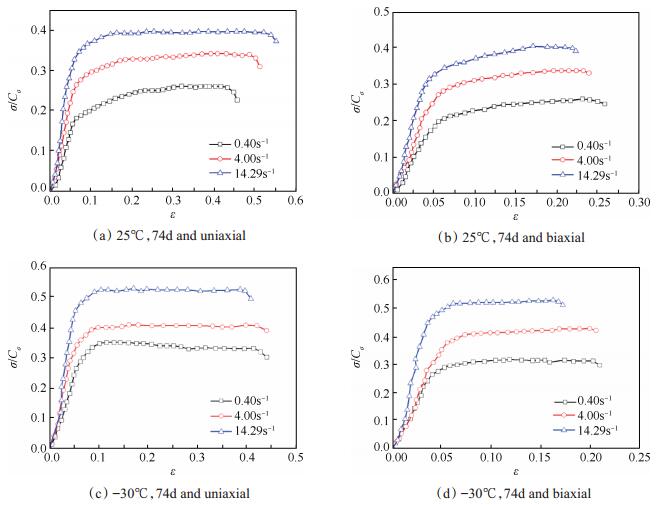
根据试验结果，获得不同温度和应变率条件下老化HTPB推进剂拉伸应力-应变曲线，其中老化74d后25℃与-30℃条件下单轴与准双轴拉伸应力-应变曲线如图 1所示。图 1及之后有关图中纵坐标均为归一化处理后无量纲数据，${C_\sigma }, {C_{{E_{{\text{bt}}}}}}, {C_{{\sigma _{{\text{bmt}}}}}}$与${C_{{\sigma _{{\text{mt}}}}}}$为归一化因子。老化后推进剂准双轴拉伸试验的力学性能曲线特性与单轴拉伸时力学性能曲线趋势保持一致，一方面，随应变增加，推进剂的应力-应变曲线仍呈现出强烈的非线性，且受温度和应变率的影响比较明显，随温度降低和应变率升高，应力值逐渐增加；另一方面，室温或较低应变率条件下，推进剂的应力-应变曲线仍呈现典型的弹性段、损伤段和破坏段3阶段变化规律特性，在-30℃高应变率条件下，推进剂的应力仍在小应变处快速达到峰值，然后迅速下降。但是与单轴拉伸试验结果相比较，准双轴拉伸时，推进剂应力-应变曲线的非线性段更为陡峭，且最大伸长率下降较为明显。

3 构建低温高应变率准双轴力学主曲线

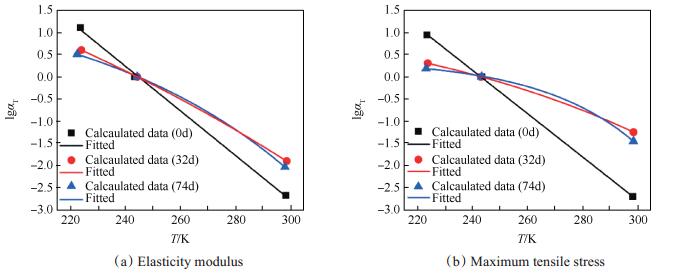
为分析低温动态加载下不同热老化时间HTPB推进剂力学性能参数主曲线，选取-30℃作为参考温度T₀，根据GJB获取推进剂力学性能主曲线方法并采用最小二乘法和Levenberg-Marquardt优化方法获得推进剂典型力学性能参数移位因子^{[15, 18]}与温度之间曲线关系，如图 2所示，其曲线表达式如表 1所示。

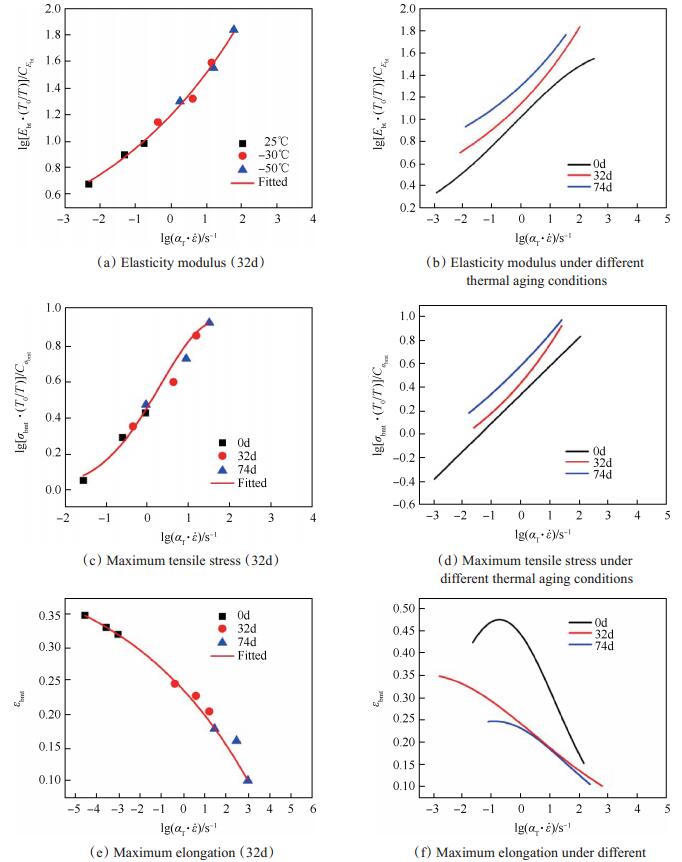
获得移位因子之后，进一步得到如图 3不同应变率与温度条件下各力学性能参数的主曲线。由图 3可知，HTPB推进剂在准双轴加载下力学性能参数主曲线与其单轴加载下趋势一致^[15]，并用如表 2所示的拟合关系式进行描述，通过曲线与数据点比较可发现，准双轴拉伸时数据离散比较大。

由图 3可知，HTPB推进剂经过热老化处理后各力学性能参数主曲线与热老化前^[15]趋势几乎相同。但是，伴随着加速老化持续进行，弹性模量和最大拉伸强度主曲线${\text{lg}}\left( {{\alpha _{\text{T}}} \cdot \dot \varepsilon } \right)$区间变窄，其中${\text{lg}}\left( {{\alpha _{\text{T}}} \cdot \dot \varepsilon } \right)$代表的是转化到参考温度下的应变率的范围大小。由此可见，经过热老化的弹性模量和最大拉伸强度主曲线只能对加载条件较小的推进剂进行描绘和评估。通过观察图 3（f）最大伸长率主曲线变化可知，热老化后主曲线范围缩小，即热老化后推进剂的材料变形能力减弱。

4 构建双轴强度准则

统一强度理论主应力表达式（${\sigma _1} \geqslant {\sigma _2} \geqslant {\sigma _3}$）^[19]

${\sigma _1} - \frac{\alpha }{{1 + b}}\left( {b{\sigma _2} + {\sigma _3}} \right) = {\sigma _{{\text{mt}}}}, {\sigma _2} \leqslant \frac{{{\sigma _1} + \alpha {\sigma _3}}}{{1 + \alpha }}$

(1)

$\frac{1}{{1 + b}}\left( {{\sigma _1} + b{\sigma _2}} \right) - \alpha {\sigma _3} = {\sigma _{{\text{mt}}}}, {\sigma _2} > \frac{{{\sigma _1} + \alpha {\sigma _3}}}{{1 + \alpha }}$

(2)

式中σ_mt为单轴最大拉伸强度；α为材料的拉压强度比（$\alpha = \frac{{{\sigma _{\text{t}}}}}{{{\sigma _{\text{c}}}}}, {\sigma _{\text{t}}}$为单轴最大拉伸强度，σ_c为单轴最大压缩强度）；b反映中间主应力对材料破坏的影响。当参数b和α取不同值时，就能得出一组适合不同材料的强度理论。此外，通过改变式（1），（2）中的主应力顺序，可得到统一强度理论的12个方程式。

板条推进剂试验件在拉伸状态下其主应力关系如下（${\sigma _1} \geqslant {\sigma _2} \geqslant {\sigma _3}$）^{[14, 17]}

${\sigma _1} = {\sigma _y} \ne 0$

(3)

${\sigma _2} = {\sigma _x} = \nu {\sigma _y}$

(4)

${\sigma _3} = {\sigma _z} = 0$

(5)

将式（3）~（5）代入式（1），（2）中，可得出HTPB推进剂准双轴拉伸时强度准则公式

${\sigma _1}\left( {1 - \frac{{\alpha b\nu }}{{1 + b}}} \right) = {\sigma _{{\text{mt}}}}$

(6)

结合式（1）~（5）及主曲线经验公式^[15]，可得出推进剂不同老化时间的准双轴拉伸主应力统一强度理论关系式

$ \begin{array}{*{20}{r}} {{\sigma _1}\left( {1 - \frac{{\alpha b\nu }}{{1 + b}}} \right) = T/{T_0} \times {{10}^{{k_6} + \frac{{{k_7}}}{{1 + {\text{exp}}\left( {{k_8}{\text{lg}}\dot \varepsilon + {l_1} \cdot T + {l_2}} \right)}}}}} \\ {\left( {{\text{Stretch}}\;{\text{without}}\;{\text{aging}}} \right)} \end{array} $

(7)

$ \begin{array}{*{20}{r}} {{\sigma _1}\left( {1 - \frac{{\alpha b\nu }}{{1 + b}}} \right) = T/{T_0} \times {{10}^{{k_6} + \frac{{{k_7}}}{{1 + {\text{exp}}\left[ {{k_8}{\text{lg}}\dot \varepsilon + {l_3}{\text{exp}}\left( {{k_4} \cdot T} \right) + {l_4}} \right]}}}}} \\ {\left( {{\text{Stretch}}\;{\text{after}}\;{\text{aging}}} \right)} \end{array} $

(8)

$ {\sigma _2} = \nu {\sigma _1} $

(9)

式中k₁，k₂，k₃，k₄，k₅，k₆，k₇，k₈和k₉是与拉压应力状态和热老化时间相关的材料常数；l₁（=k₈×k₁），l₂（=k₈×k₂+k₉），l₃（=k₈×k₃）和l₄（=k₈×k₅+k₉）同样是与拉压应力状态和热老化时间相关的材料参数。

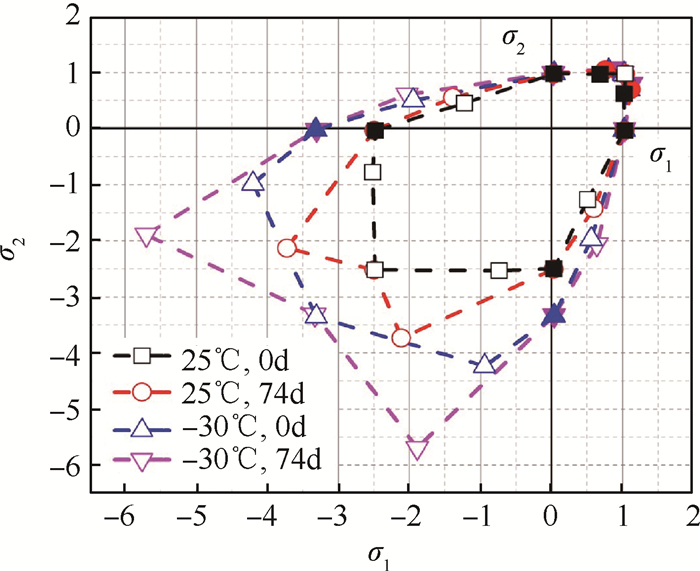
式（7），（8）左端项为理论的强度准则项，其右端项为试验推导的强度准则项，需要选择相应的α，b及ν拟合强度准则包络线，在前文的研究中发现，板条试验件可实现近似2:1的准双轴拉伸，因此ν = 0.5。根据课题组研究^[15]得到α的值在室温下约为0.4，而在-30℃下约为0.3。将热老化74dHTPB推进剂准双轴和单轴加载时最大拉伸强度代入式（7），（8）的两端，并将前期研究^[15]单轴拉压强度比α带入其中，通过拟合曲线，可以获得25℃和-30℃温度条件下b的近似值为0.3和0.6。因为单轴拉压强度比α只随着温度的变化而变化，且对于板条试验件ν近似于0.5，因此b也仅是与温度有关的数值。基于统一强度理论，将计算得到的各系数代入式（1），（2）可以求得主应力形式低温高应变率加载下HTPB推进剂的强度包络线，如图 4所示。

图 4将不同温度和热老化下的单轴最大拉伸强度规定为1，同理将双轴最大拉伸强度规定为（1，1），根据单向加载下强度拉压比α，可以推导单轴最大压缩强度为1/α，进一步归一化双轴最大压缩强度为（1/α，1/α）。根据图 4可预估多种因素影响下HTPB推进剂的结构强度。从图 4可知，当环境温度降低，HTPB推进剂的主应力形式下强度包络线范围逐渐拓展，说明其强度不断增强。其中实心点为试验所得数据，虚线及空心点为根据试验计算理论点。

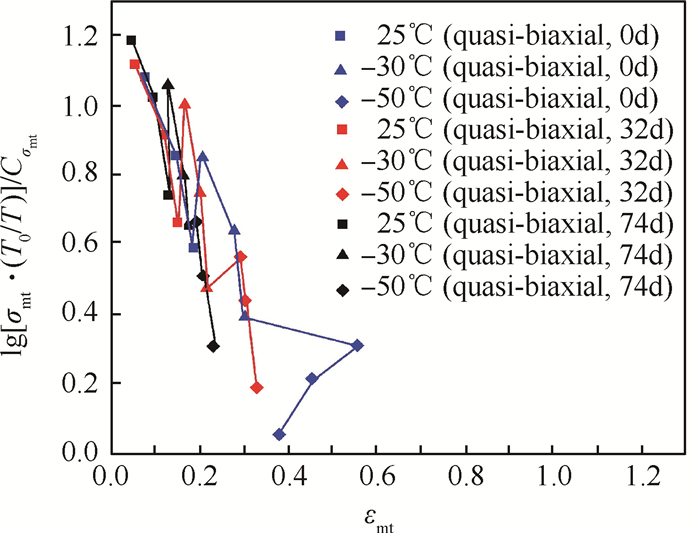
5 推进剂故障包络线分析

目前表征固体推进剂的破坏情况，包括力学性能主曲线和故障包络线。故障包络线是描述最大拉伸强度与最大伸长率的关系，将不同温度及应变率条件下的极限点连接而成。当材料的强度和伸长率包含在故障包络线范围内，说明材料的结构完整性是稳定可靠的，当处于包络线范围外，推进剂结构完整性失稳。取25℃作为参考温度，获得准双轴0d，32d和74d的故障包络线如图 5。

从图 5可知，随着热老化时间的延长，热加速老化32d和74d包络线较0d往左上方偏移，即HTPB推进剂包络线范围缩小，抵抗破坏能力降低。

6 结论

（1）本文成功开展了低温动态加载下老化后HTPB推进剂单轴与准双轴拉伸力学性能试验，获得了应力-应变曲线，温度和应变率能够显著影响老化后HTPB推进剂的低温动态拉伸力学性能，准双轴拉伸条件下推进剂的应力-应变曲线特性和单轴拉伸时趋势一致，推进剂的典型力学性能参数随温度和应变率的变化规律也和单轴拉伸时保持一致。主要区别在于准双轴拉伸条件下推进剂的最大伸长率受应变率的影响较弱。

（2）准双轴拉伸试验条件下老化前后HTPB推进剂的力学性能参数主曲线趋势相同，但是随着老化时间的加大，${\text{lg}}\left( {{\alpha _{\text{T}}} \cdot \dot \varepsilon } \right)$逐渐减小，说明热老化后HTPB推进剂主曲线只能对较小加载条件的力学行为进行预估。HTPB推进剂经过热老化后相比未老化最大伸长率范围有所缩减，说明HTPB推进剂经过热老化后材料变形逐渐减弱。因此，在分析贮存HTPB推进剂结构完整性时，主要以其最大伸长率作为是否破坏的依据。

（3）随着温度降低和热老化时间增大，推进剂强度极限线范围扩大，即HTPB推进剂强度增强；随着热老化时间的延长，包络线逐渐向左上方移动，范围逐渐缩小，抵抗破坏能力逐渐减弱。通过建立不同条件下HTPB推进剂故障包络线，可以对低温点火条件下HTPB推进剂结构完整性分析提供数据支持。

致谢: 感谢国家自然科学基金资助。