螺旋桨噪声通常可分为旋转噪声(即离散噪声)和宽频噪声两部分。旋转噪声由叶片与周期性来流相互作用引起,宽频噪声由叶片与周围流场的随机脉动相互作用产生[1]。频谱特性分析表明,涡轮螺旋桨飞机舱内噪声的主要特点是宽频噪声与一系列离散频率噪声的叠加,其中离散频率噪声占主导比重。在额定状态下,离散频率噪声为100~250Hz的长波信号,而长波信号很难通过被动隔离实现降噪。初步估计,需要将该长波噪声降低25dB才能达到同等涡扇飞机的水平[2]。对于螺旋桨长波噪声,当前较为理想的降噪方式为螺旋桨相同步降噪。螺旋桨相同步降噪原理是控制多螺旋桨飞机的几个螺旋桨之间保持一定的相角差,使各个螺旋桨产生的部分旋转噪声和振动互相抵消,达到舱内噪声最小。相对于被动噪声控制和其它主动噪声控制,相同步控制降噪不需要增加传感器和执行机构,不会增加额外重量,且降噪效果明显[3, 4]。
目前相同步控制降噪研究大多数都是基于螺旋桨噪声模型开展的,通过螺旋桨噪声模型计算出使噪声最小的最优相角,并将最优相角用于螺旋桨相同步控制[5, 6],然而螺旋桨噪声模型受飞行高度、马赫数、飞行攻角等因素的影响而动态变化,导致最优相角也动态变化[7],因此如何获得不同飞行条件下的高精度螺旋桨噪声模型是相同步降噪研究的难点。通常采用辨识的方法获取螺旋桨噪声模型,通过采集多个相角组合下的噪声值,带入噪声模型求解出模型待定的参数。在实际噪声模型辨识过程中,受飞行速度、高度、气流变化、使能和停止噪声采集时电路瞬间波动等的影响,实测数据经常会发生较大的波动,从而影响辨识模型和最优相角的准确性,进而影响到相同步降噪的效果。为减少数据波动的影响,常用的处理算法是尽可能采集多个同步相角下的噪声信息用于模型辨识,从而减少偶然数据波动对模型精度的影响[8, 9],但对于飞行条件变化时引起的数据波动缺少筛选,这影响到模型精度的进一步提高。文献[10]针对使能噪声采集和停止噪声采集时引起的瞬时极端数据波动提出一种对噪声数据截头去尾的算法,该算法对于某些场合具有明显的效果,但其研究较多基于试验结果,其截取数据的长度缺乏有效的准则。文献[11]研究了一种通过改变采样噪声数据周期数的方式提高建模精度,提出采样时间越短,相角波动对辨识精度的影响越小,但是采样时间太短将导致噪声信息丢失,从而会引入更多的随机误差,需要根据实际情况权衡两者的利弊。基于螺旋桨噪声模型获取最优相角是螺旋桨相同步降噪的关键技术,噪声模型精度对降噪效果有至关重要的影响。现有用于处理辨识数据波动的方法均是基于经验,由于缺乏统一且有效的选取理论而具有一定局限性。本文在螺旋桨噪声特征值理论的基础上提出了一种基于小波滤波和三参数正弦拟合法的最小波动时间段选取算法,该算法通过小波滤波算法从螺旋桨噪声信号中提取出低频信号,低频信号主要由叶尖通过频率(Blade-Pass Frequency,BPF)信号组成,还包括少量低幅值的其它频率信号,其中BPF信号的波动情况可以直接反映出螺旋桨噪声和相角的波动,算法通过度量一段时间内低频信号波动情况,获取波动最小的数据段用于噪声建模。
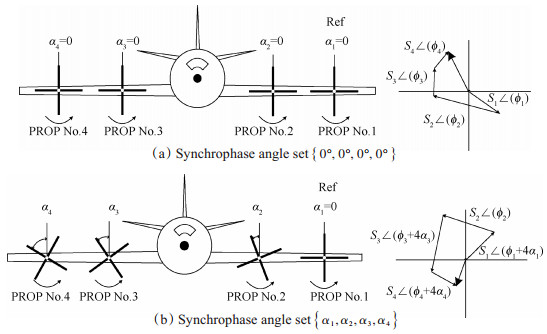
2 螺旋桨噪声值模型螺旋桨特征值理论认为,机舱某一位置的螺旋桨噪声为各个螺旋桨单独产生噪声的矢量和[4]。当螺旋桨转速同步时,噪声可以通过螺旋桨间相角组合预测。图 1(a)表示机舱内某一点在{0°,0°,0°,0°}相角组合时的BPF特征向量合成噪声的示意图,
|
Fig. 1 Propeller signature |
螺旋桨的特征值是一个复数,用来描述各个螺旋桨对噪声的贡献,特征值可以通过不同相角组合下的噪声辨识出来。螺旋桨在机舱内某一位置k处的BPF噪声为
| $ {\varphi _k} = \sum\limits_{p = 1}^p {{{\hat S}_{k,p}}{{\rm{e}}^{{\rm{i}}B{a_p}}}} $ | (1) |
式中
| $ \left[{\begin{array}{*{20}{l}} {{\varphi _1}}\\ {{\varphi _2}}\\ {...}\\ {{\varphi _K}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{{\hat S}_{1, 1}}}&{{{\hat S}_{1, 2}}}&{...}&{{{\hat S}_{1, P}}}\\ {{{\hat S}_{2, 1}}}&{{{\hat S}_{2, 2}}}&{...}&{{{\hat S}_{2, P}}}\\ {...}&{...}&{...}&{...}\\ {{{\hat S}_{K, 1}}}&{{{\hat S}_{K, 2}}}&{...}&{{{\hat S}_{K, P}}} \end{array}} \right] \times \left[{\begin{array}{*{20}{l}} {{{\rm{e}}^{{\rm{i}}B{\alpha _1}}}}\\ {{{\rm{e}}^{{\rm{i}}B{\alpha _2}}}}\\ {...}\\ {{{\rm{e}}^{{\rm{i}}B{\alpha _P}}}} \end{array}} \right] $ |
或者
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_1} = \mathit{\boldsymbol{S}} \times {\mathit{\boldsymbol{\beta }}_1}\\ {\mathit{\boldsymbol{{\rm A}}}_1} = {\left[{\begin{array}{*{20}{c}} {{\varphi _1}}&{{\varphi _2}}&{...}&{{\varphi _K}} \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{\beta }}_1} = {\left[{\begin{array}{*{20}{c}} {{{\rm{e}}^{{\rm{i}}B{\alpha _1}}}}&{{{\rm{e}}^{{\rm{i}}B{\alpha _2}}}}&{...}&{{{\rm{e}}^{{\rm{i}}B{\alpha _P}}}} \end{array}} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{S}} = \left[{\begin{array}{*{20}{c}} {{{\hat S}_{1, 1}}}&{{{\hat S}_{1, 2}}}&{...}&{{{\hat S}_{1, P}}}\\ {{{\hat S}_{2, 1}}}&{{{\hat S}_{2, 2}}}&{...}&{{{\hat S}_{2, P}}}\\ {...}&{...}&{...}&{...}\\ {{{\hat S}_{K, 1}}}&{{{\hat S}_{K, 2}}}&{...}&{{{\hat S}_{K, P}}} \end{array}} \right] \end{array} $ | (2) |
式中A1表示K个位置的复数噪声向量,S是K×P阶矩阵表示螺旋桨的特征值,β1是P列单位向量。
对于式(2)至少需要测量P组线性无关的相角组合才能求解出S值,通常会测量多于P组的相角组合以提高建模精度。对于Q(Q>P)组相角组合,螺旋桨的特征值可以用最小二乘法求得
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{\beta }}^{\rm{H}}}{\left[{\mathit{\boldsymbol{\beta }}{\mathit{\boldsymbol{\beta }}^{\rm{H}}}} \right]^{ - 1}} $ | (3) |
式中
在模型辨识的过程,需要采集某一特定相角的噪声数据段。根据文献[11]可知,噪声建模采集声音数据的时间越短,相角波动和转速偏差对辨识精度的影响越小,但减少采样时间会减少有效建模信息从而引入更多的随机误差,该文献建议至少采集5个以上螺旋桨转动周期的噪声数据。考虑到外界飞行环境的影响,直接采样一段时间(如采样1s)的噪声数据用于模型辨识可能会引起很大误差。一方面在开始使能采样时传感器电路不够稳定,需要去除噪声数据的头部段。另一方面受螺旋桨来流波动、螺旋桨间的同步相角波动和螺旋桨转速波动等的影响,噪声数据可能存在较大波动。当噪声数据波动较大时,只采集较短时间的数据段用作噪声模型辨识,数据段可能偏离真实值太远,从而导致模型预测的最优相角和实际最优相角的差大于10°,使得模型预测的最优相角降噪效果很差。
为了避免噪声数据波动大的不利影响,本文提出一种最小数据波动的噪声数据选取算法,通过度量螺旋桨噪声数据波动的大小,并从中选取出合适的数据段用于噪声模型辨识。最小数据波动的噪声数据选取算法通过采集一段时间较长的数据,采用小波变换重构出螺旋桨噪声不含BPF高阶谐波和高频噪声的低频时域信号,低频时域信号可近似为BPF信号;然后将低频信号划分为多个短时长的子段,分别对各子段进行三参数正弦拟合,计算出各拟合段的均方根误差,并从中选取出均方根误差最小的数据段用于噪声模型辨识。
由于螺旋桨噪声的主要能量集中于BPF信号,因此可通过对BPF占绝对主导的低频信号的波动情况来描述螺旋桨噪声的波动。螺旋桨噪声在不发生波动的理想状况下,低频信号近似为正弦信号。当螺旋桨噪声发生波动时,将表现为低频信号的频率和幅值围绕正弦信号的瞬时波动。此时传统的傅里叶变换所得的信号频谱是一段时间的平均特性,信号波动时,表型为频谱上多个峰值信号的幅值和频率带宽的变化。由于涉及多个变量变化,无法对噪声的瞬时波动进行直观有效的描述。而小波变换所得的时域信号能直接从时域上描述信号的波动大小,实现难度小,简明有效。
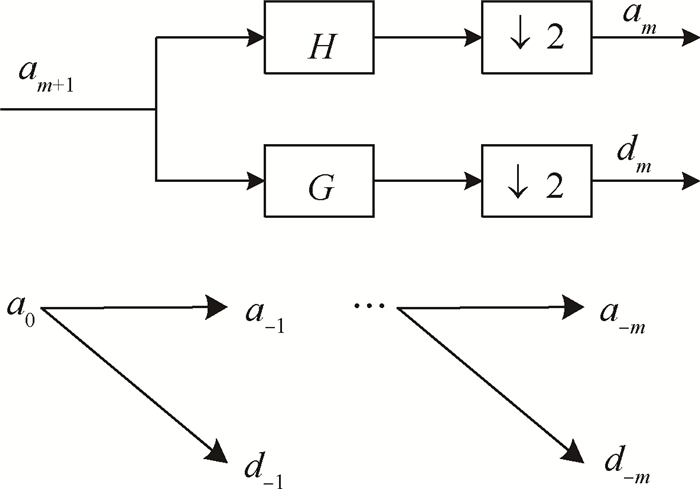
3.1 基于小波的噪声信号提取小波变换包括小波分解算法和小波重构算法两部分。小波分解算法根据不同尺度把信号序列进行多级分解,从而把信号分割成细节信号和逼近信号,如图 2所示[12, 13]。
|
Fig. 2 Wavelet decomposition algorithm |
在图 2中,a0表示原始信号向量。
| $ \begin{array}{*{20}{l}} {{a_m}\left( n \right) = \sum {h\left( {2n - k} \right){a_{m + 1}}\left( k \right)} }\\ {{d_m}\left( n \right) = \sum {g\left( {2n - k} \right){a_{m + 1}}\left( k \right)} } \end{array} $ | (4) |
am+1(n)经过低通数字滤波器H滤波后,取其偶数样本得到am(n)。am+1(n)经过高通数字滤波器G滤波后,取其偶数样本得到dm(n)。↓2表示2倍降频滤波器,h(n)表示H的冲击响应,g(n)表示G的冲击响应。
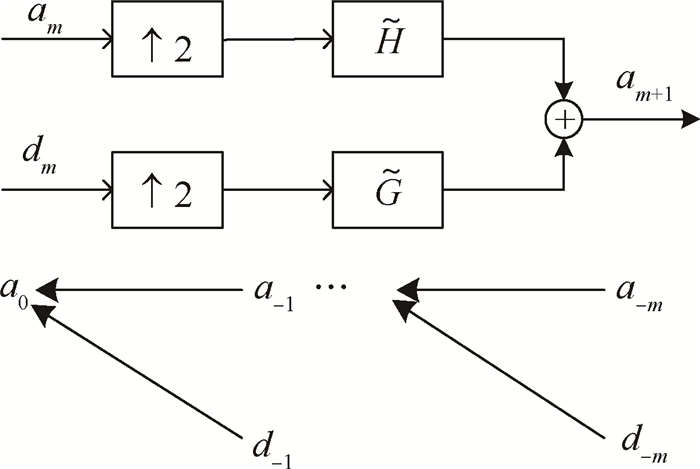
小波重构算法是分解算法的逆过程,其原理就是利用细节信号和最终的逼近信号复原最初的原始信号,重构过程如图 3所示。其中
|
Fig. 3 Wavelet reconstruction algorithm |
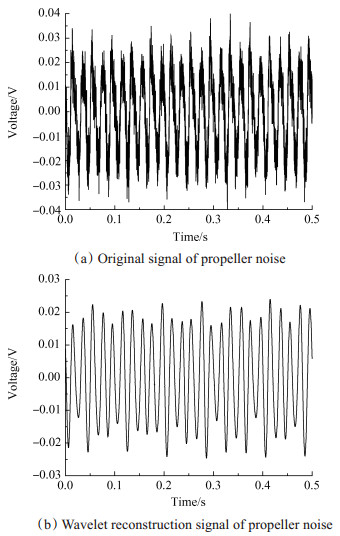
螺旋桨的噪声由螺旋桨的BPF及其高阶谐波组成,本文使用麦克风将螺旋桨的噪声信号转换为电信号,采集的电信号如图 4(a)所示。螺旋桨在1500r/min时,使用44.1kHz的采样频率采集噪声信号。根据香隆采样定律,系统可以采集22050Hz的噪声。由于人类的听觉范围在20~20000Hz,因此使用44.1kHz的采样频率可以完全覆盖人类的听觉范围。
|
Fig. 4 Original and reconstruction signal of propeller noise |
采用Mallat小波变换时,下一层逼近信号的最大通过频率为上一层逼近信号最大通过频率的一半,螺旋桨在1500r/min(50Hz)的转速下,只需对采集的噪声数据进行8层小波分解和重构,即可获得不含BPF高阶谐波的低频信号。本文对噪声数据使用db小波簇的db30小波基进行8层分解,db30小波基相当于图 4(a)中一组特定的低通滤波器H和高通滤波器G。使用db30小波基对噪声数据进行8层分解,然后对第8层信号进行重构,提取的噪声信号如图 4(b)所示。
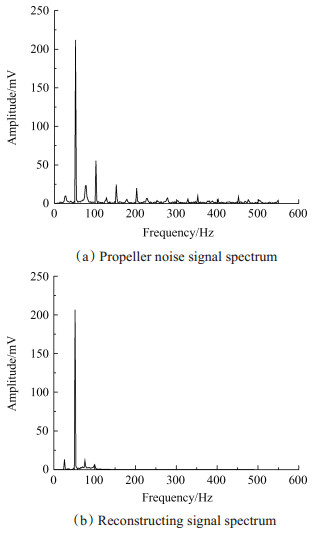
分别对图 4(a)的原始信号和图 4(b)的小波重构信号进行傅里叶变换,得到如图 5所示的频谱图,图 5(a)为原始信号的频谱图,由一系列的离散频率组成,其中幅值最大的频率为50Hz(螺旋桨BPF信号),除此之外还有BPF高阶谐波信号和少量其他低幅值信号,且BPF信号的幅值远大于其他信号。图 5(b)的小波重构信号去除了BPF高阶谐波信号和大量其他高频干扰信号,只保留了BPF信号和少量其它低频低幅值信号,因此可以将小波变换重构出的信号近似为BPF信号。在图 5(a)中BPF信号的幅值远大于其他频率的信号,这表明螺旋桨的噪声能量大部分集中于包含BPF信号的低频信号,低频信号的波动情况可以直接反映出螺旋桨噪声的波动。然而,图 5(a)中BPF的高阶谐波信号和部分低频信号也具有不可忽略的幅值,且BPF高阶谐波信号幅值和频率受扰动影响大。如4倍BPF谐波在转速发生1Hz(60r/min)波动时,其谐波频率将发生8Hz的波动,且其幅值变化无明显规律。本文使用小波变换从螺旋桨噪声提取信号,目标是提取的信号能够反映螺旋桨噪声数据的波动情况,避免将波动大的数据用于噪声模型辨识。BPF高阶谐波成分在噪声信号中能量占比小,而且波动大、规律性弱。一方面说明BPF高阶谐波不适合用于描述螺旋桨噪声数据波动;另一方面说明其他信号若含有BPF高阶谐波的噪声数据,也将不适合用于螺旋桨噪声数据波动的度量,并且当提取信号中含有BPF信号和BPF高阶谐波信号时,信号为多种波动的作用和,这增加了度量噪声波动的困难。
|
Fig. 5 Signal spectrum |
本文提出的小波提取算法,算法直接从螺旋桨噪声中获取含BPF信号的低频信号,从而有效排除了BPF高阶谐波信号和高频噪声的干扰;鉴于螺旋桨噪声能量集中于低频信号,因此低频信号其数据波动情况可以反映出螺旋桨噪声的波动。对比图 5(a)与图 5(b)的噪声低频成分,它们在25Hz和75Hz处都出现了两个较大的峰值。而图 5(b)在25Hz峰值处,相对图 5(a)的频谱宽度有较大减小;图 5(b)在75Hz处相对于图 5(a),75Hz信号幅值基本全部滤除。这说明小波滤波对于螺旋桨噪声的低频干扰成分也有显著的滤除效果,从而最大限度地保留BPF信号成分。
理想状态下,用于描述噪声波动的低频信号其频率成分只保留BPF信号,然而在图 5中,低频信号中还有少量的转速频率信号(25Hz信号)。图 4(b)中25Hz信号的幅值不到BPF信号的1/20,考虑图 4(b)中信号的幅值约为0.02,所以由25Hz信号引起的幅值波动峰值差约为0.002,实际发现图 4(b)中的峰值波动接近0.01,这说明大部分数据波动并不是由25Hz信号引起的。其原因是:在频谱图上,除了某些特定频率(如25Hz)的幅值会引起数据波动,引起数据波动的主要原因表现为频率带的宽度,而频带由噪声数据的频率波动形成。这使得使用傅里叶频谱分析噪声数据波动时,需要考虑多个频率信号的幅值和频带宽度,不仅维度大而且很不直观,难以用来度量噪声信号的波动。
引起螺旋桨噪声信号波动的原因一般有螺旋桨来流波动、螺旋桨间的相角差波动和螺旋桨转速波动。如果波动过大,该段噪声数据将不适合用于螺旋桨噪声模型辨识,故在辨识螺旋桨噪声模型时应尽量选取波动小的数据段。
3.3 正弦法噪声信号选取由于螺旋桨低频信号相对于理想正弦信号的波动大小,可用来衡量螺旋桨噪声的波动情况。因此可从实际螺旋桨低频信号中按照最小二乘法提取出螺旋桨正弦信号,并将此作为理想状态下的螺旋桨BPF信号。实际螺旋桨低频信号相对于最小二乘法拟合螺旋桨BPF信号的均方根误差,可作为螺旋桨噪声波动大小的度量。在使用最小二乘法提取螺旋桨BPF信号的操作过程中,设螺旋桨BPF信号为
| $ BPF = A{\rm{sin}}\left( {\omega t + {\beta _0}} \right) + {D_0} $ | (5) |
式中A,ω,β0和D0分别为螺旋桨BPF信号的幅值、频率、初始相位和由麦克风引起的偏差,此时有四个参数需由实际测量数据确定。在相同步控制过程中,螺旋桨转速一般波动很小。在本文的螺旋桨相同步控制实验中时,测试转速为1500r/min,转速波动只有±1r/min(±0.03Hz),频率波动为0.67%,因此频率的波动几乎可以忽略。当ω已知时,求解式(5)中的其他参数称为三参数法,当ω未知时,求解式(5)中所有的参数称为四参数法,一般三参数的计算量远小于四参数法[14]。鉴于一般相同步时螺旋桨实际转速波动很小,使用三参数法不会影响ω的精度,同时可以提高计算速度。
将式(5)展开为
| $ BPF = A{\rm{sin}}\left( {\omega t} \right) + B{\rm{cos}}\left( {\omega t} \right) + D $ | (6) |
式中ω是已知的。三参数法通过选取合适的
| $ E = \sum\limits_{i = 1}^n {{{\left[ {{y_i} - \hat A{\rm{sin}}{\omega _i} - \hat B{\rm{sin}}{\omega _i} - \hat D} \right]}^2}} $ |
则参数
| $ \begin{array}{l} \mathit{\boldsymbol{M}} = \left[{\begin{array}{*{20}{c}} {{\rm{cos}}\left( \omega \right)}&{{\rm{sin}}\left( \omega \right)}&1\\ {{\rm{cos}}\left( {2\omega } \right)}&{{\rm{sin}}\left( {2\omega } \right)}&1\\ {...}&{...}&{...}\\ {{\rm{cos}}\left( {n\omega } \right)}&{{\rm{sin}}\left( {n\omega } \right)}&1 \end{array}} \right]\\ {\mathit{\boldsymbol{x}}_0} = \left[{\begin{array}{*{20}{l}} {\hat A}\\ {\hat B}\\ {\hat D} \end{array}} \right]\;\;\;\;\;\;\;\;\mathit{\boldsymbol{y}} = \left[{\begin{array}{*{20}{l}} {{y_1}}\\ {{y_2}}\\ {...}\\ {{y_n}} \end{array}} \right] \end{array} $ |
残差平方和E用矩阵表示为
| $ E = E\left( \omega \right) = {(\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{x}}_0})^{\rm{T}}}\left( {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{x}}_0}} \right) $ |
当E最小时,可得x0的最小二乘解
| $ {{\mathit{\boldsymbol{\hat x}}}_0} = {({\mathit{\boldsymbol{M}}^{\rm{{\rm T}}}}\mathit{\boldsymbol{M}})^{ - 1}}\left( {{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{y}}} \right) $ |
拟合残差为
| $ {r_i} = {y_i} - \hat A{\rm{cos}}\left( {{\omega _i}} \right) - \hat B{\rm{sin}}\left( {{\omega _i}} \right) - \hat D $ |
均方根误差为
| $ E' = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {r_i^2} } $ |
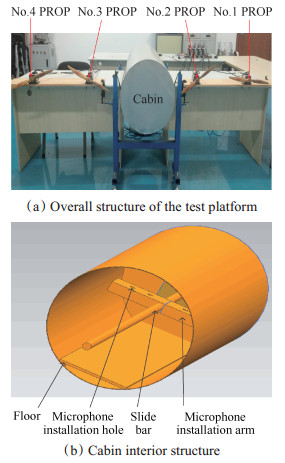
相同步降噪试验数据可通过飞行试验和地面试验获取,然而开展飞行试验研究存在试验经费大、对实验场地要求高等问题,使得飞行试验能够获得的数据有限,试验成本巨大。即使在西方发达国家,也仅有少数几个国家开展了飞行试验研究,当前国内并不具备开展飞行试验研究的条件。为了能够更高效地获得相同步降噪的数据,本文搭建如图 6所示的地面试验平台开展相同步降噪研究。图 6(a)为地面试验平台的整体结构图,试验平台使用四个电动机驱动四个螺旋桨转动,用以模拟四螺旋桨飞机的螺旋桨噪声。四螺旋桨均为两桨叶螺旋桨,从右至左依次编号为1~4。四螺旋桨中间采用薄壳圆柱体模拟机舱声学特性,这也是地面试验常用的方案[15]。圆柱体长1.5m,直径为0.5m,厚度为2mm,使用航空铝材加工制作而成。图 6(b)为模拟机舱圆柱体的内部结构图,图中底部平面用以模拟客舱地板,其麦克风安装臂上有四个麦克风安装孔,从右至左依次编号为1~4,可以同时测量四个不同点的噪声,麦克风安装臂可在滑杆上滑动和旋转,用以测量多个位置的噪声数据。
|
Fig. 6 Propeller synchrophasing test platform |
螺旋桨噪声的特征值模型一般通过辨识的方法获得噪声模型,并通过测量各螺旋桨的同步相角单独变化时的噪声数据以验证噪声模型的精度。针对如图 6的四螺旋桨试验平台,螺旋桨的噪声模型辨识选取{ 0°, 50°, 100°, 150° },{ 0°, 100°, 150°, 50° },{ 0°, 36°, 63°, 127° },{ 0°, 81°, 56°, 144° },{ 0°, 121°, 144°, 97° },{ 0°, 51°, 76°, 134° },{ 0°, 96°, 54°, 38° },{ 0°, 143°, 39°, 27°}的同步相角组合,基于式(3)进行噪声模型辨识,每一同步相角都采集10s时长的噪声数据。对于式(3)中用于噪声模型辨识的同步相角组合数显然不能小于螺旋桨个数;当同步相角组合数等于螺旋桨个数时,需确保同步相角组合线性无关;当同步相角组合数大于螺旋桨个数时,只需保证同步相角组合的秩等于螺旋桨个数;除此之外,可以任意选择用于辨识的具体同步相角。对于本文所选取的8组同步相角组合,其秩为4,等于螺旋桨的个数,因此可用于螺旋桨噪声特征值模型的辨识。
在机舱内部,螺旋桨噪声分布会随空间位置而改变,不同位置辨识所得的噪声模型将不同。相同步降噪对于特定位置点,需基于该点的噪声模型寻找使得噪声最小的最优相角实现位置点降噪;而对于机舱的多位置的空间噪声场,一般通过辨识有代表性的多个空间位置的噪声模型,取各模型的加权平均值作为机舱总体噪声模型,然后基于总体噪声模型开展全局降噪研究。因此无论是全局降噪还是位置点降噪,都需要使用位置点的噪声模型,使得如何获得位置点的高精度噪声模型是相同步降噪的基础。由于螺旋桨的噪声特征值模型在不同位置点的辨识过程完全一致,因此本文将以某一位置点为例介绍本文提出的高精度噪声模型辨识算法:本文采集圆柱体机舱内螺旋桨平面水平位置的噪声,选择麦克风安装臂上的2号麦克风数据用于分析介绍。
当前商用噪声测量仪较多使用时间长度为0.125s或1s的噪声数据计算声压级(Sound Pressure Level,SPL),如台湾的群特CENTER-322和泰仕TES1353S高精度数字噪音计。在对SPL实时性要求较高的场合,较多使用时长为0.125s的噪声数据计算SPL,即每隔0.125s进行一次SPL计算,这也和人耳听觉的生理特性近似[16]。而对SPL精度要求很高的场合,一般使用时长为1s的噪声数据计算SPL。为尽可能提高螺旋桨的噪声模型辨识精度,本文选用时长1s的噪声数据用于噪声SPL计算,时长1s的噪声数据也远大于文献[11]建议的至少采集5个以上螺旋桨转动周期的噪声数据,能够满足螺旋桨模型辨识所需数据长度要求。
传统的噪声模型辨识方式,一般从时长为L的噪声数据中选择特定的1s数据用于噪声模型辨识,如取10s时长噪声数据的5~6s数据段用于噪声模型辨识。本文提出的改进噪声模型辨识方法,时间段的选取不固定,对于任意相角组合,从时长L的噪声数据中选择出波动最小的1s时长数据用于噪声模型辨识。对于时长L的选取,L太短会影响数据的选取,尤其是在文献[10]介绍的需要截取数据首尾时;L太长将增大采样时间,降低实时性。本文通过实验发现L取10s时能够实现数据选取和实时性的均衡,如若对数据选取和实时性有特殊要求可以适当改变L的长度。
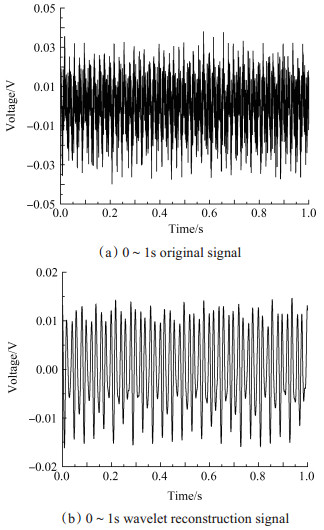
以{ 0°, 50°, 100°, 150° }相角组合数据为例,介绍最小波动数据段的选取过程。在该同步相角下采集圆柱体机舱内螺旋桨平面水平位置的噪声,10s噪声数据,其噪声数据在0~1s局部段如图 7(a)所示。
|
Fig. 7 0~1s original and reconstruction signal |
对该段数据使用小波分析重构其低频信号,重构后的信号如图 7(b)所示。重构信号主要为BPF占主导的低频信号。按照第三节介绍的正弦拟合方法,计算该段数据的均方差为0.3915。
与计算0~1s的均方差步骤相同,分别计算10s内各时间段数据的均方根,如表 1所示。由表 1可知6~7s的数据段,其均方根最小,这说明在该段时间内螺旋桨转速、噪声SPL最平稳,受外界影响影响最小,因此取该时间段的数据用于噪声模型辨识将能最大限度地提高建模精度。
|
|
Table 1 RMSE of data segment |
对于其他相角组合,本文同样采集了其相角组合下10s时长的噪声数据。按照与{ 0°, 50°, 100°, 150° }同步相角相同的处理方法,分别计算出其最小波动时间段数据,共计获得8组最小波动数据,然后将8组最小波动数据用于公式(3)的噪声模型辨识。在四螺旋桨飞机上,螺旋桨噪声只与螺旋桨间的相角差有关,与螺旋桨所处的绝对位置无关,如图 6所示,如果将1号螺旋桨作为参考螺旋桨,其同步相角一直为0°,其他三个螺旋桨的相角相对1号螺旋桨将有三个可变自由度。若三个自由度同时变化,模型精度的验证将十分复杂,需要的数据也将非常庞大,因此本文对三个自由度分别单独验证。即固定任意两自由度相角为0°,单独将另一自由度相角由0°变化到180°,记录噪声SPL随相角的变化,同时计算出辨识噪声模型的预测噪声SPL随相角的变化,对比两组数据的差值来验证噪声模型的精度。如图 6所示的四螺旋桨试验平台,可将1号,3号,4号螺旋桨相对相位角设定为0°,单独改变2号螺旋桨的相对相角,将其从0°变化至180°。在2号螺旋桨相角改变时,通过声压测量装置记录其在每一个相角下对应的噪声SPL值,同时可用螺旋桨噪声模型预测2号螺旋桨在不同相角下的噪声SPL值,对比真实值和预测值即可验证辨识噪声模型的精度。为了更全面验证辨识噪声模型的精度,可单独改变3号、4号螺旋桨的相角,记录3号、4号螺旋桨单独改变时其噪声SPL值,对比其噪声测量值与模型的预测值。
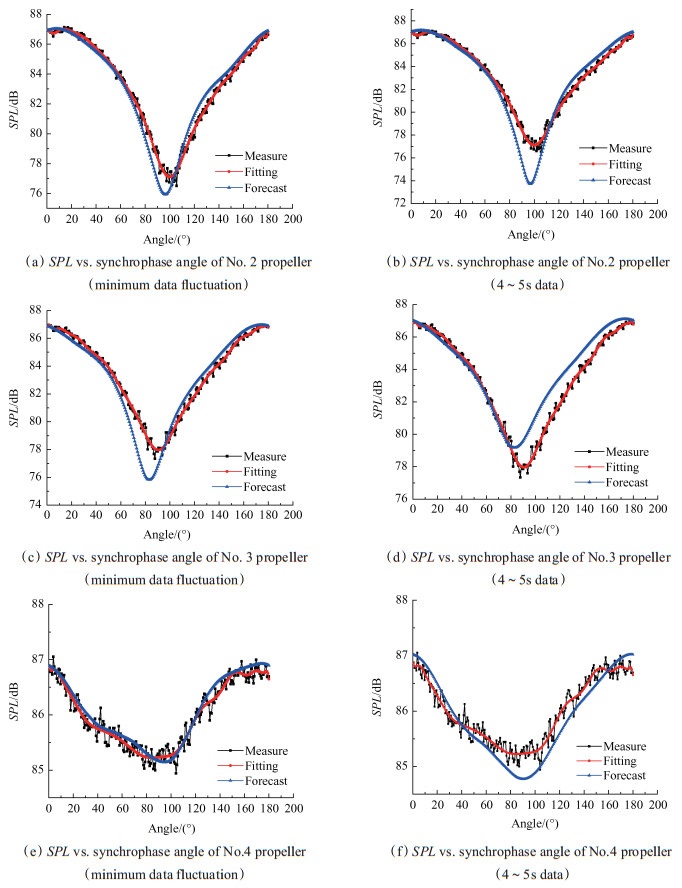
本文采用两种方法进行噪声模型辨识,第一种方法是从10s时长的数据中选取波动最小的1s时长数据段用于噪声模型辨识,第二种方法是直接取10s时长数据段中4~5s的数据用于噪声模型辨识。两种方法所获得的噪声模型,其预测噪声分别和试验测量噪声进行对比以验证其精度。模型精度验证试验结果如图 8所示,图中拟合噪声表示测量噪声的最小二乘拟合曲线,由于测量噪声可能伴随有随机干扰,因此拟合后的平滑曲线更能代表真实的噪声变化趋势。在图 8中的SPL随某螺旋桨同步相角变化,表示该螺旋桨同步相角从0°变化到180°,其他螺旋桨同步相角为0°。
|
Fig. 8 SPL changes with propeller |
对比图 8(a)和图 8(b),两者预测的使噪声SPL最小的最优相角均与真实的最优相角接近,最优相角误差在5°以内;但就预测噪声与实际噪声的一致性而言,最小数据波动辨识的噪声模型其SPL预测误差在1dB以内,而4~5s数据辨识的噪声模型其SPL预测误差在3dB以内,最小数据波动所得的噪声模型精度明显优于取4~5s数据辨识所得模型的精度;该结论对于其他图依然成立。这说明使用最小数据波动辨识所得的螺旋桨噪声模型,其精度全面优于直接选取4~5s的数据辨识所得模型的精度。对于选取4~5s数据用于噪声模型辨识,所得的噪声模型的精度稍差的现象,可能存在其他时间段(如6~7s等)的数据用于噪声模型辨识,能获得优于4~5s的效果。然而这并不具有通用性,特定(如6~7s)的数据段无法保证在任何时候都能获得良好的建模精度。本文提出的使用最小数据波动辨识噪声模型的算法可以确保用于模型辨识的数据良好,这意味着该算法可以回避转速波动、气流扰动和环境噪声扰动等瞬时干扰对建模精度的影响,从而保证辨识噪声模型的精度。
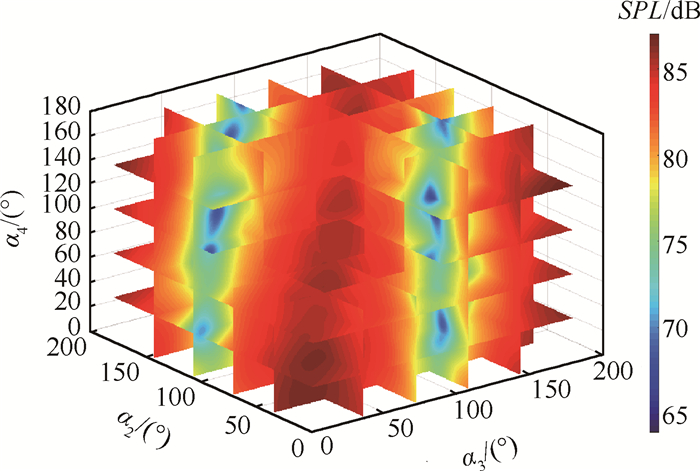
4.4 相同步降噪性能本文4.3节中辨识所得的噪声模型为螺旋桨平面水平位置第2个麦克风处的噪声模型。获得该位置的高保真噪声模型后,可开展该处的相角寻优,即寻找使该处噪声最小的同步相角,将螺旋桨控制到最优同步相角实现最优降噪。基于模型的相角寻优可使用多种算法开展,如蚁群、遗传和序列二次规划等算法寻优。本文为了更好地介绍噪声随同步相角的变化,采用遍历法进行相角寻优,遍历法的过程为将螺旋桨的相角按特定分度值进行划分,如本文介绍的两桨叶螺旋桨其相角区间为[0°,180°],按照1°的分度值划分时,4螺旋桨试验平台将有1803(5832000)种相角组合,并且分度值越小,精度越高,相角组合数越大。对于四螺旋桨试验平台,本文遍历法绘制的测量点SPL随同步相角的变化如图 9所示。
|
Fig. 9 SPL changes with synchrophase |
由图 9数据可以直接得到螺旋桨的最优相角为{ 0°, 159°, 60°, 91° },其对应的噪声SPL为63.9dB。图中使噪声最大的同步相角为{ 0°, 4°, 176°, 175° },其对应的噪声SPL为87.0dB,螺旋桨相同步降噪在该处的最大降噪幅值为23.1dB。实际测试显示最大SPL相角组合的噪声为85.3dB,最小SPL相角组合的噪声为65.8dB,两者的噪声差值约为19.5dB。其原因是实际的同步相角在最值点附件略有波动,导致SPL也时刻波动,实际测量值是一个波动平均值。这使得实际最大值将小于理论最大值,实际最小值将大于理论最大值,最终的最大降噪幅值为19.5dB,小于理论值23.1dB。然而,理论最大值和理论最小值均和试验测量值接近,这也说明本文提出的辨识算法所得的噪声模型精度良好。
对于机舱内的全局降噪优化,其过程为通过辨识机舱内多个代表性位置的噪声模型,取其加权平均值作为机舱总体噪声模型,再开展相角寻优实现全局降噪,对此本文不做详细介绍。
5 结论在地面螺旋桨相同步实验平台上,针对模拟机舱内位置点噪声开展了试验研究,得到的主要结论如下:
(1)小波分析可以有效地提取螺旋桨噪声的BPF信号,基于三参数的正弦拟合算法能够准确地度量BPF信号的波动大小,从而有效地从一段时长的噪声信号中选择出波动最小的数据段。
(2)使用波动最小的数据段用于噪声模型辨识能够回避外界瞬时扰动引起的建模误差,模型辨识精度受外界的瞬时扰动影响小。相对于传统的固定数据段辨识所得噪声模型,最小数据波动噪声模型具有更高的精度。
(3)实验位置点,使用最小数据波动辨识的噪声模型其预测的最大、最小噪声的同步相角,其对应的最大预测噪声大于实测值,最小预测噪声小于实测值。预测噪声最值与实测噪声最值不等主要来自于螺旋桨相角的不稳定,详细原因可开展下一步研究。
致谢: 感谢国家自然科学基金、南京航空航天大学研究生创新基地(实验室)开放基金资助。
| [1] |
李晓东, 孙晓峰, 胡宗安, 等. 一种亚音螺旋桨声场中间面快速算法[J]. 航空学报, 1994, 15(7): 769-773. DOI:10.3321/j.issn:1000-6893.1994.07.001 (  0) 0) |
| [2] |
Mathur G P. Active Control of Aircraft Cabin Noise[J]. Journal of the Acoustical Society of America, 1995, 97(5): 32-67.
(  0) 0) |
| [3] |
Hansen C, Snyder S, Qiu X, et al. Active Control of Noise and Vibration[M]. UK: CRC Press, 2013.
(  0) 0) |
| [4] |
Blunt DM, Rebbechi B. Propeller Synchrophase Angle Optimisation Study[C]. Rome: Proceedings of the 13th AIAA/CEA Aeroacoustics Conference, 2007.
(  0) 0) |
| [5] |
Magliozzi B. Synchrophasing for Cabin Noise Reduction of Propeller-Driven Airplanes[C]. Atlanta: Aeroacoustics Conference, 1983.
(  0) 0) |
| [6] |
Blunt D M, Rebbechi B. An Investigation into Active Synchrophasing for Cabin Noise and Vibration Reduction in Propeller Aircraft[J]. Electron Device Letters IEEE, 2006, 23(4): 306-308.
(  0) 0) |
| [7] |
Blunt D M. Altitude and Airspeed Effects on the Optimum Synchrophase Angles for a Four-Engine Propeller Aircraft[J]. Journal of Sound & Vibration, 2014, 333(16): 3732-3742.
(  0) 0) |
| [8] |
Johnston J F, Donham R E, Guinn W A. Propeller Signatures and Their Use[J]. Journal of Aircraft, 2015, 1(11): 934-942.
(  0) 0) |
| [9] |
Huang X, Wang Y, Sheng L. Synchrophasing Control in a Multi-Propeller Driven Aircraft[C]. Chicago: American Control Conference, 2015.
(  0) 0) |
| [10] |
Huang X, Sheng L, Wang Y. Propeller Synchrophase Angle Optimization of Turboprop-Driven Aircraft-An Experimental Investigation[J]. Journal of Engineering for Gas Turbines & Power, 2014, 36(11).
(  0) 0) |
| [11] |
王洋洋, 黄向华, 张天宏, 等. 一种改进的螺旋桨相同步控制噪声模型辨识方法[J]. 应用力学学报, 2014, 31(6): 933-938. (  0) 0) |
| [12] |
Mallat S G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation[J]. IEEE Transactions on Pattern Analysis & amp; Machine Intelligence, 1989, 11(7): 674-693.
(  0) 0) |
| [13] |
Mallat, Stephane G. Multifrequency Channel Decompositions of Images and Wavelet Models[J]. Signal Processing, 1989, 37(12): 2091-2110.
(  0) 0) |
| [14] |
梁志国, 孟晓风. 正弦波形参数拟合方法述评[J]. 测试技术学报, 2010, 24(1): 1-8. DOI:10.3969/j.issn.1671-7449.2010.01.001 (  0) 0) |
| [15] |
Jones J D, Fuller C R. Noise Control Characteristics of Synchrophasing, Part 2: Experimental Investigation[J]. AIAA Journal, 1986, 24(8): 1271-1277. DOI:10.2514/3.9431
(  0) 0) |
| [16] |
窦雪茹, 崔素玲. 频谱分析仪相位噪声测量原理[J]. 科技信息, 2009, 26(6): 81-81. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


