航空发动机长期在高温、高压和高转速的恶劣环境中工作, 容易发生气路突变故障影响到飞行安全[1, 2]。通过收集商用航空发动机的机载传感器数据可以对发动机各旋转部件的性能健康状态进行监视[3, 4], 检测和隔离故障以进行故障诊断与制定维修策略, 从而提高飞行安全和降低航班延误率。
航空发动机的气路健康状态常用各个部件的流量和效率的相对变化量(即健康参数)来表示, 然而由于它们无法直接测量, 只能根据机载传感器的测量值, 如两个转子转速和各个截面的压力和温度通过算法进行估计。常用的方法有滤波算法和机器学习算法两大类。
航空发动机非线性特性强, 线性卡尔曼滤波算法由于线性状态变量模型存在二次建模误差, 使得基于线性卡尔曼滤波算法的气路故障诊断精度较低。针对该问题, Zhou等[5]提出将健康参数增广到状态量, 采用固定增益的扩展卡尔曼滤波算法实现了对5个健康参数的估计。陆军等[6]以非线性模型的输出作为分段线性卡尔曼滤波器的稳态基线, 实现了对4个健康参数的估计, 提高了估计精度。陈煜等[7]提出了两种带约束的非线性卡尔曼滤波算法, 相比标准卡尔曼滤波算法也提高了一定的精度。然而, 以上文献以及许多工程实际中, 由于机载传感器热端分布较少且可测参数个数小于健康参数个数, 只能选取部分健康参数进行估计。当未估计的健康参数发生变化时, 待估计的健康参数会发生一定的偏离, 导致漏判、误判故障。
基于机器学习算法的航空发动机故障诊断技术近年来研究较热, 如极限学习机[8, 9]与神经网络[10, 11], 但都主要应用于执行机构或者传感器故障诊断上, 而非气路健康参数估计, 其主要原因为:(1)不同飞行条件, 不同风扇转速下, 相同的气路故障对输出传感器的变化不尽相同。(2)气路故障种类多, 若要准确定量估计, 需要训练样本非常庞大, 对网络要求极高。(3)机载传感器容易受到噪声的影响, 无法准确估计结果。
本文提出的神经网络修正卡尔曼滤波算法(NN-KF)结合了智能算法和卡尔曼滤波算法, 在每个采样周期内, 通过神经网络按一定概率对个体的偏移进行修正, 按粒子滤波算法加权求和计算总体的均值和协方差, 利用卡尔曼滤波算法更新所有个体, 并将均值向量作为当前时刻的估计结果, 实现了用7个可测输出估计全部10个健康参数。
2 神经网络修正卡尔曼滤波算法 2.1 无迹卡尔曼滤波算法本文先介绍一种针对非线性状态变量模型的无迹卡尔曼滤波(UKF)算法[12]。
假设非线性系统的离散时间模型为
| ${\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{f}}_{k - 1}}\left( {{\mathit{\boldsymbol{x}}_{k - 1}}, {\mathit{\boldsymbol{u}}_{k - 1}}} \right) + {{\bf{w}}_{k - 1}}\\ {{\mathit{\boldsymbol{y}}_k} = {\mathit{\boldsymbol{h}}_k}\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{u}}_k}} \right) + {\mathit{\boldsymbol{v}}_k}}$ | (1) |
式中uk, xk, yk分别为系统在k时刻的输入向量、状态向量和输出向量, wk, vk分别为系统噪声和测量噪声, 它们为不相关的高斯白噪声, 满足:wk~N(0, Qk), vk~N(0, Rk), 且与系统的状态xk无关, fk-1(·, ·), hk(·, ·)为非线性函数。UKF算法初始化
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat x}}_0^ + = E\left( {{\mathit{\boldsymbol{x}}_0}} \right)}\\ {\mathit{\boldsymbol{P}}_{x, 0}^ + = E[\left( {{\mathit{\boldsymbol{x}}_0}-\mathit{\boldsymbol{\hat x}}_0^ + } \right)\left( {{\mathit{\boldsymbol{x}}_0}-\mathit{\boldsymbol{\hat x}}_0^ + {)^{\rm{T}}}} \right]} \end{array} $ | (2) |
式中
(1) 将无迹变换产生的Sigma点代入非线性模型中进行预测
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)} = {\mathit{\boldsymbol{f}}_{k-1}}\left( {\mathit{\boldsymbol{\hat x}}_{k-1}^{\left( i \right)}, {\mathit{\boldsymbol{u}}_{k-1}}} \right)}\\ {\mathit{\boldsymbol{\hat y}}_k^{\left( i \right)} = {\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)}, {\mathit{\boldsymbol{u}}_k}} \right)}\\ {i = 1, ..., N} \end{array} $ | (3) |
式中
| $ \begin{array}{l} \bar x_k^-= \sum\limits_{i = 1}^{i = N} {W_m^{\left( i \right)}} \hat x_k^{\left( i \right)}\\ {{\bar y}_k} = \sum\limits_{i = 1}^{i = N} {W_m^{\left( i \right)}} \hat y_k^{\left( i \right)}\\ \mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{x}}, k}^-= \sum\limits_{i = 1}^{i = N} {W_c^{\left( i \right)}} \left( {\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)}-\mathit{\boldsymbol{\bar x}}_k^ - } \right){(\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)} - \mathit{\boldsymbol{\bar x}}_k^ - )^{\rm{T}}}\\ \mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{y}}, k}^ - = \sum\limits_{i = 1}^{i = N} {W_c^{\left( i \right)}} \left( {\mathit{\boldsymbol{\hat y}}_k^{\left( i \right)} - {{\mathit{\boldsymbol{\bar y}}}_k}} \right){(\mathit{\boldsymbol{\hat y}}_k^{\left( i \right)} - {{\mathit{\boldsymbol{\bar y}}}_k})^{\rm{T}}}\\ \mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{x}}y, k}^ - = \sum\limits_{i = 1}^{i = N} {W_c^{\left( i \right)}} \left( {\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)} - \mathit{\boldsymbol{\bar x}}_k^ - } \right){(\mathit{\boldsymbol{\hat y}}_k^{\left( i \right)} - {{\mathit{\boldsymbol{\bar y}}}_k})^{\rm{T}}} \end{array} $ | (4) |
式中
(2) 计算卡尔曼增益矩阵, 更新状态的估计值和协方差为
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{K}}_k} = \mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{x}}y, k}^-{{(\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{y}}, k}^-)}^{-1}}}\\ {\bar x_k^ + = \bar x_k^ - + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{y}}_k} - {{\bar {\mathit{\boldsymbol{y}}}}_k}} \right)}\\ {\mathit{\boldsymbol{P}}_k^ + = \mathit{\boldsymbol{P}}_k^ - - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{y}}, k}^ - \mathit{\boldsymbol{K}}_k^{\rm{T}}} \end{array} $ | (5) |
UKF算法通过无迹变换估计状态的先验均值和协方差, 本文的NN-KF算法借鉴粒子滤波(PF)算法[13]来估计均值和协方差:首先对上一时刻的个体按照权值进行重采样, 再按重要性密度函数对个体向量进行偏移, 然后更新个体的权值, 用这些个体来逼近当前真实的概率分布。对于PF算法个体的权值更新为
| $ \begin{array}{*{20}{l}} {f_k^{\left( i \right)} = f_{k - 1}^{\left( i \right)}\frac{{p\left( {{\mathit{\boldsymbol{y}}_k}|\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)}} \right)p\left( {\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)}|\mathit{\boldsymbol{\hat x}}_{k - 1}^{\left( i \right)}} \right)}}{{q\left( {\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)}|\mathit{\boldsymbol{\hat x}}_{k - 1}^{\left( i \right)},{\mathit{\boldsymbol{y}}_k}} \right)}}}\\ {\tilde f_k^{\left( i \right)} = f_k^{\left( i \right)}/\sum\limits_{i = 1}^N {f_k^{\left( i \right)}} } \end{array} $ | (6) |
式中fk(i)为第i个个体在第k时刻的权值,
| $ f_k^{\left( i \right)} = {\rm{exp}}\left[{C{{\left( {\mathit{\boldsymbol{\hat y}}_k^{\left( i \right)}-{\mathit{\boldsymbol{y}}_k}} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}_k^{-1}\left( {\mathit{\boldsymbol{\hat y}}_k^{\left( i \right)}-{\mathit{\boldsymbol{y}}_k}} \right)} \right] $ | (7) |
式中C为放大系数, 其他符号含义与UKF算法中相似。于是, 由PF算法可知, 将式(4)的权值Wm(i)和Wc(i)替换为
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{K}}_k} = \mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{x}}y, k}^-{{(\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{y}}, k}^-)}^{-1}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{y}}_k} - {{\mathit{\boldsymbol{\bar y}}}_k}} \right)}\\ {\mathit{\boldsymbol{\hat x}}_{k + 1}^{\left( i \right)} = \mathit{\boldsymbol{\hat x}}_k^{\left( i \right)} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{x}}_k}} \end{array} $ | (8) |
由式(8)可知, 其先验信息的好坏将直接影响滤波算法的更新方向, 尤其是当输出向量的维数小于状态向量的维数时, 一个好的先验信息能帮助稳定估计结果, 因此本文加入BP神经网络[14, 15]来修正个体的偏移方向, 获得更理想的个体以及对应的先验均值和协方差。
神经网络首先根据非线性模型:yk=hk(xk)学习输出量与状态量的非线性映射。训练完成后, 网络根据当前的测量输出计算状态量
| $ {{\mathit{\boldsymbol{\hat x}}}_k} = \mathit{\Phi }\left( {{\mathit{\boldsymbol{y}}_k}} \right) $ | (9) |
式中yk为当前测量输出向量, Φ为神经网络非线性映射,
| $ {\left( {\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)}} \right)_j} = {\left( {\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)}} \right)_j} + \lambda {\left( {{{\mathit{\boldsymbol{\hat x}}}_k}-\mathit{\boldsymbol{\hat x}}_k^{\left( i \right)}} \right)_j} $ | (10) |
式中(·)j表示该向量的第j行, λ为比例系数。将该算法定义为神经网络修正卡尔曼滤波(NN-KF)算法, 其计算流程如图 1所示。
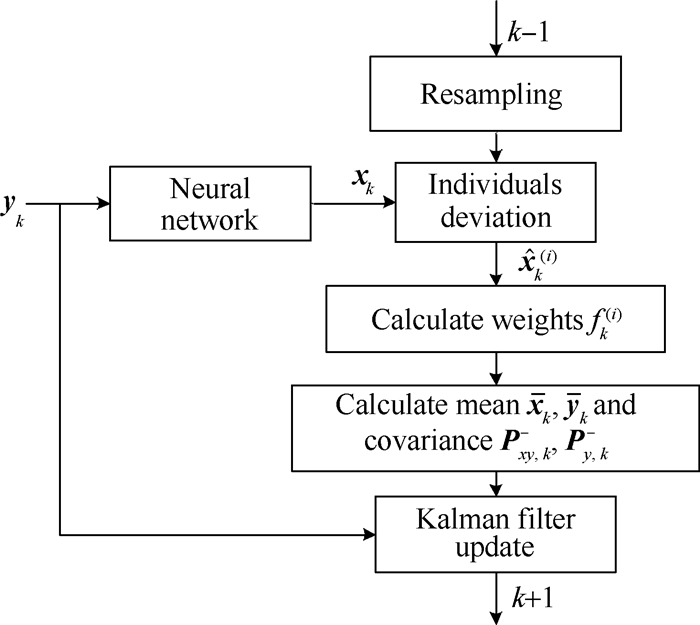
|
Fig. 1 Flowchart of NN-KF algorithm |
相比UKF算法, NN-KF算法将神经网络对状态的估计结果融入了个体中, 然后借助PF算法计算个体的权值, 改进了状态估计的均值和协方差, 使得更新过程往神经网络估计的方向偏移, 在以少估多的情况下提高了KF算法的估计精度。
3 设计点数字仿真验证 3.1 商用航空发动机模型本文数字仿真使用的航空发动机模型为某型大涵道比涡扇发动机部件级模型, 如图 2所示, 共有5个旋转部件:风扇(Fan)、低压压气机(LPC)、高压压气机(HPC)、高压涡轮(HPT)和低压涡轮(LPT)。
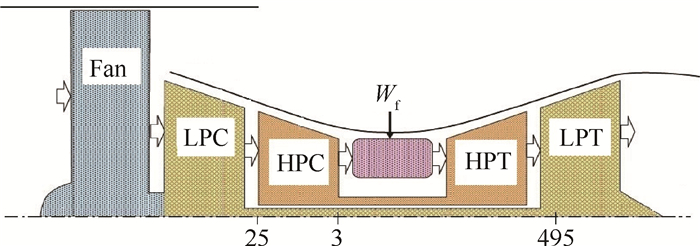
|
Fig. 2 Diagram of the high bypass ratio turbofan engine components and station designations |
待估计的健康参数为部件的效率/流量的相对变化量
| $ \left\{ {\begin{array}{*{20}{l}} {S{W_i} = \frac{{{W_i}}}{{W_i^{\rm{*}}}}-1}\\ {S{E_i} = \frac{{{\eta _i}}}{{\eta _i^{\rm{*}}}}-1} \end{array}} \right.\left( {i = 1, 2, 3, 4, 5} \right) $ | (11) |
式中Wi和ηi分别为部件流量和效率的实际值, Wi*和ηi*分别为部件没有发生故障时的流量和效率。下标1, 2, …, 5依次对应5个旋转部件。当健康参数不为0时, 表明相关气路部件发生故障, 引起性能退化。将这5个流量和5个效率健康参数作为状态量进行滤波估计, 达到估计各部件性能退化程度的目的。该型发动机与气路性能相关的机载传感器如表 1所示, 包含7个输出量以及燃油流量。
|
|
Table 1 Onboard sensors |
本文在使用NN-KF算法进行健康参数估计前, 采用BP神经网络提前训练好关于气路突变故障引起的稳态输出偏差与健康参数的变化之间的非线性映射, 然后气路故障诊断时, 该网络仅计算输出结果。训练样本选取该发动机的设计巡航飞行点(H=10.668km, Ma=0.785)下从慢车以上状态(N1=70%)到最大状态(N1=110%)的9个离散状态点, 每个状态下模拟各种气路故障。故障数据参考NASA格林研究中心的文献[16], 部件性能退化的绝对值在[1%, 5%]。训练数据共包含了9种故障模式:5种单部件(Fan, LPC, HPC, HPT, LPT)和4种多部件情况(Fan & LPC, LPC & HPC, Fan & LPC & HPC, HPT & LPT)。每种故障模式下部件的流量和效率同时退化。
训练样本的输入为表 1的7个输出量在故障前后的稳态偏差以及当前燃油流量, 输出为式(11)的10个健康参数。此外, 由于机载传感器数据含噪声, 会影响BP神经网络的估计结果, 所以加入方差为0.0022I8×8的高斯白噪声在训练样本的输入中。设置该网络的隐含层层数为1, 节点数为22, 激活函数为Tansig函数, 输出层节点数为10, 对应10个健康参数, 激活函数为Purelin函数。采用MatLab自带的Train函数以批处理方式训练该神经网络, 设置性能函数为均方误差(mse), 训练算法为Levenberg-Marquardt算法[17], 迭代次数为500, 其余都使用MatLab的默认设定。
对于NN-KF算法的控制量、状态量、输出量分别选取为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}} = {W_{\rm{f}}}}\\ {\mathit{\boldsymbol{x}} = \left[{\begin{array}{*{20}{c}} {S{W_1}}&{S{E_1}}&{S{W_2}}&{S{E_2}} \end{array}} \right.}\\ {{{\left. {\begin{array}{*{20}{c}} {S{W_3}}&{S{E_3}}&{S{W_4}}&{S{E_4}}&{S{W_5}}&{S{E_5}} \end{array}} \right]}^{\rm{T}}}}\\ {\mathit{\boldsymbol{y}} = {{\left[{\begin{array}{*{20}{c}} {{N_1}}&{{N_2}}&{{T_{25}}}&{{P_{25}}}&{{T_3}}&{{P_3}}&{{T_{495}}} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (12) |
设该算法中个体的总数为21, 偏移的概率为0.12, 比例系数λ=0.2, 对优化后的个体进行约束, 即所有效率健康参数小于等于0, 涡轮流量健康参数大于等于0[18]。将该算法与该算法中的BP神经网络、UKF算法同时进行健康参数估计, 比较三种算法的估计精度。UKF算法中无迹变换的系数选取:α=0.15, β=2, κ=0, 其控制量、状态量、输出量同式(12), 无迹变换的Sigma点个数也为21。
3.3 设计点数字仿真与分析本文的数字仿真在笔记本电脑Windows 10系统的32位MatLab R2012a下完成, 其配置为i5-6300HQ @ 2.30GHz, 4GB Ram。选取了9种气路突变故障(5种单部件、4种多部件)来验证NN-KF算法的估计精度, 如表 2。
|
|
Table 2 Fault scenarios |
数字仿真的时间为25s, 采样周期为25ms, 故障统一在第5s注入, 并假设输出传感器含高斯白噪声, 满足vk~N(0, Rk), 其中Rk=0.0022I7×7, 同时加入PID控制器调整燃油流量, 使低压转子转速保持不变。
限于篇幅, 本文首先数字仿真模拟在设计巡航飞行点的100%低压转子换算转速下发生表 2的故障情况8, NN-KF算法的健康参数估计结果如图 3(a)所示, 其协方差Py, k的迹(Trace(Py, k))与卡尔曼增益Kk的迹(Trace(K'K))随时间的变化关系如图 3(b)和图 3(c)所示。图 3(d)与图 3(e)为完全相同的机载传感器数据下, BP神经网络与UKF算法的健康参数估计结果。
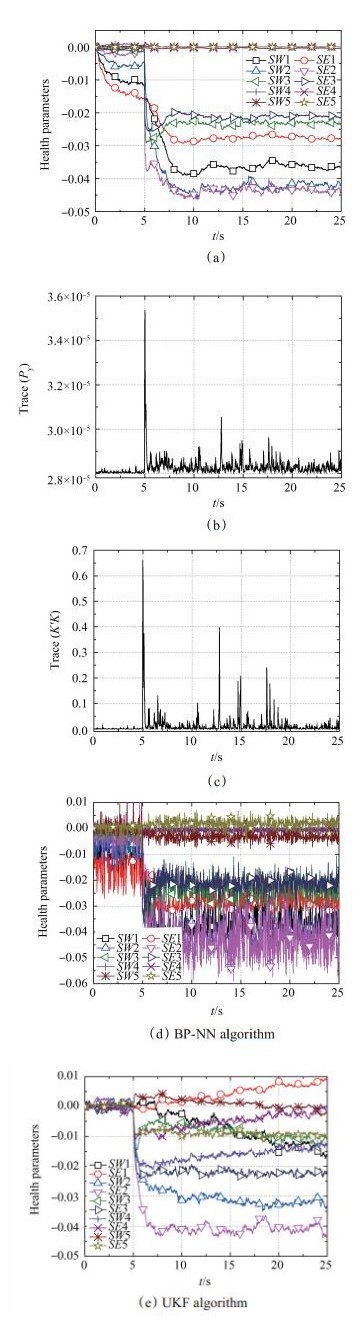
|
Fig. 3 Estimated results of fault scenario 8 |
从图 3(a)可知, 在突变故障发生后的2s内, 估计结果逐渐往真实退化方向移动, 并最终准确定位到了发生退化的6个健康参数上, 没有出现误判和漏判。从图 3(b)与图 3(c)可知, 估计的协方差Py, k在故障发生瞬间增大, 卡尔曼增益Kk也相应增大。第6s以后, 协方差矩阵的变化逐渐减小, 滤波估计结果趋于平稳。从图 3(d)中可知, BP神经网络根据燃油流量和输出偏差进行故障诊断, 对于故障定位较准确, 但是健康参数的估计精度较低。从图 3(e)中可知, UKF算法对风扇健康参数估计不准确, 也误诊了高压涡轮流量和低压涡轮效率, 估计结果也较差。
图 4(a)、图 4(b)和图 4(c)分别为故障情况9的三种算法的估计结果。对比图 4(a)、图 4(b)和图 4(c), 对于高压涡轮与低压涡轮的双部件故障模式, 本文的NN-KF算法也好于两种独立的算法。
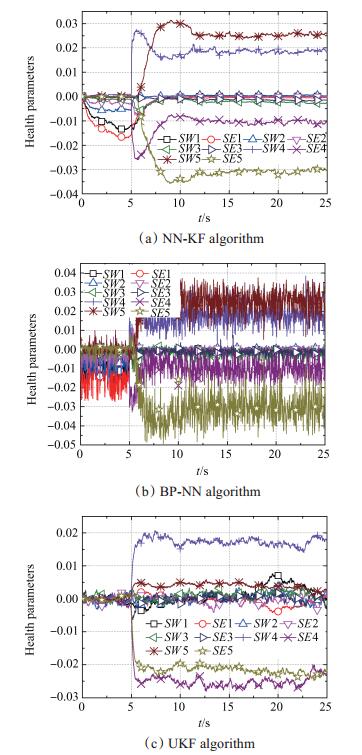
|
Fig. 4 Estimated results of fault scenario 9 |
由于商用航空发动机每次巡航飞行的高度、马赫数和低压转子转速都不一定是设计值, 为了能够继续使用NN-KF算法, 将输入给BP神经网络的输出向量偏差进行相似换算到设计巡航飞行点。参考文献[19], 计算全飞行包线内各个飞行点距离设计巡航飞行点的广义距离, 设定广义距离的阈值d≤0.07, 得到相似原理的适用范围大致由以下四个飞行点:(1)H=9.3km, Ma=0.60;(2)H=11.1km, Ma=0.90;(3)H=9.9km, Ma=0.60;(4)H=11.7km, Ma=0.90组成的平行四边形飞行区块。
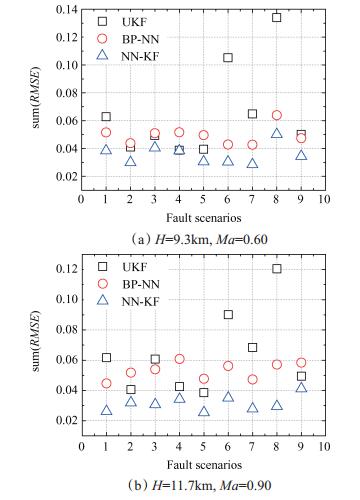
选取该飞行区块的顶点(1)和顶点(4), 每个顶点选择一个低压转子转速分别模拟表 2的9种故障模式, 将这2个飞行状态点的9种故障模式的估计精度以10个健康参数的均方根误差总和(sum(RMSE))表示如图 5(a)与图 5(b)。
| $ \begin{array}{*{20}{l}} {RMSE\left( p \right) = \sqrt {\frac{{\sum\limits_{k = 1}^{k = 1000} {{{\left( {{{\hat p}_k}-{p_k}} \right)}^2}} }}{{1000}}} }\\ {p \in \left\{ {S{W_1}, S{E_1}, S{W_2}, S{E_2}, S{W_3}, S{E_3}, S{W_4}, S{E_4}, S{W_5}, S{E_5}} \right\}}\\ {{\rm{sum}}\left( {RMSE} \right) = RMSE\left( {S{W_1}} \right) + \ldots + RMSE\left( {S{E_5}} \right)} \end{array} $ | (13) |
|
Fig. 5 Estimated errors at multiple fly points |
图 5(a)为飞行状态点(1)的误差图, 对于表 2中的9种故障模式, NN-KF算法的估计误差相比BP神经网络分别降低了25.4%, 31.5%, 20.5%, 25.6%, 38.4%, 29.3%, 33.3%, 21.5%与27.2%, 相比UKF算法分别降低了38.8%, 26.9%, 17.9%, 0.9%, 22.5%, 71.1%, 56.0%, 62.6%与31.2%。图 5(b)为飞行状态点(4)的误差图, NN-KF算法相比BP神经网络分别降低了41.4%, 38.4%, 43.1%, 43.6%, 46.7%, 37.6%, 41.1%, 48.3%与29.5%, 相比UKF算法分别降低了57.6%, 21.1%, 49.5%, 19.4%, 33.9%, 61.1%, 59.3%, 75.4%与16.7%。在计算成本方面, 该算法在25ms的采样周期内, 计算时间平均约为53ms, 其中神经网络计算约为9ms, 21个个体调用部件级模型占用约为40ms, 其余为矩阵计算。
5 结论通过本文的研究, 得到以下结论:
(1) 总结了卡尔曼滤波算法与神经网络在气路健康参数估计问题上各自存在的问题。
(2) 提出了一种利用神经网络的估计结果来修正状态估计均值与协方差的改进卡尔曼滤波算法。
(3) 多个飞行状态的数字仿真结果表明, 在机载传感器分布不均且个数小于健康参数总个数的情况下, 该混合算法相比神经网络与无迹卡尔曼滤波算法对健康参数的估计误差分别平均降低了34.6%与47.9%。
| [1] |
Mercer C R, Simon D L, Hunter G W, et al.Fundamental Technology Development for Gas-Turbine Engine Health Management[R].NASA/TM-2007-0022364.
(  0) 0) |
| [2] |
Litt J S, Simon D L, Gary S, et al, A Survey of Intelligent Control and Health Management Technologies for Aircraft Propulsion Systems[R].NASA/TM-2005-213622.
(  0) 0) |
| [3] |
Kobayashi T, Simon D L. Integration of On-Line and Off-Line Diagnostic Algorithms for Aircraft Engine Health Management[J]. Journal of Engineering for Gas Turbines & Power, 2007, 129(4): 649-659.
(  0) 0) |
| [4] |
薛薇, 郭迎清, 李睿. 航空发动机状态监视、故障诊断研究及验证[J]. 推进技术, 2011, 32(2): 271-275. (XUE Wei, GUO Ying-qing, LI Rui. Algorithm and Experimental Validation for Condition Monitoring, Fault Detection for Gas Turbine Engine[J]. Journal of Propulsion Technology, 2011, 32(2): 271-275.)
(  0) 0) |
| [5] |
Zhou G T, Su S M. Application of Improved Extended Kalman Filter for Adaptive Model of Aircraft Engine[J]. Applied Mechanics & Materials, 2015, 709: 180-185.
(  0) 0) |
| [6] |
陆军, 郭迎清, 张书刚. 基于改进混合卡尔曼滤波器的航空发动机机载自适应模型[J]. 航空动力学报, 2011, 26(11): 2593-2600. (  0) 0) |
| [7] |
陈煜, 鞠红飞, 鲁峰, 等. 涡喷发动机健康状态的带约束非线性滤波估计[J]. 推进技术, 2016, 37(4): 741-748. (CHEN Yu, JU Hong-fei, LU Feng, et al. Nonlinear Filter with Inequality Constraints for Turbojet Engine Health Estimation[J]. Journal of Propulsion Technology, 2016, 37(4): 741-748.)
(  0) 0) |
| [8] |
姜洁, 李秋红, 张高钱, 等. 基于NN-ELM的航空发动机燃油系统执行机构故障诊断[J]. 航空动力学报, 2016, 31(2): 484-492. (  0) 0) |
| [9] |
尤成新, 鲁峰, 黄金泉. 航空发动机传感器信号重构的K-ELM方法[J]. 航空动力学报, 2017, 32(1): 221-226. (  0) 0) |
| [10] |
李长征, 张瑜. 基于广义回归神经网络的传感器故障检测[J]. 推进技术, 2017, 38(9): 2130-2137. (LI Chang-zheng, ZHANG Yu. Sensor Fault Detection Based on General Regression Neural Network[J]. Journal of Propulsion Technology, 2017, 38(9): 2130-2137.)
(  0) 0) |
| [11] |
江传尚, 樊丁, 马冲. 小波网络在某型航空发动机故障诊断中的应用[J]. 航空动力学报, 2009, 24(4): 892-895. (  0) 0) |
| [12] |
Julier S J, Uhlmann J K. Unscented Filtering and Nonlinear Estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401-422. DOI:10.1109/JPROC.2003.823141
(  0) 0) |
| [13] |
朱志宇. 粒子滤波算法及其应用[M]. 北京: 科学出版社, 2010.
(  0) 0) |
| [14] |
Hecht-Nielsen.Theory of the Backpropagation Neural Network[C].Washington: International Joint Conference on Neural Networks, 1989.
(  0) 0) |
| [15] |
Demuth H, Beale M. Neural Network Toolbox-For Use with MATLAB[J]. Matlab Users Guide the Math Works, 1995, 21(15): 1225-1233.
(  0) 0) |
| [16] |
Kobayashi T, Simon D L.Hybrid Kalman Filter: A New Approach for Aircraft Engine In-Flight Diagnostics[R].NASA/TM-2006-214491.
(  0) 0) |
| [17] |
Moré J J. The Levenberg-Marquardt Algorithm:Implementation and Theory[M]. Berlin: Springer, 1978.
(  0) 0) |
| [18] |
Simon D, Simon D L. Aircraft Turbofan Engine Health Estimation Using Constrained Kalman Filtering[J]. Journal of Engineering for Gas Turbines & Power, 2003, 127(2).
(  0) 0) |
| [19] |
胡卫红, 李述清, 孙健国. 控制问题中航空发动机飞行包线区域最优划分[J]. 推进技术, 2011, 32(3): 391-395. (HU Wei-hong, LI Shu-qin, SUN Jian-guo. Flight-Envelope Optimization Partition for Aeroengines Control[J]. Journal of Propulsion Technology, 2011, 32(3): 391-395.)
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


