减重增效,提高推重比是航空发动机设计的过程中不懈追求的目标。低压涡轮轴作为航空发动机的核心部件,对其进行减重增效设计,可以有效地提高发动机性能[1]。随着新一代航空发动机对推重比要求的不断的提高,传统的金属材料在结构不变的条件下已经无法满足发动机减重增效的需求,更高性能材料的研发与应用,迫在眉睫。
新型连续纤维增强金属基复合材料具有高比刚度、比强度、耐高温和低密度等优良特性,使得其成为航空发动机关键部件选材重要的候选材料[2]。在此趋势的推动下,金属基复合材料在航空发动机轴结构上的应用成为了人们关注的焦点。而航空发动机连续纤维增强复合材料低压涡轮轴力学性能计算的准确与否,直接影响到整个发动机能否正常运行、整台发动机推重比能否提高与寿命预测的准确性及后续工作的展开。可见,研究航空发动机连续纤维增强复合材料低压涡轮轴力学性能及强度问题是十分有意义的。
金属基复合材料轴结构应用方面,20世纪80年代至90年代初,GE公司成功将SiC/Ti金属基复合材料低压轴实装于F110发动机,该低压轴质量减轻68kg,其中包括轴本身质量减轻9kg。20世纪90年代,GE公司又在XTC-76 JTDE发动机上验证了碳化硅增强的TMC低压轴,该低压轴质量较传统合金轴轻30%,刚度较钛合金轴的高40%,寿命也有所延长。英国罗罗公司也已经成功研制出SCS-6纤维增强Ti-6-4合金基复合材料,应用于欧洲联合研制的EJ200涡扇发动机[2]。德国航空航天中心材料研究所推出的SiC纤维增强钛基复合材料,强度较传统材料轴提高了70%。相较于国外,国内复合材料的应用处于起步阶段。中科院金属所成功完成SiC/Ti复合材料整体叶环成型一体化技术[1]。在国内,复合材料轴还未应用于航空发动机上。
在复合材料轴的基础研究方面,国外,AntonioF Avila对SCS-6/Ti-15-3的力学性能进行了预测,并和金属叶片强度数据进行了对比[3, 4]。Himmel对玻璃纤维增强复合材料轴进行了扭转疲劳特性试验,并得出在扭转载荷下疲劳与静强度失效与基体材料性能密切相关,而拉压疲劳载荷作用下的失效是由纤维控制的[5]。英国诺丁汉大学Hyde等[6]进行复合材料轴疲劳试验并对+45°铺层与±45°铺层情况下失效模式就行了分析。国内对金属基复合材料主轴研究处于仿真阶段,沙云东等对金属基复合材料轴承扭特性进行了研究,并得出复合材料层数不宜超过12层的结论[7~9],对金属基复合材料涡轮轴低周疲劳寿命进行了预测,并验证了预测方法的可靠性[10]。孙庆伟等利用全排列的方法航空发动机复合材料主轴铺层进行了设计,并得出复合材料轴较金属轴减重36%铺层方案[11]; 王婕等在孙庆伟的基础上将遗传算法应用到复合材料主轴的优化设计上,并验证了遗传算法的可行性较全排列法优越性结论[12]。崔广群等校核了传动轴结构的静态承扭特性[13]。
本文以航空发动机低压涡轮轴为研究背景,以常温环境下缠绕工艺成型的连续纤维增强金属基复合材料轴试验件为对象,利用有限元法对其进行模拟仿真,并与试验结果进行对比分析。
2 理论分析 2.1 复合材料力学参数预测—半经验公式半经验公式[14]用材料力学的方法求解并引入了修正系数,在计算复合材料材料宏观力学性能参数时误差较小,且半经验公式计算复合材料的宏观力学性能参数的结果较符合实际[7]。连续纤维增强复合材料轴结构试验件为纤维缠绕成型,复合材料的每一层可认为无维铺层(也成单向铺层)构成的层和结构,适用于半经验公式。下面是以单向复合材料为例预测复合材料宏观力学性能参数,1为纤维主方向,2是与纤维垂直的方向,m代表基体,f代表纤维,V为体积分数,E为杨氏模量,G为剪切模量,γ为泊松比。简化模型后所得公式为
| ${E_1} = {E_{{\rm{f}}1}}{V_{\rm{f}}} + {E_{\rm{m}}}{V_{\rm{m}}}$ | (1) |
| ${E_2} = \frac{{{E_{\rm{f}}}{E_{\rm{m}}}\left( {{V_{\rm{f}}} + {h_2}{V_{\rm{m}}}} \right)}}{{{V_{\rm{f}}}{E_{\rm{m}}} + {h_2}{V_{\rm{m}}}{E_{{\rm{f}}2}}}}$ | (2) |
式中
| ${G_{12}} = \frac{{{G_{{\rm{f}}12}}{G_{\rm{m}}}\left( {{V_{\rm{f}}} + {h_{12}}{V_{\rm{m}}}} \right)}}{{{V_{\rm{f}}}{G_{\rm{m}}} + {h_{12}}{V_{\rm{m}}}{G_{{\rm{f}}12}}}}$ | (3) |
式中
| ${G_{23}} = \frac{{{G_{{\rm{f}}23}}{G_{\rm{m}}}\left( {{V_{\rm{f}}} + {\eta _{23}}{V_{\rm{m}}}} \right)}}{{{V_{\rm{f}}}{G_{\rm{m}}} + {\eta _{23}}{V_{\rm{m}}}{G_{{\rm{f}}23}}}}$ | (4) |
式中
| ${\gamma _{21}} = {\gamma _{{\rm{f}}21}}{V_{\rm{f}}} + {\gamma _{\rm{m}}}{V_{\rm{m}}}$ | (5) |
| ${\gamma _{23}} = k\left( {{\gamma _{{\rm{f}}23}}{V_{\rm{f}}} + {\gamma _{\rm{m}}}{V_{\rm{m}}}} \right)$ | (6) |
式中
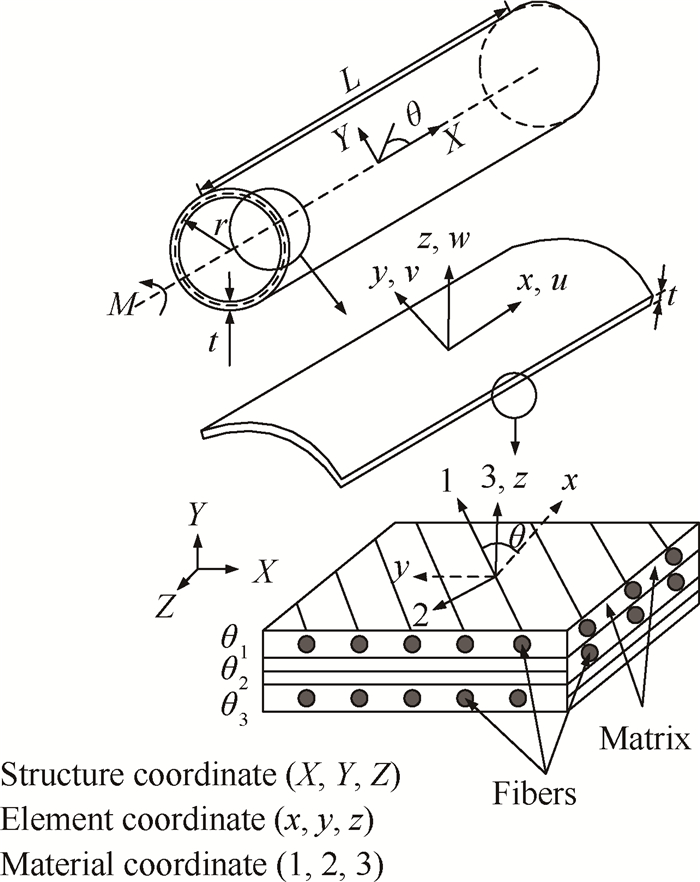
采用缠绕工艺的成型件也可以看作是一种层合结构件[4],纤维缠绕复合材料轴结构力学分析时,各个单层在整体坐标系的受力为σx,σz,τxz, 1为纤维主方向,2是与纤维垂直的方向,纤维与整体坐标系之间的夹角为θ,如图 1所示; 利用任意坐标系下单层板的应力转换关系,可以将σx,σz,τxz转换为纤维主轴方向上的应力σ1,σ2,τ12,详见式(7)。
|
Fig. 1 Relationship between fiber main shaft and structure of coordinate system[8] |
单层板材料任意坐标系下应力转换关系[8]
| $\left[{\begin{array}{*{20}{l}} {{\sigma _x}}\\ {{\sigma _z}}\\ {{\tau _{xz}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{m^2}}&{{n^2}}&{-2mn}\\ {{n^2}}&{{m^2}}&{2mn}\\ {mn}&{-mn}&{{m^2}-{n^2}} \end{array}} \right]\left[{\begin{array}{*{20}{l}} {{\sigma _1}}\\ {{\sigma _2}}\\ {{\tau _{12}}} \end{array}} \right]$ | (7) |
式中m=cosθ,n=sinθ。
对于纤维增强层状复合材料,材料坐标系下,单层材料单元节点应力应变关系可以表示为
| $\left\{ {\sigma '} \right\} = \left[{\mathit{\boldsymbol{Q}}{'_1}} \right]\left\{ {\varepsilon '} \right\}$ | (8) |
| $\left\{ {\tau '} \right\} = \left[{\mathit{\boldsymbol{Q}}{'_2}} \right]\left\{ {\gamma '} \right\}$ | (9) |
| $\left[{\mathit{\boldsymbol{Q}}{'_1}} \right] = \left[{\begin{array}{*{20}{c}} {\frac{{{E_{11}}}}{{1-{\nu _{12}}{\nu _{21}}}}}&{\frac{{{\nu _{12}}{E_{22}}}}{{1-{\nu _{12}}{\nu _{21}}}}}&0\\ {\frac{{{\nu _{21}}{E_{11}}}}{{1-{\nu _{12}}{\nu _{21}}}}}&{\frac{{{E_{22}}}}{{1 - {\nu _{12}}{\nu _{21}}}}}&0\\ 0&0&{{G_{12}}} \end{array}} \right]$ | (10) |
| $\left[{\mathit{\boldsymbol{Q}}{'_2}} \right] = \left[{\begin{array}{*{20}{c}} {{\alpha _1}{G_{13}}}&0\\ 0&{{\alpha _2}{G_{23}}} \end{array}} \right]$ | (11) |
α1和α2是剪切修正因子,假设单向弯曲的层合板沿厚度方向的横向剪切能相等。单元坐标系下层合板的本构方程为
| $\left\{ \sigma \right\} = \left[{{\mathit{\boldsymbol{Q}}_1}} \right]\left\{ \varepsilon \right\}$ | (12) |
| $\left[{{\mathit{\boldsymbol{Q}}_1}} \right] = {\left[{{\mathit{\boldsymbol{T}}_1}} \right]^{\rm{T}}}\left[{\mathit{\boldsymbol{Q}}{'_1}} \right]\left[{{\mathit{\boldsymbol{T}}_1}} \right]$ | (13) |
| $\left\{ \tau \right\} = \left[{{\mathit{\boldsymbol{Q}}_2}} \right]\left\{ \gamma \right\}$ | (14) |
| $\left[{{\mathit{\boldsymbol{Q}}_2}} \right] = {\left[{{\mathit{\boldsymbol{T}}_2}} \right]^{\rm{T}}}\left[{\mathit{\boldsymbol{Q}}{'_2}} \right]\left[{{\mathit{\boldsymbol{T}}_2}} \right]$ | (15) |
| $\left[{{\mathit{\boldsymbol{T}}_1}} \right] = \left[{\begin{array}{*{20}{c}} {{\rm{co}}{{\rm{s}}^2}\theta }&{{\rm{si}}{{\rm{n}}^2}\theta }&{{\rm{sin}}\theta {\rm{cos}}\theta }\\ {{\rm{si}}{{\rm{n}}^2}\theta }&{{\rm{co}}{{\rm{s}}^2}\theta }&{-{\rm{sin}}\theta {\rm{cos}}\theta }\\ {-2{\rm{sin}}\theta {\rm{cos}}\theta }&{2{\rm{sin}}\theta {\rm{cos}}\theta }&{{\rm{co}}{{\rm{s}}^2}\theta-{\rm{si}}{{\rm{n}}^2}\theta } \end{array}} \right]$ | (16) |
| $\left[{{\mathit{\boldsymbol{T}}_2}} \right] = \left[{\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{{\rm{sin}}\theta }\\ {-{\rm{sin}}\theta }&{{\rm{cos}}\theta } \end{array}} \right]$ | (17) |
在单元坐标系下,x,y和z轴分别代表圆柱壳的长度方向、圆周方向和径向。铺层数为n时,合应力可以定义为
| $\left\{ {\begin{array}{*{20}{l}} {\left\{ N \right\}}\\ {\left\{ M \right\}}\\ {\left\{ V \right\}} \end{array}} \right\} = \int_{ - t/2}^{t/2} {\left\{ {\begin{array}{*{20}{l}} {\left\{ \sigma \right\}}\\ {z\left\{ \sigma \right\}}\\ {\left\{ \tau \right\}} \end{array}} \right\}} {\rm{d}}z = \\ \sum\limits_{j = 1}^n {\left[ {\begin{array}{*{20}{c}} {\left( {{z_{j{\rm{t}}}} - {z_{j{\rm{b}}}}} \right)\left[ {{\mathit{\boldsymbol{Q}}_1}} \right]}&{\frac{1}{2}\left( {z_{j{\rm{t}}}^2 - z_{j{\rm{b}}}^2} \right)\left[ {{\mathit{\boldsymbol{Q}}_1}} \right]}&{\left[ {\bf{0}} \right]}\\ {\frac{1}{2}\left( {z_{j{\rm{t}}}^2 - z_{j{\rm{b}}}^2} \right)\left[ {{\mathit{\boldsymbol{Q}}_1}} \right]}&{\frac{1}{3}\left( {z_{j{\rm{t}}}^3 - z_{j{\rm{b}}}^3} \right)\left[ {{\mathit{\boldsymbol{Q}}_1}} \right]}&{}\\ {{{\left[ {\bf{0}} \right]}^{\rm{T}}}}&{{{\left[ {\bf{0}} \right]}^{\rm{T}}}}&{\left( {{z_{j{\rm{t}}}} - {z_{j{\rm{b}}}}} \right)\left[ {{\mathit{\boldsymbol{Q}}_2}} \right]} \end{array}} \right]} \left\{ {\begin{array}{*{20}{l}} {\left\{ {{\varepsilon _0}} \right\}}\\ {\left\{ k \right\}}\\ \gamma \end{array}} \right\}$ | (18) |
式中zjt和zjb分别代表第j层的中面距整个部分的顶层和底层的距离。
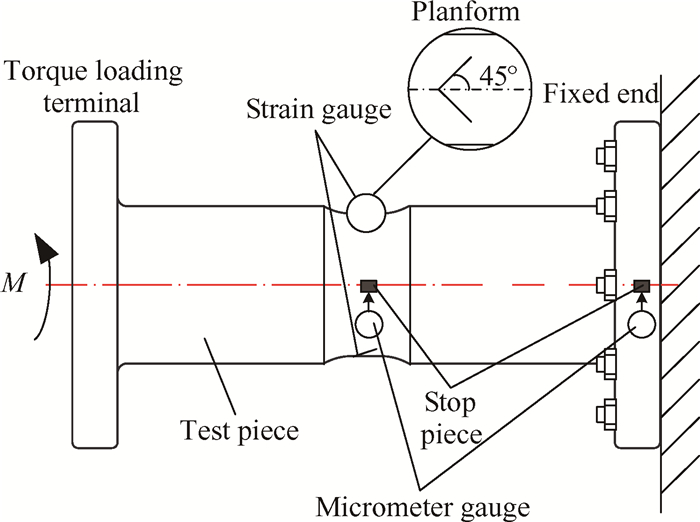
3 复合材料轴结构力学性能计算与试验验证 3.1 复合材料轴结构扭转试验简介为了对复合材料轴结构力学性能进行预测分析,对复合材料轴结构进行了常温扭转载荷作用力学性能试验与承载能力试验。复合材料轴结构扭转试验现场图如图 2所示,数据测量位置图如图 3所示。试验件一端用螺栓固定,另一端用螺栓与扭转作动筒相连,进行扭矩加载M。在施加扭转载荷的过程中,通过千分表测量复合材料轴结构中间截面绝对周向位移响应。通过图 3中应变片(与轴向成45°)进行扭转应变响应测量。

|
Fig. 2 Test site plan |
|
Fig. 3 Data measurement location map |
加载及测量要求:
(1) 试验载荷加载误差≤±2%。
(2) 应变测量设备误差≤1%,应变片测量误差≤3%。
(3) 进行刚度试验时,应分级加载(载荷谱为1,2,3,4,5kN·m),同时测量试验件周向位移及应变,载荷达最大值并完成测量后卸载。每个试验件重复至少3次,取平均值作为测量结果。
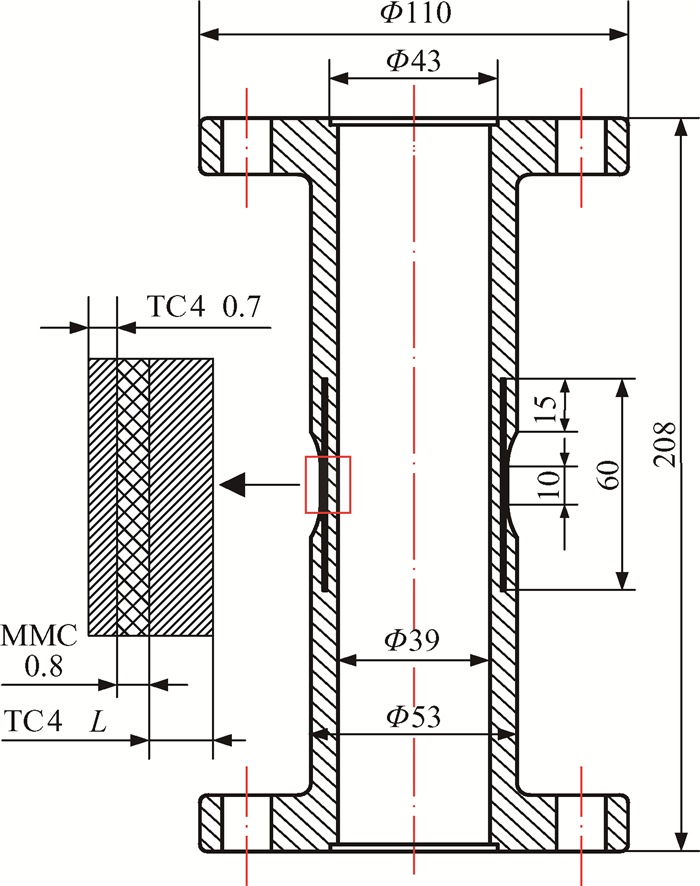
3.2 试验件及有限元模型建立复合材料轴结构扭转试验中,试验件采用纤维体积分数为43%纤维缠绕成型,其中纤维直径为100μm。轴结构试验件如图 4所示,复合材料轴段沿轴向长度为60mm,内外两层是金属(TC4),中间为复合材料层(SiC/TC4),铺层方式为:从内到外2~7层[45°,-45°,45°,-45°,45°,-45°],厚度为0.8mm,轴中间试验段长度为10mm,试验段总厚度为4.5mm。TC4金属材料和SiC纤维参数如表 1所示,其中E为弹性模量,ν为泊松比。
|
Fig. 4 Dimensions of the shafts(mm) |
|
|
Table 1 Material parameters of validation model |
根据半经验公式计算得出,SiC/TC4复合材料力学性能参数如表 2所示,其中E为弹性模量,ν为泊松比,G为剪切模量。1为纤维方向,2,3为垂直纤维的横向。
|
|
Table 2 Material parameters of SiC/TC4 |
根据轴结构试验件尺寸建立复合材料轴结构计算模型。为了简化计算,计算模型将法兰部分去除,利用Shell181单元指定复合材料每层纤维的方向、厚度与材料等属性,并同过分段操作设置最外层金属厚度来模拟试验件收缩部分,其中金属层铺层方向为任意方向。试验在常温环境下进行,仿真模型模拟试验实际工况,试验件法兰盘一端固定,试验件另一端施加载荷。在施加载荷时,将载荷加载在加载端的等效节点上。简化后模型网格划分后如图 5所示。

|
Fig. 5 Finite element modal of SiC/ TC4 composite shaft |
基于上述复合材料轴结构计算模型,计算在扭转载荷作用下复合材料轴结构试验件的响应情况及承载能力。扭矩载荷作用下,在一定的约束条件下施加阶梯扭矩载荷,载荷分别为1,2,3,4,5kN·m,分别计算不同扭矩载荷作用下的响应。通过对计算模型进行有限元计算,得到试验件危险位置应力云图,危险位置如图 6所示。

|
Fig. 6 Stress diagram of the composit shaft |
通过危险位置云图可以看出,试验件危险位置为其中间截面处,故提取计算模型中间截面位置处所有节点的应变及位移结果,并对其取平均值,与实验结果进行对比,对比数据如表 3,表 4及图 7,图 8所示。
|
|
Table 3 Strain of experimental value compared with predicted results |
|
|
表 4 Circumferential displacement of experimental value compared with predicted results(mm) |

|
Fig. 7 Strain of experimental value compared with predicted results |
|
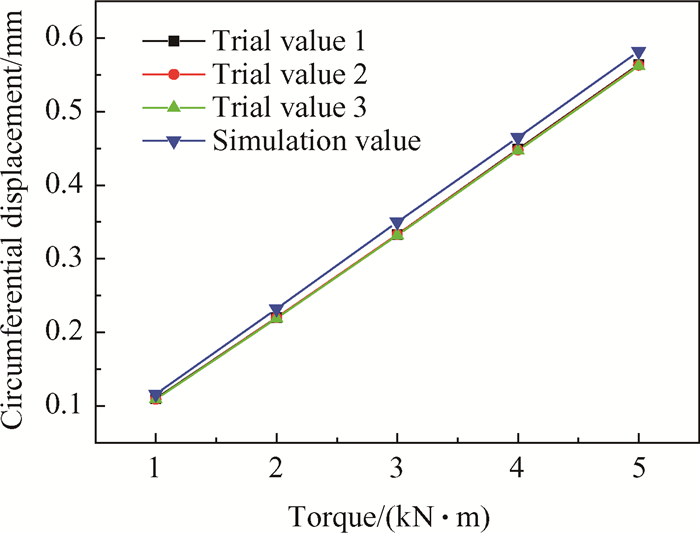
Fig. 8 Circumferential displacement of experimental value compared with predicted results |
从表 3与图 7可以看出,在扭转载荷下,复合材料轴结构应变响应试验值与仿真计算结果都随扭转荷载线性增加,说明试验件与计算模型在0~5kN·m载荷范围仍处于弹性阶段,且仿真值与试验值误差最大为5.7%左右,试验结果与仿真计算结果始终保持较高吻合度。
从表 4与图 8可以看出,仿真计算中间截面周向位移响应与试验结果位移数据都随载荷线性变化,也同样说明试验件与计算模型都在弹性阶段,最大误差控制在3.4%以内,仿真计算周向位移与试验数据吻合良好。
综上所述,所建立的仿真计算模型可以作为试验件弹性阶段仿真模型。
3.4 轴结构承载能力试验验证通过查阅《航空发动机材料手册》及中科院金属所提供的材料参数,可以得到进数轴的强度极限和复合材料单层强度极限,分别为980MPa与1800MPa。根据层合轴本构关系,将SiC/TC4复合材料层应力转化为沿纤维方向1向,垂直纤维方向2向及切向,对应应力为σ1,σ2,τ12。通过仿真计算得到复材料危险层纤维方向应力与外金属包套等效应力,结果如表 5及图 9所示,其中SEQV为等效应力。
|
|
Table 5 Strength of experimental value compared with predicted results |

|
Fig. 9 Predicted results of strength |
从表 5与图 9可以看到,当轴结构扭转载荷在9.0~9.5kN·m时,最外层TC4金属层等效应力达到975MPa,已经达到TC4金属材料强度极限980MPa,材料处于局部变形阶段。复合材料危险层在扭矩为9.2~9.4kN·m时,复合材料危险层纤维方向应力为1795~1893MPa,恰好将复合材料纤维方向层强度1800MPa包含在其范围内,说明复合材料层会在此载荷范围内达到其强度极限,与试验破坏载荷9402MPa比较接近,误差在3%以内。同时也说明此模型能适用于复合材料轴强度预测。
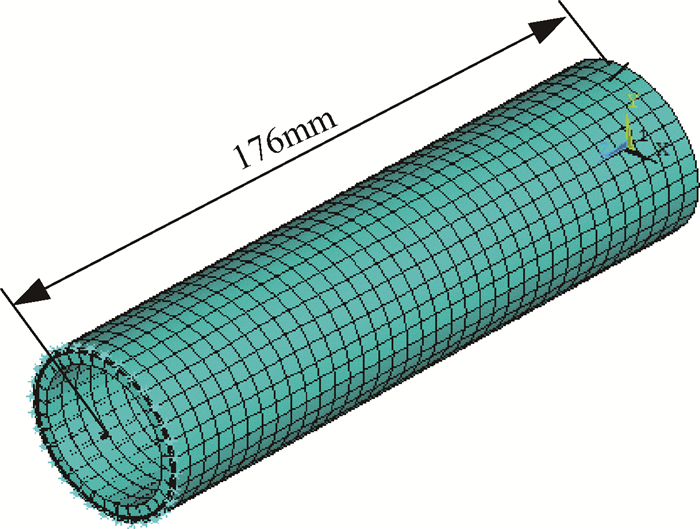
4 复合材料轴结构力学性能分析本节将研究扭转载荷作用下,铺层方案对全铺层复合材料轴结构中间截面力学性能的影响规律[15~18]。首先,对上述实验模型进行进一步简化为:总厚度为4.5mm,长度为176mm,内径为19.5mm,沿轴向都进行了复合材料铺设,复合材料铺层层数为6层,复合材料层被金属层包裹,有限元模型如图 10所示。该模型同样采用Shell181单元进行建模,一端固定,另一端施加扭矩载荷。简化后的轴结构进行结构有限元分析,在上一节验证的基础上,总结铺层角度及复合材料层位置对复合材料轴结构中间截面[11]应力、应变与复合材料轴结构扭转刚度的影响规律。
|
Fig. 10 Finite element modal of SiC/ TC4 composite shaft |
复合材料轴结构与试验件相同铺层数(6层),分析复合材料轴结构在5kN·m载荷作用下,铺层角度对复合材料轴结构中间截面力学性能影响规律。
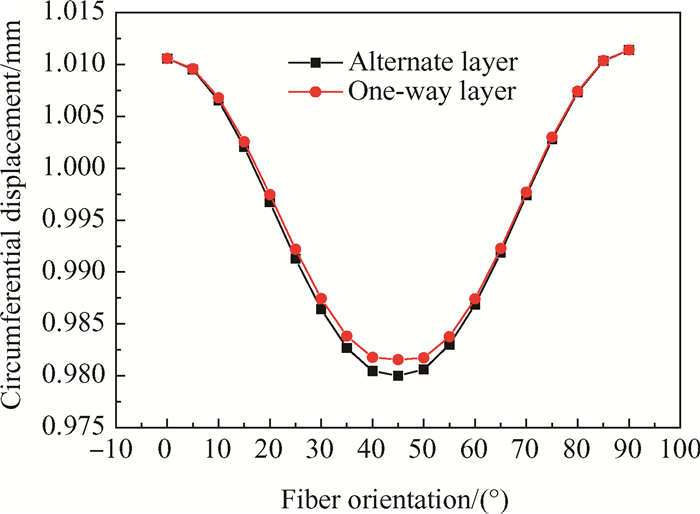
通过图 11周向位移随铺层角度的变化关系可以看出,在内外金属层厚度不变,只改变铺层角度与方式的情况下,提取轴结构中间截面表面处周向位移,发现正负交替铺层相对于单一方向铺层更有利于提高轴结构扭转刚度,并且45°铺层时周向位移最小,扭转刚度最大。
|
Fig. 11 Influence on the circumferential displacement of the composite shaft structure with different angles of layer |
在总厚度4.5mm与铺层数量不变的情况下,复合材料铺层方式为[45°/-45°]3,复材层距离内径表面的距离L(图 4)为0.5~3.2mm变化时,周向位移变化规律。
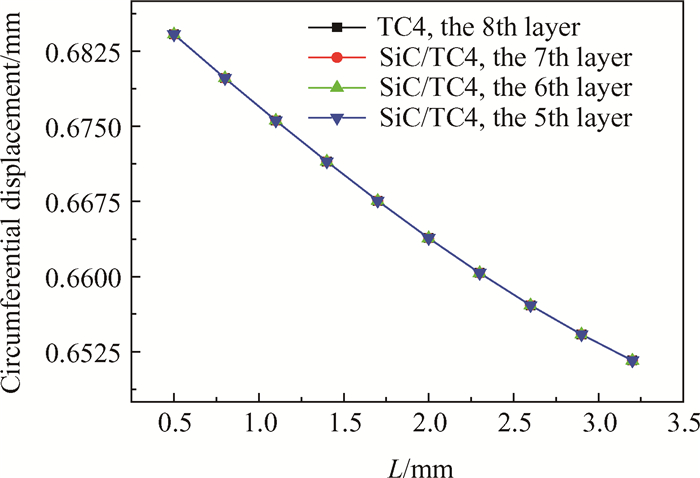
从图 12周向位移随距离L的变化关系可以看出,在5kN·m载荷作用下,随着SiC/TC4层向外推移,复合材料轴的中间截面位移持续减小。当SiC/TC4层(0.8mm复合材料层)距离复合材料轴内径表面距离L为2mm左右时,复合材料轴结构中间截面外表面周向位移减小速度放缓且随着距离增加减小速度越来越小。随着SiC/TC4层距离轴结构内径表面距离L的增加周向位移增加,SiC/TC4层第5层、第6层、第7层与金属层第8层位移数值大小几乎相同,没有随着层数不同而变化。分析原因为扭转载荷作用下,复合材料轴结构中不管SiC/TC4复合材料层位置如何变化,SiC/TC4复合材料层始终为其主要承力部分且复合材料轴结构金属层厚度在3.7mm以内,故复合材料轴结构周向位移反应主要为第7层(SiC/TC4)的周向位移。
|
Fig. 12 Influence on the circumferential displacement of the composite shaft structure with the location of MMC |
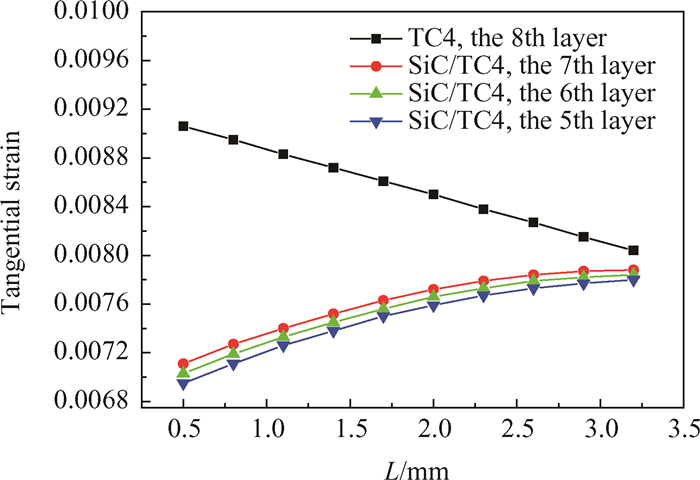
从图 13各层切应变随距离L的变化关系可以看出,在5kN·m扭转载荷作用下,随着SiC/TC4层向外推移,复合材料轴的中间截面位置处最外层金属层切应变线性减小,而复合材料层切应变逐渐增大,说明SiC/TC4层逐渐成为主要承力部分。另外SiC/TC4层距离复合材料轴内径表面距离L为2mm左右时,切应变增速放缓,说明复合材料层位于复合材料轴结构厚度的中间位置时,具有更高结构效率。
|
Fig. 13 Influence on the shear strain of the composite shaft structure with the location of MMC |
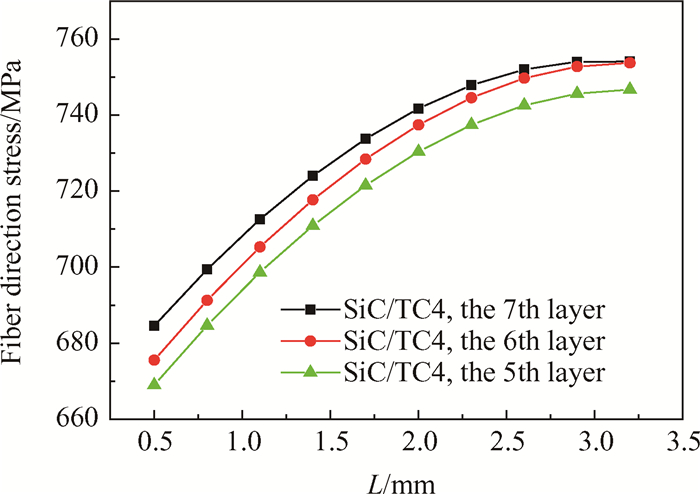
由图 14复材层各层纤维方向应力随距离L的变化关系可以看出,在5kN·m扭转载荷作用下,随着SiC/TC4层向外推移,复合材料轴结构中SiC/TC4层各层纤维方向受力逐渐增大,第7层纤维方向受力最大。且SiC/TC4层距离复合材料轴内径表面的距离L为1.5~2mm时,SiC/TC4层纤维方向受力增加速度放缓。
|
Fig. 14 Influence on the stress of the composite shaft structure with the location of MMC |
综上所述,总厚度不变复合材料轴结构在扭转载荷作用下,随着复合材料层距离复合材料轴结构内径距离L的增大,当轴结构复合材料层位于复合材料轴结构厚度的中间位置后,距离L继续增加时复合材料增强效率开始降低。从成本与收益关系对比发现,复合材料轴结构中复合材料层位于其厚度的中间位置时,具有较高的结构效率。
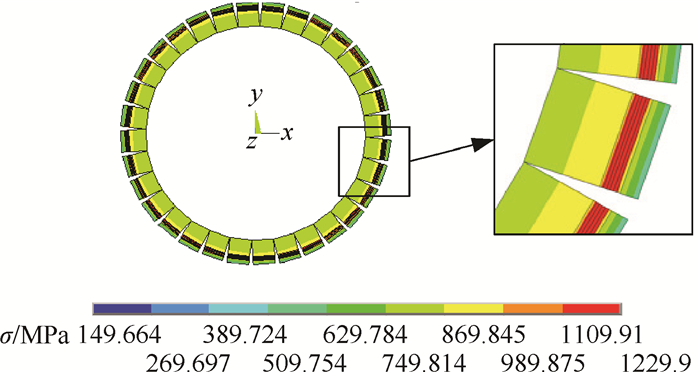
4.2 复合材料轴结构截面应力分析提取复合材料轴结构模型中间截面应力云图,如图 15所示,图中应力单位为MPa。从图 15可以看出,轴中间截面复材层应力大于内外金属层应力,复合材料层为此轴结构中主要承力部分。金属层应力越靠近复合材料,应力值越大。
|
Fig. 15 Section stress cloud diagram |
另一方面,由于金属刚度与强度远低于复合材料,可以预测随着载荷的增加,内外金属层与复合材料层交接面出容易出现失效,如图 16扭转断裂图。

|
Fig. 16 Torsional fracture diagram |
本文利用复合材料力学性能半经验公式、经典层合板理论及层合轴本构关系等相关理论方法,结合连续纤维增强复合材料轴结构试验,采用有限元法,对扭转载荷作用复合材料轴结构试验件力学性能进行了预测与对比验证,并对复合材料轴结构进行了力学性能分析。主要结论如下:
(1) 常温环境下,利用半经验公式对复合材料参数进行预测,并将材料参数带入与复合材料轴结构试验件相同的有限元模型中,进行位移与应变响应计算。通过与试验结果对比发现,仿真值与试验值总体误差在5.7%以内,说明利用半经验公式计算得出的复合材料性能参数可以较为真实反映复合材料力学性能,计算模型可靠。
(2) 正负交替铺层与单向铺层更有利提高轴结构扭转刚度,且±45°交替铺层最好。在扭转载荷作用下且复合材料轴结构总厚度不变的情况下,复材层位于复合材轴结构厚度中间位置时,复合材料轴结构效率最高。从危险位置截面应力分析结果可以看出,在扭转载荷作用下内外包套金属层与复合材料层交接面处容易出现失效。
致谢: 感谢中航产学研创新基金资助。
| [1] |
沙云东, 赵瑞霖, 贾秋月, 等. 纤维增强复合材料涡轮轴结构静强度计算与分析[J]. 机械设计与制造, 2017, 55(4): 197-201. DOI:10.3969/j.issn.1001-3997.2017.04.051 (  0) 0) |
| [2] |
梁春华. 连续纤维增强的金属基复合材料部件在航空涡扇发动机上的应用[J]. 航空制造技术, 2009, 52(15): 32-35. DOI:10.3969/j.issn.1671-833X.2009.15.001 (  0) 0) |
| [3] |
Avila A F. An Integrated Methodology and Formulations for Micro/Macro Modeling and Analysis of Metal Matrix Composites[J]. Novosibirsk State University, 1997, 5(1): 372-380.
(  0) 0) |
| [4] |
Quot A F Vila. Integrated Micro/Macro Approach for Laminate Composite Analysis: Applications to Turbine Blades[J]. AIAA Journal, 1971, 38(10): 1924-1930.
(  0) 0) |
| [5] |
Himmel N. Fatigue Life Prediction of Laminated Polymer Matrix Composites[J]. International Journal of Fatigue, 2002, 24(2): 349-360.
(  0) 0) |
| [6] |
Hyde T H, Punyong K, Becker A A. Experimental Failure Investigation for a Titanium Metal Matrix Composite with +45° and 45° Fibre Orientations[J]. Proceedings of the Institution of Mechanical Engineers Part L Journal of Materials Design & Applications, 2013, 229(1): 51-63.
(  0) 0) |
| [7] |
沙云东, 贾秋月, 骆丽, 等. 连续纤维增强金属基复合材料涡轮轴结构承扭特性分析[J]. 航空动力学报, 2016, 31(6): 1377-1384. (  0) 0) |
| [8] |
沙云东, 贾秋月, 骆丽, 等. 纤维增强复合材料轴结构铺层方案优化设计[J]. 航空动力学报, 2016, 31(12): 2933-2940. (  0) 0) |
| [9] |
沙云东, 骆丽, 贾秋月, 等. 复合材料轴结构力学性能预测及铺层方案设计[J]. 材料科学与工程学报, 2016, 34(2): 251-256. (  0) 0) |
| [10] |
沙云东, 陈祎航, 郝燕平, 等. 纤维增强复合材料涡轮轴结构疲劳寿命预测[J]. 航空动力学报, 2017, 32(4): 769-779. (  0) 0) |
| [11] |
孙庆伟, 陆山. 航空发动机复合材料主轴优化方案设计方法[J]. 复合材料学报, 2013, 30(6): 258-263. DOI:10.3969/j.issn.1000-3851.2013.06.038 (  0) 0) |
| [12] |
王婕, 陆山. 遗传与枚举混合算法对航空发动机复合材料主轴的优化设计[J]. 航空动力学报, 2015, 30(5): 1171-1177. (  0) 0) |
| [13] |
崔广群, 肖文刚, 王鹏飞. 碳纤维复合材料传动轴承扭性能研究[J]. 玻璃钢/复合材料, 2014, 44(7): 74-77. DOI:10.3969/j.issn.1003-0999.2014.07.016 (  0) 0) |
| [14] |
沃丁柱. 复合材料大全[M]. 北京: 化学工业出版社, 2000.
(  0) 0) |
| [15] |
胡晶, 李晓星, 张天敏, 等. 碳纤维复合材料传动轴承扭性能优化设计[J]. 复合材料学报, 2009, 26(6): 177-181. DOI:10.3321/j.issn:1000-3851.2009.06.030 (  0) 0) |
| [16] |
Shokrieh M M, Hasani A, Lessard L B. Shear Buckling of a Composite Drive Shaft Under Torsion[J]. AIAA Journal, 2007, 45(10): 2510-2519. DOI:10.2514/1.26351
(  0) 0) |
| [17] |
Zongjin Lu, Peter Blackmore. Cyclic Stress-Strain Behaviour of AM60B and AE44 Cast Magnesium Alloys and Its Impact on LCF Characterisation and Fatigue Analysis[J]. SAE International Journal of Materials and Manufacturing, 2014, 7(2): 446-453. DOI:10.4271/2014-01-0969
(  0) 0) |
| [18] |
Montagnier O, Hochard C. Optimisation of Hybrid High-Modulus/High-Strength Carbon Fibre Reinforced Plastic Composite Drive Shafts[J]. Materials & Design, 2013, 46(4): 88-100.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


