航空发动机属于高精密产品, 其零组件数量众多、结构复杂, 装配过程作为发动机制造过程的重要一环, 关键尺寸的装配(如叶尖间隙、转静子同轴度等)对发动机寿命和关键性指标(如推重比、耗油率等)有着重要的影响[1, 2]。而压气机转子系统作为其关键结构部件, 装配质量的优劣直接影响到发动机整机的性能及可靠性[3, 4]。现阶段在国内航空发动机领域, 发动机的装配及结构尺寸的公差设计多以早期的设计经验为主, 在实际整机装配过程中, 发动机必须进行反复的装配调试才能达到出厂要求, 这使得装配时间延长、一次装配成功率降低, 导致装配成本的增加[5]。
现阶段在公差设计及分析方面主要有极值法和统计公差法两大类方法[6]。极值法建立在零部件可以100%互换的基础上, 在求解过程中仅针对组成环的极大值和极小值进行求解, 没有考虑到组成环实际尺寸在设计公差带范围内的分布情况, 导致最终的封闭环尺寸值趋向于极端值, 使得组成环公差设计范围减小, 产品加工所要求的精密度提高, 造成加工成本的增加。统计公差法是依据组成环公差带尺寸分布特性进行封闭环和组成环公差分析的方法, 包括:(1)均方根法; (2)蒙特卡洛法; (3)卷积法; (4)Taguchi法[7, 8]。由于均方根法及卷积法在公差假设方面以及计算过程中存在明显的不足, 目前国内航空发动机装配主要采用蒙特卡洛法与Taguchi法[9]。蒙特卡洛法是在求解过程中将各个组成环的尺寸假设为某种分布, 通过随机抽取相应的尺寸样本进行试验求解封闭环尺寸, 由此为保证结果的精确度要求其抽样次数多、从而导致计算量大、计算过程比较复杂[10]。Taguchi法最大的优点就是在保证结果精确度的前提下, 尽量使用较少数量的正交试验, 降低其计算量, 并且在获得较为准确的装配成功率的基础上, 容易分析各个试验因素对于试验结果的影响大小。但其在各因素为正态分布假设的前提下, 计算所得响应函数的峰度值与假设正态分布的峰度值不符, 导致结果存在一定的误差, 并且计算复杂尺寸链的装配成功率时, 由于组成环数量众多, Taguchi法的计算量会呈指数量级的增加, 计算会更加复杂[11, 12]。
本文基于改进Taguchi法, 以航空发动机压气机级为实例, 对压气机轴向间隙进行封闭环公差分析与装配成功率的计算, 将各组成环作为正交试验的影响因素, 求解封闭环尺寸的前四阶矩, 通过求解装配响应函数的分布计算压气机一次装配成功率, 其结果分别与Taguchi法、蒙特卡洛法进行对比分析, 确定改进Taguchi法在装配成功率计算中的准确性及简单性。利用极差法对于各个组成环进行影响分析, 确定各组成环三水平因素对于装配间隙的影响大小, 获得改进Taguchi法中组成环的最优组合, 在保证压气机装配成功率的前提下, 为降低总装配成本提供了理论指导。
2 计算方法 2.1 改进Taguchi法传统Taguchi法是利用正交表挑选试验和安排试验, 通过模拟试验获取结果并对结果加以分析的过程。其优点是通过最少的试验次数得到设计参数的最优组合[13, 14]。由于Taguchi法在正交实验过程中考虑了组成环在公差带范围内的分布特性, 因此其实验结果分布较为均衡分散, 保证了试验结果较好的准确性。基本步骤是根据因素三水平准则, 假设每组组成环公差成正态分布, 且每组组成环的中高低三水平分别为
一阶原点矩
| $ {m_1} = \sum\limits_1^N {{Y_i}/N} $ | (1) |
二阶中心矩
| ${m_2} = \sum\limits_1^N {{{\left( {{Y_i} - {m_1}} \right)}^2}/N} $ | (2) |
三阶中心矩
| ${m_3} = \sum\limits_1^N {{{\left( {{Y_i} - {m_1}} \right)}^3}/N} $ | (3) |
四阶中心矩
| ${m_4} = \sum\limits_1^N {{{\left( {{Y_i} - {m_1}} \right)}^4}/N} $ | (4) |
并且其相对应的统计系数分别为
均值
| $\mu = {m_1}$ | (5) |
方差
| ${\sigma ^2} = {m_2}$ | (6) |
偏度
| $\sqrt {{\beta _1}} = {m_3}/{\left( {{m_2}} \right)^{1.5}}$ | (7) |
峰度
| ${\beta _2} = {m_4}/{\left( {{m_2}} \right)^2}$ | (8) |
在三点离散时Taguchi试验法计算得到的偏度
相应的响应函数前四阶矩分别修正为
一阶矩
| ${m_1} = \sum\limits_1^N {{\omega _i}{Y_i}} $ | (9) |
二阶矩
| ${m_2} = \sum\limits_1^N {{\omega _i}} {\left( {{Y_i} - {m_1}} \right)^2}$ | (10) |
三阶矩
| ${m_3} = \sum\limits_1^N {{\omega _i}} {\left( {{Y_i} - {m_1}} \right)^3}$ | (11) |
四阶矩
| ${m_4} = \sum\limits_1^N {{\omega _i}} {\left( {{Y_i} - {m_1}} \right)^4}$ | (12) |
式中ωi为正交试验组合中相应组成环影响因素对应水平的权重乘积。
在计算复杂尺寸链(如压气机、涡轮整体轴向装配间隙)的装配成功率时, 由于组成环众多, 改进Taguchi法和Taguchi法一样, 其计算量会呈指数量级的增加, 计算会更加复杂, 由于为保证装配的有效性, 航空发动机一般采取单元体设计理念, 在装配及设计过程中, 通常将发动机划分成相对独立装配的组件或构件, 并且在装配过程中要求其具有独立性和完全互换性, 由此提出分步正交Taguchi法的概念, 在改进Taguchi法的理论基础上, 基于发动机装配单元体化的思想, 在计算复杂尺寸链时采用分步正交的方法, 在保证装配成功率精度的前提下极大地降低了计算量。
2.2 Pearson分布理论Pearson分布由下面微分方程定义
| $\frac{{{\rm{d}}p\left( x \right)}}{{{\rm{d}}x}} = - \frac{{\left( {a + x} \right)p\left( x \right)}}{{{c_0} + {c_1}x + {c_2}{x^2}}}$ | (13) |
式中p(x)为概率密度函数, 其中a, c0, c1, c2为相应的分布参数, 它们是概率密度函数前四阶矩的函数。因此只需要得到正交试验的前四阶矩, 便可以根据Pearson微分方程(13)解得概率密度函数[17]。在利用改进Taguchi法获得装配响应函数的前四阶矩后, 可以根据Pearson理论求出装配响应函数的分布类型及其概率密度函数, 进而根据装配成功率计算公式, 求出总体响应函数的一次装配成功率。
2.3 极差分析法试验结果分析是正交试验方法的一个很重要的步骤。分析的目的是要分清各因素对指标影响的主次, 在保证压气机一次装配成功率的前提下, 根据各因素对于轴向间隙的影响来调整组成环的公差带, 进而降低总装配成本。正交试验结果分析包括方差分析法和极差法, 其中极差法就是确定出各因素的低、中、高水平对试验指标影响的主次关系, 并且筛选出试验指标的影响因素最佳方案。同时为直观展示响应函数随不同因素的变化规律, 绘制相应的水平趋势图[18~20]。
极差分析法主要包括计算与分析两部分, 相应的分析流程如图 1所示。

|
Fig. 1 Flow chart of extreme difference analysis |
其中Kjm为因素j下所对应的m水平试验指标和,
| $\begin{array}{*{20}{l}} {{R_j} = }\\ {{\rm{max}}\left( {\overline {{K_{j1}}}, \overline {{K_{j2}}}, \ldots, \overline {{K_{jm}}} } \right) - {\rm{min}}\left( {\overline {{K_{j1}}}, \overline {{K_{j2}}}, ..., \overline {{K_{jm}}} } \right)} \end{array}$ | (14) |
极差值Rj反映了第j列水平因素变动时, 实验指标的变动幅度。Rj越大说明该因素对实验指标的影响越大, 因此也就越重要[21]。
2.4 装配成功率计算模型装配成功率是指封闭环尺寸处于设计公差带范围之内的概率[22]。其中装配成功率ρ计算如下
| $\rho = \int\limits_{x \in R} {{f_x}} \left( X \right){\rm{d}}X$ | (15) |
式中x为各组成环的尺寸矢量; R为公差带宽。
本文分别采用改进Taguchi法和蒙特卡洛法计算压气机轴向间隙的装配成功率。装配成功率计算公式分别为:
(1) 改进Taguchi法装配成功率计算公式
| $P = {P_{\rm{r}}}\left( {{Y_{{\rm{min}}}} \le Y \le {Y_{{\rm{max}}}}} \right) = \int_{{Y_{{\rm{min}}}}}^{{Y_{{\rm{max}}}}} {{f_y}} \left( Y \right){\rm{d}}Y$ | (16) |
式中Ymax, Ymin分别为轴向间隙的所允许的最大值、最小值, fy(Y)为装配响应概率密度函数。
(2) 蒙特卡洛抽样求解装配成功率计算公式
| $P = {P_{\rm{r}}}\left( {{Y_{{\rm{min}}}} \le Y \le {Y_{{\rm{max}}}}} \right) = \frac{{{N_0}}}{{{N_{{\rm{total}}}}}} \times 100\% $ | (17) |
式中N0为由组成环样本计算得到的封闭环尺寸落在Ymax, Ymin之间的个数, Ntotal为总的模拟次数。
本文以航空发动机压气机为例, 基于改进Taguchi法, 依据设计准则简化压气机级装配模型, 选取整流叶片、动叶、可调静子叶片及轴承等部位的典型公差带, 构建封闭环, 创建一维尺寸链模型, 为之后分析做好简化基础。
采用改进Taguchi法, 将组成环进行分组, 求解部分响应函数的前四阶矩, 根据Pearson理论判断部分响应函数的类型, 再以部分响应函数为组成环进行正交试验求解总体响应函数。比较分步正交Taguchi法、改进Taguchi法、Taguchi法与蒙特卡洛法所得分布函数的前四阶矩, 求解装配成功率, 判断改进Taguchi法在装配分析时的优劣。
利用极差法对于所求得的正交实验表进行分析, 求解出各组成环的极差值, 分析各组成环对总体装配响应函数的影响大小。
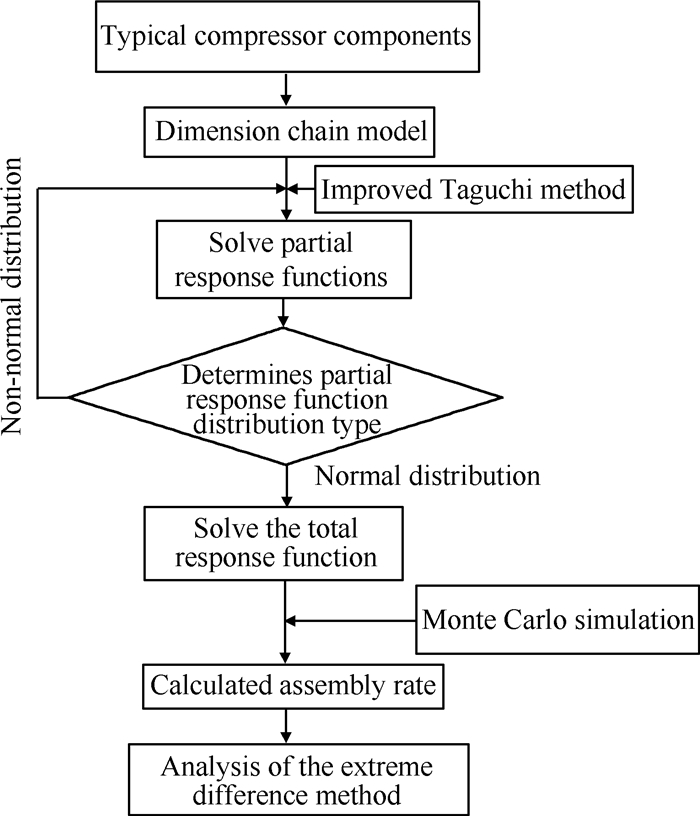
具体分析流程如图 2所示。
|
Fig. 2 Flow chart of compressor clearance analysis |
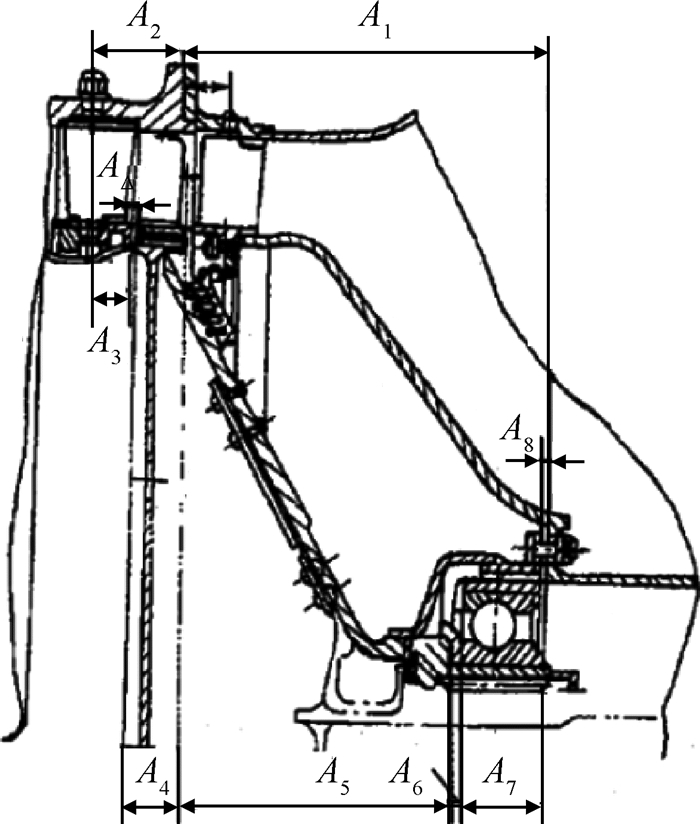
本文以航空发动机压气机组件为实例, 应用改进Taguchi法对压气机级轴向间隙的装配成功率进行计算。如图 3所示为某压气机的最后一级, A1为安装边到封严盘内环轴向安装边处距离, A2为前一级静叶轴线到安装边的距离, A3为前一级静叶轴线到静叶叶根后缘的距离, A4为动叶叶尖后缘到轴向安装边距离, A5为轴向安装边到甩油盘前侧距离, A6为甩油盘轴向厚度, A7为轴承外环右侧到内环轴向安装边处距离, A8为轴承外环右侧到内环轴向安装边距离。AΔ为封闭环轴向间隙, 该间隙与上述8个尺寸连接成封闭的尺寸组, 形成尺寸链, 其中
| $\begin{array}{l} {A_1} = {200^{ + 0.09}}{\rm{mm}}, \;{A_2} = \left( {48 \pm 0.2} \right){\rm{mm}}, \\ {A_3} = \left( {20.5 \pm 0.15} \right){\rm{mm}}, \;{A_4} = {28_{ - 0.28}}{\rm{mm}}, \\ {A_5} = \left( {152 \pm 0.1} \right){\rm{mm, }}\;{A_6} = {3.2_{ - 0.048}}{\rm{mm}}\\ {A_7} = {40^{ + 0.1}}{\rm{mm}}, \;{A_8} = {0.3_{ - 0.04}}{\rm{mm}} \end{array}$ |
|
Fig. 3 Chart of the compressor final stage |
在装配过程中要求给定间隙AΔ=3.6~3.9mm, 为装配成功。
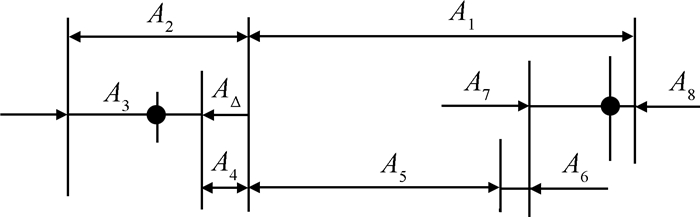
3.1 装配响应函数分析 3.1.1 部分装配响应函数求解首先依据设计准则简化压气机级装配模型, 得到一维尺寸链模型, 如图 4所示, 相应的组成环A1, A2分别为一维尺寸链增环, 组成环A3, A4, A5, A6, A7, A8分别为尺寸链减环。为便于计算, 将实例中仅存在上偏差或下偏差的组成环转化为相应的对称偏差分布。假设每个组成环尺寸在公差带范围内均服从正态分布, 则可以得到各组成环分布参数及传递比, 装配响应函数如式(18)所示[21]
| $f = {A_1} + {A_2} - {A_3} - {A_4} - {A_5} - {A_6} - {A_7} - {A_8}$ | (18) |
|
Fig. 4 Chart of simplified dimension chain model |
由于假设各个组成环在其尺寸公差范围内服从正态分布, 即尺寸的分散平均值与公差带中心一致。根据±3σ原则, 99.73%的组成环尺寸落在x±3σ范围之内, 即标准公差σ与公差带宽度T有以下关系[23]
| $6\sigma \le T$ | (19) |
式中σ为标准公差, T为公差带宽度。
根据改进Taguchi法, 各组成环低、中、高三水平因素权重分别为:1/6, 4/6, 1/6, 各组成环因素三水平分别为
|
|
Table 1 Low, medium, high levels table of constitute circles |
此实例中共存在8个装配组成环, 若直接采用改进Taguchi法进行正交试验, 则会产生6561正交样本, 样本量大、计算过程繁琐。由此采用分步正交Taguchi法的概念, 在改进Taguchi法的理论基础上, 基于发动机装配单元体化的思想, 计算尺寸链时采用分步正交的方法, 将组成环按照装配位置进行分组, 每组进行正交试验, 求得部分响应函数。
由此, 各个部分响应函数分别为:f1=A1+A2, f2=A4+A5+A6, f3=A7+A8。此时总体响应函数f为
| $f = {f_1} - {f_2} - {f_3} - {A_3}$ | (20) |
分别进行正交试验, 由于篇幅的限制本文只给出了部分响应函数f1的计算结果, 如表 2所示。
|
|
Table 2 Orthogonal test table of constitute circles A1 and A2 |
通过对正交试验表的分析, 根据式(1)~(4)分别求得三个部分响应函数f1, f2, f3的前四阶矩, 根据其四阶矩求得相应的统计系数(均值、方差值、峰度值及偏度值), 如表 3所示。
|
|
Table 3 Statistical coefficients of the partial response functions |
根据Pearson理论和表 3中的数据, 可知由改进Taguchi法求得的部分响应函数f1, f2, f3均服从正态分布, 因此可以继续使用改进Taguchi法求解封闭环的响应函数。
3.1.2 总体装配响应函数分析将部分装配响应函数f1, f2, f3和组成环A3作为总体响应函数f新的组成环, 重复上述求解的过程, 可得81个正交样本, 根据公式(1)~(8)求解出总体分布响应函数f的前四阶矩和相应的统计系数, 同时采用蒙特卡洛法对于装配响应函数进行抽样模拟试验, 模拟次数为1×105次, 计算得到分步正交Taguchi法、改进Taguchi法、Taguchi法、蒙特卡洛法的前四阶矩, 如表 4所示。
|
|
Table 4 Comparison table of statistical coefficients |
由表 4可知, 改进Taguchi法与Taguchi法相比其峰度误差由原先的12.46%降低到1.39%, 改进Taguchi法计算时所得的均值与蒙特卡洛抽样计算仅相差1.62×10-4, 方差误差为0.4787%, 可以看出改进Taguchi法较Taguchi法相比, 其结果与蒙特卡洛抽样更加接近, 更为准确。在保证精确度的前提下, 改进Taguchi法较蒙特卡洛法相比所需要的样本数量少、计算量小。而且在改进Taguchi法中, 分步正交Taguchi法计算的均值、方差与改进Taguchi法相差1.8867×10-5, 1.7724×10-5, 可以看出分步正交Taguchi法具有较高精度, 同时其样本数量大大减少, 计算量大幅度降低。
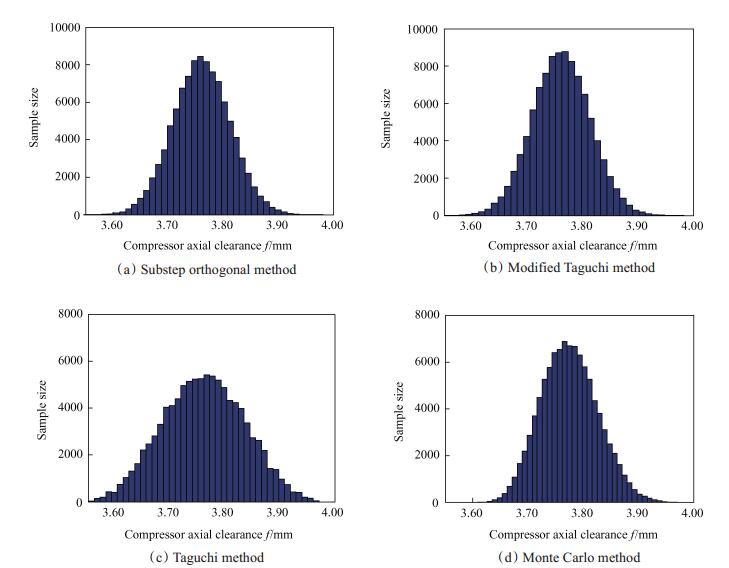
为直观表述四种统计方法所求得的总体响应函数的分布, 本文对分步正交Taguchi法、改进Taguchi法、Taguchi法、蒙特卡洛法进行抽样模拟, 如图 5所示。其中由图(b)与图(c)对比可知, 峰度值误差明显的影响了装配响应函数的分布, 进而影响到了装配成功率。由图(a)、图(b)、图(d)可知, 由于分步正交Taguchi法、改进Taguchi法及蒙特卡洛法计算所得的总体装配响应函数的前四阶矩和统计系数基本一致, 其装配间隙的分布基本一致, 装配成功率的计算精度相同。
|
Fig. 5 Clearance distribution map of four statistical methods |
根据Pearson分布理论可知, 总体分布响应函数f呈正态分布, 从而求解出改进Taguchi法的装配成功率P=Pr(3.6≤AΔ≤3.9)=99.6342%。由相应的蒙特卡洛法所得压气机一次装配成功率P=Pr(3.6≤AΔ≤3.9)=99.5520%, 可以看出, 两者计算的结果相差0.0822%, 再次验证了改进的Taguchi试验法的精确性和简便性。
3.3 各组成环对间隙因素的影响本文利用极差法对由组成环所得的正交试验表进行分析。其中Kij为各组成环第i个因素第j水平指标平均值, R为各组成环所对应的水平极差。
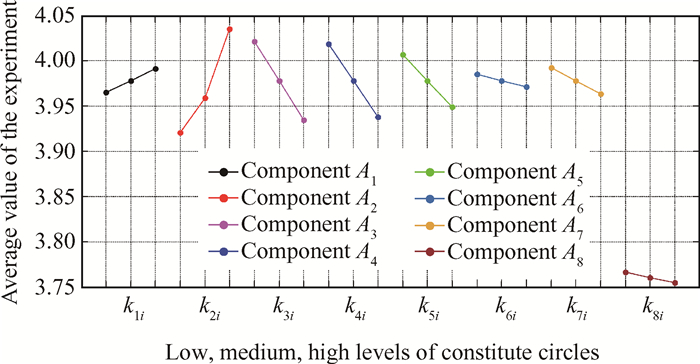
由表 5可知, 组成环A2所对应的极差值R最大, 其次是A3和A4的极差值也较大, 表明封闭环A2, A3和A4对于压气机的轴向间隙影响最为主要, 在压气机的实际装配过程中是关键尺寸, 需要重点进行公差范围的控制。A5, A7, A1, A6, A8对应的极差值R小, 是次要的影响因素。因此, 在实际装配及公差设计过程中需要对组成环A2, A3和A4的尺寸进行重点监控, 设计时尽量减小组成环A2, A3和A4的公差带, 使封闭环尺寸AΔ落在公差范围, 从而保证航空发动机压气机具有较高的装配成功率。图 6描述了各个组成环的低、中、高水平对于轴向间隙的影响趋势, Ki, j为第i个组成环的第j个水平因素的实验值, 由图可知, 根据各组成环的水平指标平均值, 轴向间隙影响因素的优水平分别为:K13, K23, K31, K41, K51, K61, K71, K81, 在改进Taguchi法正交实验中其优水平组合即为各组成环最优组合。
|
|
Table 5 Analysis result table of extreme difference analysis |
|
Fig. 6 Influence trend chart of constitute circles to the assembly clearance |
通过本文的研究与分析, 得到以下结论:
(1) 改进Taguchi法与Taguchi法相比较, 其峰度误差由原先的12.46%降低到1.39%, 其结果与蒙特卡洛法更加接近。
(2) 改进的Taguchi试验法与蒙特卡洛法相比较, 两者求解所得总体响应函数的均值及方差分别相差:1.62×10-4, 0.4787%, 根据装配成功率计算公式所求得的装配成功率相差0.0822%, 可知两者所求解精度基本相同, 而所需样本数量由105减少为6561。
(3) 分步正交Taguchi法计算的均值、方差与改进Taguchi法相差1.8867×10-5, 1.7724×10-5, 而样本数量由6561降低为126, 可知在使用改进Taguchi法时, 如果组成环较多则可以根据分步正交的思想, 采用分步正交Taguchi法在保证精确度的前提下, 可以大幅度减少计算量。
(4) 采用极差法对改进Taguchi法的试验结果进行了分析, 表明在压气机级组件的实际装配过程中, 通过加强对关键组成环尺寸A2, A3和A4的公差带范围控制而减小其它组成环尺寸因素A5, A7, A1, A6, A8的精度要求, 来保证压气机具有较高的装配成功率。
致谢: 感谢国家自然科学基金资助。
| [1] |
王晶.面向航空发动机数字化装配的公差分析技术研究[D].沈阳: 沈阳航空航天大学, 2011.
(  0) 0) |
| [2] |
桑潇潇, 廖明夫, 吴法勇, 等. 发动机轴承内环装配工艺对转子动力学特性影响的试验研究[J]. 推进技术, 2015, 36(12): 1874-1880. (SANG Xiao-xiao, LIAO Ming-fu, WU Fa-yong, et al. Experimental Study on Rotor-Dynamic Behavior Development on Aero-Engine Bearing Inner Ring Assembly Technologies[J]. Journal of Propulsion Technology, 2015, 36(12): 1874-1880.)
(  0) 0) |
| [3] |
邵锦文, 张振家, 袁宁, 等. 航空发动机涡轮叶尖间隙损失的统计设计[J]. 推进技术, 2003, 24(2): 122-124. (SHAO Jin-wen, ZHANG Zhen-jia, YUAN Ning, et al. Statical Design for Turbine Blades Tip Clearance Loss Analysis[J]. Journal of Propulsion Technology, 2003, 24(2): 122-124. DOI:10.3321/j.issn:1001-4055.2003.02.007)
(  0) 0) |
| [4] |
杨伟.轴流压气机叶片排间轴向间隙分析方法[C].成都: 中国航空学会动力分会叶轮机专业委员会学术会, 2003.
(  0) 0) |
| [5] |
陈渊博, 单福平. 公差分析在航空发动机设计中的应用研究[J]. 制造业自动化, 2017, 39(1): 69-75. DOI:10.3969/j.issn.1009-0134.2017.01.018 (  0) 0) |
| [6] |
王平, 沈晓阳. 公差分析中的统计公差方法综述[J]. 工具技术, 2008, 42(10): 43-47. DOI:10.3969/j.issn.1000-7008.2008.10.009 (  0) 0) |
| [7] |
仲昕, 杨汝清, 周兵. Accuracy Analysis of Assembly Success Rate with Monte Carlo Simulations[J]. Journal of Donghua University, 2003, 20(4): 128-131. DOI:10.3969/j.issn.1672-5220.2003.04.027 (  0) 0) |
| [8] |
费成巍, 白广忱, 范觉超, 等. 涡轮转子多尺寸装配可靠性优化分析[J]. 推进技术, 2013, 34(1): 15-18. (FEI Cheng-wei, BAI Guang-chen, FAN Jue-chao, et al. The Reliability Optimization Analysis of Turbine Rotor Multi-Dimension Assembly Reliability[J]. Journal of Propulsion Technology, 2013, 34(1): 15-18.)
(  0) 0) |
| [9] |
Chase K W, Parkinson A R. A Survey of Research in the Application of Tolerance Analysis to the Design of Mechanical Assemblies[J]. Research in Engineering Design, 1991, 3(1): 23-37.
(  0) 0) |
| [10] |
尹增谦, 管景峰, 张晓宏, 等. 蒙特卡罗方法及应用[J]. 物理与工程, 2002, 12(3): 45-49. DOI:10.3969/j.issn.1009-7104.2002.03.014 (  0) 0) |
| [11] |
D'Errico J R, Zaino N A. Statistical Tolerancing Using a Modification of Taguchi's Method[J]. Technometrics, 1988, 30(4): 397-405. DOI:10.1080/00401706.1988.10488434
(  0) 0) |
| [12] |
钱泽鹏, 于涛, 刘瑞红, 等. 基于Taguchi的公差尺寸链的优化设计[J]. 煤矿机械, 2011, 32(1): 122-124. DOI:10.3969/j.issn.1003-0794.2011.01.050 (  0) 0) |
| [13] |
曾凤章, 赵霞. 田口方法及其标准化设计[J]. 机械工业标准化与质量, 2003(11): 7-9. DOI:10.3969/j.issn.1007-6905.2003.11.004 (  0) 0) |
| [14] |
Chiang H L, Yang C B, Hsu C Y. Combining Taguchi Signal-to-Noise Ratio and Grey Relational Analysis into a Multi-Objective Optimal Model for Milling Inconel 718 Superalloy[J]. 中国机械工程学刊, 2016, 37(6): 625-633. (  0) 0) |
| [15] |
Seo H S, Kwak B M. Efficient Statistical Tolerance Analysis for General Distributions Using Three-Point Information[J]. International Journal of Production Research, 2002, 40(4): 931-944. DOI:10.1080/00207540110095709
(  0) 0) |
| [16] |
D'Errico J R, Zaino N A. Statistical Tolerancing Using a Modification of Taguchi's Method[J]. Technometrics, 1988, 30(4): 397-405. DOI:10.1080/00401706.1988.10488434
(  0) 0) |
| [17] |
陈志英, 刘勇, 周平, 等. 基于改进Taguchi方法的航空发动机装配成功率计算方法[J]. 推进技术, 2018, 39(3). (CHEN Zhi-ying, LIU Yong, ZHOU Ping, et al. Assembly Success Rate Calculation Method for Aero-Engine Based on Improved Taguchi Method[J]. Journal of Propulsion Technology, 2018, 39(3).)
(  0) 0) |
| [18] |
唐佳丽, 徐章韬. 正交试验中的极差分析与方差分析[J]. 中学数学, 2017(9): 31-34. (  0) 0) |
| [19] |
文泽军, 朱正强, 周知进, 等. 基于Taguchi正交试验的一维装配成功率计算方法及其应用[J]. 湖南科技大学学报(自然科学版), 2011, 26(3): 26-30. (  0) 0) |
| [20] |
王海宇. 飞机装配工艺学[M]. 西安: 西北工业大学出版社, 2013.
(  0) 0) |
| [21] |
王岩, 隋思涟, 王爱青. 数理统计与MATLAB工程数据分析[M]. 北京: 清华大学出版社, 2006.
(  0) 0) |
| [22] |
何勇, 方红芳. 装配成功率估算方法的研究[J]. 东华大学学报(自然科学版), 1998(1): 46-49. (  0) 0) |
| [23] |
蔡延波, 曹增强, 李志成. 复杂装配尺寸链的分析计算[J]. 现代制造工程, 2008(4): 81-84. DOI:10.3969/j.issn.1671-3133.2008.04.024 (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


