微型涡轮发动机(Micro Turbine Engine,MTE)具有重量轻、功率大、密度高等优点,可作为各种微小型导弹、无人机等飞行器的推进系统。离心压气机具有单级增压比高、稳定工作范围大、轴向长度小等优点,因此,目前国内外的微型涡轮发动机广泛采用离心式压气机[1, 2]。
受到强逆压梯度的影响,离心压气机内部容易发生大尺度的流动分离和二次流,并形成不同尺度的湍动涡结构,不仅造成机械能大幅度损失,严重时还会影响压气机的稳定工作范围,使得微型涡轮发动机的性能和工作安全性受到巨大影响[3]。许多研究者发现,不稳定的湍动涡结构对压气机的性能有重要影响[4~6],严重时会引起失速,尤其是受到泄漏流与主流剪切形成的泄漏涡结构。林峰等[7]发现压气机叶尖出现的自激(Self-induced)非定常现象与失速之间具有一定的联系。吴艳辉等[4]通过对压气机转子近失速下的非定常研究发现,泄漏涡在近失速工况下出现了泡式破碎。NASA格林研究中心的Hah等[8]研究发现,泄漏涡进入相邻叶片通道形成的低速区是引起离心压气机失速的主要原因。加拿大Vo等[9]提出了压气机失速准则,其主要判断依据和泄漏涡有密切关系。剑桥大学Hazby等[10]指出离心压气机的失速是和泄漏涡的破碎密切相关。
针对叶尖的特殊流场结构,研究人员提出了一些流动控制办法对其进行改善以提高压气机的稳定工作范围,如:机匣环向槽处理[11]、叶尖喷气[7, 12]、自循环机匣处理[13]等。尽管这些控制方法获得了一些较好的结果,但是缺乏共识,对其内在作用机理的认识还有所不足,因此,对不同型号的压气机进行处理时,得到的结论也有所差异。
对于离心式压气机转子来说,因为其流道长度相对平均叶高明显长于轴流压气机、叶尖泄漏流的积累影响较大,因此更有必要澄清叶尖泄漏流的特性,并加深对其影响压气机稳定性主要流动机理的认识。目前在这一方面的公开报道还较少,Bae[14]和李伟等[15]针对叶尖泄漏涡的不稳定性开展了机理研究,采用经验公式结合长波不稳定性理论,较好地预测了泄漏涡的频率,但其研究分别针对轴流叶栅和涡轮,且采用经验公式较为复杂,部分参数的选取对于不同的压气机有时难以预估,往往需要借助CFD或实验结果,在这种情况下难以做到一般化。本文对一台微型涡轮发动机的离心压气机进行了研究,探讨了离心压气机近失速工况下的流场特征,并采用面涡理论对泄漏涡进行建模,预测了泄漏涡的不稳定波动频率。
2 物理模型与计算方法压气机转子包含共10对大小叶片。进口叶片直径为59.5mm,出口叶片直径为98.5mm。进出口叶片高度分别为20mm和4.5mm,叶尖间隙尺寸为0.6mm,占进口叶高的3.0%。叶轮采用后弯式设计,设计点压比为2.94,流量为0.36kg/s,转速为80kr/min。
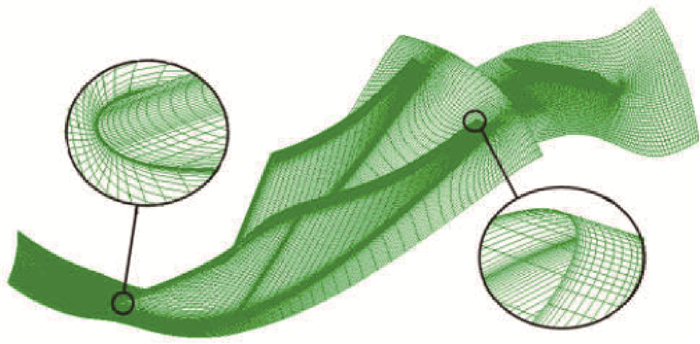
针对单叶片通道,采用AutoGrid 5进行自动网格生成,总网格数约为89万。叶片结构及其周围的网格如图 1所示。数值模拟采用NUMECA FINE求解圆柱坐标系下雷诺平均Navier-Stokes方程组,计算采用Spalart-Allmaras湍流模型。采用二阶中心差分有限体积将控制方程进行离散,并运用多重网格技术和隐式残差光顺技术加速收敛。转子通道与扩压器通道交接面采用周向混合平均法处理。在进行非定常数值模拟时,为排除转子与扩压器之间转静干涉对泄漏涡非定常性的影响,采用单转子通道进行模拟,时间步长取为1×10-5s。边界条件设置:进口给定总压为101.325kPa,总温为288K,固壁为绝热无滑移条件,出口给定静压,通过不断提高背压使得计算工况逐步逼近失速点,将计算发散时的前一个收敛工况作为近失速工况。
|
Fig. 1 Blade profile and simulation grid |
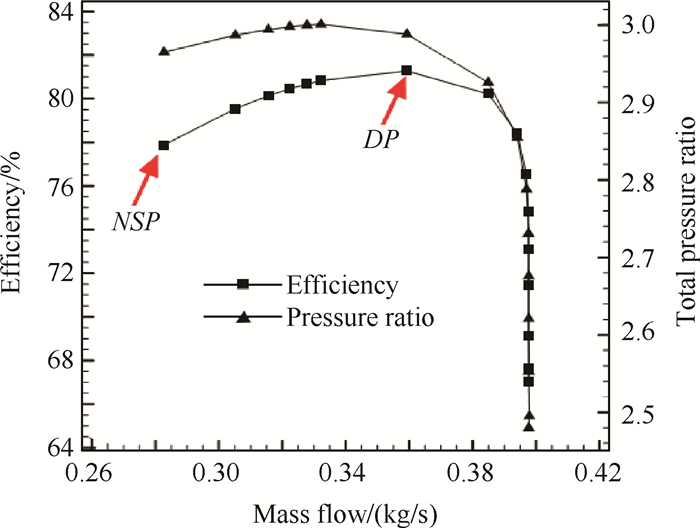
为分析近失速点的流场特征,选取设计点(Design point,DP)和近失速点(Near stall point,NSP)进行对比。压气机特性图及DP和NSP点的选取如图 2所示。
|
Fig. 2 Characteristic maps of compressors |
为了更好地观察和捕获涡结构,采用Q准则涡识别法[16],其表达式为
| $Q = \left( {\parallel \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}{\parallel ^2} - \parallel \mathit{\boldsymbol{S}}{\parallel ^2}} \right)/2$ | (1) |
式中
| ${H_{\rm{n}}} = \frac{{\mathit{\boldsymbol{\xi }} \cdot \mathit{\boldsymbol{w}}}}{{\left| \mathit{\boldsymbol{\xi }} \right| \cdot \left| \mathit{\boldsymbol{w}} \right|}}$ | (2) |
式中
|
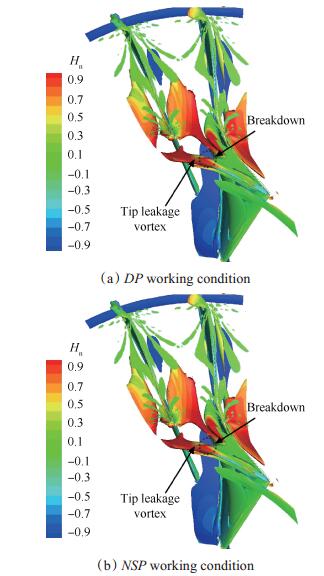
Fig. 3 Main vortex structure in compressor |
|
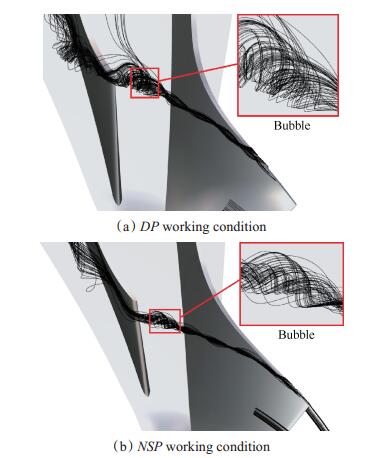
Fig. 4 Bubble structure of tip leakage vortex in compressor |
为分析泄漏涡对二次流的影响,将压气机内部通道分为两个区,将小叶片压力面和主叶片吸力面组成的通道记为通道Ⅰ,将小叶片吸力面和主叶片压力面组合的通道记为通道Ⅱ。
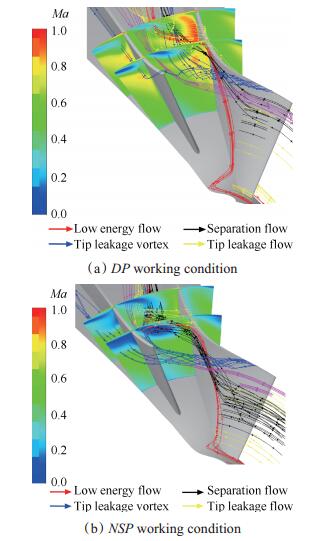
图 5为DP和NSP工况下通道Ⅰ的流场结构,可以看到在靠近机匣壁面附近,存在大范围的低速区,不同的流动结构汇入其中,主要包括部分泄漏涡、泄漏流、前缘分离流以及轮毂处的低能流。在DP工况下,这些流动结构更加贴近主叶片吸力面壁面,在通道Ⅰ中形成的低速区较小。而在NSP工况下,泄漏涡发生偏移,受到强逆压梯度及泄漏涡卷吸作用,在一定程度上会使得更多的二次流开始偏离叶片表面,结果在通道Ⅰ中形成了大范围的低速区。
|
Fig. 5 Flow structure in passage Ⅰ |
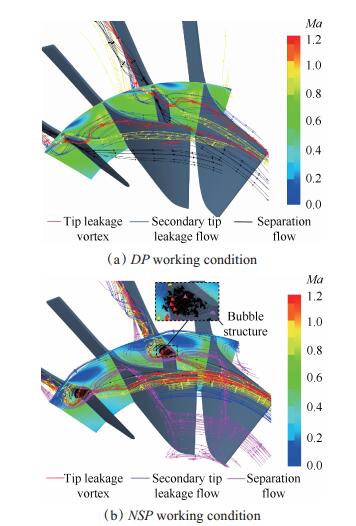
在近失速工况下,由于泄漏涡轨迹前移,更多的泄漏涡进入通道Ⅱ中,其卷吸作用也使得大量的低能流和部分二次流进入通道Ⅱ,结果使得通道Ⅱ中的流动恶化,甚至形成了回转的泡状结构,如图 6所示。结果在通道Ⅱ中造成了严重的堵塞。值得一提的是,当低能流受到泄漏涡的卷吸进入通道Ⅱ中时,不仅会造成堵塞,也会造成局部高损失区,使得压气机效率降低,这种影响要比通道Ⅰ中更为强烈[1]。关于这一点,近机匣壁面的极限流线也可以看出,如图 7所示。对于DP工况,通道Ⅱ中没有出现奇点,此时流动较为稳定,而在NSP工况下,通道Ⅱ中出现了一个节点(Nodal,N),此时流动极不稳定,而在通道Ⅰ中没有奇点形成。
|
Fig. 6 Flow structure in passage Ⅱ |

|
Fig. 7 Limiting streamline near shroud |
通过上述分析表明,泄漏涡自身在向下游发展的过程中发生破碎,尽管形成了一定的堵塞,但这并不一定是造成压气机失速的直接原因,即使在设计点也发生了泄漏涡的破碎现象。而通过对压气机近失速点流场特征分析可以发现,泄漏涡的卷吸作用在一定程度上会加重轮毂低能流的潜流和二次分离流,并造成低能流堆积在近机匣附近,这可能会引起压气机失速。
关于泄漏涡破碎和压气机失速之间的联系目前还没有共识。吴艳辉等[4]虽然发现近失速点泄漏涡发生破碎,但也没有明确指出该现象与失速之间的直接联系。NASA格林研究中Han等[18]的研究认为,破碎并不是导致压气机失速的直接原因,本文的结论与此较为接近。杜娟[19]通过研究发现,泄漏涡是否发生破碎并不影响叶顶具有特征频率的自激非定常性,而自激非定常性是失速的一种先兆。但Yamada等[20]则认为泄漏涡的破碎是引起失速的直接原因。本文将从面涡的角度出发,将泄漏涡进行简化处理,并运用与泄漏涡具有一定近似关系的机翼翼尖涡对不稳定理论进行建模,同时为从机理上更进一步认识泄漏涡提供思路。
3.2 泄漏涡面涡模型在一定情况下,泄漏涡会出现准周期变化的特征[21, 22],当流动控制激励频率与流场固有频率一致时控制效果最佳[23]。要想有效控制泄漏涡,需要知道泄漏涡的频率特征,为此,通常需要开展CFD计算或实验测量,要消耗大量的资源,难以灵活运用,本文从面涡模型出发,对泄漏涡进行建模,并运用Crow[24]翼尖涡不稳定理论建立叶轮几何参数与泄漏涡频率之间的联系。
泄漏涡并一定总是呈现出非定常的现象,林峰等[21, 25]通过研究提出了泄漏涡发生非定常波动的两个条件:(1)泄漏涡轨迹影响区达到相邻叶片压力面; (2)泄漏涡强度足够与主流抗衡并达到稳定的动态平衡状态。本文对于泄漏涡的建模以及后续的计算仅就泄漏涡具有非定常性下展开。
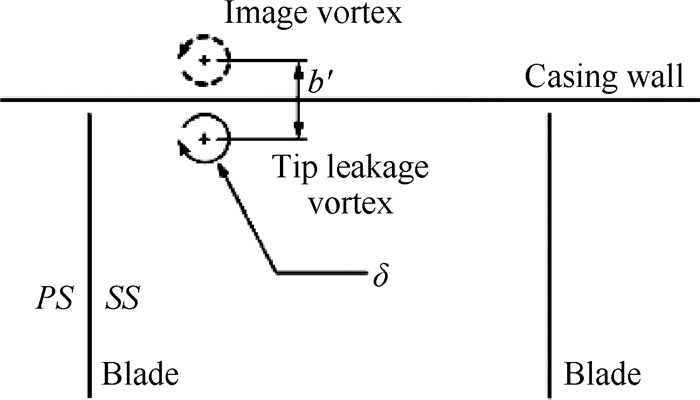
从本质上讲,泄漏涡和机翼两端翼尖涡的形成机理一致,即受到叶片(机翼)两侧压差的作用形成的。因此,在压气机机匣外侧引入一虚拟镜像涡结构,与泄漏涡形成涡对,镜像涡与泄漏涡关于机匣对称,如图 8所示。
|
Fig. 8 Tip leakage vortex and its image |
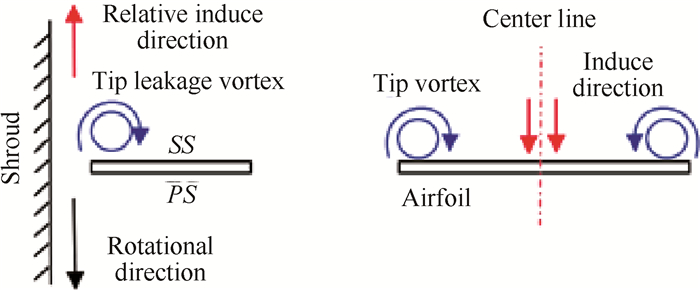
需要指出的是,压气机中的泄漏涡一侧具有固壁存在,而机翼中的翼尖涡相对应的区域并没类似的固壁,从涡对的形式上看似乎会有不同。但事实上正是由于机匣固壁的存在,使得泄漏虚拟镜像涡的引入变得较为合理,从速度诱导的概念可以较好地予以解释。若不考虑压气机机匣外侧的虚拟涡,从相对坐标系出发,由于固壁粘性作用,机匣对于泄漏涡具有与泄漏涡旋转方向一致的作用,由此产生了与之对应的速度诱导。在机翼中,两个翼尖涡的旋转方向相反,故机翼一侧的涡对另一个涡的诱导速度与机匣对泄漏涡的诱导情况一致,如图 9所示。也就是说,若不考虑虚拟涡的情况下,机匣壁面的粘性作用起到了翼尖涡对中一个涡对另一个涡的诱导作用,故在引入虚拟涡以后,可近似等效为不再考虑固壁的粘性作用。
|
Fig. 9 Induced velocity of casing and airfoil vortex pair |
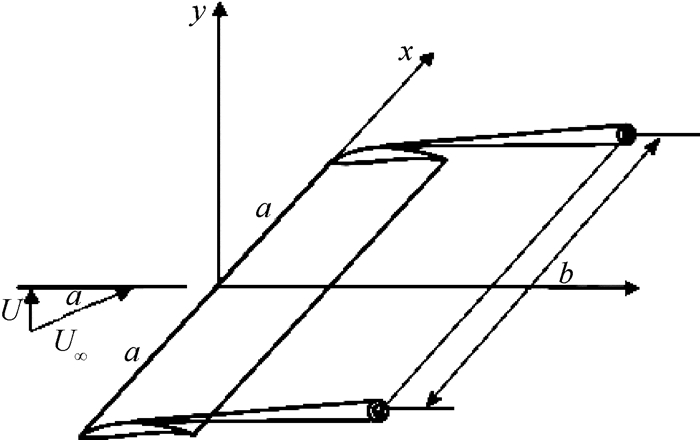
通过引入镜像涡对,建立了翼尖涡与泄漏涡之间的联系,Bae[14]最先采用了这种方案,并且通过将翼尖涡不稳定理论运用于泄漏涡中,最终较好地预测了轴流压气机叶栅的不稳定频率。反向旋转的翼尖涡对结构如图 10所示,图中
|
Fig. 10 Schematic of rolling up trailing vortices of straight wings |
采用二维面涡模型,将问题集中在研究起始时刻,即涡开始生成所在的截面,涡量分布在
| $\gamma \left( x \right) = 2Ux/\sqrt {{a^2} - {x^2}} , x \in \left[ { - a, a} \right]$ | (3) |
在涡中心位置,认为流体近似做刚体旋转运动,该涡可以认为是集中涡,则每一个集中涡的强度为
| $ \mathit{\mathit{\Gamma}} = \int_{ - a}^a {} \gamma \left( x \right){\rm{d}}x = 2Ua $ | (4) |
流体的冲量为
| $ I = \int_{ - a}^a {} x\gamma \left( x \right){\rm{d}}x = {\rm{ \mathsf{ π} }}U{a^2} $ | (5) |
该冲量又可以表示为Гb,因此根据式(4)和式(5)可以得到涡对之间的距离
| $ \frac{b}{{2a}} \approx \frac{{\rm{ \mathsf{ π} }}}{4} $ | (6) |
由于虚拟镜像涡与泄漏涡涡对的旋转方向同机翼间涡对的旋转方向相反,因此将其运用于泄漏涡中需要进行调整,这里将b替换为
| $ \frac{{2a}}{{b'}} \approx \frac{\pi }{4}\left( {或\frac{{b'}}{2} \approx \frac{{4\tau }}{\pi } \approx 1.27 {\rm{\tau}} } \right) $ | (7) |
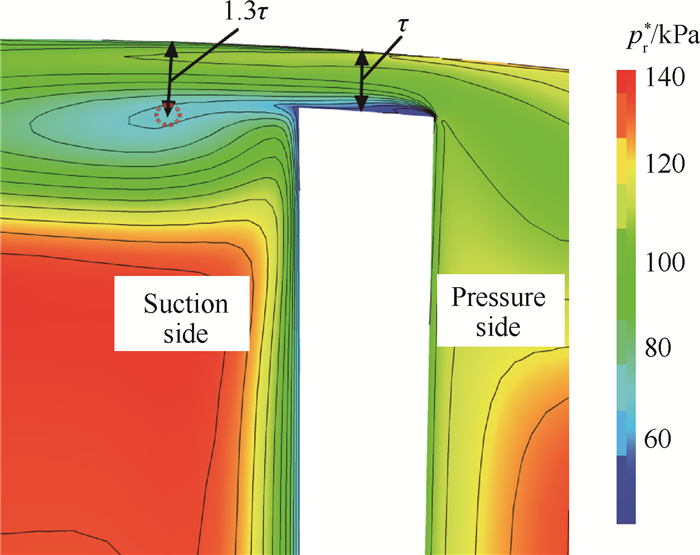
式中τ为叶尖间隙高度。为了验证该种处理方法的正确性,将式(7)的结果同计算结果进行比较。图 11给出了设计工况下25%弦长位置相对总压分布,图中
|
Fig. 11 Relative total pressure distribution at 25% chord length position |
假定涡量均匀分布,则涡强度可写为
| $ \mathit{\mathit{\Gamma}} = {\rm{ \mathsf{ π} }}{\delta ^2}\omega $ | (8) |
式中δ为涡核半径,涡核内流体做刚性运动,则旋转速度为
| $ v = \frac{{\mathit{\Gamma} r}}{{2{\rm{ \mathsf{ π} }}{\delta ^2}}} $ | (9) |
根据涡核内速度的表达式,对其进行积分,可以得到涡核内流体的动能,即
| $ {T_1} = 2 \times \frac{\rho }{2}\int_0^\delta {} {\left( {\frac{{\mathit{\Gamma} r}}{{2{\rm{ \mathsf{ π} }}{\delta ^2}}}} \right)^2}2{\rm{ \mathsf{ π} }}r{\rm{d}}r = \frac{{\rho {\mathit{\Gamma} ^2}}}{{8{\rm{ \mathsf{ π} }}}} $ | (10) |
假定涡核外气流做无旋运动,则流函数为
| $ \psi \approx \frac{\mathit{\Gamma} }{{2{\rm{ \mathsf{ π} }}}}{\rm{ln}}\left( {\frac{b}{\delta }} \right) $ | (11) |
在涡核的边界上,对流函数进行线积分,可以得到
| $ \int{{}}\frac{\partial \psi }{\partial n}\text{d}l=-\mathit{\Gamma} $ | (12) |
涡核外的动能可以表达为
| ${{T}_{2}}=-\frac{\rho }{2}\int{{}}\frac{\partial \psi }{\partial n}\text{d}l$ | (13) |
将式(11),(12)代入式(13)中,则涡核外动能可以进一步表达为
| ${T_2} \approx \frac{{\rho {\mathit{\Gamma} ^2}}}{{2{\rm{ \mathsf{ π} }}}}{\rm{ln}}\left( {\frac{b}{\delta }} \right)$ | (14) |
在初始时刻,流体的总动能等于涡核内的动能加上涡核外的动能,即
| $T = {T_1} + {T_2}$ | (15) |
式(15)中等式右边两项可以从式(10)和式(14)求得,总能T可以通过面积分求得
| $T=\frac{\rho }{2}\iint{{}}{{\mathit{\boldsymbol{u}}}^{2}}\text{d}x\text{d}y$ | (16) |
式中
| $T=\frac{\rho }{2}{{\iint{\left( \nabla \varphi \right)}}^{2}}\text{d}x\text{d}y=-2\rho \int_{0}^{a}{\varphi \frac{\partial \varphi }{\partial y}}\text{d}x$ | (17) |
其中速度势可以表示为
| $\varphi =\pm U\sqrt{{{a}^{2}}-{{x}^{2}}}$ | (18) |
法向速度为
| $\frac{\partial \varphi }{\partial y}=U$ | (19) |
将式(18),(19)代入式(17),可得
| $T=\frac{1}{2}\text{ }\!\!\pi\!\!\text{ }\rho {{U}^{2}}{{a}^{2}}=\frac{\text{ }\!\!\pi\!\!\text{ }\rho {{\mathit{\Gamma} }^{2}}}{8}$ | (20) |
联立式(10)、式(14)、式(15)和式(20),可得
| $\frac{\text{ }\!\!\pi\!\!\text{ }\rho {{\mathit{\Gamma} }^{2}}}{8}=\frac{\rho {{\mathit{\Gamma} }^{2}}}{8\text{ }\!\!\pi\!\!\text{ }}+\frac{\rho {{\mathit{\Gamma} }^{2}}}{2\text{ }\!\!\pi\!\!\text{ }}\text{ln}\frac{b}{\delta }$ | (21) |
根据式(21),可以得到涡核半径与涡对之间距离的比值为
| ${{\text{ }\!\!\pi\!\!\text{ }}^{2}}=1+4\times \text{ln}\frac{b}{\delta }或\frac{\delta }{b}\approx 0.109$ | (22) |
将
| $\frac{\delta }{{{b}'}}\approx 0.072$ | (23) |
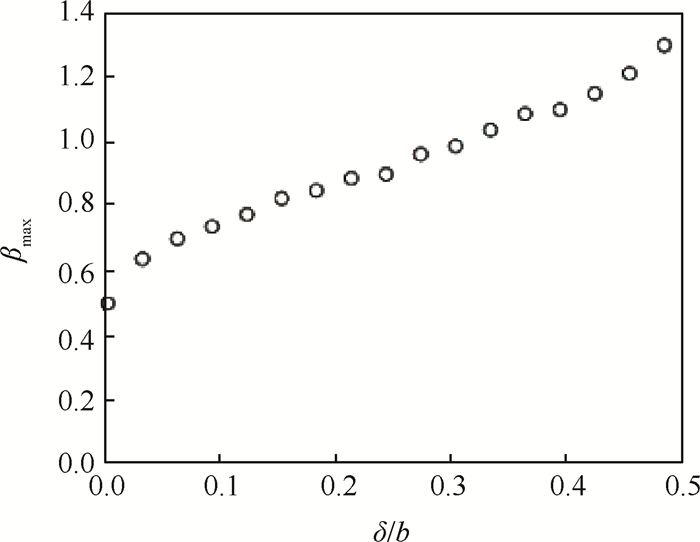
应用Crow机翼翼尖涡的不稳定性理论,通过涡核半径与涡对之间的比值,可以得到最不稳定的无量纲波长
|
Fig. 12 Most unstable wave number |
对于压气机中,需要将
| $\lambda =2\text{ }\!\!\pi\!\!\text{ }{b}'/{{\beta }_{\text{max}}}$ | (24) |
式中
| $f={{U}_{\text{r}}}/\lambda $ | (25) |
式中
通过上述过程,可以得到泄漏涡非定常的波动频率,该过程在推导的过程中没有考虑不同工况的影响,如背压。事实上,泄漏涡的行为特征与工况相关,并且其半径也是沿着弦长增长。因此可以认为这种泄漏涡面涡模型发生于泄漏涡开始生成阶段。通过上述建模过程,能够大致预测泄漏涡的频率,而不需要CFD结果或实验数据,并且从机理上提供了进一步理解泄漏涡的思路。
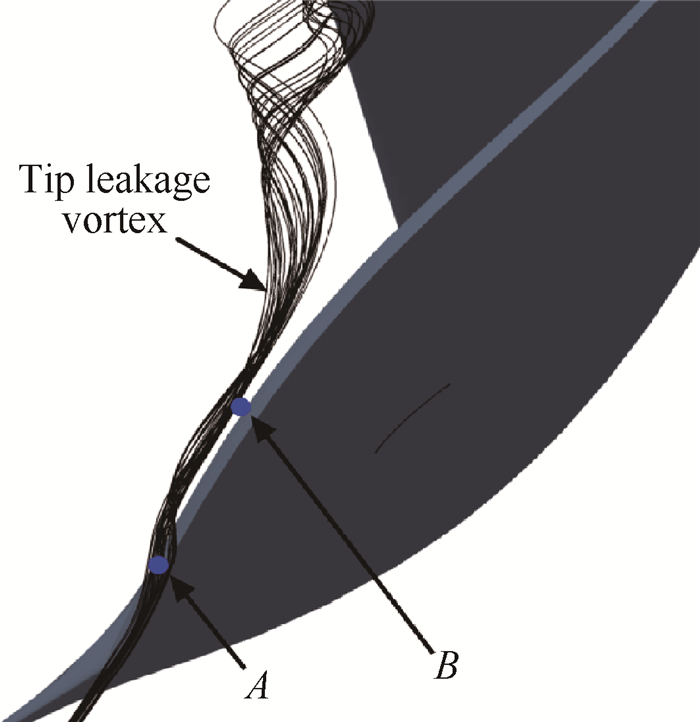
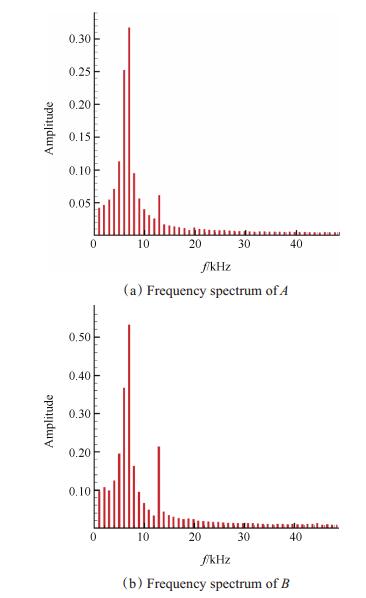
3.3 泄漏涡面涡模型的验证 3.3.1 泄漏涡面涡模型同数值模拟结果的对比为验证泄漏涡模型的准确性,对单转子单通道进行非定常数值计算,分别对3%和4%叶尖间隙高度进行计算(间隙高度与进口叶高的比值)。对于不同的间隙高度,仅通过减少叶片高度实现,其他叶片形状尺寸参数保持不变。图 13为监测点位置分布,对监测点捕获静压系数进行FFT(Fast Fourier Transform)变换,3%间隙高度计算得到的频谱图如图 14所示。从频谱图中可以看到,峰值出现在6.931kHz位置,该频率对应为泄漏涡主频,而在13.333kHz位置也有峰值出现,该频率为叶片通过频率(Blade Passing Frequency,BPF)。采用同样的方法,可以通过计算得到4%间隙高度泄漏涡的主频,其值为5.84kHz。
|
Fig. 13 Location of monitoring points |
|
Fig. 14 Frequency spectrum of monitoring points |
应用上节的泄漏涡面涡模型,在两个不同间隙下,涡半径和虚拟涡对距离之间的比值为
|
|
Table 1 Compareation between calculated frequency of leakage vortex and model prediction frequency |
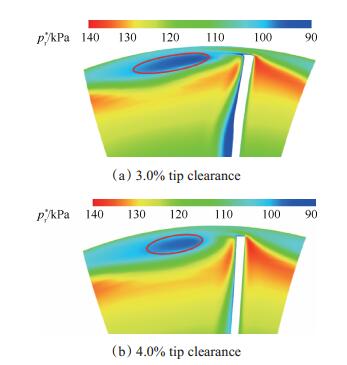
在两个间隙高度下,CFD计算频率和模型预测的频率同叶片通过频率BPF的比值介于40%~80%之间,这与Hah等[22]和Yamada等[26]得到的轴流压气机泄漏涡频率同叶片通过频率的比值相近。从表 1中还可以看出,模型在预测较大叶尖间隙时比小间隙更加接近CFD计算结果,这是由于在较小间隙情况下,泄漏涡受到机匣粘性力的作用向周向延伸,形成椭圆形结构,和模型理想的圆形具有一定差异,而在较大间隙下,泄漏涡涡核更加接近理想的圆形,因此模型预测的结果同CFD结果也较为接近。图 15给出了30%弦长截面相对总压分布,从图中可以看出4%间隙的低压区较3%间隙的低压区更加接近圆形。
|
Fig. 15 Relative total pressure at 30% chord length |
为了进一步验证模型的有效性,对NASA[27]、德国宇航院(DLR)[28]和中科院[29]三个具有代表性的公开轴流压气机实验数据与泄漏涡面涡模型预测结果进行了对比。表 2为模型预测频率与实验对比结果,从表中可以看出,模型预测的频率与实验得到的结果具有较好的吻合性:当间隙高度较大时,总体上模型的预测结果更为准确,最小偏差仅为2.8%;当间歇高度较小时,模型预测出了实际频率的大体量级,数值会偏大(和前面本文研究的离心压气机算例得到规律一致)。本文在模型建立的过程中从面涡及翼尖涡模型出发,未涉及到具体的叶型或子午流道等参数的影响,因此对离心压气机和轴流压气机的预测都适用。
|
|
Table 2 Compareation between experiment frequency of leakage vortex and model prediction frequency |
通过本文研究,得到结论如下:
(1) 在设计点和近失速工况下,泄漏涡都发生了破碎现象。但在近失速工况下受到强逆压梯度的影响,泄漏涡轨迹向额线偏转,其卷吸作用在一定程度上会使得更多的来自轮毂处的低能流和二次流汇入叶轮通道低速区,使得堵塞越为严重,通道Ⅱ中的流场较通道Ⅰ更不稳定。
(2) 在机匣外侧引入虚拟镜像涡与泄漏涡形成涡对,本文应用机翼涡对的不稳定性理论和面涡模型对泄漏涡非定常性条件下,建立了其最不稳定频率估算模型。通过CFD结果和国内外典型压气机的实验验证,表明建立的泄漏涡面涡模型具有较好的准确性,其中,针对DLR公开轴流压气机的模型预测与实际频率误差可达2.8%。相比小间隙下,当叶尖间隙高度较大时,模型预测的泄漏流频率相对更为准确,大间隙下泄漏涡涡核更加接近模型的理想形状可能是造成这种趋势原因。
致谢: 感谢国家重点基础研究发展计划“九七三”计划基金资助。
| [1] |
陈杰, 钟榈, 黄国平. 微型离心叶轮流动损失分析与削弱[J]. 推进技术, 2013, 34(7): 904-910. (CHEN Jie, ZHONG Lu, HUANG Guo-ping. Analysis and Reduction of Flow Loss in a Micro Centrifugal Impeller[J]. Journal of Propulsion Technology, 2013, 34(7): 904-910.)
(  0) 0) |
| [2] |
黄国平, 梁德旺, 何志强. 大型飞机辅助动力装置与微型涡轮发动机技术特点对比[J]. 航空动力学报, 2008, 23(2): 383-388. (  0) 0) |
| [3] |
楚武利, 刘前智, 胡春波. 航空叶片机原理[M]. 西安: 西北工业大学出版社, 2009.
(  0) 0) |
| [4] |
吴艳辉, 李清鹏, 张卓勋, 等. 轴流压气机转子近失速工况点叶尖区流动非定常性分析[J]. 推进技术, 2010, 31(5): 562-566. (WU Yan-hui, LI Qing-peng, ZHANG Zhuo-xun, et al. Unsteady Behavior of Tip Clearance Flow in an Axial Flow Compressor Rotor at near Stall Condition[J]. Journal of Propulsion Technology, 2010, 31(5): 562-566.)
(  0) 0) |
| [5] |
Lei V M, Spakovszky Z S, Greitzer E M. A Criterion for Axial Compressor Hub-Corner Stall[J]. Journal of Turbomachinery, 2008, 130(3).
(  0) 0) |
| [6] |
Suder K L, Celestina M L. Experimental and Computational Investigation of the Tip Clearance Flow in a Transonic Axial Compressor Rotor[J]. Journal of Turbomachinery, 1996, 118(2): 218-229. DOI:10.1115/1.2836629
(  0) 0) |
| [7] |
Feng L, Tong Z, Geng S, et al. A Summary of Stall Warning and Suppression Research with Micro Tip Injection[R]. ASME GT 2011-46118.
(  0) 0) |
| [8] |
Hah C, Rabe D C, Wadia A R. Role of Tip-Leakage Vortices and Passage Shock in Stall Inception in a Swept Transonic Compressor Rotor[R]. ASME GT 2004-53867.
(  0) 0) |
| [9] |
Vo H D, Tan C S, Greitzer E M. Criteria for Spike Initiated Rotating Stall[J]. Journal of Turbomachinery, 2008, 130(1).
(  0) 0) |
| [10] |
Hazby R H, Xu L. Role of Tip Leakage in Stall of a Transonic Centrifugal Impeller[R]. ASME GT 2009-59372.
(  0) 0) |
| [11] |
李相君, 楚武利, 张皓光. 高负荷跨声速轴流压气机周向浅槽处理机匣扩稳机理[J]. 推进技术, 2013, 34(5): 629-637. (LI Xiang-Jun, CHU Wu-li, ZHANG Hao-guang. Stabilizing Mechanism of Shallow Circumferential Grooves on a High Loaded Transonic Axial-Flow Compressor[J]. Journal of Propulsion Technology, 2013, 34(5): 629-637.)
(  0) 0) |
| [12] |
YANG Qi-chao, LI Lian-sheng, ZHAO Yuan-yang, et al. Experimental Investigation of an Active Control Casing Treatment of Centrifugal Compressors[J]. Experimental Thermal and Fluid Science, 2017, 83: 107-117. DOI:10.1016/j.expthermflusci.2016.12.013
(  0) 0) |
| [13] |
曹四. 机匣处理对跨声速离心压气机性能影响[J]. 推进技术, 2017, 38(4): 772-778. (CAO Si. Effects of Casing Treatment on Performance of Transonic Centrifugal Compressor[J]. Journal of Propulsion Technology, 2017, 38(4): 772-778.)
(  0) 0) |
| [14] |
Bae J. Active Control of Tip Clearance Flow in Axial Compressors[D]. Massachusetts: Massachusetts Institute of Technology, 2001.
(  0) 0) |
| [15] |
李伟, 乔渭阳, 许开富. 涡轮叶尖间隙泄漏涡不稳定性分析[J]. 推进技术, 2008, 29(2): 204-207. (LI Wei, QIAO Wei-yang, XU Kai-fu. Unsteadiness of Tip Clearance Vortex in Turbine[J]. Journal of Propulsion Technology, 2008, 29(2): 204-207. DOI:10.3321/j.issn:1001-4055.2008.02.015)
(  0) 0) |
| [16] |
胡子俊, 张楠, 姚惠之, 等. 涡判据在孔腔涡旋流动拓扑结构分析中的应用[J]. 船舶力学, 2012, 16(8): 839-846. DOI:10.3969/j.issn.1007-7294.2012.08.001 (  0) 0) |
| [17] |
Seiichi I, Masato F, Kenichiro I, et al. Vortical Flow Structure and Loss Generation Process in a Transonic Centrifugal Compressor Impeller[R]. ASME GT 2007-27791.
(  0) 0) |
| [18] |
Hah C, Hathaway M, Katz J. Investigation of Unsteady Flow Field in a Low-Speed One and a Half Stage Axial Compressor: Effects of Tip Gap Size on the Tip Clearance Flow Structure at near Stall Operation[R]. ASME GT 2014-27094.
(  0) 0) |
| [19] |
杜娟.跨音压气机/风扇转子叶顶泄漏流动的非定常机制研究[D].北京: 中国科学院研究生院, 2010. http://cdmd.cnki.com.cn/Article/CDMD-80135-2010088116.htm
(  0) 0) |
| [20] |
Yamada K, Kikuta H, Furukawa M, et al. Effects of Tip Clearance Flow on Rotating Stall Inception Process in an Axial Compressor Rotor[R]. ASME GT 2013-95479.
(  0) 0) |
| [21] |
Lin F, Du J, Chen J, et al. Flow Structures in the Tip Region for a Transonic Compressor Rotor[R]. ASME GT 2010-23025.
(  0) 0) |
| [22] |
Hah C, Bergner J, Schiffer H P. Tip Clearance Vortex Oscillation, Vortex Shedding and Rotating Instabilities in an Axial Transonic Compressor Rotor[R]. ASME GT 2008-50105.
(  0) 0) |
| [23] |
洪树立, 黄国平. 引入DMD方法研究有/无控气流分离的动态结构[J]. 航空学报, 2017, 38(8). (  0) 0) |
| [24] |
Crow S C. Stability Theory for a Pair of Trailing Vortices[J]. AIAA Journal, 1970, 8(12): 2172-2179. DOI:10.2514/3.6083
(  0) 0) |
| [25] |
Du J, Lin F, Zhang H, et al. Numerical Investigation on the Self-Induced Unsteadiness in Tip Leakage Flow for a Transonic Fan Rotor[J]. Journal of Turbomachinery-Transactions of ASME, 2010, 132(2).
(  0) 0) |
| [26] |
Yamada K, Funazaki K, Furukawa M. The Behavior of Tip Clearance Flow at Near-Stall Condition in a Transonic Axial Compressor Rotor[R]. ASME GT 2007-27725.
(  0) 0) |
| [27] |
Hah C, Voges M, Müller M W, et al. Characteristics of Tip Clearance Flow Instability in a Transonic Compressor[R]. ASME GT 2010-22101.
(  0) 0) |
| [28] |
Cahuzac A, Boudet J, Jacob M C, et al. Large-Eddy Simulation of a Rotor Tip-Clearance Flow[R]. AIAA 2002-0981.
(  0) 0) |
| [29] |
ZHANF Hong-wu, DENG Xiang-yang, CHEN Jing-yi, et al. Unsteady Tip Clearance Flow in an Isolated Axial Compressor Rotor[J]. Journal of Thermal Science, 2005, 14(3): 211-219. DOI:10.1007/s11630-005-0004-4
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


