航空发动机为了追求高推重比及高效率,涡轮入口温度逐渐攀升[1]。为了保证发动机寿命及可靠性,涡轮的传热设计十分关键。在传统涡轮设计流程中,气动设计与传热设计分开进行,可能导致后续传热设计困难[2],因而在气动设计阶段综合考虑传热设计的需求十分必要[3]。
部分文献讨论了叶片气动外形对传热性能的影响。Rajadas等[4]指出,由于主流燃气直接加热叶片,叶片型线的改变,必然导致壁面热负荷和温度的变化。Nicholson等[5]调整叶片压力面型线,降低了壁面换热系数。Nealy等[6]比较了C3X和MARK-Ⅱ叶片在相同来流及出口边界条件下的换热特性,其结论是叶片型线差异导致吸力面转捩特点不同,最终导致两者热负荷分布差异显著。杨玉骏等[7]对涡轮导叶进行敏感性分析发现通过增大叶片安装角以减小压力面型面曲率,可以一定程度降低表面换热强度,随后采用粒子群优化算法对吸力面型线进行优化,总压损失增加0.062%,单位面积换热量减小了6.3%。
随着CFD技术的发展和计算能力的提升,越来越多的研究人员尝试采用气热耦合计算方法结合优化算法对涡轮叶片进行优化或改型设计,取得了良好的效果。卢少鹏等[8]采用气热耦合优化的方法对涡轮静叶叶型进行优化,不仅提高了气动效率而且降低了叶片温度。罗磊等[9]针对某涡轮动叶的叶型和冷却结构进行了气热耦合优化设计,气动效率提高0.58%,叶片表面平均温度下降6.46K。Song等[10]采用耦合计算方法对C3X叶片的型线及冷却结构进行多学科、多目标优化,在气动效率略微下降的同时,大幅降低了叶片最高温度及最大温度梯度。Ayoubi等[11]以气膜冷却效率及气动效率为目标,对涡轮导叶吸力侧两列气膜孔的几何进行多目标优化,和原型相比,优化后冷却效率提高了100%,气动损失下降了20%。
全三维气热耦合计算能够得到精细的流场参数,但是存在网格生成难度大、计算复杂等困难,由于计算成本大,不适合在叶片设计初始阶段应用。为了在复杂流动系统耦合计算时能够兼顾效率和精度,王鹏等[12]提出了不同维数耦合的数值模拟方法。其基本思想是,对于一个复杂系统,耦合计算时将其划分为多个子系统,针对每个子系统流动特点,综合考虑实际工程评估所能接受的计算效率与精度的前提下,选择子系统的计算维数,可以是一维,也可以是二维或三维。Gu等[13]提出一种气热耦合通流设计方法,在传统通流计算的基础上引入了冷却计算模型,由此求得透平所需冷气量及主流流场参数。颜培刚等[14]等将流体网络方法应用于高性能涡轮叶片复合冷却结构的设计中,发展了流体网络分析与三维黏性流场耦合求解的计算方法。Martin等[15]开发了求解内部冷却涡轮高、低维耦合求解计算程序及多学科多目标优化设计平台,通过对普惠F110航空发动机第二级高压涡轮动叶优化设计证实了该方法有效性,优化后叶片冷却效率提高5%,蠕变寿命提高1倍,冷气流量基本保持不变。
涡轮叶片气动设计过程中叶片型线的改变将影响涡轮的传热性能,在气动设计阶段充分考虑气动设计对传热性能的影响有利于降低传热设计难度。全三维耦合计算面临内冷通道网格生成难度大、计算复杂,计算成本高等问题。本文发展一种结合一维管网程序和三维CFD的共轭传热分析方法,大大降低了计算复杂性,并对该计算方法的可靠性进行了验证。
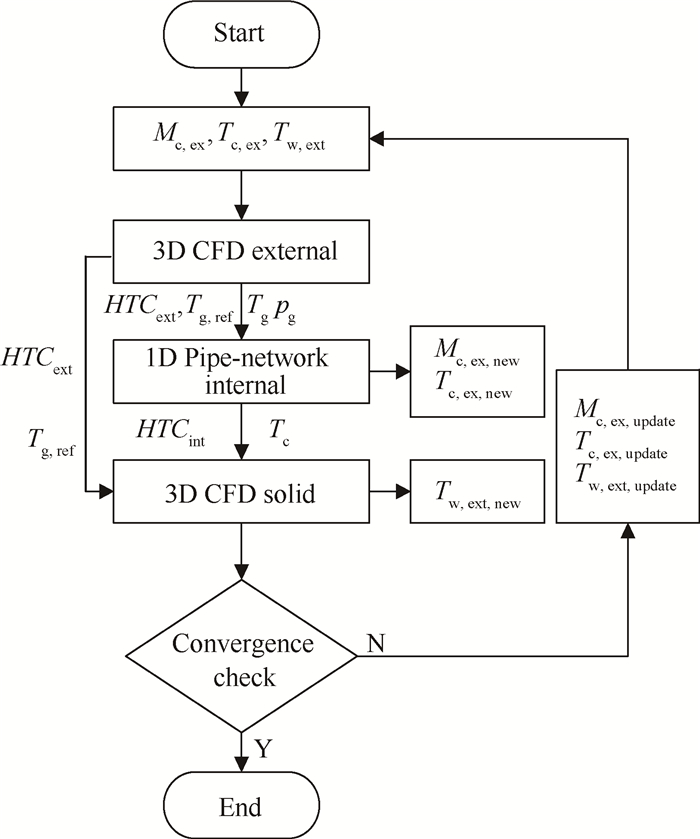
2 物理模型与计算方法管网/三维耦合计算流程由外流三维气动计算、固体域三维导热计算及内部冷却通道一维计算组成,不同计算域单独求解。图 1是管网/三维耦合计算方法的计算流程:
|
Fig. 1 Schematic diagram of the CHT procedure |
(1) 给定叶片外壁面温度
(2) 采用一维管网程序[16]对内流场进行计算,管网计算所需要的叶片外表面燃气温度
(3) 采用CFX14.5求解器对叶片固体域进行三维导热计算,导热计算内外壁面都采用第三类边界条件(壁面温度、换热系数)。外壁面燃气参考温度
(4) 判断外壁面温度,内流域冷气出口流量及温度是否满足收敛条件,若满足则耦合计算流程结束,否则更新对应参数并重复步骤(1)~(3),式(1)~(3)是参数更新公式,其中
为了保证计算过程稳定性,内流管网计算在一次外流三维气动计算完全收敛后开始。此外,每步外流计算调用上一步外流计算结果作为初场以加速收敛。
| ${M_{{\rm{c}}, {\rm{ex}}, {\rm{update}}}} = {M_{{\rm{c}}, {\rm{ex}}}}$ | (1) |
| ${T_{{\rm{c}}, {\rm{ex}}, {\rm{updata}}}} = {T_{{\rm{c}}, {\rm{ex}}, {\rm{new}}}}$ | (2) |
| ${T_{{\rm{w}}, {\rm{ext}}, {\rm{update}}}} = {T_{{\rm{w}}, {\rm{ext}}}} + a\left( {{T_{{\rm{w}}, {\rm{ext}}, {\rm{new}}}} - {T_{{\rm{w}}, {\rm{ext}}}}} \right)$ | (3) |
为了对管网/三维耦合计算方法进行验证,分别采用该方法和全三维耦合计算方法对文献[17]中MARK-Ⅱ叶片三个工况(5411,4411,4311)进行数值计算,对比不同工况下两种方法计算结果和实验数据的差别。表 1是不同工况下出口马赫数和雷诺数。相较单一工况,多工况校核的结论更具有普遍意义。另一方面,工况的变化必然导致叶片表面热负荷的变化,不同工况的数值模拟也可以考核数值计算是否能够准确预测变化的趋势。
|
|
Table 1 Outlet Mach number and Reynolds number in different conditions of MARK-Ⅱ blade |
本文的校核算例以NASA MARK-Ⅱ平面叶栅为研究对象。外部流体域工质为燃气,工质的导热系数、动力粘度和等压比热均为温度的函数。内部流体域工质为理想气体,工质物性见公式(4)~(6)。固体域材料为ASTM标准的310不锈钢,密度7900
| ${C_{p, {\rm{c}}}} = 0.093T + 995.6$ | (4) |
| ${\mu _{\rm{c}}} = 1.72 \times {10^{ - 5}}{\left( {\frac{T}{{273.11}}} \right)^{3/2}}\frac{{273.11 + 110.56}}{{T + 110.56}}$ | (5) |
| ${\lambda _{\rm{c}}} = 0.024{\left( {\frac{T}{{273.11}}} \right)^{3/2}}\frac{{273.11 + 110.56}}{{T + 110.56}}$ | (6) |
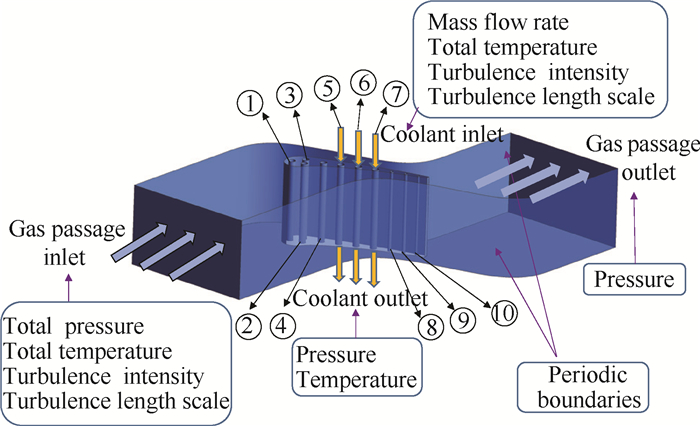
全三维耦合计算时,外流进口边界条件给定总温、总压、湍流度、湍流特征长度; 内流进口边界给定总温、流量、湍流度、湍流特征长度; 内流、外流出口边界均给定静压,见表 2。表 3和表 4分别是全三维耦合计算外流域和内流域边界条件,孔的编号见图 2,图 2为边界条件示意图。
|
|
Table 2 Boundary condition of computational domain for external flow in full 3D CHT calculation |
|
|
Table 3 Boundary condition of computational domain for internal flow in full 3-D CHT calculation |
|
|
Table 4 Boundary condition of computational domain for internal flow in pipe-network/3D CHT |
|
Fig. 2 Boundary condition schematic for full 3D CHT |
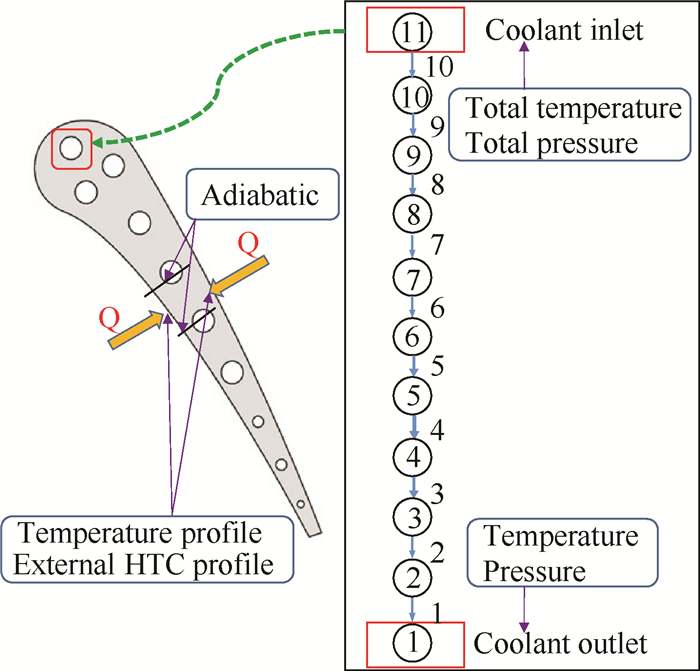
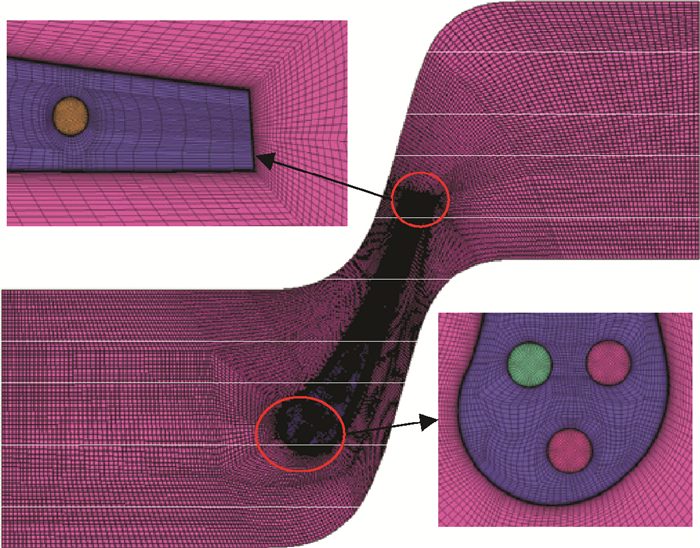
在管网/三维耦合计算流程中,不同计算域单独求解。外流域进、出口边界与全三维耦合计算相同,但是叶片壁面给定等壁温边界条件; 内流域采用一维管网程序求解,冷气通道进口边界给定总压、总温,出口边界给定静压、静温。为了求解内流温度,管网程序对叶片进行一维导热计算,因此还需要给定叶片外壁面燃气温度、换热系数; 固体域三维导热计算内外壁面都采用第三类边界条件(壁面温度、换热系数)。图 3是一维管网计算边界条件示意图。计算域均采用ICEM划分六面体网格,外流流体域边界层网格加密。图 4是计算网格示意图,流体域网格总数约170万; 固体域网格总数约70万; 内流流体域每个冷气通道网格总数约5万。
|
Fig. 3 Boundary condition schematic for pipe-network / 3D CHT procedure |
|
Fig. 4 Computational grid of MARK-Ⅱ blade |
本文分别采用
图 5为中截面型面压力分布对比,取参考压力
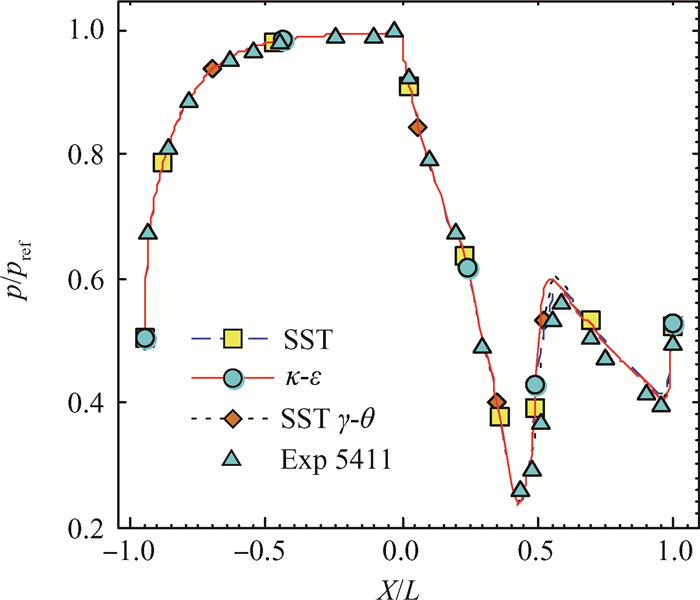
|
Fig. 5 Pressure distribution at the mid-span under 5411 operation condition for MARK-Ⅱ vane blade |
图 6为中截面摩擦系数分布对比,下方为局部放大图,回流区范围以圆圈标出示意。摩擦系数定义为式(7),其中
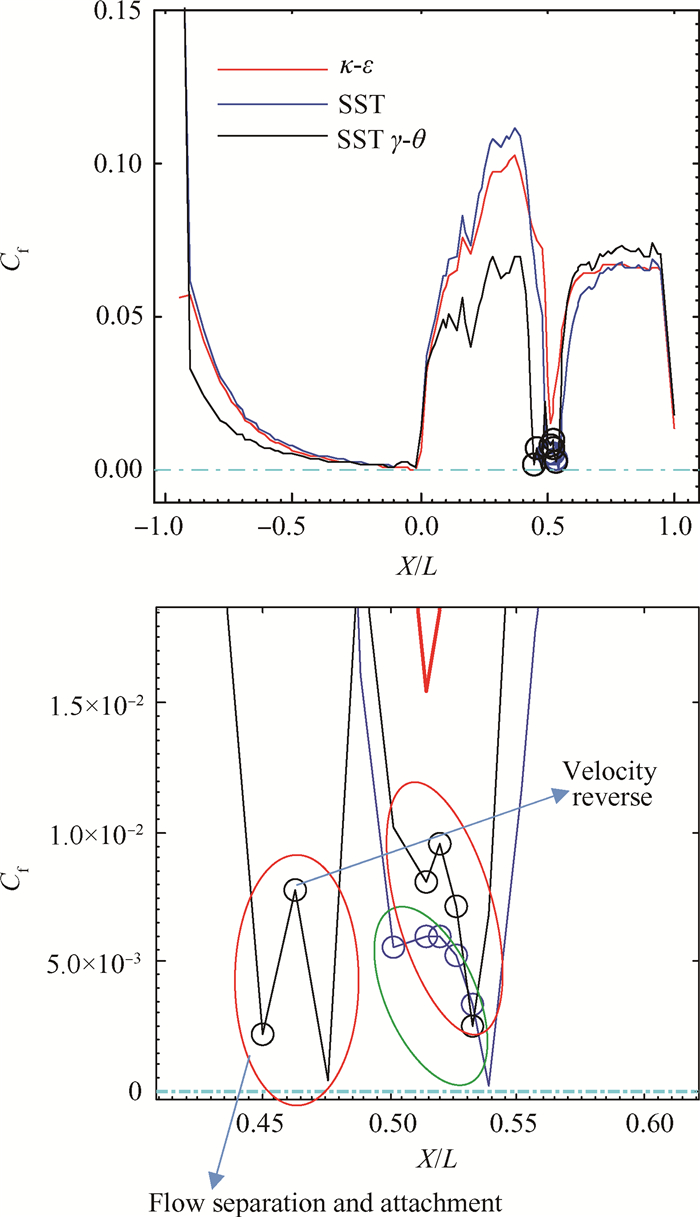
|
Fig. 6 Friction coefficient distribution at the mid-span under 5411 operation condition for MARK-Ⅱ vane blade |
图 7为中截面换热系数分布对比,换热系数定义及壁面层流区域、湍流区域换热经验式参考文献[18],
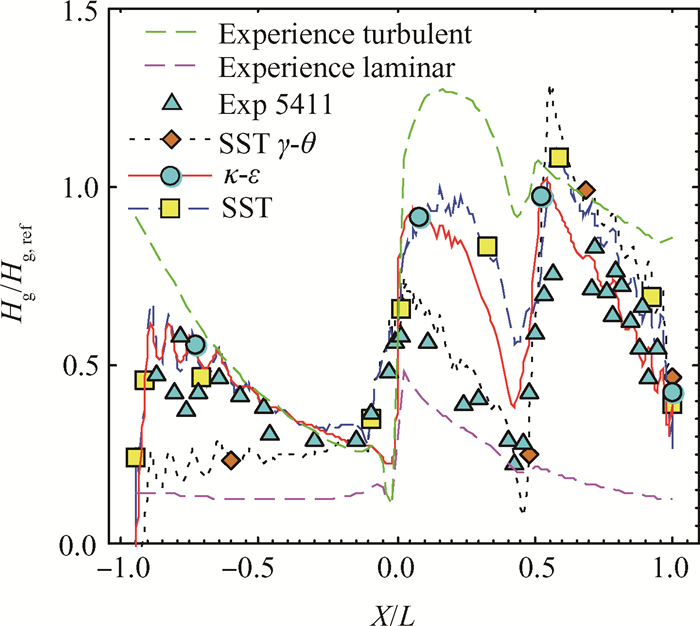
|
Fig. 7 Heat transfer coefficient distribution at the midspan under 5411 operation condition for MARK-Ⅱ vane blade |
图 8为中截面壁面温度曲线,其中,
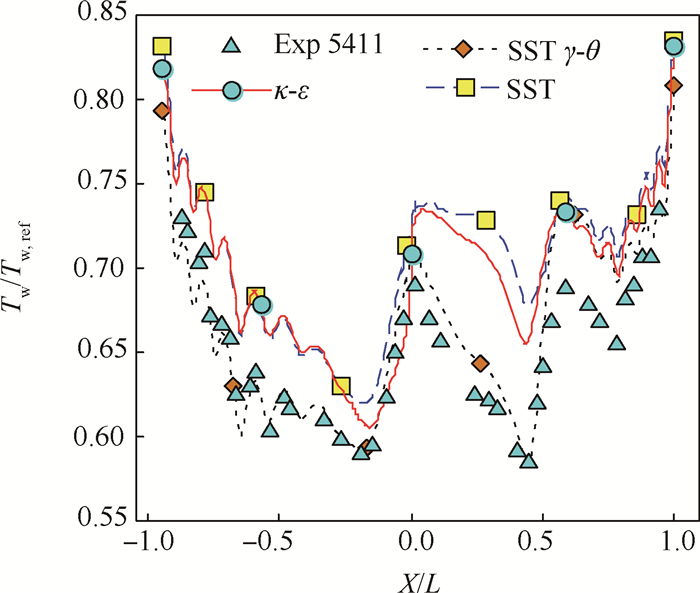
|
Fig. 8 Wall temperature distribution at the mid-span under 5411 operation condition for MARK-Ⅱ vane blade |
总体而言,
| ${C_{\rm{f}}} = \frac{{{\tau _{\rm{w}}}}}{{\rho {U^2}/2}}$ | (7) |
分别从外壁面换热系数和温度,内壁面换热系数及固体域中间截面温度分布对全三维耦合计算,管网/三维耦合计算的计算结果和实验数据进行比较。
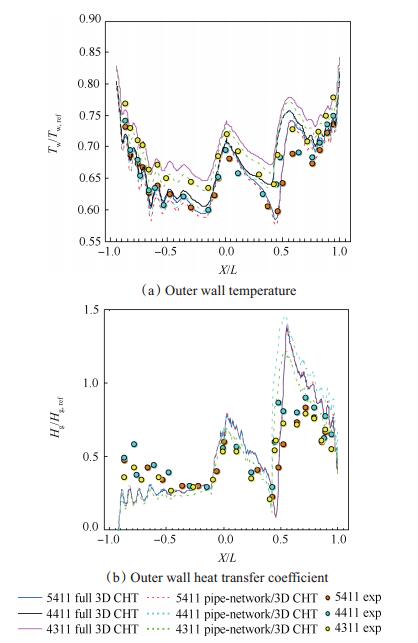
图 9(a)是不同工况中截面温度分布。两种计算方法计算结果整体趋势相同,但是管网/三维耦合计算结果较全三维耦合偏低,其中压力侧差别较吸力侧更明显。表 5是管网/三维耦合和全三维耦合壁面温度计算结果偏差的最大值,温差定义采用式(8),式(9)。不同工况(5411,4411,4311)两种计算方法得到的壁面温度最大差别分别为15.1K,16.8K,20.7K,壁面温度相差不大。
|
Fig. 9 Distribution of heat transfer coefficient and temperature of MARK-Ⅱ blade outer wall under different working conditions at mid-span |
|
|
Table 5 Maximum difference in outer wall temperature between full 3D CHT and pipe-network/3D CHT |
图 9(b)是不同工况中截面换热系数。比较4411和5411工况换热系数曲线,出口马赫数对换热系数的影响主要体现在吸力面约45%轴向弦长流动分离之后。4411工况出口马赫数低于5411工况,分离起始点及转捩结束位置相较5411工况略微前移,分离起始点后换热系数较高。比较4411和4311工况换热系数曲线,当出口雷诺数升高,叶片表面换热系数曲线整体上移。由于管网/三维耦合计算方法换热系数是通过3D CFD迭代求解获得,不同工况计算结果都与对应工况全三维耦合方法基本吻合,图中省略了4411和4311工况全三维耦合计算对应曲线。
| ${\Delta _{1 - 2, {\rm{abs}}}} = {\rm{max}}\left( {{\rm{abs}}\left( {{T_{{\rm{W}}1}} - {T_{{\rm{W}}2}}} \right)} \right)$ | (8) |
| ${\Delta _{1 - 2, {\rm{rel}}}} = {\rm{max}}\left( {{\rm{abs}}\left( {{T_{{\rm{W}}1}} - {T_{{\rm{W}}2}}} \right)/{T_{{\rm{W}}1}}} \right)$ | (9) |
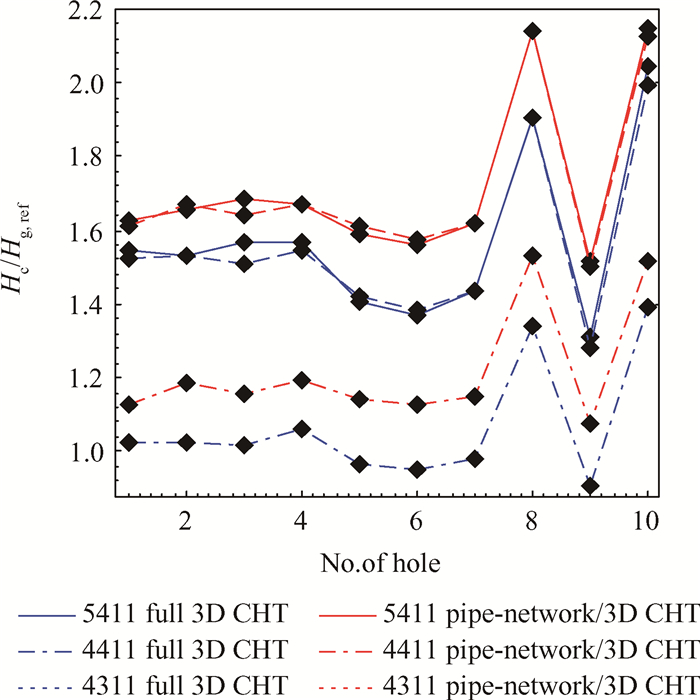
图 10是管网/三维耦合和全三维耦合计算得到的冷气通道换热系数,计算公式采用式(10),
| $ {H_{\rm{c}}} = \frac{{{q_{{\rm{cool}}, {\rm{wall}}}}}}{{{T_{{\rm{cool}}, {\rm{wall}}}} - {T_{{\rm{cool}}, {\rm{in}}, {\rm{tot}}}}}} $ | (10) |
|
Fig. 10 Wall heat transfer coefficient of cooling tube |
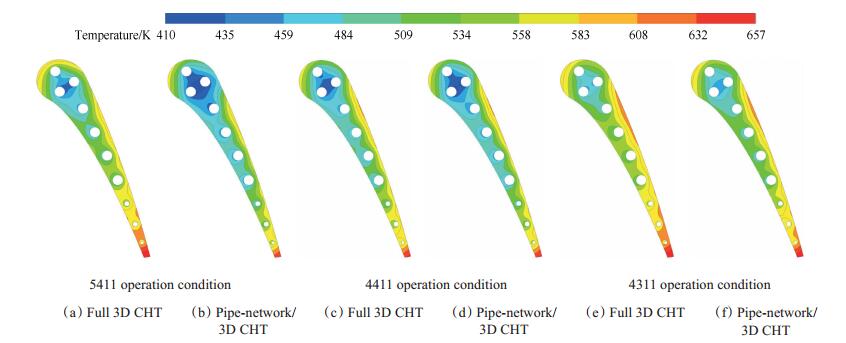
图 11是中间截面叶片固体域温度分布。管网/三维耦合与全三维耦合计算结果整体趋势相近,高温区位于叶片前缘,吸力侧转捩处及叶片尾缘。尾缘区域温度最大,第1~3个冷气通道相邻区域温度最小。但管网/三维耦合计算结果在冷气通道附近低温区域面积覆盖更大,这也证实了管网/三维耦合预测的内部通道换热较全三维耦合较强。
|
Fig. 11 Solid temperature distribution contour for MARK - Ⅱ blade under different operation conditions at mid-span |
为了避免叶片型线变化导致传热性能过度恶化,有必要在气动设计阶段应用耦合计算方法评估方案气动及传热性能。前文介绍一种结合一维管网和三维CFD的耦合计算方法,该方法相比全三维耦合计算,不需要划分复杂的冷却通道网格,降低了计算难度,节省了计算资源。将前文所述的耦合计算方法应用到涡轮叶片气动设计流程。搭建了考虑涡轮传热性能的气动优化设计平台,应用该平台对某航空发动机涡轮第二级动叶叶片型线优化设计。叶型参数化采用11参数法。经过前期网格无关性验证,耦合计算外流域网格数为250万,固体域网格为80万,一次耦合计算过程大约耗时2h(计算机CPU为i7-4790,7核)。图 12为优化前后叶型对比,表 6为优化前后性能参数对比,优化后叶片气动效率提高0.34%,冷气流量减少7.66%,而壁面平均温度仅提高1K。式(11)为气动效率公式,式中
| ${\eta _1} = \frac{{0.5{W^2}\left( {GT + GB} \right)}}{{GT\cdot HT + \sum\limits_i {} G{B_i}\cdot H{B_i}}}$ | (11) |

|
Fig. 12 Blade profile before and after optimization |
|
|
Table 6 erformance parameters before and after optimization |
通过本文研究,得到结论如下:
(1) 采用
(2) 考虑工程应用需求,发展一种基于一维管道网络法和三维CFD的耦合计算方法,在气动设计阶段快速评估传热性能。对比全三维耦合计算方法和管网/三维耦合计算方法在不同工况下的计算结果及与实验数据的差异,不同工况下,管网/三维耦合与全三维耦合计算得到的叶片型面压力和换热系数均基本吻合,叶片表面温度分布趋势一致,温度最大偏差为进口温度的3.89%。由于管网/三维耦合计算得到的冷气通道换热系数较全三维耦合偏高,管网/三维耦合计算叶片表面温度相比全三维耦合整体偏低,但是和实验结果更接近。采用管网/三维耦合求解方法分析气冷涡轮叶片共轭传热问题是可行的。
(3) 搭建适合工程应用的考虑传热性能的涡轮叶片气动优化平台,对某燃气涡轮动叶进行型线优化,在保证传热性能同时提高了叶片气动性能,气动效率提高0.34%,冷气流量下降7.66%,壁面平均温度仅提高1K。
下一步需要对叶型优化结果进行详细分析。此外,目前本文计算方法尚不能处理带气膜出流的气冷涡轮,下一步需要对该方法进一步发展。
致谢: 感谢国家自然科学基金资助。
| [1] |
尚仁操, 乔渭阳, 许开富. 气冷涡轮叶片气热耦合数值模拟研究[J]. 机械设计与制造, 2007, 45(12): 11-13. DOI:10.3969/j.issn.1001-3997.2007.12.005 (  0) 0) |
| [2] |
卢少鹏.具有气膜及气热耦合优化功能的涡轮气动设计体系研究[D].哈尔滨: 哈尔滨工业大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014084962.htm
(  0) 0) |
| [3] |
Duboue J, Liamis N, Pate L. Recent Advances in Aero-thermal Turbine Design and Analysis[C]. Las Vegas: 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, 2000.
(  0) 0) |
| [4] |
Rajadas J N, Chattopadhyay A, Pagaldipti N, et al. Shape Optimization of Turbine Blades with the Integration of Aerodynamics and Heat Transfer[J]. Mathematical Problems in Engineering, 1998, 4(1): 21-42. DOI:10.1155/S1024123X98000702
(  0) 0) |
| [5] |
Nicholson J H, Forest A E, Oldfield M L G, et al. Heat Transfer Optimized Turbine Rotor Blades—an Experimental Study Using Transient Techniques[J]. Journal of Engineering for Gas Turbines and Power, 1984, 106(1): 173-182. DOI:10.1115/1.3239531
(  0) 0) |
| [6] |
Nealy D A, Mihelc M S, Hylton L D, et al. Measurements of Heat Transfer Distribution over the Surfaces of Highly Loaded Turbine Nozzle Guide Vanes[J]. Journal of Engineering for Gas Turbines and Power, 1984, 106(1): 149-158. DOI:10.1115/1.3239528
(  0) 0) |
| [7] |
杨玉骏, 戴韧, 王蛟. 燃气透平叶型气动与传热的优化设计[J]. 航空动力学报, 2017, 32(2): 438-445. (  0) 0) |
| [8] |
卢少鹏, 迟重然, 罗磊, 等. 气热耦合条件下涡轮静叶三维优化[J]. 推进技术, 2014, 35(3): 356-364. (LU Shao-peng, CHI Zhong-ran, LUO Lei, et al. Conjugate Heat Transfer 3D Optimization for Turbine Stator[J]. Journal of Propulsion Technology, 2014, 35(3): 356-364.)
(  0) 0) |
| [9] |
罗磊, 卢少鹏, 迟重然, 等. 气热耦合条件下涡轮动叶叶型与冷却结构优化[J]. 推进技术, 2014, 35(5): 603-609. (LUO Lei, LU Shao-peng, CHI Zhong-ran, et al. Conjugate Heat Transfer Optimization for Blade Profiles and Cooling Structure in Turbine Rotor[J]. Journal of Propulsion Technology, 2014, 35(5): 603-609.)
(  0) 0) |
| [10] |
Song Y, Guo Z, Song L, et al. Multi-Objective and Multi-Disciplinary Optimization Design of Gas Turbine Blade Profile and Cooling System Using Conjugate Heat Transfer Analysis[R]. ASME GT 2014-25495.
(  0) 0) |
| [11] |
El Ayoubi C, Ghaly W, Hassan I. Aerothermal Shape Optimization for a Double Row of Discrete Film Cooling Holes on the Suction Surface of a Turbine Vane[J]. Engineering Optimization, 2015, 47(10): 1384-1404. DOI:10.1080/0305215X.2014.969725
(  0) 0) |
| [12] |
王鹏, 邹正平, 周志翔, 等. 适用于不同维数耦合的数值模拟方法研究[J]. 工程力学, 2013, 30(1): 400-406. (  0) 0) |
| [13] |
Gu C W, Li H B, Song Y. Development of an Aero-Thermal Coupled Through-Flow Method for Cooled Turbines[J]. Science China Technological Sciences, 2015, 58(12): 2060-2071. DOI:10.1007/s11431-015-5941-x
(  0) 0) |
| [14] |
Yan P G, Shi L, Wang X F, et al. Retrofit Design of Composite Cooling Structure of a Turbine Blade by Fluid Networks and Conjugate Heat Transfer Methods[J]. Science China Technological Sciences, 2013, 56(12): 3104-3114. DOI:10.1007/s11431-013-5394-z
(  0) 0) |
| [15] |
Martin T J. Computer-Automated Multi-Disciplinary Analysis and Design Optimization of Internally Cooled Turbine Blades[D]. USA: The Pennsylvania State University, 2001.
(  0) 0) |
| [16] |
迟重然, 温风波, 王松涛, 等. 涡轮动叶冷却结构设计方法Ⅱ:管网计算[J]. 工程热物理学报, 2011, 32(6). (  0) 0) |
| [17] |
Hylton L D, Milhec M S, Turner E R, et al. Analytical and Experimental Evaluation of the Heat Transfer Distribution over the Surface of Turbine Vanes[R]. NASA-CR-168015, 1983.
(  0) 0) |
| [18] |
董平.航空发动机气冷涡轮叶片的气热耦合数值模拟研究[D].哈尔滨: 哈尔滨工业大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10213-2010031090.htm
(  0) 0) |
| [19] |
邹歆, 袁新. 湍流建模对透平流热耦合模拟影响研究[J]. 工程热物理学报, 2013, 34(8): 1440-1443. (  0) 0) |
| [20] |
Bak J G, Cho J, Lee S, et al. Effects of Inlet Turbulence Conditions and Near-Wall Treatment Methods on Heat Transfer Prediction over Gas Turbine Vanes[J]. International Journal of Aeronautical & Space Sciences, 2016, 17(1): 8-19.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


