半个多世纪以来的高超声速研究极大地推动了可压缩空气动力学的发展,在此期间,超声速与高超声速气动设计方法也取得了较大的进展。特征线法、流函数坐标、残差修正、伴随方法、优化算法等在不同的时期引领了超声速气动设计的发展方向[1~3]。其中特征线法是一种数值求解超声速无粘流动的重要方法。二维特征线法在超声速流场设计中得到广泛应用[4~6],相比之下,三维特征线法的推广遇到了较大的困难。
三维特征线主要包括参考平面法[7~9]和双特征线方法[10~13]。参考平面法较双特征线方法具有一些优势:在参考平面上的有限差分网格较为简单,可以非常方便地使用特征线网格; 并且可以引入二维特征线中发展较为成熟的激波处理等技术; 与密切理论相类似,将复杂的型面进行降维设计,但参考平面法可以考虑垂直于平面的流动梯度。
国内外对三维超声速复杂气动外形的设计研究有着悠久的历史。Thompson等[14]采用变分法对三维喷管的设计问题展开了研究。Wang等[15, 16]采用CFD结合模拟退火的优化方法对三维圆转椭圆喷管的过渡型面进行了一些优化分析。此外还有一些三维喷管的直接设计方法,如等长度等截面积转换法,超椭圆面积转换法等[17, 18]。在冲压发动机进排气系统的设计领域,能够实现三维超声速气动设计且应用较为成熟的方法主要包括流线追踪技术和密切理论。
Smart等[19, 20]基于流线追踪技术和Busemann基准流场[21]提出REST进气道的设计方法,是进气道设计方法的创新。尤延铖等提出内乘波式进气道的设计概念[22],且具有较高的三维压缩效果。莫建伟等采用双向流线追踪技术,进行进出口形状均可控的三维变截面(圆转方)非对称喷管的设计[23]。
密切理论、密切轴对称理论自Jones等[24]提出以来,广泛应用于内外流压缩流场的组织。在此基础上,密切锥乘波体设计方法[25]、双密切轴对称近似设计方法[26]、三维变截面尾喷管设计方法[27]等不断出现。但在一定几何约束条件下,密切理论难以直接应用于强三维流场的精细组织。
为了进一步探索三维超声速的气动设计方法,本文从降维的三维特征线方法出发,提出三维曲面激波反问题的求解方法。为了验证设计方法的可靠性,采用参考平面法设计了锥形流和平面激波,并用泰勒麦科尔流动和斜激波关系验证了数值方法的精度; 设计了在3°来流攻角下产生圆锥激波的三维型面,并与CFD数值模拟结果进行对比。
2 参考平面解法 2.1 特征方程与相容方程柱坐标系下三维定常、无粘、可压、等熵流动的控制方程为
| $ \begin{array}{*{20}{l}} {u\frac{{\partial \rho }}{{\partial x}} + v\frac{{\partial \rho }}{{\partial r}} + \rho \frac{{\partial u}}{{\partial x}} + \rho \frac{{\partial v}}{{\partial r}} = }\\ { - \frac{w}{r}\frac{{\partial \rho }}{{\partial \phi }} - \frac{\rho }{r}\frac{{\partial w}}{{\partial \phi }} - \frac{{\rho v}}{r}} \end{array} $ | (1) |
| $ u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial r}} = - \frac{w}{r}\frac{{\partial u}}{{\partial \phi }} - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} $ | (2) |
| $ u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial r}} = - \frac{w}{r}\frac{{\partial w}}{{\partial \phi }} - \frac{{vw}}{r} - \frac{1}{{\rho r}}\frac{{\partial p}}{{\partial \phi }} $ | (3) |
| $ u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial r}} = - \frac{w}{r}\frac{{\partial w}}{{\partial \phi }} - \frac{{vw}}{r} - \frac{1}{{\rho r}}\frac{{\partial p}}{{\partial \phi }} $ | (4) |
| $ \begin{array}{*{20}{l}} {u\frac{{\partial p}}{{\partial x}} + v\frac{{\partial p}}{{\partial r}} - {a^2}\left( {u\frac{{\partial \rho }}{{\partial x}} + v\frac{{\partial \rho }}{{\partial r}}} \right) = }\\ { - \frac{w}{r}\frac{{\partial p}}{{\partial \varphi }} + {a^2}\frac{w}{r}\frac{{\partial \rho }}{{\partial \varphi }}} \end{array} $ | (5) |
此外
| $ \frac{{{u^2} + {v^2} + {w^2}}}{2} + \frac{{{a^2}}}{{\gamma - 1}} = \frac{{Ma_0^2}}{2} + \frac{1}{{\gamma - 1}} $ | (6) |
| $ \frac{p}{{{\rho ^\gamma }}}{{\rm{e}}^{ - \left( {\gamma - 1} \right)S}} = {\rm{const}} $ | (7) |
| $ \mathit{\boldsymbol{u}} \cdot \nabla S = 0 $ | (8) |
式(1)为连续方程,式(2)~式(4)为动量方程,式(5)为声速方程。其中,速度
在参考平面方法中,特征线被定义在一个参考平面内,其物理意义为马赫锥及空间流线在该平面上的投影。如果认为式(1)~式(5)的右边项都是已知的,则这些方程组仅依赖于确定参考平面的两个坐标,即为(x,r)。对这两个独立变量进行特征分析,可以推导出适用于参考平面法的特征方程和相容方程。参考面内的特征曲线也称为近特征线。沿近特征线成立的相容方程足以确定解点上除了垂直于参考平面方向的速度分量以外的所有流动参数。剩下的这一个速度分量由垂直于参考平面方向的动量方程来确定,如式(4)所示。
柱坐标系
特征方程
| $ {\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}x}}} \right)_0} = {\lambda _0} = \frac{v}{u} $ | (9) |
| $ {\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}x}}} \right)_ \pm } = {\lambda _ \pm } = {\rm{tan}}\left( {\theta \pm \mu } \right) $ | (10) |
相容方程
| $ {{\rm{d}}_ \pm }\theta \frac{{\sqrt {Ma_*^2 - 1} }}{{\rho {q^2}}}{{\rm{d}}_ \pm }p = \frac{{{F_1}c{\rm{os}}\mu \mp {F_2}{\rm{sin}}\mu }}{{{\rm{cos}}(\theta \pm \mu )}}{{\rm{d}}_ \pm }x $ | (11) |
| $\rho q{{\rm{d}}_0}q + {{\rm{d}}_0}p = \left( { - \frac{w}{r}\frac{{\partial q}}{{\partial \phi }} + \frac{{{w^2}}}{r}{\rm{sin}}\theta } \right)\rho {{\rm{d}}_0}s$ | (12) |
| $q{{\rm{d}}_0}w = \left( { - \frac{w}{r}\frac{{\partial w}}{{\partial \phi }} - \frac{{vw}}{r} - \frac{1}{{\rho r}}\frac{{\partial p}}{{\partial \phi }}} \right){{\rm{d}}_0}s$ | (13) |
| $q({{\rm{d}}_0}p - {a^2}{{\rm{d}}_0}\rho ) = ( - \frac{w}{r}\frac{{\partial p}}{{\partial \phi }} + {a^2}\frac{w}{r}\frac{{\partial \rho }}{{\partial \phi }}){\rm{d}}{s_0}$ | (14) |
式(11)中的
| ${F_1} = \frac{{{w^2}}}{{{q^2}r}}{\rm{cos}}\theta - \frac{w}{{qr}}\frac{{\partial \theta }}{{\partial \phi }}$ | (15) |
| $\begin{array}{*{20}{l}} {{F_2} = \frac{w}{{\gamma qpr}}\frac{{\partial p}}{{\partial \phi }} - \frac{w}{{{q^2}r}}\frac{{\partial q}}{{\partial \phi }} + }\\ {\frac{1}{{qr}}\frac{{\partial w}}{{\partial \phi }} + \frac{{{\rm{sin}}\theta }}{r}\left( {1 + \frac{{{w^2}}}{{{q^2}}}} \right)} \end{array}$ | (16) |
式中θ,q分别为参考平面内的流动方向角、平面速度大小,
| $Ma_{\rm{*}}^2 = \left( {{u^2} + {v^2}} \right)/{a^2}$ | (17) |
因此,从式(11)中可以看出,只有当平面马赫数大于1时,平面内的特征锥才是实的。故该方法不适用于横向速度过大的流动,因为尽管来流为超声速,但垂直于参考平面速度太大时,
从式(9)~式(16)中可以看出:参考平面法的特征方程和相容方程与二维(或者轴对称)特征线方法具有相同形式,当方程右手端的周向偏导数(
参考平面法的主要优势是简单,仅用了三条近特征线,而且流动参数在初值点上的内插是简单的线性内插,解可以在参平面内灵活地采用正步或者逆步进法。这个方法已被Moretti[28],Katskova等[29],Rakich[7, 8]成功应用于定常三维超声速流动中。
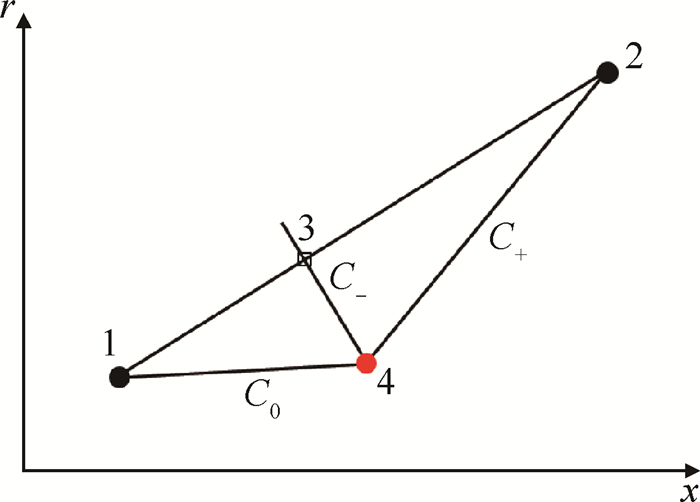
2.2 参考平面解法在参考平面内,已知图 1中直线L12为激波微元,点1和点2为已知值,其流动参数可根据斜激波关系式求得。点2发出的左行特征线
|
Fig. 1 Unit progress of tracing |
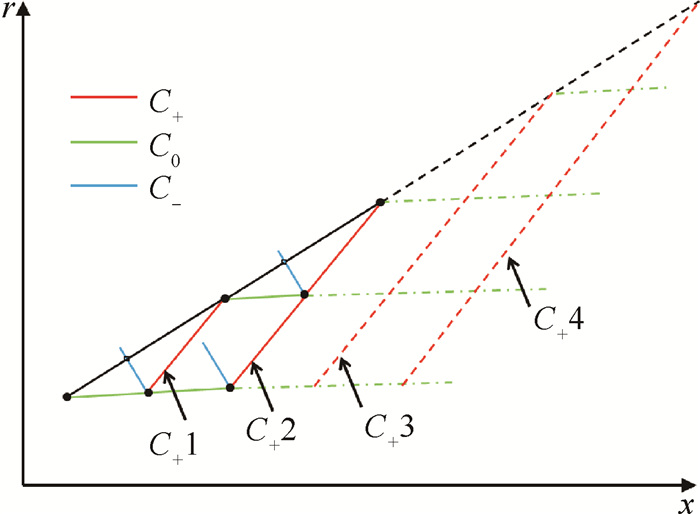
在参考平面内重复图 1所示的单元过程,可以追踪出从激波点发的左行特征线,直至参考平面内的壁面点,即为图 2中激波点至壁面流线点的红色实、虚线,记为
|
Fig. 2 Characteristics in reference plane |
n个参考平面内的左行特征线拼合成特征曲面,可用下式表达
| ${F_ + }\left( 1 \right) = \{ {C_ + }\left( 1 \right)\left( i \right)|i \le n, {\rm{}}i \in {\rm{N}}\} $ | (18) |
即
| ${\rm{Flow~field}} = \left\{ {{F_ + }\left( i \right)|i \le k, {\rm{}}i \in {\rm{N}}} \right\}$ | (19) |
式中k表示步进次数。
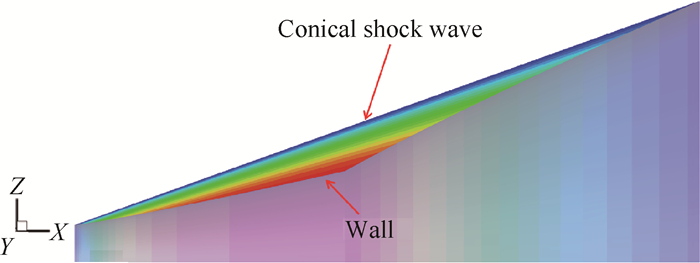
以下详细介绍三维流场的生成过程,以锥形激波的波后流场为例,流场如图 3所示,这里旨在描述算法中相关概念的三维空间结构,流场的相关参数详见2.3.1节。
|
Fig. 3 Conical shock wave and wall |
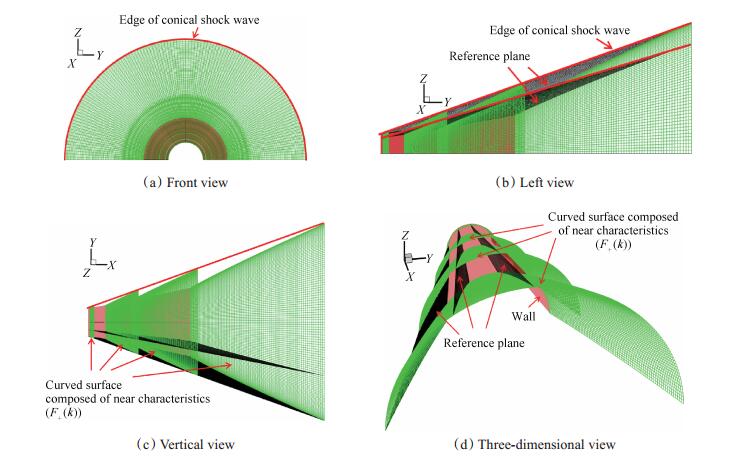
给定图 3中的锥形激波,求解对应的壁面。采用一系列参考平面(等
|
Fig. 4 Characteristic grid of conical shock at zero angle of attack |
在求解第一个步进面
采用如图 5所示的预估校正向下游空间步进,具有较好的收敛性,迭代过程为
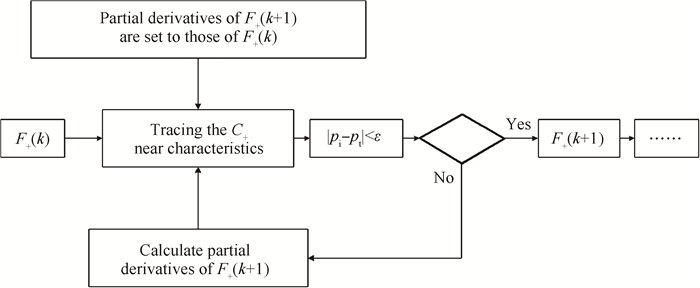
|
Fig. 5 Progress of integral iteration |
(1) 预估
(2) 完成
(3) 在曲面
(4) 返回步骤(2)直至收敛。
(5) 进行
综上所述,参考平面法通过参考面内的局部迭代和垂直于参考面的周向迭代,以及彼此间的相互嵌套完成曲面的空间步进,从而逐渐生成三维复杂型面。
2.3 精度验证为了验证设计方法的可靠性和精度,本节设计了两个算例:无攻角的锥形激波、平面激波,并与理论解进行对比验证。
2.3.1 锥形激波给定均匀来流,马赫数为4,比热比为1.25,气体常数为287J/(kg·K),流动方向为x方向。再设定锥形激波的半锥角为19.92°,锥顶点位置在(0,0,0),轴线为x轴。在相同来流马赫数下。锥面激波开始脱体时的半锥角要大于平面激波的二维斜劈角,因此所设定的锥形激波具有物理解。
为了减少计算,考虑空间的对称性,仅取锥形激波的一半进行计算:

|
Fig. 6 Conical shock wave and corresponding wall |
无攻角锥形激波的波后流场是无旋的,为锥型流,其控制方程是一个二阶非线性常微分方程(Taylor-Maccoll方程[30, 31]),因此可将其作为评判图 6流场精度的标准。图 7中展示了流场压力随球面角的关系,其中黑色点为数值积分Taylor-Maccoll方程获得的无量纲压力分布,红色的线表示参考平面法解,可以看出,对于轴对称流动,参考平面法具有非常高的计算精度,其中压力的最大相对误差为0.128%,速度误差小至3.2×10-5。
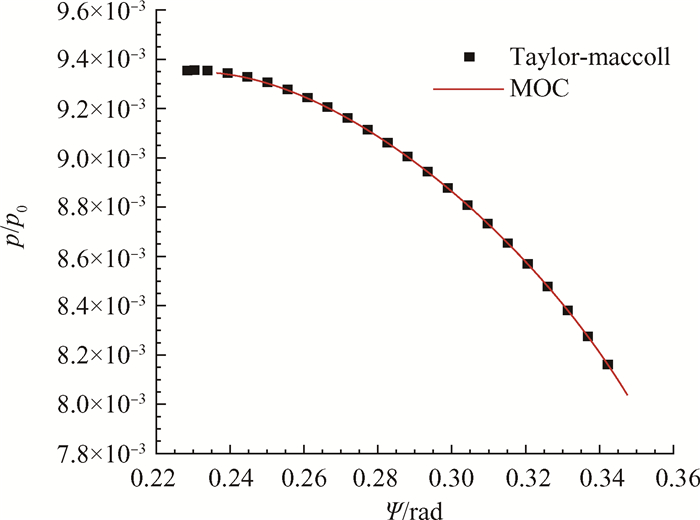
|
Fig. 7 Comparison of pressure distribution between Taylor-Maccoll flow and results from reference plane method |
上一小节中采用锥形流验证参考平面法的有效,但在该流动中,垂直于参考平面的流动梯度均为零,参考平面法实则退化成了轴对称的特征线方法。考虑到平面激波有理论解,且通过坐标变换(直角坐标系转化到柱坐标系)使得速度矢量具有周向梯度,因此采用平面激波验证周向偏导数不全为零时参考平面法的有效性。
如图 8所示,来流马赫数为4,流动参数均与上一小节相同,图中红色的平面激波过z轴,并与zx平面成19.92°夹角。初值线为x=0.1m与平面激波相贯的直线。将波后
| ${F_ + }\left( {80} \right) = \{ {C_ + }\left( {80} \right)\left( i \right)|i \le 41, {\rm{}}i \in {\rm{N}}\} $ | (20) |
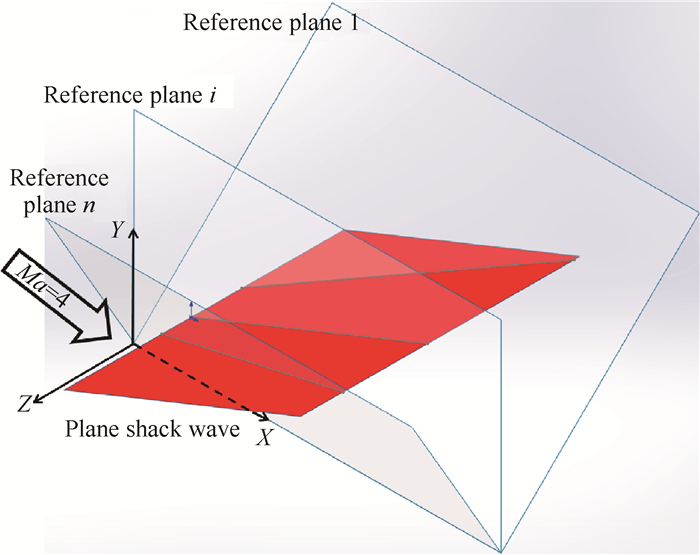
|
Fig. 8 Diagram of reference plane method for plane shock wave |
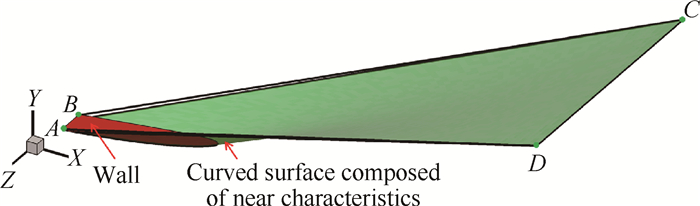
|
Fig. 9 Plane shock wave and corresponding wall |
通过与斜激波关系式对比,压力、马赫数的最大相对误差分别为6.1×10-5,4.8×10-6,在一定程度上验证了参考平面法的有效性。
3 结果与讨论高超声速飞行器在进行有攻角巡航时,进气道第一道激波的波后流场是三维的,而按照轴对称理论设计的第一道激波通常不能完全封住唇口。因此,可采用参考平面法求解三维激波反问题,使得三维激波的形状和强度得以控制。本节设计了在3°来流攻角情况下,产生圆锥激波的三维型面,即在设计状态进行3°攻角巡航时,高超声速飞行器头部产生圆锥形封口激波。
3.1 流场设计为了保证解的存在,预设锥形激波形状与2.3.1节相同,即锥形激波的半锥角为19.92°,锥顶点位置在(0,0,0)。来流马赫数为4,流动参数均与上节相同。来流存在攻角,流动方向平行于xy平面,与x轴夹角为3°,如图 10所示。

|
Fig. 10 Diagram of initial conical shock wave and the flow condition |
为了减少计算,考虑空间的对称性,仅取锥形激波的一半进行计算:

|
Fig. 11 Conical shock wave and corresponding wall |
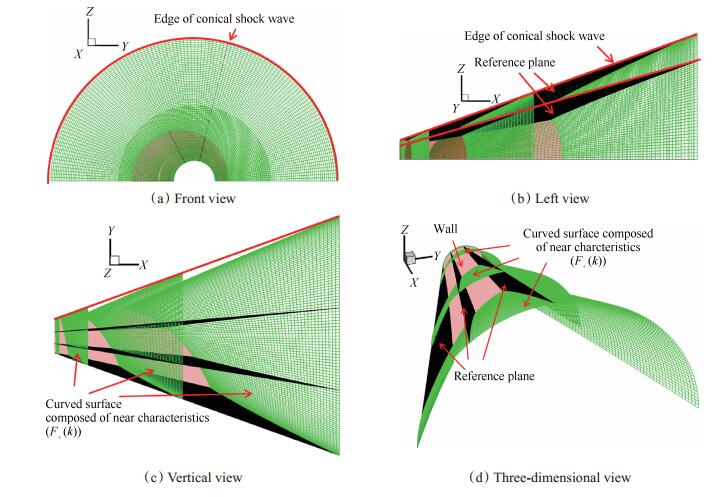
|
Fig. 12 Characteristic grid of conical shock at small angle of attack |
采用商用软件Fluent对设计的三维型面进行数值模拟,模拟的控制方程为Euler方程,网格划分如图 13(a)所示,其网格量约为262万; 作为对比,降低沿壁面法向的网格量,约为178万。三维压力场如图 13(b)所示。提取x=0.15,0.2,0.25,0.3,0.35m处的激波形状,并与设计值对比,如图 14所示,图中点表示不同空间位置处预设的激波位置,黑线表示数值模拟所得激波,可以看出,设计激波和计算激波基本一致,即:完成了在3°来流攻角情况下,产生圆锥激波的三维型面设计。
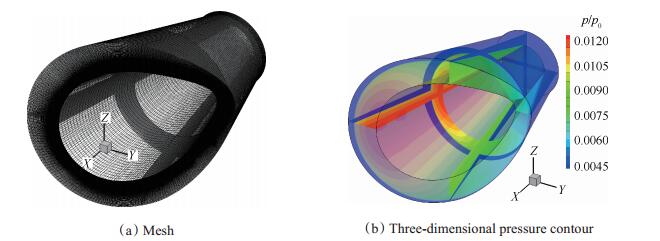
|
Fig. 13 CFD simulations |
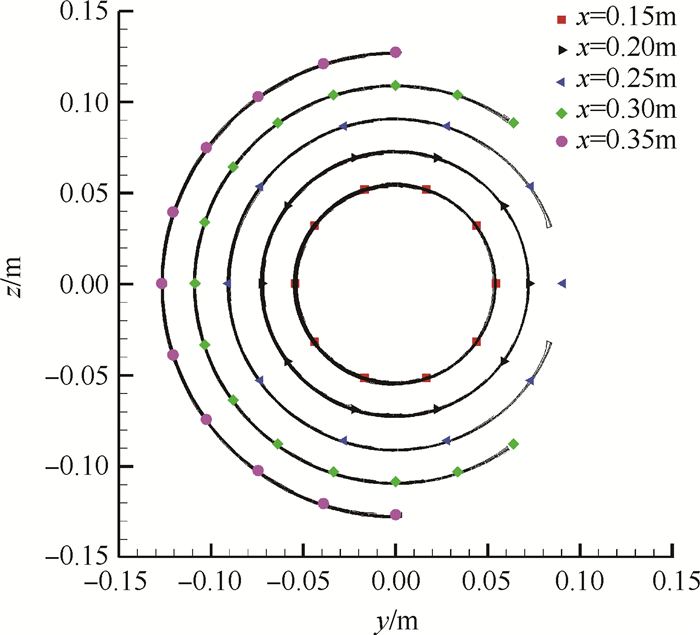
|
Fig. 14 Comparison of shock geometry between the given and simulations |
对比x=0.3m截面,y=0m和z=0.01m方向的马赫数分布,图 15所示为z=0.01m方向的马赫数分布,其中红线为参考平面法解,黑点为262万网格量下的CFD解,绿点为178万网格量下的CFD解。从图中可以看出,除了激波由于网格尺度的影响使其厚度有所不同外,结果基本一致,因此CFD解具有一定的可信性。通过对比,可得在y=0m方向压力、马赫数的最大相对误差分别为1.6%,0.27%;在z=0.01m方向压力、马赫数的最大相对误差分别为1.56%,0.35%。
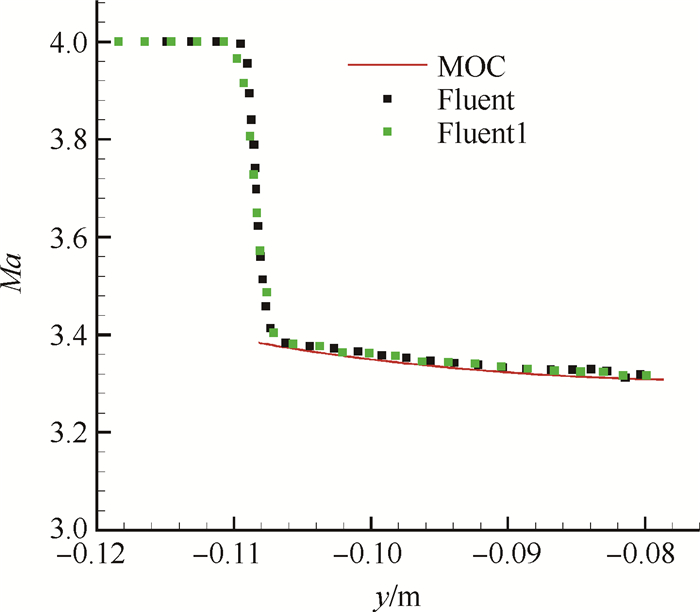
|
Fig. 15 Comparison of Mach number between reference plane method and CFD (x=0.3m, z=0.01m) |
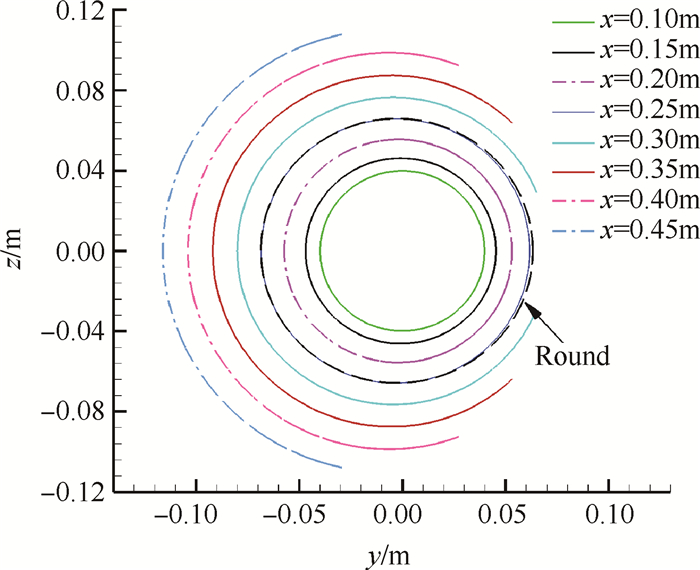
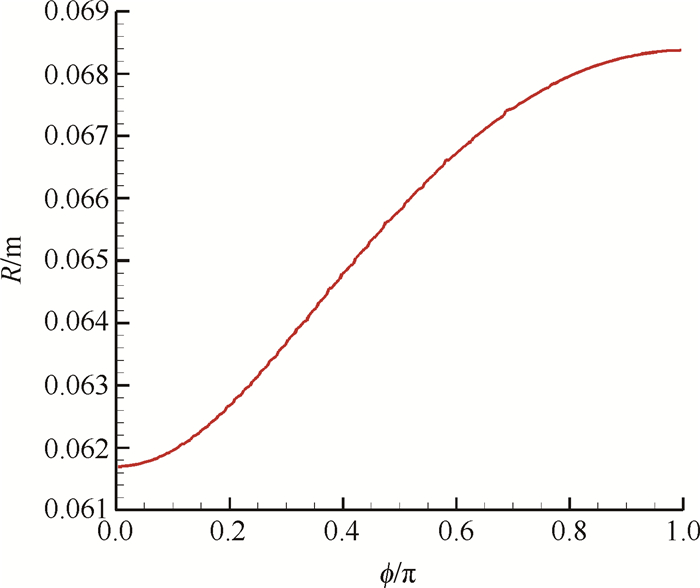
图 16为有攻角的锥形激波对应的三维型面,且在x=0.25m处叠加了一个虚线圆,定性地表明,迎风面壁面曲率半径大于背风面。图 17为x=0.25m处壁面轮廓的曲率半径,从图中可以看出,从迎风面至背风面,壁面的曲率半径逐渐减小。
|
Fig. 16 Three-dimensional construction of wall |
|
Fig. 17 Wall radius of curvature at x=0.25m |
通过本文研究,得到如下结论:
(1) 本文提出了曲面激波反问题的参考平面解法,可在每个平面内设计激波曲线,通过考虑平面法向的偏导数保证三维流动计算的准确性。
(2) 采用采用泰勒-麦科尔流动和斜激波关系式验证了该设计方法的精度,其中压力的相对误差分别为1.3×10-3,6.1×10-5。
(3) 基于参考平面法设计了在3°来流攻角下产生圆锥激波的型面,并与传统的数值模拟进行对比,流场参数最大误差不超过2%。
(4) 在有攻角超声速自由流条件下,产生圆锥激波的三维型面具有从迎风面至背风面曲率半径逐渐降低的特征。
致谢: 感谢国家自然科学基金资助。
| [1] |
Dulikravich G S. Shape Inverse Design and Optimization for Three Dimensional Aerodynamics[R]. AIAA 95-0695.
(  0) 0) |
| [2] |
Eyi S, Yumusak M. Three Dimensional Rocket Nozzle Design Using Adjoint Method[R]. AIAA 2013-4086.
(  0) 0) |
| [3] |
刘红阳.特征线追踪方法和应用[D].长沙: 国防科技大学, 2015.
(  0) 0) |
| [4] |
易仕和, 赵玉新, 何霖, 等. 超声速与高超声速喷管设计[M]. 北京: 国防工业出版社, 2013.
(  0) 0) |
| [5] |
左克罗M J, 霍夫曼J D.气体动力学[M].王汝涌等译.北京: 国防工业出版社, 1984.
(  0) 0) |
| [6] |
童秉纲, 孔祥言, 邓国华. 气体动力学[M]. 北京: 高等教育出版社, 1990.
(  0) 0) |
| [7] |
Rakich J V. Theoretical and Experimental Study of Supersonic Steady Flow around Inclined Bodies of Revolution[J]. AIAA Journal, 1970, 8(3): 511-518. DOI:10.2514/3.5698
(  0) 0) |
| [8] |
Rakich J V. Calculation of Hypersonic Flow over Bodies of Revolution at Small Angles of Attack[J]. AIAA Journal, 1965, 3(3): 458-464. DOI:10.2514/3.2886
(  0) 0) |
| [9] |
Fong J, Sirovich L. Supersonic Inviscid Flow—A Three-Dimensional Characteristics Approach[J]. Journal of Computational Physics, 1987, 68(2): 378-392. DOI:10.1016/0021-9991(87)90063-5
(  0) 0) |
| [10] |
Butler D S. The Numerical Solution of Hyperbolic Systems of Partial Differential Equations in Three Independent Variables[J]. Proceedings of the Royal Society of London A:Mathematical, Physical and Engineering Science, 1960, 255(1281): 232-252. DOI:10.1098/rspa.1960.0065
(  0) 0) |
| [11] |
Ransom V H, Hoffman J D, Thompson H D. A Second-Order Numerical Method of Characteristics for Three-Dimensional Supersonic Flow[D]. USA: Purdue University, 1970.
(  0) 0) |
| [12] |
Cline M C, Hoffman J D. Comparison of Characteristic Schemes for Three-Dimensional, Steady, Isentropic Flow[J]. AIAA Journal, 1972, 10(11): 1452-1458. DOI:10.2514/3.50389
(  0) 0) |
| [13] |
蓝庆生, 赵玉新, 赵一龙, 等. 三维超声速流动的压力反问题[J]. 空气动力学学报, 2017, 35(3): 429-435. DOI:10.7638/kqdlxxb-2016.0156 (  0) 0) |
| [14] |
Thompson H D, Murthy S N B. Design of Optimized Three-Dimensional Nozzles[J]. Journal of Spacecraft, 1966, 3(9): 1384-1393. DOI:10.2514/3.28664
(  0) 0) |
| [15] |
Wang X, Damodaran M. Optimal Three-Dimensional Nozzle Shape Design Using CFD and Parallel Simulated Annealing[J]. Journal of Propulsion and Power, 2015, 18(1): 217-221.
(  0) 0) |
| [16] |
Xing X Q, Damodaran M. Design of Three-Dimensional Nozzle Shapes Using NURBS, CFD and Hybrid Optimization Strategies[R]. AIAA 2004-4368.
(  0) 0) |
| [17] |
Meenaksh R, Hoffman J D, Murthy S N B. Design and Performance Computations in Complex 3-D Nozzles[R]. AIAA 99-0882.
(  0) 0) |
| [18] |
覃粒子, 王长辉, 刘宇, 等. 三维喷管设计[J]. 推进技术, 2005, 26(6): 499-521. (QIN Li-zi, WANG Chang-hui, LIU Yu, et al. Three-Dimensional Nozzle Design[J]. Journal of Propulsion Technology, 2005, 26(6): 499-521. DOI:10.3321/j.issn:1001-4055.2005.06.005)
(  0) 0) |
| [19] |
Smart M K. Design of Three-Dimensional Hypersonic Inlets with Rectangular-to-Elliptical Shape Transition[J]. Journal of Propulsion and Power, 1999, 15(3): 408-416. DOI:10.2514/2.5459
(  0) 0) |
| [20] |
Gollan R J, Smart M K. Design of Modular Shape-Transition Inlets for a Conical Hypersonic Vehicle[J]. Journal of Propulsion and Power, 2013, 29(4): 832-838. DOI:10.2514/1.B34672
(  0) 0) |
| [21] |
Molder S Szipiro. Busemann Inlet for Hypersonic Speeds[J]. Journal of Spacecraft and Rockets, 1966, 3(8): 1303-1304. DOI:10.2514/3.28649
(  0) 0) |
| [22] |
尤延铖, 梁德旺, 黄国平. 一种新型内乘波进气道初步研究[J]. 推进技术, 2006, 27(3): 252-256. (YOU Yan-cheng, LIANG De-wang, HUANG Guo-ping. Investigation of Internal Waverider-Derived Hypersonic Inlet[J]. Journal of Propulsion Technology, 2006, 27(3): 252-256. DOI:10.3321/j.issn:1001-4055.2006.03.015)
(  0) 0) |
| [23] |
Mo J W, Xu J L, Gu R, et al. Design of an Asymmetric Scramjet Nozzle with Circular to Rectangular Shape Transition[J]. Journal of Propulsion and Power, 2014, 30(3): 812-819. DOI:10.2514/1.B34949
(  0) 0) |
| [24] |
Jones K D, Sobieczky H, Seebass A R, et al. Waverider Design for Generalized Shock Geometries[J]. Journal of Spacecraft and Rockets, 1995, 32(6): 957-963. DOI:10.2514/3.26715
(  0) 0) |
| [25] |
赵博.乘波体飞行器气动外形设计及其数值验证[D].哈尔滨: 哈尔滨工程大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014133727.htm
(  0) 0) |
| [26] |
尤延铖, 梁德旺. 基于内乘波概念的三维变截面高超声速进气道[J]. 中国科学(E辑), 2009, 39(8): 1483-1494. (  0) 0) |
| [27] |
卢鑫, 岳连捷, 肖雅彬, 等.超燃冲压发动机三维变截面尾喷管设计[C].无锡: 第三届高超声速科技学术会议, 2010.
(  0) 0) |
| [28] |
Moretti G. Three-Dimensional Supersonic Flow Computations[J]. AIAA Journal, 1963, 1(9): 2192-2193. DOI:10.2514/3.2039
(  0) 0) |
| [29] |
Katskova O N, Chushkin P I. Three-Dimensional Supersonic Equilibrium Flow of a Gas Around Bodies at Angles of Attack[R]. NASA TT F-9790, 1965.
(  0) 0) |
| [30] |
Taylor G I, Maccoll J W. The Air Pressure on a Cone Moving at High Speeds[J]. Proceeding of the Royal Society of London, Series A, 1933, 139: 279-311.
(  0) 0) |
| [31] |
Maccoll J W. The Conical Shock Wave Formed by a Cone Moving at High Speed[J]. Proceeding of the Royal Society of London, Series A, 1937, 159: 459-472. DOI:10.1098/rspa.1937.0083
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


