2. 国防科学技术大学 高超声速冲压发动机技术重点实验室,湖南 长沙 410073
2. Science and Technology on Scramjet Laboratory, National University of Defense Technology, Changsha 410073, China
边界层抽吸是指通过将边界层部分流体除去(吸除、剥离),降低边界层厚度,增大壁面附近气流速度,从而使其更为稳健,甚至消除分离的流动控制方法。该方法一般是被动抽吸,即利用压差达到抽吸的效果,因此机构简单、易于实现,已在压气机叶片[1]、超声速进气道[2~5]、跨声速风洞实验段[6]和超声速静风洞喉道段[7]中都有成功应用的例子。特别是边界层抽吸技术在避免激波振荡和流动分离,缓解进气道流场畸变上表现出明显效果,在目前超声速飞行器中应用较为成熟,美国F-15战斗机进气道即采用了多孔散步式抽吸技术[8]。
Hamed等[9~11]和Hahn等[12]通过二维数值计算解释了抽吸位置对边界层干扰的控制效果存在差异的原因,并发现对控制激波诱导边界层分离的效果有重要影响的关键参数,包括排气孔与激波冲击点的相对位置、排气孔的尺寸与来流附面层厚度的关系、孔数、孔间距及孔的深度比以及孔轴线角度等。
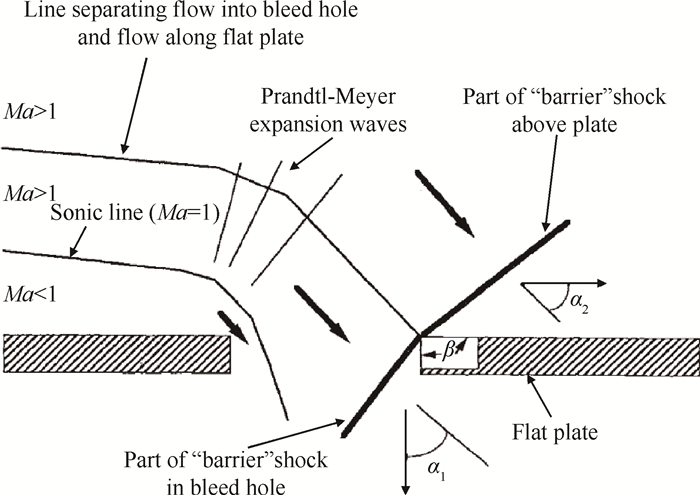
基于前人的研究基础,Rimlingert等[13]、Shih等[14]、Hamed等[15]通过CFD方法对带集气腔结构的圆形孔抽吸壁面与平板激波边界层干扰流场相互作用的流动进行了研究,并初步勾勒出抽吸控制激波/边界层干扰时抽吸孔附近的细观流场结构,如图 1所示。Chyu等[16]、Rimlingert等[17]研究了抽吸孔角度、多抽吸孔流向排列时上下游孔的相互影响、抽吸孔压比变化以及多孔排列时孔间距等参数对激波边界层干扰流场的作用机理。
|
Fig. 1 Distribution of flow field structure in the bleed slot[15] |
在边界层抽吸领域,抽吸腔压力无疑是影响边界层抽吸的重要参数。研究表明,随着抽吸腔压力的降低,抽吸流量系数逐渐增加,多孔排列产生的膨胀波和压缩波的强度逐渐增强,同时其影响范围也逐渐变大。Chyu等[16],Rimlingert等[17]研究了抽吸孔压比的变化对激波边界层干扰流场的作用机理。发现压比的变化为0.3~1.7,这代表抽吸孔处于流通与堵塞交替出现的状态。Willis等[18]通过试验测量了不同马赫数时边界层抽吸的音速流量系数Q随压比的变化规律。
在低压比时,音速流量系数随压比变化较为缓慢,甚至几乎保持不变,而随着压比的增加,音速流量系数减小的速率明显加快。Willis开展的这些试验为后续CFD边界壁面条件的处理提供了良好的数据支撑,大量研究人员都把Willis的试验结果用来验证自己研究成果的正确性。需要说明的是,上述研究者是将主流区、抽吸孔、抽吸腔一起生成网格进行计算的,而Slater[19]则是通过将抽吸区域作为一种边界条件来处理的。对90°抽吸孔的音速流量系数进行修改,发展了一种计算抽吸流量的模型,且该模型只与抽吸腔压力与来流壁面压力的比值有关,同时Slater用Willis等[18],Shaw等[20]的试验数据对自己的模型进行了验证,结果与试验几乎一致,验证了模型的准确性。
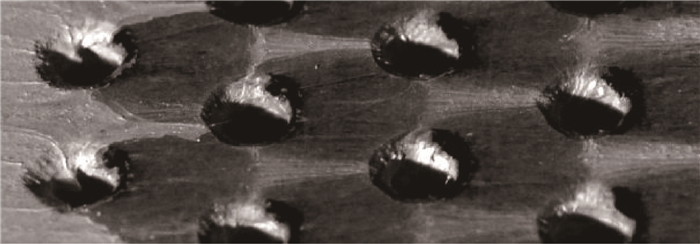
随着科技的进步,流场测量的手段也越来越丰富和精密,Oorebeek[21~23]使用了激光多普勒测速仪(LDV)、纹影技术、油流显示技术三种流场测量手段对超声速边界层抽吸孔隙内三维流动情况开展了试验研究,通过分析抽吸区域下游边界层的发展情况发现抽吸孔下游的涡对边界层的形状因子、表面摩阻系数有重要影响。如图 2所示为油流显示技术得到的抽吸孔附近流场结构图,图中颜色越深的区域表示表面摩擦越大,分析发现沿翼展方向流场结构分布较为规律,而沿流动方向颜色越来越浅,说明表面摩擦越来越小。
|
Fig. 2 Oil flow results of the flow field structure in the bleed hole[23] |
分析上述研究现状发现,关于抽吸孔隙附近流场结构的研究比较成熟,但是在试验方面的研究还并不多见,特别是使用纹影拍摄抽吸槽局部流场结构方面的研究比较稀少,并且,目前暂无关于使用NPLS拍摄抽吸槽附近局部精细流场结构的研究。
基于上述研究的不足,本文通过试验研究的方法,利用纹影和NPLS两种流动显示技术得到了不同抽吸腔反压时抽吸槽内局部流场结构。同时试验还测量了抽吸质量流量,对抽吸性能也进行了分析。
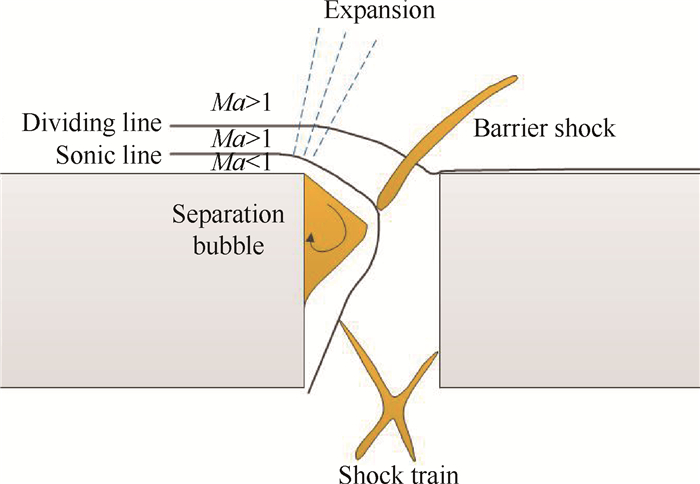
总结前人的研究成果发现,常见的抽吸槽附近流场结构组成主要包括:障碍激波,分离区,剪切层,膨胀波,激波串。具体分布如图 3所示。
|
Fig. 3 Schematic diagram of the flow field structure distribution in the bleed slot |
由于下游扰动可通过边界层内的亚声速层向上游传递,因此气流在未到达抽吸槽入口处时就已经开始向抽吸槽壁面方向偏转,这时边界层内的超声速部分运动方向也产生偏转,从而形成膨胀波。气流进入抽吸槽后,由拐角膨胀特性易知将会在抽吸槽上游壁面形成分离区,另外由于抽吸槽下游壁面的存在,对膨胀加速进入抽吸槽的气流压缩,进而产生障碍激波。从图 3中可明显看到,障碍激波结构为两段式,由平板上部分激波与抽吸槽内激波组成,且障碍激波近似为正激波。需要说明的是,图 3中激波串需要在一定抽吸腔反压条件下才会出现,另外分离区的形态与抽吸槽的尺寸及抽吸腔反压密切相关[24]。
2 试验装置 2.1 风洞试验台试验在国防科大吸气式超声速风洞上开展,如图 4所示。试验风洞由过渡段、稳定段、喷管、试验段、扩压段等部件组成。图 4中真空罐下游连接1000m3的真空球,为抽吸腔营造低反压的条件。风洞试验段可观测窗口范围为40mm×160mm。

|
Fig. 4 Supersonic wind tunnel test bench |
NPLS系统主要包括纳米粒子发生系统、脉冲片光系统、CCD成像系统和同步系统等四个子系统。纳米粒子发生系统主要指纳米粒子发生器,其主要功能在于为试验过程提供均匀的纳米粒子颗粒。经过大量调研和对多种示踪粒子试验的分析,最终选择了二氧化钛(TiO2)粒子作为粒子发生器的工作粒子,具体见文献[25]。
2.2 试验模型和条件图 5为试验段实物图,试验段入口尺寸为56mm×120mm。试验段和喷管进行了一体化设计,并对喷管和试验段壁面进行了粘性修正和消波处理。

|
Fig. 5 Physical map of the test section |
试验段采用两侧和顶部开窗的方式来满足纹影及NPLS测量对光源的需求,抽吸槽上下游分别均布6个测压点,并在下壁面焊接导管,最后通过测压管从抽吸腔引出至压力扫描阀。
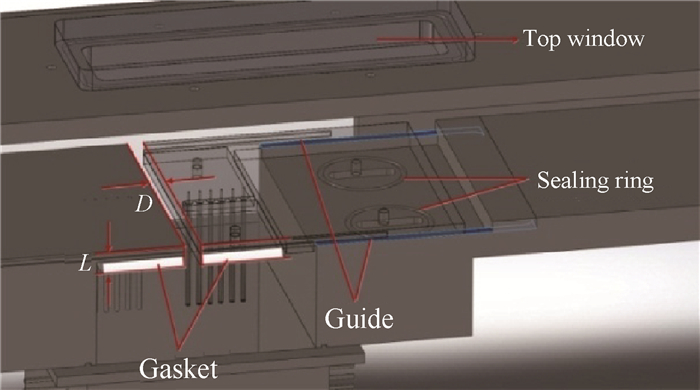
设计试验段时,考虑到试验的重复性和参数可调性,抽吸槽下游的底部平板可沿设计导轨前后移动,以此实现抽吸槽宽度D可调,图 6中蓝色部分为试验段设计的导轨,移动下游底部平板至所需宽度D后,在平板底部拧入螺钉固定,螺钉四周设计有密封圈保证气密性。另外,通过在试验段底部下壁面添加一定厚度的垫片,实现试验段抽吸槽深度L可调,垫片通过螺钉固定,如图 6所示。风洞试验段入口参数见表 1。
|
Fig. 6 Schematic diagram of the test setion |
|
|
Table 1 Entrance parameters of wind tunnel test section |
为了得到超声速来流情况下,壁面开槽进行抽吸时,抽吸槽附近的局部流场结构,首先使用了纹影技术。特别地,还使用了纳米粒子平面激光散射技术(NPLS)对抽吸槽附近的局部精细流场结构进行了显示。试验过程中,通过在抽吸腔下游管路中安装的手动蝶阀对抽吸腔反压进行手动调节。另外,通过在抽吸腔下游管路安装音速喷嘴,对抽吸的流量进行了测量。其原理是通过音速喷嘴实现声速节流,然后使用流量公式来计算流量。当音速喷嘴出口压力与入口压力比值低于0.528时,音速喷嘴达到工作条件。
流量公式为
| $\dot m = K \cdot \frac{{{p^{\rm{*}}}}}{{\sqrt {{T^{\rm{*}}}} }} \cdot {A_1} \cdot q\left( \lambda \right)$ | (1) |
式中p*为音速喷嘴入口总压,T*为音速喷嘴入口总温,A1为音速喷嘴喉道截面积,q(λ)为流量函数,标准大气条件下K=0.04042。当气流速度为声速时,流量函数q(λ)=1。因为试验过程中总温是保持不变的,此时流量公式中变量只有音速喷嘴入口总压,因此只需测量音速喷嘴入口总压即可计算流量。
对得到的抽吸流量进行无量纲处理,得到音速流量系数,用于评价抽吸性能。音速流量系数用大写字母Q表示,具体计算公式如下
| $Q = \frac{{{{\dot m}_{{\rm{real}}}}}}{{{{\dot m}_{{\rm{sonic}}}}}}$ | (2) |
式中
| ${{\dot m}_{{\rm{sonic}}}} = K \cdot \frac{{{p_0}}}{{\sqrt {{T^{\rm{*}}}} }} \cdot {A_2}$ | (3) |
式中p0为来流静压,T*为来流总温,A2为抽吸槽面积,标准大气条件下,K=0.04042。式中p0取静压而未取总压的原因是,对于壁面边界层抽吸而言,气流向抽吸孔隙内偏转时有Y向速度,这是由静压差引起的,因此用静压更合理。
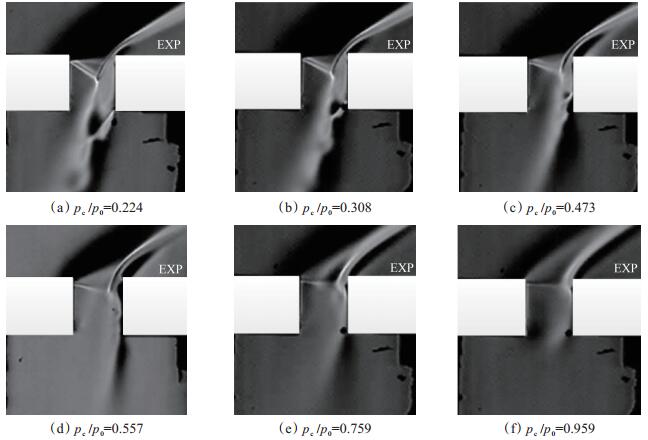
3 结果与讨论 3.1 不同压比时纹影结果图 7~图 9分别为不同抽吸槽宽度、深度时,抽吸槽内流场结构随抽吸腔反压变化情况的纹影结构图,图中pc表示抽吸腔反压,p0表示來流静压,δ表示抽吸槽入口处边界层厚度。可以发现对于超声速类型抽吸[26]而言,抽吸槽附近存在障碍激波、分离区、膨胀波、激波串等流场结构。无论抽吸槽宽度、深度如何变化,抽吸槽内流场结构随压比变化规律都是一致的。进一步分析抽吸槽内局部流场结构发现,低压比(pc/p0=0.25左右)时,抽吸腔内存在激波串,随着压比的增加,激波串长度逐渐减小。当压比超过一定值(pc/p0=0.6左右)后,激波串消失。通过分析气流经过抽吸槽时的膨胀角度以及障碍激波的位置发现,随着抽吸腔压力的增加,即压比增加,气流膨胀角度逐渐减小,且障碍激波逐渐向抽吸槽下游靠近,同时障碍激波下半段的长度逐渐减小。上述变化的原因在于抽吸腔内压力的改变通过抽吸槽内亚声速边界层向抽吸槽入口处传递,进而影响边界层的抽吸[25]。此结论不仅丰富了边界层抽吸方面的基础研究成果,对进一步明晰边界层抽吸的机理同样具有重要的参考价值。

|
Fig. 7 Schlieren results of the flow field structure in the bleed slot(δ/D=2.57, L/D=1.67) |
|
Fig. 8 Schlieren results of the flow field structure in the bleed slot(δ/D=1.54, L/D=1) |

|
Fig. 9 Schlieren results of the flow field struture in the bleed slot(δ/D=1.1, L/D=1.43) |
如图 10所示为通过NPLS技术得到的抽吸槽内局部精细流场结构图。从图中可清晰地看到抽吸槽内的分离区、剪切层、障碍激波等典型流场结构。

|
Fig. 10 NPLS results of the flow field structure in the bleed slot(δ/D=1.54, L/D=2) |
由于试验中打光方式的限制,抽吸腔内的流场结构无法通过试验显示。进一步分析试验结果发现,与通常情况一致,障碍激波为上下两段式结构,且抽吸槽内分离区外延的剪切层与障碍激波下半段几乎垂直,即障碍激波下半段可认为是正激波。之前的研究表明抽吸槽内分离区存在两种状态:开口和闭口[24]。通过分析NPLS结果,很容易发现低压比时抽吸槽内分离区为闭口状态,而高压比时抽吸槽内分离区为开口状态,且高压比的气流膨胀角度明显小于低压比情况。由于抽吸槽的存在导致抽吸槽处的边界层迅速消失,经过障碍激波后边界层又迅速发展起来。这种流场结构的变化规律与相同条件下的纹影结果一致。
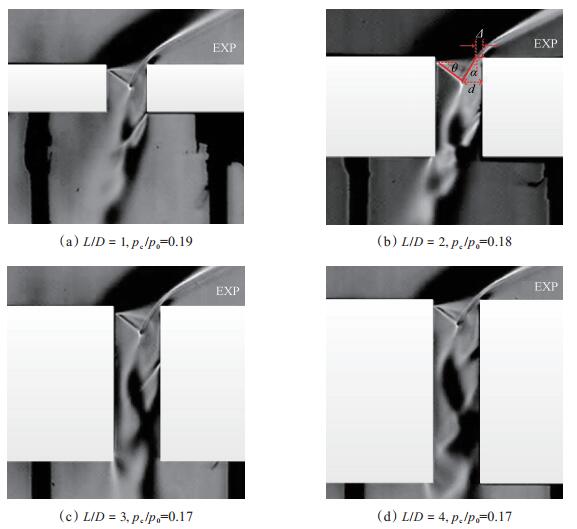
3.3 不同深宽比时纹影结果从图 11中可清楚地看到抽吸槽附近膨胀波、分离区、剪切层、障碍激波、激波串等复杂的流场结构。通过测量抽吸槽内气流的膨胀角度以及障碍激波的角度、位置等参数,得到表 2所示结果。分析易知,当抽吸腔压力达到一定值后,抽吸槽内有激波串出现,此时随着抽吸槽深宽比的增加,气流膨胀角度逐渐增加,障碍激波逐渐向上游移动。表 2中,θ,α,Δ,d分别代表气流膨胀角度、障碍激波角度、障碍激波位置、声速喉道宽度,具体见图 11(b)所示。
|
Fig. 11 Schlieren results of the flow field structure in the bleed slot with different length-to-width ratio(δ/D=1.54) |
|
|
Table 2 Parameters of the flow field at different length-to-width |
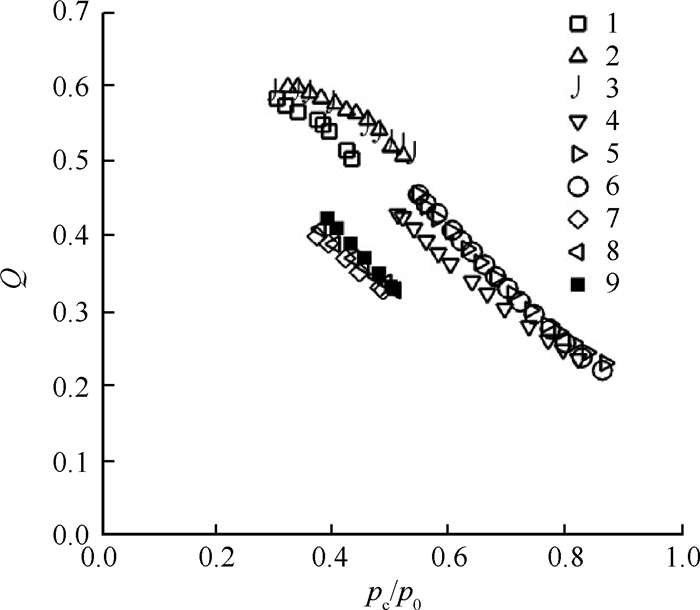
测量了不同宽度的抽吸槽在试验过程当中的抽吸流量,试验工况见表 3。经过处理得到了音速流量系数随压比的变化规律图,如图 12所示。
|
|
Table 3 Test conditions |
|
Fig. 12 Variation of sonic flow coefficient with pressure ratio at different operating conditions |
分析发现,无论抽吸槽宽度、深度如何变化,音速流量系数均随压比的增加而减小。对比工况1,2,3可发现,当L/D达到3.33后,音速流量系数不随L/D的增加而变化;对比工况4,5,6同样发现,当L/D达到2.14后,音速流量系数不随L/D的增加而变化。因此,对于一定宽度的抽吸槽而言,当抽吸槽深度超过一定值后,音速流量系数不随抽吸槽宽深比改变。需要说明的是,图 12中不同δ/D时所测得的音速流量系数分布在不同区域是由于试验所使用的音速喷嘴直径不同所致,因为不用的音速喷嘴节流程度是不一样的。
4 结论对不同宽度和深度的抽吸槽在不同抽吸腔反压情况下的流场结构开展了试验研究,同时对各个工况下音速流量系数的分布情况进行了分析,得到以下结论:
(1)通过NPLS和纹影得到了清晰的抽吸槽附近的流场结构,包括分离区、剪切层、障碍激波等。结果表明,抽吸槽内分离区存在两种状态,即开口/闭口。分离区具体处于何种状态,取决于抽吸槽的深宽比和抽吸腔反压与来流静压的比值。
(2)对于本文研究构型,当压比达到0.25左右后,抽吸腔内开始出现激波串。随着压比的增加,激波串长度逐渐减小。当压比达到0.6左右后,激波串消失。另外,随着抽吸腔反压的增加,气流膨胀角度逐渐减小,且障碍激波下半段长度逐渐减小并逐渐向抽吸槽下游靠近,音速流量系数逐渐减小。
(3)当压比在0.18附近时,随着抽吸槽深宽比的增加,抽吸槽内分离区由开口状态变为闭口状态,同时气流膨胀角度逐渐增加,障碍激波逐渐向上游移动,音速流量系数逐渐增加。
致谢: 感谢国家自然科学基金资助。
| [1] |
李俊, 刘波, 杨小东, 等. 基于CST方法的吸附式压气机叶型及抽吸方案耦合优化设计[J]. 推进技术, 2015, 36(1): 9-16. (LI Jun, LIU Bo, YANG Xiao-dong, et al. Coupling Optimization Design for Aspirated Compressor Airfoiland Aspirated Scheme Based on CST Method[J]. Journal of Propulsion Technology, 2015, 36(1): 9-16.)
(  0) 0) |
| [2] |
岳连捷, 叶青, 徐显坤, 等. 三面压缩高超进气道附面层抽吸研究[J]. 航空动力学报, 2012, 27(2): 272-278. (  0) 0) |
| [3] |
袁化成, 梁德旺. 抽吸对高超声速进气道起动能力的影响[J]. 推进技术, 2006, 27(6): 525-528. (YUAN Hua-cheng, LIANG De-wang. Effects of Bleed to the Starting Ability of Hypersonic Inlet[J]. Journal of Pro- pulsion Technology, 2006, 27(6): 525-528. DOI:10.3321/j.issn:1001-4055.2006.06.011)
(  0) 0) |
| [4] |
严红明, 钟兢军, 韩吉昂, 等. 超声速进气道喉部附面层抽吸[J]. 推进技术, 2009, 30(2): 175-181. (YAN Hong-ming, ZHONG Jing-jun, HAN Ji-ang, et al. Research on Boundary-Layer Suction in the Throat of Supersonic Inlet[J]. Journal of Propulsion Technology, 2009, 30(2): 175-181. DOI:10.3321/j.issn:1001-4055.2009.02.010)
(  0) 0) |
| [5] |
赵健, 范晓樯, 陶渊, 等. 抽吸腔中心隔板对弯曲壁面边界层抽吸性能影响研究[J]. 推进技术, 2017, 38(5): 1008-1015. (ZHAO Jian, FAN Xiao-qiang, TAO Yuan, et al. Study on the Performance Impact of Boundary Layer Bleed on the Curved Wall with Center Clapboard in the Chamber[J]. Journal of Propulsion Technology, 2017, 38(5): 1008-1015.)
(  0) 0) |
| [6] |
陈德华, 王瑞波, 刘光远, 等. 2.4m跨声速风洞槽壁试验段调试及流场校验[J]. 实验流体力学, 2013, 27(4): 66-70. DOI:10.3969/j.issn.1672-9897.2013.04.012 (  0) 0) |
| [7] |
陈植, 易仕和, 周勇为.基于喉部边界层抽吸高超声速静风洞喷管设计[C].安徽: 第十四届全国激波与激波管学术会议, 2010. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201007004014.htm
(  0) 0) |
| [8] |
Holger Babinsky, Hideaki Ogawa. SBLI Control for Wings and Inlets[J]. Shock Waves, 2008, 18(2): 89-96. DOI:10.1007/s00193-008-0149-7
(  0) 0) |
| [9] |
Hamed A, Lehnigt T. Investigation of Oblique Shock/Boundary-Layer Bleed Interaction[J]. AIAA Journal, 1992, 8(2): 418-424.
(  0) 0) |
| [10] |
Hamed A, Lehnigt T. Effect of Bleed Configuration on Shock/Laminar Boundary-Layer Interactions[J]. AIAA Journal, 1995, 33(1): 42-48. DOI:10.2514/3.12330
(  0) 0) |
| [11] |
Hamed A, Morell A, Bellamkonda G. Three-Dimensional Simulations of Bleed-Hole Rows/Shock-Wave/ Turbulent Boundary-Layer Interactions[R]. AIAA 2013-0804.
(  0) 0) |
| [12] |
Hahn T O, Shih T I-R, Chyu W J. Numerical Study of Shock-Wave/Boundary-Layer Interactions with Bleed[J]. AIAA Journal, 1993, 31(5): 869-876. DOI:10.2514/3.11698
(  0) 0) |
| [13] |
Rimlingert M J, Shih T I-R, Chyu W J. Three-Dimensional Shock-Wave/Boundary-Layer Interactions with Bleed through a Circular Hole[R]. AIAA 92-3084.
(  0) 0) |
| [14] |
Shih T I-R, Rimlingert M J. Three-Dimensional Shock-Wave/Boundary-Layer Interactions with Bleed[J]. AIAA Journal, 1993, 31(10): 1819-1826. DOI:10.2514/3.11854
(  0) 0) |
| [15] |
Hamed A, Yeuan J J, Junt Y D. Flow Characteristics in Boundary-Layer Bleed Slots with Plenum[J]. AIAA Journal, 1996, 34(2): 231-236. DOI:10.2514/3.13055
(  0) 0) |
| [16] |
Chyu W J, Rimlingert M J, Shih T I-R. Control of Shock-Wave/Boundary-Layer Interactions by Bleed[J]. AIAA Journal, 1995, 33(7): 1239-1241. DOI:10.2514/3.12886
(  0) 0) |
| [17] |
Rimlinger M J, Shih T I-P, Chyu W J. Shock-Wave/Boundary-Layer Interactions with Bleed Through Rows of Holes[J]. AIAA Journal, 1996, 34(2): 217-224. DOI:10.2514/3.13053
(  0) 0) |
| [18] |
Willis B P, Davis D O, Hingst W R. Flow Coefficient Behavior for Boundary Layer Bleed Holes and Slots[R]. AIAA 95-0031.
(  0) 0) |
| [19] |
Slater J W. Improvements in Modeling 90 Degree Bleed Holes for Supersonic Inlets[C]. Florida: 47th AIAA Aerospace Sciences Meeting, 2009. http://arc.aiaa.org/doi/abs/10.2514/1.B34333
(  0) 0) |
| [20] |
Shaw R J, Wasserbauer J F, Neumann H E. Boundary Layer Bleed System Study for a Full Scale, Mixed Compression Inlet with 45 Percent Contraction[R]. NASA TM X-3358, 1976.
(  0) 0) |
| [21] |
Oorebeek J M, Babinsky H. Flow Physics of a Normal-Hole Bled Supersonic Turbulent Boundary Layer[C]. Texas: 51th AIAA Aerospace Sciences Meeting, 2013. https://arc.aiaa.org/doi/abs/10.2514/6.2013-526
(  0) 0) |
| [22] |
Oorebeek J M, Babinsky H, Ugolotti M, et al. Comparison of Experimental and Computational Flow Structure Investigations of a Normal-Hole Bled Supersonic Boundary Layer[C]. Atlanta: 32nd AIAA Applied Aerodynamics Conference, 2014. http://arc.aiaa.org/doi/abs/10.2514/6.2014-2977
(  0) 0) |
| [23] |
Oorebeek J M, Babinsky H, Ugolotti M, et al. Experimental and Computational Investigations of a Normal-Hole-Bled Supersonic Boundary Layer[J]. AIAA Journal, 2015, 53(12): 3726-3736. DOI:10.2514/1.J053956
(  0) 0) |
| [24] |
赵健, 范晓樯, 王翼, 等.抽吸腔出口压力对抽吸孔隙内流场结构影响分析[C].成都: 第十七届全国激波与激波管学术会议, 2016.
(  0) 0) |
| [25] |
赵玉新.超声速混合层时空结构的实验研究[D].长沙: 国防科学技术大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098756.htm
(  0) 0) |
| [26] |
赵健, 范晓樯, 王翼, 等. 超声速边界层抽吸孔隙内流场结构分类[J]. 推进技术, 2017, 38(11): 2463-2470. (ZHAO Jian, FAN Xiao-qiang, WANG Yi, et al. Classification of Flow Field in Supersonic Boundary Layer Bleed Slot[J]. Journal of Propulsion Technology, 2017, 38(11): 2463-2470.)
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


