涡轮基组合循环(TBCC)发动机是国内外长期致力发展的一种全速域吸气式高超声速推进系统,具有比冲高、灵活可靠、可重复使用等优点,是大气层内远程高超声速飞行器和航天双级入轨第一级运载器的理想动力。目前,以美国NASA组合进气道模态转换试验[1, 2]、欧洲“长期先进推进概念与技术”研究计划(LAPCAT)[3]为代表的TBCC研究正通过数值模拟和地面验证机等方式开展TBCC关键技术验证工作,但是模态转换推力“鸿沟”、跨声速推力裕度不足以及高马赫数涡轮发动机设计等诸多技术难点[4]仍未彻底解决,而这些问题也是当前制约我国发展TBCC组合动力的关键因素。
根据涡轮发动机和冲压发动机的相对位置,TBCC发动机可分为串联式布局和并联式布局。串联式TBCC发动机具有结构紧凑、重量轻、迎风面积小等优点,但同时存在控制复杂的问题。对于并联式布局,模态转换期间,涡轮发动机流路和冲压发动机流路之间的相互干扰较小,难点在于组合进气道和组合喷管的调节;根据模态选择阀位于进气道的亚声速区域或超声速区域,进一步分为内并联式布局和外并联式布局。
其中,基于超燃冲压发动机技术的组合动力只能采用外并联式布局。早期开展的TBCC发动机研究主要是基于成熟的亚燃冲压发动机技术,并以串联式布局为主,20世纪90年代开展的日本HYPR计划[5]和德国SÄNGER计划[6]均通过地面整机试验验证了串联式TBCC发动机技术的可行性;同时期,在美国Beta Ⅱ两级入轨飞行器方案设计中,所采用的第一级动力则为内并联式TBCC发动机[7]。进入21世纪以来,随着双模态超燃冲压发动机技术的发展,基于高马赫数涡轮发动机和双模态冲压发动机的外并联式TBCC发动机成为美国和欧洲各国TBCC项目的主要研究对象,使用碳氢燃料,最高飞行马赫数可达6~8,例如X-43B[8],FaCET[9],SR-72等研究计划。
如何实现涡轮模态至冲压模态的平稳转换是TBCC所有布局方式的共性问题。在HYPR计划中,Miyagi等[10]提出了变循环涡扇/冲压组合发动机的模态转换策略,并给出了模态转换过程动态性能的仿真结果。黄红超等[11, 12]分别基于推力连续和流量连续原则给出了小型涡轮冲压组合发动机的模态转换过程参数调节规律。Chen等[13]基于目标规划算法开展了涡轮冲压组合发动机模态转换控制规律研究。聂聆聪等[14]提出了基于推力控制的涡轮冲压组合发动机模态转换控制规律。Daniel等[15]开发了并联式TBCC发动机的一体化动态性能仿真程序——HiTECC,并使用该程序初步分析了外并联式TBCC发动机模态转换性能。张明阳等[16]给出了内并联式TBCC发动机的模态转换策略,基本实现了模态转换期间发动机推力与空气流量的平稳过渡。由国内外公开文献可知,针对外并联式TBCC发动机模态转换过程的研究相对较少,而且已有的模态转换性能计算模型并未考虑涡轮发动机风车关闭过程,无法模拟完整的模态转换过程。
本文针对Ma7一级外并联式TBCC发动机的模态转换进行了研究,建立了外并联式TBCC发动机总体性能仿真模型,介绍了与模态转换性能模拟相关的组合进气道模态转换性能计算模型和高马赫数涡轮发动机风车性能计算模型后,基于推力连续准则提出了模态转换策略,对模态转换动态性能计算结果进行了详细分析。
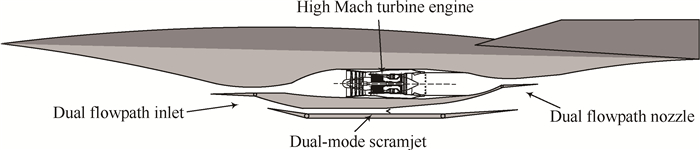
2 物理模型与计算方法 2.1 发动机构型与设计参数本文以美国空军实验室与SpaceWorks公司联合提出的双级入轨高超声速飞行器概念——Quicksat[17, 18]作为外并联式TBCC发动机模态转换性能研究的背景。所研究的外并联式TBCC发动机主要由双流路组合进气道、高马赫数涡轮发动机(HMTE)、双模态超燃冲压发动机(DMSJ)以及双流路组合尾喷管等四个子系统构成,如图 1所示。模态转换马赫数为3.75,与文献[17]给出的数值保持一致。
|
Fig. 1 Schematic diagram of the Mach 7 over-under TBCC propulsion system |
HMTE采用小涵道比、低增压比、有加力的双轴混排涡扇发动机方案,马赫数工作区间为0~3.75,在地面起飞状态下的主要设计参数如表 1所示。该涡轮发动机的马赫数工作范围明显宽于现役涡轮发动机的马赫数工作范围(0~2+),其原因在于,当飞行马赫数超过2.0后,发动机的推力主要由加力燃烧室贡献,工作原理与串联式涡扇冲压组合发动机类似。针对该涡轮发动机状态参数在宽马赫数范围内的变化规律,参考文献[19]给出的RTA发动机关键截面温度和转速随飞行马赫数(0~4)的变化规律,即在飞行马赫数较高时,由于压气机出口总温的限制,随着飞行马赫数的增加,涡轮发动机转速逐渐降低,主燃烧室加热量减小,而加力燃烧室(此时可看作冲压燃烧室)加热量逐渐增加,最终接近亚燃冲压发动机工作模式。本文主要关注模态转换性能,所以不再对涡轮模态发动机状态参数的变化规律作详细介绍。
|
|
Table 1 Main design parameters of high Mach turbine engine(HMTE) |
DMSJ的马赫数工作区间为3.75~7.0,其中在飞行马赫数5.0以下为亚燃模态,使用JP-7碳氢燃料,主要设计参数如表 2所示。
|
|
Table 2 Main design parameters of dual-mode scramjet (DMSJ) |
本文基于面向对象的模块化的发动机建模方法,开发了吸气式高速推进系统性能仿真程序——HiMach,主要用于涡轮发动机(马赫数0~4)及其组合动力的总体性能仿真和方案设计研究,可灵活搭建多种结构的串联式、并联式TBCC发动机总体性能仿真模型,可开展发动机稳态、过渡态特性计算以及控制规律研究。
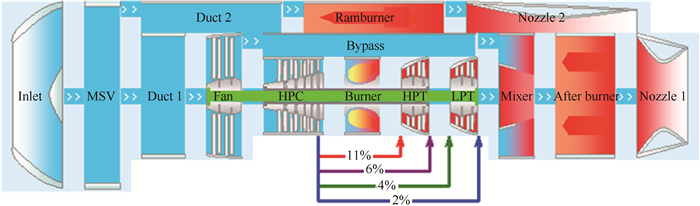
针对图 1所示的外并联式TBCC发动机,本文使用HiMach程序建立了相应的总体性能仿真模型,如图 2所示。HMTE流路主要由风扇(Fan)、压气机(HPC)、主燃烧室(Burner)、高压涡轮(HPT)、低压涡轮(LPT)、外涵道(Bypass)、混合室(Mixer)、加力燃烧室(Afterburner)以及低速喷管(Nozzle 1)等部件模型构成,其中,从压气机出口引气分别用于冷却高压涡轮导向器、高压涡轮转子、低压涡轮导向器以及低压涡轮转子,引气量分别为压气机出口空气流量的11%,6%,4%和2%。DMSJ流路主要由冲压燃烧室(Ramburner)和高速喷管(Nozzle 2)构成。组合进气道模型则由飞行器前体预压缩段(Inlet)、进气道高/低速流路分流板或者模态选择阀(MSV)、亚声速扩压段(Duct 1)以及超声速扩压段(Duct 2)等模块构成。模态选择阀由分流器部件模型表示,主要属性为分流比[16],通过分流比的取值控制TBCC发动机的工作模式。当分流比等于0时,TBCC发动机以涡轮模态工作,冲压发动机流路完全关闭;当分流比等于1.0时,TBCC发动机以冲压模态工作,涡轮发动机流路完全关闭;当分流比取值在0~1.0时,代表模态转换过程,分流比大小由两种发动机的工作状态决定。
|
Fig. 2 Over-under TBCC engine simulation model |
本文使用HiMach程序计算了外并联式TBCC发动机净比冲沿飞行轨迹的变化规律,并与文献[18]给出的相应结果进行了对比,如图 3所示。特别地,在文献[18]给出的TBCC推进系统方案中,在跨声速段开启了助推火箭,导致该段比冲大幅度降低。由图 3可以看到,除去跨声速段,本文计算得到的净比冲变化规律与文献[18]给出的结果基本一致,特别是在模态转换点,两者符合较好。

|
Fig. 3 Specific impulse variation along the flight trajectory for the Mach 7 over-under TBCC engine |
建立组合进气道模态转换性能和高马赫数涡轮发动机风车性能的计算模型是外并联式TBCC发动机模态转换性能模拟的两个重要基础,下面将分别予以介绍。
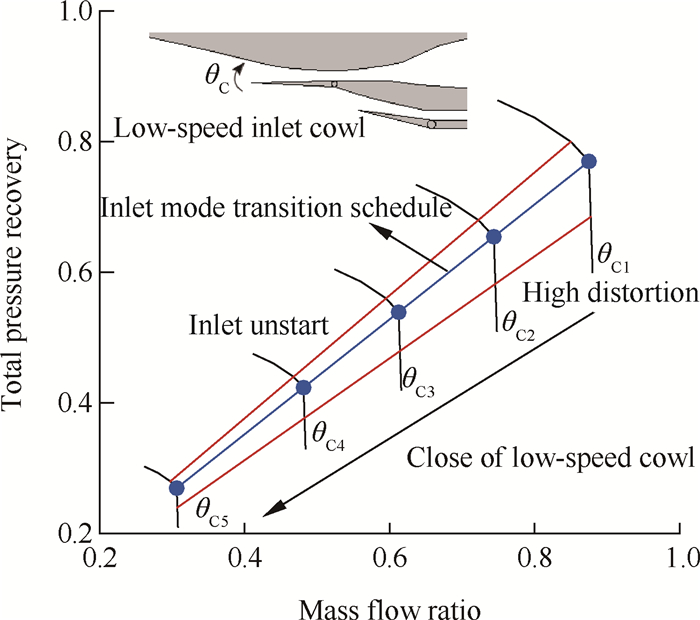
模态转换期间,组合进气道低速流路整流罩逐渐关闭,与此同时,高速流路整流罩逐渐打开,最终完成TBCC发动机由涡轮模态至冲压模态的转换。根据NASA开展的TBCC组合进气道模态转换数值模拟与试验研究工作[1, 2]可知,在组合进气道低速流路关闭的过程中,进气道低速流路的流量系数和总压恢复系数均会降低,如图 4所示的等整流罩角度θC特性。为了防止进气道进入不起动、出口流场严重畸变等工作状态,进气道模态转换工作点将位于一个由不起动边界和畸变边界限制的狭窄区间(图 4),并且根据相关试验结果[1, 2]可知,在低速流路整流板关闭或高速流路整流板打开过程中,进气道总压恢复系数与流量系数基本呈线性关系。
|
Fig. 4 Schematic mode transition characteristics for the low-speed flowpath of TBCC inlet |
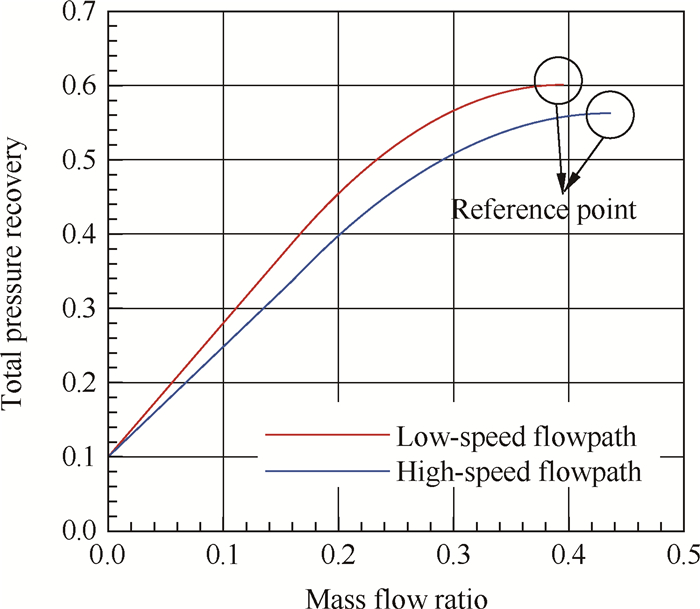
基于以上分析,本文建立了组合进气道模态转换性能的一种简化计算模型:基于相关试验或CFD数值模拟结果,以特性线的方式表示组合进气道模态转换期间总压恢复系数与流量系数的关系,特性线参考点为模态转换前涡轮模态进气道工作点(低速流路)或模态转换后冲压模态进气道工作点(高速流路)。本文基于文献[2]给出的相关试验结果,确定了组合进气道模态转换过程高/低速流路总压恢复系数与流量系数的变化规律,如图 5所示,该特性将用于后面的模态转换性能模拟。
|
Fig. 5 Variation of total pressure recovery with mass flow ratio both for low-speed and high-speed flowpath of TBCC inlet during mode transition, respectively |
涡轮发动机风车关闭过程是外并联式TBCC发动机模态转换后期所不可避免的。为此,本文建立了基于部件低转速特性匹配的涡轮发动机风车性能计算模型。该计算模型的关键在于补充旋转部件的低转速特性以及解决压比小于1.0后的效率不连续问题。
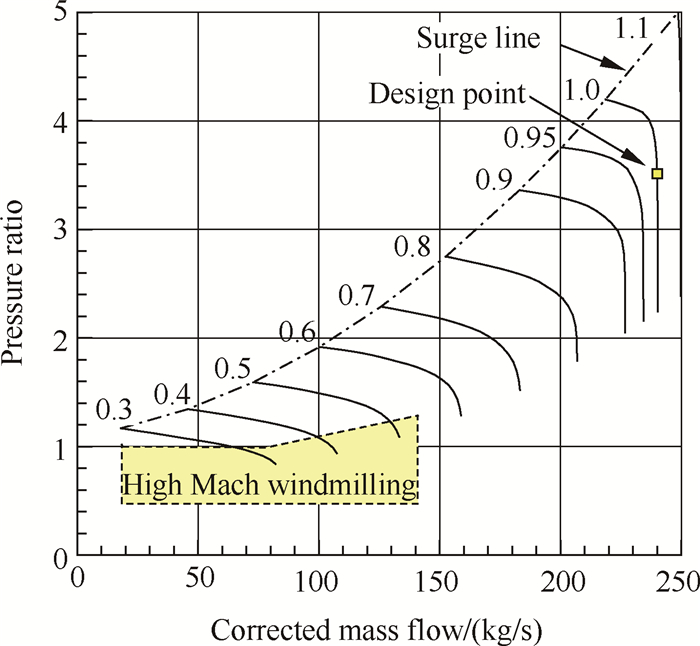
由文献[20]可知,由于模态转换点飞行马赫数较高,当涡轮发动机进入风车状态后,风扇部件工作点将位于其特性图上的低转速大流量区域,如图 6所示。因此,在对风扇慢车转速以下低转速特性进行拓展的同时,也要补充低转速大流量特性,即将低转速特性线向流量“堵塞”点方向延伸。除此之外,还应对压气机、涡轮等其它旋转部件的低转速特性进行补充,以满足高马赫数涡轮发动机风车性能模拟的需要。
|
Fig. 6 Location of matching work points on the fan characteristics map while HMTE operating in the high Mach windmilling mode |
以压缩部件为例,沿低转速特性线,随着换算流量的增加,压比pr、实际单位焓升ΔHeff以及等熵单位焓升ΔHis均下降。如图 7所示,当pr=1.0时,ΔHeff>0且ΔHis=0,则等熵效率ηis(=ΔHis/ΔHeff)等于零;当ΔHeff0且ΔHis < 0时,等熵效率为负值,并且随着压比的降低而减小;当ΔHeff=0时,等熵效率趋于无穷大;此后随着压比的进一步降低,ΔHeff和ΔHis均为负值,压缩部件开始输出轴功,等熵效率大于1.0。在发动机风车性能计算时,若采用传统的部件特性表示方法,即由相对换算转速、换算流量、压比和效率等四个特性参数表示,效率的不连续将导致发动机模型不易求解,因此本文采用了另一种特性表示方法,即由在全转速全流量范围内连续变化的换算扭矩代替等熵效率,如式(1)所示。此外,在建立发动机共同工作方程组时,由扭矩平衡方程代替原有的功率平衡方程。同理,涡轮部件特性也采用了类似的表示方法。

|
Fig. 7 Discontinuity of isentropic efficiency with pressure ratio below 1.0 for the compressors[21] |
| ${W_{{\rm{cor}}}}, {p_{\rm{r}}}, {\eta _{{\rm{is}}}} = f\left( {{{\bar n}_{{\rm{cor}}}}, \beta } \right) \Rightarrow {W_{{\rm{cor}}}}, {p_{\rm{r}}}, {T_{{\rm{cor}}}} = f\left( {{{\bar n}_{{\rm{cor}}}}, \beta } \right)$ | (1) |
式中Wcor为进口换算流量,ncor为相对换算转速,Tcor为换算扭矩(式(2)),β为部件特性插值辅助变量[21]。
| ${T_{{\rm{cor}}}} = \frac{{30}}{{{\rm{ \mathsf{ π} }} \times {N_{{\rm{cor}}, {\rm{des}}}}}}\frac{{{W_{{\rm{cor}}}} \times {\rm{\Delta }}{H_{{\rm{cor}}}}}}{{{{\bar n}_{{\rm{cor}}}}}}$ | (2) |
式中ΔHcor为换算实际单位焓升,Ncor, des为设计点换算转速。
3 结果与讨论针对本文研究的Ma7一级外并联式TBCC发动机,通过涡轮发动机燃油流量、冲压发动机燃油流量以及组合进/排气系统的变几何结构等调节变量的协同控制,实现涡轮模态至冲压模态的平稳转换。在进行模态转换性能计算时,本文假设模态转换期间飞行条件保持不变,即飞行马赫数为3.75,飞行高度为17.2km。
3.1 模态转换参数调节规律针对外并联式TBCC发动机,在设计模态转换过程的发动机参数调节规律时,需要满足以下基本要求[22]:
(1)保证推力连续变化,避免由于推力波动导致的飞行器倾覆。
(2)推进系统高/低流路稳定工作,实现气动匹配,主要体现在进/排气系统方面。
(3)实现冲压发动机稳定点火。
(4)实现涡轮发动机稳定退出工作,模态转换前涡轮发动机一般工作在全加力状态。
(5)涡轮发动机关闭后,如何避免受到高温气流的破坏。
在进行模态转换总体性能分析时,一般最为关心如何实现模态转换期间发动机总推力的连续变化,或者说,如何将TBCC发动机的推力产生由涡轮发动机平稳地过渡至冲压发动机。
首先,TBCC发动机模态转换前后的工作状态对比如表 3所示。模态转换前,TBCC发动机以全加力涡扇模态工作,冲压通道完全关闭。模态转换后,TBCC发动机以亚燃冲压模态工作,涡轮通道完全关闭。
|
|
Table 3 Operating condition comparison of turbo mode and ram mode at mode transition point |
其次,基于上述并联式TBCC发动机模态转换的基本要求,本文以发动机总推力连续变化为原则,制定了如下模态转换策略:
步骤1 当飞行器沿飞行轨迹爬升至模态转换点(Ma=3.75,H=17.2km)时,并联式TBCC发动机以全加力涡扇模态工作,同时冲压发动机通道处于完全关闭状态。
步骤2 打开进气道高速流路和喷管高速流路,逐渐增加冲压发动机通道的空气流量,但此时冲压发动机不点火,涡轮发动机仍以全加力状态工作。
步骤3 当冲压发动机空气流量增加到某一值,冲压发动机开始点火,同时减小加力燃烧供油量,逐级降低加力燃烧室出口温度,涡轮发动机以部分加力涡扇模态工作,期间通过控制冲压发动机燃烧室的供油量,保持TBCC发动机总推力恒定,通过控制高/低速流路喷管喉部面积,保持高/低速流路空气流量固定。
步骤4 当涡轮发动机加力完全关闭后,涡扇发动机开始节流,通过减小主燃烧室的燃油流量,降低涡扇发动机转速,期间通过控制冲压发动机燃烧室的供油量,保持TBCC发动机总推力恒定,但由于冲压发动机燃烧室面积的限制,燃烧室出口可能达到“堵塞”状态,此后便不能通过增加燃油流量进一步增加冲压发动机推力。
步骤5 随着涡轮发动机转速的降低,主燃烧室逐渐接近熄火边界,涡轮发动机进入风车状态。
步骤6 通过调节进气道低速流路整流罩和喷管低速流路襟板,逐渐关闭涡轮发动机通道,防止其受到高温气流的破坏。
步骤7 涡轮发动机通道完全关闭,TBCC发动机以亚燃冲压模态工作,模态转换过程结束。
上述模态转换过程可以划分为冲压发动机通道(冷通流)打开、涡轮发动机关闭加力、涡轮发动机降转和涡轮发动机通道(风车)关闭等四个阶段。根据文献[15]给出的模态转换时间量级,本文设定模态转换所需总时间为25s,模态转换每个阶段所消耗的时间如表 4所示。实际中,TBCC模态转换性能不仅取决于发动机本身的模态转换控制规律,还与高速飞行器性能相互耦合,只有在高速飞行器/TBCC推进系统一体化动态模型的基础上所得到的模态转换时间和模态转换性能才更加接近真实情况。需要指出的是,模态转换不同阶段的时间分配虽然对模态转换性能在数值上有影响,但不影响本文对模态转换期间发动机参数变化规律的分析。
|
|
Table 4 Mode transition control sequence for the over-under TBCC engine |
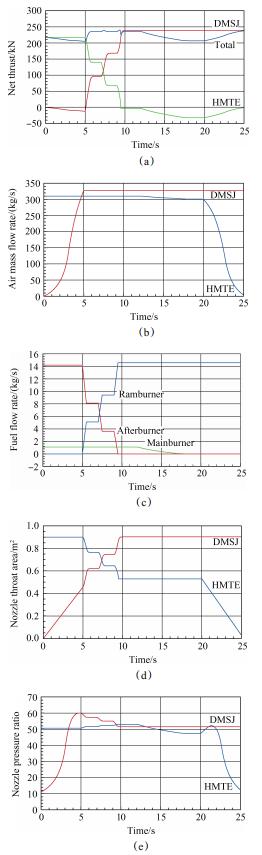
外并联式TBCC发动机的模态转换是一个动态过程,因此动态模型才能更准确地反映模态转换过程的参数变化规律。根据上述模态转换策略,本文使用HiMach程序完成了模态转换动态性能模拟,得到了模态转换期间发动机关键参数的动态变化规律,如图 8所示。
|
Fig. 8 Dynamic variation of the TBCC engine key parameters during mode transition |
由图 8(a)可知,在模态转换的第二阶段(5~12s),基本完成了TBCC发动机推力的平稳转换,即推力的产生由涡轮发动机过渡至冲压发动机,期间总推力基本保持不变。但是,在模态转换的其它阶段,总推力均出现了不同程度的下降。首先,在冲压发动机冷通流阶段(0~5s),由于冲压涵道的流动损失,冲压发动机产生负推力,并随着冲压涵道空气流量的增加而增加,在冲压燃烧室点火前达到最大值,约为模态转换后总推力的5.3%。其次,涡轮发动机在关闭加力后(9.5~25s)开始产生负推力,并在主燃烧室切断供油后,负推力达到最大值,约为模态转换后总推力的13.7%,而这也是整个模态转换期间TBCC发动机总推力的最低点。
图 8(b)~(d)给出了外并联式TBCC发动机模态转换过程的参数调节规律,包括高/低速流路空气流量、燃油流量以及喷管喉部面积等调节变量。由图 8(b)可知,在推力转换过程中(5~12s),TBCC发动机高/低速空气流量均保持不变,说明该阶段组合进气道不需要调节,而组合进气道的调节主要发生在模态转换的前期和后期,即冲压发动机通道的打开过程(0~5s)和涡轮发动机通道的关闭过程(20~25s)。在后续研究中,建议进一步细化TBCC组合进气道性能计算模型,从而得到模态转换过程组合进气道变几何结构的调节规律。由图 8(c)可知,高/低速流路燃油流量的调节主要发生在模态转换的第二阶段,与推力的转换相对应。由图 8(d)可知,涡轮发动机喷管喉部面积的调节发生在模态转换得到第二、四阶段,冲压发动机喷管喉部面积的调节发生在模态转换的前两个阶段。需要指出的是,在本文中,模态转换期间冲压发动机始终处于亚燃模态,通过喷管几何喉部的调节实现进气道与燃烧室的流量平衡;而对于冲压发动机喷管喉部不可调的情况,由文献[23]可知,则是通过在冲压发动机燃烧室形成的热力学喉道实现进气道与燃烧室的流量平衡,热力学喉道的位置与冲压燃烧室的供油量相关,并且在模态转换期间,随着供油量的增加,冲压发动机将由纯超燃模态逐渐过渡至亚燃模态。
图 8(e)给出了模态转换期间TBCC发动机高/低速流路喷管落压比的动态变化规律。模态转换第一阶段,随着冲压发动机通道的打开,组合进气道高速流路总压恢复系数逐渐增加(图 5),导致高速喷管落压比逐渐增加。模态转换第二阶段,由于加力燃烧室热阻损失降低,导致低速喷管落压比逐渐增加,同时由于冲压燃烧室热阻损失增加,导致高速喷管落压比逐渐降低。模态转换第三阶段,低速喷管落压比随着涡轮发动机转速的降低而减小。模态转换第四阶段,涡轮发动机风车阻力随着空气流量的增加而减小,但进气道低速流路总压损失却随着空气流量的减小而增加,两种因素的综合作用导致该阶段低速喷管落压比先增加后降低。
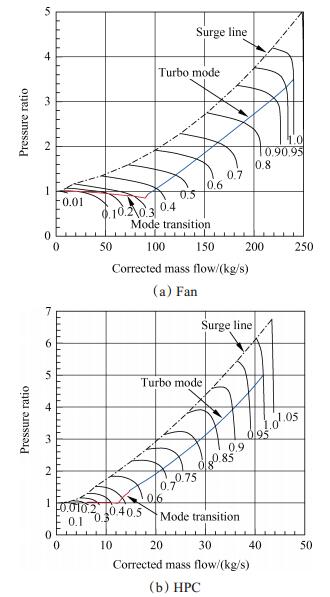
图 9给出了模态转换工作点分别在风扇和压气机部件特性图上的位置,变化规律与文献[20]给出的相关试验结果基本一致。首先,在涡轮发动机降低转速、进入风车状态的过程中,风扇和压气机的工作点均位于其特性图的低转速大流量区域,其中风扇压比小于1.0,从自由来流中提取能量并输出轴功。其次,在涡轮发动机风车关闭过程中,风扇和压气机的工作点均逐渐向压比等于1.0和换算流量等于零的方向移动,风扇压比变化幅度较大,而压气机压比始终保持在1.0左右。
|
Fig. 9 Location of mode transition work points on the characteristics map of fan and HPC, respectively |
本文建立了外并联式TBCC发动机模态转换性能计算模型,实现了由涡轮模态至冲压模态完整转换过程的动态性能模拟。通过本文的研究,得出以下结论:
(1)基于推力连续准则,确定了Ma7一级外并联式TBCC发动机的模态转换策略,基本实现了模态转换期间发动机推力与空气流量的平稳过渡。
(2)在涡轮发动机由全加力状态变化至不加力状态过程中,TBCC发动机的推力转换已基本完成,期间通过燃油流量和喷管喉部面积的协同调节可保持TBCC发动机总推力基本不变。
(3)模态转换前期处于冷通流状态的冲压发动机以及后期处于风车状态的涡轮发动机均会产生负推力,负推力最大值分别为模态转换后总推力的5.3%和13.7%。
(4)当涡轮发动机进入风车状态时,风扇和压气机的工作点均位于其特性图的低转速大流量区域,此后随着涡轮发动机空气流量的减小,风扇压比和压气机压比均趋向于1.0。
致谢: 感谢工业和信息化部民用飞机专项科研项目对本文工作的支持。
| [1] |
Saunders J D, Stueber T J, Suder K L, et al. Testing of the NASA Hypersonics Project's Combined Cycle Engine Large Scale Inlet Mode Transition Experiment (CCE LIMX)[R]. NASA/TM 2012-217217.
(  0) 0) |
| [2] |
Foster L E, Saunders J D, Sanders B W, et al. Highlights from a Mach 4 Experimental Demonstration of Inlet Mode Transition for Turbine-Based Combined Cycle Hypersonic Propulsion[R]. AIAA 2012-4143.
(  0) 0) |
| [3] |
Steelant J, Varvill R, Defoort S, et al. Achievements Obtained for Sustained Hypersonic Flight within the LAPCAT-Ⅱ Project[R]. AIAA 2015-3677.
(  0) 0) |
| [4] |
Bulman M J, Siebenhaar A. Combined Cycle Propulsion: Aerojet Innovations for Practical Hypersonic Vehicles[R]. AIAA 2011-2397.
(  0) 0) |
| [5] |
Miyagi H, Kimura H, Kishi K, et al. Combined Cycle Engine in Japanese HYPR Program[R]. AIAA 98-3278.
(  0) 0) |
| [6] |
Lederer R, Schwab R, Voss N. Hypersonic Airbreathing Propulsion Activities for S NGER[R]. AIAA 91-5040.
(  0) 0) |
| [7] |
Snyder C A, Maldonado J J. The Design and Performance Estimates for the Propulsion Module for the Booster of a TSTO Vehicle [R]. AIAA 91-3136.
(  0) 0) |
| [8] |
Lynn E S, Daric W E, Rich L D, et al. Turbine Based Combination Cycle (TBCC) Propulsion Subsystem Integration[R]. AIAA 2004-3649.
(  0) 0) |
| [9] |
Walker S, Tang M, Mamplata C. TBCC Propulsion for a Mach 6 Hypersonic Airplane[R]. AIAA 2009-7238.
(  0) 0) |
| [10] |
Miyagi H, Miyagawa H, Monji, et al. Combined Cycle Engine Research in Japanese HYPR Project[R]. AIAA 95-2751.
(  0) 0) |
| [11] |
黄红超, 王占学, 蔡元虎. 基于推力连续准则的小型涡轮冲压组合发动机模态转换过程分析[J]. 航空动力学报, 2010, 24(12): 2756-2762. (  0) 0) |
| [12] |
黄红超, 王占学, 刘增文. 基于流量连续准则的小型涡轮冲压组合发动机模态转换过程分析[J]. 西北工业大学学报, 2010, 28(2): 234-239. DOI:10.3969/j.issn.1000-2758.2010.02.016 (  0) 0) |
| [13] |
Chen M, Tang H L, Zhu Z L. Goal Programming for Stable Mode Transition in Tandem Turbo-Ramjet Engines[J]. Chinese Journal of Aeronautics, 2009, 22(5): 486-492. DOI:10.1016/S1000-9361(08)60130-2
(  0) 0) |
| [14] |
聂聆聪, 李岩, 戴冬红, 等. 涡轮冲压组合发动机模态转换多变量控制研究[J]. 推进技术, 2017, 38(5): 968-974. (NIE Ling-cong, LI Yan, DAI Dong-hong, et al. Study on Mode Transition Multi-Variable Control for Turbine-Based Combined Cycle Engine[J]. Journal of Propulsion Technology, 2017, 38(5): 968-974.)
(  0) 0) |
| [15] |
Daniel A H, Eric J G. Integrated Turbine-Based Combined Cycle Dynamic Simulation Model[C]. Arlington, VA: 58th Joint Army-Navy-NASA-Air-Farce (JANNAF) Interagency Propulsion, 2011.
(  0) 0) |
| [16] |
张明阳, 王占学, 刘增文, 等. Ma4一级内并联式TBCC发动机模态转换性能分析[J]. 推进技术, 2017, 38(2): 315-322. (ZHANG Ming-yang, WANG Zhan-xue, LIU Zeng-wen, et al. Analysis of Mode Transition Performance a Mach 4 Over-Under TBCC Engine[J]. Journal of Propulsion Technology, 2017, 38(2): 315-322.)
(  0) 0) |
| [17] |
Bradford J E, Charania A, Wallace J, et al. Quicksat: A Two-Stage to Orbit Reusable Launch Vehicle Utilizing Air-Breathing Propulsion for Responsive Space Access[R]. AIAA 2004-5950.
(  0) 0) |
| [18] |
Eklund D R, Boudreau A H, Bradford J E. A Turbine-Based Combined Cycle Solution for Responsive Space Access[R]. AIAA 2005-4186.
(  0) 0) |
| [19] |
Bartolotta P A, McNelis N B, Shafer D G. High Speed Turbines: Development of a Turbine Accelerator (RTA) for Space Access[R]. AIAA 2003-6943.
(  0) 0) |
| [20] |
Sosounov V A, Tskhovrebov M M, Solonin V I, et al. The Study of Experimental Turboramjets[R]. AIAA 92-3720.
(  0) 0) |
| [21] |
Kurzke J. How to Get Component Maps for Aircraft Gas Turbine Performance Calculations[R]. ASME 96-GT-164.
(  0) 0) |
| [22] |
Peter J O. Mode Transition Design Considerations for an Airbreathing Combined-Cycle Hypersonic Vehicle[R]. AIAA 2008-2621.
(  0) 0) |
| [23] |
陈玉春, 刘小勇, 黄兴, 等. 基于集总参数方程的超燃冲压发动机性能计算模型[J]. 推进技术, 2012, 33(6): 840-846. (CHEN Yu-chun, LIU Xiao-yong, HUANG Xing, et al. A Model Based on Lumped Parameter Method for Scramjet Performance Computation[J]. Journal of Propulsion Technology, 2012, 33(6): 840-846.)
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

